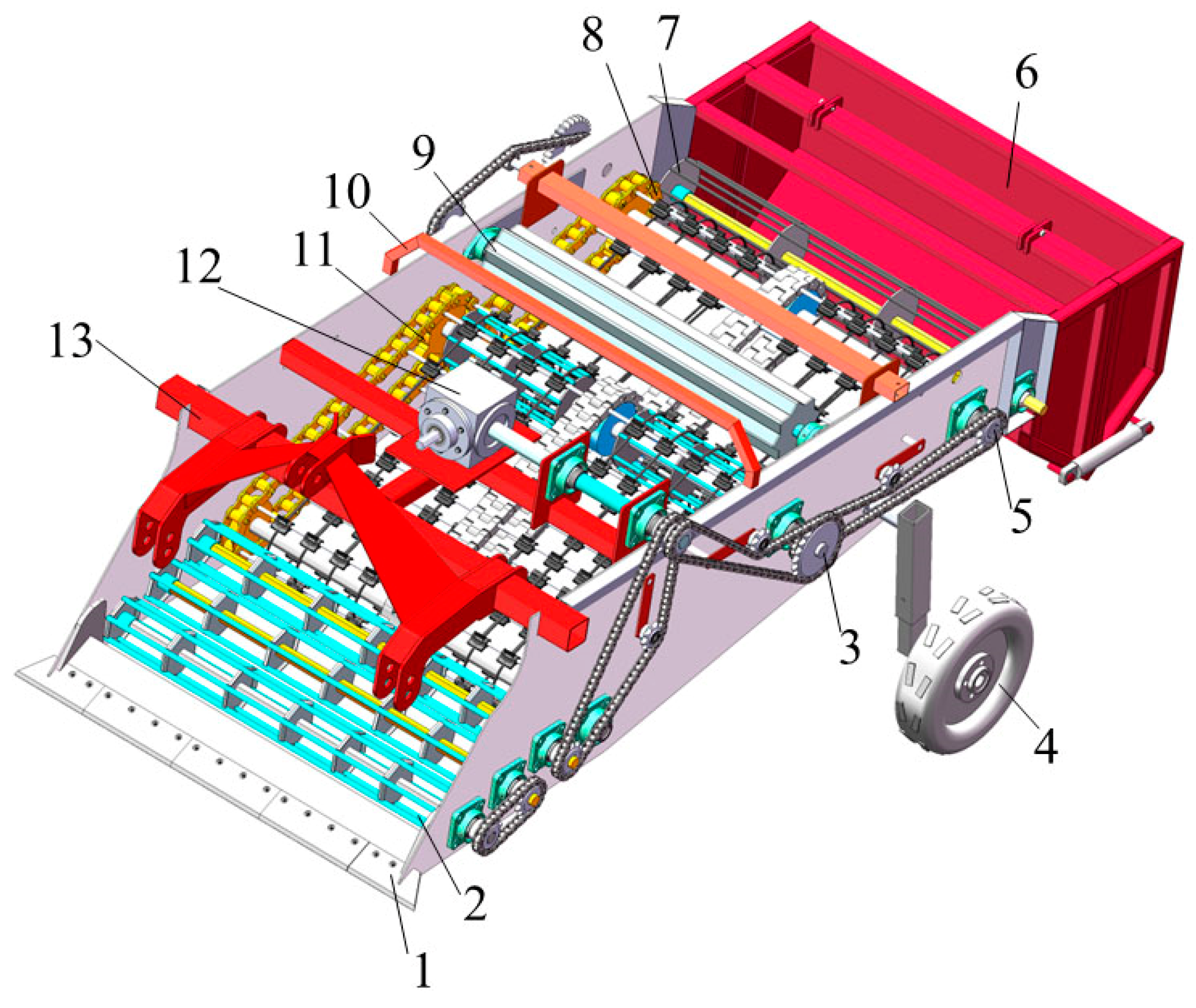
3.1. Design of the Digging Shovel
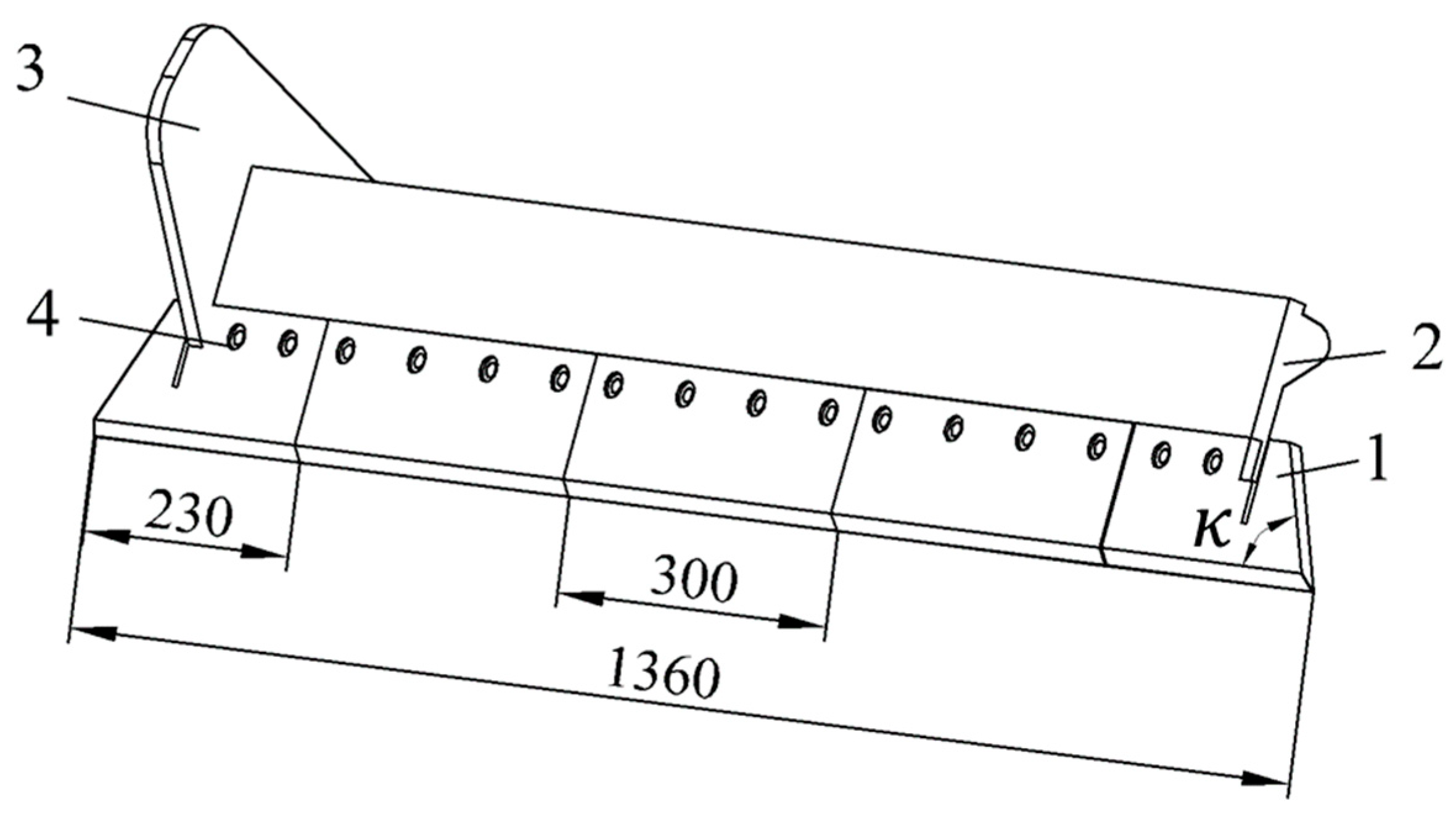
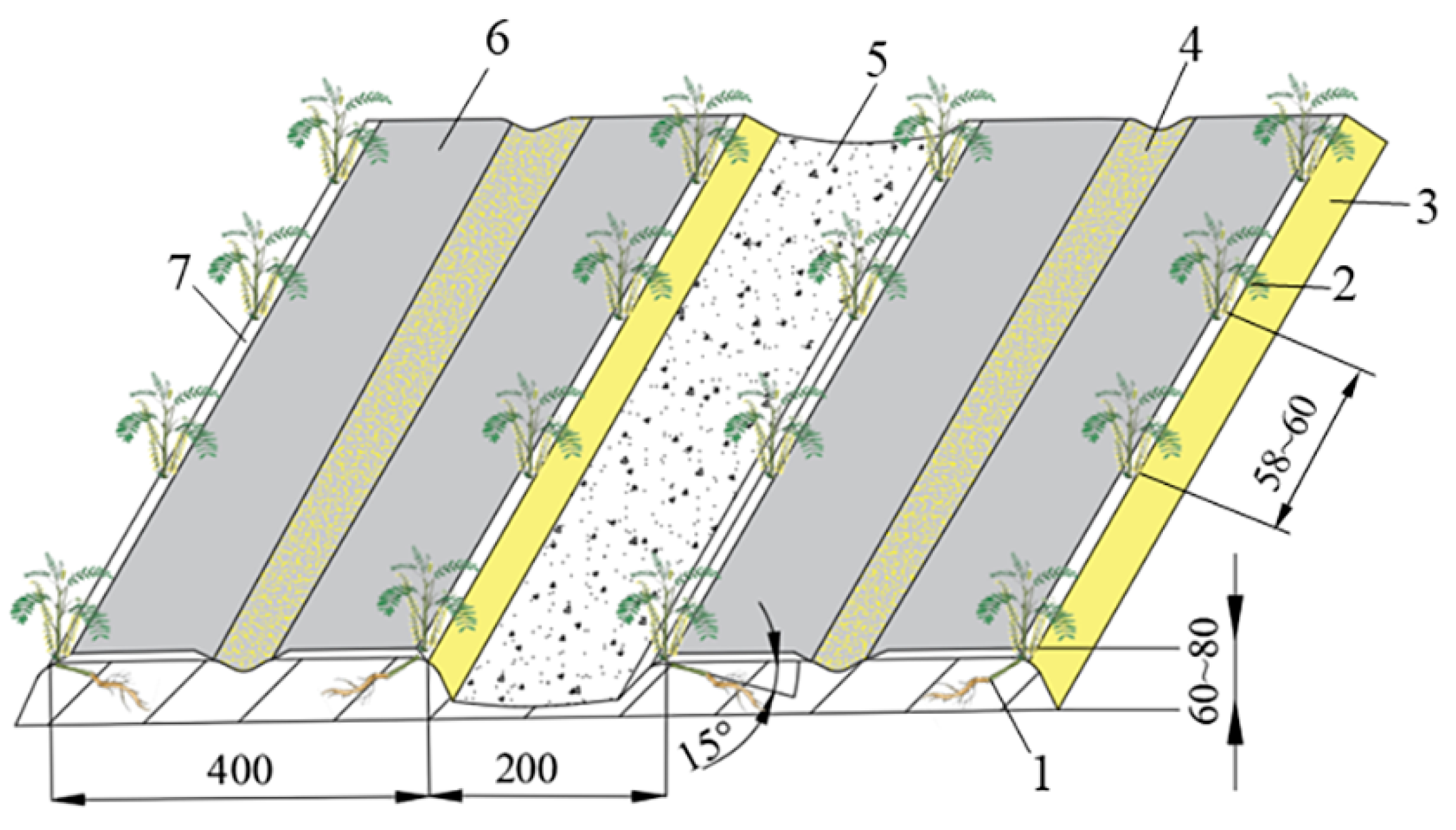
The primary production area of Astragalus is located in the northwest Loess Plateau region in China, where the plant demonstrates lower soil-fertility requirements. In order to adapt to the planting mode and meet the agronomic requirements, the designed Astragalus digger can harvest two plant rows at once; the ridge width is 400 mm, the row spacing is 200 mm. The root system of Astragalus is distributed in a branching pattern, with lengths between 50 and 150 mm. Considering the driving error of the equipment, the width of the excavator was set to 1360 mm (see
Figure 2). It consists of multiple shovel blades, and the shovel head is fixed onto a positioning plate, which is then fixed onto the side plate of the machine body. In comparison to a single shovel, this multiple-shovel arrangement offers the advantages of reducing digging resistance and being a simple structure that is easy to manufacture. However, if there are too many shovels, they are prone to deformation during operation. Conversely, if there are too few shovels, material will be wasted during replacement. As a good compromise, five separate single shovels have been adopted. For convenient servicing, the entire digging shovel is designed with two types of shovel blades. Because the two end shovel blades have blade inclination angles, to ensure soil penetration performance their length was set to 230 mm, while the length of the middle shovel was 300 mm.
The determination of the inclination angle of the shovel blade is related to the mixture of medicine and soil and the friction angle of the shovel surface, which satisfies the following relationship, according to the following equation [
17]:
The rolling friction coefficient between soil and steel ranges from 0.5 to 0.7 [
18]. Suppose the friction coefficient is 0.7 [
19], then the friction angle
is about 35°. In order to improve the ability to break the soil and reduce the resistance of digging, the inclination angle
of the digging-shovel blade was set to between 20° and 40°.
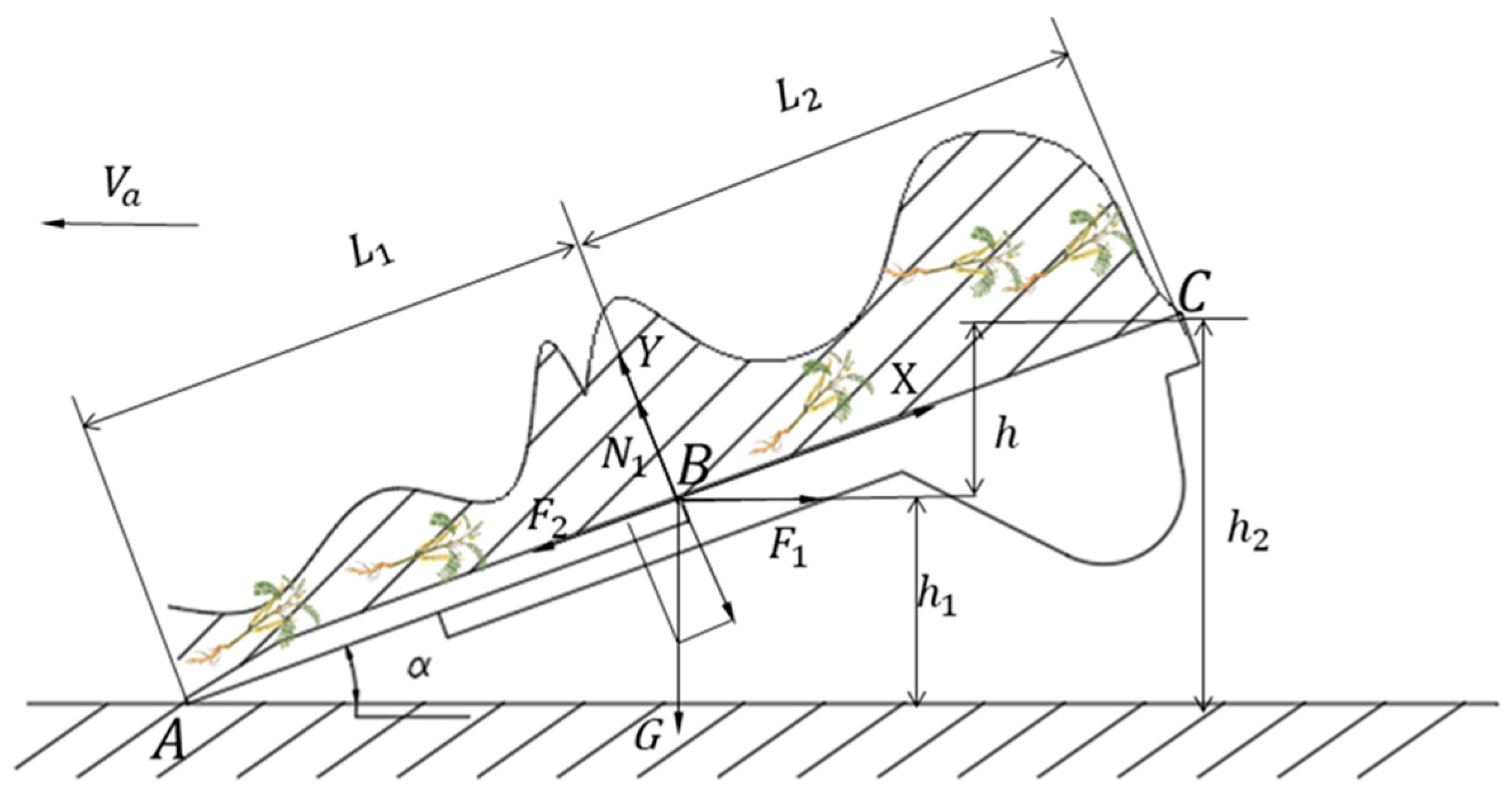
The design of the digger shovel is based on shape parameters, primarily involving the shovel length (
L1 +
L2) and the inclination angle of the digger shovel. The force distribution on the digging shovel is shown in
Figure 3. According to this figure, the equilibrium equations on each direction are as follows:
where
is the force on the digger when pushing soil forward (N);
is the vertical force of the digging shovel on the soil (N);
G is the gravity on the soil (N);
is the friction force acting on the shovel surface (N);
is the friction coefficient between the soil and digging shovel,
; and
is the angle between the digging shovel and the ground.
From Equation (1) we further obtain:
The length
of the front end of the digging shovel can be expressed using the following relationship:
To ensure that the digger can cut the soil block and have good sliding–cutting performance, while also ensuring that the rear end of the digger has sufficient height from the ground and that it does not touch the ground, the designed digging depth
h1 is set to 200 mm. In turn, the length
of the rear section of the shovel can be calculated using energy conservation, assuming that the Astragalus–soil mixture moves along the shovel surface at the forward speed
of the unit to point
B (see
Figure 3):
where
m is the mass of the Astragalus rhizome–soil mixture (kg);
Assuming that the velocity
V of the soil–Astragalus mixture, as it moves along the shovel surface from point
B to point
C, becomes zero, the soil starts accumulating at point
C. The energy at point
B is utilized to overcome the work
W1 required for lifting the soil–Astragalus mixture to a height
h and the work
W2 needed to overcome friction along the digging-shovel surface
L2. According to the conservation of energy, the equation can be formulated as follows:
The total length
L of the digging shovel can be expressed as:
where
is the friction angle between soil and steel, (30°~36°) [
20];
g is gravitational acceleration; (m/s
2) and the forward speed
V of the unit is 1.0 m/s.
To ensure optimal soil-penetration performance and seamless backward transportation of the soil–Astragalus mixture, the angle of the digging shovel can be adjusted using the ground wheel. The recommended adjustable angle for the flat digging shovel, denoted as α, is within the range of 30° to 40°, and the speed of gravitational acceleration g was determined as 9.8 m s−2.
Based on the calculation and analysis of the above parameters, the total length of the designed digging shovel L was determined to be 320 mm, for which it satisfies best the soil–Astragalus excavation needs.
3.2. Roller-Screen Device
3.2.1. Design and Working Principle of the Roller Screen
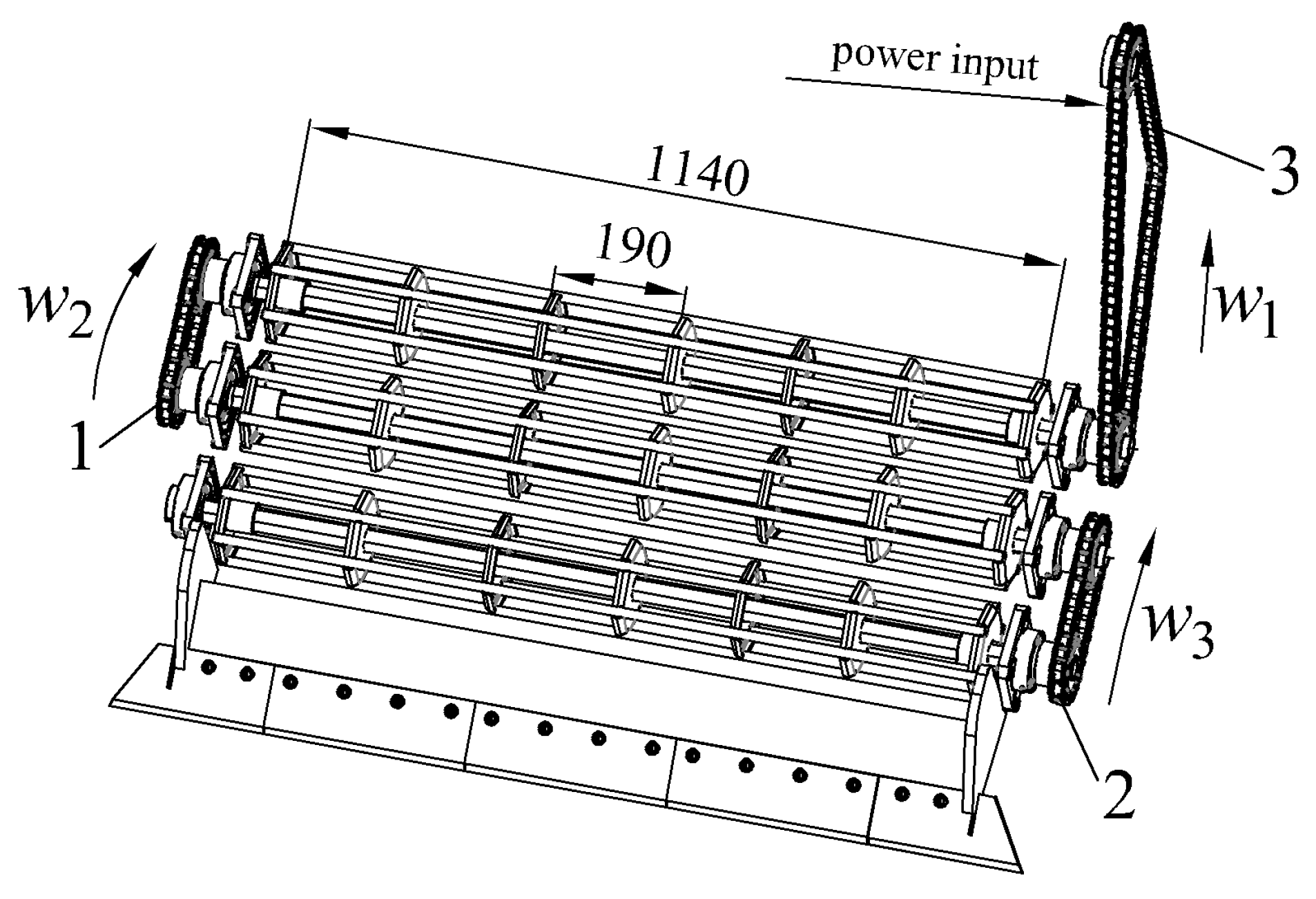
In the actual work process, when the size of the soil block exceeds the clearance interval on the conveyor belt, it becomes challenging for the soil block to dislodge during the transmission process. Consequently, it ends up progressing through the subsequent conveying stages alongside the Astragalus, leading to a higher likelihood of soil blocks becoming mixed with the Astragalus. This mixing adversely affects the quality of the harvest. To address the above-mentioned issues, a roller screen, as illustrated in
Figure 4, has been incorporated at the rear end of the digger. It primarily consists of a driving sprocket, rollers and link chains. Three sets of roller devices are evenly installed on the frame, with transmission sprockets located at both ends of each conveyor roller, facilitating a step-by-step power transmission. Additionally, these rollers are equipped with protective shells for the sprockets, safeguarding them against soil blockage.
The material of the rod is 65 Mn steel with a diameter of 10 mm. The fixed plate is made of 5 mm-thick 65 Mn steel plate, bent at 90°. Its hexagonal shape can fully disperse the pressure on each side, and thus increase the stability of the structure. The angle between adjacent sides is 120°, and a semi-circular structure with a diameter of 10 mm is cut at the angle. The rod is welded to the semi-circular structure on the fixed plate. The cross-sectional design of the drive shaft is a hexagonal shape with a side length of 20 mm, and the roller-screen device is fixed on the frame through the drive shaft.
Power from the tractor’s Power Take Off (PTO) is transmitted to input chain 2 through the gearbox (
Figure 4). This chain drives the third roller, causing it to rotate, and simultaneously transferring power to chain 1. Chain 1, in turn, drives the second roller while transferring power to chain 3. Finally, chain 3 drives the first roller to complete the cycle. This sequence creates a “right-left-right” rotation pattern for the rollers. This roller screen device effectively increases the movement of the separation device on the soil, sifting out soil and stones. This reduces work resistance and improves the overall work efficiency.
Based on the intended working width of the equipment, the final drum-screen length is set at 1140 mm. To reinforce the steel bars and prevent soil from adhering to them, thereby reducing crushing efficiency and harvesting output, hexagonal reinforcement plates are welded to the vertical shaft at regular intervals. These plates are spaced 190 mm apart and connected to the connecting rods by welding. The rollers are arranged consecutively, with each pair angled slightly upwards. During operation, the sprocket drives the rollers to rotate in a clockwise direction, effectively crushing the soil.
3.2.2. Roller-Screen Force Analysis
To guarantee the smooth movement of excavated Astragalus onto the conveyor belt chain, it is crucial to determine the optimal speed of the roller screen. This can be achieved by analyzing the forces acting on the mixture on the roller screen, treating the combined soil and Astragalus scooped up per unit time as individual particles.
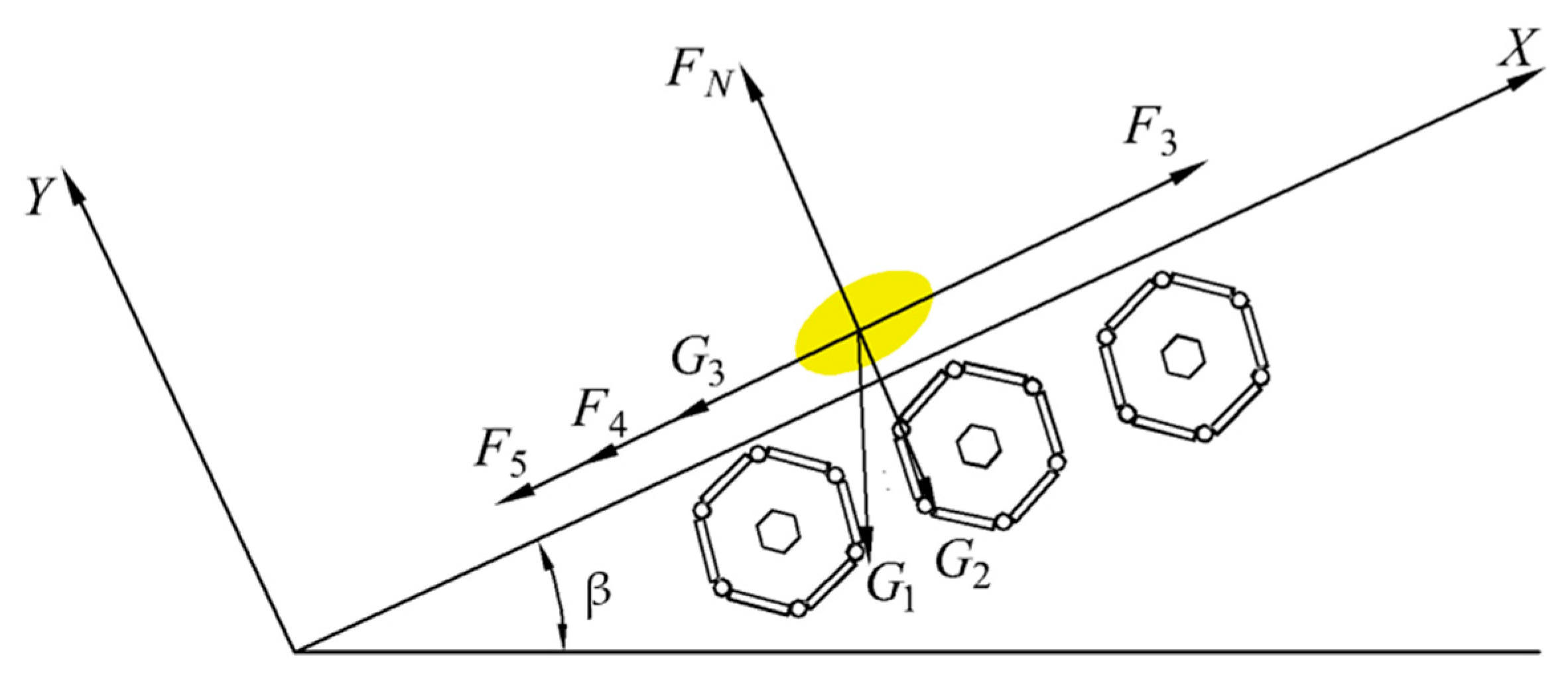
Figure 5 depicts the force analysis for the roller screen’s transport process.
Figure 5 shows the following: β: angle between the roller screen and the ground (degrees);
FN: force exerted by the roller screen on a particle (N);
F3: conveying force received by Astragalus (N);
F4: frictional force due to rolling during Astragalus movement (N);
F5: frictional force generated at the neck of the roller screen on Astragalus (N);
G1: gravitational force acting on a particle (N); and
G3 and
G2: components of gravity in the
X and
Y axes, respectively (N).
With these notations, the following equations can be written:
where
is the number of roller sieves in contact with Astragalus (
= 3);
q is the mass of a single roller screen (
= 4.9 kg);
is the sliding friction between particles and roller screens (
= 26.5°);
is the equivalent friction coefficient of the roller bearing (
= 0.15);
is the diameter of the roller journal (mm); and
D is the diameter of the roller (mm).
Based on the same
Figure 5, we can further write:
where
is the rolling friction coefficient (
= 0.05), and
is the friction coefficient between the soil and the roller screen (
= 0.6) [
21].
According to Equations (8)–(10), the condition to ensure smooth upward transportation of particles is:
The formula for meeting the critical speed for smooth transportation of particles is:
For the roller diameter D = 150 mm, journal diameter d = 32 mm, angle between the roller screen and the ground β = 20°, and mass of Astragalus and soil blocks per unit time 500 kg, the calculated critical speed of the roller screen is 137.2 rpm. However, to accommodate operational needs in various plots, the operating speed was set to 150 rpm.
If we treat the mixture of Astragalus and soil (which needs to be continuously separated and transported upwards) as a single particle, the analysis shows that to achieve stable upward transport, at least three roller supports must be employed. The root and stem growth length (
L₃) of Astragalus is between 200 mm and 600 mm, and for the upper limit
L₃ = 600 mm, the approximate spacing between the rollers should be:
To ensure timely separation of the roller spacing, it is necessary to match the assembly pitch of the drive sprocket. Therefore, the roller-shaft spacing was taken as b = 170 mm.
3.2.3. Simulation Parameter Setting for Roller-Screen Operation Stroke
To assess the effectiveness of installing a roller screen in improving separation efficiency, a comparative analysis was conducted using the discrete element method (DEM) in a simulated experiment. Two models were created: one equipped with a roller screen and another without. The material composition of the models should be 65 Mn steel. Experiments were then run with both models to compare their separation performance. For the contact model between soil particles and each other, as well as between soil particles and the separation device, the Hertz-Mindlin (no-slip) model [
22] was chosen. The relevant simulation parameters were set as specified in
Table 2 [
23].
Two plot model diagrams, each measuring 8000 mm (length) × 1400 mm (width) × 600 mm (height), were created in SolidWorks 2020 based on the characteristics of harvest plots in the northwest region. These models were then imported into EDEM 2020 software. A particle factory, aligned with the plot height, was set up within EDEM. A total of 1.5 million soil particles were generated and allowed to fall freely under the influence of gravity within the plots. The entire simulation ran for 9 s.
3.2.4. Simulation Process and Result Interpretation
Prior to initiating the simulation, two filtering models had to be established within SolidWorks and saved in the .stp format. Subsequently, these models were imported into EDEM software, as depicted in
Figure 6. Additionally, the roller-screen speed was set to 150 rpm. For both the roller screen and the conveyor chain, the forward speed was set to 1.0 m/s, and the conveyor-chain speed was set to 2.2 m/s. In the simulation of the roller-screen operation, the effects of material wear and frictional heat transfer were neglected.
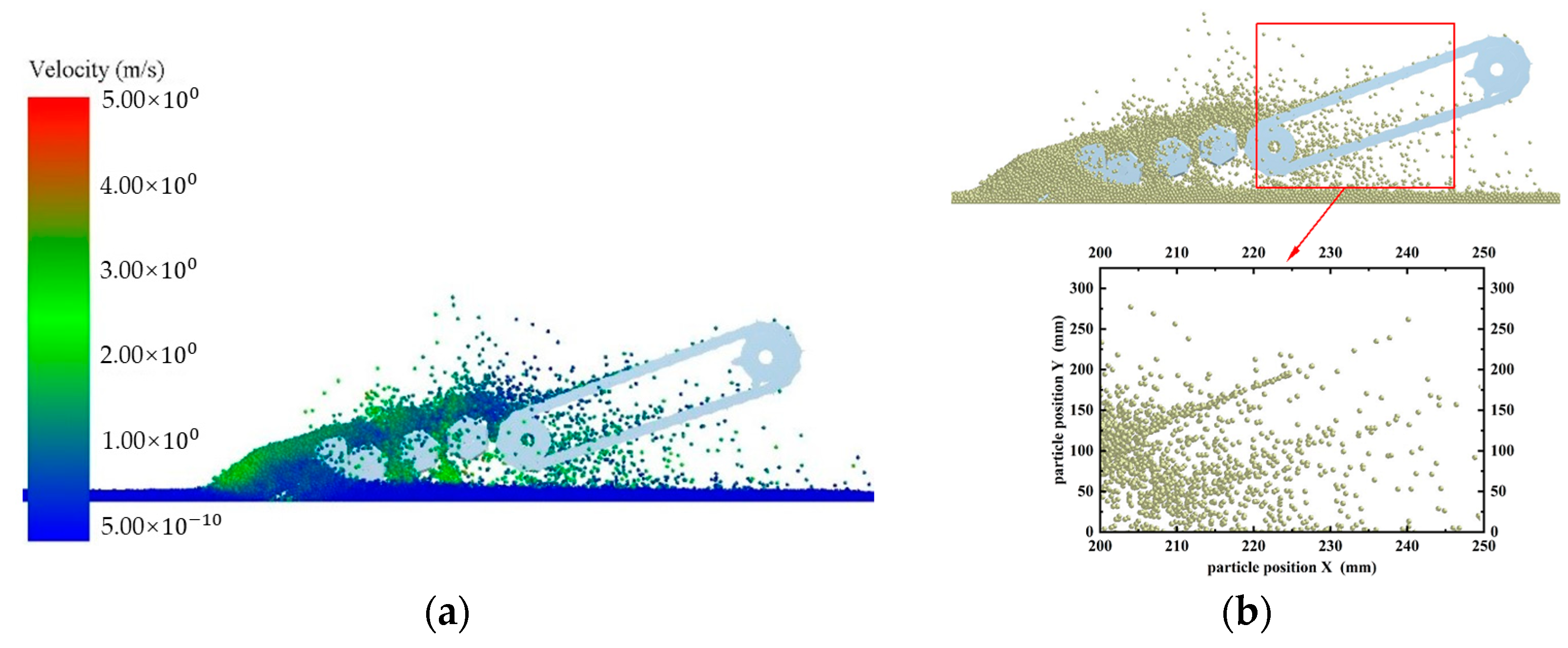
The effect of soil particles entering the conveyor chain when different simulation devices operate stably is shown in
Figure 7 and
Figure 8. From these simulation diagrams it can be seen that the particle density entering the conveyor chain when the roller screen is installed is smaller than that when the roller screen is not installed. To determine the screening efficiency of the roller screen, data collection and processing during the experimental process were carried out through the post-processing module of the discrete element simulation software EDEM 2020. Due to the inability to directly calculate the number of particles screened by the roller-screen device, the screening efficiency of the roller screen can be indirectly calculated by measuring the number of particles falling into the conveyor chain. Data collection was conducted at the initial positions of two different models of conveyor chains. Using the Grid Bin Group option of the Setup Selections module, a measuring box with a width and length of 700 mm and 540 mm was set every 1 s along the direction of motion of the roller-screen device from the initial stage position. The total time was set to 9 s. The number of particles passing through each box was measured, and a data table was output to calculate the screening efficiency. The results are shown in
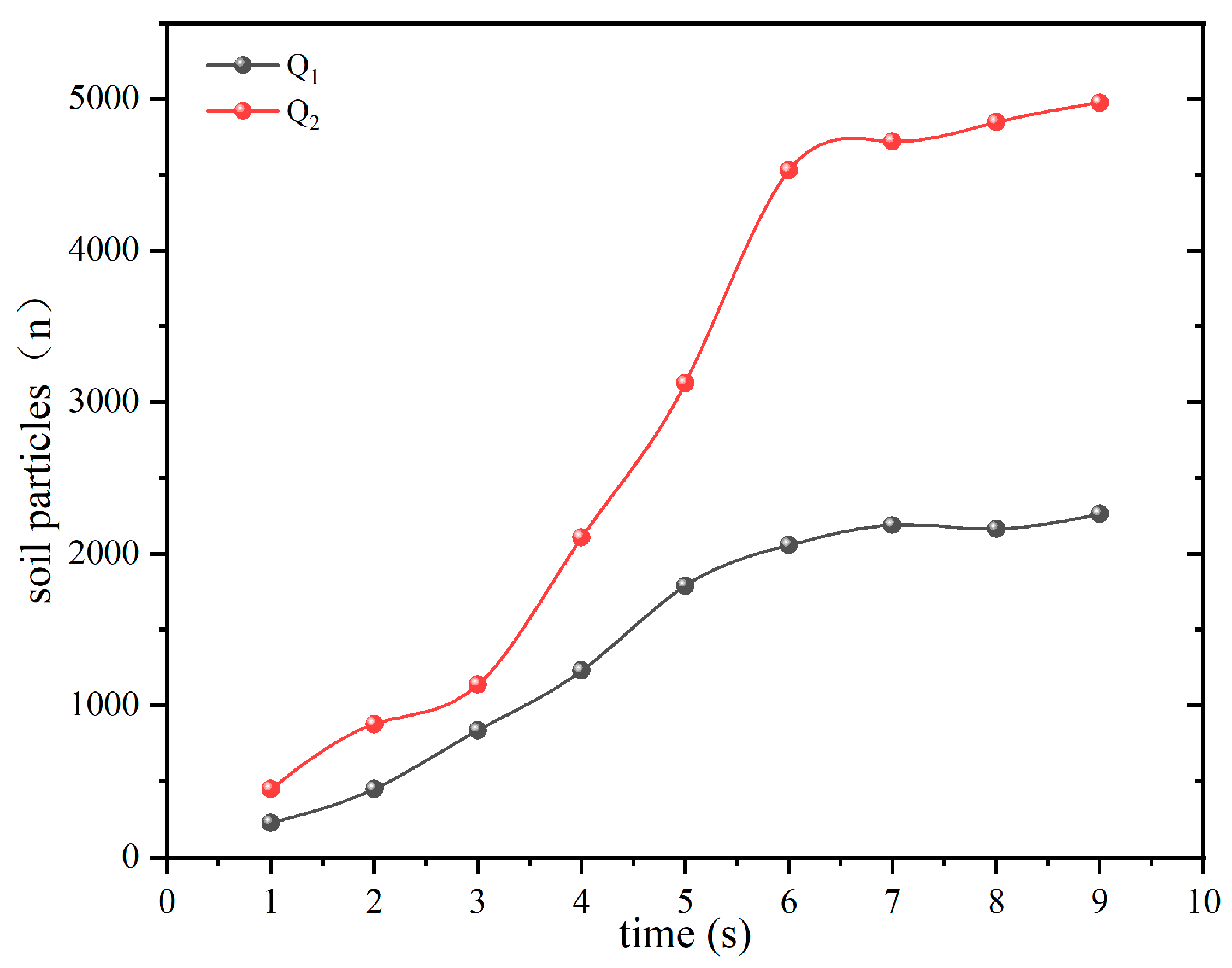
Figure 9.
The Q
1 line represents the number of soil particles measured without the installation of the roller screen, while the Q
2 line represents the number of soil particles measured with the installation of the roller screen. In both cases, the particle numbers tend to stabilize after about 6 s. Without a roller-screen device, the number of particles measured during the stable period is between 4500 and 5000. With a roller-screen device, the number of particles measured is between 2000 and 2500. The actual number of particles has been gathered in
Table 3.
After the number of particles entering the conveyor chain from two different devices had stabilized, the screening efficiency of the roller screen was calculated for the simulation time between 6 and 9 s. The formula used was:
where
is the screening efficiency of the roller screen, (%);
is the number of soil particles measured by installing a roller-screen device; and
is the number of soil particles measured without the installation of a roller-screen device.
According to Equation (15), the screening efficiency of the roller screen is approximately 56.3%.
Figure 7b shows that that soil particles directly enter the conveyor-chain device through the digger shovel, resulting in low particle dispersion and high density, which increases the operational resistance of the conveyor-chain device and affects the permeability of the soil. As can be seen in
Figure 8b, the soil particles entering the conveyor chain after screening have a high degree of dispersion. The main reason for this situation is that the roller screen exerts a greater force on soil particles during high-speed rotation, and the soil particles are subjected to greater centrifugal and shear forces, increasing the interaction between particles and resulting in dispersion and separation effects. Meanwhile, the high-speed rotation of the roller screen also increases the impact force on soil particles, resulting in a higher horizontal particle velocity and greater dispersion of soil particles. The pore structure of the soil will also become looser, increasing the soil permeability and thus providing a good growth environment for the next crop of Astragalus membranaceus.
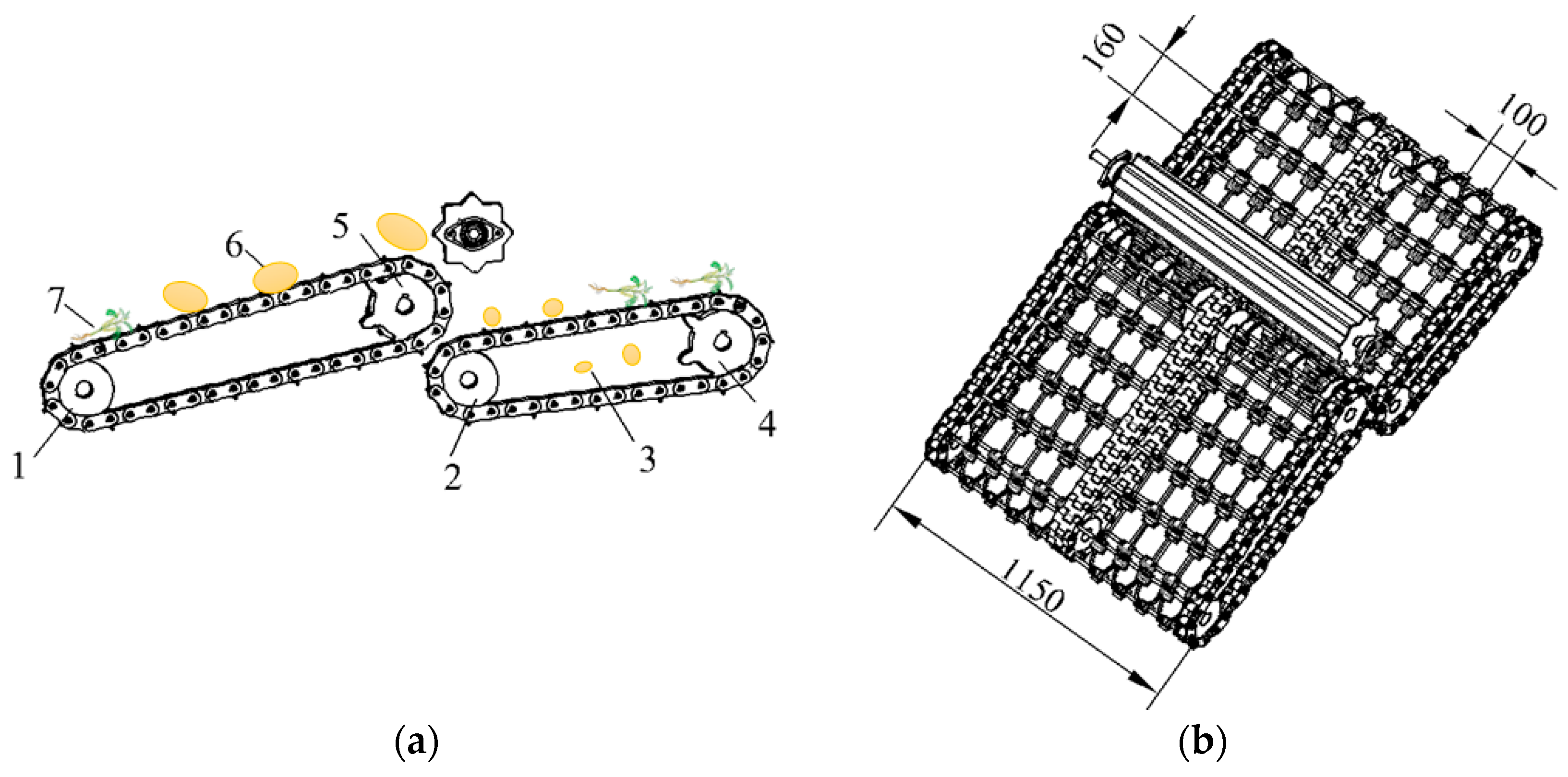
3.3. Flexible Separation-Conveyor Device
As shown in
Figure 10, the Astragalus digger implements a two-stage conveyor-chain separation operation. Digging out the mixture of Astragalus–soil with a shovel, it enters the conveyor chain through a roller screen. The installation angle of the conveyor chain directly determines the yield of Astragalus. This structure mainly consists of a first-stage conveyor chain, a second-stage conveyor chain and a flexible screen.
The length of the rhizomes of Astragalus is mostly above 200 mm, so the separation gap is designed to be 160 mm × 100 mm, and the total length of the separation rod is 1050 mm. To ensure fixed spacing during the separation process, the separation rods are fixed through the holes in the conveyor chain and can rotate. This ensures that the distance between the separation rods does not change during the normal operation of the conveyor chain.
The first stage of the conveyor chain mainly separates the mixture screened by the roller screen, and transports Astragalus rhizomes mixed with larger soil blocks backwards. A soil-crushing device installed behind the first-level conveyor chain will break the larger soil blocks. The broken soil then falls onto the second-level separation device, along with Astragalus. The soil blocks are separated in the gaps of the second-level separation device, and Astragalus is collected into the collection box as the conveyor operates.
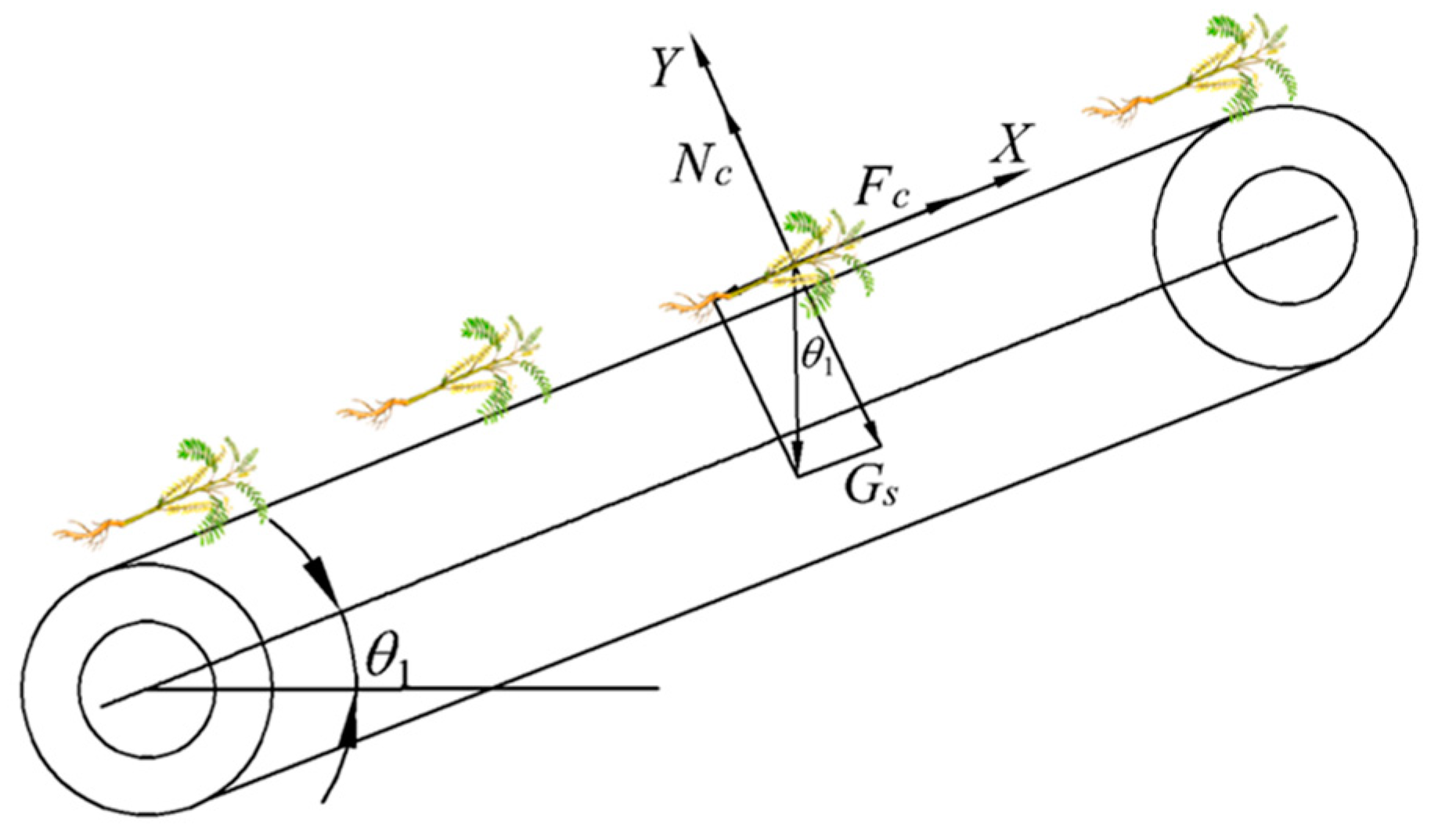
3.3.1. Calculation of Installation Angle of the Conveyor Chain
When the mixture is transported along the separation device, a suitable installation angle is required to ensure that medicinal materials do not slide down in the opposite direction of the conveyor chain. The installation angle is determined through the force analysis of Astragalus on the conveyor chain. When the inclination angle of the conveyor chain is at the critical value
, the Astragalus is slipping backwards, corresponding to the force configuration as shown in
Figure 11.
The equilibrium equations are the following:
where
is the critical inclination angle of medicinal materials sliding on the conveyor belt (°);
is the weight of medicinal materials (N);
is the frictional force between the medicinal materials and the conveyor belt (N);
is the support force of the conveyor chain upon the medicinal materials (N); and
is the static friction coefficient between medicinal materials and the conveyor chain.
The static coefficient of friction
c between the medicinal plants and the conveyor chain is 0.45 [
24], and the critical inclination angle for medicinal materials to slip on the conveyor chain is 24.9°. If the installation angle is too big, the harvest is prone to rolling, while if the angle is too small, the overall size of the machine will be too long and power consumption will increase. Therefore, the installation angle in working condition was set to 30°, which exceeds the critical inclination angle, causing the medicinal material to slide downwards.
To solve this problem, a flexible screen was installed on the conveyor chain to facilitate the smooth transportation of Astragalus along the lifting direction. The flexible screen can additionally reduce the vibration damage and the deformation and fracture of the Astragalus during the separation process, thus maintaining its structural integrity and improving the efficiency of separation.
The screen strips between the conveying rods are shown in
Figure 12. There are 12 mm through holes at both ends of the sieve chain, which are connected by rubber rods with a length of 124 mm and a diameter of 8 mm. The sieve chains are embedded and connected, and the rods pass through the through holes of the rubber mesh and connect to the chain. The diameter of Astragalus is generally between 0.5 and 3 cm. Considering factors such as shaking during operation, to achieve the conveying process the designed height of the end of the sieve is 30 mm. Therefore, even if the angle of the conveyor chain exceeds the critical inclination angle during operation, the medicinal materials will not slide downwards during the conveying process. Compared with the more common straight-rod installation, this arrangement allows the medicinal materials to be better maintained in a fixed position during the separation and transportation process, reducing its damage rate.
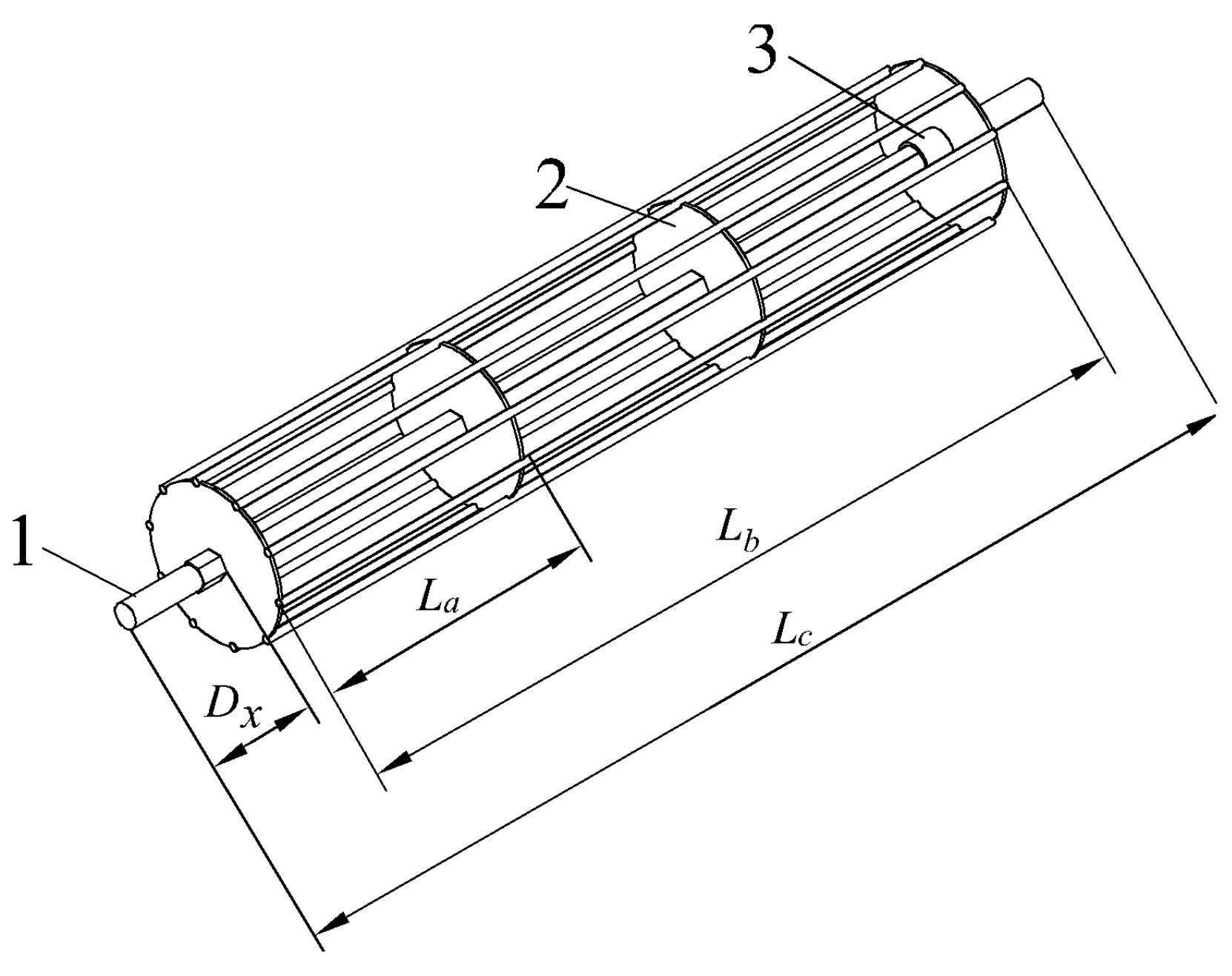
3.3.2. Rear Soil-Crushing Roller Device
In order to achieve better separation between medicinal materials and soil, a soil-crushing roller was installed at the rear end of the second-stage conveyor chain. Considering that there are fewer remaining soil blocks at the end of the conveyor, combined with the overall size and weight of the machine, the designed soil-crushing roller is a rod type. These rods not only save materials but also reduce the weight of the soil-crushing device.
As shown in
Figure 13, the soil-crushing roller consists of a driving shaft, a fastening ring, a disc, and a rod. The soil-crushing roller is driven by the active shaft of the second-stage conveyor chain. When the digger operates, the soil-crushing roller begins to rotate and breaks down larger soil blocks into smaller particles. According to the width of the machine operation, the length
of the soil-crushing roller shaft is designed to be 1400 mm. Compared to traditional circular shafts, this device uses a hexagonal shaft, which provide more bearing area where the reinforced disks are assembled, and to resist better torsional loads. The shaft is also lighter weight, thereby reducing manufacturing costs and the required actuating power.
The distance between the disc and the side frame is 137 mm, and the actual working width is 1120 mm, choosing an appropriate size based on specific land conditions and soil conditions, and selecting a diameter of 200 mm. The soil-crushing roller is evenly divided into three sections horizontally, and each section is welded with a disc that plays a reinforcing role on the soil-crushing rod. The length D of each section is 372 mm, and 10 soil-crushing rods with a diameter of 12 mm are evenly distributed around them, which are attached by welding.
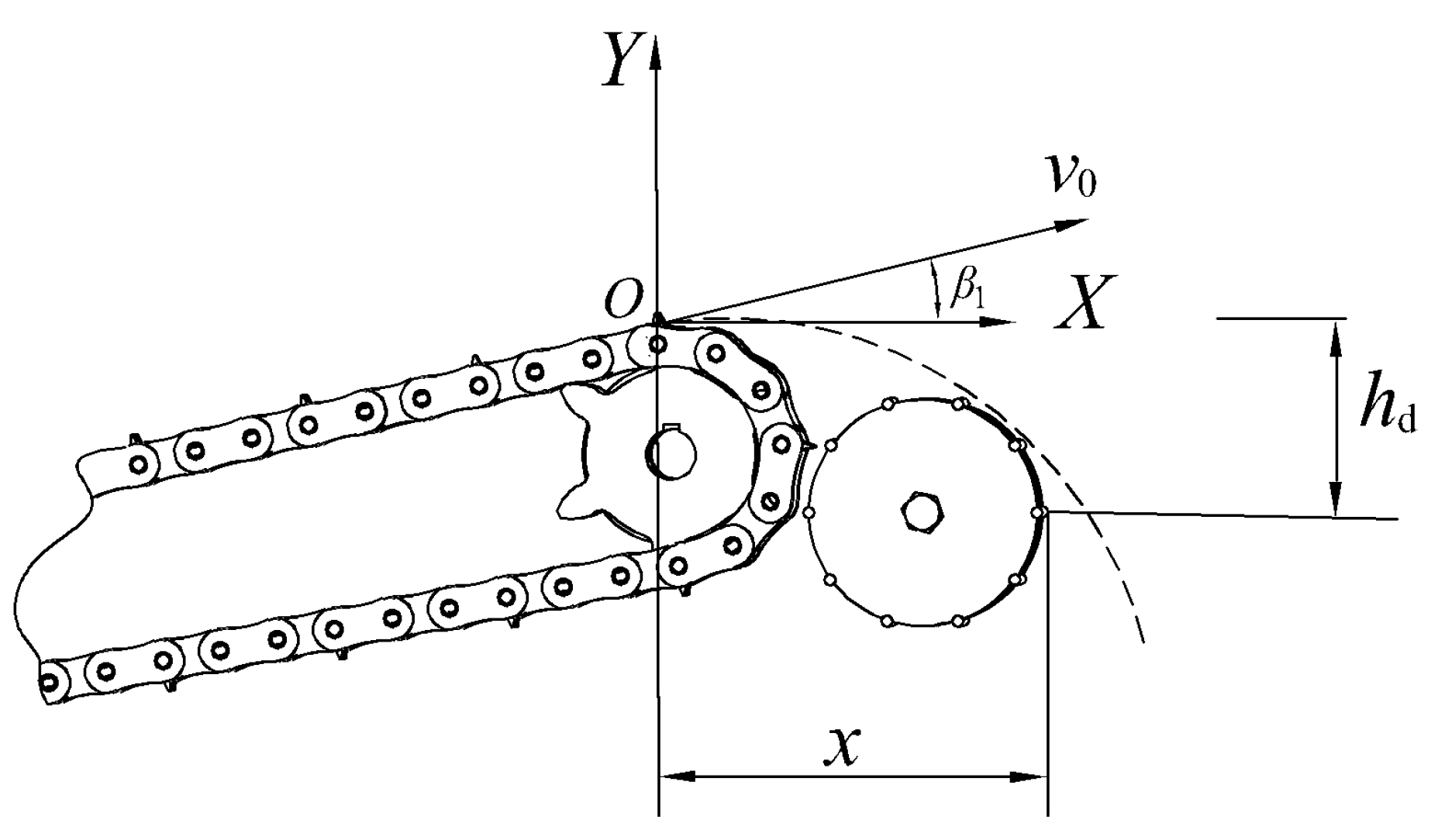
Astragalus is transported to the end of the second-stage conveyor chain and thrown backwards at a certain speed. To ensure that the installation of the rear soil-crushing device does not affect the thrown material, the horizontal displacement of Astragalus during throwing needs to be considered. Therefore, a motion analysis was conducted, as shown in
Figure 14.
Due to the angle between the conveyor chain and the ground, when Astragalus is transported to point
O and thrown out of the second-stage conveyor chain, its velocity is the same as the velocity of the conveyor chain. Ignoring the impact of collisions and air resistance between Astragalus, the soil blocks and the conveyor chains, the Astragalus is thrown out and undergoes uniform linear motion in the horizontal direction. In the vertical direction, it first reaches the highest point and then undergoes uniform acceleration with a linear motion downwards. The equation of motion for reaching the highest point in the vertical direction is as follows:
where
is the mass of Astragalus (kg);
is the vertical rise height (mm);
is the angle between the second-stage conveyor chain and the ground level (°); and
is gravitational acceleration (m/
).
According to the installation angle of the first-level conveyor chain, the installation angle of the second-level conveyor device is taken as 30° and the speed of the second-level conveyor chain is taken as 2 m/s. By substituting it into the above formula, the maximum height of rise is calculated to be 50 mm.
According to the installation position of the rear soil-crushing roller device, taking
as 300 mm and
as 200 mm, then there is the following formula:
where
is the actual horizontal distance, (mm).
Substituting this into Equation (18), the calculated value is x = 391 mm, which is greater than the farthest distance x for installing the soil-crushing device, thus satisfying the operating conditions.
3.4. Crushed-Soil Roller
Given the large amount of soil and numerous soil blocks, combined with the actual harvesting situation of Astragalus in northern arid areas of China, a soil-crushing roller was installed at the end of the first-stage conveyor chain. This can crush the compacted soil blocks, achieving the effect of crushing the soil and reducing the working resistance of the machinery.
Figure 15 shows the structural diagram of the soil-crushing roller device of the Astragalus digger, which consists mainly of a soil-crushing roller, driving shaft, support rod and fixed plate. The structural dimensions and spatial position of the soil-crushing roller directly affect the quality of the soil crushing. Cylindrical soil-crushing rollers have limited soil-crushing capacity, and are not ideal for treating randomly-shaped-soil treatment, resulting in low soil-crushing efficiency. Therefore, this device is welded with Q235B angle iron with a thickness of 3 mm and a side length of 40 × 40 mm. The advantage is its sturdy structure, which is suitable for handling large and hard soil blocks. It can also be customized according to actual needs. The drive shaft passes through the covers at both ends of the roller and is connected to one side of the gear. The two ends of the roller are connected to a fixed plate at a distance of 40 mm from the frame. The two ends of the support rod are fixed to the frames on both sides with 10 mm bolts and welded to the fixed plate to fix the soil-crushing roller. The roller-screen device is driven by the active shaft of the secondary conveyor chain. In non-sticky heavy soil, the device can be disassembled through bolts [
25], thus reducing the power consumption of the unit.
3.4.1. Calculation of Diameter of Soil-Crushing Roller
As shown in
Figure 15, the soil block can be approximated as a circle with a diameter of
d. To press the soil block into the soil-crushing roller, the following condition needs to be met:
where
is the friction,
, (N).
is the friction coefficient between the soil-crushing roller and the material in contact.
Then, the following inequality (20) can be derived:
According to the geometric diagram, it can be inferred that
Combining Formulas (21) and (22) into inequality (20) we obtain the following:
According to Equation (24), the minimum diameter
of the soil-crushing roller is related to the friction coefficient
, soil block diameter
, and the vertical distance Z between the soil-crushing roller and the sieve. Based on actual measurements of soil mixtures, the friction coefficient
was taken between 0.5 and 0.7 [
18]. The minimum diameter of the soil block that can be sieved by the conveyor chain is 100 mm. In order to achieve the function of crushing soil, it is required that the vertical distance between the roller and the screen is less than 100 mm. Therefore, the distance
between the roller and the sieve was 80 mm, the diameter of the soil block was 100 mm, and the diameter of the soil-crushing roller was 40–180 mm. The larger the diameter of the soil-crushing roller, the better the soil-crushing effect. However, if the diameter is too large, the power consumption increases. A good compromise that satisfies the harvesting conditions was a 160 mm diameter of the soil-crushing roller.
3.4.2. Calculation of the Width of the Soil-Crushing Roller
The length of the soil-crushing roller can be determined according to the actual agricultural requirements of planting. The Astragalus digger can achieve two rows of digging and the working width can be calculated according to formula (25):
where
is the average line spacing (mm);
is the average width of ridge surface (mm);
is the standard deviation (mm); and
is the tractor driving deviation (mm).
Under the real-time control of the operator, the driving deviation of the tractor can be controlled within 30 mm. The comprehensive standard deviation formula is
where
is the standard deviation of line spacing (mm) and
is the standard deviation of the average width of the ridge surface (mm).
Based on actual measurement data, the calculated standard deviation is 6.23 mm, which can be taken as 6 mm, the average line spacing
is 200 mm, and the average width of the ridge surface is 400 mm. Combining the agronomic requirements of two rows of ridges with a bottom width of 1000 mm, the actual working width of the soil-crushing roller calculated is
A, which is 1078 mm. The effective working width of the soil-crushing roller should be slightly larger than the width of the ridges at both ends [
26], and the effective working width
A should be taken as 1150 mm.
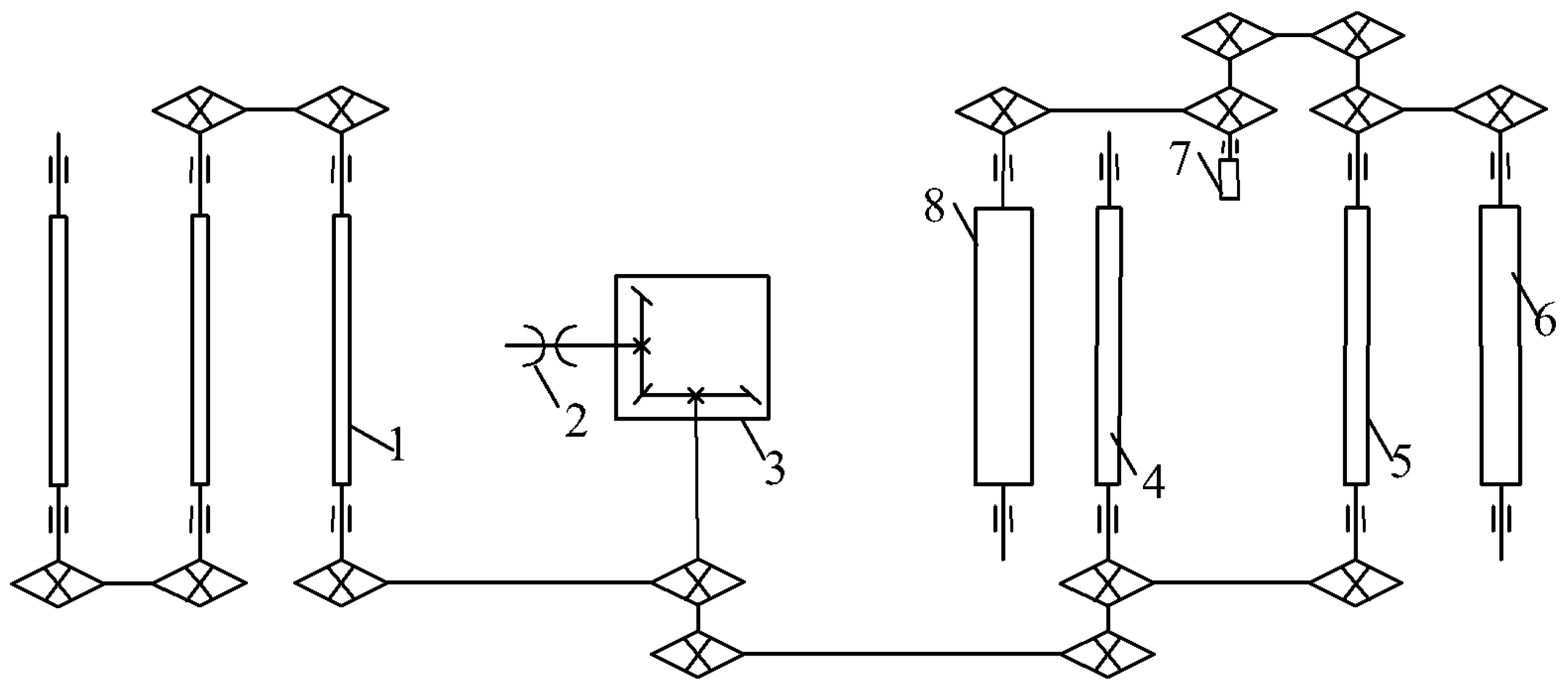
3.5. The Transmission System
The transmission system of the Astragalus digger employs predominantly chain transmission, and is illustrated in
Figure 16. The tractor conveys power to the digger’s gearbox, which changes the transmission direction. Power is sequentially transmitted to the front roller screen and the rear conveyor chain, facilitating the functions of digging, transportation, and cleaning.
The rated speed of the tractor engine power-output shaft is 540 rpm, and the speed of each sprocket in the chain drive is calculated with
where
is the speed of driving wheel (r/min);
is the speed of driven wheel (r/min);
is the teeth number of the driving sprocket; and
is the teeth number of the driven sprocket.
Among them, the gear on the output shaft of the gearbox which is matched with the first-stage conveying device has 10 teeth. The number of teeth on the sprocket of the first-stage conveying drive shaft is 27. The number of teeth on the gear of the second-stage conveying device is 9, and the number of teeth on the gear of the second-stage conveying drive shaft is 10. Based on the number of teeth in the sprocket and the speed of the power-conveying shaft, the speed of the driving shaft of the first-stage conveying device is calculated as 193 rpm, while the speed of the driving shaft of the second-stage conveying device is 174 rpm. Given the speed of the driving shaft, the linear speed of the conveyor chain can be calculated with the following:
where
is the linear speed of the conveyor chain (mm/min), and
is the radius of the driving wheel (mm).
Among them, the radius of the driving wheel of the first- and second-stage conveying devices is 110 mm. The calculated linear speed of the first-stage conveying device is 2.2 m/s, and the linear speed of the second-stage conveying device is 2 m/s. To ensure the normal operation of the conveying process, it is necessary to meet the requirement that the linear velocity of the soil–Astragalus mixture on the screen is greater than the horizontal-separation velocity on the screen when the unit moves forward [
27], that is:
According to Formula (28), the linear speed of the first-stage conveyor chain is 2.2 m/s, and the linear speed of the second-stage conveyor chain is 2 m/s. The horizontal angle between the first- and second-stage conveyor chains and the ground is 30°, and the speed at which the tractor drives the digger forward is 0.5 to 1.5 m/s. Both levels of conveyor screens meet the conveying requirements.