Analysis of Mechanical Properties of Functional Parts of Goat Hoofs under Multi-Slope
Abstract
1. Introduction
2. Materials and Methods
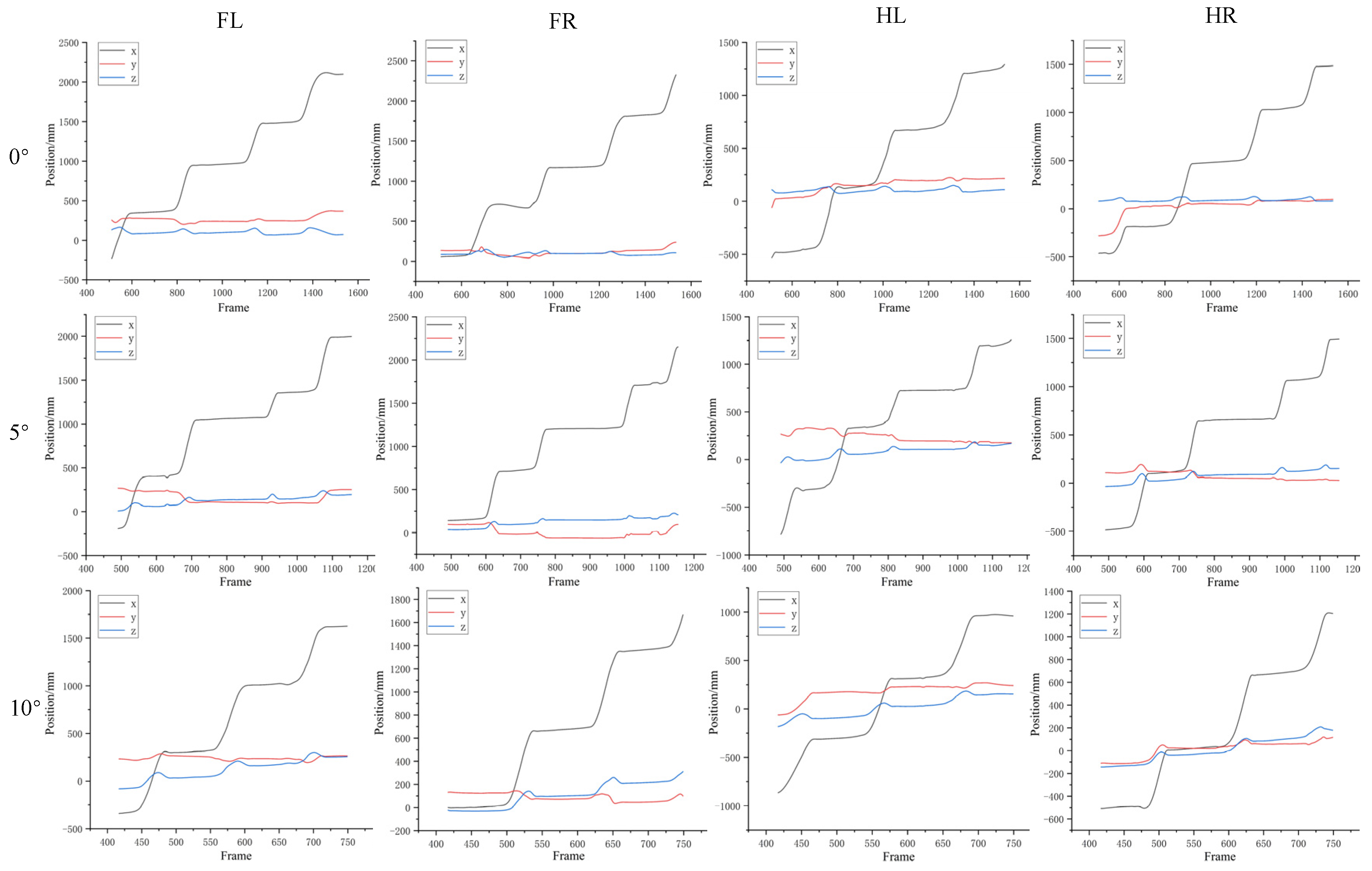
2.1. Acquisition and Analysis of Pressure Cloud Maps of Hoof Sole
2.2. Acquisition and Analysis of the Pressure Data of the Characteristic Functional Parts of Hoof Sole
2.3. Data Processing and Analysis
3. Results and Discussions
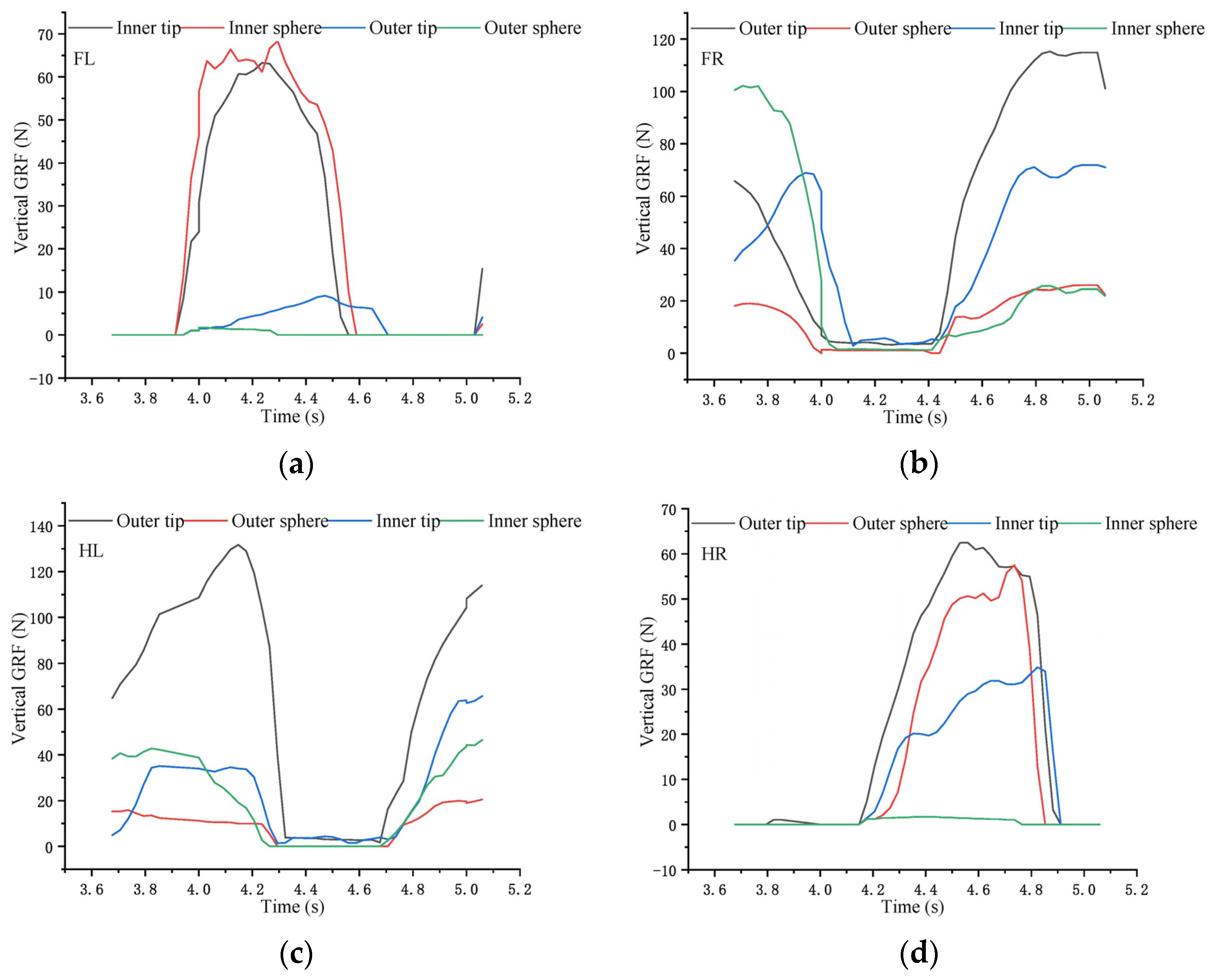
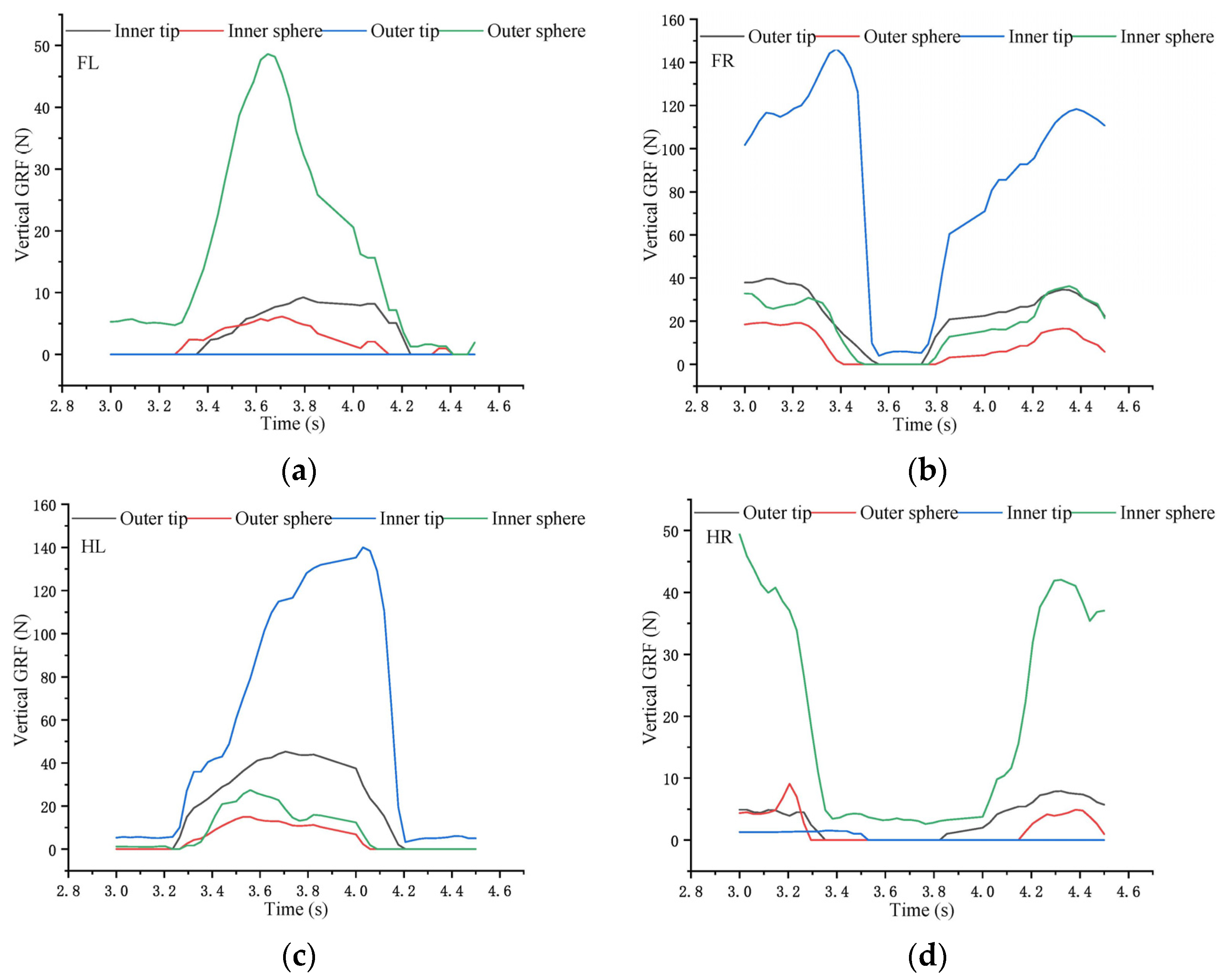
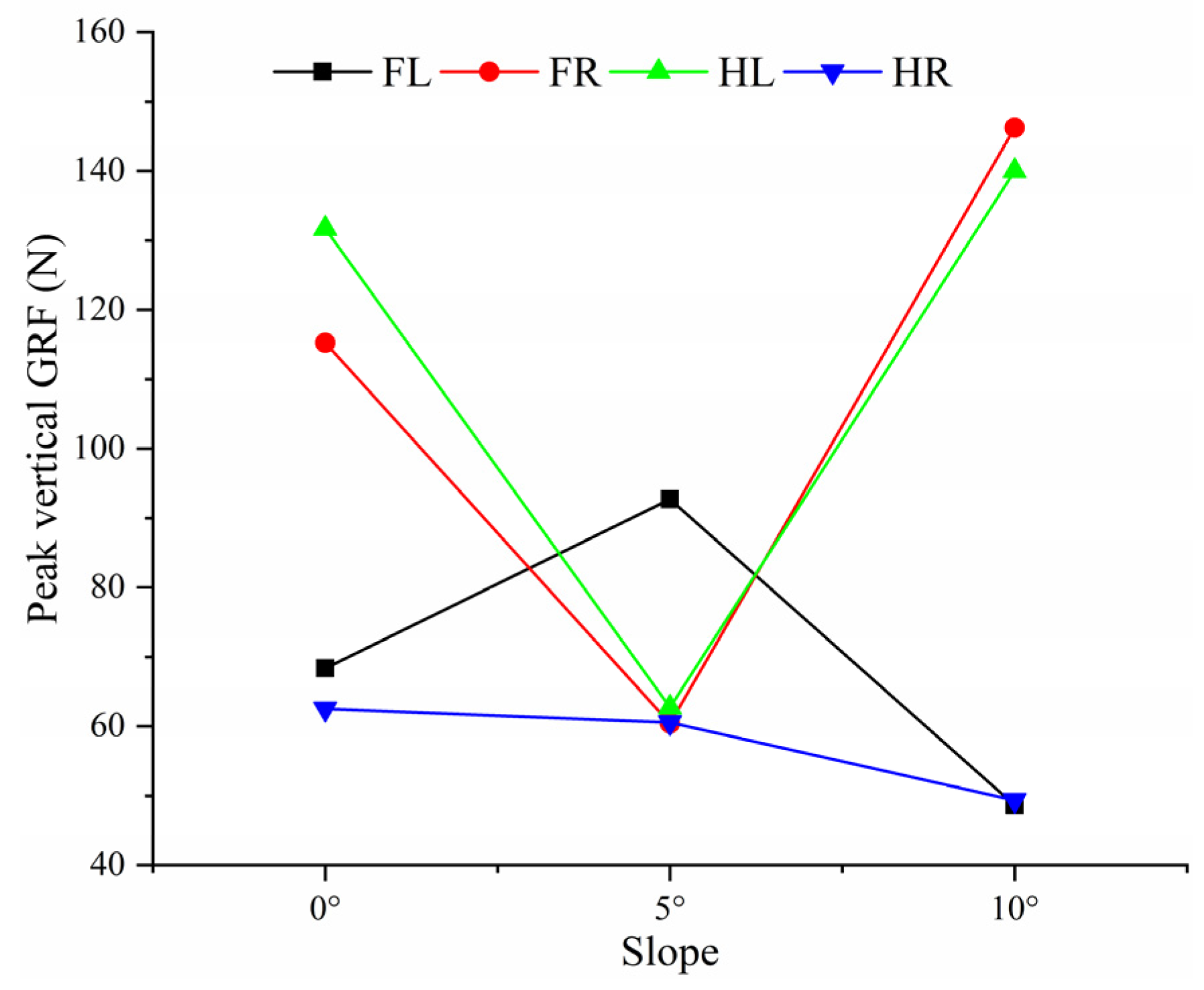
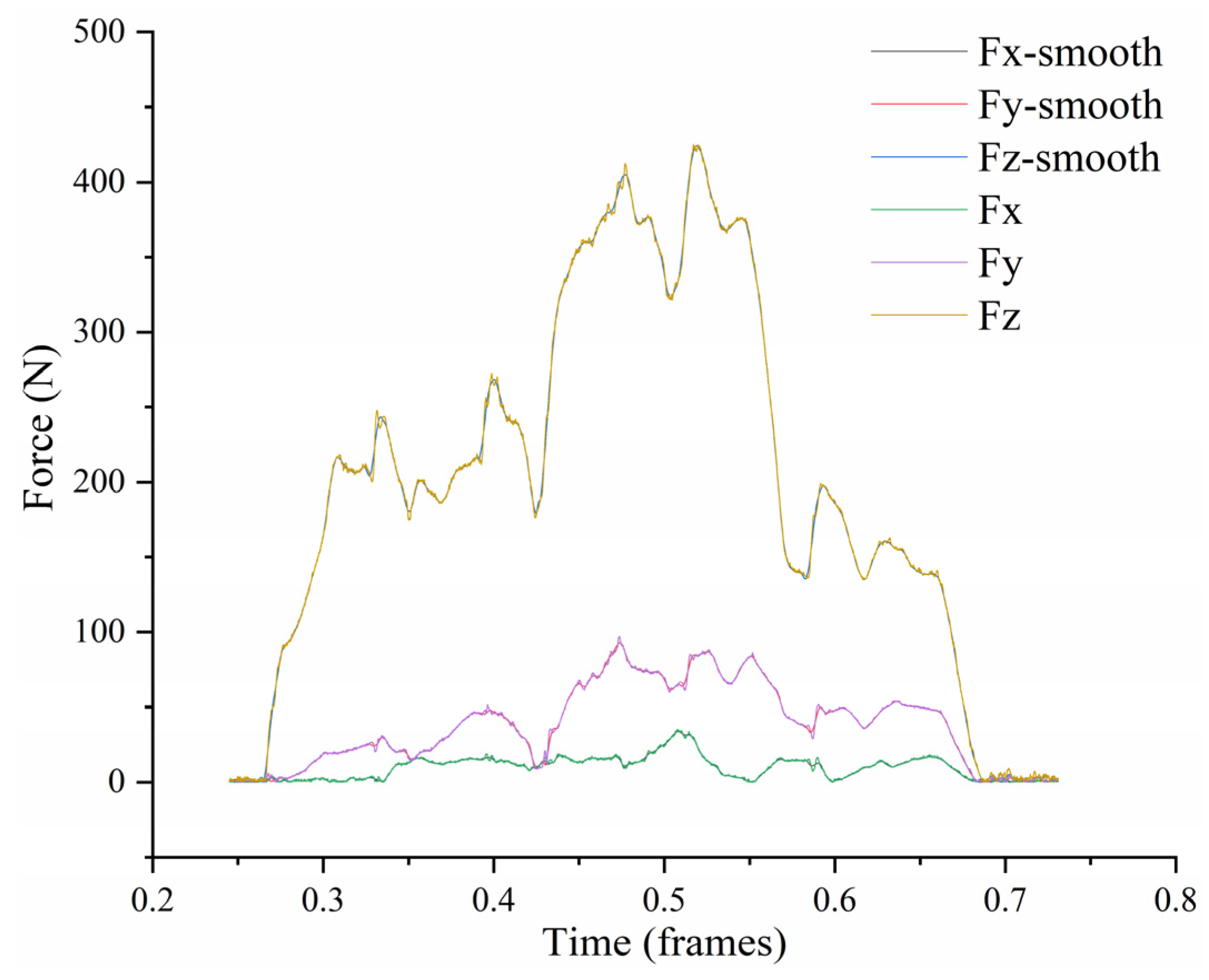
3.1. Analysis of the Vertical GRF of Characteristic Functional Parts of Goat Hoof under Multi-Slope
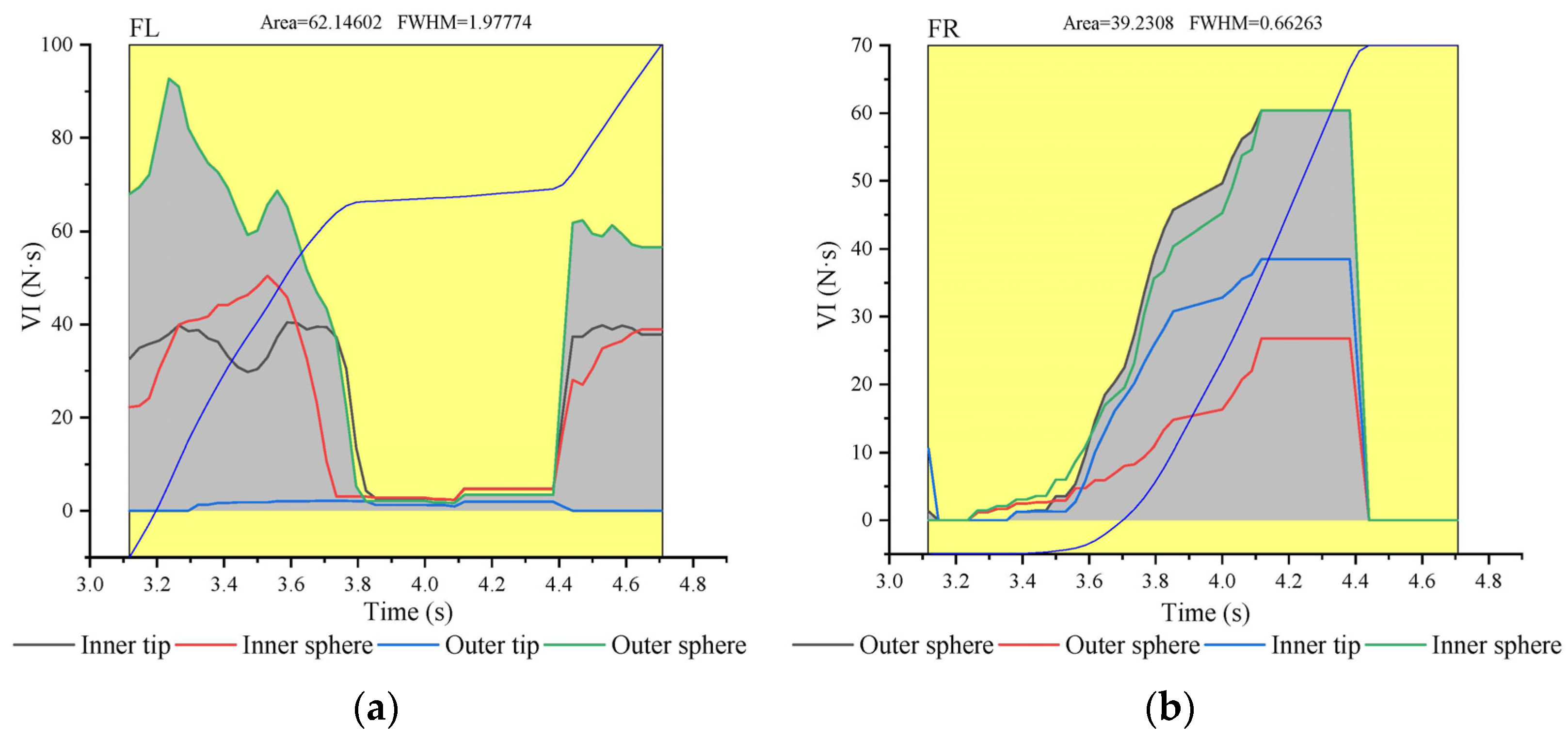
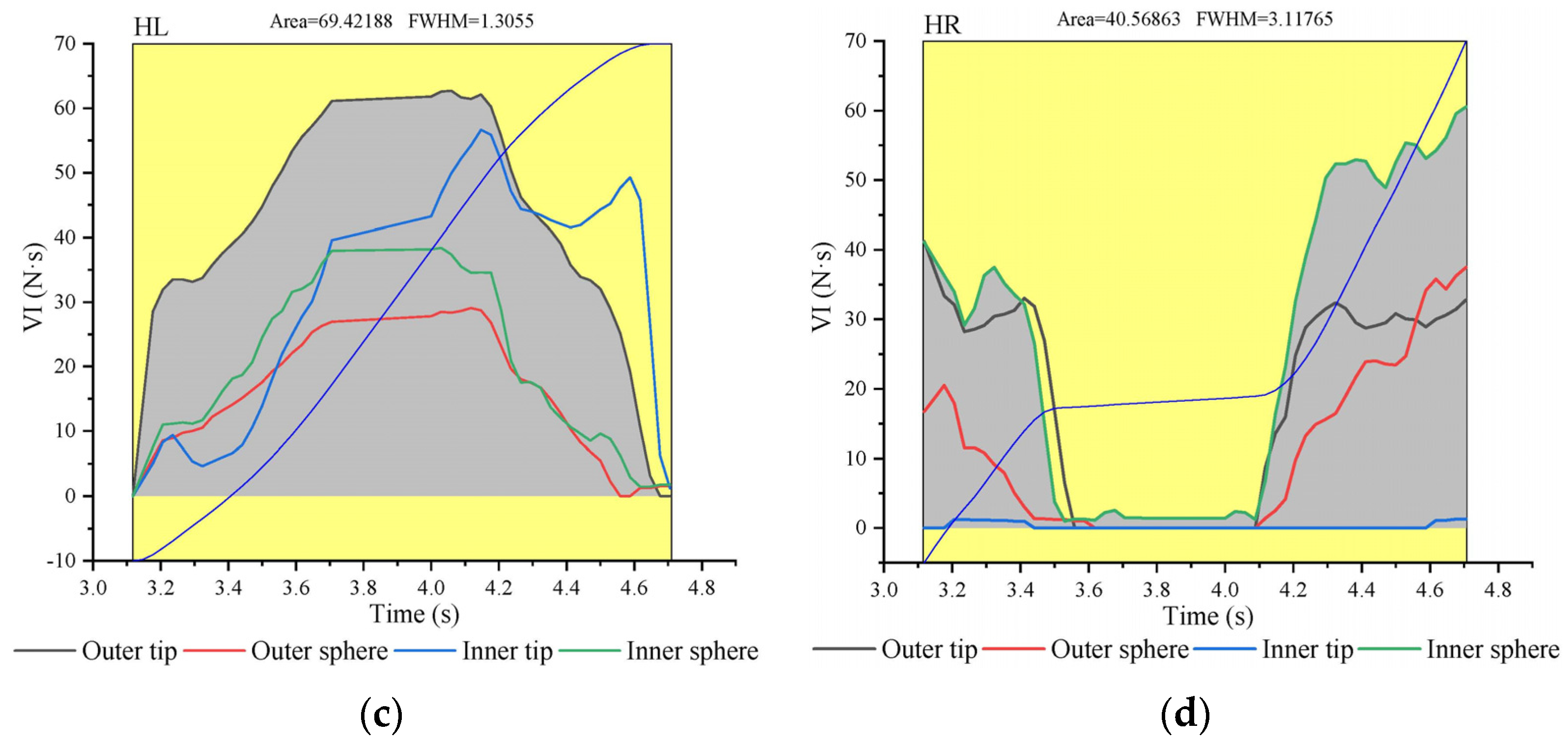
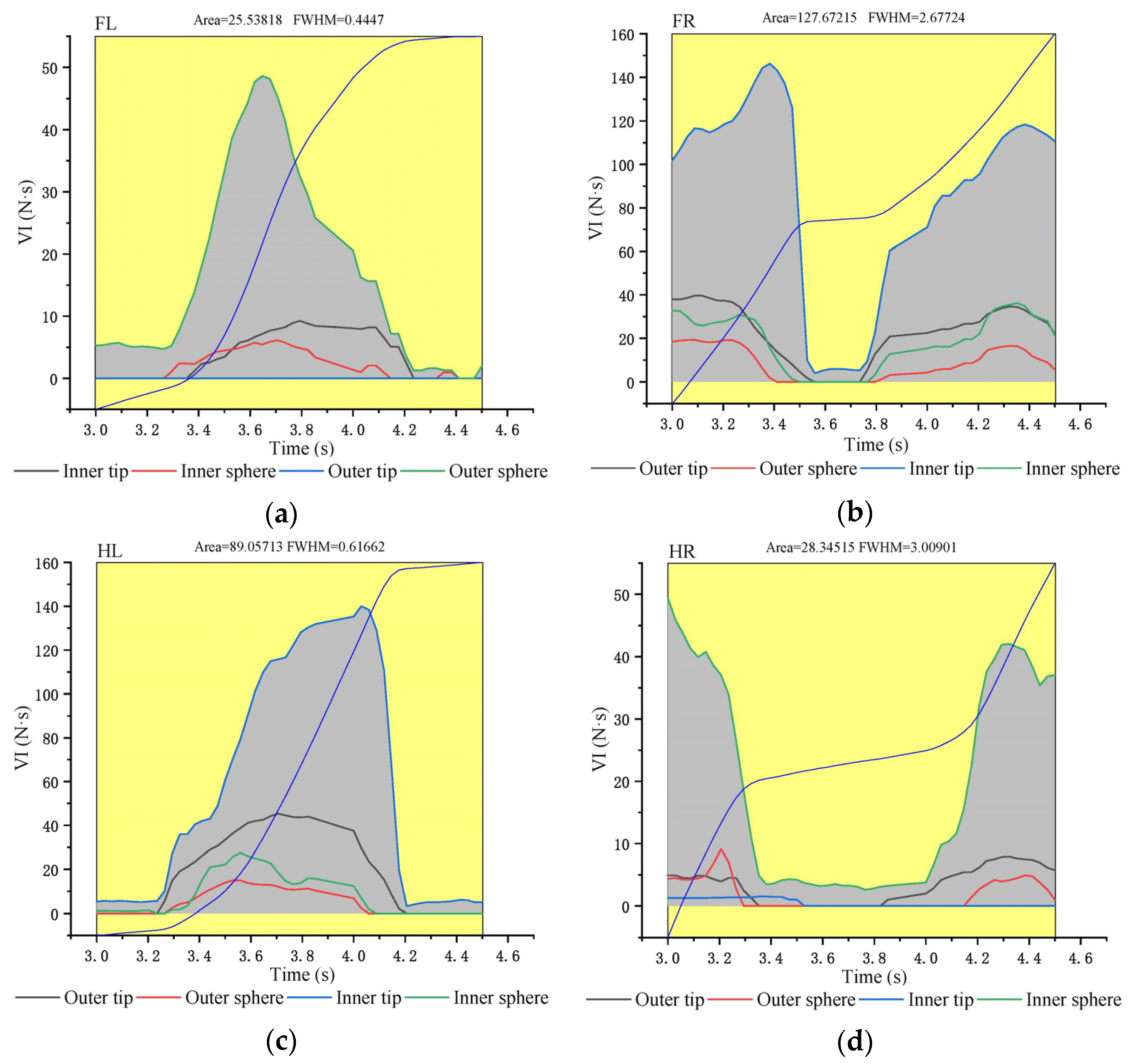
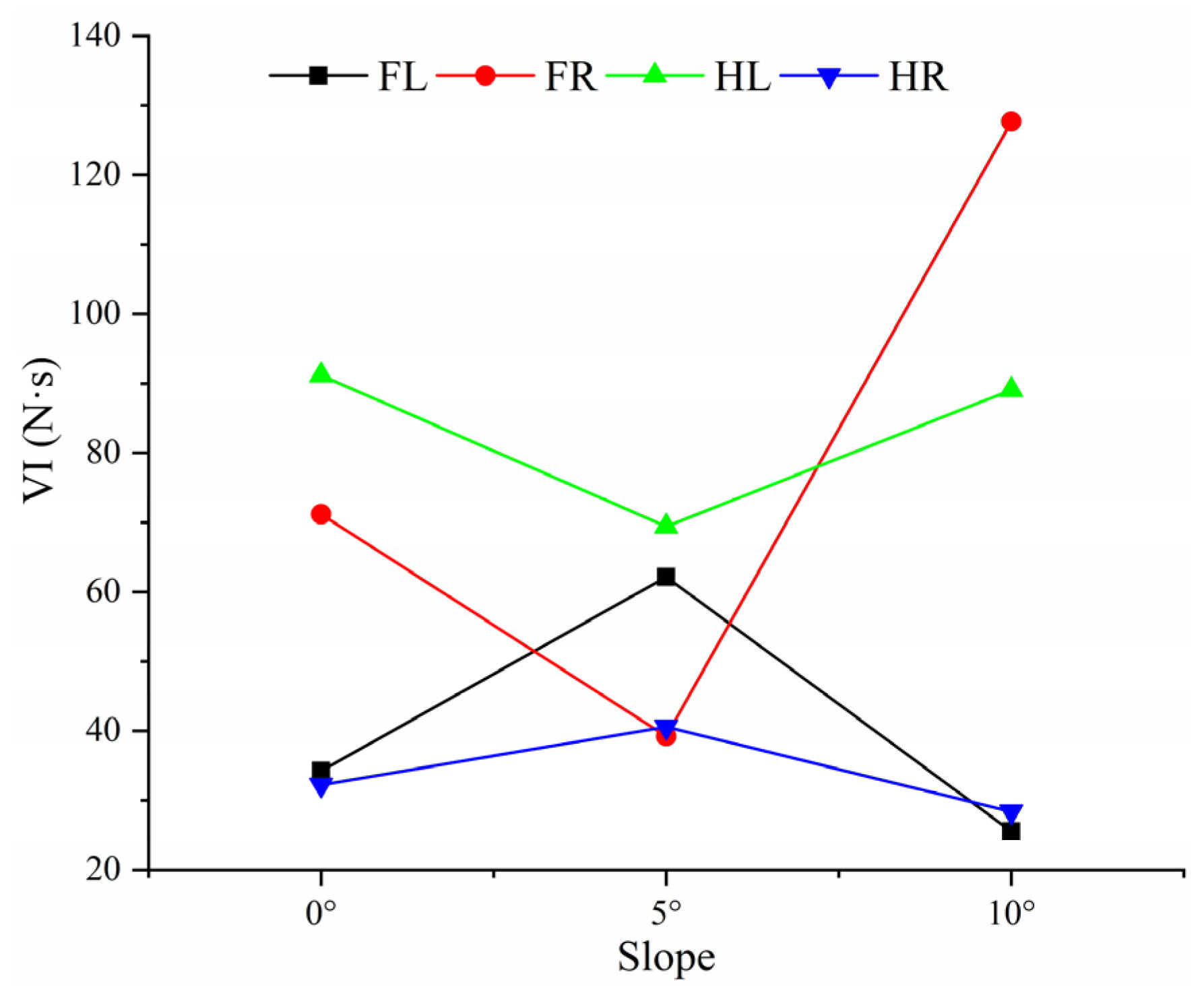
3.2. Analysis of the VI of Characteristic Functional Parts of Goat Hoofs Bottom under Multi-Slope
3.3. Comparative Analysis of the Vertical GRF and VI of Characteristic Functional Parts of Goat Hoof under Multi-Slope
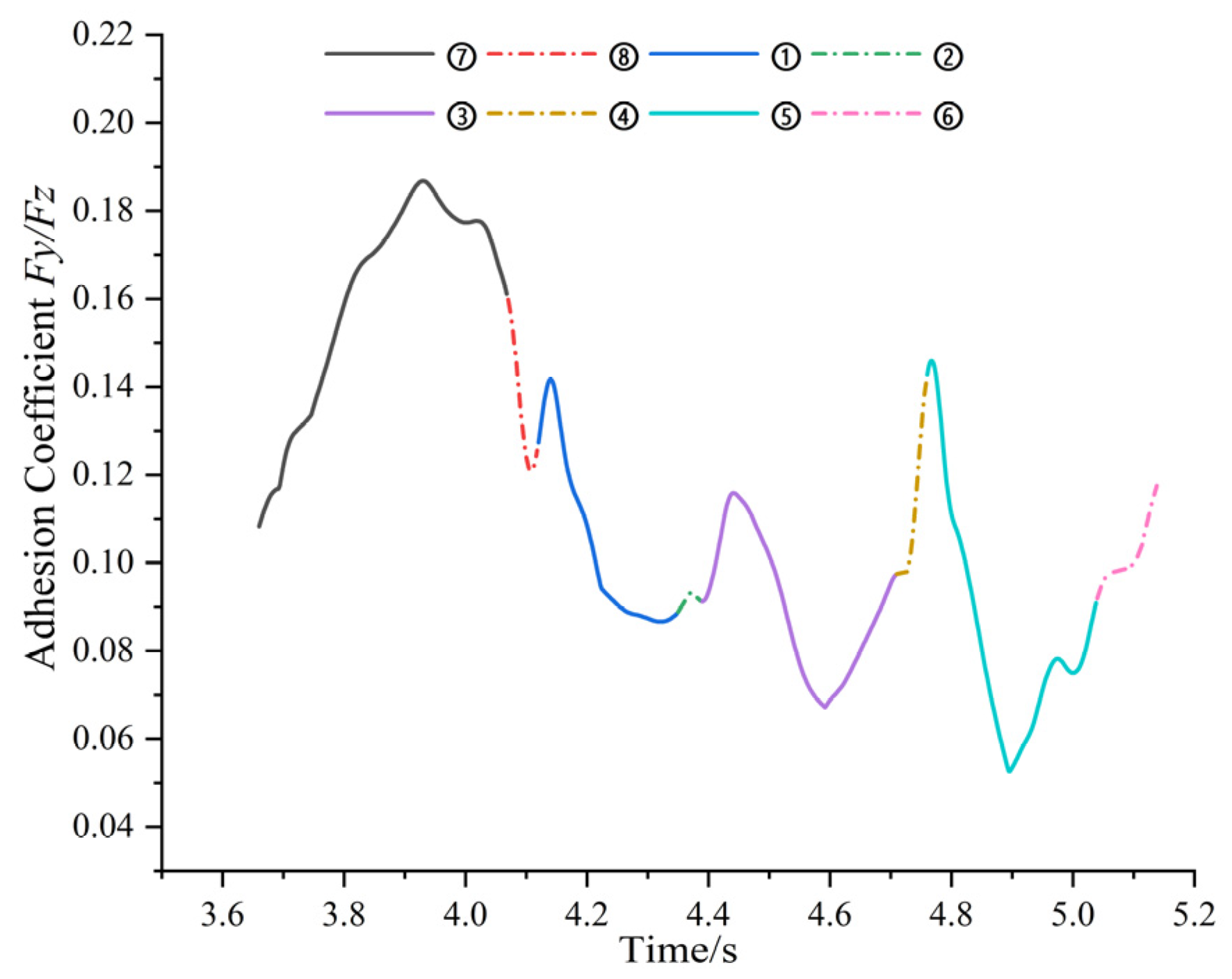
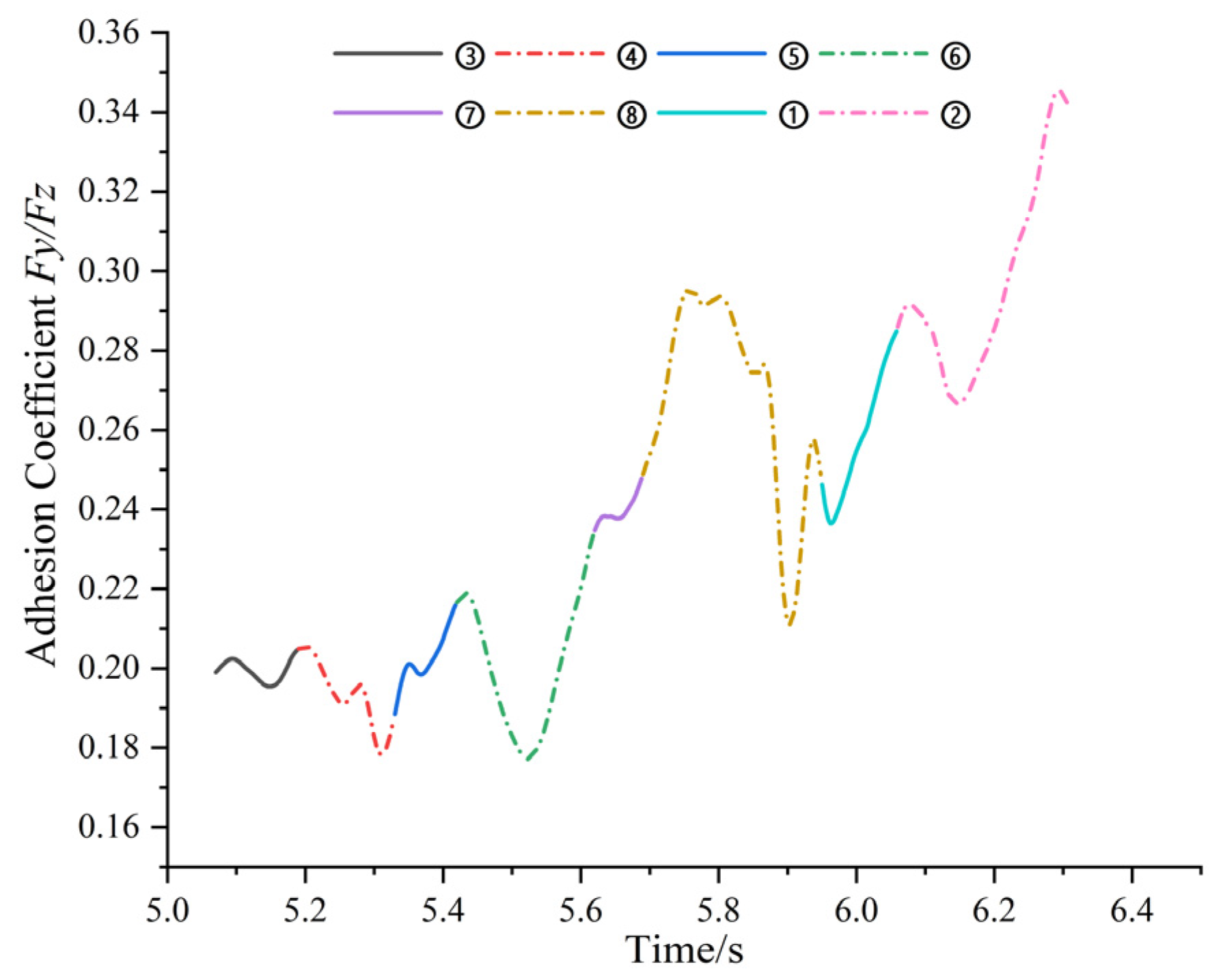
3.4. Analysis of Adhesion Coefficient of Goat Hoof Bottom under Multi-Slope
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- He, J.; Wu, D.L.; Ma, J.S.; Wang, H.K.; Yang, Y.L. The influence law of grouser shape on soil slide sinkage when tracked vehicle travels on soft road. J. Multi-Body Dyn. 2019, 234, 225–237. [Google Scholar] [CrossRef]
- Li, J.Z.; Liu, S.J.; Dai, Y. Effect of grouser height on tractive performance of tracked mining vehicle. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2459–2466. [Google Scholar] [CrossRef]
- Shaikh, S.A.; Li, Y.M.; Zheng, M.; Chandio, F.A.; Ahmad, F.; Tunio, M.H.; Abbas, I. Effect of grouser height on the tractive performance of single grouser shoe under different soil moisture contents in clay loam terrain. Sustainability 2023, 13, 1156. [Google Scholar] [CrossRef]
- Xue, L.; Xie, B.F.; Lin, F.; Cheng, S.; Li, L.; Liu, M.H.; Li, J. Field traction performance test analysis of bionic paddy wheel and vaned wheel. Biomimetics 2022, 7, 185. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Pang, H.; Ji, Q.L.; Li, G.Y.; Dong, W.C.; Wen, L.G.; Li, J.Q. Structure design and traction trafficability analysis of multi-posture wheel-legs bionic walking wheels for sand terrain. J. Terramech. 2020, 91, 31–43. [Google Scholar] [CrossRef]
- Cai, Q.; Ma, W.B.; Rao, Q.H.; Li, G.X. Optimization design of bionic grousers for the crawled mineral collector based on the deep-sea sediment. Mar. Georesour. Geotechnol. 2020, 38, 48–56. [Google Scholar]
- Liang, C.; Ji, L.; Mousavi, H.; Sandu, C. Evaluation of tire traction performance on dry surface based on tire-road contact stress. In 30th SIAR International Congress of Automotive and Transport Engineering: Science and Management of Automotive and Transportation Engineering (SWAT); Universitatea Craiova: Craiova, Romania, 2020. [Google Scholar]
- Xu, F.; Rao, Q.H.; Ma, W.B. Track shoe structure optimization of deep-sea mining vehicle based on new rheological calculation formulae of sediment. Mech. Based Des. Struct. Mach. 2019, 47, 479–496. [Google Scholar] [CrossRef]
- Gan, L.J.; Huang, Q.Q.; Chen, S. Design and traction performance research on the ostrich-foot sandy track shoe. Mech. Sci. Technol. Aerosp. Eng. 2022, 41, 673–680. [Google Scholar]
- Zhang, R.; Li, G.Y.; Qiao, Y.; Jiang, L.; Li, J.Q. Analysis for effect of tire tread element of imitation reindeer plantar morphology on tire anti-skid performance. Trans. Chin. Soc. Agric. Eng. 2019, 35, 47–54. [Google Scholar]
- He, Y.H.; Han, D.L.; Li, G.Y.; Luo, G.; Zhang, R. Bionic design and performance analysis of adaptive low vibration walking wheel. Trans. Chin. Soc. Agric. Mach. 2018, 49, 418–426. [Google Scholar]
- Wang, G.L.; Mei, Y.; Zhou, H.C.; Liu, C.Z. Vibration reduction mechanism of cat claw pad and its bionic application in tire pattern. J. Vib. Shock 2022, 41, 128–136. [Google Scholar]
- Liu, C.Z.; Li, Y.Q.; Sun, Y.F.; Xie, M.Y.; Xu, C.W. Crown design of radial tire bio-inspired by cat paw pads. Mech. Sci. Technol. Aerosp. Eng. 2022, 41, 186–191. [Google Scholar]
- Li, Y.L.; Liu, C.Z.; Yuan, Y.; Li, Y.Q.; Sun, Y.F. Cat-paw pad bionic design of motorcycle tire crown. Mech. Sci. Technol. Aerosp. Eng. 2020, 39, 1505–1510. [Google Scholar]
- Han, D.L.; Zhang, R.; Yu, G.L.; Jiang, L.; Li, D.; Li, J.Q. Study on bio-inspired feet based on the cushioning and shock absorption characteristics of the ostrich foot. PLoS ONE 2020, 15, e0236324. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.W.; Liu, S.W.; Mei, T.; Wu, X.; Li, Y. Design and analysis of a bio-inspired tracked wall-climbing robot with spines. Robot 2019, 41, 526–533. [Google Scholar]
- Ma, S.S. Bionic Research in Surface of Traveling-Sand Wheel Based on Adhesion Property of Ostrich Planta; Jilin University: Changchun, China, 2017. [Google Scholar]
- Xu, P.; Ding, L.; Gao, H.B.; Zhou, R.Y.; Li, N. Environmental characterization and path planning for legged robots considering foot-terrain interaction. J. Mech. Eng. 2020, 56, 21–33. [Google Scholar]
- Liu, X.Y.; Kui, H.L.; Qian, Z.H.; Ren, L. Vertical ground reaction force characteristics of blue sheep based on different slopes walking. J. Zhejiang Univ. 2021, 55, 1668–1675, 1704. [Google Scholar]
- Liu, X.Y.; Kui, H.L.; Qian, Z.H.; Ren, L. Hoof pressure distribution pattern of blue sheep during walking on different slopes: A subject-specific analysis. Front. Vet. Sci. 2021, 8, 633509. [Google Scholar] [CrossRef]
- Li, G.Y.; Zhang, R.; Han, D.L.; Pang, H.; Yu, G.L.; Cao, Q.Q.; Wang, C.; Kong, L.X.; Wang, C.J.; Dong, W.C.; et al. Forelimb joints contribute to locomotor performance in reindeer (Rangifer tarandus) by maintaining stability and storing energy. PeerJ 2020, 8, e10278. [Google Scholar] [CrossRef]
- Rifkin, R.E.; Grzeskowiak, R.M.; Mulon, P.Y.; Adair, H.S.; Biris, A.S.; Dhar, M.; Anderson, D.E. Use of a pressure-sensing walkway system for biometric assessment of gait characteristics in goats. PLoS ONE 2019, 14, e0223771. [Google Scholar] [CrossRef]
- Fahie, M.A.; Cortez, J.C.; Ledesma, M.; Su, Y.H. Pressure mat analysis of walk and trot gait characteristics in 66 normal small, medium, large, and giant breed dogs. Front. Vet. Sci. 2018, 5, 256. [Google Scholar] [CrossRef] [PubMed]
- Pitti, L.; Oosterlinck, M.; Díaz-Bertrana, M.L.; Carrillo, J.M.; Rubio, M.; Sopena, J.; Santana, A.; Vilar, J.M. Assessment of static posturography and pedobarography for the detection of unilateral forelimb lameness in ponies. BMC Vet. Res. 2018, 14, 151. [Google Scholar] [CrossRef]
- Oosterlinck, M.; Dumoulin, M.; Van de Water, E.; Pille, F. Biomechanical aspects of farriery in horses. Vlaams Diergeneeskd. Tijdschr. 2017, 86, 256–265. [Google Scholar]
- Panagiotopoulou, O.; Pataky, T.C.; Day, M.; Hensman, M.C.; Hensman, S.; Hutchinson, J.R.; Clemente, C.J. Foot pressure distributions during walking in African elephants (Loxodonta Africana). R. Soc. Open Sci. 2016, 3, 160203. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q. Study on Anti-Slip and Buffer Characteristics of Goat Foot and Design of Bionic Foot; Jilin University: Changchun, China, 2019. [Google Scholar]
- Qian, Z.H.; Miao, H.B.; Shang, Z.; Ren, L.Q. Foot-ground contact analysis of German shepherd dog in walking, trotting and jumping gaits. J. Jilin Univ. 2014, 44, 1692–1697. [Google Scholar]
- Zhang, F.; Cui, X.H.; Wang, S.Q.; Sun, H.X.; Wang, J.J.; Wang, X.Y.; Fu, S.L.; Guo, Z.J. Analysis of kinematic characteristics of Saanen goat spine under multi-slope. Biomimetics 2022, 7, 181. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zhang, C.C.; Teng, S.; Cui, X.H.; Ali, S.; Wang, X.Y. Research on the adhesive performance of a biomimetic goat hoof track shoe pattern. Biomimetics 2022, 7, 80. [Google Scholar] [CrossRef]
- Zhang, F.; Teng, S.; Wang, Y.F.; Guo, Z.J.; Wang, J.J.; Xu, R.L. Design of bionic goat quadruped robot mechanism and walking gait planning. Int. J. Agric. Biol. Eng. 2020, 13, 32–39. [Google Scholar] [CrossRef]










| First Touchdown | Second Touchdown | |||||
|---|---|---|---|---|---|---|
| Touch the Ground | Touch the Ground Completely | Off the Ground | Touch the Ground | Touch the Ground Completely | Off the Ground | |
| HR |  |  |  | 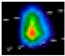 |  |  |
| FR |  |  |  |  |  | 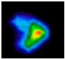 |
| HL | 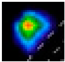 |  |  |  |  |  |
| FL |  | 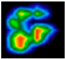 |  |  |  |  |
| Gait Sequence | FL | HL | FR | HR |
|---|---|---|---|---|
| ① | 0 | 1 | 1 | 1 |
| ② | 0 | 1 | 1 | 0 |
| ③ | 1 | 1 | 1 | 0 |
| ④ | 1 | 1 | 0 | 0 |
| ⑤ | 1 | 1 | 0 | 1 |
| ⑥ | 1 | 0 | 0 | 1 |
| ⑦ | 1 | 0 | 1 | 1 |
| ⑧ | 0 | 0 | 1 | 1 |
| ⑨ | 0 | 1 | 1 | 1 |
| 0°(N) | 5°(N) | 10°(N) | The Variation from 0° to 5° | The Variation from 5° to 10° | The Variation from 0° to 10° | |
|---|---|---|---|---|---|---|
| FL | 68.36 Inner sphere | 92.70 Outer sphere | 48.62 Outer sphere | +24.34 | −44.08 | −19.74 |
| FR | 115.23 Outer tip | 60.42 Outer tip | 146.20 Inner tip | −54.81 | +85.78 | +30.97 |
| HL | 131.67 Outer tip | 63.73 Outer tip | 139.99 Inner tip | −67.94 | +76.26 | +8.32 |
| HR | 62.51 Outer tip | 60.53 Inner sphere | 49.35 Inner sphere | −1.98 | −11.18 | −13.16 |
| 0°(N·s) | 5°(N·s) | 10°(N·s) | The Variation from 0° to 5° | The Variation from 5° to 10° | The Variation from 0° to 10° | |
|---|---|---|---|---|---|---|
| FL | 34.22 Inner sphere | 62.15 Outer sphere | 25.54 Outer sphere | +27.93 | −36.61 | −8.68 |
| FR | 71.17 Outer tip | 39.23 Outer tip | 127.67 Inner tip | −31.94 | +88.44 | +56.50 |
| HL | 91.17 Outer tip | 69.42 Outer tip | 89.06 Inner tip | −21.75 | +19.64 | −2.11 |
| HR | 32.24 Outer tip | 40.57 Inner sphere | 28.35 Inner sphere | +8.33 | −12.22 | −3.89 |
| Index | Force | Moving | Lowess | Loess | Sgolay | Rlowess | Rloess |
|---|---|---|---|---|---|---|---|
| SNR | 45.6737 | 47.7935 | 49.9087 | 48.6220 | 46.7867 | 48.6099 | |
| 34.8124 | 36.9723 | 39.6110 | 37.6773 | 33.3548 | 36.3560 | ||
| 52.2374 | 54.6334 | 57.6871 | 55.4155 | 47.6820 | 54.7717 | ||
| 55.0299 | 57.7477 | 61.5511 | 58.8012 | 52.0127 | 56.9574 | ||
| 57.7372 | 62.3959 | 67.0735 | 65.2911 | 49.4790 | 56.9990 | ||
| 61.0407 | 65.5280 | 70.1179 | 68.3453 | 53.7918 | 63.0567 | ||
| RMSE | 0.0196 | 0.0153 | 0.0120 | 0.0139 | 0.0172 | 0.0140 | |
| 0.0199 | 0.0155 | 0.0115 | 0.0143 | 0.0236 | 0.0167 | ||
| 0.0381 | 0.0289 | 0.0203 | 0.0264 | 0.0644 | 0.0285 | ||
| 0.0383 | 0.0280 | 0.0181 | 0.0248 | 0.0542 | 0.0307 | ||
| 0.1080 | 0.0632 | 0.0369 | 0.0453 | 0.2794 | 0.1176 | ||
| 0.1014 | 0.0605 | 0.0357 | 0.0437 | 0.2337 | 0.0804 | ||
| R2 | 0.9756 | 0.9850 | 0.9908 | 0.9876 | 0.9811 | 0.9876 | |
| 0.9879 | 0.9926 | 0.9960 | 0.9937 | 0.9831 | 0.9915 | ||
| 0.9914 | 0.9951 | 0.9976 | 0.9959 | 0.9755 | 0.9952 | ||
| 0.9952 | 0.9974 | 0.9989 | 0.9980 | 0.9903 | 0.9969 | ||
| 0.9970 | 0.9990 | 0.9996 | 0.9995 | 0.9798 | 0.9964 | ||
| 0.9984 | 0.9994 | 0.9998 | 0.9997 | 0.9917 | 0.9990 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Wang, X.; Cui, X.; Qiu, Y.; Teng, S.; Ali, S.; Fu, S. Analysis of Mechanical Properties of Functional Parts of Goat Hoofs under Multi-Slope. Agriculture 2024, 14, 451. https://doi.org/10.3390/agriculture14030451
Zhang F, Wang X, Cui X, Qiu Y, Teng S, Ali S, Fu S. Analysis of Mechanical Properties of Functional Parts of Goat Hoofs under Multi-Slope. Agriculture. 2024; 14(3):451. https://doi.org/10.3390/agriculture14030451
Chicago/Turabian StyleZhang, Fu, Xinyue Wang, Xiahua Cui, Yubo Qiu, Shuai Teng, Shaukat Ali, and Sanling Fu. 2024. "Analysis of Mechanical Properties of Functional Parts of Goat Hoofs under Multi-Slope" Agriculture 14, no. 3: 451. https://doi.org/10.3390/agriculture14030451
APA StyleZhang, F., Wang, X., Cui, X., Qiu, Y., Teng, S., Ali, S., & Fu, S. (2024). Analysis of Mechanical Properties of Functional Parts of Goat Hoofs under Multi-Slope. Agriculture, 14(3), 451. https://doi.org/10.3390/agriculture14030451






