Investigation of the Kinetic Dynamics in the Intermittent Microwave–Hot-Air Combined Drying of Peanut Pods

Abstract

The drying process is crucial for maintaining the quality of peanut pods and mitigating the risk of mold proliferation. The aim of this study was to investigate the kinetic characteristics of a synergistic intermittent microwave and a hot-air-drying technique, with an emphasis on enhancing efficiency and reducing energy consumption. A comprehensive analysis was performed on key parameters—including moisture content, moisture ratio, drying rate, and effective moisture diffusion coefficient—to elucidate moisture migration during the drying process. The findings indicated that higher microwave power significantly accelerates the drying rate while substantially shortening the drying time for peanut pods. The effective moisture diffusion coefficient was found to range from 0.987 × 10⁻⁹ to 1.227 × 10⁻⁹ m²/s, with the Verma model demonstrating superior accuracy in predicting drying behavior. The experiment achieved a minimum specific energy consumption of 12,535 kJ/kg and a maximum thermal efficiency of 18.1% at a microwave power density of 0.8 W/g combined with a temperature of 40 °C. However, the observed thermal efficiency was lower than that in previous studies, mainly due to the suboptimal regulation of experimental parameters. Future research should focus on optimizing these parameters and further exploring the impact of this drying method on energy consumption to achieve more efficient and sustainable peanut drying.

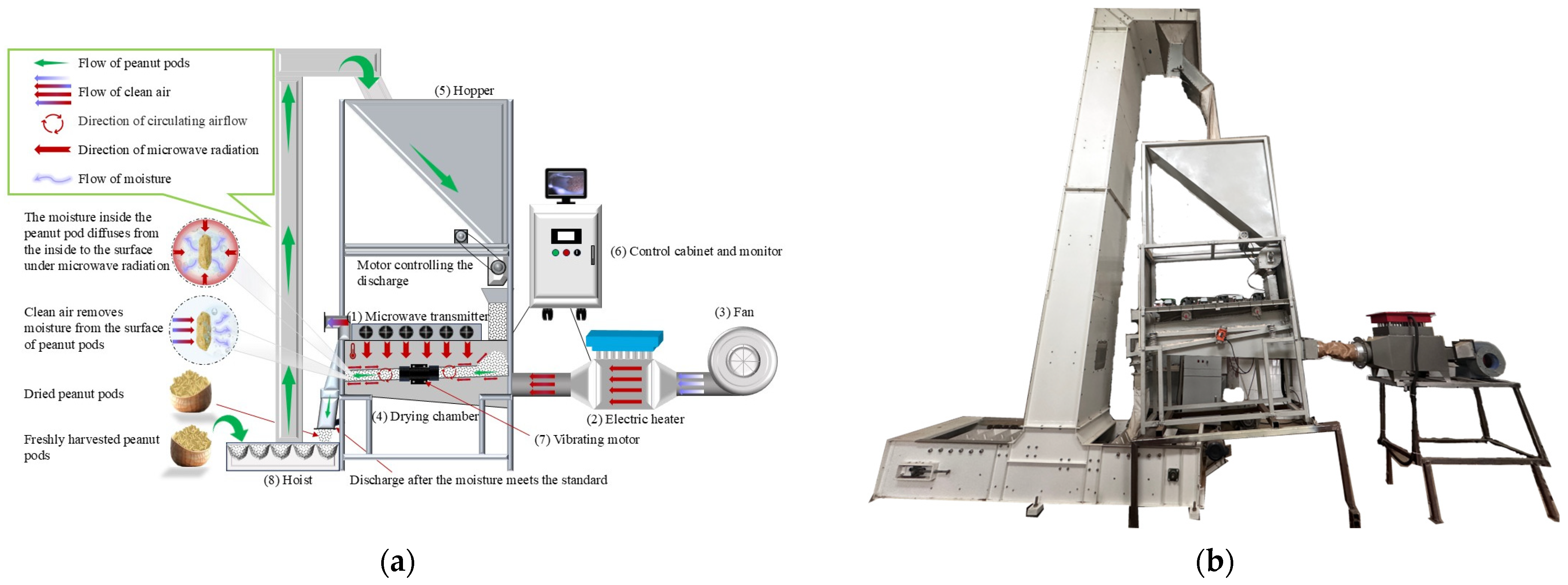
1. Introduction

Peanut (also known as groundnut) is a crucial cash crop recognized for its high nutritional value and diverse applications, with cultivation occurring in over 100 countries worldwide. According to data from the FAO and the National Bureau of Statistics of China, the area under peanut cultivation in China was approximately 4.68 million hectares in 2022, accounting for 15.32% of the global total. China also ranked first in peanut production, yielding around 18.33 million tons, which constituted approximately 33.79% of the total global output [1,2,3]. The economic value of peanuts is primarily derived from their substantial oil and protein content, which range from 16% to 36% for protein, and around 50% for fat, along with being rich in many nutrients, such as unsaturated fatty acids [4].

The moisture content of freshly harvested peanut pods is high (about 45% wet base moisture content), making it susceptible to some harmful microorganisms and deterioration [5]. Thus, drying peanut pods after harvest is essential; the effectiveness of this drying process significantly influences the quality, safety, and convenience of subsequent peanut processing and storage [6]. While traditional drying methods, such as natural drying and hot-air drying, are extensively used in many regions, they remain plagued by numerous challenges. These challenges, such as prolonged drying time, inefficient drying, uneven moisture distribution, and high energy consumption, severely compromise both the drying efficiency and economic benefits of peanuts [7,8]. As a result, the advancement of more efficient drying technologies has emerged as a key area for contemporary research.

In recent years, microwave drying technology has gained widespread attention due to its ability to significantly enhance drying efficiency and reduce drying time. Microwave drying works by directly applying microwave radiation to the material, causing rapid evaporation of moisture, thereby improving the drying process [9,10]. Compared with traditional drying methods, microwave drying allows the material to be heated more deeply and thoroughly and minimizes the thermal gradient [11,12]. However, relying solely on microwave drying can result in the surface overheating as well as uneven heating overall. By alternating between hot air and microwave drying, more uniform drying can be achieved in a shorter time, reducing uneven moisture distribution, and effectively lowering excessive energy consumption. Additionally, intermittent drying helps to stabilize temperature fluctuations during the drying process, thus preventing over-drying or quality degradation on the surface of the peanut pods. This ultimately improves the drying quality and enhances the economic benefits of the final product. In summary, the technique of intermittently introducing microwave energy during the hot-air-drying process combines the rapid heating capabilities of microwaves with the uniform drying characteristics of hot air, resulting in thorough material drying and a stabilized drying environment that reduces surface overheating and promotes uniform drying [13]. In previous studies, Ling et al. [14] identified the optimal process parameters for the intermittent microwave–hot-air drying of peanuts through a response surface optimization analysis. The optimal conditions were established as T = 45 °C, MW = 1.25 W/g, and an intermittent ratio of 1.10 [5]. Their findings demonstrated that this intermittent drying technique is highly efficient, ensuring both effective drying and the preservation of peanut quality, and indicate that this drying technology can effectively reduce costs while ensuring high quality in peanut production. Additionally, studies involving other materials, such as apple [15], taro [16], potato [17], oleifera seeds [18], papaya [19], jujube [20], and rice [21], have demonstrated that intermittent microwave–hot-air drying yields significant improvements in drying efficiency and can substantially shorten the drying time.

Although this drying technology offers significant theoretical advantages compared with traditional drying methods, such as the potential to improve energy efficiency, reduce drying time, and better preserve product quality, currently, this method has not been widely studied. Moreover, research specifically focusing on the drying kinetics of peanut pods is still scarce. Most existing studies have concentrated on only microwave or hot-air drying, with the performance of peanut pods under this combined drying process not having been fully validated. Furthermore, as an important agricultural product, peanut pods have unique drying characteristics. By contrast, this study not only analyzes the microwave–hot-air-drying process but investigates key factors in drying kinetics, such as the moisture diffusion coefficient, and conducts an energy analysis, including specific energy consumption and thermal efficiency. These analyses contribute to a deeper understanding of the drying process and provide theoretical support for optimizing drying conditions for peanut pods.

In this study, an intermittent microwave drying method was used to examine its effects on the drying kinetics of peanut pods, and single-factor tests were employed to compare the influences of microwave power and temperature on energy consumption and thermal efficiency. The goal of this research was to reveal the dynamic mechanisms of combined intermittent microwave and hot-air drying, to assess their potential, to optimize the technological parameters involved in the drying process, and to explore technologies appropriate for peanut pod drying. Furthermore, this work aspires to contribute to the advancement of drying technologies for agricultural products, to facilitate the modernization of agricultural post-harvest processing, to enhance the economic value of these products, and to minimize energy consumption, thereby offering valuable references for related domains.

2. Materials and Methods

2.1. Material Pretreatment

The experimental material comprised peanut pods (variety Zhanyou 75) sourced from Zhanjiang City, Guangdong Province. After undergoing a rigorous selection process to ensure uniform size and flawless appearance, the pods were packaged, sealed, and stored in a 4 °C temperature-controlled refrigerator for subsequent use. The initial moisture content was approximately 45% (wet basis), as determined using the standard oven method, which involved maintaining a temperature of 130 °C for over 8 h [22]. The quantity of material utilized in this experiment amounts to 6 kg.

2.2. Experimental Set-Up

The drying process in this study was carried out using a custom 5HWZL-type microwave–hot-air-drying platform, as depicted in Figure 1b. To achieve uniform drying throughout the procedure, the effective area of the drying bed was calculated, determining that approximately 6 kg of peanut pods were needed to fully occupy the bed. The microwave transmitter power range was set to between 0 and 7.2 kW.

The platform configuration, shown in Figure 1a, is composed of the following components: (1) a microwave transmitter, (2) an electric heater, (3) a fan, (4) a drying chamber, (5) a hopper, (6) a control cabinet and monitor, (7) a vibrating motor, and (8) a hoist. In addition to the drying platform, several instruments were utilized during the experiment, including an electronic scale, an electric blast drying oven, an anemometer, and a microwave detector. The accuracy and measurement ranges of these instruments are provided in

Table 1. The precision and measurement ranges of the instruments used in the experiments.

Instrument	Model	Range	Precision
Electronic scale	988 (Omar)	0.1~30 kg	±5/10 g
	JY5002 (Liang ping)	0~500 g	±0.01 g
	FA1004 (Hang ping)	0~100 g	±0.1 mg
Electric heating blast drying oven	DGF30/7-IA	0~300 °C	-
Anemometer	TSI 9545 (VelociCalc)	0~30 m/s	±0.015 m/s
Microwave Detector	825 (VICTOR)	0~9.99 mW/cm2	±1 dB
Fork-shaped digital meter	606B+ (VICTOR)	−20~1000 °C	-

.

2.3. Drying Procedure

Prior to the experiment, freshly harvested peanuts were removed from refrigeration and allowed to acclimate to room temperature. A batch-cycle single-factor experiment was then conducted, with each experimental group consisting of 6 kg of fresh peanuts. Samples were collected every 20 min throughout the experiment. Before the experiment began, three bags of peanuts were selected from the sample and placed in a sealed bag as representatives of the initial moisture content of this experiment, and 3–4 peanut capsules were taken from each bag. As seen in Figure 1b, 6 kg of peanut pods were first put into the material rack of the elevator, and then, the elevator lifted them into the hopper of the test stand, which was guided into the drying chamber by the control material valve. After the peanuts entered the drying chamber, the peanut pods were vibrated and evenly distributed into a thin layer (0.02 m) by the vibration motor, the operating parameters were adjusted according to the test design specifications, and the dryer was started for drying. The drying was stopped when the moisture content of the peanut pods reached 10% or lower.

The preliminary experiments showed that improper control of the microwave and temperature parameters would lead to a rapid increase in the peanuts’ internal and external temperatures. This sharp rise would then accelerate fat oxidation and nutrient degradation, negatively impacting the peanuts’ flavor and texture while also altering their color and reducing nutritional value. Moreover, elevated settings resulted in higher energy consumption and production costs. On the other hand, inadequate ventilation speeds could hinder efficient moisture removal. To maintain a controlled environment, the laboratory used an air conditioning system to ensure consistent experimental conditions, with the temperature set at T = 25 ± 1 °C and RH = 68 ± 1%.

For our experiments, we set microwave power levels at 0.4 W/g, 0.6 W/g, and 0.8 W/g, combined with temperatures of 40 °C and 45 °C, a fixed air velocity of 0.7 m/s (this air velocity is the apparent air velocity calculated based on an air flow rate of 1110 m³/h and a cross-sectional area of 0.4354 m²), and a microwave intermittent ratio of 0.3 (the intermittent microwave power usage ratio refers to the portion during each cycle where the microwave is on for 30% of the time and off for 70% of the time, with each cycle lasting ten minutes). Based on these combinations, we conducted intermittent microwave–hot-air drying experiments.

2.4. Drying Kinetics

2.4.1. Moisture Content Determination

In this study, for each drying condition, we randomly extracted 3–4 uniformly sized peanut pod samples from the fluidized bed at 20-min intervals during the drying process, repeating this procedure three times. The collected samples were then stored in sealed bags to ensure proper preservation. After completing the drying tests, the final moisture content was measured using an electrically heated blast drying oven.

Moisture content can be calculated using the following equation [5]:

$$Moisturecontent\left(\%w.b.\right)={\displaystyle \frac{m_t-m_c}{m_t}}\times 100\%$$

(1)

where m_t denotes the mass of the peanut pods desiccated at time t (kg) and mc represents the mass after drying (kg).

2.4.2. Drying Rate Determination

During the drying process, the moisture content changes over time. The formula for calculating the drying rate (DR) is as follows [23]:

$$DR={\displaystyle \frac{M_{t+dt}-M_t}{dt}}$$

(2)

M_t+dt and M_t indicate moisture content at t + dt and t, respectively, and dt is the time taken for the change to occur.

2.4.3. Moisture Ratio Determination

The moisture ratio (MR) can be expressed as follows [24]:

$$MR={\displaystyle \frac{\left(M_t-M_e\right)}{\left(M_i-M_e\right)}}$$

(3)

where M_e represents the equilibrium moisture content, M_t denotes the moisture content at time t, and M_i indicates the initial moisture content (wet basis).

When assessing the drying rate, the decline curve of the moisture ratio or moisture content functions as a clear and precise instrument. Nevertheless, the inherent fluctuations and instability of microwave energy during the drying process pose considerable challenges in ascertaining the equilibrium moisture content. Consequently, the expression for the moisture ratio can be streamlined into the following equation [24]:

$$MR={\displaystyle \frac{M_t}{M_i}}$$

(4)

2.4.4. Effective Moisture Diffusivity Evaluation

Moisture diffusivity characterizes the capacity for moisture removal through migration and diffusion during the drying process. Given that the length of a peanut pod is considerably greater than its thickness, mass transfer is assumed to occur unidirectionally. Fick’s second law of diffusion elucidates the behavior of moisture diffusion throughout the drying process, represented by the following equation. This law operates under the premise that moisture moves in a singular direction while maintaining a stable effective diffusion coefficient [25].

$${\displaystyle \frac{\partial M}{\partial t}}=D_{eff}{\displaystyle \frac{{\partial }^{2}M}{\partial x^2}}$$

(5)

The primary mechanism for moisture transport to surface evaporation is diffusion. In this experiment, the evaporation of moisture from peanut pods is modeled as transport through a finite cylinder. To assess the diffusion of moisture during the drying process, the MR can be calculated using a formula based on Fick’s law of diffusion [26,27]:

$$MR={\displaystyle \frac{8}{{\pi }^2}}{\displaystyle \sum _{n_1=0}^{\infty }\frac{1}{\left(2n+1\right)}}\exp \left[-{\displaystyle \frac{{\pi }^2{\left(2n_1+1\right)}^2}{4L^2}}{D}_{eff}t\right]{\displaystyle \sum _{n_{2=1}}^{\infty }\frac{4}{{\lambda }_{n_2}^2}}\exp \left(-{\displaystyle \frac{{\lambda }_{n_2}^2}{R^2}}{D}_{eff}t\right)$$

(6)

In this equation, D_eff signifies the moisture diffusion coefficient (measured in m²/s, while t represents the drying time (in seconds). R indicates the radius of the cylinder’s bottom surface (in meters), and L refers to the thickness of the material, calculated as the average of the two test groups, n₁ and n₂. Furthermore, λ_n2 corresponds to the root of Bessel’s function, where λ₁ is determined to be 2.4048 according to the relevant tabulated values.

For longer durations of drying, the aforementioned equation can be further reduced to the following expression [26]:

$$MR={\displaystyle \frac{32}{{\pi }^2{\lambda }_1^2}}\exp \left[-\left({\displaystyle \frac{{\lambda }_1^2}{R^2}}+{\displaystyle \frac{{\pi }^2}{4L^2}}\right)D_{eff}t\right]$$

(7)

Taking the logarithm of both sides of the equation and the first term, the following equation can be obtained [26]:

$$\ln MR=-\left({\displaystyle \frac{{\lambda }_1^2}{R^2}}+{\displaystyle \frac{{\pi }^2}{4L^2}}\right)D_{eff}t+\ln {\displaystyle \frac{32}{{\pi }^2{\lambda }_1^2}}$$

(8)

where MR refers to the moisture ratio and D_eff signifies the moisture diffusion coefficient. It is important to note that D_eff is linearly correlated with the drying time, where the slope K can be defined as follows [26]:

$$K=-\left({\displaystyle \frac{{\lambda }_1^2}{R^2}}+{\displaystyle \frac{{\pi }^2}{4L^2}}\right)D_{eff}$$

(9)

2.5. Drying Kinetic Models and Validation

Table 2. Several thin-layer drying kinetic models commonly used for drying peanut pods.

Model No.	Model Name	Model Formula	Ref.
1	Page	$MR=\exp (-k{t}^n)$	[29]
2	Lewis	$MR=\exp (-kt)$	[30]
3	Henderson	$MR=a\exp (-kt)$	[31]
4	Diffusion Approximation	$MR=a\exp (-kt)+(1-a)\exp (-kbt)$	[32]
5	Verma et al.	$MR=a\exp (-kt)+(1-a)\exp (-gt)$	[32]

Note: a, b, k, n, and g are the coefficients of the model equation.

summarizes the five most widely used drying kinetic models in thin-layer drying processes. To assess the fitting accuracy of these drying kinetic models, we employed three assessment metrics: the determination coefficient (R²), the residual sum of squares (SSE), and the root mean square error (RMSE). Generally, a coefficient of determination close to 1, along with a lower residual sum of squares and RMSE, indicates a better fit for the model. Through these calculations, we can quantitatively evaluate each model’s suitability for describing the drying process of peanut pods, calculated using the following equations [5,28]:

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^N{\left(M{R}_{pre,i}-M{R}_{\exp ,i}\right)}^2}}{{\displaystyle \sum _{i=1}^N{\left(\overline{M{R}_{\exp ,i}}-M{R}_{pre,i}\right)}^2}}}$$

(10)

$$SSE={\displaystyle \sum _{i=1}^N(M{R}_{\exp ,i}-M{R}_{pre,i}}{)}^2$$

(11)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{\left(M{R}_{\exp ,i}-M{R}_{pre,i}\right)}^2}}$$

(12)

where MR_exp,i refers to the moisture content measured in the experiments, MR_pre,i indicates the moisture content predicted by the model, and N represents the total count of experimental observations.

2.6. Energy Determination

2.6.1. Specific Energy Consumption

Specific energy consumption (SEC) is a critical metric that reflects the energy expenditure associated with the drying apparatus. It evaluates the energy efficiency of the system by calculating the ratio of total energy consumed throughout the drying process to the mass of the moisture evaporated from the sample. In this context, the energy consumption during drying is bifurcated into two segments: microwave and hot-air drying. According to the first law of thermodynamics, the equation for specific energy consumption can be expressed as follows [5,24]:

$$SEC={\displaystyle \frac{Q_t}{m_{evap}}}$$

(13)

$$Q_t=E_{a,in}+E_{mic}$$

(14)

$$m_{evap}={\displaystyle \frac{m_0\left(M_i-M_f\right)}{100-M_f}}$$

(15)

In this context, t denotes the drying time (in seconds), Q_t represents the heat energy consumed (in kilojoules), and m_evap refers to the mass of the moisture evaporated from the grain during the drying process (in kilograms).

Furthermore, the heat energy transfer rate (kJ/s) associated with the air entering and exiting the drying chamber can be articulated based on the ambient temperature as follows [5,33]:

$${\stackrel{·}{E}}_{a,in}=\stackrel{·}{m_{a,in}}\left(c_{da}+c_{vap}{\omega }_{a,in}\right)\left(T_{a,in}-T_0\right)$$

(16)

where $c_{da}$ denotes the specific heat capacity of dry air (kJ/(kg·K)); $c_{vap}$ represents the specific heat capacity of water vapor (kJ/(kg·K)); ${\omega }_{a,in}$ refers to the absolute humidity of the inlet air (kg/m³); $T_{a,in}$ represents the temperature of the hot air entering the system (K); and $T_0$ represents the ambient temperature (K).

The mass flow rate (kJ/s) of dry air can be formulated as follows [33,34]:

$$\stackrel{·}{m}={\rho }_{da}{v}_a{A}_{ven}$$

(17)

where ρ is the dry air density (kg/m³), v is the air velocity (m/s), and A is the air flow area (m²).

The electrical energy consumption of the magnetron can be quantified using the following expression [5,34]:

$$E_{mic}=P_{0}t$$

(18)

where P₀ represents the microwave power produced by the magnetron, measured in kilowatts (kW), and t is the duration, measured in minutes.

According to the manufacturer’s data, the magnetron achieves an efficiency of around 70% when converting electrical energy into microwave energy.

2.6.2. Heat Efficiency

Thermal efficiency (η) serves as a critical metric for evaluating energy efficiency, defined as the ratio of the heat energy utilized for water evaporation (Q_evap) to the total heat energy consumed by the system (Q_t, in kJ). The energy efficiency of the drying system is calculated using the following equation [35]:

$$\eta ={\displaystyle \frac{Q_{evap}}{Q_t}}\times 100\%$$

(19)

$$Q_{evap}=h_{fg}\times m_{evap}$$

(20)

where $h_{fg}$ is the latent heat during the vaporization of water (2260 kJ/kg).

2.7. Data Processing

Data organization for the experiments was carried out using Excel; MATLAB 2021a and Origin 2021 were utilized to model the drying curves mathematically and to generate corresponding graphs.

3. Results

3.1. Moisture Content

As depicted in Figure 2, the moisture content of the peanuts consistently declined over time during the drying process. During intermittent microwave–hot-air drying, the absence of a noticeable slow-drying phase during the microwave stage is likely due to the strong penetration capability of microwaves. These microwaves induce high-frequency molecular vibrations within the peanut pods, generating internal heat through friction, which expedites moisture evaporation. As the intensity of the intermittent microwaves rises, the drying time is substantially reduced. This reduction may be explained by the intensified microwave electric field, which allows more energy to be absorbed by the moisture and converted into heat. This process intensifies the movement of moisture, further accelerating its evaporation and diffusion. Additionally, hot air not only provides heat but removes surface moisture through convection, decreasing the retention time of moisture at the surface and promoting further migration and evaporation. Consequently, the temperature within the material rises more rapidly, resulting in higher steam pressure, faster moisture diffusion rates, and improved drying efficiency.

3.2. Drying Rate

During peanut drying via intermittent microwave–hot-air drying, the wet basis moisture content decreased from 45% (w.b.) to around 10% (w.b.). As demonstrated in Figure 3, increasing the intermittent microwave power density significantly accelerates the drying process. This is due to the intensified microwave energy, which accelerates moisture evaporation and improves the overall efficiency of mass and heat transfer. Additionally, increasing the temperature is crucial for sustaining a consistent evaporation rate during the low-moisture phase. However, the drying rate curve in Figure 3 shows that under different temperature conditions, temperature has little effect on the drying rate. The structure of the peanut pod also has a significant impact on the moisture removal rate, likely due to variations in the texture and surface area—factors that are critical in the mass and heat transfer processes. This structural influence results in a slower drying rate during the later stages of the process [36]. In this study, the drying time was found to be significantly shorter when using a higher microwave power, primarily due to the strong penetrating ability of microwave energy, which allows heat to penetrate more deeply, thereby enhancing the diffusion of moisture within the peanut pods [37].

3.3. Moisture Ratio

As shown in Figure 4, with increases in intermittent microwave power density and temperature, the moisture content in peanut pods decreased significantly, mainly due to the change in moisture gradient and relative humidity. Microwave heating increases the energy of water molecules, causing violent vibrations that generate heat inside the peanut, thus accelerating the outward migration of free water. This process increases the water gradient, which increases the driving force of outward diffusion, resulting in a large amount of free water loss. In addition, with the increase in drying temperature, the removal rate of free water is accelerated, which is conducive to its diffusion. At the same time, the high temperatures reduce the relative humidity of the surrounding air and increase the water vapor pressure difference between the inside and outside of the peanut pod. The synergistic effect of these factors promotes the migration of moisture from inside to outside the pod, intensifying the moisture gradient and accelerating the drying process [38,39].

3.4. Moisture Effective Diffusivity Evaluation

The moisture diffusion coefficient is a crucial parameter for assessing the rate of moisture movement within a material, remaining largely unaffected by specific drying techniques [40]. As shown in

Table 3. Effective diffusion coefficients of moisture for each variable.

Experiment No.	Drying Parameters	Coefficient of Determination (R2)	Slope of the Fitted Equation (K)	Deff (m2/s)
1	0.4 W/g, 40 °C	0.99532	−1.2061 × 10−4	0.822 × 10−9
2	0.4 W/g, 45 °C	0.99551	−1.214 × 10−4	0.828 × 10−9
3	0.6 W/g, 40 °C	0.99435	−1.321 × 10−4	0.901 × 10−9
4	0.6 W/g, 45 °C	0.99414	−1.448 × 10−4	0.987 × 10−9
5	0.8 W/g, 40 °C	0.9888	−1.554 × 10−4	1.059 × 10−9
6	0.8 W/g, 45 °C	0.99768	−1.801 × 10−4	1.227 × 10−9

, despite the higher R² values and better fit, the K values became more negative with the change in drying conditions, indicating that the drying rate and the moisture diffusion coefficient changed more rapidly as the microwave power and temperature increased. An increase in intermittent microwave power density significantly accelerates and homogenizes the heating process within the material. This enhancement notably raises the moisture gradient between the interior and surface, facilitating effective moisture diffusion from the inside to the outside. At a constant temperature of 40 °C, the moisture diffusion coefficient increases from 0.822 × 10⁻⁹ to 1.059 × 10⁻⁹ m²/s. Additionally, higher temperatures further amplify the temperature difference between the hot air and the peanut surface, generating a stronger driving force for moisture evaporation and diffusion, which increases the effective diffusion coefficient from 0.828 × 10⁻⁹ to 1.227 × 10⁻⁹ m²/s. Since evaporation primarily occurs at the surface, the migration of moisture from inside the pod to the surface typically lags behind the evaporation rate, resulting in deceleration of the drying rate during the later stages. Therefore, microwave heating effectively promotes the migration of moisture from inside the pod to the surface, enhancing the overall drying rate. Moreover, elevated temperatures further accelerate moisture removal from within the peanuts. The combination of microwave heating with hot-air drying not only increases the drying rate but optimizes moisture migration pathways, significantly improving the efficiency of the drying process. However, in-depth analyses and experimental verification of the mechanism of change in the moisture diffusion coefficient are lacking, especially for the microscopic mechanism of moisture migration.

3.5. Drying Model Fit and Validation

3.5.1. Fitting Results

The experimental data for peanut pods under various factors, along with the fitting results of five selected models (refer to Table 2) that describe the kinetics of thin-layer drying and the evaluation metrics R², RMSE, and SSE, are presented in

Table 4. Page fitting results under different drying conditions.

Model	Drying Parameters	Model Parameter		R2	RMSE	SSE
		k	n
Page	0.4 W/g, 40 °C	0.01617	0.85677	0.99739	0.01387	0.00231
	0.4 W/g, 45 °C	0.01755	0.84282	0.99865	0.0099	0.00118
	0.6 W/g, 40 °C	0.01957	0.83891	0.99876	0.00968	0.00103
	0.6 W/g, 45 °C	0.01608	0.88355	0.99741	0.01435	0.00206
	0.8 W/g, 40 °C	0.02098	0.85684	0.9983	0.01191	0.00128
	0.8 W/g, 45 °C	0.01438	0.94852	0.99905	0.00935	0.00069

,

Table 5. Lewis fitting results under different drying conditions.

Model	Drying Parameters	Model Parameter	R2	RMSE	SSE
		k
Lewis	0.4 W/g, 40 °C	0.00806	0.98803	0.02853	0.01058
	0.4 W/g, 45 °C	0.00819	0.98724	0.02928	0.01114
	0.6 W/g, 40 °C	0.00909	0.98704	0.03001	0.0108
	0.6 W/g, 45 °C	0.00929	0.99178	0.02438	0.00654
	0.8 W/g, 40 °C	0.0109	0.98989	0.02754	0.00759
	0.8 W/g, 45 °C	0.01141	0.99812	0.01239	0.00138

,

Table 6. Henderson fitting results under different drying conditions.

Model	Drying Parameters	Model Parameter		R2	RMSE	SSE
		a	k
Henderson	0.4 W/g, 40 °C	0.96092	0.00769	0.99137	0.02521	0.00763
	0.4 W/g, 45 °C	0.95356	0.00774	0.99199	0.02414	0.00699
	0.6 W/g, 40 °C	0.95595	0.00862	0.99122	0.0258	0.00732
	0.6 W/g, 45 °C	0.96984	0.00896	0.99379	0.02222	0.00494
	0.8 W/g, 40 °C	0.96834	0.0105	0.99202	0.02579	0.00599
	0.8 W/g, 45 °C	0.99103	0.0113	0.99826	0.01265	0.00128

,

Table 7. Diffusion Approximation fitting results under different drying conditions.

Model	Drying Parameters	Model Parameter			R2	RMSE	SSE
		a	k	b
Diffusion Approximation	0.4 W/g, 40 °C	0.19795	0.0296	0.21754	0.99624	0.01664	0.00332
	0.4 W/g, 45 °C	0.18229	0.03543	0.18554	0.99541	0.01827	0.00401
	0.6 W/g, 40 °C	0.23809	0.03052	0.22748	0.99672	0.01577	0.00274
	0.6 W/g, 45 °C	0.14554	0.03802	0.20774	0.99705	0.01532	0.00235
	0.8 W/g, 40 °C	0.70536	0.01669	0.24626	0.99631	0.01754	0.00277
	0.8 W/g, 45 °C	0.84568	0.01361	0.31057	0.99863	0.01122	0.00101

and

Table 8. Verma fitting results under different drying conditions.

Model	Drying Parameters	Model Parameter			R2	RMSE	SSE
		a	k	g
Verma et al.	0.4 W/g, 40 °C	0.19793	0.0296	0.00644	0.99807	0.01246	0.00171
	0.4 W/g, 45 °C	0.18224	0.03564	0.00661	0.99906	0.00866	0.00082
	0.6 W/g, 40 °C	0.23799	0.03053	0.00694	0.9992	0.00814	0.00066
	0.6 W/g, 45 °C	0.14548	0.03803	0.0079	0.99783	0.01386	0.00173
	0.8 W/g, 40 °C	0.70521	0.01669	0.00411	0.9997	0.00533	0.00023
	0.8 W/g, 45 °C	0.84517	0.01361	0.00424	0.99945	0.00763	0.00041

.

Table 4, Table 5, Table 6, Table 7 and Table 8 present the key metrics used to evaluate the model fit, assessing the performance of five models in describing the dynamics of the thin-layer drying of peanut pods. The primary evaluation criteria include the coefficient of determination (R²), root mean square error (RMSE), and sum of squared errors (SSE) [5]. The fitting results vary across different drying conditions, with the following observations: The Page model (Table 4) shows a slight fitting bias under high-temperature conditions (e.g., 45 °C). Although the R² values are high (up to 0.99905), the RMSE and SSE values increase slightly under certain drying conditions, particularly at low microwave power (0.4 W/g). This suggests that the Page model may not fully capture the complex variations in the drying process. The Lewis model (Table 5) performs well under low power (0.4 W/g) and low temperature (40 °C), exhibiting high R² values (ranging from 0.98803 to 0.99812). However, as temperature and power increase, the fitting quality declines, with corresponding increases in RMSE and SSE values. This indicates that the Lewis model is less suitable for high-power and high-temperature drying conditions and struggles to accommodate the nonlinear nature of moisture migration during drying. The Henderson model (Table 6) demonstrates a strong fitting performance under high-power conditions (0.8 W/g, 45 °C), with an R² value of 0.99826 and low RMSE and SSE values, particularly at 45 °C. However, under low-power and low-temperature conditions, the model’s performance decreases, suggesting that it has limited adaptability to varying drying conditions. The Diffusion Approximation model (Table 7) consistently achieves R² values above 0.995 across different drying conditions, yet its RMSE and SSE values are higher compared to the other models, especially at low temperatures (40 °C) and low microwave power (0.4 W/g). This suggests that while the Diffusion Approximation model is effective at describing the diffusion process of moisture, it does not fully capture the nonlinear characteristics of the drying process.

By contrast, the Verma model (Table 8) delivers the best fitting results across all experimental conditions. The R² values for this model are consistently close to 1, and both the RMSE and SSE values are low, particularly at 0.8 W/g microwave power and 45 °C (R² = 0.99945, RMSE = 0.00763, SSE = 0.00041). These results demonstrate that the Verma model accurately captures the moisture diffusion dynamics during the drying of peanut pods. Furthermore, the residuals are evenly distributed and conform to a normal distribution, reinforcing the model’s ability to accurately represent the dynamics of the intermittent microwave–hot-air-drying process. Therefore, the Verma model shows great potential for optimizing the drying process of peanut pods, particularly in applications involving microwave–hot air intermittent drying technology.

3.5.2. Model Validation

To assess the model’s ability to accurately represent the changes in the moisture ratios of peanuts during intermittent microwave and hot-air drying, we plotted the predicted and measured moisture ratios under various conditions in a scatter plot, which can be used to intuitively explain the relationship between the predicted value and the measured value, with the measured moisture ratio on the horizontal axis and the predicted moisture ratio on the vertical axis (Figure 5). A close relationship can be seen between the model predictions and actual measurements, with data points evenly distributed around the line y = x, confirming the accuracy of the model proposed by Verma et al. in the context of intermittent microwave–hot-air drying. These graphs provide a visual validation of the model, offering an intuitive and quantitative basis for assessing its predictive performance.

3.6. Specific Energy Consumption

As shown in Figure 6, the specific energy consumption (SEC) and average drying rate of peanut pods during microwave–hot-air drying are significantly influenced by various drying parameters. As seen in the figure, as intermittent microwave power increases, the SEC gradually decreases, while the average drying rate first increases and then decreases with increasing microwave power. This trend highlights the complex interplay between drying power and drying efficiency.

The SEC ranges from 12,535 to 17,466.2 kJ/kg, with lower values associated with higher microwave power. The increase in microwave power accelerates the rise in the internal temperature of the peanut pods, which in turn promotes moisture diffusion and evaporation. Specifically, microwave heating amplifies the internal temperature gradient, creating a stronger driving force for moisture migration from the interior to the exterior of the material. This enhances moisture diffusion, while the increased moisture concentration gradient further accelerates evaporation, leading to higher drying rates. Additionally, the elevated partial pressure of moisture vapor within the material facilitates the evaporation process, reducing the drying time and consequently lowering the SEC. However, while increasing the temperature boosts evaporation rates, it can also aggravate the temperature difference between the hot air and the peanut pod. This increased temperature difference may reduce the heat transfer efficiency. Excessively high temperatures can lead to rapid evaporation of surface moisture, creating a vapor barrier that hinders heat transfer into the material. As a result, the drying process slows down, and more energy is required to overcome this barrier, which in turn increases the SEC. Thus, balancing microwave power and temperature is crucial for optimizing drying efficiency and minimizing energy consumption. These findings emphasize that controlling both parameters effectively is essential for achieving an optimal drying process that conserves energy while maintaining high drying rates.

3.7. Thermal Efficiency

As presented in

Table 9. Thermal efficiency across various drying conditions.

No	Microwave Power Density (W/g)	Temperature (°C)	Thermal Efficiency (%)
1	0.4	40	15.5%
2	0.6	40	15.9%
3	0.8	40	18.1%
4	0.4	45	12.9%
5	0.6	45	13.5%
6	0.8	45	15.9%

, the thermal efficiency of peanut pods progressively improves with increasing intermittent microwave power density, with the highest being 18.1%. This enhancement is attributed to the capability of microwaves to penetrate the material uniformly and deeply, which boosts the heating and evaporation processes of moisture, thereby improving energy utilization efficiency. Additionally, the rising moisture gradient promotes effective diffusion, while increased moisture vapor partial pressure facilitates vapor escape; the interplay of these factors further enhances the drying rate. Nonetheless, although higher temperatures can accelerate surface moisture evaporation, excessively high temperatures may compromise thermal efficiency. Specifically, excessive heat input can lead to energy waste and, in the latter stages of drying, when the internal moisture content is reduced, elevated temperatures can cause densification of the peanut shell’s internal structure. This densification impedes moisture migration, slows the drying rate, and increases energy consumption, ultimately leading to reduced thermal efficiency. Therefore, optimizing the drying process and improving energy efficiency require careful regulation of microwave power density and temperature to achieve optimal energy utilization and drying performance.

4. Discussion

This study involved a comprehensive investigation into the dynamic characteristics of peanut drying using intermittent microwave–hot-air drying. By analyzing the key parameters that influence moisture content, drying rate, moisture diffusion coefficient, and energy consumption in peanut pods, we found that both the microwave power density and temperature significantly affect the drying behavior of peanut pods. These findings offer valuable theoretical insights for optimizing the drying process.

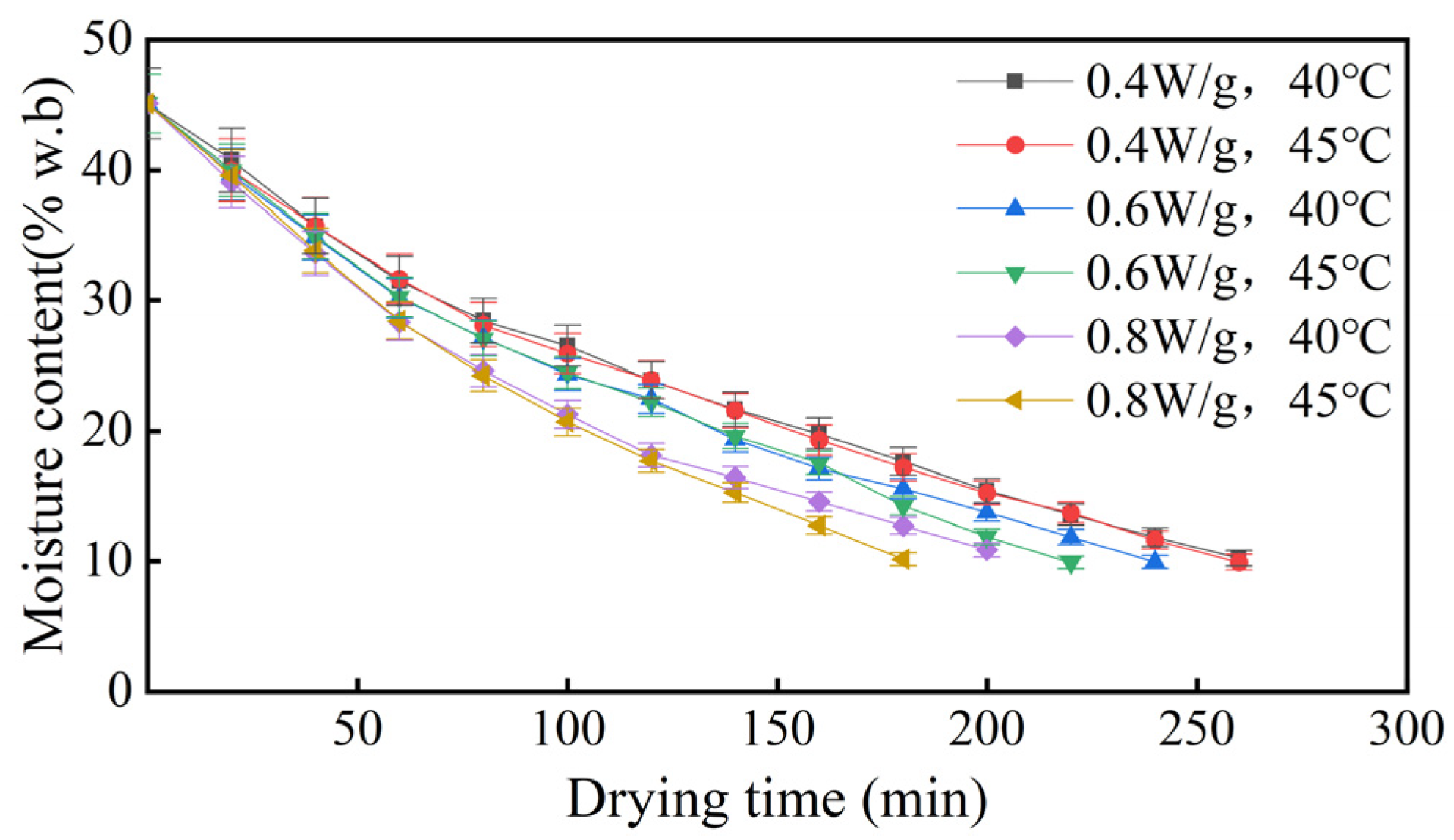
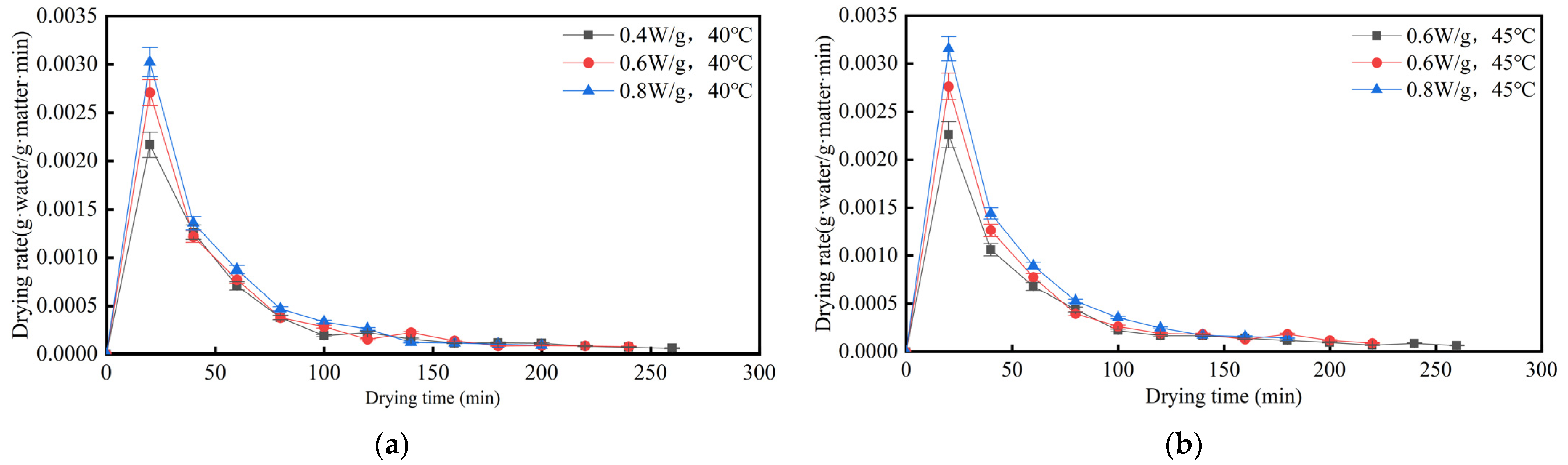
Firstly, the increase in microwave power density and temperature enhances the migration and evaporation of moisture within peanut pods by elevating the internal temperature and pressure [41,42]. This acceleration promotes the evaporation of surface moisture, increases the moisture gradient, and may alter the microstructure of the peanut pod, thereby reducing its moisture content [43,44]. Similar findings have been reported by other researchers [14,45]. During the early stages of drying, peanut pods hold a considerable amount of moisture. With increasing microwave power and temperature, the thermal movement of the internal moisture accelerates, which raises the evaporation rate and accelerates the drying rate [46]. Nonetheless, over time, the amount of free moisture diminishes, leading to a decrease in the rate of moisture diffusion. At this point, evaporation demands additional energy to disrupt the bound moisture and the moisture adsorbed within the material [5]. This shift results in the moisture content reaching equilibrium quicker, ultimately slowing both the drying rate and the moisture ratio [47]. The effective moisture diffusivity ranges from 0.987 × 10⁻⁹ to 1.227 × 10⁻⁹ m²/s, which aligns with previous studies and confirms the efficacy of the intermittent microwave–hot-air-drying method [5,47,48,49]. The Verma model demonstrated the best fit in this study, indicating its effectiveness in describing moisture migration in peanut pods, consistent with evaluations of this model in the drying processes of peanuts and other foods found in the literature.

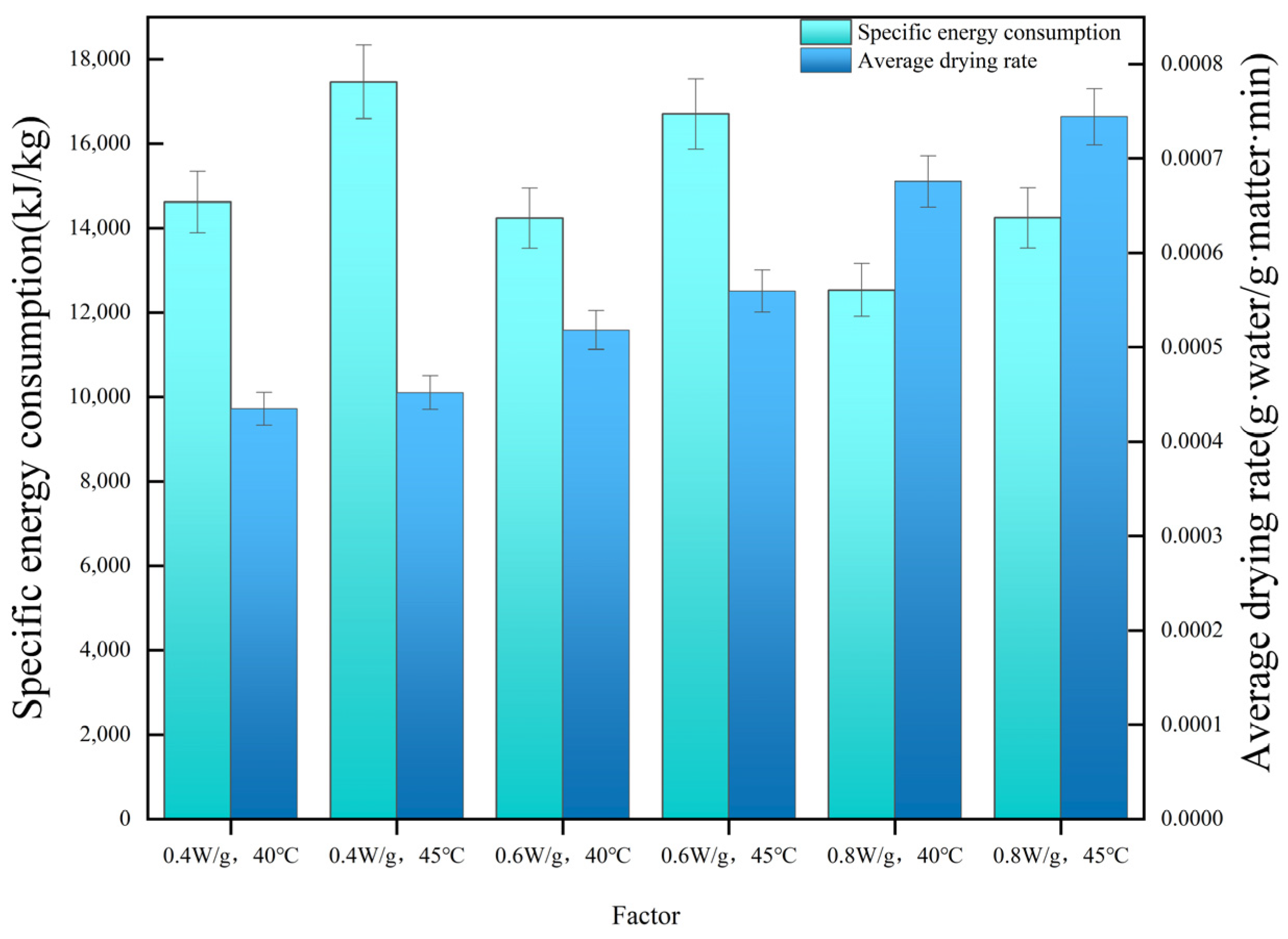
Secondly, in the thermodynamic assessment, the lowest specific energy consumption (12,535 kJ/kg) and the highest thermal efficiency (18.1%) were recorded at a microwave power density of 0.8 W/g and a temperature of 40 °C. This finding demonstrates that careful control of drying parameters can significantly improve energy utilization efficiency. Nonetheless, the lower thermal efficiency observed in this study, compared with the thermal efficiency in other studies, may indicate that the experimental conditions were not optimal, underscoring the importance of fine-tuning drying parameters in future investigations.

In summary, this study identifies several limitations in the investigation of peanut-drying kinetics using a combination of intermittent microwave and hot-air drying. The selected test parameters did not encompass all potential drying conditions, which limits a comprehensive understanding of the underlying drying mechanisms. Additionally, factors such as peanut variety, size, and initial moisture content were not considered, yet these can significantly influence drying efficacy in practical applications. Future research should aim to broaden the range of parameters studied and account for the diversity of peanut varieties. Moreover, the thermal efficiency observed in this study is lower compared with that in other studies, suggesting that the amount of energy consumed during drying needs to be improved. Future investigations should explore advanced drying technologies and methods, including intelligent control systems and multi-stage drying strategies, to further reduce energy consumption and enhance drying quality. Research into thermal energy recovery and reuse during the peanut-drying process could also contribute to improved energy efficiency and reduced production costs, ultimately leading to a more efficient and sustainable drying process.

5. Conclusions

In this study, a specifically designed batch microwave–hot-air-drying system was utilized to explore the drying kinetics of peanuts. We conducted a comprehensive analysis of key parameters, including moisture content, drying rate, moisture effective diffusion coefficient, thermal efficiency, and specific energy consumption. The experimental results demonstrated that the effective moisture diffusion coefficient ranged from 0.987 × 10⁻⁹ to 1.227 × 10⁻⁹ m²/s. We found that the Verma model yielded the best fitting results, with an R² of 0.9997, signifying its effectiveness in accurately modeling the drying process of peanuts. With regard to energy consumption, setting the microwave power at 0.8 W/g and maintaining a temperature of 40 °C resulted in a minimal unit energy consumption of 12,535 kJ/kg, while achieving a thermal efficiency of 18.1%. Nonetheless, the relatively low thermal efficiency is attributed to suboptimal experimental parameter configurations. Therefore, future research should focus on further optimizing drying parameters to enhance thermal efficiency and minimize energy consumption, thereby increasing the feasibility and economic advantages of this drying technology.