Next Article in Journal
Long-Term Simulated Direct N2O Emissions from German Oilseed Rape Cultivation below the IPCC Emission Factor
Previous Article in Journal
Dam Age Differentially Affects Immune Response of Her Calf to Bovine Respiratory Disease Vaccination
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agriculture
Volume 14
Issue 1
10.3390/agriculture14010069
agriculture-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study on the Relationship between Crack Initiation and Crack Bifurcation in Walnut Shells Based on Energy

by
Xiaolan Man
1,
Long Li
1,
Hong Zhang
1,2,3,*,
Haipeng Lan
1,2,3,
Xiuwen Fan
1,2,3,
Yurong Tang
1,2,3 and
Yongcheng Zhang
1,2,3
1
College of Mechanical Electrification Engineering, Tarim University, Alaer 843300, China
2
Key Laboratory of Modern Agricultural Engineering, Tarim University, Alaer 843300, China
3
Key Laboratory of Tarim Oasis Agriculture, Tarim University, Ministry of Education, Alaer 843300, China
*
Author to whom correspondence should be addressed.
Agriculture 2024, 14(1), 69; https://doi.org/10.3390/agriculture14010069
Submission received: 5 December 2023 / Revised: 23 December 2023 / Accepted: 27 December 2023 / Published: 29 December 2023
(This article belongs to the Section Agricultural Product Quality and Safety)
Browse Figures
Versions Notes

Abstract

:
Clarifying the dissipated energy required for crack expansion is an effective way to control material crushing. Therefore, based on the material fracture probability model and fractal theory, the energy range required for crack extension was determined, and the morphology of the cracks was quantified. This study investigates the influence of walnut size on crack propagation characteristics; this includes its effects on the crack initiation threshold energy, representing resistance to crack initiation, and the crack bifurcation threshold energy, representing resistance to crack bifurcation. The results show that crack extension has a well-defined threshold energy below which cracks do not initiate or bifurcate. The size of walnuts significantly impacts crack propagation characteristics, showing that both crack initiation threshold energy and crack bifurcation threshold energy decrease with increasing walnut sizes. In addition, there is a positive correlation function between the crack initiation threshold energy and the crack bifurcation threshold energy. The experimental results can offer fresh insights into material fracture prediction and serve as a reference for numerical simulations.

1. Introduction

Walnuts are mainly composed of two parts, the shell and the kernel, and they are attracting increasing attention due to their multiple health benefits and wide range of applications in food and medicine [1,2]. However, walnut kernels, which are even more important to people, contain a lot of nutrients and are usually encased in a hard and thick shell [3]. Therefore, shell-breaking is an important process in the primary processing of walnuts to obtain high-quality kernels and their by-products [4]. Unfortunately, the quality of walnut shell breaking and processing can be reduced due to the uncontrolled crushing of walnut shells, including over- and under-crushing. Therefore, there is an urgent need for new walnut shell-breaking methods in order to specifically control shell cracking and improve shell-breaking performance, which requires a good understanding of the walnut shell-crushing mechanism.
Understanding fracture characteristics, including fracture threshold energy and fracture force, is important for understanding and accurately determining the crushing process of walnuts. Among them, fracture threshold energy refers to the ability of the material to resist the occurrence of fracture, and crack initiation energy is a key parameter for determining whether a walnut is crushed or not. In order to control the crushing state of walnuts and improve crushing quality, many studies have investigated the fracture threshold energy of walnuts at the particle scale via single-particle uniaxial load tests. For example, Sharifan et al., Koyuncu et al., and Man et al. [5,6,7] clarified the fracture threshold energy of walnuts and its influencing factors under the assumption that walnuts are not damaged. However, walnuts are inevitably subject to minor collisions during transportation, sorting, and other processes, causing damage to the walnuts. The presence of damage was suspected to influence the fracture threshold energy and the evolutionary behavior of cracks in walnuts, which may influence the crushing effect. Therefore, the fracture threshold energies determined based on the assumption that damage does not exist usually do not provide accurate information about determining walnut breakage. Thus, it is necessary to systematically study the fracture threshold energy, which considers the damage to walnuts. Rumpf et al. [8] developed a model to determine the fracture threshold energy based on the Monte Carlo method under the consideration of damage. However, the model has difficulty in obtaining the relevant parameters due to the large number of parameters. Vogel et al. (2005), Lecoq et al. (1999) [9,10] made a number of simplifications to the model and developed a dimensionless fracture probability model to successfully obtain the granite fracture threshold energy. However, whether the model can be applied with the determination of the fracture threshold energy of walnuts and the analysis of the fracture threshold energy of walnuts considering the damage scenario has not been reported.
In walnut shell-breaking processing, more bifurcations are often required to achieve crushing than compared to a single crack. However, existing studies have focused more on the rate, morphology, and number of walnut crack extensions. For example, Li et al. [11] quantitatively characterized the irregularity of walnut bifurcation based on fractal theory. The rate of walnut crack expansion and the number of bifurcations were analyzed via numerical simulations carried out by Hang et al. [12]. In fact, one would prefer that the loading energy required for crack bifurcation be known in advance in order to better control fragmentation [13,14,15,16]. Mecholsky et al. [17] proposed a method for determining the threshold energy for crack bifurcation based on fractal theory. The method was successfully applied to determine the energy of walnut crack bifurcations by Li et al. [11]. However, it is well known that the process of crushing walnuts inevitably begins with the cracking of the material, followed by the bifurcation of cracks. Apparently, crack bifurcation in walnuts is controlled by their cracking. However, previous studies on the threshold energy of walnut crack bifurcation were performed while ignoring the effects of cracking, which usually does not provide comprehensive information about the walnut-crushing process. Therefore, the determination of cracking and bifurcation threshold energies is very important to fully understand and accurately capture the walnut-crushing process. Nevertheless, until now, limited documented information is available on the effect of walnut cracking on crack bifurcation; in particular, the relationship between crack-opening energy and crack bifurcation energy has not been clarified.
In order to further analyze the mechanism of crack extension, an attempt is made to explain the process of crack initiation and crack bifurcation from the point of view of energy. In Section 2, a comprehensive description is provided regarding the drop hammer impact experiment, along with the quantification of crack bifurcation coefficients using fractal dimension. In Section 3, the effect of the walnut’s size on crack initiation energy and crack bifurcation threshold energy was discussed. Finally, the relationship between crack initiation energy and crack bifurcation threshold energy was established. This study provides (i) an improved understanding of the crushing mechanisms of walnuts under impact loading conditions and (ii) a theoretical reference for the optimization of operating conditions.

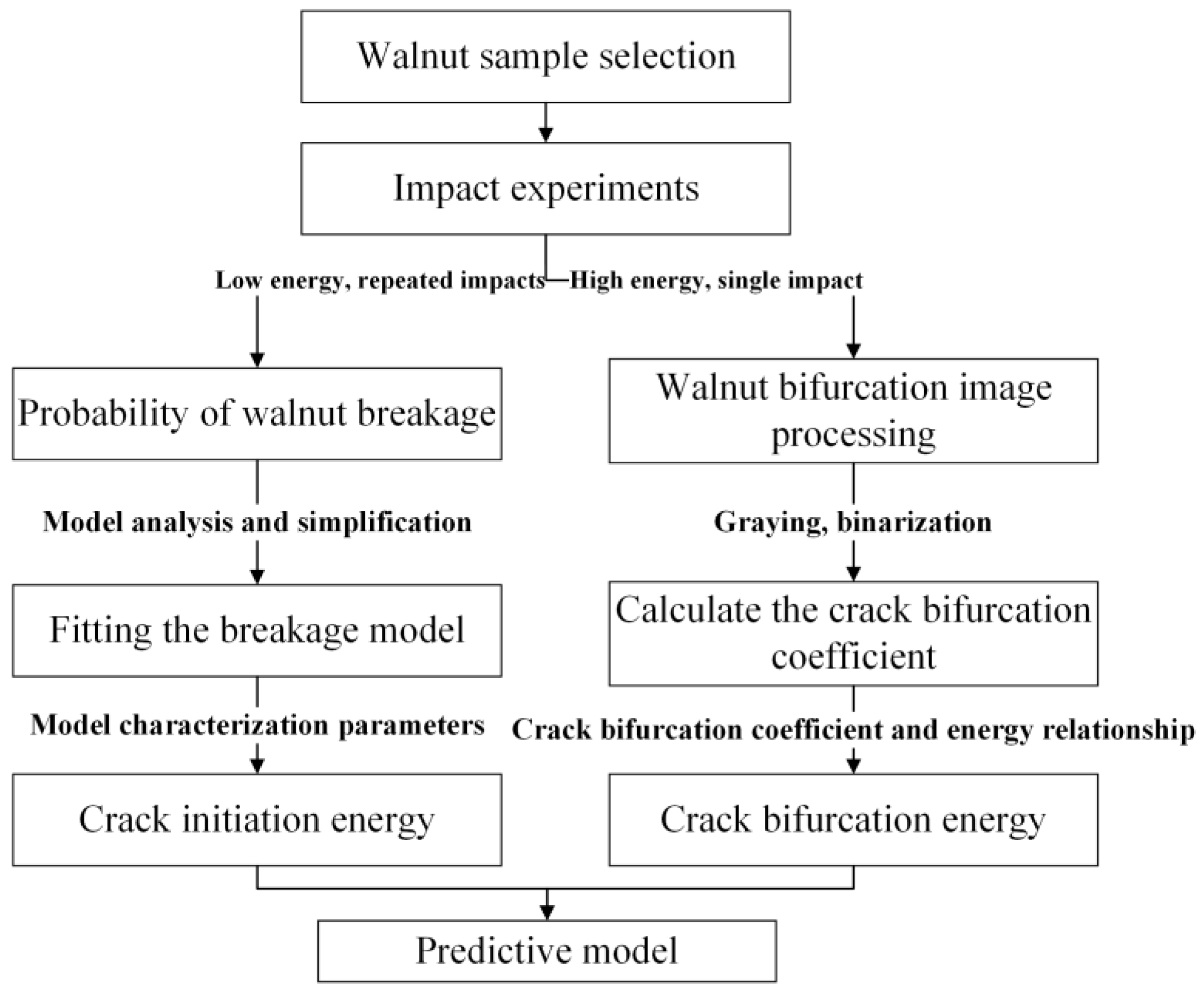
2. Materials and Methods

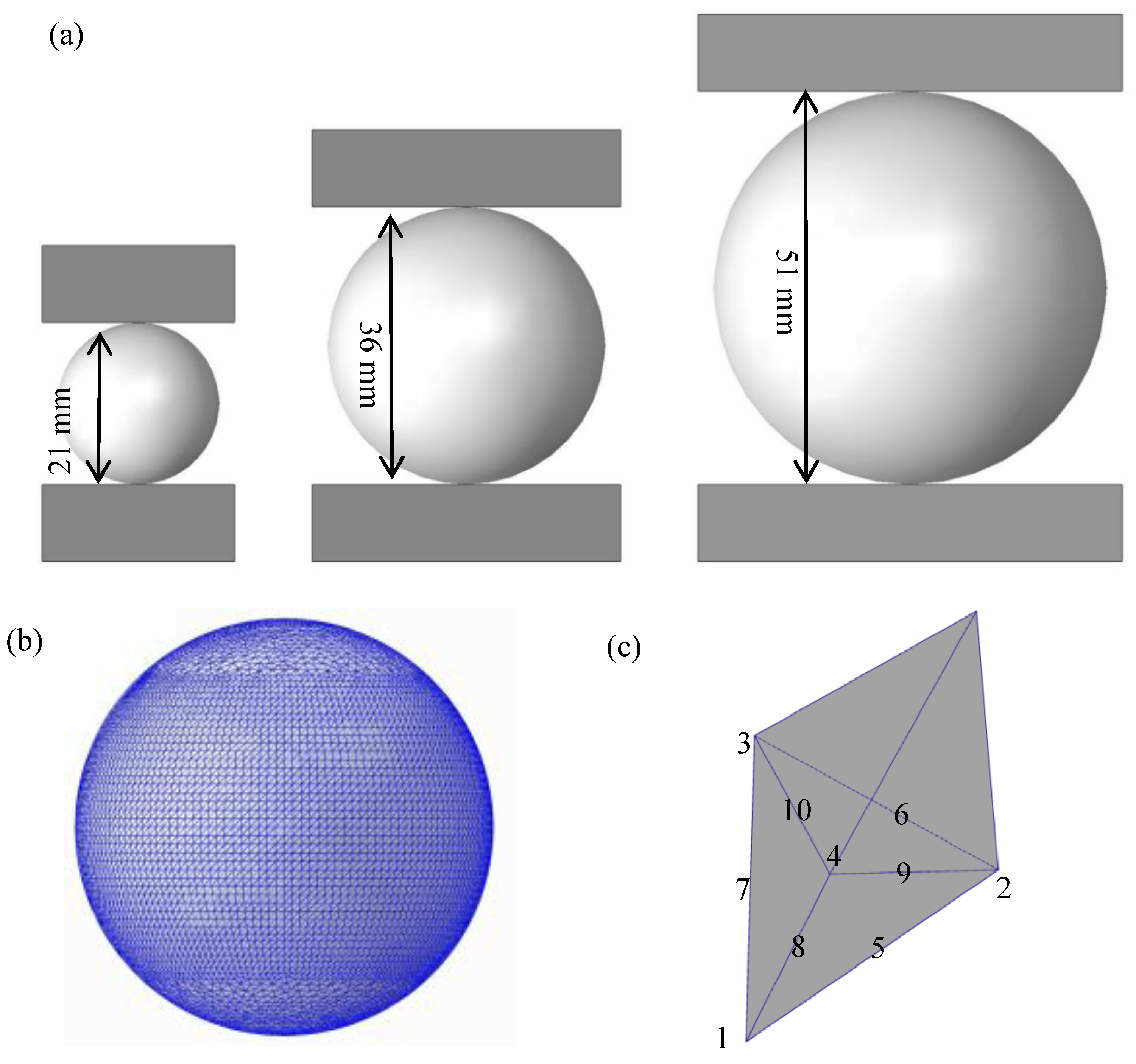
2.1. Preparation of the Walnut Samples

Taking walnuts as an example here, the crack expansion mechanisms of nut material subjected to impact are initially explored. ‘Wen 185’, which is a typical cultivar in local markets, was selected and used as the experimental sample. During the 2022 harvest season, freshly harvested walnuts (Juglans regia L.) were gathered from the Wensu Walnut Experimental Station, which is situated in Xinjiang, China, at coordinates 41°27′67″ N latitude, 80°24′17″ E longitude, and an altitude of 1056 m, as depicted in Figure 1. Similarly to other cultivars [18,19], these walnut constituents encompass both the kernel and thinner shell, and they are delineated by a convex suture line, dividing it into halves (as indicated by the red dotted line in Figure 1). However, considering the intricate shape of the kernel and the unique gap between the shell and kernel, this study primarily concentrates on analyzing the shell’s failure for the sake of simplicity (i.e., crack initiation and crack bifurcation). The moisture content of walnut samples was measured by drying them with the help of an air-ventilated oven (DGH-9053A type, Yiheng, Shanghai, China). After hot air drying, the walnuts had a moisture content of 9 to 10.5 percent (wet basis). At this moisture level, the walnuts exhibited good elastic mechanical properties, similarly to brittle materials. Table 1 presents a summary of the remaining physical parameters pertaining to the walnut.
Typically, theoretical and simulated research [20,21] simplifies walnuts into a spherical shape. Therefore, following the methodology in [18], the equivalent spheroid diameter was derived by measuring dimensional parameters (length, width, and thickness, as illustrated in Figure 1) for two hundred walnuts. Notably, the distribution of the equivalent spheroid diameter exhibits a notable adherence to the normal distribution, spanning sizes ranging from 30 to 44 mm, as depicted in Figure 2. A size range of 30–44 mm was chosen and subsequently subdivided evenly into 8 groups with a 2 mm interval. This categorization aimed to elucidate the impact of walnut size on its crack characteristics. Precisely, the 37 mm size represents an average within the 36–38 mm range. In accordance with our prior research [21], the walnut samples were placed in sealed bottles before each experiment and stored in a climate-controlled room at 60% relative humidity and 21 °C to sustain consistent moisture content. It is important to highlight that particular conditions, such as maintaining identical walnut sizes and moisture content, were upheld to ensure reproducibility with respect to results. Additionally, in order to clearly represent the entire process of the experiment, a flowchart of the walnut impact experiment and the related energy determination was drawn, as shown in Figure 3.

2.2. Calculation of Fractal Dimension

Fractal geometry provides a method for quantitatively describing complex and disordered systems with some intrinsic regularity that is widespread in nature. Fractal geometry breaks through the framework of traditional Euclidean space and extends the ideal and simplified description of classical geometric integer dimensions to fractional dimensions, thus more accurately portraying the essential characteristics of an object or phenomenon. The birth of fractal geometry provided a completely new approach to the study of crack irregularities.
Based on fractal theory, Mecholsky et al. (2020) [13] proposed a crack bifurcation coefficient that quantifies the irregular state of crack bifurcation; i.e., the smaller the crack bifurcation coefficient, the lower the degree of crack bifurcation irregularity (i.e., the smaller the crack bifurcation). At the same time, the crack bifurcation coefficient provides important information about the stress or energy threshold. Currently, numerous methods have been proposed for calculating the fractal dimension [19]. However, compared to various other methods (e.g., island method, scale method, etc.), the box-counting method is one of the most well-established algorithms for determining the fractal dimension due to its simplicity [22]. As per the method proposed by Mecholsky et al. (2020) [13], the crack bifurcation coefficients mentioned above were determined.
The calculation of the fractal dimension is divided into three parts, including image processing, pixel coverage, and model solving. Initially, given the intricate morphology of crack surfaces, image processing techniques, involving grayscale and binary processing, were employed to extract the crack’s outline. For ease of use, the initial crack images were captured utilizing cameras from mobile phones. The phone is equipped with a 1200-megapixel video camera and an LED flashlight. In addition, crack images were processed using an image processing program developed based on MATLAB R2018b software. Secondly, building upon image processing, the procedure primarily involves enclosing the entire specimen within a large square box and subsequently dividing this box into smaller uniform square segments. Thirdly, the size of the small square boxes was adjusted for various counting trials. Ultimately, the count of boxes traversed by a crack was documented with respect to varying sizes of small square boxes. It is important to note that this analysis considered the complete propagation of the crack, encompassing both the original unbranched crack near the origin site and all subsequent branches. Therefore, following the aforementioned procedures, the fractal dimension could be computed using Equation (1):
C B C = log ( N L , C B C ) log ( L max , C B C L C B C )
where NL denotes the number of all boxes covering the crack. L denotes the size of the small square boxes. Lmax signifies the size of the large square box needed to enclose the entire specimen. Typically, the fractal dimension of the crack bifurcation is determined by fitting the slope of the plot log(NL) vs. log(Lmax/L) for each sample, as shown in Figure 4.

2.3. Drop Hammer Impact Experiment

The aim of this paper is to elucidate the threshold energy for crack expansion after material fracture, including the threshold energy needed for crack initiation and bifurcation. Obviously, the formation of cracks and the occurrences of bifurcations are prerequisites. Therefore, the impact energy for satisfying the initial fracture and crack bifurcation occurrence must be appropriate for analyzing the respective fracture energy thresholds. The first is the determination of the loading energy in the impact experiments, which was obtained via a pre-experiment carried out on the impact crushing of walnuts. Specifically, the walnuts were impacted using different energies so that an initial fracture in two, or three, impacts was realized in order to obtain the loading energy required for the experiment. The method of determining the loading energy of walnut crack bifurcation was the same as that in the previous section, and different loading energies were selected for the impact experiments to record the loading energy when the walnut exhibited crack bifurcation. The specific loading energies for this study are listed in Table 2. In addition, it is necessary to mention that all experiments were carried out by means of a drop hammer impact test machine.
As a matter of fact, the determination of the appropriate loading energy via pre-experimentation has been carried out in previous studies and will not be repeated in this paper [5]. In addition, the main experiments of this study were also carried out using a falling hammer impact test machine to perform impact experiments at different impact energies and walnut sizes.
The drop hammer impact tester primarily consists of essential components, such as an air compressor, an aluminum drop hammer, a lifting device, an anti-twice impact mechanism, and a control console, as depicted in Figure 5. The anti-twice impact device functions by activating a pneumatic limiting stopper, which is coordinated via a set of infrared emission and receiving diodes. This mechanism effectively immobilizes the drop hammer after a singular impact event. It is important to note that the force restricting the stopper, thereby preventing the drop hammer from rebounding, is generated by the air compressor. In addition, considering the unevenness of the walnut’s surface, as shown in Figure 1, it is necessary to paste the walnut specimen on the target plate with a double-sided adhesive to ensure the same loading point for each impact experiment. Previous studies have highlighted the dependence of fracture energy and breakage extent on the direction of loading applied to the walnut’s surface [23,24]. Consequently, impact loading was applied along the walnut surface’s thickness direction, which holds practical significance for shell breaking in real-world production scenarios. To ensure statistically robust and representative outcomes, 200 individual walnut samples were subjected to testing at each impact energy level. It is worth mentioning that throughout all drop experiments, the impact angles were consistently maintained at 90° (i.e., normal direction). In this context, this study assumes a notable disparity in stiffness between the drop hammer and the walnut. Moreover, it is crucial to highlight that the height adjustment of the drop hammer was carried out to achieve varying impact energies.

3. Results and Discussion

It is well known that the energy required for crack extensions in brittle materials is a key parameter for measuring the resistance of a material to crack extension. This parameter provides crucial insights into various aspects of material fracture mechanisms, including fracture toughness, fracture modes, et cetera. Research has demonstrated that the crack extension energy in brittle materials adheres to a size effect, meaning that with larger sizes, the crack extension energy decreases [25,26]. Walnuts differ significantly from conventional brittle materials in material composition and chemical properties, and it remains to be seen whether they exhibit a size effect. Therefore, in the following sections, we will discuss the effect of walnut size on crack extension energy in detail, including crack initiation energy and crack bifurcation energy.

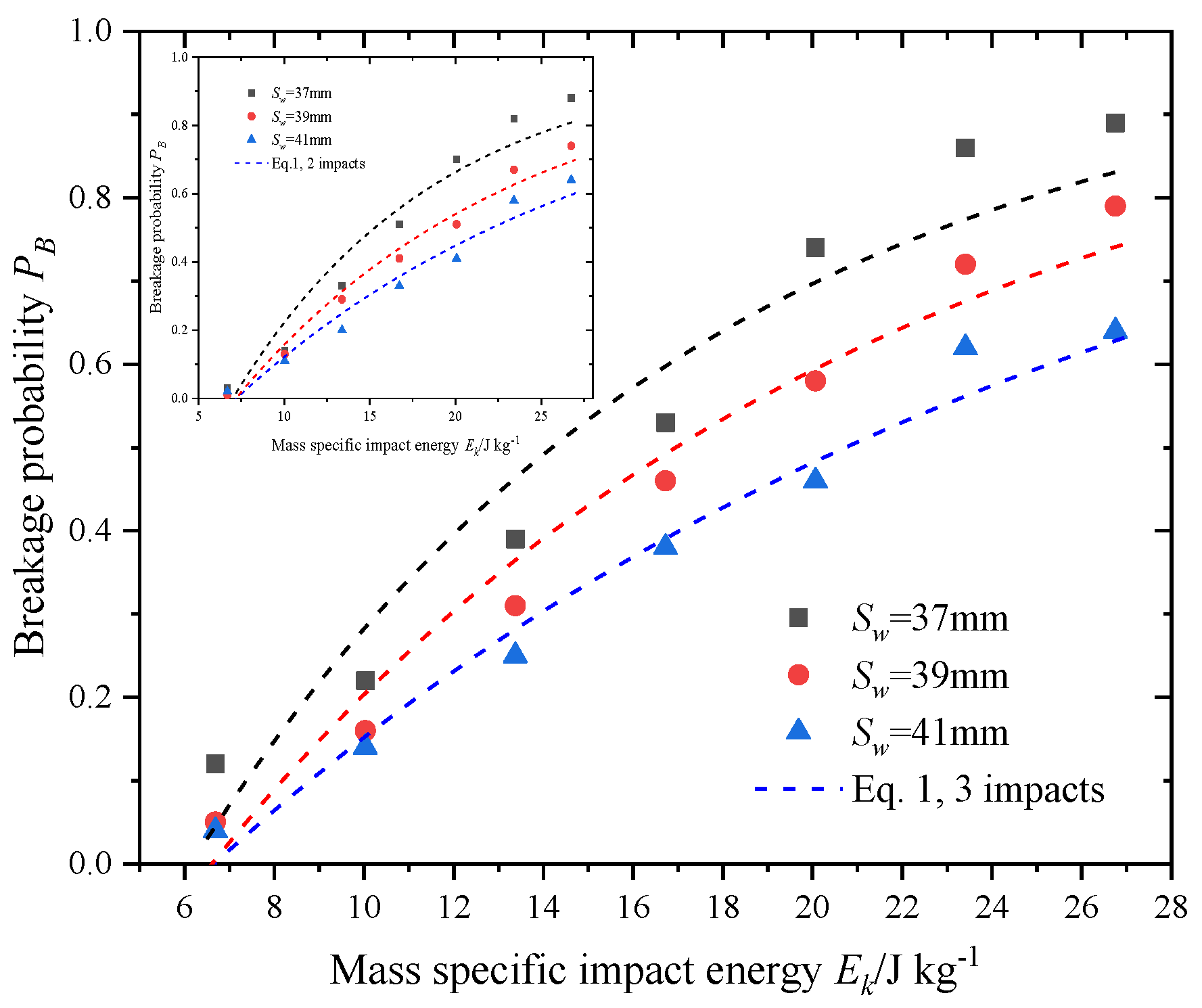
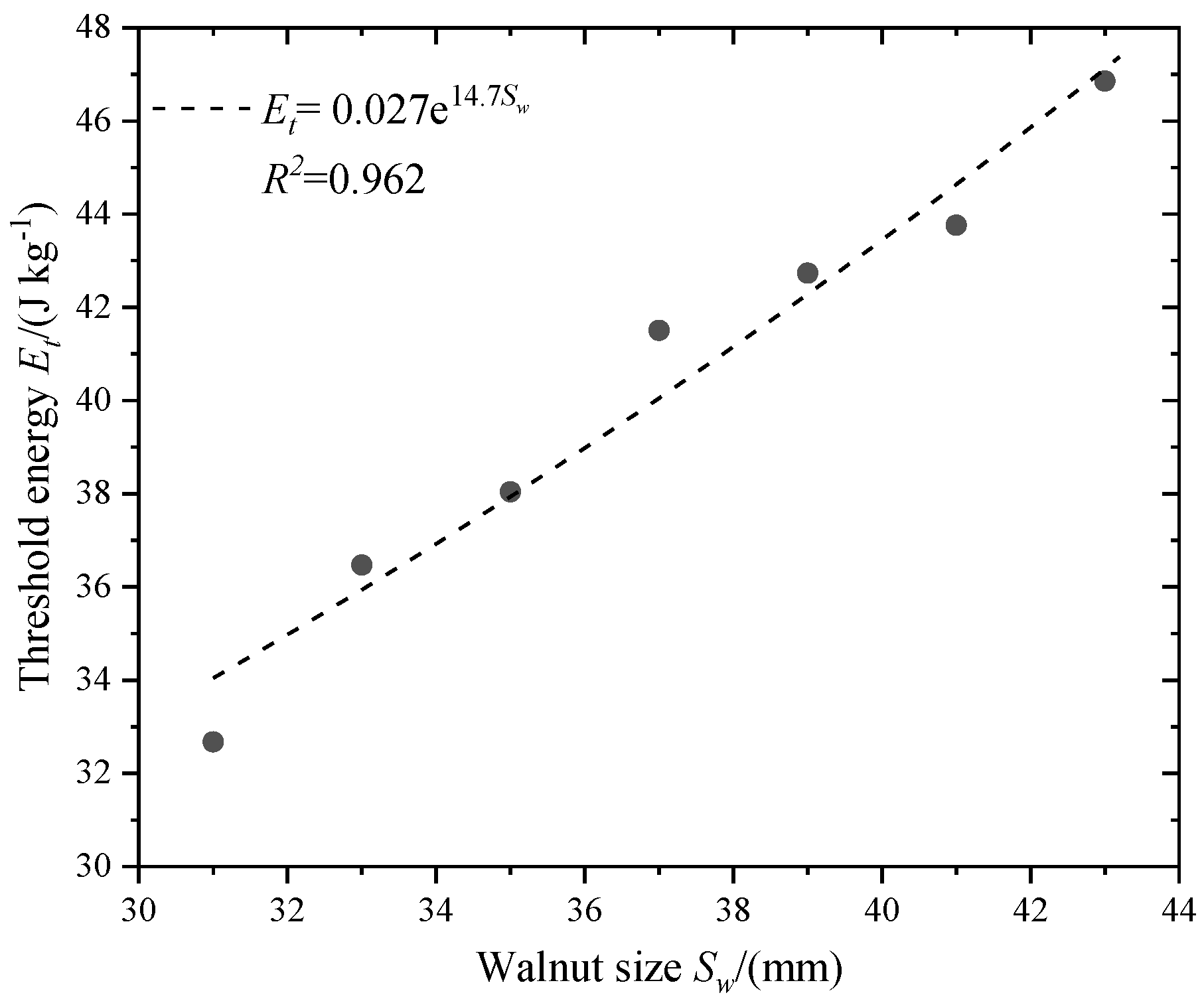
3.1. Crack Initiation Energy

It has been shown that there exists an energy threshold for particle fracture [18]; i.e., when the loading energy is lower than this threshold, initiating crack growth is difficult, whereas if the impact energy is greater than the threshold, it will contribute to particle crack growth. Correspondingly, some selection functions used to determine the energy threshold were also proposed [7,27], and they all correlate the breakage probability with impact energy. In fact, there are realities that have to be taken into account in which the initial fracture of the material occurs, forming a crack extension often as a result of multiple impacts. For example, walnuts fracture after being subjected to multiple impacts during processing, including repeated walnut–machine and walnut–walnut impacts. Therefore, considering the case of multiple impacts is mandatory when determining the crack extension threshold. Coincidentally, Vogel and Peukert (2005) proposed a fracture mechanics model based on the generalized dimensional analysis method combined with the Monte Carlo method, and their model takes the effects of multiple impacts into account. The model is based on the idea of a limit and solves the fracture threshold energy by assuming the fracture’s probability. Specifically, the threshold energy is the fracture energy corresponding to the fracture probability when it is extremely low. In addition, the inference process and the use of the model are described in detail by Vogel and Peukert (see Ref. [12]). The derived model can be written as follows:
P B = 1 − exp − c o n s t . S w k 1 + E E T 1 − v T 2 1 − v 2 1 5 × 1 − v 2 E ρ v S 2 2 1 5 E k − E m , min v S 2 2
where PB is the breakage probability of the walnut. Ek is the mass-specific impact energy incurred by the walnut, J/kg. Sw is the walnut’s size, mm. k is the number of impacts experienced by a walnut. E and ET are the Young’s modulus of the particle and target material, respectively, Pa. v and vT are the Poisson ratio of the particle and target material, respectively: dimensionless. ρ is particle density, kg/m3. v is impact velocity, m/s. vS denotes strength, m/s. It is worth noting that 1 + E E T 1 − v T 2 v 2 1 5 1 − v 2 E ρ v S 2 2 1 5 1 v S 2 2 in the model is completely dependent on the nature of the material and the independent stress conditions; therefore, it can be assumed to be a fixed material constant, fMat. Em,min is the mass-ratio threshold impact energy used to determine whether the walnut is capable of undergoing initial crack expansion due to impact. In other words, Em,min represents the energy required for this crack to expand. Obviously, below Em,min, the cracks do not extend (i.e., the particles do not fracture) because the particles are able to absorb the strain energy [9,28].
In order to analyze the threshold energy of walnut crack initiation, the fracture probability distribution of walnuts at different sizes was investigated, as shown in Figure 6. Note that Figure 6 shows the fracture probabilities obtained in the case of three impacts, where the small figure shows the fracture probability after two impacts, and the lines in the figure denote the fit of Equation (2) relative to the experimental data. The model agrees well with the results of multiple impact experiments.
As observed in the figure, the walnut-crushing probability trend is the same; i.e., the crushing probability of walnuts increases with an increase in impact energy. It is worth noting that the walnut’s size makes a significant difference; i.e., the larger the walnut size, the lower the probability of fracture, as shown in the small graph in Figure 6.
Taking the Em,min obtained from Equation (3) and plotting it in Figure 7, the energy value of the walnut crack initiation is obtained as a function of size. It is easy to see that the energy value of the walnut crack initiation increases linearly with an increase in size. The reason for this may be due to the structural stability of the shell; the larger its size, the more structurally stable it is. Similar conclusions were reached in the study of Liu et al. (2022) [29]. It is worth noting that the interval of energy values for walnut crack initiation is 4.784–7.888 J kg−1, which is quite different from the fracture energy of walnut. This is because there are other energies that are essential for material fracture, including elastic potential energy and thermal energy. This is because the fracture energy encompasses not only the energy associated with crack propagation but also elastic potential energy, thermal energy, and more.

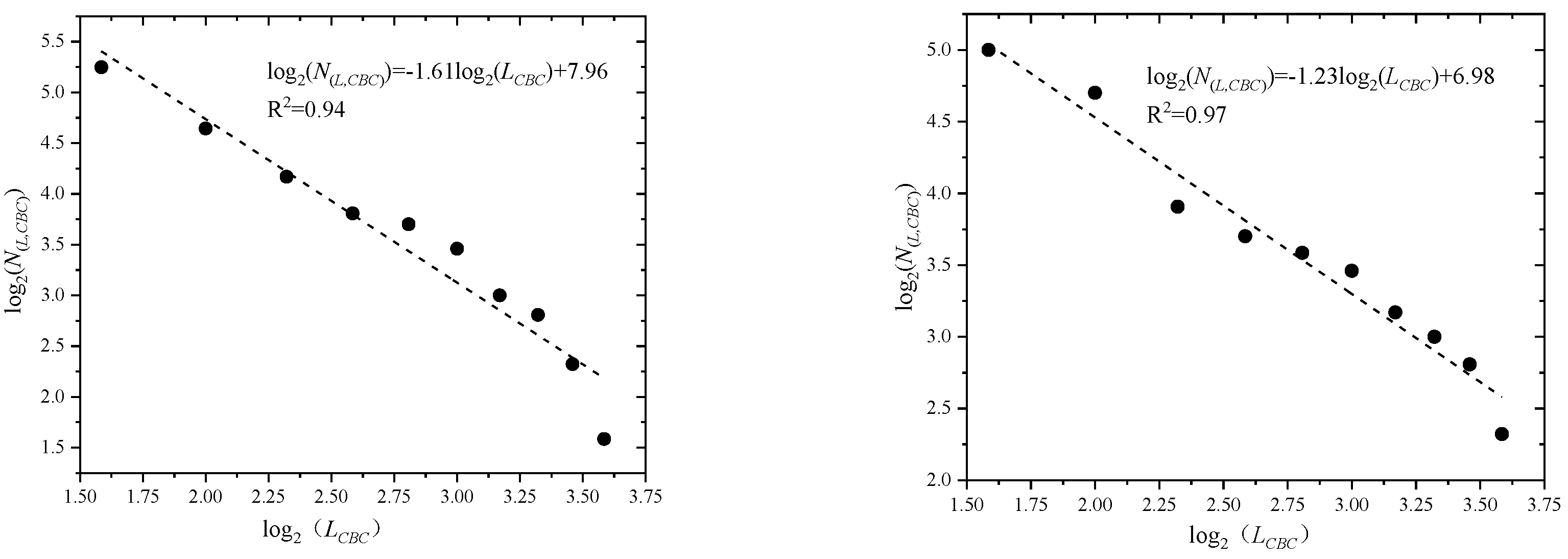
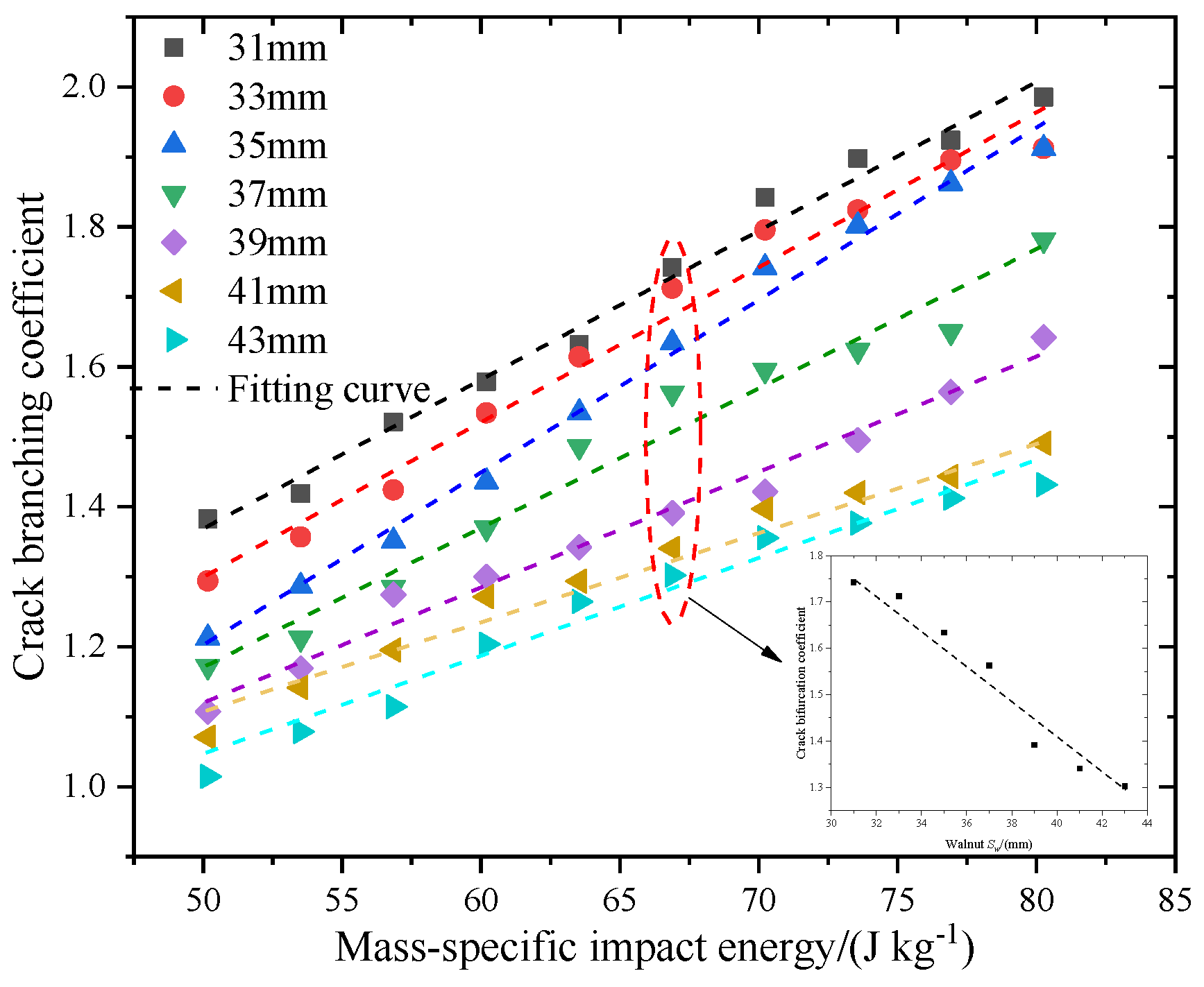
3.2. Crack Bifurcation Coefficient

Figure 8 depicts snapshots of crack bifurcation at various walnut sizes. It is evident that with an increase in walnut size, the alteration in crack bifurcation becomes apparent, signifying a decrease in the number of fragments, as depicted in Figure 8a–c. Therefore, this suggests that the expansion in walnut size limits crack bifurcation, subsequently decreasing the occurrence of crack branching. As a result, it can be inferred that the coefficient of crack bifurcation could indirectly be gauged by assessing the number of fragments, as illustrated in Figure 8a–c. This observation finds support in the findings of Ref. [30].
In order to quantitatively analyze the sensitivity of material size to crack bifurcation, the CBC for different walnut sizes is given in Figure 9. As shown in the figure, CBC decreases linearly with an increase in walnut size. In other words, the number of crack bifurcations is greater for smaller sizes than for larger sizes. Research has demonstrated that material micro-morphology, particularly when larger micro-cracks or micro-voids are present, significantly contributes to crack bifurcation. Therefore, according to the size effect, the larger the size of the walnut, the more prone it is to bifurcation, which is widely observed in brittle particles, such as concrete, rock, and glass particles [31,32]. However, the current emergence of this non-dimensional effect may be attributed to the fact that the challenges associated with crack propagation are offset by the increased structural stability resulting from the larger size. Hence, this study posits that the bifurcation of cracks in hollow shell particles is primarily influenced by their structural stability rather than the micro-morphology of walnuts.
In order to verify the validity of the estimation above and consider walnut samples with irregular shapes and uneven surfaces, uniaxial compression experiments using standard samples with different sizes were conducted with the help of the finite element method (FEM), as shown in Figure 10. Note that the standard sample was a spherical shell made out of polymethyl methacrylate (PMMA), which is the reason why the inside of the PMMA material is more uniform and has no pore structure and natural micro-cracks [33]. It should be emphasized that compared with the experimental methods (e.g., additive manufacturing), the spherical shell is easier to construct using finite element software ABAQUS 2022. Here, the element type with C3D10 was meshed using Tet Free mesh generation methods. A mesh size of 1 mm was selected for the calculation, which takes both computational costs and simulation accuracy into account. The main parameters obtained from previous publications for PMMA materials are summarized and listed in Table 3.
For the sake of simplicity, more details about the simulation method and progress, as well as parameter settings, can be referred to in Refs. [33,34].
Figure 11 shows the fracture energy of a spherical shell at different sizes. Note that the symbols denote the experimental data, and the curves represent the fitting results. It is clear that the fracture energy exponentially increases with an increase in spherical shell size, implying that the larger the spherical shell, the higher the resistance to breakage effects, and the better the structural stability. Clearly, disregarding the initial micro-crack, the structural stability of the spherical shell progressively intensifies with size augmentation. This implies that the fracture of the spherical shell primarily hinges on the loss of structural stability. This suggests that the fracture of the spherical shell predominantly relies on the diminishment of its structural stability. Likewise, as proposed by Liu et al. (2022) [29], the primary failure modes of pressure hulls under seawater pressure include yields due to inadequate material strength (similarly to the scenario discussed in this work) and instability arising from insufficient structural stiffness. In summary, the simulated analyses sufficiently verify the guess mentioned above, in which the failure mechanisms result in a decrease in structural stability relative to an increase in walnut size.
Consequently, it can be inferred that the impact of walnut size on crack bifurcation is correlated with walnut strength (i.e., larger walnuts possess higher strength). Therefore, in contrast to the microscopic characteristics of walnuts, the occurrence of crack bifurcation in hollow shell particles is chiefly governed by their size. The uniaxial compression experiments of macadamia nuts at different sizes were carried out by Koya et al. [35]. The results showed that the strength of macadamia nuts increased with an increase in size. Similar findings were validated in the papers by Ogunsina and Wang et al. [36,37]. Summarizing the previous studies and the experimental results in this paper, the fracture energy of nuts has a non-size effect; i.e., the larger the size, the greater the resistance to fracture. Wang et al. [37] provide an explanation from a biological point of view; i.e., the larger the size of the nut, the harder the shell has to be in order to protect the kernel from insect beaks, drop impacts, etc.
In contrast, the coefficient of crack bifurcation (CBC) demonstrates a linear increase with the augmentation of mass-specific impact energy, as illustrated in the inset of Figure 9. This occurs because the increase in impact energy facilitates the creation of more defects in the material, consequently leading to the formation of crack bifurcations; thus, the greater impact energy leads to a larger CBC. To obtain a more profound understanding of CBC, a mathematical model concerning CBC and energy has been formulated, building upon existing findings.
C B C = a s E k + E i
It is worth noting that as is a material parameter that represents the sensitivity of the crack bifurcation to the loading energy [13]. Ei is the zero intercept. The constant Ei is related to the threshold energy for bifurcation. We consider the boundary conditions of the model; i.e., when CBC is 1, the crack only undergoes extension and does not produce a bifurcation. We can let CBC converge to 1 to obtain the threshold energy Et for crack bifurcation: i.e., the crack will not bifurcate when the loading energy is less than Et.
Accordingly, as shown by the dashed line in Figure 9, Equation (3) fits the CBC and impact energy well; e.g., a crack bifurcation threshold of 41.5 J kg−1 is obtained when the walnut size is 37 mm. Applying a comparable approach, the threshold energy dictating crack bifurcation for various walnut sizes was determined and graphed in Figure 12. The graph illustrates a non-linear increase in the threshold energy corresponding to the walnut size’s increment, spanning a range from 32.677 to 46.853 J kg−1. Coincidentally, the relationship between threshold energy and size corresponds to the simulation’s outcomes, displaying exponential functions in both cases. On the one hand, this helps illustrate the veracity of the simulation’s results. Furthermore, this reaffirms the validity of the earlier hypothesis that structural stability increases with size. Evidently, the fitting model holds promise in providing valuable theoretical insights for determining threshold energy values for other hollow shell particles.

3.3. Correlation and Discussion

It is well known that the crack extension process in brittle materials has distinct stages compared to plastic materials [38]. Macroscopic crack initiation represents the initial phase of the overall expansion process, resulting from the energy-driven enlargement of pre-existing micro-defects or micro-voids within the material [39]. After a certain length of crack extension, crack bifurcation takes place when the crack’s tip encounters non-uniform stress or energy distributions, particularly when a substantial amount of energy is injected [40,41]. It is evident that there is a connection between crack initiation and bifurcation, as both fundamentally rely on energy as the driving force. Despite these similarities, there are still significant differences in crack initiation and bifurcation; i.e., the energy required for crack initiation and bifurcation can vary depending on the number and direction of crack bars.
In order to clarify the connections and differences between the different stages of crack expansion, the threshold energy for crack initiation and crack bifurcation at different walnut sizes is plotted in Figure 13. As mentioned previously, crack bifurcation is the subsequent stage following crack initiation, implying that crack initiation is a prerequisite for crack bifurcation. Thus, the threshold energy for crack bifurcation necessarily includes the energy of pre-crack initiation. According to the energy conservation theorem, the absolute energy required for crack bifurcation is obtained via Equation (4):
E a = E t − E m , m i n
where Ea is the absolute crack bifurcation energy. Overall, the energy required for crack expansion is reported to increase linearly with increasing walnut size. In addition, the crack bifurcation threshold increases exponentially as the crack initiation threshold increases, as observed in the small box shown in Figure 13. The results show that the higher the crack initiation energy, the higher the crack bifurcation energy. Possible reasons for this are that the number of cracks has increased in the first place, and the energy required for crack expansion has increased. This phenomenon can be attributed to a couple of factors: Firstly, an increase in the total number of cracks leads to an increase in the energy required for crack expansion. Secondly, the expansion between multiple cracks can be constrained by each other, further increasing the difficulty of crack expansion.
In this paper, the crushing process of walnuts is discretized to reveal the crushing mechanism of walnuts from the two stages of crack extension and crack bifurcation, and the relationship between crack extension and crack bifurcation is explained based on the law of energy conservation. The results can provide theoretical guidance for numerical simulations concerning the crushing process of thin-shelled materials and help predict crack bifurcations. In addition, the results of the study can provide data support for the design of walnut impact shell breakers. As a matter of fact, the crushing process of the shell material is dynamically changing, particularly with respect to the processes of crack extension and bifurcation. In order to better clarify the mechanism of crack extension and bifurcation, it is necessary to study the crushing process dynamically with the help of a high-speed camera. Therefore, future work needs to invest more effort in high-speed imaging methods to dynamically reveal the material’s crushing mechanism.

4. Conclusions

In this study, the fracture probability of walnuts after impact was first analyzed, and a probabilistic model was fitted to obtain the threshold energy for crack initiation. The irregularity of the crack bifurcation was then quantified using the crack bifurcation system, and the threshold energy of the crack bifurcation was obtained via modeling. On this basis, the effect of walnut size on crack initiation and crack bifurcation was investigated via laboratory-scale experiments, and the main findings are as follows.
The threshold interval for crack initiation in the walnut size interval was 4.784–7.888 J kg−1, and the threshold interval for crack bifurcation was 32.677–46.636 J kg−1. In addition, walnut size conforms to an inversely proportional function for both crack initiation and crack bifurcation thresholds. The thresholds for crack initiation and crack bifurcation have a linear relationship, and the larger the threshold for crack initiation, the larger the threshold for crack bifurcation.
Meanwhile, the results of the study can be embedded in future numerical simulations to model the crack germination, extension, and bifurcation of walnuts during crushing under impact, which could provide a theoretical basis for elucidating the crack evolution mechanism of walnuts under impact. This study provides important information for the understanding of the walnut-crushing processes under impact, and it has practical value in the walnut processing industry for the optimization of shell-breaking process parameters and improvements in crushing quality.

Author Contributions

Conceptualization, L.L.; methodology, L.L.; software, H.L.; investigation, X.M.; resources, Y.Z.; data curation, X.M.; writing—original draft preparation, X.M.; writing—review and editing, X.M. and H.Z.; validation, L.L.; visualization, L.L.; formal analysis, Y.T.; supervision, H.L.; project administration, X.F.; funding acquisition, H.Z., Y.Z. and X.F. All authors have read and agreed to the published version of the manuscript.

Funding

This work has been financially supported and encouraged by the Shishi Science and Technology Program (Grant Nos. 2021ZB01, 2022ZB05, and 2022ZB07), the Bingtuan Science and Technology Program (Grant Nos. 2022CB08 and 2018CB014), and the Modern Agricultural Engineering Key Laboratory at the Universities of Education Department of Xinjiang Uygur Autonomous Region (Grant No. TDNG2022101).

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Acknowledgments

The authors thank Haipeng Lan from Tarim University for thesis supervision. The authors are grateful to the anonymous reviewers for their comments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Udayarajana, C.T.; Mohana, K.; Nisha, P. Tree nuts: Treasure mine for prebiotic and probiotic dairy free vegan products. Trends Food Sci. Technol. 2022, 124, 208–218. [Google Scholar] [CrossRef]
  2. Gama, T.; Wallace, H.M.; Trueman, S.J.; Hosseini-Bai, S. Quality and shelf life of tree nuts: A review. Sci. Hortic. 2019, 242, 116–126. [Google Scholar] [CrossRef]
  3. Chen, C.; Pan, Z.L. Postharvest processing of tree nuts: Current status and future prospects-a comprehensive review. Compr. Rev. Food Sci. F 2022, 21, 1702–1731. [Google Scholar] [CrossRef] [PubMed]
  4. Zhang, H.; Liu, H.L.; Zeng, Y.; Tang, Y.R.; Zhang, Z.G.; Che, J. Design and Performance Evaluation of a Multi-Point Extrusion Walnut Cracking Device. Agriculture 2022, 12, 1494. [Google Scholar] [CrossRef]
  5. Sharifian, F.; Derafshi, M.H. Mechanical Behavior of Walnut under Cracking Conditions. J. Appl. Sci. 2008, 8, 886–890. [Google Scholar] [CrossRef]
  6. Koyuncu, M.A.; Ekinci, K.; Savran, E. Cracking Characteristics of Walnut. Biosyst. Eng. 2004, 87, 305–311. [Google Scholar] [CrossRef]
  7. Man, X.L.; Li, L.; Zeng, Y.; Tang, Y.R.; Yang, J.L.; Fan, X.W.; Zhang, Y.C.; Zhang, H.; Su, G.G.; Wang, J.P. Mechanical impact characteristics of hollow shell granule based on continuous damage theory. Powder Technol. 2023, 429, 118946. [Google Scholar] [CrossRef]
  8. Rumpf, H. Physical aspects of comminution and new formulation of a law of comminution. Powder Technol. 1973, 7, 145–159. [Google Scholar] [CrossRef]
  9. Vogel, L.; Peukert, W. From single particle impact behaviour to modelling of impact mills. Chem. Eng. Sci. 2005, 60, 5164–5176. [Google Scholar] [CrossRef]
  10. Lecoq, O.; Guigon, P.; Pons, M. A grindability test to study the influence of the material processing on the impact behaviour. Powder Technol. 1999, 105, 21–29. [Google Scholar] [CrossRef]
  11. Li, L.; Mao, B.Q.; Zeng, Y.; Tang, Y.T.; Man, X.L.; Fan, X.W.; Zhang, Y.C.; Zhang, H. Experimental study on crack irregularity of hollow shell particle under impact loading. Powder Technol. 2023, 427, 118704. [Google Scholar] [CrossRef]
  12. Han, B.W.; Su, G.G.; Zeng, Y.; Yang, J.; Fan, X.W.; Zhang, Y.C.; Zhang, H.; Wang, J.F. FDEM investigation on the crack propagation characteristics of walnut shell under multi-contact loadings. Front. Mater. 2023, 10, 1293683. [Google Scholar] [CrossRef]
  13. Shen, Q.; Rao, Q.; Zhang, Q.; Li, Z.; Yi, W. A New Method for Predicting Double-Crack Propagation Trajectories of Brittle Rock. Int. J. Appl. Mech. 2021, 13, 2150026. [Google Scholar] [CrossRef]
  14. Reinhardt, H.W.; Xu, S. A practical testing approach to determine mode II fracture energy GIIF for concrete. Int. J. Fract. 2000, 105, 107–125. [Google Scholar] [CrossRef]
  15. Momber, A.W. Deformation and fracture of rocks loaded with spherical indenters. Int. J. Fract. 2004, 125, 263–279. [Google Scholar] [CrossRef]
  16. Bouzeboudja, H.; Melbouci, B.; Bouzeboudja, A. Experimental Study of Crushed Granular Materials by the Notion of Fractal Dimension in 2D and 3D. Geotech. Geol. Eng. 2022, 40, 2009–2031. [Google Scholar] [CrossRef]
  17. Delellis, D.P.; Mecholsky, N.A.; Mecholsky, J.J., Jr.; Quinn, G.D. A fractal analysis of crack branching in borosilicate glass. J. Am. Ceram. Soc. 2020, 103, 5283–5290. [Google Scholar] [CrossRef]
  18. Chen, C.; Zhang, W.; Venkitasamy, C.; Khir, R.; McHugh, T.; Pan, Z. Walnut structure and its influence on the hydration and drying characteristics. Drying Technol. 2019, 38, 975–986. [Google Scholar] [CrossRef]
  19. Altuntas, E.; Özkan, Y. Physical and Mechanical Properties of Some Walnut (Juglans regia L.) Cultivars. Int. J. Food Eng. 2008, 4, 1–13. [Google Scholar] [CrossRef]
  20. Lu, Y.; Liu, S.; Weng, L.; Li, Z.; Xu, L. Fractal analysis of cracking in a clayey soil under freeze-thaw cycles. Eng. Geol. 2016, 208, 93–99. [Google Scholar] [CrossRef]
  21. Rosa, A.F.; Arago, F.; Motta, L. Effects of particle size distribution and lithology on the resistance to breakage of ballast materials, Constr. Build. Mater. 2020, 267, 121015. [Google Scholar] [CrossRef]
  22. Zeng, Y.; Jia, F.G.; Meng, X.Y.; Han, Y.L.; Xiao, Y.W. The effects of friction characteristic of particle on milling process in a horizontal rice mill. Adv. Powder Technol. 2018, 29, 1280–1291. [Google Scholar] [CrossRef]
  23. Zeng, Y.; Mao, B.Q.; Li, A.Q.; Han, Y.L.; Jia, F.G. DEM investigation of particle flow in a vertical rice mill: Influence of particle shape and rotation speed. Powder Technol. 2022, 399, 117115. [Google Scholar] [CrossRef]
  24. Zeng, Y.; Jia, F.G.; Chen, P.Y.; Qiu, H.L.; Han, Y.L.; Meng, X.Y.; Xiao, Y.W. Effects of convex rib height on spherical particle milling in a lab-scale horizontal rice mill. Powder Technol. 2019, 342, 1–10. [Google Scholar] [CrossRef]
  25. Cherepanov, G.P.; Balankin, A.S.; Ivanova, V.S. Fractal fracture mechanics-a review. Eng. Fract. Mech. 1995, 51, 997–1033. [Google Scholar] [CrossRef]
  26. Zheng, G.M.; Zhao, J.; Li, L.; Cheng, X.; Wang, M. A fractal analysis of the crack extension paths in a Si3N4 ceramic tool composite. Int. J. Refract. Met. Hard Mater. 2015, 51, 160–168. [Google Scholar] [CrossRef]
  27. Gharibzahedi, S.M.T.; Mousavi, S.M.; Hamedi, M. Mechanical behaviour of Persian Walnut and its kernel under compression loading: An experimental and computational study. J. Food Process. Preserv. 2012, 36, 423–430. [Google Scholar] [CrossRef]
  28. Han, Y.L.; Li, G.R.; Jia, F.G.; Meng, X.Y.; Chu, Y.H.; Chen, P.Y.; Bai, S.G.; Zhao, H.W. Analysis of breakage behavior of rice under impact. Powder Technol. 2021, 394, 533–546. [Google Scholar] [CrossRef]
  29. Rajpoot, D.; Tandaiya, P.; Narayan, R.L.; Ramamurty, U. Size effects and failure regimes in notched micro-cantilever beam fracture. Acta Mater. 2022, 234, 118041. [Google Scholar] [CrossRef]
  30. Yu, H.; Zhou, B.; Zhu, L.; Yan, J.; Li, J.; Zhang, J. Mathematical law of size effect on the flexural property of ceramics. Ceram. Int. 2022, 48, 769–775. [Google Scholar] [CrossRef]
  31. Rozenblat, Y.; Grant, E.; Levy, A.; Kalman, H.; Tomas, J. Selection and breakage functions of particles under impact loads. Chem. Eng. Sci. 2012, 71, 56–66. [Google Scholar] [CrossRef]
  32. Capece, M.; Bilgili, E.; Davé, R.N. Formulation of a Physically Motivated Specific Breakage Rate Parameter for Ball Milling via the Discrete Element Method. AIChE J. 2014, 60, 2404–2415. [Google Scholar] [CrossRef]
  33. Liu, D.; Zhu, H.T.; Liu, F.; Cao, J.Q.; Ding, Z.J.; Zhang, Y. Buckling failure analysis of PMMA spherical pressure hull. Ocean Eng. 2022, 245, 110465. [Google Scholar] [CrossRef]
  34. Mecholsky, J.J., Jr.; Linhart, R.; Kwitkin, B.D. On the fractal nature of crack branching in MgF2. J. Mater. Res. 1998, 13, 3153–3159. [Google Scholar] [CrossRef]
  35. Jacquet, N.; Tardif, N.; Elguedj, T.; Garnier, C. Buckling of thick elasto-visco-plastic egg shells under external pressure: Experiments and bifurcation analysis. Int. J. Solids Struct. 2022, 257, 111591. [Google Scholar] [CrossRef]
  36. Hirata, R.; Ooi, A.; Tada, E.; Nishikata, A. Influence of the degree of saturation on carbon steel corrosion in soil. Corros. Sci. 2021, 189, 109568. [Google Scholar] [CrossRef]
  37. Wang, L.; Zhu, Z.M.; Zhou, L.; Gao, W.T.; Dong, Y.Q.; Niu, C.Y.; Ai, T. Study the effect of circular hole on dynamic fracture properties of cracked PMMA specimen under impact loads. Int. J. Impact Eng. 2021, 156, 103948. [Google Scholar] [CrossRef]
  38. Kazarinov, N.A.; Bratov, V.A.; Morozov, N.F.; Petrov, Y.V.; Balandin, V.V.; Iqbald, M.A.; Gupta, N.K. Experimental and numerical analysis of PMMA impact fracture. Int. J. Impact Eng. 2020, 143, 103597. [Google Scholar] [CrossRef]
  39. Koya, O.A.; Faborode, M.O. Mathematical modelling of palm nut cracking based on Hertz’s theory. Biosyst. Eng. 2005, 91, 471–478. [Google Scholar] [CrossRef]
  40. Bobaru, F.; Zhang, G. Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. Int. J. Fract. 2015, 196, 59–98. [Google Scholar] [CrossRef]
  41. Gao, J.; Bai, Y.; Fan, H.; Song, G.; Zou, X.; Zheng, Y.; He, X. Phase-field simulation of microscale crack propagation/deflection in SiCf/SiC composites with weak interphase. J. Am. Ceram. Soc. 2023, 106, 4877–4890. [Google Scholar] [CrossRef]
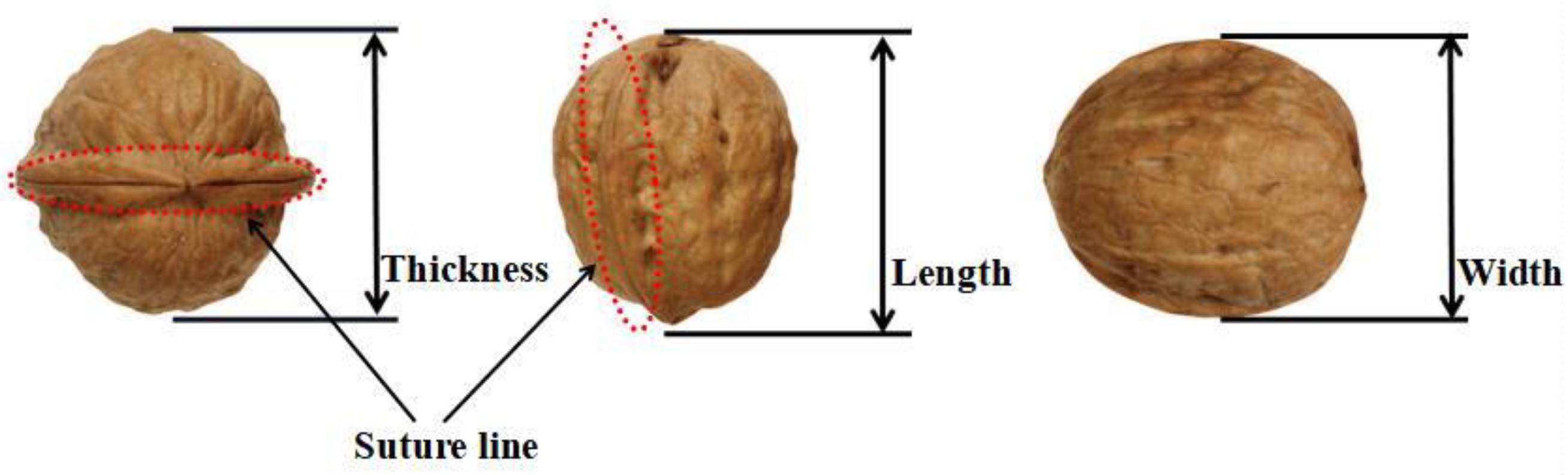
Agriculture 14 00069 g001
Figure 1. Snapshots of the walnut: three principal sizes of a walnut.
Figure 1. Snapshots of the walnut: three principal sizes of a walnut.
Agriculture 14 00069 g001
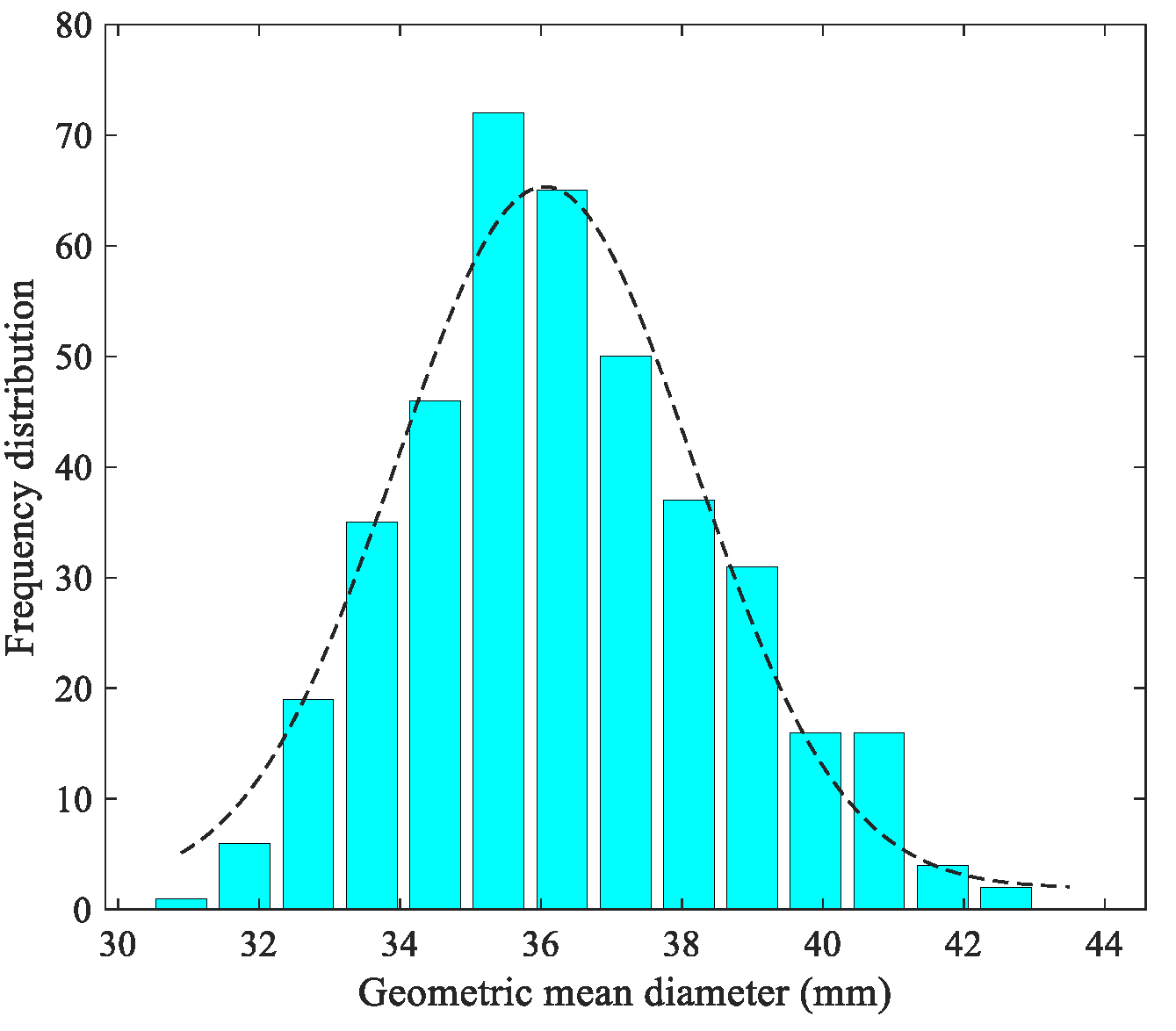
Agriculture 14 00069 g002
Figure 2. Statistical distribution of the equivalent spheroid diameter of walnuts.
Figure 2. Statistical distribution of the equivalent spheroid diameter of walnuts.
Agriculture 14 00069 g002
Agriculture 14 00069 g003
Figure 3. Steps of the walnut impact experiment and the determination of threshold energy.
Figure 3. Steps of the walnut impact experiment and the determination of threshold energy.
Agriculture 14 00069 g003
Agriculture 14 00069 g004
Figure 4. The number of small square boxes as a function of the size calculation of CBC. Here, walnut sizes are 33 mm and 39 mm.
Figure 4. The number of small square boxes as a function of the size calculation of CBC. Here, walnut sizes are 33 mm and 39 mm.
Agriculture 14 00069 g004
Agriculture 14 00069 g005
Figure 5. Snapshots showing the configuration of the drop hammer impact tester.
Figure 5. Snapshots showing the configuration of the drop hammer impact tester.
Agriculture 14 00069 g005
Agriculture 14 00069 g006
Figure 6. Variations in breakage probability with mass-specific impact energies under different walnut sizes.
Figure 6. Variations in breakage probability with mass-specific impact energies under different walnut sizes.
Agriculture 14 00069 g006
Agriculture 14 00069 g007
Figure 7. The threshold energy for crack initiation as a function of walnut size.
Figure 7. The threshold energy for crack initiation as a function of walnut size.
Agriculture 14 00069 g007
Agriculture 14 00069 g008
Figure 8. Snapshots of the crack bifurcation of cracked surfaces: (a) Sw = 37 mm, (b) Sw = 39 mm, and (c) Sw = 41 mm when the mass-specific impact energy is 63.54 J kg−1.
Figure 8. Snapshots of the crack bifurcation of cracked surfaces: (a) Sw = 37 mm, (b) Sw = 39 mm, and (c) Sw = 41 mm when the mass-specific impact energy is 63.54 J kg−1.
Agriculture 14 00069 g008
Agriculture 14 00069 g009
Figure 9. Variations in the crack bifurcation coefficient with respect to mass-specific impact energies under different walnut sizes.
Figure 9. Variations in the crack bifurcation coefficient with respect to mass-specific impact energies under different walnut sizes.
Agriculture 14 00069 g009
Agriculture 14 00069 g010
Figure 10. (a) A spherical shell with different sizes during compression experiments; (b) finite element discretization of the shell; (c) 10-node tetrahedral element.
Figure 10. (a) A spherical shell with different sizes during compression experiments; (b) finite element discretization of the shell; (c) 10-node tetrahedral element.
Agriculture 14 00069 g010
Agriculture 14 00069 g011
Figure 11. The fracture energy as a function of spherical shell size.
Figure 11. The fracture energy as a function of spherical shell size.
Agriculture 14 00069 g011
Agriculture 14 00069 g012
Figure 12. The threshold energy for crack bifurcation as a function of walnut size.
Figure 12. The threshold energy for crack bifurcation as a function of walnut size.
Agriculture 14 00069 g012
Agriculture 14 00069 g013
Figure 13. The threshold energy as a function of walnut size.
Figure 13. The threshold energy as a function of walnut size.
Agriculture 14 00069 g013
Table 1. Walnut characteristic parameters.
Table 1. Walnut characteristic parameters.
Walnut Size/(mm)Length
/(mm)		Width
/(mm)		Thickness
/(mm)		SphericityAverage Mass of Walnut Shell/(g)
3135.76 ± 1.1629.65 ± 0.9630.22 ± 1.130.91 ± 0.083.57
3336.73 ± 1.0830.8 ± 0.9832.06 ± 1.250.93 ± 0.13.95
3539.94 ± 1.0833.12 ± 0.8734.28 ± 1.130.92 ± 0.114.19
3740.16 ± 1.1634.76 ± 1.0335.68 ± 1.20.94 ± 0.174.46
3941.92 ± 1.0136 ± 0.7537.78 ± 1.180.93 ± 0.174.99
4143.57 ± 1.2139.74 ± 1.1139.78 ± 1.210.94 ± 0.095.35
4343.57 ± 1.2143.27 ± 1.0743.27 ± 1.070.95 ± 0.095.81
Table 2. The loading energy used in the experiment.
Table 2. The loading energy used in the experiment.
Bifurcation experiment (J kg−1)50.16253.50656.8560.19563.53966.88370.22773.57176.91580.26
Cracking experiment (J kg−1)6.68810.03213.37616.7220.06523.40926.753
Table 3. Physical parameters and their values in FEM simulations.
Table 3. Physical parameters and their values in FEM simulations.
Plexiglas PropertiesValues
Density1.2 × 103 (kg m3)
Elasticity modulus3100 (MPa)
Poisson ratio0.37
Brittle crackingDirect stress after crackingDirect cracking strain
36.80
34.13.33 × 10−6
21.16.67 × 10−6
Direct cracking failure strain1 × 10−6
Brittle shearShear retention factorCrack opening strain
10
0.50.001
0.250.002
0.1250.003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Man, X.; Li, L.; Zhang, H.; Lan, H.; Fan, X.; Tang, Y.; Zhang, Y. Study on the Relationship between Crack Initiation and Crack Bifurcation in Walnut Shells Based on Energy. Agriculture 2024, 14, 69. https://doi.org/10.3390/agriculture14010069

AMA Style

Man X, Li L, Zhang H, Lan H, Fan X, Tang Y, Zhang Y. Study on the Relationship between Crack Initiation and Crack Bifurcation in Walnut Shells Based on Energy. Agriculture. 2024; 14(1):69. https://doi.org/10.3390/agriculture14010069

Chicago/Turabian Style

Man, Xiaolan, Long Li, Hong Zhang, Haipeng Lan, Xiuwen Fan, Yurong Tang, and Yongcheng Zhang. 2024. "Study on the Relationship between Crack Initiation and Crack Bifurcation in Walnut Shells Based on Energy" Agriculture 14, no. 1: 69. https://doi.org/10.3390/agriculture14010069

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop