Abstract
Harvesting is an integral component of the agricultural cycle, necessitating the use of high-performance grain harvester combines, which are utilized for a short period each year. Given the seasonality and significant cost involved, list prices ranging from a quarter to almost a million euros, a fact-based investment assessment decision-making process is essential. However, there is a paucity of research studies forecasting the remaining value of grain harvester combines in recent years. This study proposes a straightforward methodology based on public information that employs various parametric and non-parametric models to develop a robust and user-friendly model that can assist decision makers, such as farmers, contractors, sellers, and finance and insurance entities, in optimizing their harvesting operations. The model employs a power regression mode, with RMSE of 1.574 and RSqAdj of 0.8457 results, to provide accurate and reliable insights for informed decision-making. The robust model transparency enables us to easily create a mainstreamed spreadsheet-based dashboard tool.
1. Introduction
Making the right investments in capital assets, such as machinery, is critical to long-term success [1]. Due to the seasonal nature of agricultural work, agricultural machinery is used during brief time periods during the year. Machinery costs include the cost of ownership, operation, and penalties for lack of timeliness. Ownership costs include depreciation of the machine, interest on the investment and cost of taxes, insurance, and housing of the machine. Depreciation is the reduction in the value of a machine value with time and use. It is often the largest single cost of machine ownership [2].
The harvesting operation, cutting, threshing, separating, cleaning, and residue management of the grain (rice, wheat, corn, soybeans, barley, oats, sorghum, dry beans, canola, etc.) can be performed by one machine in a single pass over the field commonly known as combines [3].
Drawing from the analysis of [4], as reported by [5], it is noteworthy that combines rank third in Euros among the largest agricultural machinery categories, following tractors and machine parts (Figure 1). Given this significant contribution to the agricultural sector, it is imperative to focus on forecasting the remaining value of combines.
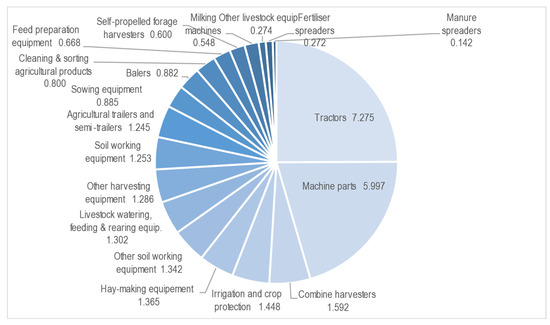
Figure 1.
European (EU 27) agricultural machinery production (in thousands of million EUR) by product family in 2020.
Having a thorough understanding of the combine cost of ownership is paramount to establishing the most efficient usage strategy as it is the key factor in order to opt (1) to acquire the good by means of either paying in full or using conventional finance schemes or financial leases; (2) to acquire the usage by means of either operational leases or machine rental; or (3) acquire the task by means of custom hiring the requested task. The usage strategy evaluation might have consequences on the machine type selection (tangential or axial separation and/or threshing), machine size (therefore, performance), brand and model, as it might be different for each of the above-mentioned usage strategies.
Isaac et al. (2006) created a combine harvester econometric model to determine the maximum harvested net income and the optimum forward speed for a given harvesting scenario. For the base case, the machinery cost was 48% of the total harvest cost, and the combine ownership cost was the highest machinery cost, comprising 40% of the total harvest cost [6].
The current manufacturer’s portfolio offering has a list price from slightly above a quarter million EUR to slightly below one million EUR (Figure 2); therefore, it is quite an investment that requires thorough analysis.
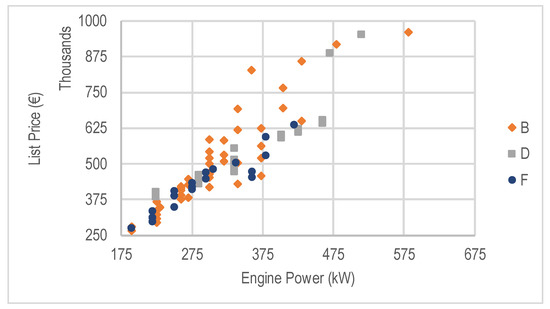
Figure 2.
Grain harvesting combine list prices in Germany.
1.1. Previous Studies
When compared to the passenger car industry in Europe [7], the number of used combine sales in the region is relatively small [8]. The amount of large passenger car operators (financing, leasing, and renting entities) as well as independent pre-owned passenger car resellers is vastly superior to that of the agricultural machinery and even more so to combines. Moreover, the statistical sample of used combine sales is significantly fragmented due to the extensive variety of available models and options. This high level of fragmentation, in conjunction with the limited availability of large datasets, makes it challenging to access the requisite information for conducting comprehensive empirical studies [9]. As a result, researchers and industry practitioners alike face significant hurdles in gaining a clear understanding of the European used combine market and the factors that affect its performance. Therefore, it is imperative that future studies adopt rigorous research methodologies and utilize a broad range of data sources to obtain more accurate and detailed insights into this market.
Several studies have been conducted to develop models that accurately predict the residual value of agricultural equipment, such as combines. The models proposed by ASAE in 1979 and Weersink and Sauber in 1983 [9] were both based on age, with the latter also taking into account engine type and power, brand, usage, and technological level. These models were exponential in nature. In 1981, Leatham and Baker [10] developed a Cobb–Douglas model based on age, header size, and manufacturer.
Cross and Perry conducted several studies in the 1990s [11,12] that explored different variables, such as usage, condition, auction typology, geographical location, and economic indicators. They developed models using Box–Cox and double square root transformations. In 1996, Unterschultz and Mumey [13] used a Cobb–Douglas model based on age and manufacturer.
More recently, in 2004, Wu and Perry [14] developed a Box–Cox model based on age, production year, and manufacturer. In 2020, Kay, Edwards, and Duffy [15] developed a model based on ASABE [16], which, in turn, was based on Cross and Perry’s double square root from 1996 [12]. It is clear that there is a necessity to update the grain harvester and combine the remaining value analysis.
1.2. Current Issues
The manufacturer’s product portfolio has evolved in complexity to the extent that it includes similar engine power, threshing, separating, cleaning, grain and residue management systems, as well as traction systems (wheels and tracks) that exert a significant influence on the selling price (Table 1).

Table 1.
A 300 kW combine list price (List Price relative to B|Ca|005 most cost-sensitive proposition as 1).
Divergent demands from the market for various productivity, efficiency, maintenance, and repair requirements arise due to the distinct characteristics of the engine power, threshing, separating, cleaning, and grain and residue management systems, as well as traction systems (wheels and tracks) in combines, even if they possess the same engine power, resulting in differing residual values. Consequently, assessing the residual value of these varied combines solely based on their engine power might pose challenges.
The lifespan of the combine series is considerably influenced by the off-road diesel engine emission regulations [17,18,19,20] established by the European Commission (EC). Meanwhile, the off-road diesel emission regulations have impacted the cost [21,22], and it is not farfetched to assume that new emission regulations will incur additional associated costs [23], despite the implementation of the latest European emission regulation. The implementation cost of the off-road diesel engine emission regulations exhibits a significant increase due to the allocation of fixed costs to a smaller number of engines, as depicted in Figure 3.

Figure 3.
Combine list prices in Germany compared to Euro zone inflation (HICP) (1997 HICP and price increase value reference as 1).
1.3. Goal
The primary objective of this research is to devise a residual value computation approach and framework that adequately fulfills three fundamental requisites. Firstly, the model must rely solely on publicly available information to ensure accessibility for all stakeholders, including owners, users, marketers, financiers, and insurers. Secondly, the model should offer robust forecasting capabilities to support informed decision making regarding usage strategies. Finally, to facilitate ease of use, the model must have low cognitive requirements, enabling all stakeholders to make fact-based decisions on optimizing the input and output relationship of grain harvester combines from the leading Original Equipment Manufacturers (OEMs), including Claas, John Deere, and New Holland, in the primary markets of Western Europe [8]. Through developing such a model, this study aims to provide a valuable tool to support decision making in the grain harvester combine market, thereby enhancing the productivity and profitability of stakeholders in this industry.
2. Materials and Methods
2.1. Dataset
In order to conduct a thorough analysis, it is essential to have access to accurate and comprehensive data. Unfortunately, there is currently a lack of transactional European information on combines, making it challenging to perform a proper analysis [8].
Therefore, this study relies on data from professional retailers who advertise their grain combine harvesters on online platforms, such as https://www.agriaffaires.com/, https://www.mascus.com/, and https://www.tractorpool.com/ (retrieved 15 July 2022). The data is limited to machines manufactured by Claas, John Deere, and New Holland and advertised in Austria, Belgium, Denmark, Finland, France, Germany, Italy, Lithuania, Netherlands, Norway, Poland, Spain, Sweden, and the United Kingdom.
To ensure data accuracy, the grain combine harvester models was aligned with the original equipment manufacturer’s official nomenclature, and redundant advertisements were removed.
To estimate the transactional values of agricultural used equipment in a specific set of countries, interviews were conducted with subject matter experts familiar with the local markets. These experts confirmed that the average surrendered negotiating gap in these markets was approximately 10%, depending on various factors, such as sales terms and conditions, trade-in value, machine appeal, and proximity to the end of the sales window. This negotiating gap value was subsequently used to transform the advertised prices of the agricultural used equipment gathered from the relevant web portals into estimated transactional values.
To validate the accuracy of the estimated transactional values, further enquiries and appraisals were conducted, which confirmed the results of the advertised to transactional price conversion. The consulted subject matter experts also provided valuable insights into the local market dynamics and the factors influencing the negotiation process.
The use of subject matter experts to estimate transactional values in the agricultural used equipment market proved to be a reliable and effective approach. By leveraging their expertise and insights into the local market conditions and negotiation practices, it has been possible to estimate transactional values with a high degree of accuracy, even in markets where comprehensive data is not readily available.
The resulting dataset consists of 1197 unique combine observations, with particular attention paid to data standardization, parsing, and deduplication (data enrichment was not necessary as only advertisements including age, hours and (“&”/”^”) price were collected).
2.2. Data Systematization and Preprocessing
Calculating the residual value (RV), as described by Herranz-Matey and Ruiz-Garcia [24], gives the following equation:
2.2.1. New Equivalent Combine
In the context of combine models, a series refers to a group of combines that share fundamental features, such as wheelbase and mass, separating, threshing, and grain and residue management systems, and are primarily distinguished by their engine power. With technological advancements, newer series is introduced with enhancements aimed at improving efficacy and/or efficiency. However, the new series may not always have a direct replacement model with similar features to the older series, which may have been discontinued due to changes in technology. The retail price of a new model in a series includes inflation changes, regulatory compliance costs, and additional features deemed necessary by the market (see Table 2).

Table 2.
Model genealogy sample.
Acquiring the retail price of contemporary models is relatively effortless for the domain experts who will employ the methodology outlined in this investigation, as it can be accessed through certain manufacturers’ websites and/or obtained through a dealer’s quotation.
2.2.2. Combine Family
Manufacturers include some price-impacting options, such as land-leveling machines, flat level, tires, or rubber tracks are included in the names, while others include the several threshing and or separating systems in the model name, whereas others do not.
In addition, there is variability in the number of sales across different product lines, which results in distinct discrepancies in online advertisements. This allows for the subdivision of the product lines into several families that share common features and specifications (see Table 3).

Table 3.
Family model details.
Integrating the new equivalent combine and combine family has played a crucial role in consolidating a dataset of 1197 combines for this research.
2.3. Data Analysis
The aim of this study is to achieve the most accurate results possible by utilizing accessible tools and methodology. However, to ensure that the best results are obtained, it is essential to evaluate more advanced models and tools. Therefore, various models and subtypes were assessed, as previously mentioned, by utilizing different variables and validation methods.
The models analyzed included ensemble methods (Bagged Trees and Boosted Trees), Gaussian Process Regression (GPR) (Exponential, Matern 5/2, Rational Quadratic, Squared Exponential), Kernel (Least Square Regressions and Supported Vector Machines), Linear Regressions (Linear and Robust Linear), Neural Network (Bilayered, Medium, Narrow, Trilayered and Wide), Supported Vector Machine (SVM) (Coarse Gaussian, Cubic, Fine Gaussian, Linear, Median, and Quadratic), and Tree (Fine and Medium).
The fitted models were tested with varying numbers of predictor variables, ranging from 2 (age and hours by tractor family) to 9 (age, hours, model, current equivalent model, brand, country, wheelbase, and engine power).
Cross-over validation (3, 5, 7, and 9 folds) and holdout validation (5%, 10%, 15%, 20%, and 25%) were used with 5% test data, and machine learning optimization was incorporated.
In addition, the following parametric models were evaluated for all the combine families.
Linear (lin-lin):
Logarithmic (lin-log):
Power (log-log):
Exponential (log-lin):
Double square root:
Polynomial 12:
Polynomial 21:
Polynomial 22:
In this regression analysis, the performance of different models was evaluated using the Root Mean Squared Error (RMSE) and Adjusted Coefficient of Determination (RSqAdj) metrics. RMSE was chosen to standardize the error in the same units as the outcome variable, facilitating the interpretation of the model’s accuracy. A lower RMSE value indicates a closer fit of the model to the regression line, thus higher accuracy. When a model is perfectly accurate, the RMSE value will be zero.
The adjusted coefficient of determination (RSqAdj) metric is a better evaluation measure than coefficient of determination (RSq), as it accounts for the number of predictor variables used to predict the dependent variable. RSqAdj is a statistical measure that indicates the proportion of variance in the dependent variable explained by the regression model. In contrast, the RSqAdj considers the number of predictor variables used and adjusts the RSq value to penalize the inclusion of irrelevant variables that may inflate the RSq value [25].
3. Results
The performance of various models with different numbers of predictors was assessed using Root Mean Square Error (RMSE) as the evaluation metric. The results indicated that models with seven predictors outperformed those with three, five, and other predictors. Additionally, hold-out validation produced better RMSE values compared to cross-validation. Among the different types of models tested, Exponential Gaussian Process Regression (GPR) exhibited the most consistent RMSE results across all variables and validation methods. Specifically, the best non-parametric model was identified as Exponential Gaussian Process Regression with 7 predictors and 5% hold-out validation, as it yielded the best RMSE and RSqAdj results (as indicated by rhomboid dots in Figure 4).

Figure 4.
Nonparametric tested models, validations, and predictors with best RMSE and RSqAdj results.
Thus, the optimal non-parametric model was determined to be the Exponential Gaussian Process Regression with 7 predictors, validated using 5% hold-out, with an RMSE of 0.0557 and an RSqAdj of 0.9281.
In light of the suggested methodology for power regression models that rely on two predicting variables of combine families, it became necessary to examine more sophisticated models. To this end, the combine families that yielded the best power regression model Root Mean Square Error (RMSE) results were subjected to the same fitted models, with a 5% hold-out validation serving as the data sets.
The Optimized Gaussian Process Regressions of the combine family grouped two predictors (age and hours) for the considered combine families. The results were consistently favorable for each of the combine families (Figure 5).
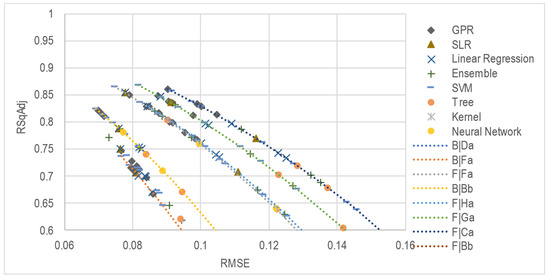
Figure 5.
Nonparametric tested models with two predictors (age and hours) of combine families with best RMSE and RSqAdj results.
We recommend the power regression model (5), as it offered the best RMSE and RSqAdj determination results (Table 4 and Figure 6).

Table 4.
Combine power regression results.

Figure 6.
Combine power regression results.
The combine family grouped two predictors (age and hours) of the considered combine families modeled with Gaussian process regressions optimized with machine learning provided very favorable RMSE and RSqAdj, but even when optimized with machine learning, its performance is surpassed by the proposed residual value power linear regression (Table 5).

Table 5.
Combine family two predictors’ parametric and nonparametric regression results.
4. Discussion
This present study evaluated the robustness of the posited power regression model through comparisons with previously referenced regression models that provided sufficient details for processing the dataset. Additionally, regression models were fitted to the complete dataset using multiple variables and validations, as well as to combine families using the same two predictors (age and hours) employed in the proposed power linear regression. Whenever sufficient details were provided, the previous studies’ regression models were employed to process the complete dataset. (Table 6).

Table 6.
Previous studies results.
The suggested power regression model (with RMSE = 0.0854 and RSqAdj = 0.8342) exhibits superior predictive robustness. Prior research has incorporated brand and power, in addition to years of age and hours of usage, to forecast residual value behavior. However, Table 1 indicates that power alone is insufficient to differentiate residual value behavior as similar combine families from the same brand with identical power specifications can exhibit distinct threshing, separating, and grain handling technologies as ground propulsion systems. The suggested power residual value regression model addresses this issue by considering all these aspects at the model level and categorizing them into combine families, which provides a sturdier foundation for the results (Figure 7).

Figure 7.
Proposed residual value power linear regression for combine family B|Ba.
In comparison to the preceding studies, this research exhibits improved RMSE and adjusted coefficient of determination (RSqAdj) as it accounts for more than the brand, power, and specification levels (threshing, separating, and grain handling and ground propulsion systems) and relates them to an equivalent new model, providing a precise price reference that encompasses variations in inflation and production costs. This approach establishes a more solid basis for producing results that are robust and reliable.
Methodology and Model Derived Grain Combine Harvester Remaining Value Forecaster Tool
The primary objectives of this present study are to enhance the ease of use and robustness of the forecast, thereby enabling all stakeholders to evaluate the residual value of a grain combine harvester quickly and accurately. To this end, a power remaining value regression has been proposed, which can be transformed into a powerful yet straightforward tool utilizing the same mainstream spreadsheet employed for calculating the power regressions. The regression coefficients apply to any combined family at any age and hours, rendering comparisons between families effortless by implementing filters (or slicers) and creating charts.
High-performance machines (high-performance tangential threshing and walker separation (F|Ca and F|Da) and rotary threshing and separation (F|Ba) even more show) suffer quicker residual value loss compared to more conventional combines (F|Fa and F|Ga) of the same brand (which makes it a fairer comparison, eliminating brand market perception) (Figure 8).

Figure 8.
Residual value (value as new =1) comparison of Brand F combine families with 150 h per year (HPY).
The same effect can be seen when concentrating on high-performance machines. High-performing rotary combines (D|Ba) lose value faster than high-performance tangential threshing and walker separation (D|Da and D|DEa) of the same brand (Figure 9).

Figure 9.
Residual value (value as new = 1) comparison of Brand D high performance combine families with 150 h per year (HPY).
The same behavior can be observed in mid-size combines, where rotary separation combines (B|Da) show faster residual value loss compared to walker separation families (B|Ea and B|Fa), while all three families from the same brand share the same tangential separating system (Figure 10).

Figure 10.
Residual value (value as new = 1) comparison of Brand B combine families with 150 h per year (HPY).
The high-performance combine family B|Ba pioneered the market by offering a rubber-tracked version, family B|Bb. The rubber-track option implies a bigger initial investment. The residual value of the former is higher compared to the latter (Figure 11).
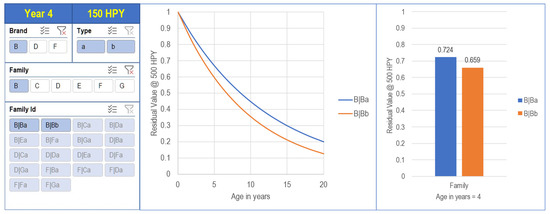
Figure 11.
Residual value (value as new =1) comparison of Brand B high performance combine families B|Ba featuring tires and B|Bb featuring rubber tracks with 150 h per year (HPY).
Not all combines are created equal, and neither are their performance capacities nor the cost of operation. The proposed power residual value regression clearly states that the cost of ownership is also not created equal, showing significant differences.
Therefore, it is mandatory to analyze if the costs derived from higher performance-enhancing features are truly compensated by the actual performance. There might be harvesting conditions that make a certain feature a must-have “ticket to the game”, therefore, unavoidable; meanwhile, in others, it might be a nice-to-have “capricious hype”; only a thorough analysis will ascertain which one is which.
5. Conclusions
This study introduces a combine-based and family-grouped methodology that overcomes the limitations of previous residual value analyses relying on auctions and advertisements to gather data. By focusing on the main drivers of combine value, namely age and usage, and using more sophisticated regression models (linear, exponential, ordinary least squares, Box–Cox, and double square root), the proposed power regression curve provides a robust RMSE of 0.0854 and an RSqAdj of 0.8342, which outperforms all the previous studies and models tested in this study. This present methodology takes into account the specifications of each combine model while considering the price increase caused by emission regulations and specification advancements. This is achieved by comparing the retail price of used combines to the retail price of equivalent new combines. Furthermore, to compensate for the limited statistical population, the models are grouped into family units or subdivided based on significant differences within combine models. The proposed power regression model is uncomplicated and requires only a simple internet search on used equipment websites and two enquiries to sellers, making it effortless to obtain information that is later processed transparently in a universally known software. Despite its simplicity, this power regression model has not been surpassed by more advanced models, including those utilizing machine learning optimization.
This study enables farmers, contractors, sellers, and financial and insurance entities to make informed decisions on harvesting tasks (e.g., purchasing, renting, leasing, or custom hiring) by accessing public information and using a user-friendly yet robust model. Future studies could explore methods of increasing the dataset size by incorporating auction results as a source of transactional information, given the establishment of a correlation between retail and wholesale prices. Additionally, it would be advantageous to evaluate this system with other self-propelled agricultural machines, such as roots, vegetables, forage harvesters, and sprayers.
Author Contributions
Conceptualization, I.H.-M.; methodology, I.H.-M. and L.R.-G.; validation, I.H.-M.; formal analysis, I.H.-M. and L.R.-G.; investigation, I.H.-M. and L.R.-G.; resources, I.H.-M.; data curation, I.H.-M.; writing—original draft preparation, I.H.-M. and L.R.-G.; writing—review and editing, I.H.-M. and L.R.-G.; supervision, L.R.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
If necessary, we can provide raw data.
Acknowledgments
The authors thank Pilar Linares for her support and “Tractores y Máquinas” (https://www.tractoresymaquinas.com) for providing the IT infrastructure for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- FAO. Handbook on Agricultural Cost of Production Statistics; FAO: Rome, Italy, 2016. [Google Scholar]
- Strivastava, A.K.; Goering, C.E.; Rohrbach, R.P.; Buckmaster, D.R. Machinery Selection and Management. In Engineering Principles of Agricultural Machines; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2006; Chapter 15; pp. 525–552. [Google Scholar]
- Strivastava, A.K.; Goering, C.E.; Rohrbach, R.P.; Buckmaster, D.R. Grain Harvesting. In Engineering Principles of Agricultural Machines; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2006; Chapter 12; pp. 403–436. [Google Scholar]
- AXEMA. Economic Report; AXEMA: Paris, France, 2022. [Google Scholar]
- CEMA. European Agricultural Machinery Industry Key Figures; CEMA: Brussels, Belgium, 2022. [Google Scholar]
- Isaac, N.E.; Quick, G.R.; Birrell, S.J.; Edwards, W.M.; Coers, B.A. Combine Harvester Econometric Model with Forward Speed Optimization. Appl. Eng. Agric. 2006, 22, 25–31. [Google Scholar] [CrossRef]
- ACEA. Economic and Market Report. State of the EU Auto Industry. Full-Year 2021; European Automobile Manufacturers’ Association (ACEA): Brussels, Belgium, 2022. [Google Scholar]
- CEMA. Economic Press Release Tractor Registrations 2021; CEMA Aisbl—European Agricultural Machinery: Brussels, Belgium, 2022. [Google Scholar]
- Weersink, A.; Stauber, S. Optimal Replacement Interval and Depreciation Method for a Grain Combine. West. J. Agric. Econ. 1988, 13, 18–28. [Google Scholar]
- Leatham, D.J.; Baker, T.G. Empirical Estimates of the Effects of Inflation on Salvage Values, Cost and Optimal Replacement of Tractors and Combines. North Cent. J. Agric. Econ. 1981, 3, 109–117. [Google Scholar] [CrossRef]
- Cross, T.L.; Perry, G.M. Depreciation Patterns for Agricultural Machinery. Am. J. Agric. Econ. 1995, 77, 194–204. [Google Scholar] [CrossRef]
- Cross, T.L.; Perry, G.M. Remaining Value Functions for Farm Equipment. Appl. Eng. Agric. 1996, 12, 547–553. [Google Scholar] [CrossRef]
- Unterschultz, J.; Mumey, G. Reducing Investment Risk in Tractors and Combines with Improved Terminal Asset Value Forecasts. Can. J. Agric. Econ. 1996, 44, 295–309. [Google Scholar] [CrossRef]
- Wu, J.; Perry, G.M. Estimating Farm Equipment Depreciation: Which Functional Form Is Best? Am. J. Agric. Econ. 2004, 86, 483–491. [Google Scholar] [CrossRef]
- Kay, R.D.; Edwards, W.M.; Duffy, P.A. Farm Management, 7th ed.; McGraw-Hill: New York, NY, USA, 2020. [Google Scholar]
- ASABE. Agricultural Machinery Management Data ASAE Standard D497.7 Agricultural Machinery Management Data; American Society of Agricultural and Biological Engineers: Joseph, MI, USA, 2020. [Google Scholar]
- EC. Directive 97/68/EC of the European Parliament and of the Council of 16 December 1997; European Commission (EC): Brussels, Belgium, 1997. [Google Scholar]
- EC. Directive 2000/25/EC of the European Parliament; European Commission (EC): Brussels, Belgium, 2000. [Google Scholar]
- EC. Directive 2004/26/EC of the European Parliament and of the Council of 21 April 2004 Amending Directive 97/68/EC; European Commission (EC): Brussels, Belgium, 2004. [Google Scholar]
- EC. Directive 2009/30/EC of the European Parliament and of the Council of 23 April 2009 Amending Directive 98/70/EC; European Commission (EC): Brussels, Belgium, 2009. [Google Scholar]
- Posada, F.; Chambliss, S.; Blumberg, K. Cost of Emission Reduction Technologies for Heavy Duty Diesel Vehicles; The International Council on Clean Transportation (ICCT): Washington, DC, USA, 2016. [Google Scholar]
- Lynch, L.A.; Hunter, C.A.; Zigler, B.T.; Thomton, M.J.; Reznicek, E.P. On-Road Heavy-Duty Low-NOx Technology Cost Study; Technical Report NREL/TP-5400-76571; National Renewable Energy Laboratory (NREL), U.S. Department of Energy: Golden, CO, USA, 2020. [Google Scholar]
- Posada, F.; Isenstadt, A.; Badshah, H. Estimated Cost of a Diesel Emissions-Control Technology to Meet Future California Low NOx Standards in 2024 and 2027; The International Council of Clean Transportation: Washington, DC, USA, 2020. [Google Scholar]
- Herranz-Matey, I.; Ruiz-Garcia, L. A New Method and Model for the Estimation of Residual Value of Agricultural Tractors. Agriculture 2023, 13, 409. [Google Scholar] [CrossRef]
- McCarthy, R.V.; McCarthy, M.M.; Ceccucci, W.; Halawi, L. Applying Predictive Analytics; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-030-14037-3. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).