Behavioral Analysis of Mowing Workers Based on Hilbert–Huang Transform: An Auxiliary Movement Analysis of Manual Mowing on the Slopes of Terraced Rice Fields
Abstract
1. Introduction
2. Related Studies and Hypotheses
2.1. Human Movement Analysis
2.2. Hilbert–Huang Transform
3. Methodology
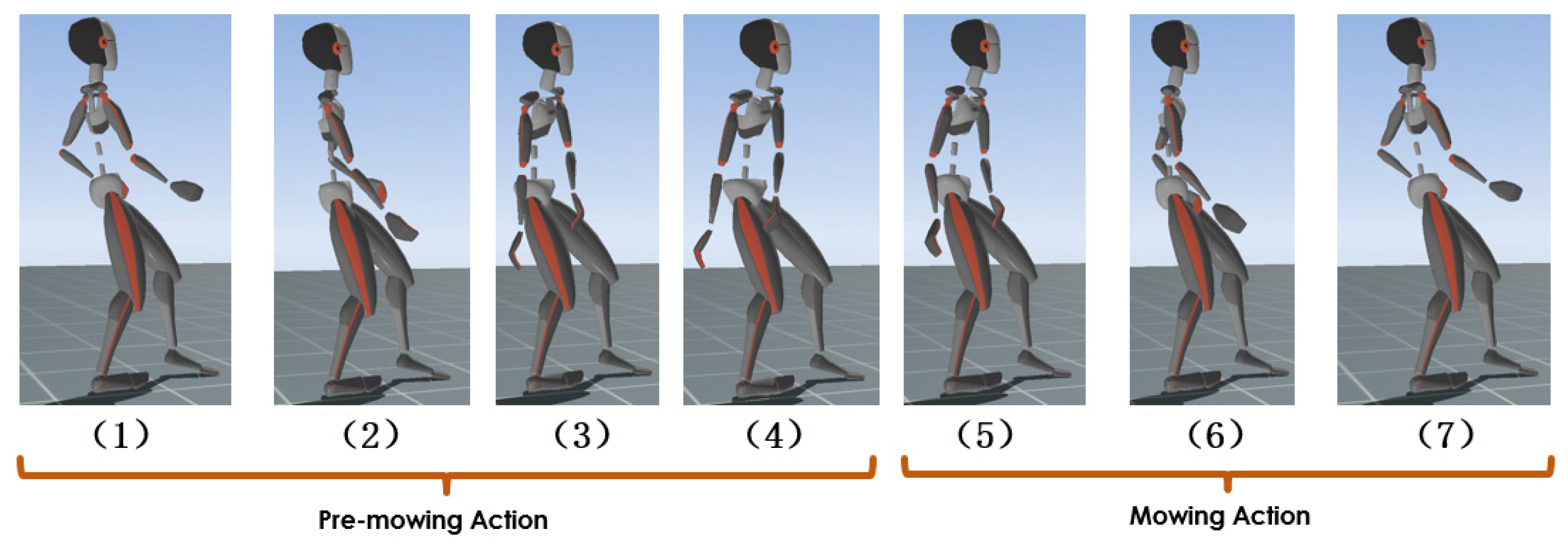
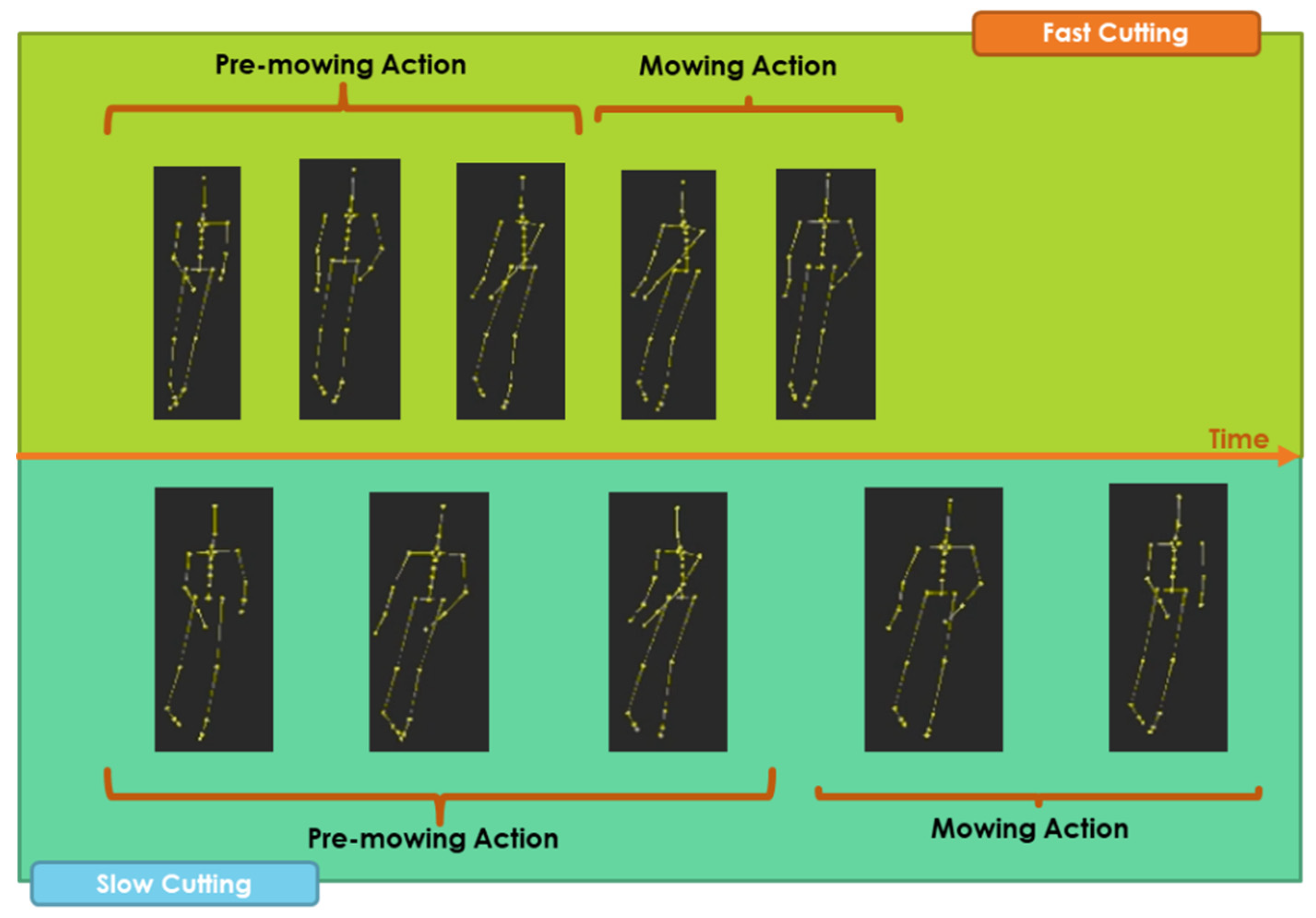
3.1. Definition: Mowing Motion on Slopes and Pre-Cutting Actions
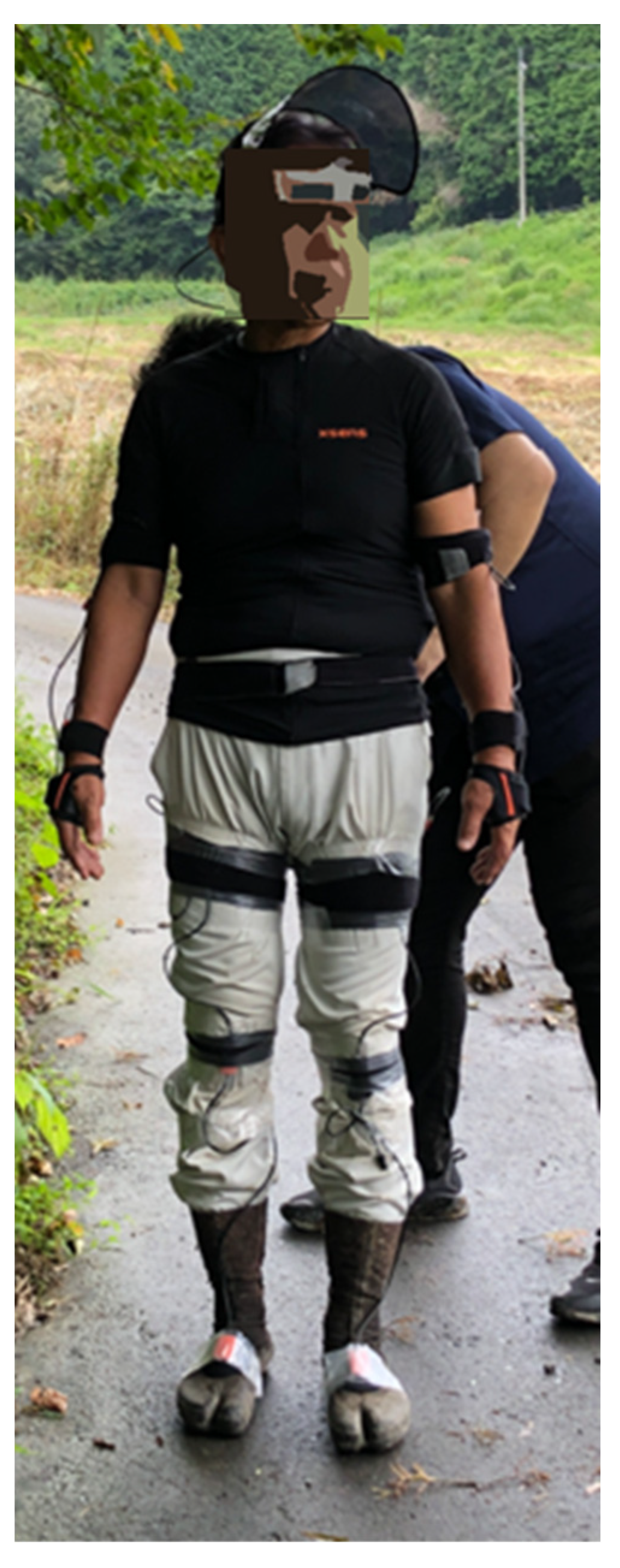
3.2. Device: Body Motion Capture MVN
3.3. Method: Hilbert–Huang Transform
3.3.1. Hilbert–Huang Transform
3.3.2. Empirical Mode Decomposition
- The difference between the local extrema and zero crossings should not exceed one.
- The mean value of the upper and lower envelopes derived from the local extrema should equal zero.
- Compute the residuals. (Initially, ).
- 2.
- Initialize and retrieve .
- (a)
- The envelope connecting the maxima of and the envelope connecting the minima are obtained by cubic spline interpolation, and the average of and is subtracted from .
- (b)
- If satisfies the convergence condition it is added to the IMF set, . Otherwise, steps (a) and (b) are repeated.
- 3.
- Repeat steps 1 and 2 until all IMFs are extracted.
3.3.3. Multivariate Empirical Mode Decomposition
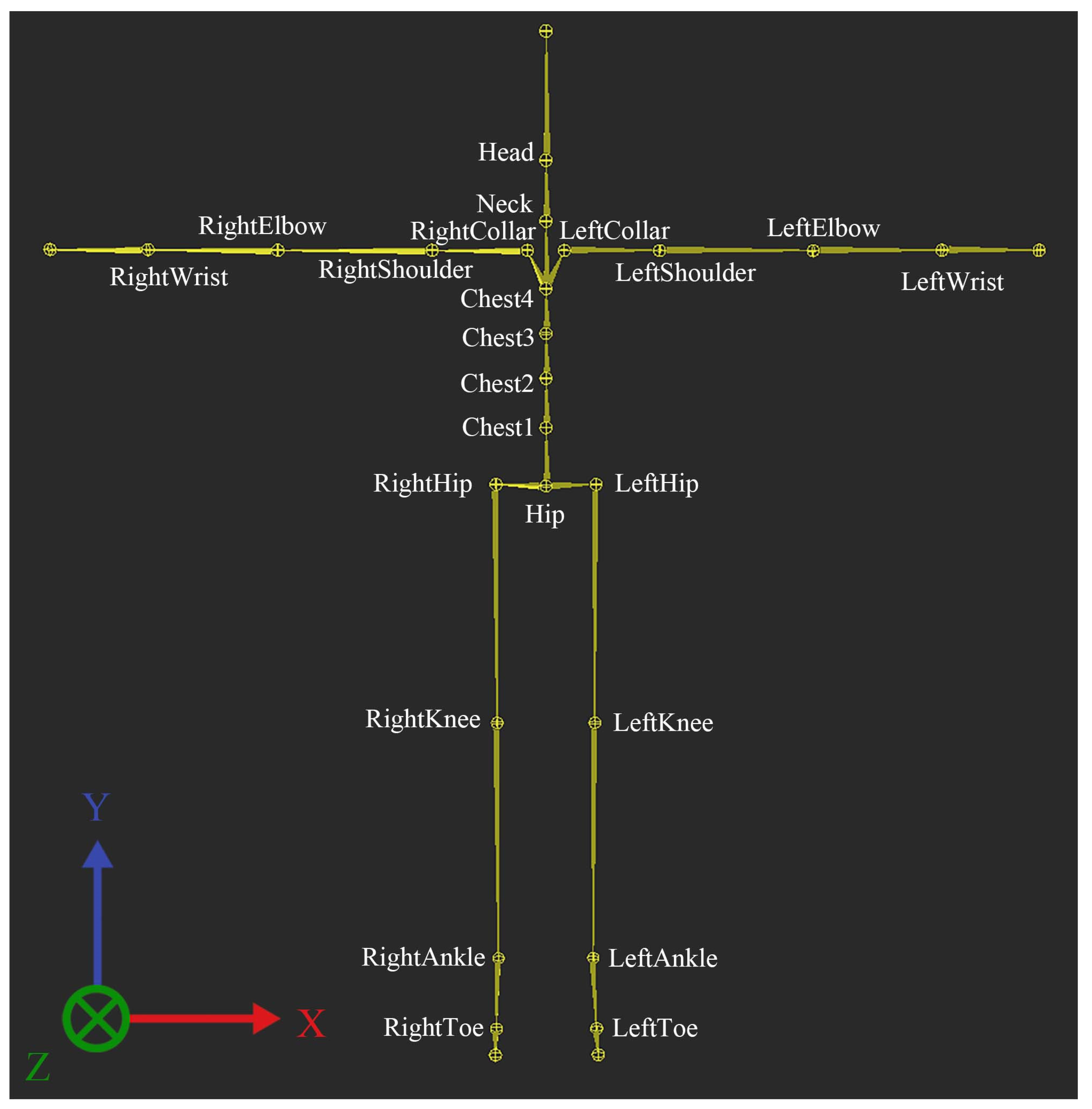
3.3.4. Joint Structure
3.3.5. Mowing Motion Decomposition
3.3.6. Average Amplitude and Frequency
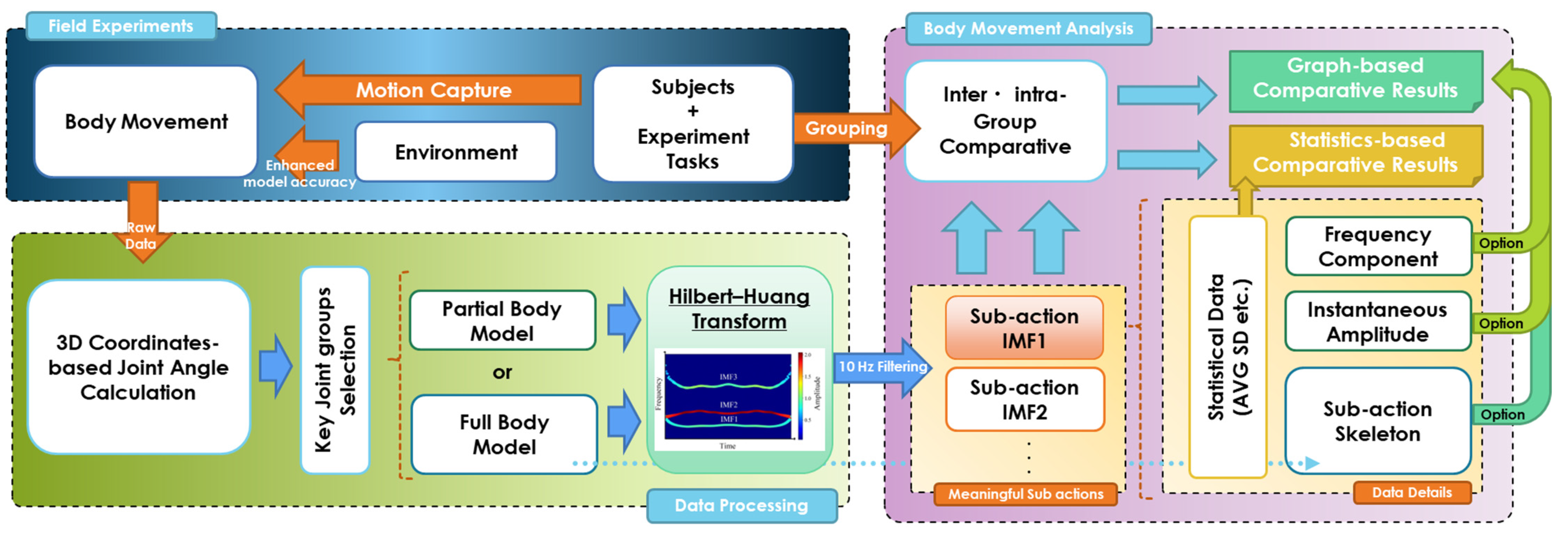
3.4. Model: Joint Angular Calculation-based Body Movement Analysis
- Field experiments: The purpose of the vast majority of human behavior comparison experiments is to find out the similarities and differences between different subject groups. Therefore, this model argues that in the field experiment stage, it is necessary to group subjects in advance for the purpose of the experiment and to collect the environmental data of the experimental site as objectively as possible. This will enhance the 3D model accuracy captured by the devices for the final human body movements.
- Data processing: After receiving the raw data of body movements, this model does not put the data into machine learning or other black-box algorithms directly. Instead, the model calculates all the joint angles of the subject’s body based on their original 3D coordinates before the analysis and then selects the most relevant parts to represent their body movement characteristics data for calculation according to the experimental purpose. Based on this, the corresponding model (full or partial) will be selected, and the HHT movement decomposition method will be used to decompose the target body movements to obtain the raw overall statistics and time-series-based graphical data for the following analysis.
- Body movement analysis: Because not all sub-actions have an obvious purpose, some minor redundant actions that are not even perceptible to humans need to be eliminated before the analysis (10 Hz filtering). In combination with the previous grouping of subjects, the model classifies all meaningful sub-actions (IMF1, IMF2,...) of the relevant data into two types (statistic data and graph data) before the between and within groups comparative analyses. Different types of sub-action data can be analyzed in different comparative ways. This will facilitate model users’ interpretation and discussion of the purpose and effect of the target sub-action from different perspectives of the whole and time series.
4. Field Experiments and Dataset
4.1. Field Experiments
4.2. Dataset
5. Data Processing and Analysis
5.1. HHT-based Actions Decomposition and Classification
5.2. Differences between Workers with Different Mowing Experience
5.2.1. Differences between Workers with Different Mowing Experience (Fast)
5.2.2. Differences between Workers with Different Mowing Experience (Slow)
5.3. Falling Risk Analysis
5.3.1. Falling Risk Analysis for Pre-Cutting SD_hip (Freq. Fast)
5.3.2. Falling Risk Analysis for Pre-Cutting SD_hip (Amp. Fast)
5.3.3. Falling Risk Analysis for Pre-Cutting SD_hip (Freq. Slow)
5.3.4. Falling Risk Analysis for Pre-Cutting SD_hip (Amp. Slow)
6. Discussion & Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yasushi, U.; Koujirou, I.; Yuuki, I. Development of Remote Control Paddy Ridge Mower in Nagano Prefecture, System/Control/Information. Inst. Syst. Control. Inf. Eng. 2021, 65, 471–476. [Google Scholar] [CrossRef]
- Iwano, Y. Development of the mowing robot of trimmer type. In Proceedings of the SICE Annual Conference 2010, Taipei, Taiwan, 18–21 August 2010; pp. 1349–1352. [Google Scholar]
- Open Access Report, Ministry of Agriculture, Forestry, and Fisheries of Japan, Agriculture and Forestry Census. Available online: https://www.maff.go.jp/j/tokei/sihyo/data/08.html (accessed on 29 May 2022).
- Ministry of Agriculture, Forestry, and Fisheries. Outline of Agricultural Work Death Accidents that Occurred in 2018. Agricultural Work Fatal Accident Investigation. pp. 1–11. Available online: https://www.maff.go.jp/j/seisan/sien/sizai/s_kikaika/anzen/attach/pdf/index-101.pdf (accessed on 29 May 2022).
- Ministry of Agriculture, Forestry, and Fisheries. Farm Work Accident That Happened in This Way IV. Investigation of Agricultural Work Accident. p. 41. Available online: http://www.maff.go.jp/j/seisan/sien/sizai/s_kikaika/anzen/23taimen.html (accessed on 29 May 2020).
- Suenaga, E.; Sumiyoshi, Y.; Takada, S.; Umin, K. Two cases of serious cardiovascular disease found after orthopedic consultation. Orthop. Surg. Disaster Surg. 2017, 66, 900–903. [Google Scholar]
- Wu, B.; Zhu, Y.; Nishimura, S.; Jin, Q. Analyzing the Effects of Driving Experience on Prebraking Behaviors Based on Data Collected by Motion Capture Devices. IEEE Access 2020, 8, 197337–197351. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Bruderlin, A.; Williams, A. Motion signal processing. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August 1995. [Google Scholar]
- Troje, N.F. Decomposing biological motion: A framework for analysis and synthesis of human gait patterns. J. Vis. 2002, 2, 371–387. [Google Scholar] [CrossRef]
- Aminian, K.; Najaf, B. Capturing human motion using body-fixed sensors: Outdoor measurement and clinical applications. Comput. Animat. Virtual Worlds 2004, 15, 79–94. [Google Scholar] [CrossRef]
- Dong, R.; Cai, D.; Ikuno, S. Motion capture data analysis in the instantaneous frequency-domain using Hilbert–Huang transform. Sensors 2020, 20, 6534. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.; Chen, Y.; Cai, D.; Nakagawa, S.; Higaki, T.; Asai, N. Robot motion design using bunraku emotional expressions—Focusing on Jo-Ha-Kyū in sounds and movements. Adv. Robot. 2020, 34, 299–312. [Google Scholar] [CrossRef]
- Dong, R.; Chang, Q.; Ikuno, S. A deep learning framework for realistic robot motion generation. Neural Comput. Appl. 2021. [Google Scholar] [CrossRef]
- Wu, B.; Wu, Y.; Nishimura, S.; Jin, Q. Analysis on the Subdivision of Skilled Mowing Movements on Slopes. Sensors 2022, 22, 1372. [Google Scholar] [CrossRef]
- Wu, B.; Wu, Y.; Aoki, Y.; Nishimura, S. Mowing Patterns Comparison: Analyzing the Mowing Behaviors of Elderly Adults on an Inclined Plane via a Motion Capture Device. IEEE Access 2020, 8, 216623–216633. [Google Scholar] [CrossRef]
- Google. Mediapipe. Available online: https://google.github.io/mediapipe/ (accessed on 29 May 2022).
- Zhang, S.; Chen, W.; Chen, C.; Liu, Y. Human deep squat detection method based on MediaPipe combined with Yolov5 network. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 6404–6409. [Google Scholar] [CrossRef]
- Ma, J.; Ma, L.; Ruan, W.; Chen, H.; Feng, J.A. Wushu Posture Recognition System Based on MediaPipe. In Proceedings of the 2022 2nd International Conference on Information Technology and Contemporary Sports (TCS), Guangzhou, China, 24–26 June 2022; pp. 10–13. [Google Scholar] [CrossRef]
- Cockcroft, J.; Scheffer, C. Determining the Feasibility of Measuring Outdoor Road Cycling Kinematics Using Inertial Motion Capture Technology. SAIEE Afr. Res. J. 2011, 102, 31–39. [Google Scholar] [CrossRef]
- Wouda, F.J.; Giuberti, M.; Bellusci, G.; Maartens, E.; Reenalda, J.; Van Beijnum BJ, F.; Veltink, P.H. On the Validity of Different Motion Capture Technologies for the Analysis of Running. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; pp. 1175–1180. [Google Scholar] [CrossRef]
- Huang, E.N.; Shen, S.S.P. Hilbert–Huang Transform and Its Applications, 2nd ed.; World Scientific Publishing: Singapore, 2014. [Google Scholar]
- Rilling, G.; Flandrin, P.; Gonçalves, P.; Lilly, J.M. Bivariate empirical mode decomposition. IEEE Signal Process. Lett. 2007, 14, 936–939. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Empirical Mode Decomposition for Trivariate Signals. IEEE Trans. Signal Process. 2010, 58, 1059–1068. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. R. Soc. 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- Bracewell, R.N. Fourier Transform and Its Applications; McGraw-Hill Inc Press: New York, NY, USA, 1978. [Google Scholar]
- Wu, B.; Zhu, Y.; Dong, R.; Sato, K.; Ikuno, S.; Nishimura, S.; Jin, Q. Pre-braking behaviors analysis based on Hilbert–Huang transform. CCF Trans. Pervasive Comp. Interact. 2022. [Google Scholar] [CrossRef]
- Yang, Y.; Hao, F.; Pang, B.; Min, G.; Wu, Y. Dynamic Maximal Cliques Detection and Evolution Management in Social Internet of Things: A Formal Concept Analysis Approach. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1020–1032. [Google Scholar] [CrossRef]
- Hao, F.; Yang, Y.; Mi, G.; Loia, V. Incremental Construction of Three-way Concept Lattice for Knowledge Discovery in Social Networks. Inf. Sci. 2021, 578, 257–280. [Google Scholar] [CrossRef]
- Li, M.; Chen, S.; Chen, X.; Zhang, Y.; Wang, Y.; Tian, Q. Symbiotic graph neural networks for 3d skeleton-based human action recognition and motion prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3316–3333. [Google Scholar] [CrossRef]
- Zhou, F.; De la Torre, F.; Hodgins, J.K. Hierarchical aligned cluster analysis for temporal clustering of human motion. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 582–596. [Google Scholar] [CrossRef]
- Boashsah, B. Estimating and interpreting the instantaneous frequency of a signal. II. Algorithms and Applications. Proc. IEEE 1992, 80, 540–568. [Google Scholar] [CrossRef]
- Niu, J.; Liu, Y.; Jiang, W.; Li, X.; Kuang, G. Weighted average frequency algorithm for Hilbert–Huang spectrum and its application to micro-Doppler estimation. IET Radar Sonar Navig. 2012, 6, 595–602. [Google Scholar] [CrossRef]
- Dong, R.; Ni, S.; Ikuno, S. Non-linear frequency analysis of COVID-19 spread in Tokyo using empirical mode decomposition. Sci. Rep. 2022, 12, 2175. [Google Scholar] [CrossRef] [PubMed]
- Lee, J. “Hip Height and Sprinting,” How to Run Faster… at any Age. Part 3. Available online: https://speedendurance.com/2012/01/31/hip-height-and-sprinting/ (accessed on 22 December 2022).
- Thorpe, S.; Fize, D.; Marlot, C. Speed of processing in the human visual system. Nature 1996, 381, 520–522. [Google Scholar] [CrossRef] [PubMed]


| No. | Body Height | Arm Span | Hip Height | Age | Experience |
|---|---|---|---|---|---|
| 1 | 165 | 163 | 90 | 74 | 40 years~ |
| 2 | 165 | 161 | 97 | 66 | 40 years~ |
| 3 | 176 | 167 | 107 | 68 | 8 years~ |
| 4 | 163 | 170 | 90 | 46 | 6 years~ |
| 5 | 176 | 167 | 107 | 69 | 10 years~ |
| No. | Measure | Abbreviations | No. | Measure | Abb. |
|---|---|---|---|---|---|
| 1 | Hip | Hip | 12 | Right Toe | Rtoe |
| 2 | Chest1-4 | Chest1-4 | 13 | Left Collar | Lcollar |
| 3 | Neck | Neck | 14 | Left Shoulder | Lshoulder |
| 4 | Head | Head | 15 | Left Elbow | Lelbow |
| 5 | Right Collar | Rcollar | 16 | Left Wrist | Lwrist |
| 6 | Right Shoulder | Rshoulder | 17 | Left Hip | Lhip |
| 7 | Right Elbow | Relbow | 18 | Left Knee | Lknee |
| 8 | Right Wrist | Rwrist | 19 | Left Ankle | Lankle |
| 9 | Right Hip | Rhip | 20 | Left Toe | Ltoe |
| 10 | Right Knee | Rknee | 21 | ||
| 11 | Right Ankle | Rankle | 22 |
| S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|
| IMF 1 | 3.023 | 4.683 | 4.589 | 3.325 | 3.718 | 2.097 |
| IMF 2 | 2.871 | 3.375 | 2.979 | 2.122 | 2.217 | 2.035 |
| IMF 3 | 1.852 | 2.040 | 1.833 | 1.55 | 1.249 | 2.078 |
| IMF 4 | 1.035 | 1.158 | 0.999 | 0.900 | 0.707 | 1.511 |
| IMF 5 | 0.613 | 0.703 | 0.574 | 0.517 | 0.442 | 0.959 |
| IMF 6 | 0.355 | 0.436 | 0.371 | 0.28 | 0.247 | 0.601 |
| IMF 7 | 0.178 | 0.242 | 0.190 | 0.153 | 0.139 | 0.347 |
| IMF 8 | 0.097 | 0.133 | 0.100 | 0.080 | 0.072 | 0.191 |
| IMF 9 | 0.052 | 0.069 | 0.057 | 0.044 | 0.038 | 0.104 |
| IMF 10 | 0.031 | 0.038 | 0.031 | 0.022 | 0.024 | 0.056 |
| Measure | Mowing Experience | N | Mean Rank | U | W | Z | p | Effect Size |
|---|---|---|---|---|---|---|---|---|
| Hip_freq * | Novice | 43 | 49.19 | 293 | 888 | −4.49 | 0.00 | −0.51225 |
| Experienced | 34 | 26.12 | ||||||
| Chest_freq * | Novice | 43 | 49.47 | 281 | 876 | −4.62 | 0.00 | −0.52642 |
| Experienced | 34 | 25.76 | ||||||
| Chest2_freq * | Novice | 43 | 48.93 | 304 | 899 | −4.38 | 0.00 | −0.49915 |
| Experienced | 34 | 26.44 | ||||||
| Chest3_freq | Novice | 43 | 49.26 | 290 | 885 | −4.52 | 0.00 | −0.51556 |
| Experienced | 34 | 26.03 | ||||||
| Chest4_freq * | Novice | 43 | 49.44 | 282 | 877 | −4.61 | 0.00 | −0.52492 |
| Experienced | 34 | 25.79 | ||||||
| Neck_freq * | Novice | 43 | 47.93 | 347 | 942 | −3.94 | 0.00 | −0.4489 |
| Experienced | 34 | 27.71 | ||||||
| Head_freq * | Novice | 43 | 49.77 | 268 | 863 | −4.75 | 0.00 | −0.54131 |
| Experienced | 34 | 25.38 | ||||||
| Rcollar_freq * | Novice | 43 | 47.23 | 377 | 972 | −3.63 | 0.00 | −0.4138 |
| Experienced | 34 | 28.59 | ||||||
| Rshoulder_freq * | Novice | 43 | 46.21 | 421 | 1016 | −3.18 | 0.00 | −0.36239 |
| Experienced | 34 | 29.88 | ||||||
| Relbow_freq * | Novice | 43 | 46.98 | 388 | 983 | −3.52 | 0.00 | −0.41273 |
| Experienced | 34 | 28.91 | ||||||
| Rwrist_freq * | Novice | 43 | 45.37 | 457 | 1052 | −2.81 | 0.01 | −0.32343 |
| Experienced | 34 | 30.94 | ||||||
| Lcollar_freq * | Novice | 43 | 46.37 | 414 | 1009 | −3.25 | 0.00 | −0.376 |
| Experienced | 34 | 29.68 | ||||||
| Lshoulder_freq * | Novice | 43 | 44.33 | 502 | 1097 | −2.35 | 0.02 | −0.26769 |
| Experienced | 34 | 32.26 | ||||||
| Lelbow_freq * | Novice | 43 | 47.65 | 359 | 954 | −3.82 | 0.00 | −0.43487 |
| Experienced | 34 | 28.06 | ||||||
| Lwrist_freq * | Novice | 43 | 45.91 | 434 | 1029 | −3.05 | 0.00 | −0.34724 |
| Experienced | 34 | 30.26 | ||||||
| Rhip_freq * | Novice | 43 | 44.60 | 490 | 1085 | −2.47 | 0.01 | −0.28172 |
| Experienced | 34 | 31.91 | ||||||
| Rknee_freq * | Novice | 43 | 51.42 | 197 | 792 | −5.48 | 0.00 | −0.62428 |
| Experienced | 34 | 23.29 | ||||||
| Rankle_freq * | Novice | 43 | 46.49 | 409 | 1004 | −3.30 | 0.00 | −0.37641 |
| Experienced | 34 | 29.53 | ||||||
| Rtoe_freq ‡ | Novice | 43 | 42.88 | 564 | 1159 | −1.71 | 0.09 | −0.19521 |
| Experienced | 34 | 34.09 | ||||||
| Lhip_freq * | Novice | 43 | 47.53 | 364 | 959 | −3.77 | 0.00 | −0.42962 |
| Experienced | 34 | 28.21 | ||||||
| Lknee_freq * | Novice | 43 | 47.26 | 376 | 971 | −3.64 | 0.00 | −0.41544 |
| Experienced | 34 | 28.56 | ||||||
| Lankle_freq * | Novice | 43 | 47.79 | 353 | 948 | −3.88 | 0.00 | −0.44194 |
| Experienced | 34 | 27.88 | ||||||
| Ltoe_freq * | Novice | 43 | 45.05 | 471 | 1066 | −2.67 | 0.01 | −0.33933 |
| Experienced | 34 | 31.35 |
| Measure | Mowing Experience | N | Mean Rank | U | W | Z | p | Effect Size |
|---|---|---|---|---|---|---|---|---|
| Hip_amp | Novice | 43 | 37.47 | 665 | 1611 | −0.68 | 0.50 | −0.077 |
| Experienced | 34 | 40.94 | ||||||
| Chest_amp | Novice | 43 | 36.95 | 643 | 1589 | −0.90 | 0.37 | −0.103 |
| Experienced | 34 | 41.59 | ||||||
| Chest2_amp | Novice | 43 | 37.44 | 664 | 1610 | −0.69 | 0.49 | −0.078 |
| Experienced | 34 | 40.97 | ||||||
| Chest3_amp | Novice | 43 | 37.16 | 652 | 1598 | −0.81 | 0.42 | −0.092 |
| Experienced | 34 | 41.32 | ||||||
| Chest4_amp | Novice | 43 | 36.88 | 640 | 1586 | −0.93 | 0.35 | −0.106 |
| Experienced | 34 | 41.68 | ||||||
| Neck_amp | Novice | 43 | 38.95 | 729 | 1675 | −0.02 | 0.98 | −0.002 |
| Experienced | 34 | 39.06 | ||||||
| Head_amp | Novice | 43 | 39.88 | 693 | 1288 | −0.39 | 0.70 | −0.044 |
| Experienced | 34 | 37.88 | ||||||
| Rcollar_amp | Novice | 43 | 38.26 | 699 | 1645 | −0.33 | 0.74 | −0.037 |
| Experienced | 34 | 39.94 | ||||||
| Rshoulder_amp * | Novice | 43 | 34.28 | 528 | 1474 | −2.08 | 0.04 | −0.237 |
| Experienced | 34 | 44.97 | ||||||
| Relbow_amp * | Novice | 43 | 28.56 | 282 | 1228 | −4.61 | 0.00 | −0.525 |
| Experienced | 34 | 52.21 | ||||||
| Rwrist_amp * | Novice | 43 | 29.63 | 328 | 1274 | −4.13 | 0.00 | −0.471 |
| Experienced | 34 | 50.85 | ||||||
| Lcollar_amp | Novice | 43 | 42.40 | 585 | 1180 | −1.50 | 0.13 | −0.171 |
| Experienced | 34 | 34.71 | ||||||
| Lshoulder_amp * | Novice | 43 | 34.53 | 539 | 1485 | −1.97 | 0.05 | −0.224 |
| Experienced | 34 | 44.65 | ||||||
| Lelbow_amp | Novice | 43 | 35.26 | 570 | 1516 | −1.65 | 0.10 | −0.188 |
| Experienced | 34 | 43.74 | ||||||
| Lwrist_amp ‡ | Novice | 43 | 34.95 | 557 | 1503 | −1.78 | 0.07 | −0.203 |
| Experienced | 34 | 44.12 | ||||||
| Rhip_amp | Novice | 43 | 39.86 | 694 | 1289 | −0.38 | 0.70 | −0.043 |
| Experienced | 34 | 37.91 | ||||||
| Rknee_amp | Novice | 43 | 40.35 | 673 | 1268 | −0.59 | 0.55 | −0.068 |
| Experienced | 34 | 37.29 | ||||||
| Rankle_amp | Novice | 43 | 34.67 | 545 | 1491 | −1.91 | 0.06 | −0.217 |
| Experienced | 34 | 44.47 | ||||||
| Rtoe_amp | Novice | 43 | 35.95 | 600 | 1546 | −1.34 | 0.18 | −0.153 |
| Experienced | 34 | 42.85 | ||||||
| Lhip_amp | Novice | 43 | 38.58 | 713 | 1659 | −0.18 | 0.85 | −0.021 |
| Experienced | 34 | 39.53 | ||||||
| Lknee_amp | Novice | 43 | 35.47 | 579 | 1525 | −1.56 | 0.12 | −0.178 |
| Experienced | 34 | 43.47 | ||||||
| Hip_amp | Novice | 43 | 41.65 | 617 | 1212 | −1.17 | 0.24 | −0.133 |
| Experienced | 34 | 35.65 | ||||||
| Chest_amp | Novice | 43 | 38.14 | 694 | 1640 | −0.38 | 0.70 | −0.043 |
| Experienced | 34 | 40.09 |
| Measure | Mowing Experience | N | Mean Rank | U | W | Z | p | Effect Size |
|---|---|---|---|---|---|---|---|---|
| Hip_freq | Novice | 43 | 37.86 | 682 | 1628 | −0.50 | 0.62 | −0.05728 |
| Experienced | 34 | 40.44 | ||||||
| Chest_freq * | Novice | 43 | 44.07 | 513 | 1108 | −2.24 | 0.03 | −0.25485 |
| Experienced | 34 | 32.59 | ||||||
| Chest2_freq | Novice | 43 | 44.12 | 511 | 1106 | −2.26 | 0.02 | −0.25719 |
| Experienced | 34 | 32.53 | ||||||
| Chest3_freq * | Novice | 43 | 43.63 | 532 | 1127 | −2.04 | 0.04 | −0.23264 |
| Experienced | 34 | 33.15 | ||||||
| Chest4_freq * | Novice | 43 | 43.58 | 534 | 1129 | −2.02 | 0.04 | −0.2303 |
| Experienced | 34 | 33.21 | ||||||
| Neck_freq | Novice | 43 | 42.07 | 599 | 1194 | −1.35 | 0.18 | −0.15431 |
| Experienced | 34 | 35.12 | ||||||
| Head_freq | Novice | 43 | 43.02 | 558 | 1153 | −1.77 | 0.08 | −0.20224 |
| Experienced | 34 | 33.91 | ||||||
| Rcollar_freq | Novice | 43 | 40.98 | 646 | 1241 | −0.87 | 0.38 | −0.09937 |
| Experienced | 34 | 36.50 | ||||||
| Rshoulder_freq | Novice | 43 | 37.77 | 678 | 1624 | −0.54 | 0.59 | −0.06196 |
| Experienced | 34 | 40.56 | ||||||
| Relbow_freq | Novice | 43 | 42.47 | 582 | 1177 | −1.53 | 0.13 | −0.17418 |
| Experienced | 34 | 34.62 | ||||||
| Rwrist_freq | Novice | 43 | 41.60 | 619 | 1214 | −1.15 | 0.25 | −0.13093 |
| Experienced | 34 | 35.71 | ||||||
| Lcollar_freq | Novice | 43 | 42.23 | 592 | 1187 | −1.43 | 0.15 | −0.16249 |
| Experienced | 34 | 34.91 | ||||||
| Lshoulder_freq | Novice | 43 | 41.91 | 606 | 1201 | −1.28 | 0.20 | −0.14613 |
| Experienced | 34 | 35.32 | ||||||
| Lelbow_freq ‡ | Novice | 43 | 43.33 | 545 | 1140 | −1.91 | 0.06 | −0.21744 |
| Experienced | 34 | 33.53 | ||||||
| Lwrist_freq ‡ | Novice | 43 | 43.16 | 552 | 1147 | −1.84 | 0.07 | −0.20926 |
| Experienced | 34 | 33.74 | ||||||
| Rhip_freq | Novice | 43 | 41.19 | 637 | 1232 | −0.96 | 0.33 | −0.10989 |
| Experienced | 34 | 36.24 | ||||||
| Rknee_freq | Novice | 43 | 42.60 | 576 | 1171 | −1.59 | 0.11 | −0.1812 |
| Experienced | 34 | 34.44 | ||||||
| Rankle_freq | Novice | 43 | 42.65 | 574 | 1169 | −1.61 | 0.11 | −0.18354 |
| Experienced | 34 | 34.38 | ||||||
| Rtoe_freq | Novice | 43 | 38.49 | 709 | 1655 | −0.23 | 0.82 | −0.02572 |
| Experienced | 34 | 39.65 | ||||||
| Lhip_freq | Novice | 43 | 41.81 | 610 | 1205 | −1.24 | 0.21 | −0.14145 |
| Experienced | 34 | 35.44 | ||||||
| Lknee_freq | Novice | 43 | 40.67 | 659 | 1254 | −0.74 | 0.46 | −0.08417 |
| Experienced | 34 | 36.88 | ||||||
| Lankle_freq | Novice | 43 | 40.19 | 680 | 1275 | −0.52 | 0.60 | −0.05962 |
| Experienced | 34 | 37.50 | ||||||
| Ltoe_freq | Novice | 43 | 40.40 | 671 | 1266 | −0.62 | 0.54 | −0.07014 |
| Experienced | 34 | 37.24 |
| Measure | Mowing Experience | N | Mean Rank | U | W | Z | p | Effect Size |
|---|---|---|---|---|---|---|---|---|
| Hip_amp | Novice | 43 | 35.70 | 589 | 1535 | −1.46 | 0.15 | -0.166 |
| Experienced | 34 | 43.18 | ||||||
| Chest_amp * | Novice | 43 | 34.28 | 528 | 1474 | −2.08 | 0.04 | −0.23731 |
| Experienced | 34 | 44.97 | ||||||
| Chest2_amp * | Novice | 43 | 34.77 | 549 | 1495 | −1.87 | 0.06 | −0.21276 |
| Experienced | 34 | 44.35 | ||||||
| Chest3_amp * | Novice | 43 | 34.35 | 531 | 1477 | −2.05 | 0.04 | −0.23381 |
| Experienced | 34 | 44.88 | ||||||
| Chest4_amp * | Novice | 43 | 34.14 | 522 | 1468 | −2.14 | 0.03 | −0.24433 |
| Experienced | 34 | 45.15 | ||||||
| Neck_amp | Novice | 43 | 36.65 | 630 | 1576 | −1.04 | 0.30 | −0.11807 |
| Experienced | 34 | 41.97 | ||||||
| Head_amp | Novice | 43 | 37.00 | 645 | 1591 | −0.88 | 0.38 | −0.10054 |
| Experienced | 34 | 41.53 | ||||||
| Rcollar_amp | Novice | 43 | 38.47 | 708 | 1654 | −0.24 | 0.81 | −0.02689 |
| Experienced | 34 | 39.68 | ||||||
| Rshoulder_amp * | Novice | 43 | 30.84 | 380 | 1326 | −3.60 | 0.00 | −0.41033 |
| Experienced | 34 | 49.32 | ||||||
| Relbow_amp * | Novice | 43 | 24.19 | 94 | 1040 | −6.53 | 0.00 | −0.74467 |
| Experienced | 34 | 57.74 | ||||||
| Rwrist_amp * | Novice | 43 | 26.93 | 212 | 1158 | −5.32 | 0.00 | −0.60672 |
| Experienced | 34 | 54.26 | ||||||
| Lcollar_amp * | Novice | 43 | 47.40 | 370 | 965 | −3.70 | 0.00 | −0.42202 |
| Experienced | 34 | 28.38 | ||||||
| Lshoulder_amp * | Novice | 43 | 33.37 | 489 | 1435 | −2.48 | 0.01 | −0.2829 |
| Experienced | 34 | 46.12 | ||||||
| Lelbow_amp | Novice | 43 | 38.00 | 688 | 1634 | −0.44 | 0.66 | −0.05027 |
| Experienced | 34 | 40.26 | ||||||
| Lwrist_amp * | Novice | 43 | 32.56 | 454 | 1400 | −2.84 | 0.00 | −0.32382 |
| Experienced | 34 | 47.15 | ||||||
| Rhip_amp | Novice | 43 | 41.23 | 635 | 1230 | −0.98 | 0.32 | −0.11223 |
| Experienced | 34 | 36.18 | ||||||
| Rknee_amp | Novice | 43 | 41.09 | 641 | 1236 | −0.92 | 0.36 | −0.10521 |
| Experienced | 34 | 36.35 | ||||||
| Rankle_amp * | Novice | 43 | 34.33 | 530 | 1476 | −2.06 | 0.04 | −0.23497 |
| Experienced | 34 | 44.91 | ||||||
| Rtoe_amp | Novice | 43 | 36.05 | 604 | 1550 | −1.30 | 0.19 | −0.14847 |
| Experienced | 34 | 42.74 | ||||||
| Lhip_amp | Novice | 43 | 36.65 | 630 | 1576 | −1.04 | 0.30 | −0.11807 |
| Experienced | 34 | 41.97 | ||||||
| Lknee_amp | Novice | 43 | 36.33 | 616 | 1562 | −1.18 | 0.24 | −0.13444 |
| Experienced | 34 | 42.38 | ||||||
| Lankle_amp | Novice | 43 | 40.47 | 668 | 1263 | −0.65 | 0.52 | −0.07365 |
| Experienced | 34 | 37.15 | ||||||
| Ltoe_amp ‡ | Novice | 43 | 34.91 | 555 | 1501 | −1.81 | 0.07 | −0.20575 |
| Experienced | 34 | 44.18 |
| Measure | Unstandardized Coef. | Standardized Coef. | T | Sig. | |
|---|---|---|---|---|---|
| B | Std. Error | Beta | |||
| (Constant) | 4.220 | 1.760 | 2.398 | 0.017 | |
| Ankle_height | 0.109 | 0.023 | 0.250 | 4.680 | 0.000 |
| Lhip_freq | 0.196 | 0.034 | 0.255 | 5.749 | 0.000 |
| Head_amp | −0.021 | 0.005 | −0.165 | −3.834 | 0.000 |
| Lankle_freq | 0.140 | 0.046 | 0.140 | 3.014 | 0.003 |
| Foot_or_Shoe_length | −0.239 | 0.062 | −0.204 | −3.854 | 0.000 |
| Head_freq | 0.108 | 0.040 | 0.121 | 2.714 | 0.007 |
| Measure | Unstandardized Coef. | Standardized Coef. | T | Sig. | |
|---|---|---|---|---|---|
| B | Std. Error | Beta | |||
| (Constant) | −66.549 | 4.873 | −13.658 | 0.000 | |
| Rankle_amp | 0.389 | 0.041 | 0.324 | 9.551 | 0.000 |
| Body_height | 0.384 | 0.028 | 0.385 | 13.807 | 0.000 |
| Chest2_amp | 1.669 | 0.190 | 0.280 | 8.787 | 0.000 |
| Lankle_amp | 0.277 | 0.040 | 0.230 | 6.950 | 0.000 |
| Measure | Unstandardized Coef. | Standardized Coef. | T | Sig. | |
|---|---|---|---|---|---|
| B | Std. Error | Beta | |||
| (Constant) | 1.602 | 0.468 | 3.424 | 0.001 | |
| Rankle_freq | 0.207 | 0.041 | 0.196 | 5.022 | 0.000 |
| Lhip_freq | 0.189 | 0.036 | 0.203 | 5.247 | 0.000 |
| Neck_freq | 0.147 | 0.042 | 0.135 | 3.541 | 0.000 |
| Hip_height | −0.025 | 0.005 | −0.215 | −5.052 | 0.000 |
| Lcollar_freq | 0.150 | 0.039 | 0.141 | 3.835 | 0.000 |
| Lankle_freq | 0.138 | 0.043 | 0.128 | 3.235 | 0.001 |
| Age | 0.018 | 0.006 | 0.136 | 3.199 | 0.001 |
| Measure | Unstandardized Coef. | Standardized Coef. | T | Sig. | |
|---|---|---|---|---|---|
| B | Std. Error | Beta | |||
| (Constant) | 0.430 | 0.318 | 1.352 | 0.177 | |
| Lankle_amp | 0.999 | 0.048 | 0.653 | 20.909 | 0.000 |
| Ltoe_amp | −0.516 | 0.064 | −0.209 | −8.022 | 0.000 |
| Rankle_amp | 0.312 | 0.046 | 0.218 | 6.852 | 0.000 |
| Rknee_amp | −0.081 | 0.013 | −0.161 | −5.987 | 0.000 |
| Lcollar_amp | 0.577 | 0.118 | 0.134 | 4.877 | 0.000 |
| Exp | −0.059 | 0.014 | −0.113 | −4.328 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Wu, Y.; Dong, R.; Sato, K.; Ikuno, S.; Nishimura, S.; Jin, Q. Behavioral Analysis of Mowing Workers Based on Hilbert–Huang Transform: An Auxiliary Movement Analysis of Manual Mowing on the Slopes of Terraced Rice Fields. Agriculture 2023, 13, 489. https://doi.org/10.3390/agriculture13020489
Wu B, Wu Y, Dong R, Sato K, Ikuno S, Nishimura S, Jin Q. Behavioral Analysis of Mowing Workers Based on Hilbert–Huang Transform: An Auxiliary Movement Analysis of Manual Mowing on the Slopes of Terraced Rice Fields. Agriculture. 2023; 13(2):489. https://doi.org/10.3390/agriculture13020489
Chicago/Turabian StyleWu, Bo, Yuan Wu, Ran Dong, Kiminori Sato, Soichiro Ikuno, Shoji Nishimura, and Qun Jin. 2023. "Behavioral Analysis of Mowing Workers Based on Hilbert–Huang Transform: An Auxiliary Movement Analysis of Manual Mowing on the Slopes of Terraced Rice Fields" Agriculture 13, no. 2: 489. https://doi.org/10.3390/agriculture13020489
APA StyleWu, B., Wu, Y., Dong, R., Sato, K., Ikuno, S., Nishimura, S., & Jin, Q. (2023). Behavioral Analysis of Mowing Workers Based on Hilbert–Huang Transform: An Auxiliary Movement Analysis of Manual Mowing on the Slopes of Terraced Rice Fields. Agriculture, 13(2), 489. https://doi.org/10.3390/agriculture13020489







