Responses of Soybean Water Supply and Requirement to Future Climate Conditions in Heilongjiang Province
Abstract
:1. Introduction
2. Materials and Methods
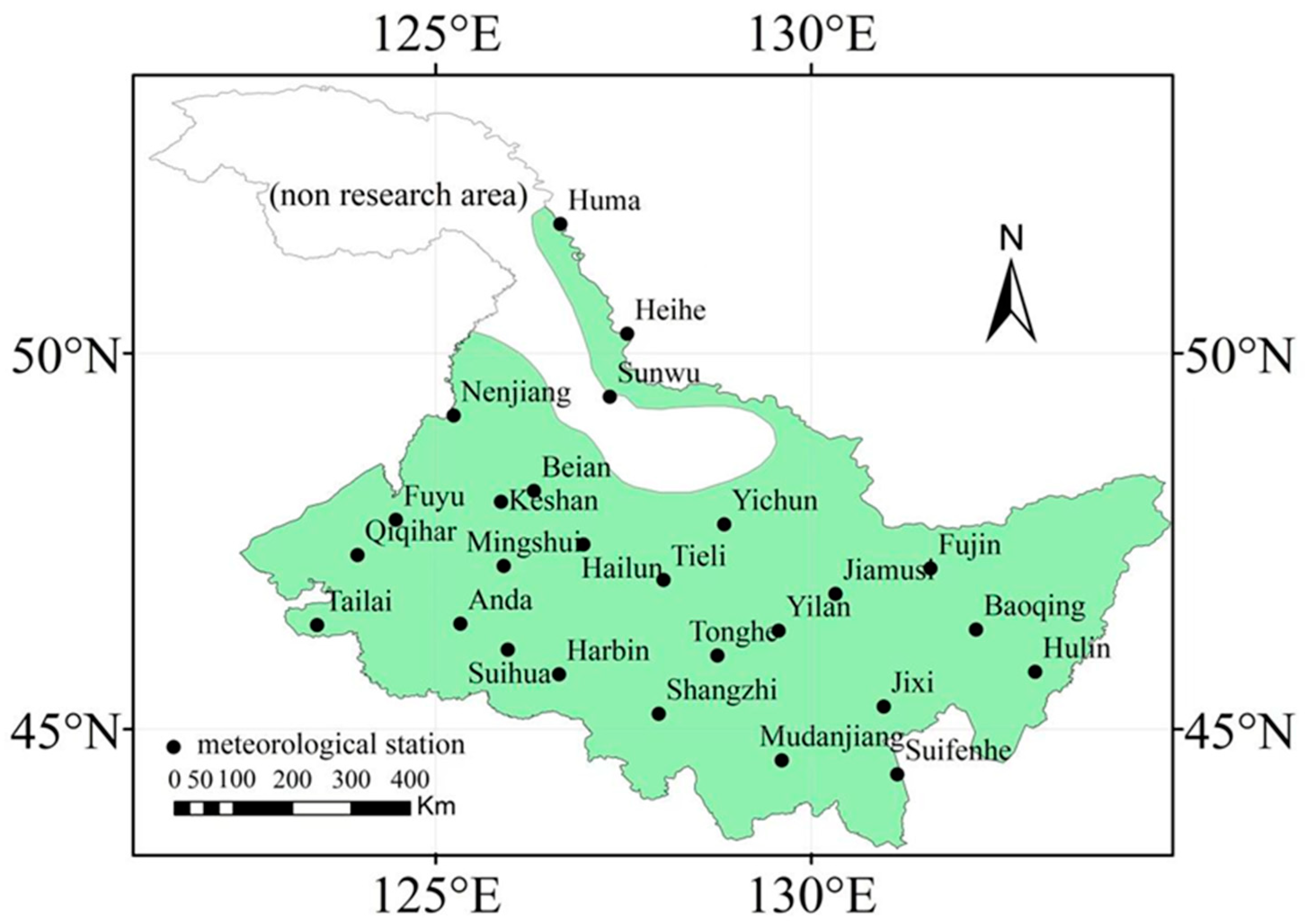
2.1. Study Region and Datasets
2.2. Division of Soybean Growth Period
2.3. Soil Parameters
2.4. Effective Precipitation (Pe)
2.5. Crop Water Requirement (ETc)
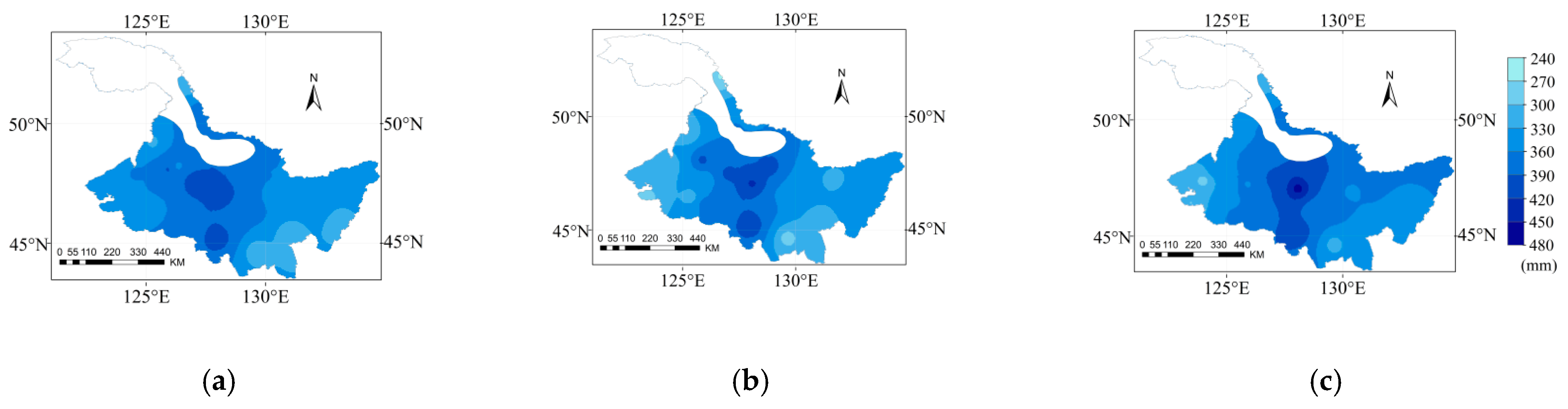
2.6. Irrigation Water Requirement (Ir)
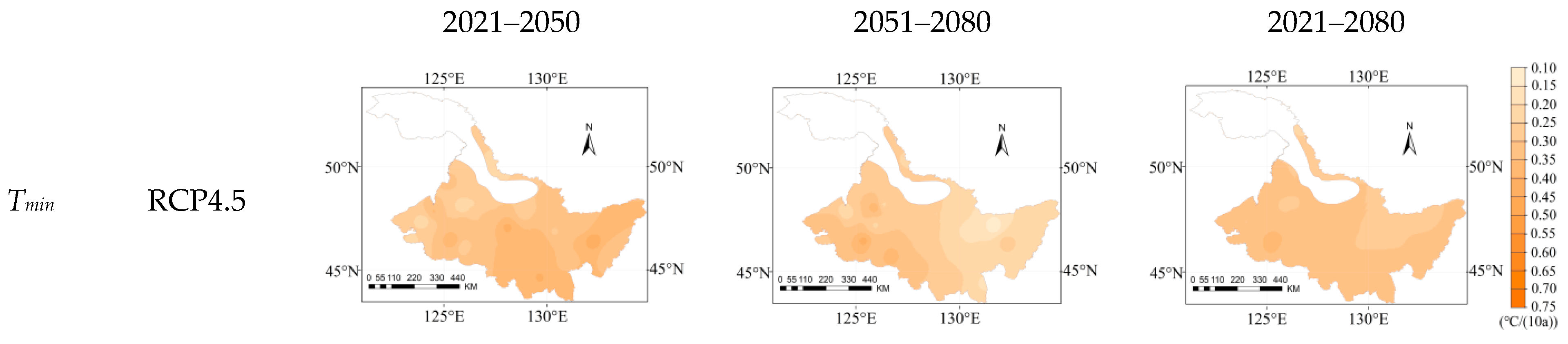
2.7. Climate Tendency Rate
2.8. Coupling Degree of ETc and Pe (CD)
2.9. Mann–Kendall Trend Test
2.10. Data Processing
3. Results
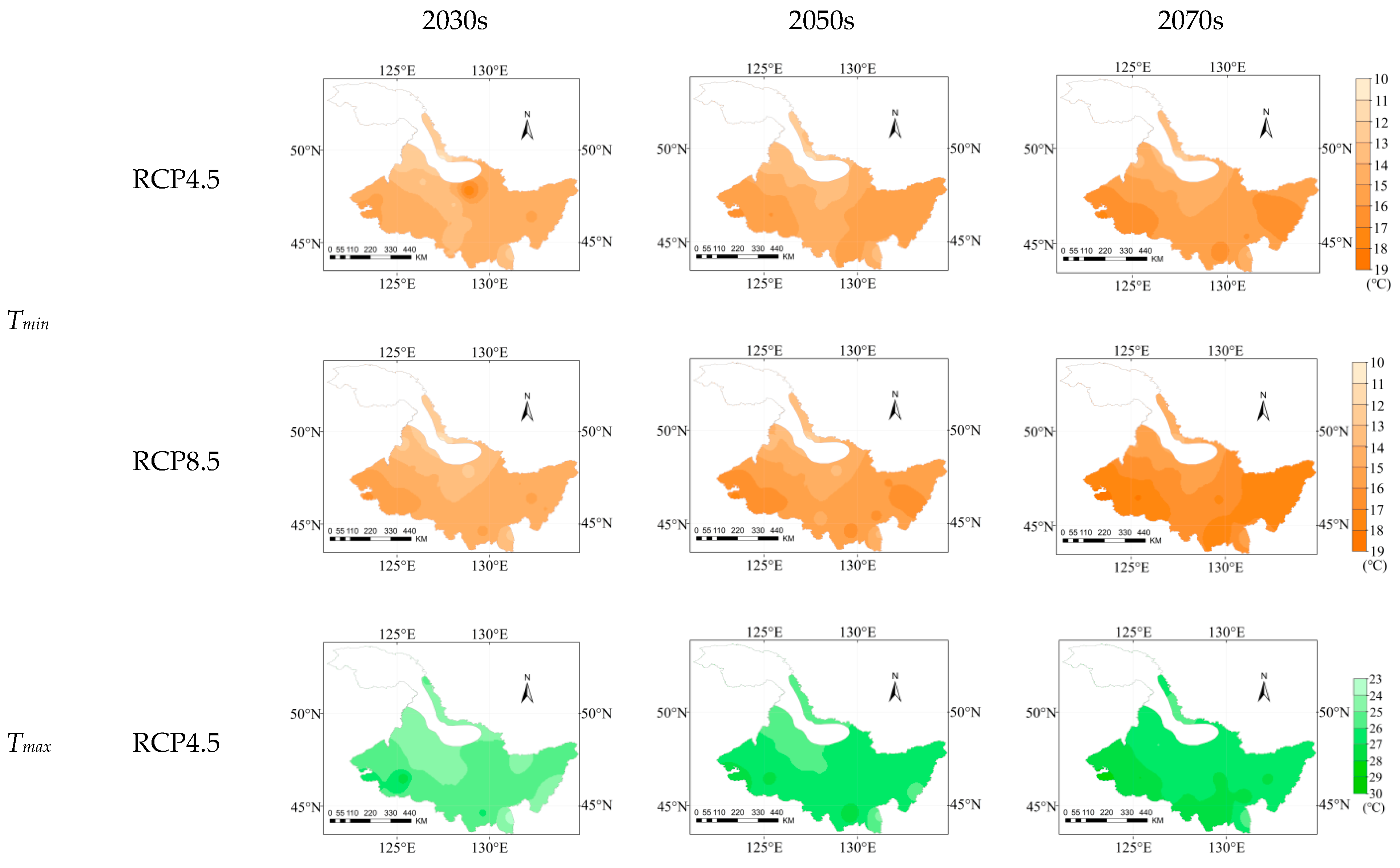
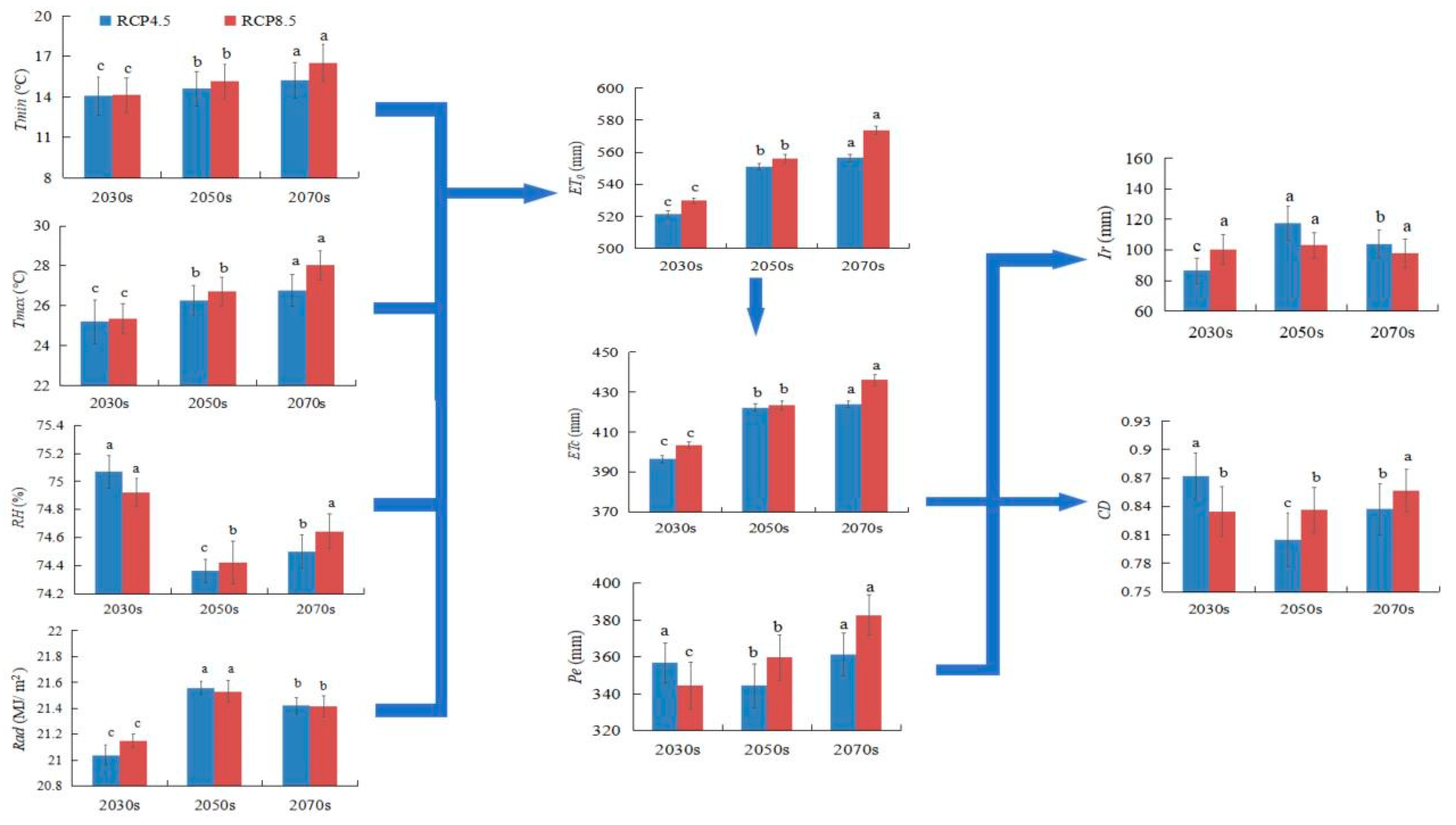
3.1. Spatial and Temporal Variation of Future Meteorological Factor
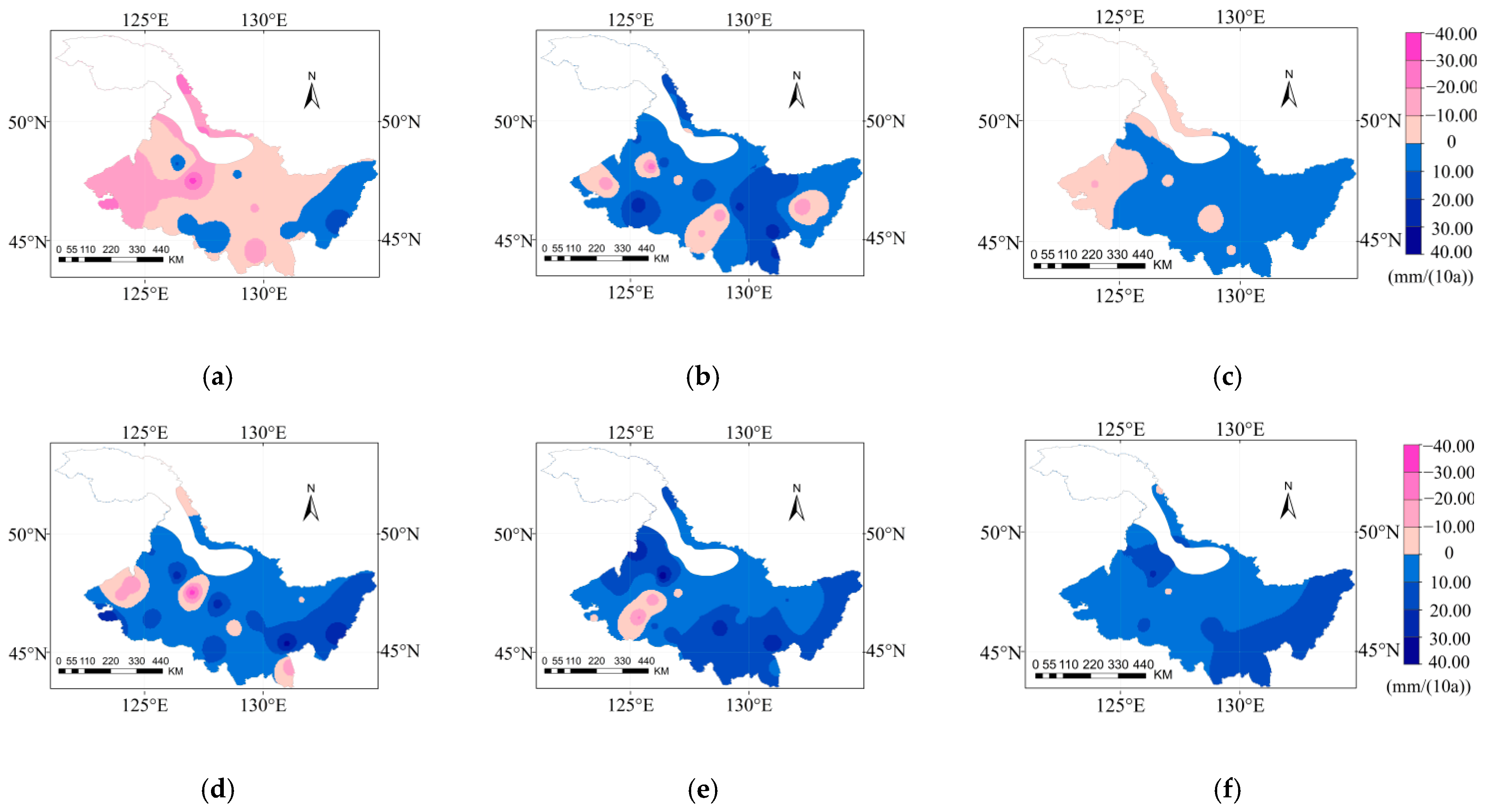
3.2. Spatial and Temporal Variation of ET0
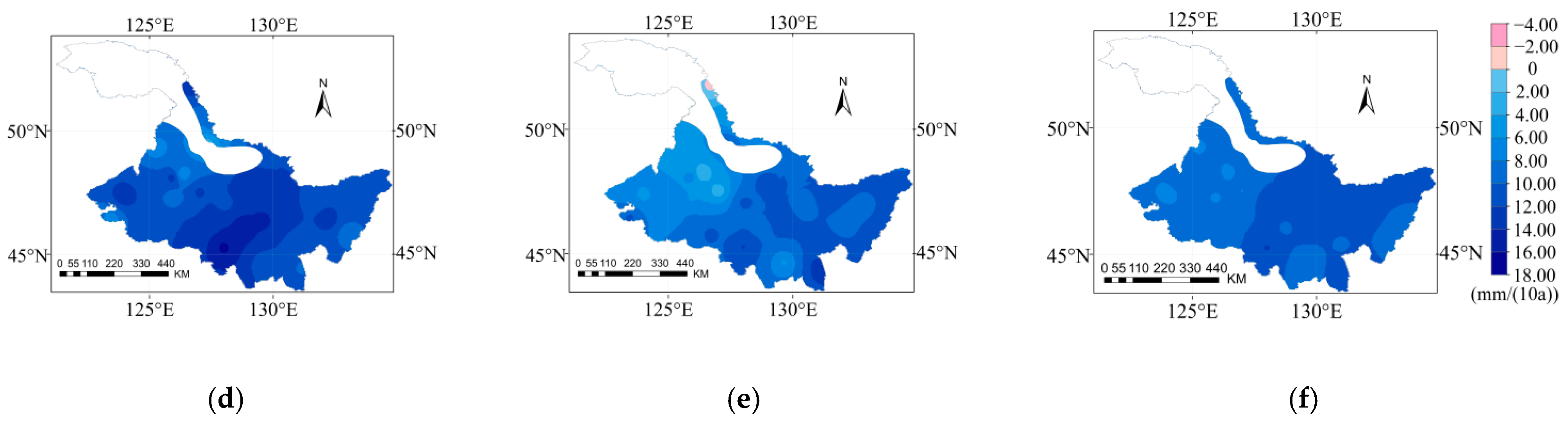
3.3. Spatial and Temporal Variation of ETc
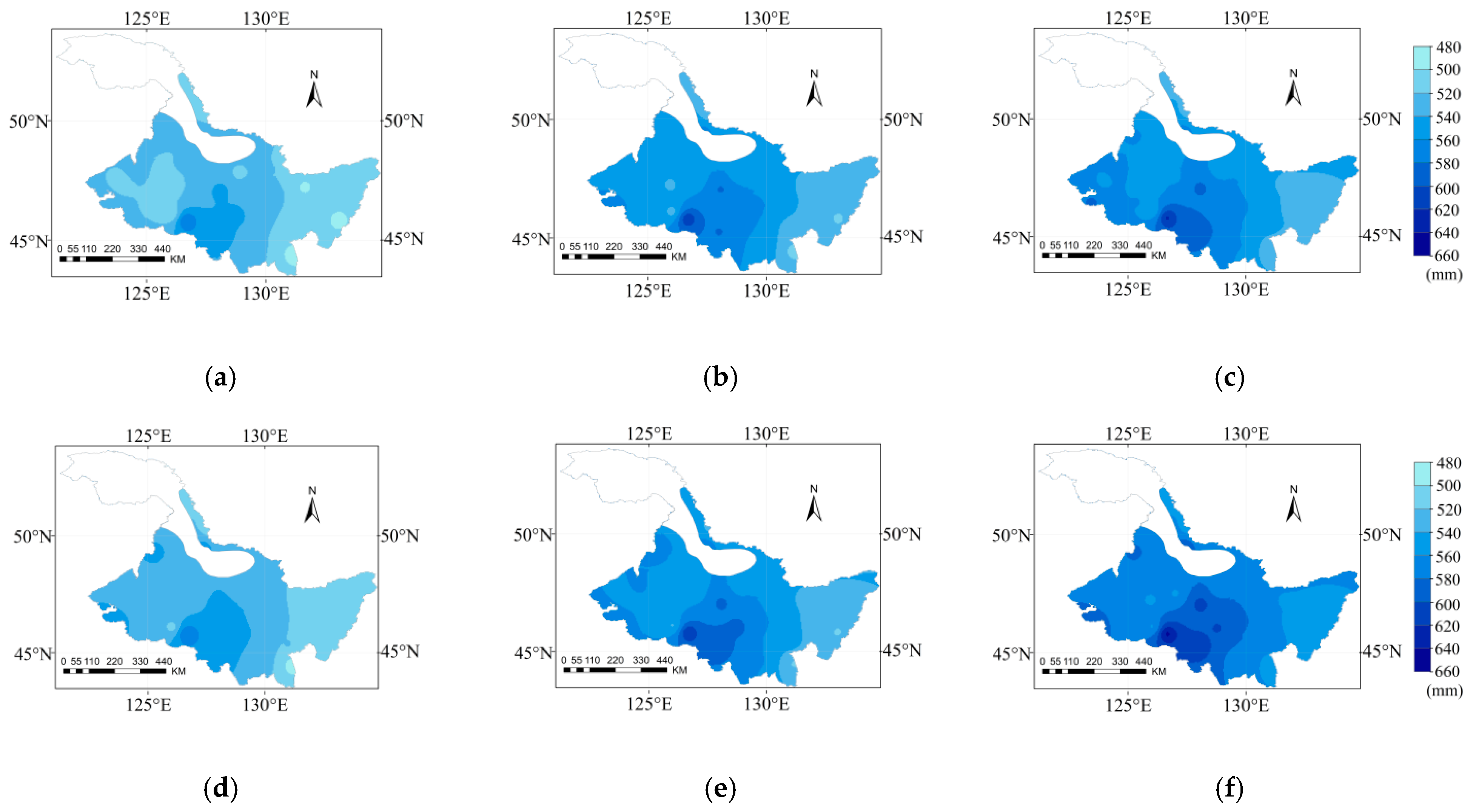
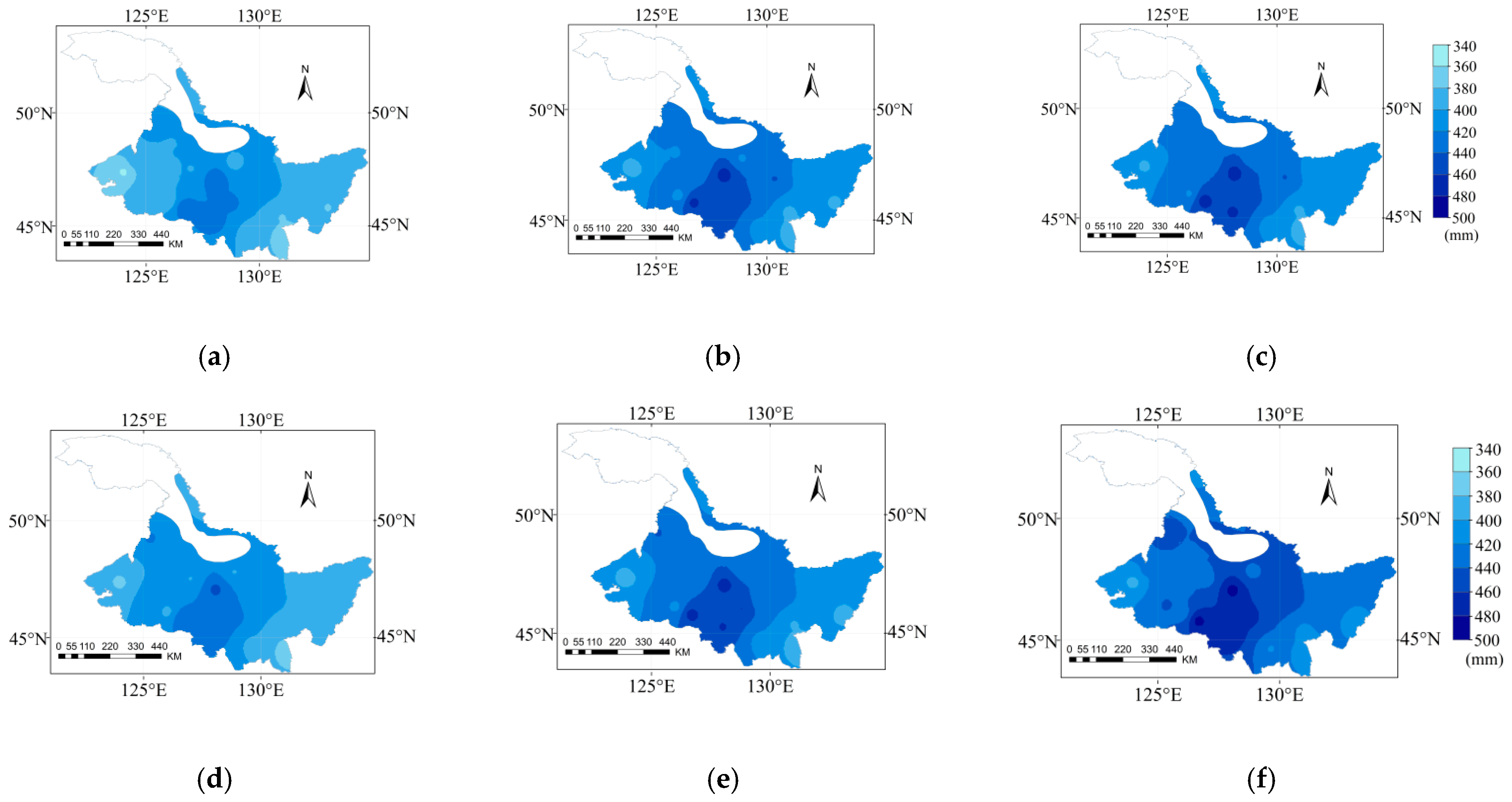
3.4. Spatial and Temporal Variation of Pe
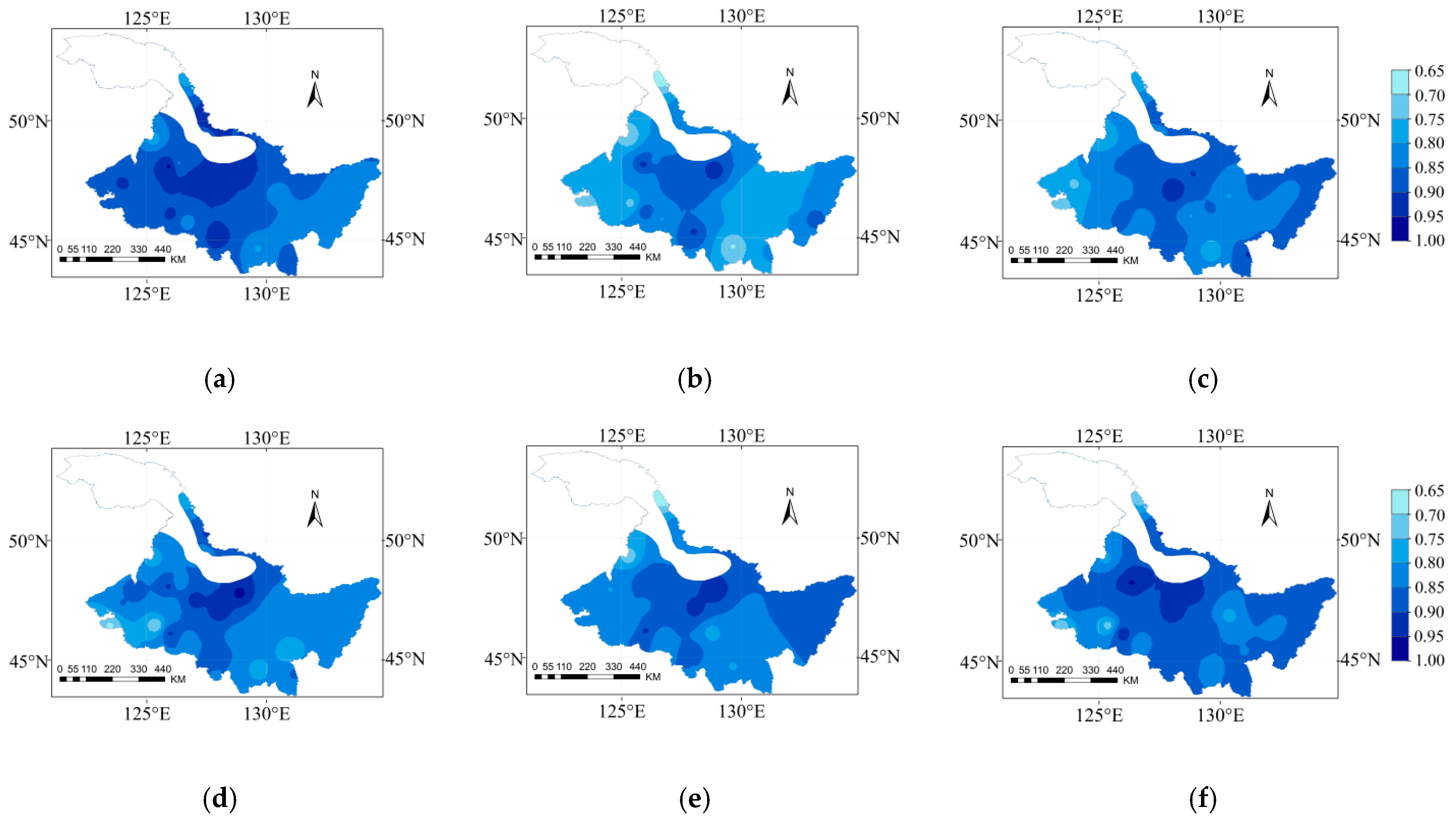
3.5. Spatial and Temporal Variation of CD
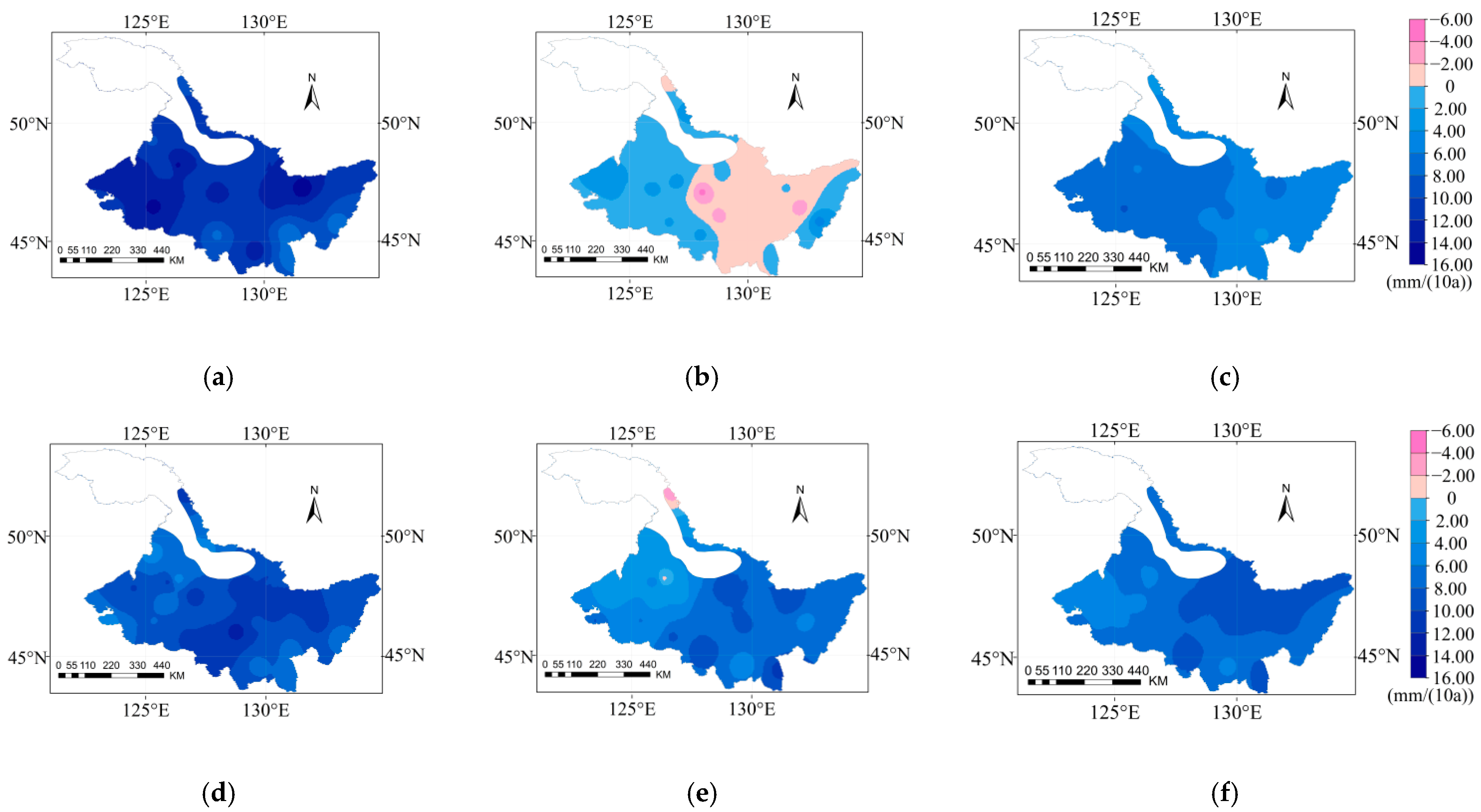
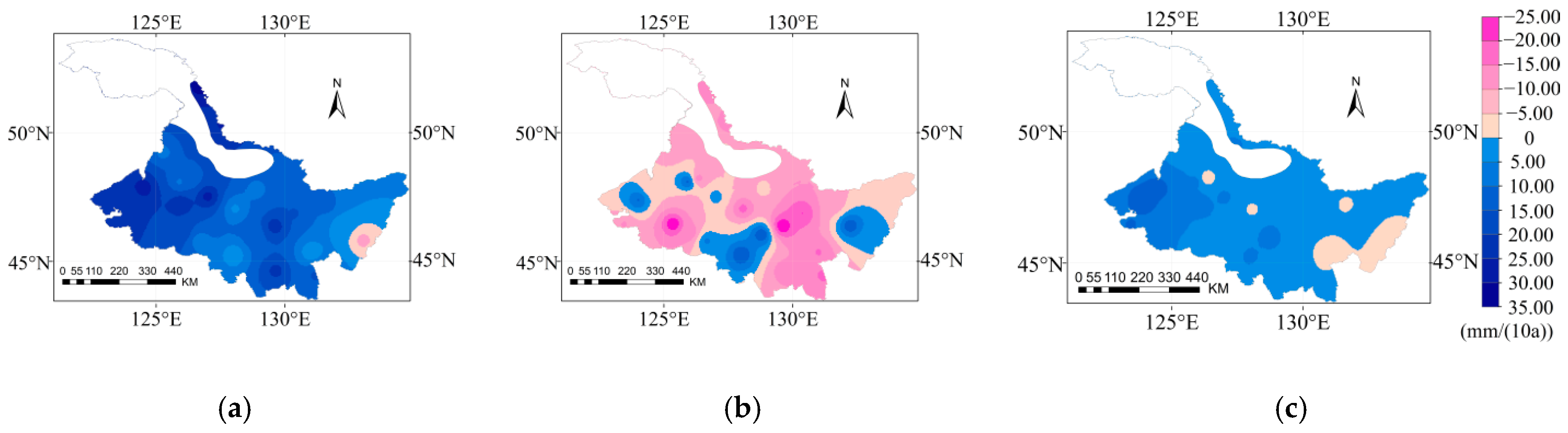
3.6. Spatial and Temporal Variation of Ir
3.7. Effect of Climate Change on Water Supply and Requirement
4. Discussion
4.1. Soybean ETc and Meteorological Factors
4.2. Soybean ETc, Pe, and Ir
4.3. Uncertainties and Limitations of the Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.Y. Impact of climate change on grain production in China. Chin. Agric. Sci. Bull. 2021, 12, 51–57. (In Chinese) [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Global Warming of 1.5 °C; Impacts of 1.5 °C of Global Warming on Natural and Human Systems. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2018; in press. [Google Scholar]
- Wang, T.; Du, C.; Nie, T.; Sun, Z.; Zhu, S.; Feng, C.; Dai, C.; Chu, L.; Liu, Y.; Liang, Q. Spatiotemporal analysis of maize water requirement in the Heilongjiang Province of China during 1960–2015. Water 2020, 12, 2472. [Google Scholar] [CrossRef]
- Tang, C.X. Influence of rainfall weather on agricultural production and countermeasures. Agric. Dev. Equip. 2019, 10, 68–69. (In Chinese) [Google Scholar]
- Bouras, E.; Jarlan, L.; Khabba, S.; Er-Raki, S.; Dezetter, A.; Sghir, F.; Tramblay, Y. Assessing the impact of global climate changes on irrigated wheat yields and water requirements in a semi-arid environment of Morocco. Sci. Rep. 2019, 9, 19142. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, W.; Zhuang, Q.; Luo, Y. Adaptation of paddy rice in China to climate change: The effects of shifting sowing date on yield and irrigation water requirement. Agric. Water Manag. 2020, 228, 105890. [Google Scholar] [CrossRef]
- Wang, W.G.; Sun, F.Z.; Peng, S.Z.; Xu, J.Z.; Luo, Y.F.; Jiao, X.Y. Simulation of response of rice irrigation water demand to climate change. Trans. Chin. Soc. Agric. Eng. 2013, 14, 90–98. (In Chinese) [Google Scholar]
- Acharjee, T.K.; Ludwig, F.; van Halsema, G.; Hellegers, P.; Supit, I. Future changes in water requirements of Boro rice in the face of climate change in North-West Bangladesh. Agric. Water Manag. 2017, 194, 172–183. [Google Scholar] [CrossRef]
- Cheshmberah, F.; Zolfaghari, A.A. The Effect of Climate Change on Future Reference Evapotranspiration in Different Climatic Zones of Iran. Pure Appl. Geophys. 2019, 176, 3649–3664. [Google Scholar] [CrossRef]
- Ti, J.; Yang, Y.; Yin, X.; Liang, J.; Pu, L.; Jiang, Y.; Wen, X.; Chen, F. Spatio-Temporal Analysis of Meteorological Elements in the North China District of China during 1960–2015. Water 2018, 10, 789. [Google Scholar] [CrossRef] [Green Version]
- Nie, T.; Tang, Y.; Jiao, Y.; Li, N.; Wang, T.; Du, C.; Zhang, Z.; Chen, P.; Li, T.; Sun, Z.; et al. Effects of Irrigation Schedules on Maize Yield and Water Use Efficiency under Future Climate Scenarios in Heilongjiang Province Based on the AquaCrop Model. Agronomy 2022, 12, 810. [Google Scholar] [CrossRef]
- Lyu, J.; He, Q.-Y.; Chen, Q.-W.; Cheng, R.-R.; Li, G.; Otsuki, K.; Yamanaka, N.; Du, S. Distinct transpiration characteristics of black locust plantations acclimated to semiarid and subhumid sites in the Loess Plateau, China. Agric. Water Manag. 2022, 262, 107402. [Google Scholar] [CrossRef]
- Nkomozepi, T.; Chung, S.-O. Assessing the trends and uncertainty of maize net irrigation water requirement estimated from climate change projections for Zimbabwe. Agric. Water Manag. 2012, 111, 60–67. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, D.L.; Wang, B.; Feng, P.; Bai, H.; Tang, J. Climate change impact on yields and water use of wheat and maize in the North China Plain under future climate change scenarios. Agric. Water Manag. 2020, 238, 106238. [Google Scholar] [CrossRef]
- Yang, X.; Jin, X.; Chu, Q.; Pacenka, S.; Steenhuis, T.S. Impact of climate variation from 1965 to 2016 on cotton water requirements in North China Plain. Agric. Water Manag. 2021, 243, 106502. [Google Scholar] [CrossRef]
- Chen, D.W. Advances in Prediction and Calculation of Crop Water Demand. Hydro Sci. Cold Zone Eng. 2021, 4, 171–174. (In Chinese) [Google Scholar]
- Wang, Y.; Shao, X.H.; Li, Y.H. Research progress on real-time prediction method of reference crop water requirement. J. Anhui Agric. Sci. 2008, 36, 13919–13920. (In Chinese) [Google Scholar] [CrossRef]
- Tavakoli, A.R.; Moghadam, M.M.; Sepaskhah, A.R. Evaluation of the AquaCrop model for barley production under deficit irrigation and rainfed condition in Iran. Agric. Water Manag. 2015, 161, 136–146. [Google Scholar] [CrossRef]
- FAO. OECD-FAO Agricultural Outlook; OECD Publishing, Food and Agriculture Organization of the United Nations: Rome, Italy, 2009; pp. 2011–2020. [Google Scholar]
- Lu, X.P.; Duan, S.Q.; Ma, X.Y.; Bai, S.M. Comparative Study on Calculation of Maize Water Demand by Single and Double Crop Coefficient Method. Water Sav. Irrig. 2012, 11, 18–21. (In Chinese) [Google Scholar]
- Zhang, L.; Tan, F.; Li, S.; Huo, Z. Potential dynamic of irrigation water requirement for rice across Northeast China. Theor. Appl. Climatol. 2020, 142, 1283–1293. [Google Scholar] [CrossRef]
- Wu, J.B.; Ma, Y.F.; Zheng, H.X.; Cao, X.S. Estimation of maize evapotranspiration in semi-arid region based on modified crop coefficient model. J. Water Resour. Archit. Eng. 2020, 18, 25–29. (In Chinese) [Google Scholar]
- Zhang, J.P.; Wang, C.Y.; Yang, X.G.; Zhao, Y.X.; Liu, Z.J.; Wang, J.; Chen, Y.Y. Prediction of the impact of future climate change on maize water demand in Northeast China. Trans. Chin. Soc. Agric. Eng. 2009, 25, 50–55. (In Chinese) [Google Scholar]
- Nie, T.Z.; Zhang, Z.X.; Qi, Z.J.; Chen, P.; Lin, Y.Y.; Sun, Z.Y. Spatial-temporal distribution characteristics of rice water demand in Heilongjiang Province from 1960 to 2015. Trans. Chin. Soc. Agric. Mach. 2019, 50, 279–290. (In Chinese) [Google Scholar]
- Jin, X. Application of Penman Formula in Crop Water Demand Calculation. Jianghuai Water Resour. Sci. Technol. 2018, 1, 28–30. (In Chinese) [Google Scholar]
- Awal, R.; Fares, A.; Bayabil, H. Assessing Potential Climate Change Impacts on Irrigation Requirements of Major Crops in the Brazos Headwaters Basin, Texas. Water 2018, 10, 1610. [Google Scholar] [CrossRef] [Green Version]
- Hong, E.-M.; Nam, W.-H.; Choi, J.-Y.; Pachepsky, Y.A. Projected irrigation requirements for upland crops using soil moisture model under climate change in South Korea. Agric. Water Manag. 2016, 165, 163–180. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.B.; Roy, D.; Maniruzzaman, M.; Biswas, J.C.; Naher, U.A.; Haque, M.M.; Kalra, N. Response of crop water requirement and yield of irrigated rice to elevated temperature in Bangladesh. Int. J. Agron. 2021, 2021, 9963201. [Google Scholar] [CrossRef]
- Sunil, A.; Deepthi, B.; Mirajkar, A.B.; Adarsh, S. Modeling future irrigation water demands in the context of climate change: A case study of Jayakwadi command area, India. Model. Earth Syst. Environ. 2021, 7, 1963–1977. [Google Scholar] [CrossRef]
- Goodarzi, M.; Abedi-Koupai, J.; Heidarpour, M. Investigating Impacts of Climate Change on Irrigation Water Demands and Its Resulting Consequences on Groundwater Using CMIP5 Models. GroundWater 2019, 57, 259–268. [Google Scholar] [CrossRef]
- Chen, P.; Nie, T.; Chen, S.; Zhang, Z.; Qi, Z.; Liu, W. Recovery efficiency and loss of 15N-labelled urea in a rice-soil system under water saving irrigation in the Songnen Plain of Northeast China. Agric. Water Manag. 2019, 222, 139–153. [Google Scholar] [CrossRef]
- Chen, P.; Xu, J.; Zhang, Z.; Wang, K.; Li, T.; Wei, Q.; Li, Y. Carbon pathways in aggregates and density fractions in Mollisols under water and straw management: Evidence from 13C natural abundance. Soil Biol. Biochem. 2022, 169, 108684. [Google Scholar] [CrossRef]
- Heilongjiang Provincial People’s Government. Heilongjiang Yearbook; Editorial Department: Harbin, China, 2020; pp. 244–245. ISSN 1008-0791.
- Li, J.Y.; Wang, X.L.; Wang, Z.B.; Nie, T.Z. Spatial and Temporal Distribution of Soybean Water Demand and Drought in Heilongjiang Province in Recent 50 Years. Trans. Chin. Soc. Agric. Mach. 2020, 51, 223–237. (In Chinese) [Google Scholar]
- Hu, H.J.; Wang, M.; Yin, X.G.; Jiang, Y.L.; Wen, X.Y.; Chen, F. Analysis on Temporal and Spatial Variation Characteristics of Soybean Water Demand in Northeast Agricultural Region under Climate Change. Zhongguo Nongye Daxue Xuebao 2017, 22, 21–31. (In Chinese) [Google Scholar]
- Accumulated Temperature Zone of Crop Varieties in Heilongjiang Province. Available online: http://www.hljagri.gov.cn/ (accessed on 2 September 2020).
- Area Layout Planning of High-Quality and High-yield Main Food Crops in Heilongjiang Province in 2015. Available online: http://dszz.hljagri.gov.cn/tjxxw/jrtj/tzgg/201501/ (accessed on 2 September 2020).
- Smith, M. CROPWAT: A Computer Program for Irrigation Planning and Management; FAO: Rome, Italy, 1992. [Google Scholar]
- FAO. Crop Evapotranspiration for Computing Crop Water Requirement; FAO Irrigation & Drainage Paper: Rome, Italy, 1998; p. 56. [Google Scholar]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Change 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Bahmani, S.; Bajic, I.V.; HajShirmohammadi, A. Joint Decoding of Unequally Protected JPEG2000 Bitstreams and Reed-Solomon Codes. IEEE Trans. Image Process. 2010, 19, 2693–2704. [Google Scholar] [CrossRef] [PubMed]
- Tsakmakis, I.D.; Zoidou, M.; Gikas, G.D.; Sylaios, G.K. Impact of Irrigation Technologies and Strategies on Cotton Water Footprint Using AquaCrop and CROPWAT Models. Environ. Process. 2018, 5, S181–S199. [Google Scholar] [CrossRef]
- Dubrau, A.W.; Hendren, L.J. Taming MATLAB. Acm Sigplan Notice 2012, 47, 503–522. [Google Scholar] [CrossRef]
- Xiao, Z.L. A comparative study of using MATLAB and SPSS software to solve regression analysis. Shanxi Youth 2016, 18, 58–59. (In Chinese) [Google Scholar]
- Farooq, N.; Gheewala, S.H. Assessing the impact of climate change on sugarcane and adaptation actions in Pakistan. Acta Geophys. 2020, 68, 1489–1503. [Google Scholar] [CrossRef]
- Li, Y.; Qu, H.J.; Su, W.Y.; Gao, Z.P.; Wu, J.M. Response of Crop Irrigation Water Demand in Typical Area of Huanghuai Plain under HadGEM2-ES Climate Model. Water Resour. Power 2017, 35, 119–122. (In Chinese) [Google Scholar]
- Jalota, S.K.; Sood, A.; Chahal, G.B.S.; Choudhury, B.U. Crop water productivity of cotton (Gossypium hirsutum L.)–wheat (Triticum aestivum L.) system as influenced by deficit irrigation, soil texture and precipitation. Agric. Water Manag. 2006, 84, 137–146. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, D.; Zhang, H.; Asseng, S.; Yin, T.; Qiu, X.; Ye, Z.; Liu, L.; Tang, L.; Cao, W.; et al. Separating the impacts of heat stress events from rising mean temperatures on winter wheat yield of China. Environ. Res. Lett. 2021, 16, 124035. [Google Scholar] [CrossRef]
- Paul, M.; Dangol, S.; Kholodovsky, V.; Sapkota, A.R.; Negahban-Azar, M.; Lansing, S.L. Modeling the Impacts of Climate Change on Crop Yield and Irrigation in the Monocacy River Watershed, USA. Climate 2020, 8, 139. [Google Scholar] [CrossRef]
- Durodola, O.S.; Mourad, K.A. Modelling the Impacts of Climate Change on Soybeans Water Use and Yields in Ogun-Ona River Basin, Nigeria. Agriculture 2020, 10, 593. [Google Scholar] [CrossRef]
- Soares, D.; Rolim, J.; Fradinho, M.J.; Paço, T.A.D. Climate Change Impacts on Irrigation Requirements of Preserved Forage for Horses under Mediterranean Conditions. Agronomy 2020, 10, 1758. [Google Scholar] [CrossRef]
- Luo, X.; Xia, J.; Yang, H. Modeling water requirements of major crops and their responses to climate change in the North China Plain. Environ. Earth Sci. 2015, 74, 3531–3541. [Google Scholar] [CrossRef]
- Gao, J.; Yang, X.; Zheng, B.; Liu, Z.; Zhao, J.; Sun, S.; Li, K.; Dong, C. Effects of climate change on the extension of the potential double cropping region and crop water requirements in Northern China. Agric. For. Meteorol. 2019, 268, 146–155. [Google Scholar] [CrossRef]
- Mainuddin, M.; Kirby, M.; Chowdhury, R.A.R.; Shah-Newaz, S.M. Spatial and temporal variations of, and the impact of climate change on, the dry season crop irrigation requirements in Bangladesh. Irrig. Sci. 2015, 33, 107–120. [Google Scholar] [CrossRef]
- Bouregaa, T. Impact of climate change on yield and water requirement of rainfed crops in the Setif region. Manag. Environ. Qual. Int. J. 2019, 30, 851–863. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L.; Niu, Z.; Zhang, M.; Li, C.a.; Li, J. The effects of projected climate change and extreme climate on maize and rice in the Yangtze River Basin, China. Agric. For. Meteorol. 2020, 282, 107867. [Google Scholar] [CrossRef]
- Ma, J.Q.; Li, P.F.; Liu, L. Experimental Study on Crop Coefficient of Summer Maize in Henan Province. Water Sav. Irrig. 2016, 4, 24–27. (In Chinese) [Google Scholar]







| Agrometeorological Station | Lini (Days) | Ldev (Days) | Lmid (Days) | LLate (Days) | Total Growth Day (Days) | Meteorological Station |
|---|---|---|---|---|---|---|
| Qinggang | 24 | 31 | 59 | 16 | 130 | Anda, Suihua |
| Hulin | 27 | 30 | 60 | 17 | 134 | Hulin |
| Boli | 35 | 24 | 16 | 16 | 125 | Jixi, Mudanjiang, Suifenhe |
| Bayan | 29 | 24 | 62 | 23 | 138 | Tonghe, Shangzhi |
| Heihe | 32 | 25 | 59 | 17 | 133 | Heihe, Sunwu |
| Harbin | 34 | 32 | 67 | 17 | 150 | Haerbin |
| Nenjiang | 29 | 27 | 60 | 17 | 133 | Nenjiang |
| Longjiang | 20 | 27 | 63 | 22 | 132 | Qiqihar, Tailai |
| Huma | 33 | 18 | 57 | 17 | 125 | Huma |
| Qingan | 28 | 21 | 63 | 28 | 140 | Tieli |
| Tangyuan | 27 | 28 | 65 | 16 | 136 | Yinlan |
| Beian | 28 | 26 | 65 | 15 | 134 | Keshan, Beian |
| Baiquan | 27 | 27 | 55 | 23 | 132 | Mingshui |
| Jiayin | 30 | 24 | 57 | 16 | 127 | Yichun |
| Hailun | 28 | 29 | 63 | 19 | 139 | Hailun |
| Jiamusi | 28 | 32 | 62 | 17 | 139 | Jiamusi |
| Fuyu | 32 | 32 | 57 | 14 | 135 | Fuyu |
| Baoqing | 22 | 28 | 60 | 19 | 129 | Baoqing |
| Fujin | 29 | 25 | 60 | 21 | 135 | Fujin |
| Items | Scenarios | Periods | Tmin | Tmax | RH | Rad |
|---|---|---|---|---|---|---|
| ET0 | RCP4.5 | 2030s | −0.176 | −0.522 * | −0.769 ** | 0.790 ** |
| 2050s | 0.087 | 0.779 ** | −0.727 ** | 0.892 ** | ||
| 2070s | 0.057 | 0.926 ** | −0.863 ** | 0.912 ** | ||
| 2030s–2070s | 0.898 ** | 0.982 ** | −0.831 ** | 0.908 ** | ||
| RCP8.5 | 2030s | −0.059 | 0.405 | −0.450 * | 0.508 * | |
| 2050s | −0.386 | 0.852 ** | −0.924 ** | 0.963 ** | ||
| 2070s | −0.473 * | 0.854 ** | −0.885 ** | 0.929 ** | ||
| 2030s–2070s | 0.971 ** | 0.991 ** | −0.226 | 0.697 ** | ||
| ETc | RCP4.5 | 2030s | −0.291 | 0.548 * | −0.826 ** | 0.849 ** |
| 2050s | −0.089 | 0.598 ** | −0.780 ** | 0.892 ** | ||
| 2070s | −0.091 | 0.790 ** | −0.798 * | 0.823 ** | ||
| 2030s–2070s | 0.855 ** | 0.960 ** | −0.873 ** | 0.939 ** | ||
| RCP8.5 | 2030s | −0.214 | 0.298 | −0.595 ** | 0.649 ** | |
| 2050s | −0.395 | 0.739 ** | −0.820 ** | 0.884 ** | ||
| 2070s | −0.489 * | 0.726 ** | −0.841 ** | 0.890 ** | ||
| 2030s–2070s | 0.962 ** | 0.984 ** | −0.851 ** | 0.716 ** | ||
| Pe | RCP4.5 | 2030s | −0.240 | −0.338 | 0.140 | −0.114 |
| 2050s | 0.390 | 0.025 | −0.487 | −0.436 | ||
| 2070s | −0.149 | −0.223 | 0.255 | −0.208 | ||
| 2030s–2070s | 0.167 | −0.021 | 0.387 ** | −0.306 * | ||
| RCP8.5 | 2030s | 0.206 | 0.081 | 0.136 | −0.142 | |
| 2050s | 0.099 | −0.344 | 0.375 | −0.339 | ||
| 2070s | 0.482 * | −0.001 | −0.248 | −0.306 | ||
| 2030s–2070s | 0.810 ** | −0.793 ** | −0.110 | −0.324 * | ||
| Ir | RCP4.5 | 2030s | 0.152 | 0.287 | −0.184 | 0.167 |
| 2050s | −0.283 | 0.291 | −0.698 ** | 0.693 ** | ||
| 2070s | −0.016 | 0.381 | −0.434 | 0.419 | ||
| 2030s–2070s | 0.409 ** | 0.590 ** | −0.841 ** | 0.824 ** | ||
| RCP8.5 | 2030s | −0.232 | −0.078 | −0.209 | 0.209 | |
| 2050s | −0.231 | 0.434 | −0.547 * | 0.550 * | ||
| 2070s | −0.531 * | 0.268 | −0.489 * | 0.582 ** | ||
| 2030s–2070s | −0.140 | 0.094 | −0.400 ** | 0.283 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Nie, T.; Tang, Y.; Lu, D.; Wang, T.; Zhang, Z.; Chen, P.; Li, T.; Meng, L.; Jiao, Y.; et al. Responses of Soybean Water Supply and Requirement to Future Climate Conditions in Heilongjiang Province. Agriculture 2022, 12, 1035. https://doi.org/10.3390/agriculture12071035
Li N, Nie T, Tang Y, Lu D, Wang T, Zhang Z, Chen P, Li T, Meng L, Jiao Y, et al. Responses of Soybean Water Supply and Requirement to Future Climate Conditions in Heilongjiang Province. Agriculture. 2022; 12(7):1035. https://doi.org/10.3390/agriculture12071035
Chicago/Turabian StyleLi, Na, Tangzhe Nie, Yi Tang, Dehao Lu, Tianyi Wang, Zhongxue Zhang, Peng Chen, Tiecheng Li, Linghui Meng, Yang Jiao, and et al. 2022. "Responses of Soybean Water Supply and Requirement to Future Climate Conditions in Heilongjiang Province" Agriculture 12, no. 7: 1035. https://doi.org/10.3390/agriculture12071035
APA StyleLi, N., Nie, T., Tang, Y., Lu, D., Wang, T., Zhang, Z., Chen, P., Li, T., Meng, L., Jiao, Y., & Cheng, K. (2022). Responses of Soybean Water Supply and Requirement to Future Climate Conditions in Heilongjiang Province. Agriculture, 12(7), 1035. https://doi.org/10.3390/agriculture12071035







