Abstract
Affected by the temporal and spatial changes of natural resources, human activities, and social economic system policies, there are many uncertainties in the development, utilization, and management process of irrigation district agricultural water resources, which will increase the complexity of the use of irrigation district agricultural water resources. Decision makers find it challenging to cope with the complexity of fluctuating water supplies and demands that are critical for water resources’ allocation. In response to these issues, this paper presents an optimization modeling approach for agricultural water allocation at an irrigation district scale, considering the uncertainties of water supply and demand. The minimum cross-entropy method was used to estimate the parameters of hydrologic frequency distribution functions of water supply and demand, which are the basis for agricultural water resources’ optimal allocation and the evaluation of water resources’ carrying capacity in the Hetao Irrigation District. Interval Linear Fractional Programming was used to find water availability, shortage, and use efficiency in different irrigation areas of the Hetao Irrigation District (HID) under different scenarios. The denominator of fractional planning is the environmental goal, and the numerator is the economic goal; so, the objective function of fractional programming is the utility rate required in the post-optimization analysis. Future water availability and shortage scenarios are adopted consistent with the Representative Concentration Pathways’ (RCPs’) framework, and future water use scenarios are developed using the Shared Socioeconomic Pathways’ (SSPs’) framework. Results revealed that under SSP1, the annual water consumption increased from 30 billion m3 to 60 billion m3, almost doubling in Urad. The annual water consumption under SSP2 and SSP3 increased slightly, from 30 billion m3 to about 50 billion m3. The amount of water available for well irrigation in Urad decreased from 300 to 250 billion m3, while the amount of water available for canal irrigation in Urad remained at 270 billion m3 from 2010 s to 2030 s, only dropping to 240 billion m3 in 2040 s. The entropy-weight-based Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) method was applied to evaluate agricultural water resources’ allocation schemes because it can avoid the subjectivity of weight determination and can reflect the dynamic changing trend of irrigation district agricultural water resources’ carrying capacity. The approach is applicable to most regions, such as the Hetao Irrigation District in the Upper Yellow River Basi with limited precipitation, to determine water strategies under the changing environment.
1. Introduction
Ecological economics, landscape ecology, and agricultural sustainable development are the theoretical bases of a water-saving ecological irrigation district [1]. The target system of water-saving ecological irrigation district construction includes high agricultural productivity, functional irrigation district, water and soil environmental health, reasonable allocation and efficient utilization of water resources, high biodiversity, and optimal water resources’ ecological and economic service functions [2,3]. The reasonable allocation of multiple agricultural water resources and improvement of water resources’ utilization efficiency, soil health quality maintenance and controlled irrigation, ecosystem and biodiversity restoration, comprehensive treatment of pollution sources and gradual interception control, water landscape and water culture construction in the irrigation district, and participatory innovation management are supporting technologies to achieve the goal of the system of water-saving ecological irrigation district construction [2,3,4]. Ecological irrigation district management includes the following aspects: water shortage, water pollution, flooding, ecological deterioration, economy development, environmental protection, and climate adaptation. The complexities of an integrated ecological irrigation district management are related to many factors, including dynamic and interactive relationships between different aspects, and multi-objective, multi-stage, and multi-uncertainty aspects in the process of ecological irrigation district planning and management. Effective system analysis methods, for example, robust simulation and optimization tools, are needed in the construction of a water-saving ecological irrigation district. The theoretical basis, research content, and research tools of the research on the optimal allocation of water resources are constantly enriched [3]. Among them, research on agricultural water resources can be divided into four categories according to different research scales, namely, the optimal allocation of water resources in multi-irrigation districts, the optimal scheduling of water resources in irrigation canals, the optimal allocation of water and soil resources for multi-crops, and the optimization of crop irrigation schedules [4]. Christine Sweetapple et al., established the multi-objective optimization of a wastewater treatment plant control to reduce greenhouse gas emissions. Zarghami and Szidarovszky coupled stochastic and fuzzy methods by orderly weighted average calculation and established a stochastic, fuzzy, multi-criteria decision-making model to deal with the multiple uncertainties encountered in water resources’ management. Guo et al., fully considered the multi-objectives and uncertainty in the process of optimizing water distribution in a canal system and used multi-objective programming and a genetic algorithm to optimize the water distribution process of a three-level system of the trunk branch-lateral in the Xijun Irrigation District in the middle reaches of the Heihe River. Aiming at the nonlinear and uncertain characteristics in the optimal allocation of irrigation water resources and considering the interests of decision-making subjects at different levels in the irrigation area, Li et al., respectively constructed an Interval Linear Fractional Programming (ILFP) model considering the interests of the upper managers to obtain the maximum irrigation water productivity and Interval Quadratic Programming (IQP) model considering the interests of the lower tier farmers to obtain a maximum yield. Taking the middle reaches of the Heihe River as the research object, Li comprehensively considered the characteristics of four different water use scales in the middle reaches of the Heihe River to establish an optimization model to optimize the allocation of agricultural water resources in the middle reaches of the Heihe River. Aiming at improving irrigation water use efficiency, Zhang et al., used a multi-objective model to optimize the planting structure of six main crops in Minqin County, Gansu Province. Combined with the virtual water theory, Su et al., optimized the irrigation water volume for seven main crops in the Shiyang River Basin. Zhang et al., established an optimization model of irrigation water resources for three administrative regions in the middle reaches of the Heihe River and three main crops in the administrative region based on a two-layer model; they made an attempt to combine research with different study scales. Shang optimized the winter wheat irrigation system in Beijing based on the farmland water balance simulation model, crop water production function, and water sensitivity index accumulation function. Yin et al., established multi-objective, optimization-based reactive nitrogen transport modeling for the water–environment–agriculture nexus in a basin-scale coastal aquifer. In the above research on optimal allocation of system resources and risk management models in irrigation districts under uncertainty, most of them used multi-objective optimization models [4,5,6,7,8,9,10]. However, the determination of the objective function of the multi-objective optimization model, especially the determination of multi-objective weight parameters, has always been a challenge. To overcome the limitations of multi-objective optimization programming, an interval linear fractional programming model is established through coupling interval parameter programming and linear fractional programming. The denominator of fractional planning is the environmental goal, and the numerator is the economic goal, which reflects the correlation between two goals very well. In addition, the objective function of fractional programming is the utility rate required in the post-optimization analysis, which fully reflects the interaction between the environmental dimension and the economic dimension [5,6,9].
Therefore, in response to the above anxieties, this study aimed to develop an interval linear fractional programming (ILFP) model combined with POMCE and Clayton copula estimation for solving the problem of allocation of agricultural water in the Hetao Irrigation District under uncertain conditions [7,8,10]. The main content of this research included the following: (1) the establishment of an ILFP model through the integration of the methods of interval parameter programming and linear fractional programming into an optimization model; (2) the introduction of the POMCE to express distribution functions of rainfall and evaporation, and the formulation of the concept of Clayton copula that spatializes all elements of estimating the joint probability distribution function (JPDF) of rainfall and evaporation; (3) the combination of the ILFP model with the POMCE and Clayton copula estimation and applying it to the Hetao Irrigation District (HID) in the Yellow River Basin for managing agricultural water allocation; and (4) the utilization of the entropy-weight-based TOPSIS method to evaluate the water resources’ carrying capacity of the Hetao Irrigation District (HID). Therefore, optimal schemes can help manage limited water resources under different irrigation methods and shared socioeconomic pathways (SSPs) in irrigation districts; these findings are helpful for decision makers to promote agricultural sustainable development in arid and semi-arid areas. The framework of this study is shown in Figure 1.
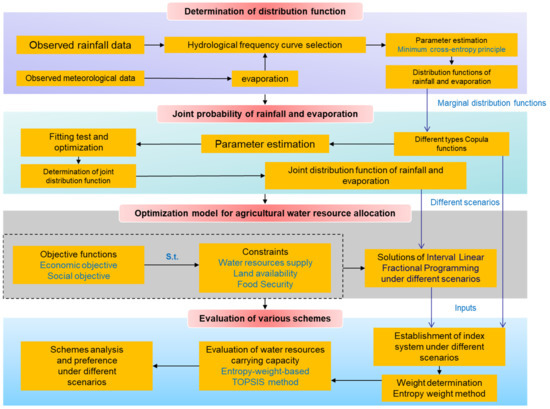
Figure 1.
Decision-making framework of resource management for the Hetao Irrigation District.
This paper is organized as follows. Section 2 describes the methodology of estimating the joint probability distribution function (JPDF) of rainfall and evaporation, including the minimum cross-entropy principle, the copula function, the formulation of an ILFP model and its solution process, and the entropy-weight-based TOPSIS method. Section 3 provides the problem details, modeling framework, and data collection of the Hetao Irrigation District. The results, analysis, and discussions are presented in Section 4, and the paper is concluded in Section 5.
2. Methods
2.1. Minimum Cross-Entropy Principle
POMCE is a powerful principle with the building blocks of the entropy theory. The minimum cross-entropy principle was formulated by Kullback and Leibler (1951) and detailed by Kullback (1959). We consider a probability distribution Q = {q_1, q_2,⋯, q_N} for a random variable X, which takes on N values [11]. To derive the distribution P = {p_1, p_2,⋯, p_N} of X, we should minimize the distance between P and Q. As the distance between P and Q is closer, the uncertainty will be greater. The principle of minimum cross-entropy is expressed as
where D is the cross-entropy or distance.
If no prior distribution is obtainable in the shape of constraints and Q is chosen to be a uniform distribution, Equation (1) takes the form
where H is the Shannon entropy.
In Equations (2) and (3), minimizing D (P, Q) is equal to maximizing H. Since D is a convex function, its global and local minimum are equivalent.
A posterior distribution P is acquired by combining a prior Q with specified constraints, and minimization of cross-entropy results asymptotically from Bayes’ theorem [11,12].
POMCE involves two major concepts. One is a prior probability distribution and the other is a measure of distance.
POMCE is a measure between two probability distributions. One of them is related to the system to be characterized and is assumed to be unknown. The other is related to the model chosen to describe the system, for example, concretely. For the models to characterize a system, the set of moments are considered. The mean and any symmetrical part of the covariance matrix of the scheme are called constraints.
The POMCE measure is gained by minimizing the discrimination information while considering the given prior distribution, extending all probabilistic descriptions of the system that agree with the given constraints. One of the causes is of root square sense as the measure of distance [11,12,13].
2.2. Copula Function
When random variables with different marginal probability distributions are not independent of each other, it becomes very difficult to model the joint distribution. At this time, under multiple random variables with known marginal probability distributions, the copula function is a very good tool to model their correlation.
Sklars gave this theory in 1959: Any multivariate joint distribution can be written according to univariate marginal distribution functions and one copula, which represents the dependence structure between the two variables. In this way, the randomness and coupling of variables are separated. Among them, the randomness of random variables is described by the marginal probability distribution, and the coupling characteristics between random variables are represented by the copula function. In other words, correlation properties of a joint distribution are completely determined by its copula function.
Assuming X_1, X_2,⋯, X_N are N random variables, their respective marginal distributions are F_1 (x_1), F_2 (x_2),⋯, F_N (x_N) and their joint distribution is H(x_1, x_2,⋯, x_N), then there is a function that “connects” the marginal distribution and the joint distribution C(∙), making H(x_1, x_2,⋯, x_N) = C(F_1 (x_1), F_2 (x_2),⋯, F_N (x_N)), according to the inverse transformation of the CDF of the edge distribution, which is x_i = F_i(−1) (u_i) (i = 1, 2,⋯, N). The expression form of the copula function can be obtained: C(u_1, u_2,⋯, u_N) = H[F(−1) (u_1), F_2(−1) (u_2),⋯, F_N(−1) (u_N)].
There are many kinds of copula functions, such as Frank copula, t-copula, Clayton copula, Gumbel copula, and Gaussian copula [14,15].
2.3. Interval Linear Fractional Programming (ILFP)
2.3.1. Interval Parameter Programming (IPP)
Interval parameter programming (IPP) addresses the problems of uncertainty that cannot be studied through probabilistic and possibilistic analyses. However, it cannot provide adequate information about the nature of output uncertainty, and all the uncertainties are forced into one arithmetic interval. The typical IPP model is:
where f± is the objective function, a±, b±, c± are the interval coefficients, X± is the interval decision variable, “±” represents the interval value, “+” is the upper bound, and “−” is the lower bound.
2.3.2. Linear Fractional Programming (LFP)
Linear fractional programming (LFP) refers to a mathematical programming whose objective function is a fractional function under linear constraints. The typical LFP model is:
where f(x) is the objective function; A∈R(m × n); b∈Rm; p, q, x∈Rn; α, β∈R; and rank A = m.
2.3.3. ILFP
An interval linear fractional programming model is established by coupling interval parameter programming and linear fractional programming. Its representation is presented as follows:
where f± is the objective function; X± is the independent variable of model; C±, D±, α±, β±, A±, B± are interval parameters; and A−, A+ are known matrices. Then, A± = [A−, A+] = {A∈R(m × n) a_ij− ≤ a_ij ≤ a_ij+}, a_ij± is an element in matrix A±, and a_ij− and a_ij+ are the upper and lower bounds of a_ij±. Other interval parameters can also be expressed in this way [16,17,18].
The solution of an interval linear fractional programming model is based on the following three fundamental theorems.
Theorem 1: Let A = [A−, A+], B = [B−, B+], Amv = (A− + A+)/2, and Bmv = (B− + B+)/2. Then, according to expression (1), for any parameter A, B, the lower bound model solution set is expressed as P_ = {A− X ≤ B−, X ≥ 0}, the upper bound model solution set is expressed as P+ = {A+ X ≤ B+, X ≥ 0}, and the median model solution set is expressed as Pmv = {Amv X ≤ Bmv, X ≥ 0}, giving P_− ⊆P_mv⊆P_+.
Theorem 2: If X± ≥ 0, D± X+ β± > 0, and f± (X) > 0, then, for each interval parameter, the upper limit expression of the objective function can be obtained as maxf+ (X) = (C+ X+ α+)/(D− X+ β−) and the lower bound expression is maxf− (X) = (C− X + α−)/(D+ X+ β+). When Cmv = (C− + C+)/2, then Dmv = (D− + D+)/2, αmv, and βmv. By analogy, the median expression of the objective function is maxfmv (X) = (Cmv X+ αmv)/(Dmv X+ βmv), giving f− ≤ fmv ≤ f+.
Theorem 3: When f± (X) > 0, the partial derivative of the objective function with respect to the independent variable can be represented as f+/x_j = (c_j+ − d_j− f+)/(∑_(i = 1)n〖d_i− x_j〗). When d_j± > 0, if c_j+∈(−∞, d_j− f_(P_mv)+), then, if and only if x_j → x_j+, f → f+. If c_j+∈[d_j− f_(P_mv)+, +∞), then, if and only if〖x〗_j → x_j−, f → f+.
2.4. Entropy-Weight-Based TOPSIS Method
In the first step, a decision matrix D containing n attributes and m options is established.
Step 2: Use the entropy method to modify the weight of each attribute.
Entropy was first introduced into thermodynamics by R. Clausius in 1865 as a physical concept, usually called thermodynamic entropy. After Shannon founded the theory of information, the concept of entropy had a new interpretation, which is now generally called information entropy. It has been widely used in financial engineering, social economy, and other fields. Entropy can be used to explain the uncertainty of the discrete distribution function Pl. For the k-th attribute, its uncertainty can be expressed as:
Among them, m is the scheme where .
For the calculation index difference coefficient, , normalize the difference coefficient, .
If the decision maker focuses on the importance of the attribute , the following formula can be used to modify its weight:
where is the entropy weight of the evaluation index and is a certain attribute to which the decision maker in the evaluation index system pays attention.
where is the standardized decision matrix and is the decision matrix after adding entropy weight.
The fourth step is to find positive and negative ideal solutions. The positive ideal solution refers to the largest positive effect indicator and the smallest negative effect indicator in each column. Similarly, the negative ideal solution refers to the smallest positive effect indicator and the largest negative effect indicator in each column.
Step 5: Calculate the distance and for each plan between the positive ideal solution plan and the negative ideal solution plan.
Step 6: Calculate the average value of the distance between each scheme and the negative ideal solution scheme. The expression is:
The schemes are classified according to the value. The larger the value is, the higher the efficiency of the scheme will be [18,19,20].
3. Application
3.1. Study Area and Data Collection
The Hetao Irrigation District is located in the southern part of Bayannaoer City, just as the Figure 2 shows, with Langshan Mountain in the Yinshan Mountains to the north and the alluvial fan at the southern foot of Wula Mountain, the Yellow River in the south, the suburbs of Baotou in the east, and the Ulan Buh Desert in the west. Wuliangsuhai is located in Wulate Front Banner, Bayannaoer City, at the east end of the Hetao Plain, 22 km away from Wulashan Town.
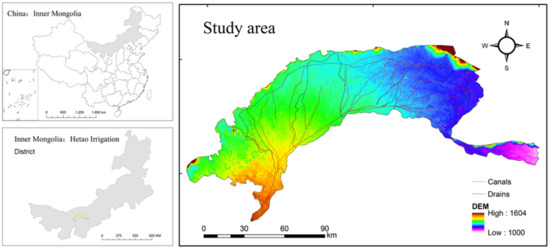
Figure 2.
The geographical position of study area.
The planned area has a mid-temperate continental climate and is located on a plateau. Affected by Mongolian high pressure, there is heavy sand and low rainfall. The annual average temperature is 3.7–7.6 °C, the annual precipitation is 100–300 mm, the average evaporation is 2032–3179 mm, and the annual average wind speed is 3 m/s, with mostly a northwest wind and a northeast wind.
The planned area belongs to the Yellow River system. According to Project Planning Report of Hetao Irrigation District, the Yellow River passes through the southern end of Bayannaoer City, enters Ershililiuzi in Dengkou County of Bayannaoer City, and exits at the Labor Canal of Wulate Front Banner in the east. The total length of the territory is 340 km, and the average annual runoff is 237 million m3, accounting for 71.6% of the city’s average annual runoff.
The planning scope includes Linhe City and six banner counties, including the entire area of Wuyuan County, Dengkou County, Hangjinhou Banner, and the southern foot of Yinshan Mountain in Urd Front, Middle, and Back Banners. The planned total population is 1.5717 million, accounting for 93% of the city’s total population. Social-economic data involved in the optimization model were selected from the Bayannaoer Statistical Yearbook 2018 and related references. In 2018, the city’s GDP of Bayannaoer was CNY 81.31 billion, and the GDP of the main banner counties within the planning area reached CNY 67.48 billion, accounting for 83% of the city’s GDP. The ratio of tertiary production is 20.2:53.4:41.1. Agriculture has developed in an all-around way. In 2018, the total output value of agriculture, forestry, the animal industry, and the fishery industry was CNY 16.28 billion, accounting for 23.2% of the city’s total output value. The total sown area of crops in the city is 11.128 million mu, of which the sown area of grain is 5.375 million mu, and the total grain output is 5.24 billion jin [16,17,19].
3.2. Parameter Estimation
Based on the rainfall and evaporation data of the Wu Liang Su Hai Ecological Positioning Station, the changes of rainfall and evaporation from 2000 to 2020 are depicted in Figure 3. In this research, the Pearson III distribution function is employed to describe the hydrological distribution of rainfall and evaporation. Based on the minimum cross-entropy principle for Pearson III distribution function, the MATLAB (MathWorks, Natick, MA, USA) program is applied to estimate the related parameters. The scale, shape, and location parameters for annual rainfall were 12.98, 3.56, and 16.66, respectively [16]. Thus, the distribution function of rainfall was expressed as:
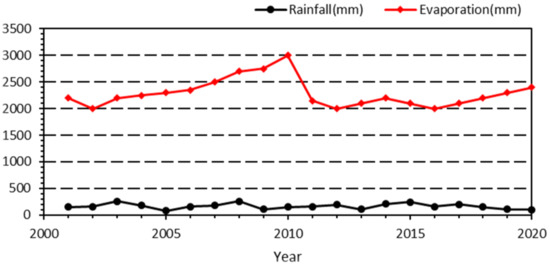
Figure 3.
Changes of rainfall and evaporation.
The scale, shape, and location parameters for evaporation were 14.62, 5.88, and 296.87, respectively. Thus, the distribution function of evaporation was expressed as:
These two distributions were regarded as marginal distributions of the rainfall and evaporation’s joint distribution function.
3.3. Joint Probability of Water Supply and Water Demand
Based on the marginal distribution functions of rainfall and evaporation, the commonly used t-copula, Gaussian copula and Archimedean copula (including the Clayton copula, Gumbel copula and Frank copula in this study, which are continually used in hydrology-related analysis) were selected to establish the joint distribution function. This article sought to select a best copula function from the Clayton copula function, Gumbel copula function, Frank copula function, t-copula function, and Gaussian copula function. The specific equations of these copula functions are expressed in Appendix A. In this research, a non-probabilistic measure for goodness of approximation, named Euclidean distance (d2), was used to evaluate the performance of each copula function. The value of d2 was 0.0372, 0.0593, 0.183, 0.0587, and 0.2064 corresponding to the above copula functions [17,18,19]. The results showed that, for the Clayton copula, the value of d2 was the smallest; thus, the Clayton copula was selected, and the joint distribution function of rainfall and evaporation could be expressed as:
where U represents the runoff, V represents the evaporation. In this research, = −3.6.
And the joint probability density function of rainfall and evaporation can be expressed as:
Based on the joint probability distribution function and joint probability density function, the 3D image of c(u,v) and C(u,v) was drawn, as the Figure 4 shows:
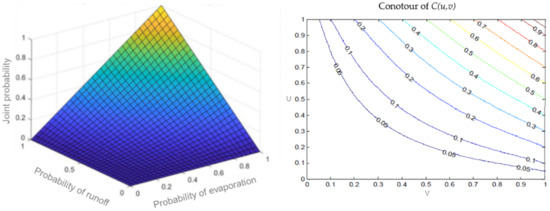
Figure 4.
Joint distribution of runoff and evaporation.
3.4. Agricultural Water Resource Optimal Allocation under Uncertainty
Agricultural water resources planning is an effective means to construct ecological irrigation districts [15]. It can make a reasonable allocation of agricultural water resources from an overall perspective, improve the utilization efficiency of agricultural water resources, and solve the problem of agricultural water shortage to a certain extent [16,17,18]. When optimizing the allocation of agricultural water resources, the expected goals are usually set first, building a model according to the actual situation. Finally, according to the objective function value that satisfies the constraints, it provides a decision-making basis for decision makers [17]. However, in most cases, the target demand for agricultural water resources’ allocation is not a single demand; different requirements will make the model results completely different [18]. Therefore, in order to avoid the drawbacks of the agricultural water resource optimization model simply pursuing economic benefits, research at home and abroad have introduced multi-objective planning into the agricultural water resources’ optimal allocation, seeking to explore the results of optimal allocation of agricultural water resources from different target angles [19]. At present, the more common multi-objective optimization methods include the target weight method, gray analysis method, compromise constraint method, entropy weight coefficient method, fuzzy optimization theory, evolutionary algorithm, etc. [20]. These methods have promoted the research progress of multi-objective optimization models for agricultural water resources, but most of the above methods have a lack of a unified and objective scientific basis for the determination of coefficients and the calculation of objective function weights [21]. Making the model results susceptible to the subjective factors of the researcher, the introduction of linear fractional programming can weaken the influence of subjective factors. In addition, due to the complexity of the agricultural water resources system, the related socio-economic and ecological environment system, and the current technical conditions, it is difficult to use absolutely accurate data in the model application process. Due to the random distribution and fuzzy characteristics of the uncertain parameters of the model, the interval uncertainty method can reflect the uncertainty of the model parameters to a certain extent and can easily reflect the uncertainty in the output results in the form of interval values. This research intended to establish an interval linear fractional programming model through coupling interval parameter programming and linear fractional programming. We conducted research on the multi-objective optimal allocation of agricultural water resources in an irrigation distract in order to better reflect the uncertainty in the process of optimal allocation of agricultural water resources and to reduce the degree to which the multi-objective optimal allocation model is affected by subjective parameter calculations and inaccurate data [22,23,24]. The objectives of the optimization model can be expressed as follows.
The above objective is subjected to the following constraints:
- (1)
- Water availability constraint
- (2)
- Water demand constraint
- (3)
- Land availability constraint
- (4)
- Drip irrigation water quantity constraint
- (5)
- Crop price constraint
- (6)
- Food security constraint
Model Hypothesis: There is a non-linear correlation between the cost of crop flood irrigation and water price, which is where ,
(RBM), and (kg) represent utility rate, economic objective and environmental objective, respectively; is the index of different areas; is the kind of crops; . is the yield (kg); is the price of crops (RMB/kg); is the planting cost (RMB); is the irrigation area, which is the decision variable (ha); is the water rights’ transfer and increased crop drip irrigation planting area (ha); is the crop drip irrigation yield (kg); is the drip irrigation cost (RMB); , , and are the parameters of chemical oxygen demand, ammonia nitrogen, total nitrogen, and total phosphorus, respectively, that inflow the river; , , and are emissions per unit area of chemical oxygen demand, ammonia nitrogen, total nitrogen and total phosphorus, respectively (kg/ha); is the water availability (m3); is the incoming water quantity (m3); is the water demand (m3); and are minimum and maximum water demand (m3); is the water availability efficiency (%); and are the minimum and maximum irrigation areas, respectively, (ha); is the drip irrigation water quantity per planting area (m3/ha); is the water rights’ transfer water quantity (m3); and are the minimum and maximum price of crops (RMB/kg); is the population for subarea and crop ; is the food demand per capita (kg/capita); and is the agricultural water price (RMB/m3).
The process of solving the interval linear fractional programming model is as follows. (1) Take the median value for all interval values in the model objective function and constraint conditions. Construct the median sub-model and solve the feasible solution of the median sub-model . (2) Determine the upper and lower limits of the independent variable interval , the objective function interval , and the corresponding relationship between the upper and lower limits of the parameter interval in the constraint condition. (3) Convert the interval linear fractional programming model into an upper limit sub-model and lower limit sub-model, respectively. (4) Connect the feasible solution obtained by solving the median sub-model in step (2). Use constraint to solve the upper and lower limit sub-models. Obtain the final interval solution based on the feasible solution obtained from the upper and lower limit sub-models [23,24,25].
4. Result Analysis and Discussion
4.1. Water Scarcity in the HID
Figure 5 presents from 2010 to 2050, under RCP8.5, in the Wuyuan irrigation area. Whether it is the upper or lower bound, there is almost no water shortage in summer, while the water shortage in spring is more serious than that in autumn and winter, about 250 million m3 to 300 million m3. In the Dengkou irrigation area, there is almost no water shortage problem. In the Linhe irrigation area, the water shortage in winter is the most serious, about 50 million m3 to 200 million m3. In the Hangjinhou irrigation area and the Urad irrigation area, the water shortage in winter is also the most serious, 200 million m3 to 300 million m3 and 210 million m3 to 300 million m3, respectively [26,27].
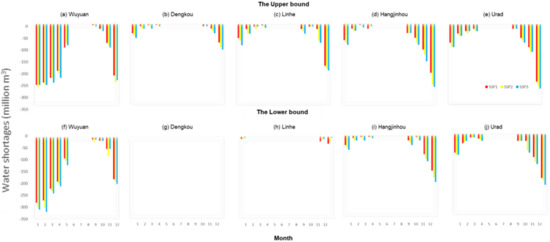
Figure 5.
Average monthly water shortage in five areas of the Hetao Irrigation District from 2010 to 2050 (RCP8.5).
4.2. Regional Water Use in the HID
Figure 6 shows, with 2010 and 2020 as the baseline scenarios, the forecast of water use for different irrigation methods in the Dengkou irrigation area and the Urad irrigation area from 2030 to 2050; trend analysis was carried out. The annual water consumption in the Dengkou irrigation area peaked around 2030 at 20 billion m3 under all three SSPs and declined thereafter. However, in 2050, the annual water consumption under SSP2 and SSP3 was about 10 billion m3, falling faster than 15 billion m3 under SSP1. The annual water consumption in the Urad irrigation area showed an upward trend under three pathways. Under SSP1, the annual water consumption increased from 30 billion m3 to 60 billion m3, almost doubling. The annual water consumption under SSP2 and SSP3 increased slightly, from 30 billion m3 to about 50 billion m3. The water consumption of drip irrigation increased significantly from 2010 to 2050, and the water consumption of furrow irrigation remained basically unchanged. The water consumption of traditional border irrigation was about 5 billion m3 in 2050, which was lower than that in 2010 [25,26,27].
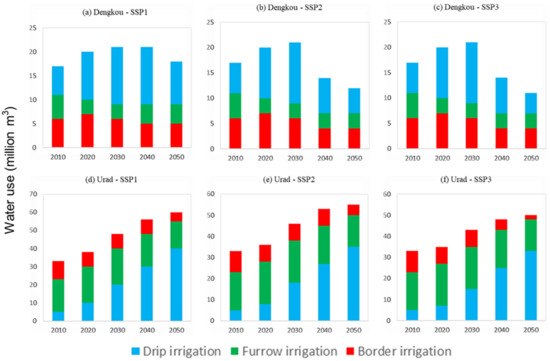
Figure 6.
Irrigation water consumption prediction of three methods for the Dengkou and Urad irrigation areas under different scenarios.
4.3. Water Availability Changes in the HID
Figure 7a,b shows the water availability in the Dengkou and Urad irrigation areas from 2010 s to 2040 s for both well and canal irrigation. In general, the available water volume in Dengkou and Urad decreased from 2010 s to 2040 s. The available water volume of well irrigation decreased from 50 billion m3 to 45 billion m3 in Dengkou, and the available water volume of canal irrigation decreased from 48 billion m3 to 40 billion m3 in Dengkou, with a small degree of decline. The amount of water available in Urad decreased more than that in Dengkou [28]. Specifically, the amount of water available for well irrigation in Urad decreased from 300 billion m3 to 250 billion m3 while the amount of water available for canal irrigation in Urad remained at 270 billion m3 from 2010 s to 2030 s, only dropping to 240 billion m3 in 2040 s.
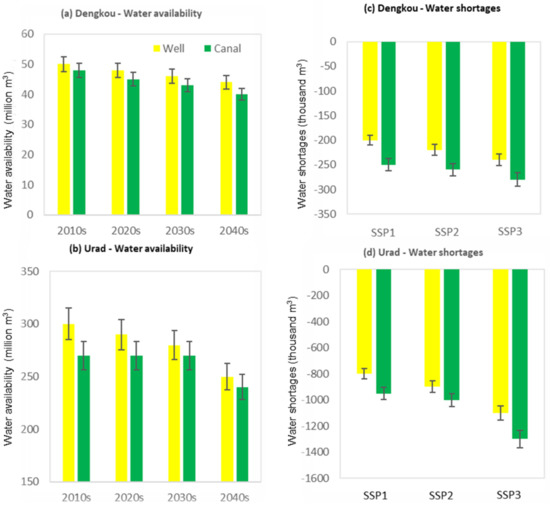
Figure 7.
Annual average water availability of two irrigation methods in two irrigation areas (a,b) and annual average water shortage from 2010 to 2050 under the SSPs (c,d).
4.4. Water Shortages in the HID
Correspondingly, Figure 7c,d shows that from SSP1 to SSP3, the water shortage in Dengkou and Urad increased, and the water shortage in canal irrigation was more than that in well irrigation for both irrigation areas. Specifically, the water shortage of well irrigation at Dengkou increased from 200 million m3 under SSP1 to 250 million m3 under SSP3, and the water shortage at Dengkou of canal irrigation increased from 250 million m3 under SSP1 to 280 million m3 under SSP3. In the Urad irrigation area, the water shortage of well irrigation increased from 800 million m3 under SSP1 to 1.100 million m3 under SSP3, and the water shortage under SSP1 and SSP2 was similar, both 1.000 million m3, and greatly increased to 1.300 million m3 under SSP3 [29].
4.5. Evaluation of Water Resources’ Carrying Capacity in the HID
According to results obtained from the optimization model and the TOPSIS entropy weight coefficient method, the water resources’ carrying capacity of the Hetao Irrigation District was analyzed. Considering that the numerator in the optimization model is the economic goal and the denominator is the environmental goal, we analyzed the water resources’ carrying capacity of the Hetao Irrigation District from the perspective of sustainable development. The design of the evaluation index system should follow the principles of systematics, representativeness, and quantification. There are, at least, dozens of indicators involved in the evaluation of water resources’ carrying capacity in an irrigation district. For comprehensive evaluation, a few indicators should be selected to reflect the most important and comprehensive information. Each indicator should be independent, comparable, and universal. Therefore, as Table 1 shows, the indicator system included three dimensions: economy, environment, and society. Each dimension contained three parameters. For the economic dimension, the benefits of unilateral water, water production efficiency, and crop output were selected. For the social dimension, it contained the three parameters of the proportion of green and high-quality agricultural products, land productivity, and resource consumption per unit of GDP. For the environmental dimension, the aging rate of the engineering facilities, Global Warming Potential per output, and agricultural non-point pollution discharge were involved. According to the entropy-weight-based TOPSIS method, the water resources’ carrying capacity prices for five different areas in the HID were obtained, as shown in the Figure 8. This research divided the price of water resources’ carrying capacity into five grades: [0, 0.2) means I grade, [0.2, 0.4) means II grade, [0.4, 0.6) means III grade, [0.6, 0.8) means IV grade, and [0.8, 1.0) means V grade. The higher the grade means the better the water resources’ carrying capacity. From the Figure 8, the water resources’ carrying capacity in the Yichang subarea was the worst, with the average value containing the three dimensions being 0.3; in the Yongji subarea, it was the best, with the average value containing the three dimensions being 0.6 [30]. The water resources’ carrying capacities of the Jiefangzha subarea and Yongji subarea were higher than the average value; the other three irrigation areas’ water resources’ carrying capacities were lower than the average value. The social dimension was in a high ratio of the water resources’ carrying capacity in the Wulanbuhe, Jiefangzha, and Urad irrigation areas; however, the proportion of the three dimensions was basically the same for water resources’ carrying capacity in the other two subareas.

Table 1.
Index system and weights.
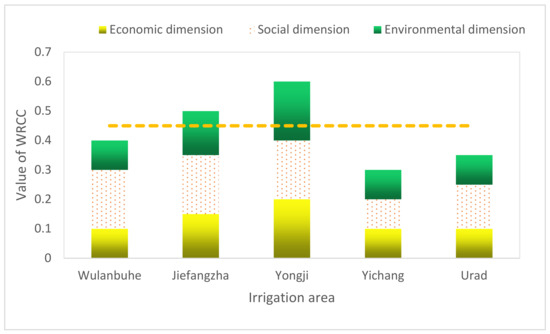
Figure 8.
Water resource carrying capacity for different subareas in HID. (Note: (1) WRCC means water resource carrying capacity; and (2) the yellow, dashed line is the average value of WRCC in the different subareas of HID).
In comparison with bi-level, multi-objective optimization model (BMPSOM) for optimizing a crop planting structure in “Optimal management of cultivated land coupling remote sensing-based expected irrigation water forecasting”, the ILFP was short of the “Yield constraint”. Therefore, it cannot be used for a crop planting structure programming. However, it contained “Water demand constraint” and “Drip irrigation water quantity constraint”; so, the water availability changes of the different irrigation methods in the HID can be obtained.
5. Conclusions
In this paper, a decision-making framework for resource management in the Hetao Irrigation District was designed [31]. The minimum cross-entropy principle was used in the parameter prediction process of rainfall and evaporation distribution functions [31,32]. Through the optimization selection of five copula functions, the Clayton copula was used to determine the parameter of probability density function and joint distribution function of rainfall and evaporation [32,33,34]. The determination of the weight parameters of the objective function in the multi-objective optimization model has always been a challenge [35,36,37,38]. Therefore, in the uncertainty optimization model module, we adopted the interval linear fractional programming model [39,40]. The numerator of the objective function is the economic goal, the denominator is the environmental goal, and the result is the utility rate in economics, which is used for post-optimization analysis [41,42]. In the post-optimization analysis, taking 2010 to 2020 as the baseline scenario and 2020 to 2050 as the forecast scenario, the obtained results included the upper and lower limits of the average monthly water shortage in five irrigation areas of the Hetao Irrigation District and the water consumption, availability, and shortage of Dengkou and Urad under border irrigation, furrow irrigation, drip irrigation, and a well–canal combination under different RCPs and SSPs [43]. Based on the optimization results, through the entropy-weight-based TOPSIS method, an index system including three dimensions of economy, society, and environment was established to deeply analyze the dynamic change of the water resources’ carrying capacity of the Hetao Irrigation District [44,45].
The results of the case study showed that the established model framework based on interval linear fractional planning can objectively reflect the uncertainty and complexity in the planning and management of agricultural water resources in the Hetao Irrigation District [39,44]. The results demonstrated the applicability and feasibility of using the minimum cross-entropy principle and the entropy-weight-based TOPSIS method on agricultural water resources’ management in an irrigation district in northeast China. It can provide decision support for the construction of a high-quality ecological irrigation district in arid and semi-arid areas under the conditions of climate change and human activities [40,43,44,45]. This study aimed to construct a modeling framework for agricultural water resources’ management; however, specific details for some sections were simplified. Such as the objective functions and constraints of the optimization model were simple, the relationship between leaders and followers was not reflected, cropping area constraints and food demand constraints should have been considered, and the dynamics of the modeling framework were overlooked. These deserves future research to improve the framework.
Author Contributions
The study and the writing of the manuscript were carried out with contributions from all the authors. Writing—original draft preparation, Y.Z.; supervision, P.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by National Natural Science Foundation of China’s continuation of funding projects for innovative research groups (No. 51621061) and National Natural Science Foundation of China (Grant Numbers: 52130902, 51909264, and 52009133).
Conflicts of Interest
The authors declare no conflict of interest and are grateful to Chenglong Zhang and Hang Zhao in the Centre for Agricultural Water Research in China, China Agricultural University, for their support and encouragement in our research.
Appendix A

Table A1.
Equations of the copula functions in this study.
Table A1.
Equations of the copula functions in this study.
| Function Name | C(u,v) | Interpretation |
|---|---|---|
| Clayton copula | and . is the Kendall coefficient of rank correlation, and the same below. | |
| Gumbel copula | and . | |
| Frank copula | and . | |
| t-copula | is the inverse function t distribution function while the degree of freedom is k; ρ is the correlation coefficients between variables. | |
| Gaussian copula | is the inverse function of standard normal distribution function; ρ is the correlation coefficients between variables. |
References
- Li, Y.; Huang, G. An inexact two-stage mixed integer linear programming method for solid waste management in the City of Regina. J. Environ. Manag. 2006, 81, 188–209. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.H.; Chi, G.F.; Li, Y.P. Long-Term Planning of an Integrated Solid Waste Management System under Uncertainty—Ι. Model Development. Environ. Eng. Sci. 2005, 22, 823–834. [Google Scholar] [CrossRef]
- Huang, G.H.; Chi, G.F.; Li, Y.P. Long-Term Planning of an Integrated Solid Waste Management System under Uncertainty—ΙΙ. A North American Case Study. Environ. Eng. Sci. 2005, 22, 835–853. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, P.; Liu, X.; Adeloye, A.J. Simulation and optimization coupling model for soil salinization and waterlogging control in the Urad irrigation area, North China. J. Hydrol. 2022, 607, 127408. [Google Scholar] [CrossRef]
- Gu, J.J.; Guo, P.; Huang, G.H. Inexact stochastic dynamic programming method and application to water resources management in Shandong China under uncertainty. Stoch. Hydrol. Hydraul. 2013, 27, 1207–1219. [Google Scholar] [CrossRef]
- Gu, J.J.; Guo, P.; Huang, G.H.; Shen, N. Optimization of the industrial structure facing sustainable development in resource-based city subjected to water resources under uncertainty. Stoch. Hydrol. Hydraul. 2013, 27, 659–673. [Google Scholar] [CrossRef]
- Tong, F.; Guo, P. Simulation and optimization for crop water allocation based on crop water production functions and climate factor under uncertainty. Appl. Math. Model. 2013, 37, 7708–7716. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Fang, S.Q.; Zhang, L.D. An inexact fuzzy parameter two-stage stochastic programming model for irrigation water allocation under uncertainty. Stoch. Hydrol. Hydraul. 2013, 27, 1441–1452. [Google Scholar] [CrossRef]
- Fang, S.Q.; Guo, P.; Li, M.; Zhang, L. Bi-level Multi-objective Programming Applied to Water Resources Allocation. Math. Prob. Eng. 2013, 2013, 837919. [Google Scholar] [CrossRef]
- Guo, P.; Chen, X.; Tong, L.; Li, J.; Li, M. An optimization model for a crop deficit irrigation system under uncertainty. Eng. Optim. 2012, 46, 1–14. [Google Scholar] [CrossRef]
- Hashimoto, T.; Loucks, D.P.; Stedinger, J.R. Robustness of water resources systems. Water Resour. Res. 1982, 18, 21–26. [Google Scholar] [CrossRef]
- McKinney, D.C.; Loucks, D.P. Network design for predicting groundwater contamination. Water Resour. Res. 1992, 28, 133–147. [Google Scholar] [CrossRef]
- Loucks, D.P. Modeling and managing the interactions between hydrology, ecology and economics. J. Hydrol. 2005, 328, 408–416. [Google Scholar] [CrossRef]
- Revelle, C.S.; Loucks, D.P.; Lynn, W.R. Linear programming applied to water quality management. Water Resour. Res. 1968, 4, 1–9. [Google Scholar] [CrossRef]
- Fedra, K.; Loucks, D.P. Interactive Computer Technology for Planning and Policy Modeling. Water Resour. Res. 1985, 21, 114–122. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, G.H.; Cai, Y.P. Multi-Source Multi-Sector Sustainable Water Supply Under Multiple Uncertainties: An Inexact Fuzzy-Stochastic Quadratic Programming Approach. Water Resour. Manag. 2013, 27, 451–473. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, G.; Cai, Y.; Yang, Z. A non-probabilistic programming approach enabling risk-aversion analysis for supporting sustainable watershed development. J. Clean. Prod. 2016, 112, 4771–4788. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, G.H.; Cai, Y.P. A Fuzzy Evacuation Management Model Oriented Toward the Mitigation of Emissions. J. Environ. Inform. 2015, 25, 117–125. [Google Scholar] [CrossRef]
- Dong, C.; Huang, G.; Tan, Q. A robust optimization modelling approach for managing water and farmland use between anthropogenic modification and ecosystems protection under uncertainties. Ecol. Eng. 2015, 76, 95–109. [Google Scholar] [CrossRef]
- Wang, R.; Li, Y.; Tan, Q. A review of inexact optimization modeling and its application to integrated water resources management. Front. Earth Sci. 2015, 9, 51–64. [Google Scholar] [CrossRef]
- Dong, C.; Huang, G.H.; Tan, Q.; Cai, Y. Coupled planning of water resources and agricultural land-use based on an inexact-stochastic programming model. Front. Ear. Sci. 2014, 8, 70–80. [Google Scholar] [CrossRef]
- Ren, C.; Guo, P.; Li, M.; Li, R. An innovative method for water resources carrying capacity research—Metabolic theory of regional water resources. J. Environ. Manag. 2016, 167, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Ren, C.; Guo, P.; Yang, G.; Li, R.; Liu, L. Spatial and Temporal Analyses of Water Resources Use Efficiency Based on Data Envelope Analysis and Malmquist Index: Case Study in Gansu Province, China. J. Water Resour. Plan. Manag. 2016, 142, 04016066. [Google Scholar] [CrossRef]
- Ren, C.F.; Li, R.H.; Zhang, L.D.; Guo, P. Multi-objective stochastic fractional goal programming model for water resources optimal allocation among industries. J. Water Res. Plan. Manag. 2016, 142, 04016036. [Google Scholar] [CrossRef]
- Ren, C.F.; Guo, P.; Li, M.; Gu, J.J. Optimization of Industrial Structure Considering the Uncertainty of Water Resources. Water Resour. Manag. 2013, 27, 3885–3898. [Google Scholar] [CrossRef]
- Gui, Z.; Zhang, C.; Li, M.; Guo, P. Risk analysis methods of the water resources system under uncertainty. Front. Agric. Sci. Eng. 2015, 2, 205–215. [Google Scholar] [CrossRef]
- Gui, Z.; Li, M.; Guo, P. Simulation-Based Inexact Fuzzy Semi-Infinite Programming Method for Agricultural Cultivated Area Planning in the Shiyang River Basin. J. Irrig. Drain. Eng. 2017, 143, 05016011. [Google Scholar] [CrossRef]
- Guo, P.; Chen, X.; Li, M.; Li, J. Fuzzy chance-constrained linear fractional programming approach for optimal water allocation. Stoch. Hydrol. Hydraul. 2014, 28, 1601–1612. [Google Scholar] [CrossRef]
- Guo, P.; Wang, X.; Zhu, H.; Li, M. Inexact Fuzzy Chance-Constrained Nonlinear Programming Approach for Crop Water Allocation under Precipitation Variation and Sustainable Development. J. Water Resour. Plan. Manag. 2014, 140, 05014003. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Liu, X.; Huang, G.; Huo, Z. A decision-support system for cropland irrigation water management and agricultural non-point sources pollution control. Desalination Water Treat. 2014, 52, 5106–5117. [Google Scholar] [CrossRef]
- Zhang, L.D.; Guo, P.; Fang, S.Q.; Li, M. Monthly Optimal Reservoirs Operation for Multi-crop Deficit Irrigation under Fuzzy Stochastic Uncertainties. J. Appl. Math. 2014, 2014, 105391. [Google Scholar]
- Fu, Y.; Li, M.; Guo, P. Optimal Allocation of Water Resources Model for Different Growth Stages of Crops under Uncertainty. J. Irrig. Drain. Eng. 2014, 140, 05014003. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, P. Integrated agriculture water management optimization model for water saving potential analysis. Agric. Water Manag. 2016, 170, 5–19. [Google Scholar] [CrossRef]
- Liu, C.; Rubæk, G.H.; Liu, F.; Andersen, M.N. Effect of partial root zone drying and deficit irrigation on nitrogen and phosphorus uptake in potato. Agric. Water Manag. 2015, 159, 66–76. [Google Scholar] [CrossRef]
- Liu, C.; Liu, F.; Ravnskov, S.; Rubaek, G.H.; Sun, Z.; Andersen, M.N. Impact of Wood Biochar and Its Interactions with Mycorrhizal Fungi, Phosphorus Fertilization and Irrigation Strategies on Potato Growth. J. Agron. Crop Sci. 2016, 203, 131–145. [Google Scholar] [CrossRef]
- Liu, C.; Ravnskov, S.; Liu, F.; Rubæk, G.H.; Andersen, M.N. Arbuscular mycorrhizal fungi alleviate abiotic stresses in potato plants caused by low phosphorus and deficit irrigation/partial root-zone drying. J. Agric. Sci. 2018, 156, 46–58. [Google Scholar] [CrossRef]
- Liu, C.; Liu, F.; Andersen, M.N.; Wang, G.; Wu, K.; Zhao, Q.; Ye, Z. Domestic wastewater infiltration process in desert sandy soil and its irrigation prospect analysis. Ecotoxicol. Environ. Saf. 2020, 208, 111419. [Google Scholar] [CrossRef]
- Huang, W.; Dai, L.M.; Baetz, B.W.; Cao, M.F.; Razavi, S. Interval Binary Programming Model for Noise Control within an Urban Environment. J. Environ. Inform. 2013, 21, 93–101. [Google Scholar] [CrossRef]
- Huang, W.; Walker, W.S.; Kim, Y. Junction potentials in thermolytic reverse electrodialysis. Desalination 2015, 369, 149–155. [Google Scholar] [CrossRef]
- Huang, W.; Baetz, B.W.; Razavi, S. A GIS-Based Integer Programming Approach for the Location of Solid Waste Collection Depots. J. Environ. Inform. 2016, 28, 39–44. [Google Scholar] [CrossRef][Green Version]
- Huang, W.; Kim, Y. Electrochemical techniques for evaluating short-chain fatty acid utilization by bioanodes. Environ. Sci. Pollut. Res. 2016, 24, 2620–2626. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Huang, W.; Huang, G.; Huang, K.; Zhou, X. A PCM-based stochastic hydrological model for uncertainty quantification in watershed systems. Stoch. Hydrol. Hydraul. 2015, 29, 915–927. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, W.; Huang, G.H.; Li, Z.; Li, Y.P.; Wang, X.Q.; Cheng, G.H.; Jin, L. A Stepwise-Cluster Forecasting Approach for Monthly Stream flows Based on Climate Teleconnections. Stoch. Environ. Res. Risk Assess. 2015, 29, 1557–1569. [Google Scholar] [CrossRef]
- Miao, D.Y.; Huang, W.W.; Li, Y.P.; Yang, Z.F. An Inexact Two-Stage Water Quality Management Model for Supporting Sustainable Development in a Rural System. J. Environ. Inform. 2014, 24, 52–64. [Google Scholar]
- Miao, D.Y.; Huang, W.W.; Li, Y.P.; Yang, Z.F. Planning Water Resources Systems under Uncertainty Using An Interval-Fuzzy De Novo Programming Method. J. Environ. Inform. 2014, 24, 11–23. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).