Abstract
With the development of precision agriculture (PA), low-altitude and low-volume spraying based on unmanned aerial vehicles (UAVs) is playing an increasingly important role in the control of crop diseases, pests, and weeds. However, the aerial spraying quality and droplet drift are affected by many factors, some of which are controllable (e.g., flight and spraying parameters) and some of which are not (e.g., environmental parameters). In order to study the influence of spraying parameters on the UAV-based spraying performance, we propose a UAV-compatible spraying system and a customized experimental platform in this work. Through single-factor test and Box–Behnken response surface methods, four influencing factors, namely spraying height, flow rate, distance between nozzles, and pulse width modulation (PWM) duty cycle, were studied under indoor conditions. Variance analysis and multiple quadratic regression fitting were performed on the test data by using Design-Expert 8.0.5B software, and quadratic polynomial regression models of effective spraying width, droplet coverage density, coefficient of variation, and droplet coverage rate were established. Based on the Z-score standardization, a mathematical model of the comprehensive score with four factors was established to evaluate the spraying quality and predict optimal spraying parameters. Test results indicate that the effect intensity of four influencing factors from strong to weak is PWM duty cycle, flow rate, distance between nozzles, and spraying height, and their optimal values are 98.65%, 1.74 L/min, 1.0 m, and 1.60 m, respectively. Additionally, verification experimental results demonstrate that the deviation between the predicted comprehensive score and the actual value was less than 6%. This paper can provide a reference for the design and optimization of UAV spraying systems.
1. Introduction
Over the past few decades, traditional agriculture has been evolving towards precision agriculture (PA), which is characterized by applying the right treatment in the right place at the right time [1,2]. Throughout the whole growth circle of crops, labor-intensive and high-risk agrochemical spraying is one of the most indispensable operations to control the emergence and spread of pests, diseases, or weeds. However, the abuse of agrochemicals, especially pesticides, has caused great damage to the agricultural ecosystem. Determining how to suppress the increase in pesticide usage by improving the application efficiency and then promoting the sustainable development of agriculture is a worldwide challenge in this century [3]. Although terrestrial agricultural machinery plays the main role in field spraying, its accessibility in unstructured farmland, especially with late-stage high-stem crops, limits its efficiency in curbing disease, pest, or weed outbreaks.
With the advance of robotics and sensing technologies, agricultural robots (Agri-robots) have shown great potential in closing the crop yield gap and promoting sustainable agricultural development [4,5]. With the unique characteristics of high flexibility and maneuverability, unmanned aerial vehicles (UAVs) stand out among various Agri-robots and have proven to be a powerful platform to conduct field surveys and aerial management [6,7,8]. For example, UAVs have been widely used in different agricultural applications, such as soil mapping, crop identification, and biotic/abiotic monitoring [9,10,11,12,13]. Specifically, UAV-based agrochemical spraying has drawn extensive attention in the agricultural community [14,15]. Generally, there are two strategies for UAV-based spraying, namely uniform spraying and spot spraying. Uniform spraying aims to cover the entire area with the same dosage of agrochemicals. Most of the previous research work can be classified into this category. For instance, to achieve the highest droplet deposition volume and droplet uniformity, Guo et al. [16] conducted an orthogonal experiment to find the optimal combination of flight parameter, drop size, and crop phenotype. Furthermore, some researchers have focused on applying adaptive methods to aerial pesticide spraying. Faiçal et al. [17] introduced a series of optimization algorithms, such as genetic algorithm, particle swarm algorithm, and hill-climbing algorithm, to optimize the UAV’s flight route according to the dynamically changing weather conditions. Variable-rate application is another adaptive approach to achieve area-even spraying [18,19,20]. Wang et al. [21] realized the dynamic adjustment of flow rate following the real-time change of flight speed and improved the uniformity of the deposition distribution. With the development of agricultural information technology, spatial and temporal variabilities of farmland are becoming more and more accessible. Spot spraying takes the spatiotemporal variabilities into account and only performs appropriate treatment on specific sites. Richardson et al. [22] developed a UAV spot spraying system for applying pesticides to individual plants and proposed a method for quantifying and analyzing the 2D pattern of droplet deposition. Compared to uniform spraying, spot spraying is more conducive to improving agrochemical utilization and reducing dosage. For both uniform spraying and spot spraying, it is necessary to study the influence of operating parameters on spraying quality.
Spraying width, size of droplets, volume of deposition, droplet coverage density, droplet distribution uniformity, and droplet coverage rate are among the main metrics used to evaluate the UAV-based spraying quality. However, they can be affected by many factors, which can be roughly divided into three aspects: environmental parameters, flight parameters, and spraying parameters. Among them, in-situ environmental parameters, including crosswind speed and direction, are usually uncontrollable and have a direct impact on droplet deposition and drift [23,24]. Flight parameters, such as flight speed, flight height, and downwash, determine the deposition and distribution of droplets [25,26,27]. Additionally, some spraying parameters, such as spraying flow and nozzle specifications, directly influence the characteristics of droplets and spraying efficiency [28,29,30].
Agricultural scientists have carried out many studies to investigate the impact of different operating parameters on the quality of UAV spraying. Chen, et al. [24] studied the impact mechanism of the wind field in X-, Y-, and Z-directions on the distribution characteristics of aerial spraying droplet deposition on a rice canopy. Field experimental results demonstrated that the wind field in the Z-direction has the most significant effect on droplet deposition, followed by the Y-direction and then the X-direction. Ahmad et al. [25] and Tang et al. [26] investigated the influences of flight parameters, such as flight speed and flight height, on the droplet deposition and off-target drift. At present, most of the studies with field experiments only focused on a few influencing factors, such as flight speed, flight height, and spraying flow [31,32]. The main reason is that many factors cannot be precisely controlled in a real field environment. Additionally, it has been proven that the interactions of various factors also have a significant impact on UAV-based spraying quality.
Another limitation of previous studies is that most of the relevant works are based on specific spraying systems with fixed spraying parameters to study the impact of flight parameters and environmental parameters on spraying quality, while ignoring the optimization of spraying system parameters. However, the optimization of the spraying system is fundamental and critical for UAV spraying.
This work specifically focused on the analysis of the influence of parameters of a spraying system designed for UAV spraying application on the spraying quality based on Box–Behnken response surface method. A customized platform was constructed for simulating the flight of UAVs. Four-factor–three-level factorial tests were conducted to investigate the interaction of four spraying parameters, namely spraying height, flow rate, distance between nozzles, and pulse width modulation (PWM) duty cycle, on spraying quality. This study aims to provide a reference for the design and optimization of UAV spraying systems.
2. Materials and Methods
2.1. Design and Control Methods of Spraying System
In order to study the influence of different operating parameters on spraying quality, a spraying system for UAV spraying application was designed as shown in Figure 1. The spraying system is mainly composed of a tank, a micro diaphragm pump (MDP) (PLD-1206, max pressure: 1 MPa, max flow: 4 L/min), a pressure sensor (KY-3, measure range: 0–1 MPa, precision: ±0.25%), a flow sensor (MJ-HW41C, measure range: 0.25–2.5 L/min, precision: ±5%), two electric centrifugal nozzles (ECNs) (LXPT-03, nominal voltage: 12 V, max speed: 16,000 r/min), and the spraying controller (STM32F407, STMicroelectronics). The MDP is responsible for transporting the spray material from the tank to the ECNs. The ECN atomizes the spraying material into droplets with a minimum diameter of less than 100 μm through the centrifugal force generated by the high-speed rotation of the embedded motor. The main reason for choosing this type of nozzle is that the size of the droplet diameter can be controlled by adjusting the duty cycle of the PWM control signal. Additionally, droplets with 100–150 μm diameter are generally required for ultra-low-volume UAV spraying according to [33] other related works.
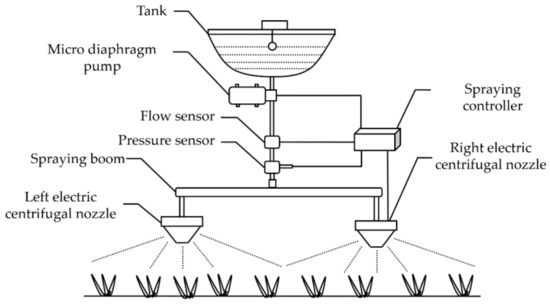
Figure 1.
Schematic view of the spraying system designed for UAV spraying application.
For the spraying system we designed, the spraying height, flow rate, distance between nozzles, and rotation speed of ECNs are the four controllable parameters. The spraying height and flow rate are set with reference to the values commonly used in other works. The selection of installing space between the two ECNs is mainly based on common UAV sizes. Motor speed inside ECN directly determines the centrifugal force and indirectly affects the droplet diameter and spraying width. It can be controlled by configuring the duty cycle of the PWM signal.
The control method of spraying system is shown in Figure 2. A microcontroller unit (MCU) with ARM Cortex-M4 kernel is used as the spraying controller. Two Ultra battery elimination circuit (UBEC) modules are deployed to stabilize the output voltage of the 6S lithium battery into constant 5 and 12 V, respectively. The 5 V powers the MCU, wireless data transmission module, pressure sensor, and flow sensor; the 12 V powers ECNs and MDP. The inputs of the MCU are connected to the flow sensor, pressure sensor and wireless data transmission module, and the outputs are connected to the MDP and ECN through three electronic speed controllers (ESCs). The MCU can output three independent PWM waves with adjustable duty cycle to control the rotational speed of the internal motors of the MDP and ECNs. The wireless data transmission module is used to build a direct communication bridge between the spray controller and the host computer. Based on LabVIEW, a control software running (as shown in Figure 3) on the host computer was developed to monitor the entire system and send control commands.
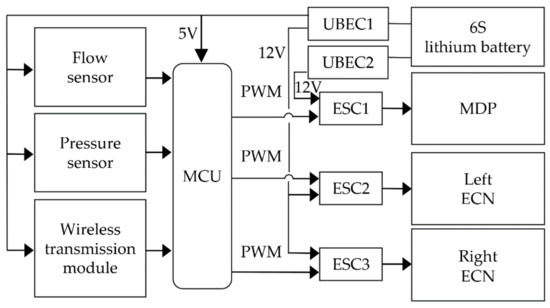
Figure 2.
Schematic of spraying control system.

Figure 3.
The control software running on the host computer.
2.2. Design of Test Platform
As shown in Figure 4, an indoor test platform was designed and constructed to study the effects of spraying height, flow rate, distance between nozzles, and PWM duty cycle on spraying performance of the proposed spraying system. The test platform is 4 m long, 5 m wide, and 3 m high. It is mainly composed of a gantry with nozzles, sliding carrier, liner slide, servo motor, motor controller, and pulleys. The servo motor drives the sliding carrier with water-sensitive paper (WSP) through the wire rope and pulleys to pass through the spraying field at 2.0 m/s. To avoid contamination of the WSP by droplets before the spraying field reaches a steady state, plastic film is used on both ends of the test platform to shield the sliding carrier.
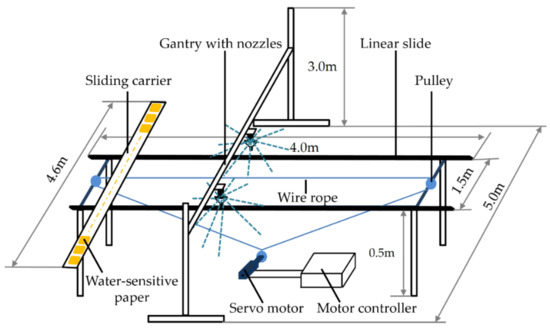
Figure 4.
Schematic diagram of the structure of the spraying platform.
2.3. Test Methods
The multifactor and multilevel orthogonal experiment was the core test method in this work. The spraying height, flow rate, distance between nozzles, and PWM duty cycle of ECNs were the four factors, and the effective spraying width, droplet coverage density, coefficient of variation, and droplet coverage rate were considered as response values. The indoor test is shown in Figure 5. For each test, the spraying height and the distance between nozzles were manually adjusted according to the experimental schedules. The target flow and PWM duty cycle of the nozzles were set by remote control software. The servo motor controller communicated with the spraying controller through the RS232 communication protocol and received the control instruction from the host computer to execute start, accelerate, brake, and stop.

Figure 5.
On-site picture of indoor test.
To ensure the safety of indoor tests, all experiments were carried out with water instead of agrochemicals. Pieces of water-sensitive paper (26 × 76 mm, Syngenta, Switzerland) were used to collect the droplets and calculate their coverage density and coverage rate. Twenty-four sampling points were evenly arranged at 20 cm intervals on the sliding carrier, and a single piece of WSP was fixed at each sampling point. After each test, all 24 pieces of WSP were collected, labeled, and sealed separately for subsequent analysis.
In view of the immaturity of UAV-based spraying technology, there is currently no internationally recognized method for evaluating the quality of UAV spraying. According to the definitions in the China civil aviation standard “Agricultural Aviation Operation Quality and Technical Indicators Part I: Spraying Operations-MH/T1002.1-2016”, low-volume and ultra-low-volume spraying means that the usage of agrochemical is 5–30 L/ha and 0–5 L/ha, respectively. Droplet coverage density in ultra-low-volume pesticide spraying is 15–40/cm2, and the droplet distribution uniformity is less than 70%. Combining our research experience and methods in related works, in this study, when the droplet coverage density at the sampling point is greater than 15/cm2, it is considered an effective sampling point. A WSP sample with sedimentary droplets is shown in Figure 6a, and the corresponding processed image is shown in Figure 6b. The individual droplet size, the droplet distribution, the total number of droplets, the droplet coverage density, and the droplet coverage rate can be extracted by DepositScan, a publicly available scanning program that can quickly evaluate deposit distribution on images of WSP [34].

Figure 6.
Image processing for WSP samples. (a) Raw and (b) processed images of a WSP with droplets. Note: Blue areas in raw image and black points in processed image are the traces after the droplets were deposited on WSP.
Droplet coverage density (CD) is the total number of deposited droplets per cm2. The droplet distribution uniformity is expressed by the coefficient of variation (CV) of the droplet coverage density. The smaller the CV, the more uniform the droplet distribution is. The calculation formula is as follows:
where CV is the coefficient of variation, S is the standard deviation of the droplet coverage density, CD is the droplet coverage density of a single sample, and CDavg is the average droplet coverage density of all samples within a single test.
Droplet coverage rate (CR) is the ratio of total area that droplets covered per cm2; it can be computed by (3):
where CR is the droplet coverage rate, ai represents the area of a single droplet, and A stands for the entire area of the selected region.
The effective spraying width represents the total spraying width of both left and right ECNs and can be obtained by counting the number of effective sampling points:
where SW is the effective spraying width, ∑num.sample represents the total number of samples between the leftmost and rightmost effective samples, and 0.2 refers to the interval between WSP samples with the unit of m. The width of WSP is ignored.
2.4. Analysis Method
The main purpose of this work is to find the optimal combination of four influencing factors which can yield the best spraying quality. This is a typical multifactor, multilevel factorial study. The use of overall experimental methods to solve multifactor and multilevel optimization problems usually results in too many total trials that are unpractical to conduct. Orthogonal experimental design (OED), central composite design (CCD), and Box–Behnken design (BBD) are the three most used factorial experimental design methods. According to the orthogonality, OED selects some representative points from the overall experiments to find the best combination of factors and levels. It pays attention to how to arrange the experiment scientifically and reasonably. However, it cannot find a clear functional expression between the factor and the response value, so it cannot find the optimal combination of factors and the optimal value of the response value in the entire interval. CCD and BBD are the two most important response surface design methods, both of which can construct regression equations between factors and response values. CCD is particularly useful in sequential experiments because it is possible to add pivot points and center points to previous factor experiments to build a new work. BBD usually has fewer design points, so its operating cost is lower than that of CCD with the same number factor. In this work, there was no order requirement for 4-factor and 3-level experiments, and we hoped to establish an accurate regression equation of the four spraying parameters and spraying quality through as few experiments as possible. Therefore, Box–Behnken response surface analysis method was the best option for this study. In addition, Design-Expert 8.0.5B (Stat-Ease Inc., Minneapolis, MN, USA) was introduced to schedule BBD tests and analyze experimental results.
Taking effective spraying width SW, average droplet coverage density CDavg, coefficient of variation CV, and droplet coverage rate CR as reference values, the effects of spraying height X1, flow rate X2, distance between nozzles (the distance between left and right ECNs) X3, and PWM duty cycle of ECN X4 on spraying performance of the spraying system were investigated. In this work, the PWM duty cycle of the left ECN and right ECN is always configured to the same value. Firstly, single-factor tests were designed and conducted to find the maximum and minimum levels of each factor (detailed in Section 3.1). Secondly, BBD was deployed to design the 4-factors and 3-levels test (detailed in Section 3.2). Thirdly, based on the test results, quadratic polynomial mathematical models were obtained with the help of analysis of variance (ANOVA). Then, through Z-score standardization, a mathematical model of comprehensive score that integrates the four response values was established and the optimal operating parameters were solved. The Z-score standardization for the positive correlation response value data can be described as Formula (5), where is the standardized data, is the average of raw data x, and σ means the standard deviation. The standardized treatment formula for the negative correlation response value data can be described as Formula (6).
Finally, a set of optimal values of the four factors and the corresponding comprehensive score could be solved. The spraying quality with the predicted values was evaluated by the verification tests. The deviation between the predicted comprehensive score and the actual value was used to estimate the prediction accuracy of the model.
3. Results
3.1. Results of Single-Factor Test
We carried out a series of single-factor tests to determine the level scope of each factor. The test results in Table 1 show the following: (a) Taking X1 as the investigating factor, when X1 increases from 1.0 to 1.8 m, SW is basically stable at 2.6 m, and CDavg, CR, and the droplet distribution uniformity are improved. When X1 reaches 2 m, CDavg and CR begin to decrease, and the uniformity of droplet distribution begins to deteriorate. (b) Taking the flow rate X2 as the investigating factor, as X2 increases, the CR gradually increases. However, the maximum value of SW appears when X2 reaches 1.7 L/min, and the minimum value of the CV occurs when X2 reaches 1.4 L/min. (c) Taking the distance between nozzles X3 as the investigating factor, as X3 increases, SW gradually increases, while CV first decreases and then increases, and the minimum value is taken at 1.6 m. (d) Taking PWM duty cycle X4 as the investigating factor, with the increase in X4, SW changes in a small range, and the CDavg and the uniformity of droplet coverage distribution are improved.

Table 1.
Design and results of single-factor tests.
Considering the results of the single-factor test and the limitation of the actual operating environment, the level values of the four factors are configured as follows: spraying height X1: 1.0–2.0 m, flow rate X2: 0.50–2.00 L/min, distance between nozzles X3: 0.8–2.2 m, PWM duty cycle X4: 50–100%. The final four factors and three levels of the Box–Behnken tests are shown in Table 2.

Table 2.
Factor level of Box–Behnken tests.
3.2. Results Analysis of Response Surface Test
A total of 29 tests were designed by BBD in Design-Expert 8.0.5B. Of these, numbers 1, 11, 15, 24, and 29 are the central point tests, and the others are the factorial tests. All tests were carried out in accordance with the order of the test sequence. The results in Table 3 were analyzed using the method of quadratic multiple regression fitting.

Table 3.
Design and results of Box–Behnken tests.
Through parameter optimization, the quadratic polynomial regression equations of effective spraying width SW, average droplet coverage density CDavg, coefficient of variation CV, and droplet coverage rate CR were respectively obtained for the true values of spraying height X1, flow rate X2, distance between nozzles X3, and PWM duty cycle X4.
The correlation coefficient R2 of equation CDavg and CR are greater than 0.9, indicating that the quadratic polynomial could accurately represent the effect of changes in operating parameters on droplet coverage density and droplet coverage rate. Z-score standardization was used to standardize the four response values (in Table 3) obtained in each experiment. Then, by adding the four standardized response values, a comprehensive score was obtained, which can be used to represent the spraying performance of the spraying system under different operating parameters. The quadratic polynomial regression equation of comprehensive score (CS) of the true values of X1, X2, X3, and X4 is as follows:
The results of ANOVA for quadratic regression equations of response surface are listed in Table 4. The results demonstrate the following: (a) The integrated regression model is correct as the model has a significant p-value. (b) X2, X4, and X22 reach significance level. (c) According to the F value, it can be inferred that the influence intensity of four factors from strong to weak is X4 > X2 > X3 > X1. (d) Although the interactions between the four factors are not significant, X2 and X4 is the main interaction. The interaction effects of X2X4, X2X3, and X3X4 on the comprehensive score are shown in Figure 7a, Figure 7b, and Figure 7c, respectively. In Figure 7a, the comprehensive score increases first and then decreases with the increase in X2, but it shows a linear change with the changes of X3 (Figure 7b) and X4 (Figure 7c), indicating that the interactions of X2X4, X2X3, and X3X4 have a nonsignificant influence on the model.

Table 4.
ANOVA for quadratic regression equations of response surface.
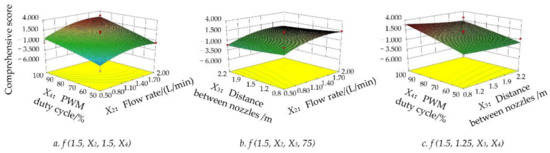
Figure 7.
Response surface plots of interaction of three factors.
Taking the highest comprehensive score as the goal of optimization, the optimized operating parameters of the spraying system can be predicted by solving and analyzing the extreme value of the regression model. The optimal parameters are as follows: spraying height X1, 1.60 m; flow rate X2, 1.74 L/min; distance between nozzles X3, 1.0 m; PWM duty cycle in nozzle X4, 98.65%. The predictive value of the comprehensive score is 3.182.
To facilitate the verification tests, the PWM duty cycle was adjusted to 100%, and the model prediction results were verified according to the above optimal conditions. The test results are shown in Table 5. The experimental data were added after Z-score standardization, and the comprehensive average score was 3.205. Compared with the predicted value of the model, the relative error is 0.74%, which indicates that the regression equation model is reliable and predictable.

Table 5.
Results of verification tests.
4. Discussion
In general, the spraying technology based on UAVs is still in the preliminary research stage. Although some achievements have been made so far, there are still many problems that need to be solved. Firstly, some of the UAVs used in related research are commercialized, and some are privately customized. These UAVs have a variety of shapes, sizes, and driving methods, which increases the difficulty of studying the influence of the UAVs’ flight parameters on the spraying quality. Secondly, except for some commercial agricultural UAVs, such as DJI MG-P and T series, other agricultural UAVs used for scientific research are usually equipped with customized nonstandardized spraying systems. This means that the optimal spraying parameters vary in different studies. Thirdly, UAV-based spraying quality is affected by many factors, and there are no uniform standards that are recognized by the global agricultural community that can be used to evaluate it.
Spraying height, flight speed, flow rate, and drop size are controllable in indoor or outdoor experiments. Their influence on spraying quality is the research focus of most published papers [15,25,26,28,31,32]. For example, in 2016, Xue et al. [15] developed an automatic aerial spraying system for an N-3-type unmanned helicopter. They investigated the performance of UAV spraying through a series of outdoor experiments, in which the main test parameters were set as follows: flight speed 3–6 m/s, flight height 3–7 m, and spraying flow of each centrifugal rotary atomizer (total 2) 0.6–1 L/min. Test results revealed that the CV of UAV-based spraying performance is lower than 60%. However, the spraying quality is sensitive to experimental configurations, and the optimal combination of operating parameters in this study may not be applicable to other UAV-based spraying systems. In addition, downwash and crosswinds also have a significant impact on deposition patterns and off-target drift [23,24,35]. What makes this area of study more complicated is that UAV spraying quality is usually affected by the interaction of multiple factors, and it is unrealistic to accurately reveal the interaction mechanism by conducting real field experiments, especially given the uncertainty of environmental parameters and the instability of flight attitude. For example, the dynamically changing downwash airflow is determined by various factors such as ambient wind, crop canopy, flight speed, flight altitude, flight attitude, and drone modalities. Sometimes, it is necessary or even inevitable to study the influence of some factors in certain specific ideal environments. Although such research results are different from the real situation, they can provide a certain reference for the optimization of system parameters.
Zhang et al. [36] developed an indoor spraying platform to simulate UAV aerial spraying. The system was tested at three different moving speeds, 0.3, 0.6, and 1.0 m/s, during which the wind speed and flow rate remained constant at 5.7 m/s and 1.16 L/min, respectively. Although they introduced the downwash airflow by installing a propeller above each nozzle, the wind speed could not adapt to the change of the moving speed, which would reduce the interpretability of the experimental results.
This work mainly studies the effect of spraying parameters on spraying quality and proposes a spraying parameter optimization method. The influences of other factors, such as downwash and crosswind, are not in the scope of this research. Spraying height, flow rate, distance between nozzles, and PWM duty cycle of ECNs are the four investigating factors, and the effective spraying width, coefficient of variation, droplet coverage density, and droplet coverage rate are the main metrics used to evaluate the spraying quality. Analysis results in Table 5 demonstrate that the optimal parameters are as follows: spraying height, 1.60 m; flow rate, 1.74 L/min; distance between nozzles, 1.0 m; PWM duty cycle of ECN, 98.65%. With these configurations, the effective spraying width SW, average droplet coverage density CDavg, coefficient of variation CV, and droplet coverage rate CR are 2.9 m, 68.4 No./cm2, 32.65%, and 21.77%, respectively. Once the spraying system is mounted on the UAV, the 1.6 m spraying height can not only ensure flight safety, but also help reduce the drift of the droplets. Taking the 2.0 m/s moving speed of the gantry in our designed platform and the 2.9 m effective spraying width (Table 5) into account, the flow rate of 1.74 L/min results in the dosage of agrochemical at 50 L/ha, which is inconsistent with the 15–20 L/ha commonly used for low-volume UAV spraying. However, our research results still can provide a reference for real-field UAV-based spraying, and the flow rate can be further reduced with the increase in flight speed and the involvement of downwash. The 1.0 m nozzle spacing, on the one hand, is compatible with most agricultural UAVs; on the other hand, it can maintain the adjacent overlap of the left and right nozzles. The 98.65% PWM duty cycle means the ECN almost works at the full speed, and the minimum droplet diameter can reach 100 μm or less. This is beneficial to improve the droplet coverage density and coverage uniformity.
There are a few limitations in this work. The first one is that we studied the cross-effects of four spray parameters on spraying quality through simulation experiments in an indoor environment. However, field trials are needed to verify the results because the real farmland environment is more complicated, and many parameters cannot be precisely controlled. Another one is that we did not consider the impact of the downwash airflow. The main reason is that the intensity and distribution characteristics of the downwash airflow are affected by many factors and cannot be accurately simulated.
5. Conclusions
In this work, a specially customized platform and a spraying system designed for UAV spraying applications were proposed. Under indoor environmental conditions, the influence of operating parameters of the spraying system on the spraying quality was studied by combining the single-factor test and Box–Behnken response surface methodology. Test data were standardized by Z-score, and a comprehensive score was used to evaluate the spraying performance. Variance analysis and multiple quadratic regression fitting were performed on the test data by using Design-Expert 8.0.5B software. The mathematical model of the comprehensive score with four factors was established to predict the optimal operating parameters, which can be listed as follows: spraying height, 1.60 m; flow rate, 1.74 L/min; distance between nozzles, 1.0 m; duty cycle of PWM in nozzle, 98.65%. Verification test results showed that the deviation between the predicted comprehensive score and the actual value was less than 6%, which indicated that the response surface method for the working parameters of the application system was reasonable and feasible. Overall, this work will contribute to the design and optimization of spraying systems for UAV spraying applications. In the following research, we will equip this spraying system on a UAV to carry out real field spraying experiments and verify the real spraying performance under this set of optimized parameters.
Author Contributions
D.W., W.C. and S.X. designed the research. D.W. and Z.L. participated in the measurements and data analysis. D.W. wrote the first draft of the manuscript. Z.L., S.X. and W.C. revised and edited the final version of the manuscript. D.W. and S.X. are responsible for funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (32001424), Shenzhen Science and Technology Program (JCYJ20210324102401005), and China Postdoctoral Science Foundation (2020M682989).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge Junxiong Zhang and Wei Li from China Agricultural University for supporting this work.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Gebbers, R.; Adamchuk, V.I. Precision agriculture and food security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef] [PubMed]
- Maes, W.H.; Steppe, K. Perspectives for remote sensing with unmanned aerial vehicles in precision agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Lechenet, M.; Dessaint, F.; Py, G.; Makowski, D.; Munier-Jolain, N. Reducing pesticide use while preserving crop productivity and profitability on arable farms. Nat. Plants 2017, 3, 1–6. [Google Scholar] [CrossRef] [PubMed]
- King, A. Technology: The future of agriculture. Nature 2017, 544, S21–S23. [Google Scholar] [CrossRef] [Green Version]
- Vougioukas, S.G. Agricultural robotics. Annu. Rev. Control Robot. Auton. Syst. 2019, 2, 365–392. [Google Scholar] [CrossRef]
- Sylvester, G. (Ed.) E-Agriculture in Action: Drones for Agriculture; Food and Agriculture Organization of the United Nations and International Telecommunication Union: Bangkok, Thailand, 2018. [Google Scholar]
- Xiongkui, H.; Bonds, J.; Herbst, A.; Langenakens, J. Recent development of unmanned aerial vehicle for plant protection in East Asia. Int. J. Agric. Biol. Eng. 2017, 10, 18–30. [Google Scholar]
- Huang, Y.; Thomson, S.J.; Hoffmann, W.C.; Lan, Y.; Fritz, B.K. Development and prospect of unmanned aerial vehicle technologies for agricultural production management. Int. J. Agric. Biol. Eng. 2013, 6, 1–10. [Google Scholar]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Mukherjee, A.; Misra, S.; Raghuwanshi, N.S. A survey of unmanned aerial sensing solutions in precision agriculture. J. Netw. Comput. Appl. 2019, 148, 102461. [Google Scholar] [CrossRef]
- Yang, N.; Yang, S.; Cui, W.; Zhang, Z.; Zhang, J.; Chen, J.; Chen, J.; Ma, Y.; Lao, C.; Song, Z.; et al. Effect of spring irrigation on soil salinity monitoring with UAV-borne multispectral sensor. Int. J. Remote Sens. 2021, 42, 8952–8978. [Google Scholar] [CrossRef]
- Srivastava, K.; Bhutoria, A.J.; Sharma, J.K.; Sinha, A.; Pandey, P.C. UAVs technology for the development of GUI based application for precision agriculture and environmental research. Remote Sens. Appl. Soc. Environ. 2019, 16, 100258. [Google Scholar] [CrossRef]
- Srivastava, K.; Pandey, P.C.; Sharma, J.K. An approach for route optimization in applications of precision agriculture using uavs. Drones 2020, 4, 58. [Google Scholar] [CrossRef]
- Kharim, M.N.A.; Wayayok, A.; Shariff, A.R.M.; Abdullah, A.F.; Husin, E.M. Droplet deposition density of organic liquid fertilizer at low altitude UAV aerial spraying in rice cultivation. Comput. Electron. Agric. 2019, 167, 105045. [Google Scholar] [CrossRef]
- Xue, X.; Lan, Y.; Sun, Z.; Chang, C.; Hoffmann, W.C. Develop an unmanned aerial vehicle based automatic aerial spraying system. Comput. Electron. Agric. 2016, 128, 58–66. [Google Scholar] [CrossRef]
- Guo, S.; Li, J.; Yao, W.; Hu, X.; Wei, X.; Long, B.; Wu, H.; Li, H. Optimization of the factors affecting droplet deposition in rice fields by rotary unmanned aerial vehicles (UAVs). Precis. Agric. 2021, 22, 1918–1935. [Google Scholar] [CrossRef]
- Faiçal, B.S.; Freitas, H.; Gomes, P.H.; Mano, L.Y.; Pessin, G.; de Carvalho, A.C.; Krishnamachari, B.; Ueyama, J. An adaptive approach for UAV-based pesticide spraying in dynamic environments. Comput. Electron. Agric. 2017, 138, 210–223. [Google Scholar] [CrossRef]
- Wang, L.; Lan, Y.; Yue, X.; Ling, K.; Cen, Z.; Cheng, Z.; Liu, Y.; Wang, J. Vision-based adaptive variable rate spraying approach for unmanned aerial vehicles. Int. J. Agric. Biol. Eng. 2019, 12, 18–26. [Google Scholar] [CrossRef]
- Lian, Q.; Tan, F.; Fu, X.; Zhang, P.; Liu, X.; Zhang, W. Design of precision variable-rate spray system for unmanned aerial vehicle using automatic control method. Int. J. Agric. Biol. Eng. 2019, 12, 29–35. [Google Scholar] [CrossRef]
- Wen, S.; Zhang, Q.; Deng, J.; Lan, Y.; Yin, X.; Shan, J. Design and experiment of a variable spray system for unmanned aerial vehicles based on PID and PWM control. Appl. Sci. 2018, 8, 2482. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Zhang, J.; Li, W.; Xiong, B.; Zhang, S.; Zhang, W. Design and test of dynamic variable spraying system of plant protection UAV. Trans. Chin. Soc. Agric. 2017, 5, 86–93. [Google Scholar]
- Richardson, B.; Rolando, C.A.; Kimberley, M.O. Quantifying spray deposition from a UAV configured for spot spray applications to individual plants. Trans. ASABE 2020, 63, 1049–1058. [Google Scholar] [CrossRef]
- Wang, G.; Han, Y.; Li, X.; Andaloro, J.; Chen, P.; Hoffmann, W.C.; Han, X.; Chen, S.; Lan, Y. Field evaluation of spray drift and environmental impact using an agricultural unmanned aerial vehicle (UAV) sprayer. Sci. Total Environ. 2020, 737, 139793. [Google Scholar] [CrossRef]
- Chen, S.; Lan, Y.; Jiyu, L.; Zhou, Z.; Liu, A.; Mao, Y. Effect of wind field below unmanned helicopter on droplet deposition distribution of aerial spraying. Int. J. Agric. Biol. Eng. 2017, 10, 67–77. [Google Scholar]
- Ahmad, F.; Qiu, B.; Dong, X.; Ma, J.; Huang, X.; Ahmed, S.; Chandio, F.A. Effect of operating parameters of UAV sprayer on spray deposition pattern in target and off-target zones during outer field weed control application. Comput. Electron. Agric. 2020, 172, 105350. [Google Scholar] [CrossRef]
- Tang, Y.; Hou, C.J.; Luo, S.M.; Lin, J.T.; Yang, Z.; Huang, W.F. Effects of operation height and tree shape on droplet deposition in citrus trees using an unmanned aerial vehicle. Comput. Electron. Agric. 2018, 148, 1–7. [Google Scholar] [CrossRef]
- Lou, Z.; Xin, F.; Han, X.; Lan, Y.; Duan, T.; Fu, W. Effect of unmanned aerial vehicle flight height on droplet distribution, drift and control of cotton aphids and spider mites. Agronomy 2018, 8, 187. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Lan, Y.; Zhou, Z.; Ouyang, F.; Wang, G.; Huang, X.; Deng, X.; Cheng, S. Effect of droplet size parameters on droplet deposition and drift of aerial spraying by using plant protection UAV. Agronomy 2020, 10, 195. [Google Scholar] [CrossRef] [Green Version]
- Musiu, E.M.; Qi, L.; Wu, Y. Spray deposition and distribution on the targets and losses to the ground as affected by application volume rate, airflow rate and target position. Crop Prot. 2019, 116, 170–180. [Google Scholar] [CrossRef]
- Xin, F.; Zhao, J.; Zhou, Y.; Wang, G.; Han, X.; Fu, W.; Deng, J.; Lan, Y. Effects of dosage and spraying volume on cotton defoliants efficacy: A case study based on application of unmanned aerial vehicles. Agronomy 2018, 8, 85. [Google Scholar] [CrossRef] [Green Version]
- Liao, J.; Zang, Y.; Luo, X.; Zhou, Z.; Lan, Y.; Zang, Y.; Gu, X.; Wu, W.; Hewitt, A.J. Optimization of variables for maximizing efficacy and efficiency in aerial spray application to cotton using unmanned aerial systems. Int. J. Agric. Biol. Eng. 2019, 12, 10–17. [Google Scholar] [CrossRef]
- Meng, Y.; Su, J.; Song, J.; Chen, W.H.; Lan, Y. Experimental evaluation of UAV spraying for peach trees of different shapes: Effects of operating parameters on droplet distribution. Comput. Electron. Agric. 2020, 170, 105282. [Google Scholar] [CrossRef]
- Civil Aviation Administration of China. Agricultural Aviation Operation Quality and Technical Indicators Part I: Spraying Operations (MH/T 1002.1-2016). National Public Service Platform for Standards Information 2016. 03.220.50. Available online: http://hbba.sacinfo.org.cn/stdDetail/e8993d4d62653dc7eaa6dd22500412d4 (accessed on 31 December 2021).
- Zhu, H.; Salyani, M.; Fox, R.D. A portable scanning system for evaluation of spray deposit distribution. Comput. Electron. Agric. 2011, 76, 38–43. [Google Scholar] [CrossRef]
- Li, J.; Shi, Y.; Lan, Y.; Guo, S. Vertical distribution and vortex structure of rotor wind field under the influence of rice canopy. Comput. Electron. Agric. 2019, 159, 140–146. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; He, Y.; Liu, F.; Cen, H.; Fang, H. Near ground platform development to simulate UAV aerial spraying and its spraying test under different conditions. Comput. Electron. Agric. 2018, 148, 8–18. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).