The authors unintentionally missed the citation of the chapter by Hofstee J. W., Speelman L., Scheufler B. “1.4-Fertilizer Distributors” in the “CIGR Handbook of Agricultural Engineering—Volume III, Plant Production Engineering” edited by “The International Commission of Agricultural Engineering, Stout B.A. Texas A&M University U.S.A., Cheze B. Ministry of Agriculture Fisheries and Food France” and published by “American Society of Agricultural Engineers: St. Joseph MI, U.S.A.” in 1999, and thus they wish to apologize to the authors of the uncited work and to make the following corrections to [1]:
Original version
- 2.1.
- Theoretical Considerations
A spinning disc spreader consists of one or two rotating discs with two or more vanes mounted on them. The spreader has a hopper, usually cone shaped, above the disc(s) and the fertilizer is fed in a stream by gravity or by means of a conveyor mechanism to the disc(s). The disc distributes the fertilizer by throwing it away with velocities normally in the range 15–50 ; for some spreaders the velocity may be up to 70 . These high velocities are required to obtain large effective working widths.
The important design factors of the spinning disc are disc radius (rd), feed radius (r0), pitch angle (β0) of the vane, cone angle of the disc (a) and the shape of the vane (straight in the present case). The radius of the disc of most spreaders is 0.30–0.45 m. The angular velocity of most discs is 42–105 . The feed radius determines the starting position of particles on the disc. The pitch angle is the angle between vane and the radial line. This angle has a large influence on particle motion. The cone angle is the angle between the disk surface and the horizontal plane. A positive cone angle (6° in the present case) means the particles are discharged with a vertical velocity component that usually projects the particles a longer distance.
The motion of a particle on a spinning disc can be described by a differential equation derived from the forces acting on the particle according to D’Alembert’s Principle.
If is the particle mass (kg) and the acceleration due to gravity (m), we consider the following forces (Figure 1):
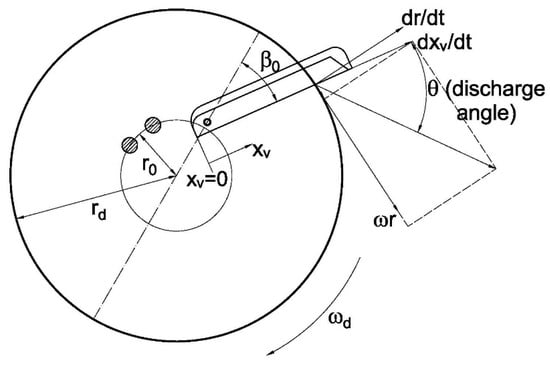
Figure 1.
Geometry, kinematics, and dynamics of a spinning disc fertilizer.
- weight ; N
- centrifugal force ; N
- inertial force ; N
- Coriolis force ; N
- friction ; N (Friction occurs when one of the above forces has a component perpendicular to the direction of motion).
Depending on the following variables:
- Residence time: the time elapsing between the moment the particle begins to move on the disc and the moment the particle leaves the disc;
- Rotation angle of the disc: the angular rotation of the disc during the residence time;
- Tangential velocity: the circumferential velocity of the tip of the vane;
- Velocity along the vane ;
- Radial velocity: the velocity of the particle in a radial direction .
The final result of the acceleration of particles along the vane of a spinning disc can be summarized by two main parameters:
- Discharge velocity: the absolute velocity at which the particle is discharged, equal to the vector addition of the velocity along the vane and the tangential velocity;
- Discharge angle: the angle between the radial direction and the discharge direction.
The coefficient of friction, a major physical property of fertilizer that affects the motion of particles on a disc, significantly influences the value of these parameters. An increase in the coefficient of friction results in an increase in residence time and a decrease in velocity along the vane. A lower velocity along the vane decreases the radial velocity, the discharge velocity and consequently the discharge angle. The magnitude of these effects is also greatly influenced by other parameters, such as the rotational velocity of the disc.
- References
- 25.
- EN 13739-2:2011 European Standard. Agricultural Machinery—Solid Fertilizer Broadcasters and Full Width Distributors—Environmental Protection—Part 2: Test Methods; CEN: Bruxelles, Belgium, 2011.
- 26.
- Kleinman, K.; Horton, N.J. SAS and R. Data Management, Statistical Analysis, and Graphics; CRR Press-Taylor & Francis Group: Boca Raton, FL, USA, 2010.
- 27.
- Hofstee, J.W.; Huisman, W. Handling and spreading of fertilizers: Part 1, Physical properties of fertilizer in relation to particle motion. J. Agric. Eng. Res. 1990, 62, 9–24.
Corrected version
- 2.1.
- Theoretical Considerations
The considered disc fertilizer spreader consists of a single rotating disc having two straight vanes mounted on it. A hopper having a dosing outlet and a stirrer feeds the disc with the fertilizer. Usually, the fertilizer is thrown away from the disc-vanes device with a speed ve that ranges between 15–50 m·s−1 with a maximum value that, in some case, can reach 70 m·s−1 with higher speeds related to wider working widths [25]. The fertilizer particle eject speed is directly related (Figure 1) to the angular speed of the disc ωd and to specific design factors of the spreader itself such as: (i) the disc radius rd; (ii) the fertilizer feed point radius r0; (iii) the angle between each vane and the corresponding radius (pitch angle β0) and (iv) the cone angle of the rotating disc.
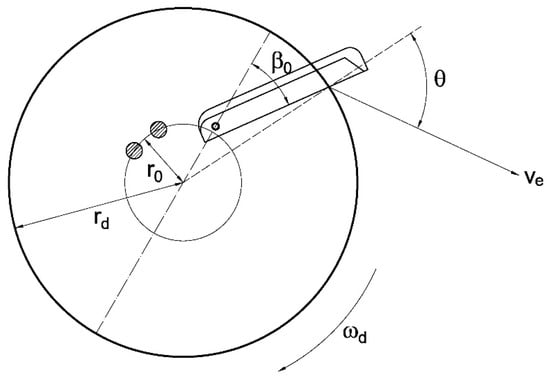
Figure 1.
Geometry, kinematics, and dynamics of a spinning disc fertilizer.
Taking into account the D’Alembert’s Principle, the motion of a single fertilizer particle is described by a differential equation which considers all the forces that act on it [25]. Among these forces, the friction force plays a significant role in the present study. It depends on the particle weight and on the fertilizer physical characteristics. An increase of the friction force due mainly to an increase of the friction coefficient between the fertilizer particle and the disc-vanes device, leads to both a lower eject speed ve and a smaller eject angle θ [25].
- References
- 25.
- Hofstee, J.W.; Speelman, L.; Scheufler, B. 1.4-Fertilizer Distributors. In CIGR Handbook of Agricultural Engineering; The International Commission of Agricultural Engineering, Stout, B.A., Cheze, B., Eds.; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1999; Volume III, pp. 240–268.
- 26.
- EN 13739-2:2011 European Standard. Agricultural Machinery—Solid Fertilizer Broadcasters and Full Width Distributors—Environmental Protection—Part 2: Test Methods; CEN: Bruxelles, Belgium, 2011.
- 27.
- Kleinman, K.; Horton, N.J. SAS and R. Data Management, Statistical Analysis, and Graphics; CRR Press-Taylor & Francis Group: Boca Raton, FL, USA, 2010.
- 28.
- Hofstee, J.W.; Huisman, W. Handling and spreading of fertilizers: Part 1, Physical properties of fertilizer in relation to particle motion. J. Agric. Eng. Res. 1990, 62, 9–24.
The authors would like to apologize for any inconvenience caused to the readers by these changes. The published version will be updated on the article webpage, with a reference to this correction notice.
Reference
- Przywara, A.; Santoro, F.; Kraszkiewicz, A.; Pecyna, A.; Pascuzzi, S. Experimental Study of Disc Fertilizer Spreader Performance. Agriculture 2020, 10, 467. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).