Prioritizing Patient Selection in Clinical Trials: A Machine Learning Algorithm for Dynamic Prediction of In-Hospital Mortality for ICU Admitted Patients Using Repeated Measurement Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Study Size
2.3. Descriptive Statistics
2.4. Machine Learning Models
Models Description
- (1)
- Model A: MixRFb model using RDW as a predictor and also considering the following as features: (a) age, (b) gender, (c) time (days of ICU stay), (d) any comorbidity. The selection of covariates for the MixRFb algorithm was guided by their clinical relevance and availability in routine ICU practice. Age is widely recognized as a predictor of ICU mortality, capturing baseline patient severity and physiological derangements [35]. RDW was included as it reflects systemic inflammation and oxidative stress, which are critical in predicting outcomes in critically ill patients [26]. Comorbidities were considered to account for underlying health conditions that influence mortality risk [36]. In this study, we included the presence of at least one comorbidity, such as diabetes [37], cardiovascular disease [38], or respiratory disease [39], as these specific conditions are strongly associated with ICU mortality and provide clinically interpretable variables while simplifying data collection in high-pressure ICU environments. Gender was included to evaluate potential sex-related differences in outcomes, while days in ICU capture longitudinal changes in patient status [40].
- (2)
- Model B: MixRFb model using SAPS as a predictor because it is widely recognized as a robust predictor of ICU mortality, capturing baseline patient severity and physiological derangements [41].
- (3)
- Model C: Classical RF model using RDW as a predictor and also including the following as features: (a) age, (b) gender, (c) time (days of ICU stay), (d) any comorbidity.
2.5. Model Training Validation Workflow
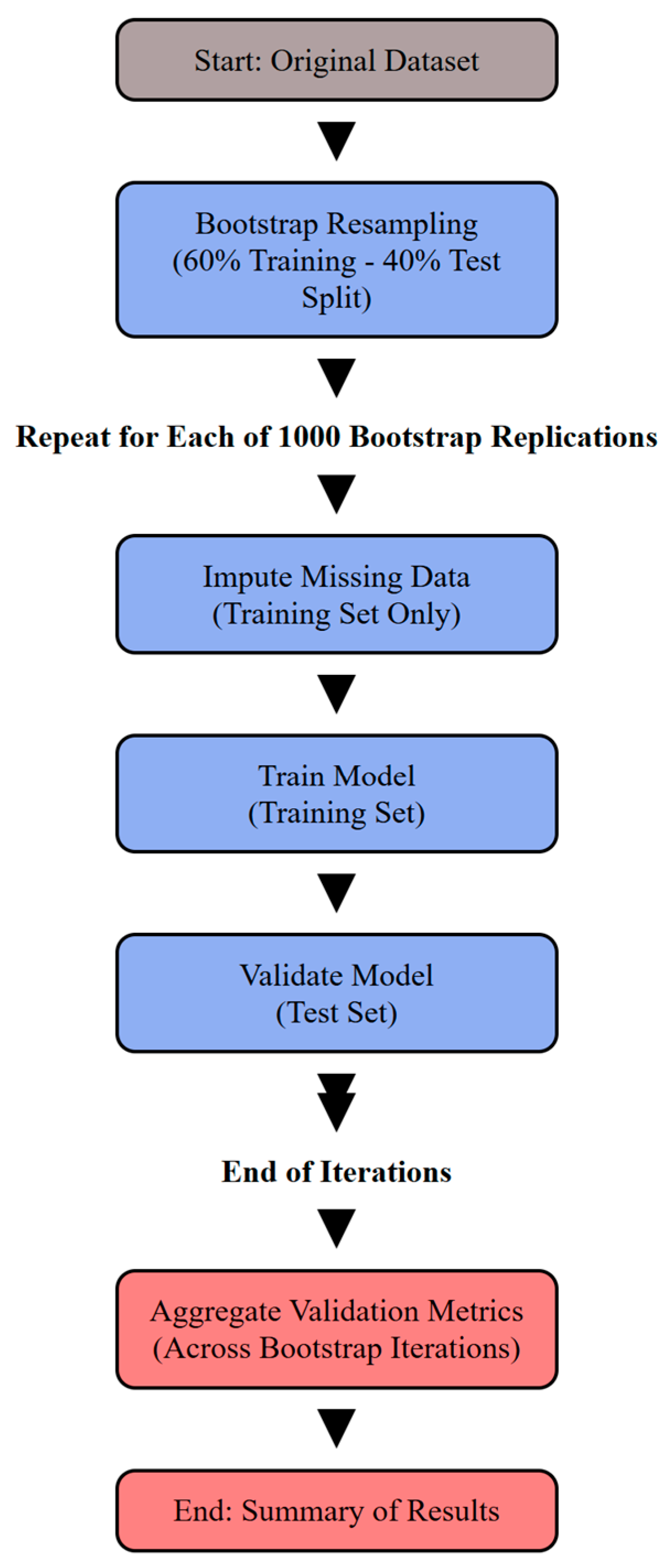
2.5.1. Model Validation via Bootstrap Resampling
2.5.2. Handling Missing Data
2.5.3. Measures of Performance
2.6. Variable Importance
2.7. Sensitivity Analyses
- ✓ Standalone Variable Predictive Analysis. The standalone predictive power of individual variables was evaluated by fitting a MixRFb model using variables selected based on their prominence in a multi-way importance analysis, which identified them as leading predictors. The analysis involved fitting the model for each variable independently to assess their predictive capability.
- ✓ Sensitivity Analysis with Recurrent Neural Network. A Recurrent Neural Network (RNN) was implemented as a sensitivity analysis to handle repeated measurement data via MLT. The model incorporated four features: age, gender, days in ICU, and RDW. The RNN was configured with a batch size of 286 and five time points with a discrete outcome.
- ✓ Sensitivity Analysis with Generalized Linear Mixed Effect Model. A sensitivity analysis with a simple mixed-effect model was also performed.
- ✓ Descriptive ROC Analysis. A descriptive Receiver Operating Characteristic (ROC) analysis was conducted to evaluate the performance of traditional SAPS and RDW as standalone predictors. ROC curves were generated for each variable independently to assess their predictive capacity.
2.8. Shiny Application Development
3. Results
3.1. Model Performances
3.1.1. Training
- ✓ Model A (MixRFb incorporating RDW and other covariates): The training AUC was 0.882 (95% CI: 0.860–0.904), indicating a strong predictive performance. This result is graphically represented in Figure 2, Panel A.
- ✓ Model B (MixRFb using SAPS as a predictor): This model showed a reduced training performance, with an AUC of 0.814 (95% CI: 0.790–0.838), suggesting that while SAPS is a useful predictor, the addition of RDW and other covariates in Model A improves prediction accuracy.
- ✓ Model C (Classical RF using RDW as a predictor): Although not incorporating repeated measurement data, this model demonstrated a training AUC of 0.835 (95% CI: 0.812–0.858).
3.1.2. Validation
3.2. Variable Contribution
3.3. Sensitivity Analyses
- ✓ Using SAPS alone: The ROC curve analysis for SAPS as a standalone predictor displayed an AUC of 0.683 (95% CI: 0.655–0.711), underlining a weaker predictive capability.
- ✓ Using RDW alone: RDW’s predictive ability for mortality was the lowest, with an AUC of 0.555 (95% CI: 0.527–0.583), suggesting limited utility when used without modeling patterns and interaction with additional predictors.
3.4. Shiny App
4. Discussion
Study Limitations and Future Research Developments
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ICU | Intensive Care Unit |
| RCTs | Randomized Controlled Trials |
| ARDS | Acute Respiratory Distress Syndrome |
| VAP | Ventilator-Associated Pneumonia |
| AKI | Acute Kidney Injury |
| APACHE | Acute Physiology and Chronic Health Evaluation Score |
| SAPS | Simplified Acute Physiology Score |
| MPM | Mortality Probability Models |
| ML | Machine Learning |
| RDW | Red Blood Cell Distribution Width |
| OR | Odds Ratio |
| CI | Confidence Intervals |
| MixRFb | Mixed Effects Random Forest for Binary Data |
| RF | Random Forest |
| MICE | Missing Imputation Chain |
| AUC | Area Under ROC Curve |
| OOB | Out-Of-Bag |
| VIP | Variable Importance Plot |
References
- Delaney, A.; Angus, D.C.; Bellomo, R.; Cameron, P.; Cooper, D.J.; Finfer, S.; Harrison, D.A.; Huang, D.T.; Myburgh, J.A.; Peake, S.L.; et al. Bench-to-Bedside Review: The Evaluation of Complex Interventions in Critical Care. Crit. Care 2008, 12, 210. [Google Scholar] [CrossRef] [PubMed]
- Granholm, A.; Alhazzani, W.; Derde, L.P.G.; Angus, D.C.; Zampieri, F.G.; Hammond, N.E.; Sweeney, R.M.; Myatra, S.N.; Azoulay, E.; Rowan, K.; et al. Randomised Clinical Trials in Critical Care: Past, Present and Future. Intensive Care Med. 2022, 48, 164–178. [Google Scholar] [CrossRef]
- François, B.; Clavel, M.; Vignon, P.; Laterre, P.-F. Perspective on Optimizing Clinical Trials in Critical Care: How to Puzzle out Recurrent Failures. J. Intensive Care 2016, 4, 67. [Google Scholar] [CrossRef]
- Ali, N.A.; Wolf, K.M.; Hammersley, J.; Hoffmann, S.P.; O’Brien, J.M.; Phillips, G.S.; Rashkin, M.; Warren, E.; Garland, A.; on behalf of the Midwest Critical Care Consortium Continuity of Care in Intensive Care Units. A Cluster-Randomized Trial of Intensivist Staffing. Am. J. Respir. Crit. Care Med. 2011, 184, 803–808. [Google Scholar] [CrossRef] [PubMed]
- Luce, J.M.; Cook, D.J.; Martin, T.R.; Angus, D.C.; A Boushey, H.; Curtis, J.R.; E Heffner, J.; Lanken, P.N.; Levy, M.M.; Polite, P.Y.; et al. The Ethical Conduct of Clinical Research Involving Critically Ill Patients in the United States and Canada: Principles and Recommendations. Am. J. Respir. Crit. Care Med. 2004, 170, 1375–1384. [Google Scholar] [CrossRef] [PubMed]
- Yamga, E.; Mantena, S.; Rosen, D.; Bucholz, E.M.; Yeh, R.W.; Celi, L.A.; Ustun, B.; Butala, N.M. Optimized Risk Score to Predict Mortality in Patients with Cardiogenic Shock in the Cardiac Intensive Care Unit. J. Am. Hear. Assoc. 2023, 12, e029232. [Google Scholar] [CrossRef] [PubMed]
- Boussina, A.; Shashikumar, S.P.; Malhotra, A.; Owens, R.L.; El-Kareh, R.; Longhurst, C.A.; Quintero, K.; Donahue, A.; Chan, T.C.; Nemati, S.; et al. Impact of a Deep Learning Sepsis Prediction Model on Quality of Care and Survival. Npj Digit. Med. 2024, 7, 14. [Google Scholar] [CrossRef] [PubMed]
- Villar, J.; Ferrando, C.; Tusman, G.; Berra, L.; Rodríguez-Suárez, P.; Suárez-Sipmann, F. Unsuccessful and Successful Clinical Trials in Acute Respiratory Distress Syndrome: Addressing Physiology-Based Gaps. Front. Physiol. 2021, 12, 774025. [Google Scholar] [CrossRef] [PubMed]
- Koshiaris, C.; Archer, L.; Lay-Flurrie, S.; Snell, K.I.; Riley, R.D.; Stevens, R.; Banerjee, A.; Usher-Smith, J.A.; Clegg, A.; Payne, R.A.; et al. Predicting the Risk of Acute Kidney Injury in Primary Care: Derivation and Validation of STRATIFY-AKI. Br. J. Gen. Pr. 2023, 73, e605–e614. [Google Scholar] [CrossRef] [PubMed]
- Knaus, W.A.; Zimmerman, J.E.; Wagner, D.P.; Draper, E.A.; Lawrence, D.E. APACHE—Acute Physiology and Chronic Health Evaluation: A Physiologically Based Classification System: Crit. Care Med. 1981, 9, 591–597. [Google Scholar] [CrossRef] [PubMed]
- Gall, J.-R.L.; Loirat, P.; Alperovitch, A.; Glaser, P.; Granthil, C.; Mathieu, D.; Mercier, P.; Thomas, R.; Villers, D. A Simplified Acute Physiology Score for ICU Patients. Crit. Care Med. 1984, 12, 975–977. [Google Scholar] [CrossRef] [PubMed]
- Lemeshow, S. Mortality Probability Models (MPM II) Based on an International Cohort of Intensive Care Unit Patients. JAMA 1993, 270, 2478. [Google Scholar] [CrossRef]
- Zhai, Q.; Lin, Z.; Ge, H.; Liang, Y.; Li, N.; Ma, Q.; Ye, C. Using Machine Learning Tools to Predict Outcomes for Emergency Department Intensive Care Unit Patients. Sci. Re.p 2020, 10, 20919. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Yao, Y.; Zhou, J.; Diao, X.; Chen, H.; Cai, K.; Ma, X.; Wang, S. Dynamic APACHE II Score to Predict the Outcome of Intensive Care Unit Patients. Front. Med. 2022, 8, 744907. [Google Scholar] [CrossRef]
- Atallah, L.; Nabian, M.; Brochini, L.; Amelung, P.J. Machine Learning for Benchmarking Critical Care Outcomes. Healthc. Inform. Res. 2023, 29, 301–314. [Google Scholar] [CrossRef] [PubMed]
- Sikora, A.; Zhang, T.; Murphy, D.J.; Smith, S.E.; Murray, B.; Kamaleswaran, R.; Chen, X.; Buckley, M.S.; Rowe, S.; Devlin, J.W. Machine Learning vs. Traditional Regression Analysis for Fluid Overload Prediction in the ICU. Sci. Rep. 2023, 13, 19654. [Google Scholar] [CrossRef] [PubMed]
- Makino, M.; Yoshimoto, R.; Ono, M.; Itoko, T.; Katsuki, T.; Koseki, A.; Kudo, M.; Haida, K.; Kuroda, J.; Yanagiya, R.; et al. Artificial Intelligence Predicts the Progression of Diabetic Kidney Disease Using Big Data Machine Learning. Sci. Rep. 2019, 9, 11862. [Google Scholar] [CrossRef]
- Chen, Z.; Li, T.; Guo, S.; Zeng, D.; Wang, K. Machine Learning-Based in-Hospital Mortality Risk Prediction Tool for Intensive Care Unit Patients with Heart Failure. Front. Cardiovasc. Med. 2023, 10, 1119699. [Google Scholar] [CrossRef] [PubMed]
- Hong, W.S.; Rudas, A.; Bell, E.J.; Chiang, J.N. Association of Red Blood Cell Distribution Width with Hospital Admission and In-Hospital Mortality Across All-Cause Adult Emergency Department Visits. JAMIA Open 2023, 6, ooad053. [Google Scholar] [CrossRef] [PubMed]
- Fontana, V.; Spadaro, S.; Villois, P.; Righy Shinotsuka, C.; Fogagnolo, A.; Nobile, L.; Vincent, J.-L.; Creteur, J.; Taccone, F.S. Can Red Blood Cell Distribution Width Predict Outcome After Cardiac Arrest? Minerva Anestesiol. 2018, 84, 693–702. [Google Scholar] [CrossRef]
- Yonemoto, S.; Hamano, T.; Fujii, N.; Shimada, K.; Yamaguchi, S.; Matsumoto, A.; Kubota, K.; Hashimoto, N.; Oka, T.; Senda, M.; et al. Red Cell Distribution Width and Renal Outcome in Patients with Non-Dialysis-Dependent Chronic Kidney Disease. PLoS ONE 2018, 13, e0198825. [Google Scholar] [CrossRef] [PubMed]
- Valko, L.; Baglyas, S.; Podmaniczky, E.; Prohaszka, Z.; Gal, J.; Lorx, A. Exploring Red Cell Distribution Width as a Biomarker for Treatment Efficacy in Home Mechanical Ventilation. BMC Pulm. Med. 2022, 22, 115. [Google Scholar] [CrossRef]
- Fogagnolo, A.; Spadaro, S.; Taccone, F.S.; Ragazzi, R.; Romanello, A.; Fanni, A.; Marangoni, E.; Franchi, F.; Scolletta, S.; Volta, C.A. The Prognostic Role of Red Blood Cell Distribution Width in Transfused and Non-Transfused Critically Ill Patients. Minerva Anestesiol. 2019, 85, 1159–1167. [Google Scholar] [CrossRef] [PubMed]
- Valenti, A.C.; Vitolo, M.; Imberti, J.F.; Malavasi, V.L.; Boriani, G. Red Cell Distribution Width: A Routinely Available Biomarker with Important Clinical Implications in Patients with Atrial Fibrillation. CPD 2021, 27, 3901–3912. [Google Scholar] [CrossRef]
- She, Y.; Li, Y.; Chen, S.; Chen, Y.; Zhou, L. Red Blood Cell Distribution Width Predicts In-Hospital Mortality in Patients with a Primary Diagnosis of Seizures in the ICU: A Retrospective Database Study. Neurol. Sci. 2022, 43, 499–506. [Google Scholar] [CrossRef] [PubMed]
- Horne, B.D.; Anderson, J.L.; Muhlestein, J.B.; Ridker, P.M.; Paynter, N.P. Complete Blood Count Risk Score and Its Components, Including RDW, Are Associated with Mortality in the JUPITER Trial. Eur. J. Prev. Cardiolog. 2015, 22, 519–526. [Google Scholar] [CrossRef] [PubMed]
- Lee, J. Patient-Specific Predictive Modeling Using Random Forests: An Observational Study for the Critically Ill. JMIR Med. Inform. 2017, 5, e3. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Szymczak, S. A Review on Longitudinal Data Analysis with Random Forest. Brief. Bioinform. 2023, 24, bbad002. [Google Scholar] [CrossRef]
- Dankl, D.; Rezar, R.; Mamandipoor, B.; Zhou, Z.; Wernly, S.; Wernly, B.; Osmani, V. Red Cell Distribution Width Is Independently Associated with Mortality in Sepsis. Med. Princ. Pr. 2022, 31, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Wang, Y.-G.; Drovandi, C.; Cao, T. Predictions of Machine Learning with Mixed-Effects in Analyzing Longitudinal Data Under Model Misspecification. Stat. Methods Appl. 2023, 32, 681–711. [Google Scholar] [CrossRef]
- Chen, A.; Zhao, Z.; Hou, W.; Singer, A.J.; Li, H.; Duong, T.Q. Time-to-Death Longitudinal Characterization of Clinical Variables and Longitudinal Prediction of Mortality in COVID-19 Patients: A Two-Center Study. Front. Med. 2021, 8, 661940. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gamazon, E.R.; Pierce, B.L.; Stranger, B.E.; Im, H.K.; Gibbons, R.D.; Cox, N.J.; Nicolae, D.L.; Chen, L.S. Imputing Gene Expression in Uncollected Tissues Within and Beyond GTEx. Am. J. Hum. Genet. 2016, 98, 697–708. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by random forest. R News 2002, 2, 18–22. [Google Scholar]
- van Buuren, S.; Groothuis-Oudshoorn, K. Mice: Multivariate Imputation by Chained Equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Gonçalves-Pereira, J.; Oliveira, A.; Vieira, T.; Rodrigues, A.R.; Pinto, M.J.; Pipa, S.; Martinho, A.; Ribeiro, S.; Paiva, J.-A. Critically Ill Patient Mortality by Age: Long-Term Follow-up (CIMbA-LT). Ann. Intensive Care 2023, 13, 7. [Google Scholar] [CrossRef] [PubMed]
- Forte, J.C.; Van Der Horst, I.C.C. Comorbidities and Medical History Essential for Mortality Prediction in Critically Ill Patients. Lancet Digit. Health 2019, 1, e48–e49. [Google Scholar] [CrossRef]
- Siegelaar, S.E.; Hickmann, M.; Hoekstra, J.B.; Holleman, F.; DeVries, J.H. The Effect of Diabetes on Mortality in Critically Ill Patients: A Systematic Review and Meta-Analysis. Crit. Care 2011, 15, R205. [Google Scholar] [CrossRef]
- Rocha, B.; Cunha, G.; Maltes, S.; Moura, A.N.N.E.; Coelho, F.; Torres, J.; Santos, P.; Monteiro, F.; Monteiro, F.; Almeida, G.; et al. Cardiovascular Disease in an Intensive Care Unit: Patterns of an Often Fatal Omen. Eur. Heart J. 2021, 42, ehab724-1520. [Google Scholar] [CrossRef]
- Grangier, B.; Vacheron, C.-H.; De Marignan, D.; Casalegno, J.-S.; Couray-Targe, S.; Bestion, A.; Ader, F.; Richard, J.-C.; Frobert, E.; Argaud, L.; et al. Comparison of Mortality and Outcomes of Four Respiratory Viruses in the Intensive Care Unit: A Multicenter Retrospective Study. Sci. Rep. 2024, 14, 6690. [Google Scholar] [CrossRef] [PubMed]
- Merdji, H.; Long, M.T.; Ostermann, M.; Herridge, M.; Myatra, S.N.; De Rosa, S.; Metaxa, V.; Kotfis, K.; Robba, C.; De Jong, A.; et al. Sex and Gender Differences in Intensive Care Medicine. Intensive Care Med. 2023, 49, 1155–1167. [Google Scholar] [CrossRef] [PubMed]
- Le Gall, J.-R. A New Simplified Acute Physiology Score (SAPS II) Based on a European/North American Multicenter Study. JAMA J. Am. Med. Assoc. 1993, 270, 2957. [Google Scholar] [CrossRef]
- Lin, Z.; Lawrence, W.R.; Huang, Y.; Lin, Q.; Gao, Y. Classifying Depression Using Blood Biomarkers: A Large Population Study. J. Psychiatr. Res. 2021, 140, 364–372. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Li, F.; Xin, H.; Zhang, J.; Fu, M.; Zhou, J.; Lian, Z. Prediction Model of In-Hospital Mortality in Intensive Care Unit Patients with Heart Failure: Machine Learning-Based, Retrospective Analysis of the MIMIC-III Database. BMJ Open 2021, 11, e044779. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Torres, V.; Royuela, A.; Múñez-Rubio, E.; Gutierrez-Rojas, Á.; Mills-Sánchez, P.; Ortega, A.; Tejado-Bravo, S.; García-Sanz, J.; Muñoz-Serrano, A.; Calderón-Parra, J.; et al. Red Blood Cell Distribution Width as Prognostic Factor in Sepsis: A New Use for a Classical Parameter. J. Crit. Care 2022, 71, 154069. [Google Scholar] [CrossRef] [PubMed]
- Duggal, A.; Scheraga, R.; Sacha, G.L.; Wang, X.; Huang, S.; Krishnan, S.; Siuba, M.T.; Torbic, H.; Dugar, S.; Mucha, S.; et al. Forecasting Disease Trajectories in Critical Illness: Comparison of Probabilistic Dynamic Systems to Static Models to Predict Patient Status in the Intensive Care Unit. BMJ Open 2024, 14, e079243. [Google Scholar] [CrossRef]
- Vallet, H.; Guidet, B.; Boumendil, A.; De Lange, D.W.; Leaver, S.; Szczeklik, W.; Jung, C.; Sviri, S.; Beil, M.; Flaatten, H. The Impact of Age-Related Syndromes on ICU Process and Outcomes in Very Old Patients. Ann. Intensive Care 2023, 13, 68. [Google Scholar] [CrossRef]
- Said, A.S.; Spinella, P.C.; Hartman, M.E.; Steffen, K.M.; Jackups, R.; Holubkov, R.; Wallendorf, M.; Doctor, A. RBC Distribution Width: Biomarker for Red Cell Dysfunction and Critical Illness Outcome? Pediatr. Crit. Care Med. 2017, 18, 134–142. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Li, W.; Ke, W. Association between Red Blood Cell Distribution Width and All-Cause Mortality in Unselected Critically Ill Patients: Analysis of the MIMIC-III Database. Front. Med. 2023, 10, 1152058. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.; Bradley, J.; Smith, S.; McPeake, J.; Walsh, T.; Haines, K.; Leggett, N.; Hart, N.; McAuley, D. Do Critical Illness Survivors with Multimorbidity Need a Different Model of Care? Crit. Care 2023, 27, 485. [Google Scholar] [CrossRef] [PubMed]
- Waqas, M.; Humphries, U.W. A Critical Review of RNN and LSTM Variants in Hydrological Time Series Predictions. MethodsX 2024, 13, 102946. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Zhou, H.; Tang, Q. Red Blood Cell Distribution Width: A Novel Predictive Indicator for Cardiovascular and Cerebrovascular Diseases. Dis. Markers 2017, 2017, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chew, G.M.; Shikuma, C.M.; Gangcuangco, L.M.A.; Souza, S.A.; Shiramizu, B.; Nakamoto, B.K.; Gong, T.; Mannem, S.R.; Mitchell, B.I.; et al. Red Blood Cell Distribution Width as an Easily Measurable Biomarker of Persistent Inflammation and T Cell Dysregulation in Antiretrovirally Treated HIV-Infected Adults. HIV Clin. Trials 2018, 19, 172–176. [Google Scholar] [CrossRef] [PubMed]
- Knaus, W.A.; Draper, E.A.; Wagner, D.P.; Zimmerman, J.E. APACHE II: A Severity of Disease Classification System. Crit. Care Med. 1985, 13, 818–829. [Google Scholar] [CrossRef]
- Hothorn, T.; Hornik, K.; Zeileis, A. Unbiased Recursive Partitioning: A Conditional Inference Framework. J. Comput. Graph. Stat. 2006, 15, 651–674. [Google Scholar] [CrossRef]
- Xia, R. Comparison of Random Forests and Cforest: Variable Importance Measures and Prediction Accuracies. Master’s Thesis, Utah State University, Logan, UT, USA, 2009. [Google Scholar] [CrossRef]




| Variables | Survival (n = 207) | Death (n = 79) | Total (N = 286) | OR | CI 95% | p-Value |
|---|---|---|---|---|---|---|
| Age (years) (median [IQR]) | 69.0 [59.0–78.0] | 74.0 [66.0–79.0] | 71.0 [61.0–78.0] | 1.03 | [1.00; 1.05] | 0.022 |
| Gender, n (%) | 1.27 | [0.71; 2.25] | 0.496 | |||
| Male (Ref.) | 117 (63.9%) | 39 (58.2%) | 156 (62.4%) | |||
| Female | 66 (36.1%) | 28 (41.8%) | 94 (37.6%) | |||
| Diabetes, n (%) | 1.89 | [1.04; 3.42] | 0.046 | |||
| No (Ref.) | 135 (73.8%) | 40 (59.7%) | 175 (70.0%) | |||
| Yes | 48 (26.2%) | 27 (40.3%) | 75 (30.0%) | |||
| Cardiovascular disease, n (%) | 1.59 | [0.91; 2.84] | ||||
| No (Ref.) | 95 (51.9%) | 27 (40.3%) | 122 (48.8%) | 0.138 | ||
| Yes | 88 (48.1%) | 40 (59.7%) | 128 (51.2%) | |||
| Respiratory disease, n (%) | 0.92 | [0.44; 1.84] | ||||
| No (Ref.) | 145 (79.2%) | 54 (80.6%) | 199 (79.6%) | 0.953 | ||
| Yes | 38 (20.8%) | 13 (19.4%) | 51 (20.4%) | |||
|
SAPS (median [IQR]) | 36.0 [27.0; 46.0] | 46.5 [39.0; 54.0] | 40.0 [29.0; 50.0] | 1.05 | [1.03; 1.08] | <0.001 |
| Any comorbidity, n (%) | 1.56 | [0.85; 2.97] | 0.197 | |||
| No (Ref.) | 67 (36.6%) | 18 (26.9%) | 85 (34.0%) | |||
| Yes | 116 (63.4%) | 49 (73.1%) | 165 (66.0%) |
| AUC | F1 | |
|---|---|---|
| Model A | 0.87 [0.85–0.88] | 0.76 [0.72–0.78] |
| Model B | 0.8 [0.79–0.83] | 0.72 [0.69–0.74] |
| Model C | 0.78 [0.8–0.81] | 0.66 [0.72–0.77] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedarzani, E.; Fogangolo, A.; Baldi, I.; Berchialla, P.; Panzini, I.; Khan, M.R.; Valpiani, G.; Spadaro, S.; Gregori, D.; Azzolina, D. Prioritizing Patient Selection in Clinical Trials: A Machine Learning Algorithm for Dynamic Prediction of In-Hospital Mortality for ICU Admitted Patients Using Repeated Measurement Data. J. Clin. Med. 2025, 14, 612. https://doi.org/10.3390/jcm14020612
Pedarzani E, Fogangolo A, Baldi I, Berchialla P, Panzini I, Khan MR, Valpiani G, Spadaro S, Gregori D, Azzolina D. Prioritizing Patient Selection in Clinical Trials: A Machine Learning Algorithm for Dynamic Prediction of In-Hospital Mortality for ICU Admitted Patients Using Repeated Measurement Data. Journal of Clinical Medicine. 2025; 14(2):612. https://doi.org/10.3390/jcm14020612
Chicago/Turabian StylePedarzani, Emma, Alberto Fogangolo, Ileana Baldi, Paola Berchialla, Ilaria Panzini, Mohd Rashid Khan, Giorgia Valpiani, Savino Spadaro, Dario Gregori, and Danila Azzolina. 2025. "Prioritizing Patient Selection in Clinical Trials: A Machine Learning Algorithm for Dynamic Prediction of In-Hospital Mortality for ICU Admitted Patients Using Repeated Measurement Data" Journal of Clinical Medicine 14, no. 2: 612. https://doi.org/10.3390/jcm14020612
APA StylePedarzani, E., Fogangolo, A., Baldi, I., Berchialla, P., Panzini, I., Khan, M. R., Valpiani, G., Spadaro, S., Gregori, D., & Azzolina, D. (2025). Prioritizing Patient Selection in Clinical Trials: A Machine Learning Algorithm for Dynamic Prediction of In-Hospital Mortality for ICU Admitted Patients Using Repeated Measurement Data. Journal of Clinical Medicine, 14(2), 612. https://doi.org/10.3390/jcm14020612









