Time-to-Event Modeling for Survival Prediction of Osimertinib as the First- and Second-Line Therapy
Abstract
1. Introduction
2. Materials and Methods
2.1. Literature Search
2.2. Study Selection
2.3. Data Extraction
2.4. Modeling Analysis
2.5. Model Development
2.6. Covariate Model
2.7. Model Evaluation
2.8. Simulation
2.9. Risk of Bias and Quality Assessment
3. Results
3.1. Characteristics of the Included Studies
3.2. Risk of Bias and Quality Assessment of Reconstructed Data
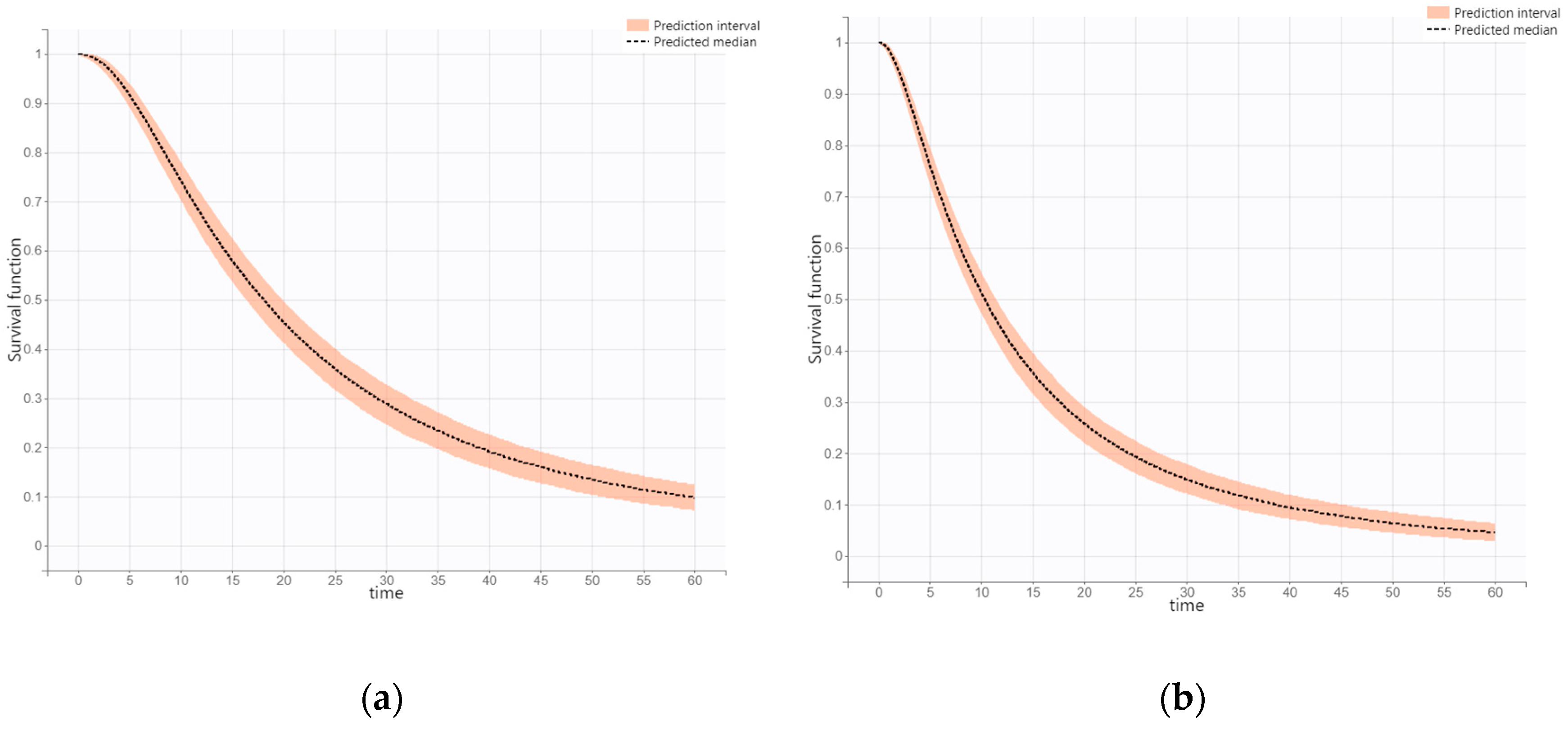
3.3. Overall Survival (OS)
3.4. Progression-Free Survival (PFS)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Torre, L.A.; Bray, F.; Siegel, R.L.; Ferlay, J.; Lortet-Tieulent, J.; Jemal, A. Global cancer statistics, 2012. CA Cancer J. Clin. 2015, 65, 87–108. [Google Scholar] [CrossRef] [PubMed]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Schiller, J.H.; Harrington, D.; Belani, C.P.; Langer, C.; Sandler, A.; Krook, J.; Zhu, J.; Johnson, D.H. Comparison of four chemotherapy regimens for advanced non–small-cell lung cancer. N. Engl. J. Med. 2002, 346, 92–98. [Google Scholar] [CrossRef]
- Zhou, C.; Wu, Y.; Chen, G.; Feng, J.; Liu, X.-Q.; Wang, C.; Zhang, S.; Wang, J.; Zhou, S.; Ren, S. Final overall survival results from a randomised, phase III study of erlotinib versus chemotherapy as first-line treatment of EGFR mutation-positive advanced non-small-cell lung cancer (OPTIMAL, CTONG-0802). Ann. Oncol. 2015, 26, 1877–1883. [Google Scholar] [CrossRef]
- Fukuoka, M.; Wu, Y.-L.; Thongprasert, S.; Sunpaweravong, P.; Leong, S.-S.; Sriuranpong, V.; Chao, T.-Y.; Nakagawa, K.; Chu, D.-T.; Saijo, N. Biomarker analyses and final overall survival results from a phase III, randomized, open-label, first-line study of gefitinib versus carboplatin/paclitaxel in clinically selected patients with advanced non–small-cell lung cancer in Asia (IPASS). J. Clin. Oncol. 2011, 29, 2866–2874. [Google Scholar] [CrossRef]
- Yang, J.C.-H.; Wu, Y.-L.; Schuler, M.; Sebastian, M.; Popat, S.; Yamamoto, N.; Zhou, C.; Hu, C.-P.; O’Byrne, K.; Feng, J. Afatinib versus cisplatin-based chemotherapy for EGFR mutation-positive lung adenocarcinoma (LUX-Lung 3 and LUX-Lung 6): Analysis of overall survival data from two randomised, phase 3 trials. Lancet Oncol. 2015, 16, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Mok, T.S.; Wu, Y.-L.; Thongprasert, S.; Yang, C.-H.; Chu, D.-T.; Saijo, N.; Sunpaweravong, P.; Han, B.; Margono, B.; Ichinose, Y. Gefitinib or carboplatin–paclitaxel in pulmonary adenocarcinoma. N. Engl. J. Med. 2009, 361, 947–957. [Google Scholar] [CrossRef]
- Sequist, L.V.; Yang, J.C.-H.; Yamamoto, N.; O’Byrne, K.; Hirsh, V.; Mok, T.; Geater, S.L.; Orlov, S.; Tsai, C.-M.; Boyer, M. Phase III study of afatinib or cisplatin plus pemetrexed in patients with metastatic lung adenocarcinoma with EGFR mutations. J. Clin. Oncol. 2013, 31, 3327–3334. [Google Scholar] [CrossRef] [PubMed]
- Pao, W.; Chmielecki, J. Rational, biologically based treatment of EGFR-mutant non-small-cell lung cancer. Nat. Rev. Cancer 2010, 10, 760–774. [Google Scholar] [CrossRef]
- Gazdar, A. Activating and resistance mutations of EGFR in non-small-cell lung cancer: Role in clinical response to EGFR tyrosine kinase inhibitors. Oncogene 2009, 28, S24–S31. [Google Scholar] [CrossRef]
- Juchum, M.; Günther, M.; Laufer, S.A. Fighting cancer drug resistance: Opportunities and challenges for mutation-specific EGFR inhibitors. Drug Resist. Updates 2015, 20, 12–28. [Google Scholar] [CrossRef] [PubMed]
- Engel, J.; Becker, C.; Lategahn, J.; Keul, M.; Ketzer, J.; Mühlenberg, T.; Kollipara, L.; Schultz-Fademrecht, C.; Zahedi, R.P.; Bauer, S. Insight into the inhibition of drug-resistant mutants of the receptor tyrosine kinase EGFR. Angew. Chem. Int. Ed. 2016, 55, 10909–10912. [Google Scholar] [CrossRef] [PubMed]
- Soria, J.-C.; Ohe, Y.; Vansteenkiste, J.; Reungwetwattana, T.; Chewaskulyong, B.; Lee, K.H.; Dechaphunkul, A.; Imamura, F.; Nogami, N.; Kurata, T. Osimertinib in untreated EGFR-mutated advanced non–small-cell lung cancer. N. Engl. J. Med. 2018, 378, 113–125. [Google Scholar] [CrossRef]
- Ramalingam, S.S.; Vansteenkiste, J.; Planchard, D.; Cho, B.C.; Gray, J.E.; Ohe, Y.; Zhou, C.; Reungwetwattana, T.; Cheng, Y.; Chewaskulyong, B. Overall survival with osimertinib in untreated, EGFR-mutated advanced NSCLC. N. Engl. J. Med. 2020, 382, 41–50. [Google Scholar] [CrossRef]
- U.S. Food and Drug Administration. TAGRISSO (Osimertinib) Highlights of Prescribing Information; U.S. Food and Drug Administration: Rockville, MD, USA, 2018. [Google Scholar]
- Ettinger, D.S.; Wood, D.E.; Aisner, D.L.; Akerley, W.; Bauman, J.; Chirieac, L.R.; D’Amico, T.A.; DeCamp, M.M.; Dilling, T.J.; Dobelbower, M. Non–small cell lung cancer, version 5.2017, NCCN clinical practice guidelines in oncology. J. Natl. Compr. Cancer Netw. 2017, 15, 504–535. [Google Scholar] [CrossRef]
- Holford, N. A time to event tutorial for pharmacometricians. CPT Pharmacomet. Syst. Pharmacol. 2013, 2, e43. [Google Scholar] [CrossRef] [PubMed]
- Stewart, L.A.; Clarke, M.; Rovers, M.; Riley, R.D.; Simmonds, M.; Stewart, G.; Tierney, J.F. Preferred reporting items for a systematic review and meta-analysis of individual participant data: The PRISMA-IPD statement. JAMA 2015, 313, 1657–1665. [Google Scholar] [CrossRef]
- Liu, N.; Zhou, Y.; Lee, J.J. IPDfromKM: Reconstruct individual patient data from published Kaplan-Meier survival curves. BMC Med. Res. Methodol. 2021, 21, 111. [Google Scholar] [CrossRef]
- Van Wijk, R.C.; Simonsson, U.S. Finding the right hazard function for time-to-event modeling: A tutorial and Shiny application. CPT Pharmacomet. Syst. Pharmacol. 2022, 11, 991–1001. [Google Scholar] [CrossRef]
- Gao, L.; Chen, R.; Li, T.; Li, L.; Zheng, Q. Quantitative Analysis of the Efficacy of PARP Inhibitors as Maintenance Therapy in Recurrent Ovarian Cancer. Front. Pharmacol. 2021, 12, 771836. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: Berlin/Heidelberg, Germany, 1998; pp. 199–213. [Google Scholar]
- Lindbom, L.; Ribbing, J.; Jonsson, E.N. Perl-speaks-NONMEM (PsN)—A Perl module for NONMEM related programming. Comput. Methods Programs Biomed. 2004, 75, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Sterne, J.A.; Savović, J.; Page, M.J.; Elbers, R.G.; Blencowe, N.S.; Boutron, I.; Cates, C.J.; Cheng, H.-Y.; Corbett, M.S.; Eldridge, S.M. RoB 2: A revised tool for assessing risk of bias in randomised trials. BMJ 2019, 366, l4898. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; He, Y.; Li, W.; Zhang, H.-l.; Zhou, Q.; Wang, B.; Liu, C.; Walding, A.; Saggese, M.; Huang, X. Osimertinib versus comparator EGFR TKI as first-line treatment for EGFR-mutated advanced NSCLC: FLAURA China, a randomized study. Target. Oncol. 2021, 16, 165–176. [Google Scholar] [CrossRef]
- Ahn, M.J.; Tsai, C.M.; Shepherd, F.A.; Bazhenova, L.; Sequist, L.V.; Hida, T.; Yang, J.C.; Ramalingam, S.S.; Mitsudomi, T.; Jänne, P.A. Osimertinib in patients with T790M mutation-positive, advanced non–small cell lung cancer: Long-term follow-up from a pooled analysis of 2 phase 2 studies. Cancer 2019, 125, 892–901. [Google Scholar] [CrossRef]
- Mok, T.S.; Wu, Y.-L.; Ahn, M.-J.; Garassino, M.C.; Kim, H.R.; Ramalingam, S.S.; Shepherd, F.A.; He, Y.; Akamatsu, H.; Theelen, W.S. Osimertinib or platinum–pemetrexed in EGFR T790M–positive lung cancer. N. Engl. J. Med. 2017, 376, 629–640. [Google Scholar] [CrossRef]
- Papadimitrakopoulou, V.; Mok, T.; Han, J.-Y.; Ahn, M.-J.; Delmonte, A.; Ramalingam, S.; Kim, S.; Shepherd, F.; Laskin, J.; He, Y. Osimertinib versus platinum–pemetrexed for patients with EGFR T790M advanced NSCLC and progression on a prior EGFR-tyrosine kinase inhibitor: AURA3 overall survival analysis. Ann. Oncol. 2020, 31, 1536–1544. [Google Scholar] [CrossRef]
- Lin, J.J.; Cardarella, S.; Lydon, C.A.; Dahlberg, S.E.; Jackman, D.M.; Jänne, P.A.; Johnson, B.E. Five-year survival in EGFR-mutant metastatic lung adenocarcinoma treated with EGFR-TKIs. J. Thorac. Oncol. 2016, 11, 556–565. [Google Scholar] [CrossRef]
- Wu, Y.-L.; Planchard, D.; Lu, S.; Sun, H.; Yamamoto, N.; Kim, D.-W.; Tan, D.; Yang, J.-H.; Azrif, M.; Mitsudomi, T. Pan-Asian adapted Clinical Practice Guidelines for the management of patients with metastatic non-small-cell lung cancer: A CSCO–ESMO initiative endorsed by JSMO, KSMO, MOS, SSO and TOS. Ann. Oncol. 2019, 30, 171–210. [Google Scholar] [CrossRef] [PubMed]
- Cho, B.C.; Chewaskulyong, B.; Lee, K.H.; Dechaphunkul, A.; Sriuranpong, V.; Imamura, F.; Nogami, N.; Kurata, T.; Okamoto, I.; Zhou, C. Osimertinib versus standard of care EGFR TKI as first-line treatment in patients with EGFRm advanced NSCLC: FLAURA Asian subset. J. Thorac. Oncol. 2019, 14, 99–106. [Google Scholar] [CrossRef]
- Kim, E.S.; Melosky, B.; Park, K.; Yamamoto, N.; Yang, J.C. EGFR tyrosine kinase inhibitors for EGFR mutation-positive non-small-cell lung cancer: Outcomes in Asian populations. Future Oncol. 2021, 17, 2395–2408. [Google Scholar] [CrossRef]
- Chan, S.-K.; Choi, H.C.-W.; Lee, V.H.-F. Overall survival benefits of first-line treatments for Asian patients with advanced EGFR-mutated NSCLC harboring L858R mutation: A systematic review and network meta-analysis. JTO Clin. Res. Rep. 2022, 3, 100322. [Google Scholar] [CrossRef] [PubMed]
- Brown, K.; Comisar, C.; Witjes, H.; Maringwa, J.; de Greef, R.; Vishwanathan, K.; Cantarini, M.; Cox, E. Population pharmacokinetics and exposure-response of osimertinib in patients with non-small cell lung cancer. Br. J. Clin. Pharmacol. 2017, 83, 1216–1226. [Google Scholar] [CrossRef] [PubMed]
- Planchard, D.; Brown, K.H.; Kim, D.-W.; Kim, S.-W.; Ohe, Y.; Felip, E.; Leese, P.; Cantarini, M.; Vishwanathan, K.; Jänne, P.A. Osimertinib Western and Asian clinical pharmacokinetics in patients and healthy volunteers: Implications for formulation, dose, and dosing frequency in pivotal clinical studies. Cancer Chemother. Pharmacol. 2016, 77, 767–776. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.; Lin, Y.W.; Schmidt, H.; Sunnaker, M.; Van Maanen, E.; Huang, X.; Rukazenkov, Y.; Tomkinson, H.; Vishwanathan, K. Population Pharmacokinetics of Osimertinib in Patients With Non-Small Cell Lung Cancer. Pharmacol. Res. Perspect. 2025, 13, e70098. [Google Scholar] [CrossRef]
- Mauro, M.J.; Davis, C.; Zyczynski, T.; Khoury, H.J. The role of observational studies in optimizing the clinical management of chronic myeloid leukemia. Ther. Adv. Hematol. 2015, 6, 3–14. [Google Scholar] [CrossRef]

| Treatment | First-Line | Second-Line | ||||
|---|---|---|---|---|---|---|
| Study | FLAURA | FLAURA Updated OS | FLAURA China | AURA2 + AURA Extension | AURA3 | AURA3 Updated OS |
| Author | J.-C. Soria et al. [13] | S.S. Ramalingam et al. [14] | Ying Cheng et al. [25] | MJ Ahn et al. [26] | T.S. Mok et al. [27] | VA Papadimitrakopoulou et al. [28] |
| Publication year | 2018 | 2020 | 2021 | 2019 | 2017 | 2020 |
| Race (n, (%)) | White 101 (36) Asian 174 (62) Other 4 (1) | Asian 71 (100) Non-Asian 0 (0) | White 101 (36) Asian 174 (62) Black or African American 4 (1) Other 7 (2) Not reported 4 (1) | White 89 (32) Asian 182 (65) Other 8 (3) | ||
| Sample size per arm (n) | 279 | 71 | 129 | 279 | ||
| Male (%) | 36 | 39 | 32 | 38 | ||
| Age (year) | 64 | 60 | 63 | 62 | ||
| ECOG PS 0/1 (%) | 40/60 | 10/90 | 37/63 | NA | ||
| OS (mon.) | 38.6 | 33.1 | 26.5 | 26.8 | ||
| PFS (mon.) | 18.9 | 17.8 | 9.7 | 10.1 | ||
| First-Line | ||||
| Parameter | Base Model | Covariate Model (Final Model) | ||
| Estimate | RSE (%) | Estimate | RSE (%) | |
| Fixed effect | ||||
| Te_pop | 44.31 (95% CI, 39.97–48.42) | 5.10 | 41.69 (95% CI, 38.16–46.62) | 5.07 |
| p_pop | 2.56 (95% CI, 2.06–3.5) | 13.6 | 2.25 (95% CI, 1.77–3.55) | 10.4 |
| beta_Te_Race_global | NA | NA | 0.19 (95% CI, 0.016–0.39) | 50.0 |
| Standard Deviation of the Random Effects | ||||
| omega_Te | 0.58 (95% CI, 0.35–0.85) | 24.1 | 0.44 (95% CI, 0.22–0.98) | 22.9 |
| omega_p | 0.54 (95% CI, 0.39–0.82) | 25.4 | 0.54 (95% CI, 0.42–0.75) | 15.1 |
| Second-Line | ||||
| Parameter | Base Model | Covariate Model (Final Model) | ||
| Estimate | RSE (%) | Estimate | RSE (%) | |
| Fixed Effect | ||||
| Te_pop | 27.47 (95% CI, 25.43–30.57) | 4.58 | NA | NA |
| p_pop | 3.5 (95% CI, 2.71–4.67) | 13.2 | NA | NA |
| beta_Te_Race_global | NA | NA | NA | NA |
| Standard Deviation of the Random Effects | ||||
| omega_Te | 0.6 (95% CI, 0.53–0.75) | 9.42 | NA | NA |
| omega_p | 0.75 (95% CI, 0.57–1) | 14.2 | NA | NA |
| First-Line | Second-Line | |||
|---|---|---|---|---|
| Parameter | Final Model | Final Model | ||
| Estimate | RSE (%) | Estimate | RSE (%) | |
| Fixed Effect | ||||
| Te_pop | 18.03 (95% CI, 15.97–19.94) | 5.83 | 10.31 (95% CI, 9.25–11.71) | 5.89 |
| p_pop | 5.88 (95% CI, 4.67–9.23) | 18.8 | 5.92 (95% CI, 3.76–7.62) | 21.9 |
| beta_Te_Race_global | NA | NA | NA | NA |
| Standard Deviation of the Random Effects | ||||
| omega_Te | 0.8 (95% CI, 0.68–0.93) | 8.69 | 0.93 (95% CI, 0.84–1.08) | 6.85 |
| omega_p | 0.81 (95% CI, 0.58–1.1) | 19.3 | 0.74 (95% CI, 0.38–0.99) | 16.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kim, H.; Lee, H.; Hahn, J.; Chang, M.J. Time-to-Event Modeling for Survival Prediction of Osimertinib as the First- and Second-Line Therapy. J. Clin. Med. 2025, 14, 4077. https://doi.org/10.3390/jcm14124077
Lee S, Kim H, Lee H, Hahn J, Chang MJ. Time-to-Event Modeling for Survival Prediction of Osimertinib as the First- and Second-Line Therapy. Journal of Clinical Medicine. 2025; 14(12):4077. https://doi.org/10.3390/jcm14124077
Chicago/Turabian StyleLee, Sungjae, Heungjo Kim, Hongjae Lee, Jongsung Hahn, and Min Jung Chang. 2025. "Time-to-Event Modeling for Survival Prediction of Osimertinib as the First- and Second-Line Therapy" Journal of Clinical Medicine 14, no. 12: 4077. https://doi.org/10.3390/jcm14124077
APA StyleLee, S., Kim, H., Lee, H., Hahn, J., & Chang, M. J. (2025). Time-to-Event Modeling for Survival Prediction of Osimertinib as the First- and Second-Line Therapy. Journal of Clinical Medicine, 14(12), 4077. https://doi.org/10.3390/jcm14124077






