A Review of Intraocular Lens Power Calculation Formulas Based on Artificial Intelligence
Abstract
1. Introduction
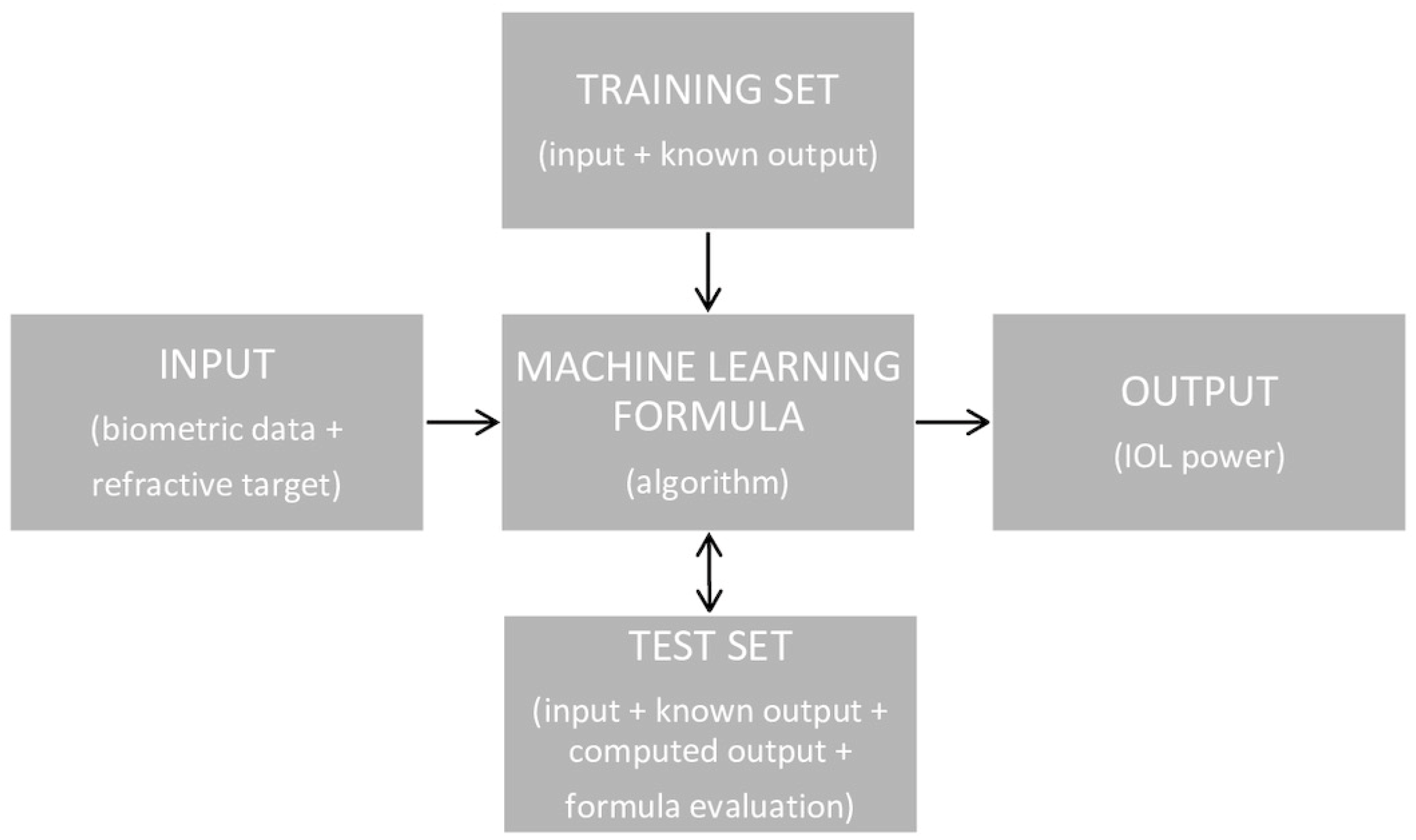
2. Methods
2.1. Formula Findings
2.2. The Hill-RBF Formula
2.3. The Karmona Formula
2.4. The Nallasamy Formula
2.5. The FullMonte Method
2.6. The Ladas Super Formula AI
2.7. The PEARL-DGS Formula
2.8. The Kane Formula
2.9. The Hoffer QST Formula
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aristodemou, P.; Sparrow, J.M.; Kaye, S. Evaluating refractive outcomes after cataract surgery. Ophthalmology 2019, 126, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Rocha-de-Lossada, C.; Colmenero-Reina, E.; Flikier, D.; Castro-Alonso, F.J.; Rodriguez-Raton, A.; García-Madrona, J.L.; Peraza-Nieves, J.; Sánchez-González, J.M. Intraocular lens power calculation formula accuracy: Comparison of 12 formulas for trifocal hydrophilic intraocular lens. Eur. J. Ophthalmol. 2021, 31, 2981–2988. [Google Scholar] [CrossRef]
- Alio, J.L.; Grzybowski, A.; El Aswad, A.; Romaniuk, D. Refractive lens exchange. Surv. Ophthalmol. 2014, 59, 579–598. [Google Scholar] [CrossRef] [PubMed]
- Doshi, D.; Limdi, P.; Parekh, N.; Gohil, N. A Comparative Study to Assess the Predictability of Different IOL Power Calculation Formulas in Eyes of Short and Long Axial Length. J. Clin. Diagn. Res. 2017, 11, NC01–NC04. [Google Scholar] [CrossRef] [PubMed]
- Melles, R.B.; Holladay, J.T.; Chang, W.J. Accuracy of Intraocular Lens calculation Formulas. Ophthalmology 2018, 125, 169–178. [Google Scholar] [CrossRef]
- Nemeth, G.; Modis, L., Jr. Accuracy of the Hill-radial basis function method and the Barrett Universal II formula. Eur. J. Ophthalmol. 2021, 31, 566–571. [Google Scholar] [CrossRef]
- Kane, J.X.; Van Heerden, A.; Atik, A.; Petsoglou, C. Accuracy of 3 new method for intraocular lens power selection. J. Cataract. Refract. Surg. 2017, 43, 333–339. [Google Scholar] [CrossRef]
- Ladas, J.G.; Siddiqui, A.A.; Devgan, U.; Jun, A.S. A 3-D “Super Surface” Combining Intraocular Lens Formulas to Generate a “Super Formula” and Maximize Accuracy. JAMA Ophthalmol. 2015, 133, 1431–1436. [Google Scholar] [CrossRef]
- Debellemanière, G.; Dubois, M.; Gauvin, M.; Wallerstein, A.; Brenner, L.F.; Rampat, R.; Saad, A.; Gatinel, D. The PEARL-DGS Formula: The Development of an Open-source Machine Learning-based Thick IOL Calculation Formula. Am. J. Ophthalmol. 2021, 232, 58–69. [Google Scholar] [CrossRef]
- Carmona-Gonzalez, D.; Castillo-Gomez, A.; Palomino-Bautista, C. Comparison of the accuracy of 11 intraocular lens power calculation formulas. Eur. J. Ophthalmol. 2021, 31, 2370–2376. [Google Scholar] [CrossRef]
- Nemeth, G.; Kemeny-Beke, A.; Modis, L., Jr. Comparison of accuracy of different intraocular lens power calculation methods using artificial intelligence. Eur. J. Ophthalmol. 2022, 32, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Voytsekhivskyy, O.V.; Hoffer, K.J.; Savini, G.; Tutchenko, L.P.; Hipólito-Fernandes, D. Clinical Accuracy of 18 IOL Power Formulas in 241 Short Eyes. Curr. Eye Res. 2021, 46, 1832–1843. [Google Scholar] [CrossRef]
- Lee, A.C.; Quazi, M.A.; Pepose, J.S. Biometry and intraocular lens power calculation. Curr. Opin. Ophthalmol. 2008, 19, 13–17. [Google Scholar] [CrossRef] [PubMed]
- Stopyra, W. Effectiveness, Sensitivity and Specificity of Intraocular Lens Power Calculation Formulas for Short Eyes. Turk. J. Ophthalmol. 2022, 52, 201–207. [Google Scholar] [CrossRef]
- Koch, D.D.; Hill, W.; Abulafia, A.; Wang, L. Pursuing perfection in intraocular lens calculations: I. Logical approach for classifying IOL calculation formulas. J. Cataract. Refract. Surg. 2017, 43, 717–718. [Google Scholar] [CrossRef]
- Norrby, S. Sources of error in intraocular lens power calculation. J. Cataract. Refract. Surg. 2008, 34, 368–376. [Google Scholar] [CrossRef] [PubMed]
- Grzybowski, A. Artificial Intelligence in Ophthalmology; Springer Nature: Cham, Switzerland, 2021; pp. 1–286. ISBN 978-3-030-78601-4. [Google Scholar] [CrossRef]
- Rajesh, A.E.; Davidson, O.Q.; Lee, C.S.; Lee, A.Y. Artificial Intelligence and Diabetic Retinopathy: AI Framework, Prospective Studies, Head-to-head Validation, and Cost-effectiveness. Diabetes Care 2023, 46, 1728–1739. [Google Scholar] [CrossRef]
- Ting, D.S.W.; Pasquale, L.R.; Peng, L.; Campbell, J.P.; Lee, A.; Raman, R.; Tan, G.S.W.; Schmetterer, L.; Keane, P.A.; Wong, T.Y. Artificial intelligence and deep learning in ophthalmology. Br. J. Ophthalmol. 2019, 103, 167–175. [Google Scholar] [CrossRef]
- Ramessur, R.; Raja, L.; Kilduff, C.L.; Kang, S.; Li, J.P.O.; Thomas, P.B.; Sim, D.A. Impact and Challenges of Integrating Artificial Intelligence and Telemedicine into Clinical Ophthalmology. Asia-Pac. J. Ophthalmol. 2021, 10, 317–327. [Google Scholar] [CrossRef]
- Hipólito-Fernandes, D.; Luís, M.E.; Serras-Pereira, R.; Gil, P.; Maduro, V.; Feijão, J.; Alves, N. Anterior chamber depth, lens thickness and intraocular lens calculation formula accuracy: Nine formulas comparison. Br. J. Ophthalmol. 2022, 106, 349–355. [Google Scholar] [CrossRef]
- Connell, B.J.; Kane, J.X. Comparison of the Kane formula with existing formulas for intraocular lens power selection. BMJ Open Ophthalmol. 2019, 4, e000251. [Google Scholar] [CrossRef]
- Gatinel, D.; Debellemanière, G.; Saad, A.; Dubois, M.; Rampat, R. Determining the Theoretical Effective Lens Position of Thick Intraocular Lenses for Machine Learning-Based IOL Power Calculation and Simulation. Transl. Vis. Sci. Technol. 2021, 10, 27. [Google Scholar] [CrossRef]
- Carmona-González, D.; Palomino-Bautista, C. Accuracy of a new intraocular lens power calculation method based on artificial intelligence. Eye 2021, 35, 517–522. [Google Scholar] [CrossRef]
- Taroni, L.; Hoffer, K.J.M.; Pellegrini, M.; Lupardi, E.; Savini, G. Comparison of the New Hoffer QST with 4 Modern Accurate Formulas. J. Cataract. Refract. Surg. 2023, 49, 378–384. [Google Scholar] [CrossRef]
- Shammas, H.J.; Taroni, L.; Pellegrini, M.; Shammas, M.C.; Jivrajka, R.V. Accuracy of never IOL power formulas in short and long eyes using sum-of-segment biometry. J. Cataract. Refract. Surg. 2022, 48, 1113–1120. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Stein, J.; Nallasamy, N. Evaluation of the Nallasamy formula: A stacking ensemble machine learning method for refraction prediction in cataract surgery. Br. J. Ophthalmol. 2023, 107, 1066–1071. [Google Scholar] [CrossRef] [PubMed]
- Kane, J.X.; Melles, R.B. Intraocular lens formula comparison in axial hyperopia with a high-power intraocular lens of 30 or more diopters. J. Cataract. Refract. Surg. 2020, 46, 1236–1239. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Wang, L.; Kane, J.X.; Li, J.; Liu, L.; Wu, M. Accuracy of Artificial Intelligence Formulas and Axial Length Adjustments for Highly Myopic Eyes. Am. J. Ophthalmol. 2021, 223, 100–107. [Google Scholar] [CrossRef]
- Ang, R.T.; Rapista, A.B.; Remo, J.M.; Tan-Daclan, M.T.; Cruz, E. Clinical outcomes and comparison of intraocular lens calculation formulas in eyes with long axial myopia. Taiwan J. Ophthalmol. 2021, 12, 305–311. [Google Scholar] [CrossRef]
- Savini, G.; Di Maita, M.; Hoffer, K.J.; Næser, K.; Schiano-Lomoriello, D.; Vagge, A.; Di Cello, L.; Traverso, C.E. Comparison of 13 formulas for IOL power calculation with measurements from partial coherence interferometry. Br. J. Ophthalmol. 2021, 105, 484–489. [Google Scholar] [CrossRef]
- Hou, M.; Ding, Y.; Liu, L.; Li, J.; Liu, X.; Wu, M. Accuracy of intraocular lens power calculation in primary angle-closure disease: Comparison of 7 formulas. Graefe’s Arch. Clin. Exp. Ophthalmol. 2021, 259, 3739–3747. [Google Scholar] [CrossRef]
- Hill, W. Hill-RBF Calculator. Available online: https://rbfcalculator.com (accessed on 28 October 2023).
- Carmona-González, D. Karmona Calculator. Available online: https://karmona-iol.com (accessed on 8 October 2023).
- Clarke, G.P.; Burmeister, J. Comparison of intraocular lens computations using a neural network versus the Holladay formula. J. Cataract. Refract. Surg. 1997, 23, 1585–1589. [Google Scholar] [CrossRef] [PubMed]
- Cassidy, J.; Nouri, A.; Betz, V.; Lilge, L. High-performance, robustly verified Monte Carlo simulation with FullMonte. J. Biomed. Opt. 2018, 23, 1–11. [Google Scholar] [CrossRef]
- Siddiqui, A.A.; Juthani, V.; Kang, J.; Chuck, R.S. The future of intraocular lens calculations: Ladas super formula. Ann. Eye Sci. 2019, 4, 19. [Google Scholar] [CrossRef]
- Stopyra, W. Comparison of the accuracy of six intraocular lens power calculation formulas for eyes of axial length exceeding 25.0 mm. J. Fr. Ophthalmol. 2021, 44, 1332–1339. [Google Scholar] [CrossRef]
- Stopyra, W. The accuracy of intraocular lens power calculation formulas for eyes longer than 25.00 mm and the correlation between method accuracy and eye axial length. Klin. Oczna 2021, 123, 129–133. [Google Scholar] [CrossRef]
- Debellemanière, G.; Saad, A.; Gatinel, D. PEARL DGS Calculator. IOL Solver. Available online: https://iolsolver.com (accessed on 28 October 2023).
- Cooke, D.L.; Cooke, T.L. Approximating sum-of-segments axial length from a traditional optical low-coherence reflectometry measurement. J. Cataract. Refract. Surg. 2019, 45, 351–354. [Google Scholar] [CrossRef] [PubMed]
- Kane, J. Kane Calculator. Available online: https://iolformula.com (accessed on 28 October 2023).
- Darcy, K.; Gunn, D.; Tavassoli, S.; Sparrow, J.; Kane, J.X. Assessment of the accuracy of new and updated intraocular lens power calculation formulas in 10930 eyes from the UK National Health Service. J. Cataract. Refract. Surg. 2020, 46, 2–7. [Google Scholar] [CrossRef]
- Tan, X.; Zhang, J.; Zhu, Y.; Xu, J.; Oiu, X.; Yang, G.; Liu, Z.; Luo, L.; Liu, Y. Accuracy of New Generation Intraocular Lens Calculation Formulas in Vitrectomized Eyes. Am. J. Ophthalmol. 2020, 217, 81–90. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; Liu, Z.; Yang, G.; Oiu, X.; Xu, J.; Jin, G.; Li, Y.; Zhang, S.; Tan, X.; et al. Accuracy of new-generation intraocular lens calculation formulas in eyes undergoing combined silicone oil removal and cataract surgery. J. Cataract. Refract. Surg. 2021, 47, 593–598. [Google Scholar] [CrossRef]
- Hipólito-Fernandes, D.; Elisa Luís, M.; Gil, P.; Maduro, V.; Feijão, J.; Yeo, T.K.; Voytsekhivskyy, O.; Alves, N. VRF-G, a New Intraocular Lens Power Calculation Formula: A 13-Formulas Comparison Study. Clin. Ophthalmol. 2020, 14, 4395–4402. [Google Scholar] [CrossRef]
- Hipólito-Fernandes, D.; Luís, M.E.; Maleita, D.; Gil, P.; Maduro, V.; Feijão, J.; Costa, L.; Marques, N.; Branco, J.; Alves, N. Intraocular lens power calculation formulas accuracy in combined phacovitrectomy: An 8-formulas comparison study. Int. J. Retin. Vitr. 2021, 7, 47. [Google Scholar] [CrossRef] [PubMed]
- Chang, P.; Qian, S.; Wang, Y.; Li, S.; Yang, F.; Hu, Y.; Liu, Z.; Zhao, Y. Accuracy of new-generation intraocular lens calculation formulas in eyes with variations in predicted refraction. Graefe’s Arch. Clin. Exp. Ophthalmol. 2022, 261, 127–135. [Google Scholar] [CrossRef]
- Pellegrini, M.; Furiosi, L.; Salgari, N.; D’Angelo, S.; Zauli, G.; Yu, A.C.; Busin, M. Accuracy of intraocular lens power calculation for cataract surgery after deep anterior lamellar keratoplasty. Clin. Exp. Ophthalmol. 2022, 50, 17–22. [Google Scholar] [CrossRef] [PubMed]
- Hoffer, K.J.; Aramberri, J.; Haigis, W.; Olsen, T.; Savini, G.; Shammas, H.J.; Bentow, S. Protocols for studies of intraocular lens formula accuracy. Am. J. Ophthalmol. 2015, 160, 403–405.e1. [Google Scholar] [CrossRef]
- Tsessler, M.; Cohen, S.; Wang, L.; Koch, D.D.; Zadok, D.; Abulafia, A. Evaluating the prediction accuracy of the Hill-RBF 3.0 formula using a heteroscedastic statistical method. J. Cataract. Refract. Surg. 2022, 48, 37–43. [Google Scholar] [CrossRef]
- Savini, G.; Taroni, L.; Hoffer, K.J. Recent developments in intraocular lens power calculation methods-update 2020. Ann. Transl. Med. 2020, 8, 1553. [Google Scholar] [CrossRef] [PubMed]
- Xia, T.; Martinez, C.E.; Tsai, L.M. Update on Intraocular Lens Formulas and Calculations. Asia-Pac. J. Ophthalmol. 2020, 9, 186–193. [Google Scholar] [CrossRef]
- Guttierez, L.; Lim, J.S.; Foo, L.L.; Ng, W.Y.; Yip, M.; Lim, G.Y.S.; Wong, M.H.Y.; Fong, A.; Rosman, M.; Mehta, J.S.; et al. Application of artificial intelligence in cataract management current and future directions. Eye Vis. 2022, 9, 3. [Google Scholar] [CrossRef]
- Stopyra, W.; Langenbucher, A.; Grzybowski, A. Intraocular Lens Power Calculation Formulas—A Systematic Review. Ophthalmol. Ther. 2023, 12, 2881–2902. [Google Scholar] [CrossRef]
- Guo, D.; He w Wei, L.; Song, Y.; Qi, J.; Yao, Y.; Chen, X.; Huang, J.; Lu, Y.; Zhu, X. The Zhu-Lu formula: A machine learning-based intraocular lens power calculation formula for highly myopic eyes. Eye Vis. 2023, 10, 26. [Google Scholar] [CrossRef] [PubMed]
- Kenny, P.I.; Kozhaya, K.; Truong, P.; Weikert, M.P.; Hill, W.E.; Koch, D.D. Efficacy of segmented axial length and artificial intelligence approaches to intraocular lens power calculation in short eyes. J. Cataract. Refract. Surg. 2023, 49, 697–703. [Google Scholar] [CrossRef] [PubMed]
- Stopyra, W. Analysis of accuracy of twelve intraocular lens power calculation formulas for eyes with axial hyperopia. Saudi J. Ophthalmol. 2023, 37, 125–130. [Google Scholar] [CrossRef] [PubMed]
- Voytsekhivskyy, O.V.; Hoffer, K.J.; Tutchenko, L.; Cooke, D.L.; Savini, G. Accuracy of 24 IOL Power Calculation Methods. J. Refract. Surg. 2023, 39, 249–256. [Google Scholar] [CrossRef]
- Li, T.; Stein, J.; Nallasamy, N. AI-powered effective lens position prediction improves the accuracy of existing lens formulas. Br. J. Ophthalmol. 2022, 106, 1222–1226. [Google Scholar] [CrossRef]
- Cione, F.; De Bernardo, M.; Gioia, M.; Oliviero, M.; Santoro, A.G.; Caputo, A.; Capasso, L.; Paglianulo, S.; Rosa, N. A No-History Multi-Formula Approach to Improve the IOL Power Calculation after Laser Refractive Surgery: Preliminary Results. J. Clin. Med. 2023, 12, 2890. [Google Scholar] [CrossRef]


| Formula | Logical Approach Classification | Variables Utilized | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AL | K | KmA | KmP | ACD | LT | CCT | WTW | G | |||
| FullMonte | Hybrid | C | C | C | C | ||||||
| Ladas | Hybrid | C | C | C | |||||||
| Hill-RBF | 1.0 | AI | C | C | C | ||||||
| 2.0 | C | C | C | ||||||||
| 3.0 | C | C | C | O | O | O | O | ||||
| PEARL-DGS | Hybrid | C | C | C | C | C | C | ||||
| Kane | Hybrid | C | C | C | O | O | C | ||||
| Karmona | AI | C | C | O | C | O | C | C | |||
| Hoffer QST | Hybrid | C | C | C | C | ||||||
| Nallasamy | AI | C | C | C | C | O | C | ||||
| Study | MAE | |||||||
|---|---|---|---|---|---|---|---|---|
| Hill-RBF | Karmona | Nallasamy | Kane | Ladas | Hoffer QST | PEARL-DGS | FullMonte | |
| Kane et al., 2017; (3122 eyes) [7] | 0.407 | 0.402 | 0.428 | |||||
| Connell and Kane, 2019; (864 eyes) [22] | 0.346 | 0.329 | ||||||
| Darcy et al., 2020; (10,930 eyes) [43] | 0.387 | 0.377 | ||||||
| Carmona-González et al., 2020; (481 eyes) [10] | 0.33 | 0.30 | 0.32 | |||||
| Hipólito-Fernandes et al., 2020; (695 eyes) [21] | 0.337 | 0.315 | 0.312 | |||||
| Savini et al., 2020; (200 eyes) [31] | 0.287 | 0.265 | 0.286 | |||||
| Rocha-de-Lossada et al., 2020; (171 eyes) [2] | 0.283 | 0.276 | 0.308 | 0.263 | ||||
| Cheng et al., 2020; (370 eyes) [29] | 0.46 | 0.34 | ||||||
| Kane and Melles, 2020; (182 eyes) [28] | 0.709 | 0.533 | ||||||
| Nemeth and Modis, 2020; (186 eyes) [6] | 0.36 | |||||||
| Tan et al., 2020; (111 eyes) [44] | 0.72 | 0.74 | ||||||
| Hou et al., 2021; (129 eyes) [32] | 0.44 | 0.41 | 0.51 | |||||
| Carmona-González et al., 2021; (260 eyes) [24] | 0.3 | 0.24 | ||||||
| Ang et al., 2021; (183 eyes) [30] | 0.34 | 0.39 | ||||||
| Nemeth et al., 2021; (114 eyes) [11] | 0.36 | 0.42 | 0.41 | |||||
| Zhang et al., 2021; (211 eyes) [45] | 0.55 | 0.57 | ||||||
| Hipólito-Fernandes et al., 2021; (828 eyes) [46] | 0.342 | 0.324 | 0.344 | |||||
| Voytsekhivskyy et al., 2021; (241 eyes) [12] | 0.413 | 0.387 | 0.468 | 0.421 | ||||
| Hipólito-Fernandes et al., 2021; (220 eyes) [47] | 0.364 | 0.377 | ||||||
| Debellemanière et al., 2021; (4242 eyes) [9] | 0.303 | 0.286 | ||||||
| Chang et al., 2022; (79 eyes) [48] | 0.40 | 0.46 | ||||||
| Shammas et al., 2022; (595 eyes) [26] | 0.31 | 0.30 | 0.31 | 0.29 | ||||
| Pellegrini et al., 2022; (82 eyes) [49] | 1.10 | 1.05 | ||||||
| Taroni et al., 2023 (1259 eyes) [25] | 0.38 | 0.36 | 0.36 | |||||
| Li et al., 2023 (6893 eyes) [27] | 0.31 | 0.33 | ||||||
| Study | % ±0.5 D | |||||||
|---|---|---|---|---|---|---|---|---|
| Hill-RBF | Karmona | Nallasamy | Kane | Ladas | Hoffer QST | PEARL-DGS | FullMonte | |
| Kane et al., 2017; (3122 eyes) [7] | 69.6 | 69.8 | 66.6 | |||||
| Connell and Kane, 2019; (864 eyes) [22] | 75.3 | 77.9 | ||||||
| Darcy et al., 2020; (10930 eyes) [43] | 71.2 | 72.0 | ||||||
| Carmona-González et al., 2020; (481 eyes) [10] | 76.1 | 80.0 | 79.8 | |||||
| Hipólito-Fernandes et al., 2020; (695 eyes) [21] | 77.9 | 81.6 | 79.9 | |||||
| Savini et al., 2020; (200 eyes) [31] | 85.0 | 86.5 | 84.5 | |||||
| Rocha-de-Lossada et al., 2020; (171 eyes) [2] | 85.4 | 84.8 | 81.3 | 86.0 | ||||
| Cheng et al., 2020; (370 eyes) [29] | 69.5 | 75.0 | ||||||
| Kane and Melles, 2020; (182 eyes) [28] | 44.0 | 58.5 | ||||||
| Nemeth and Modis, 2020; (186 eyes) [6] | 83.6 | |||||||
| Tan et al., 2020; (111 eyes) [44] | 59.8 | 49.5 | ||||||
| Hou et al., 2021; (129 eyes) [32] | 69.0 | 71.3 | 60.5 | |||||
| Carmona-González et al., 2021; (260 eyes) [24] | 80.8 | 90.4 | ||||||
| Ang et al., 2021; (183 eyes) [30] | 80.9 | 75.4 | ||||||
| Nemeth et al., 2021; (114 eyes) [11] | 84.2 | 80.7 | 79.8 | |||||
| Zhang et al., 2021; (211 eyes) [45] | 65.9 | 64.5 | ||||||
| Hipólito-Fernandes et al., 2021; (828 eyes) [46] | 76.7 | 79.3 | 76.9 | |||||
| Voytsekhivskyy et al., 2021; (241 eyes) [12] | 67.7 | 72.2 | 66.0 | 68.5 | ||||
| Hipólito-Fernandes et al., 2021; (220 eyes) [47] | 71.6 | 74.1 | ||||||
| Debellemanière et al., 2021; (4242 eyes) [9] | 87.4 | |||||||
| Chang et al., 2022; (79 eyes) [48] | 70.9 | 65.8 | ||||||
| Shammas et al., 2022; (595 eyes) [26] | 81.5 | 80.3 | 80.7 | 81.7 | ||||
| Pellegrini et al., 2022; (82 eyes) [49] | 32.5 | 37.0 | ||||||
| Taroni et al., 2023 (1259 eyes) [25] | 74.7 | 76.3 | 76.3 | |||||
| Li et al., 2023 (6893 eyes) [27] | 80.2 | 77.7 | ||||||
| Study | Limitations | Parameter | Formula | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hill | Karm | Nall | Kane | Ladas | HQST | DGS | FullM | |||
| Rocha-de-Lossada et al., 2021; 171 eyes [2] | Small sample size, two eyes per patient included (against Hoffer recommendation) (Hoffer et al., 2015) [50] Phaco performed by one surgeon | MAE | 0.28 | 0.28 | 0.31 | 0.26 | ||||
| ±0.5 D | 85.4 | 84.8 | 81.3 | 86.0 | ||||||
| ±1.0 D | 98.8 | 100 | 98.3 | 100 | ||||||
| Shammas et al., 2022; 595 eyes [26] | Small sample size of short and long eyes Lack of extremely short and long eyes Biometry with the Argos (Alcon, Fort Worth, TX, USA) biometer (sum-of-segment methodology for AL) | MAE | 0.31 | 0.30 | 0.31 | 0.29 | ||||
| ±0.5 D | 81.5 | 80.3 | 80.7 | 81.7 | ||||||
| ±1.0 D | 99.5 | 99.7 | 99.8 | 99.8 | ||||||
| Hipólito-Fernandes et al., 2020; 828 eyes [46] | The same model of implanted IOL Preoperative optical biometry with optical low-coherence reflectometry (OLCR)—Lenstar LS- 900® (Haag-Streit AG, Köniz, Switzerland) | MAE | 0.34 | 0.32 | 0.34 | |||||
| ±0.5 D | 76.7 | 79.3 | 76.9 | |||||||
| ±1.0 D | 97.6 | 97.7 | 97.2 | |||||||
| Carmona-González et al., 2021; 481 eyes [10] | Small sample size of short and long eyes | MAE | 0.33 | 0.30 | 0.32 | |||||
| ±0.5 D | 76.1 | 80.0 | 79.8 | |||||||
| ±1.0 D | 97.5 | 98.1 | 96.9 | |||||||
| Kane et al., 2017; 3122 Eyes [7] | Single IOL model (Hill-RBF and Barrett Universal II have been developed or reformulated based on data using this particular IOL type) Lack of full optimization of the lens constant for each formula | MAE | 0.41 | 0.40 | 0.42 | |||||
| ±0.5 D | 69.6 | 69.8 | 66.6 | |||||||
| ±1.0 D | 94.3 | 94.3 | 93.0 | |||||||
| Voytsek hivskyy et al., 2021; 241 eyes [12] | Only short eyes (lack of medium and long eyes) Small sample size of very short eyes | MAE | 0.41 | 0.39 | 0.47 | 0.42 | ||||
| ±0.5 D | 67.7 | 72.2 | 66.0 | 68.5 | ||||||
| ±1.0 D | 93.8 | 95.4 | 88.4 | 93.8 | ||||||
| Savini et al., 2020; 200 eyes [31] | Lack of LT data does not show the full capabilities of formulas that can utilize this parameter, such as Kane, Pearl-DGS, and Hill-RBF Small sample size Phaco performed by one surgeon | MAE | 0.29 | 0.27 | 0.29 | |||||
| ±0.5 D | 85.0 | 86.5 | 84.5 | |||||||
| ±1.0 D | 99.5 | 99.0 | 98.5 | |||||||
| Darcy et al., 2020; 10,930 [43] eyes | Absence of LT, CCT, and WTW measurements | MAE | 0.39 | 0.38 | ||||||
| ±0.5 D | 71.2 | 72.0 | ||||||||
| ±1.0 D | 94.9 | 95.2 | ||||||||
| Carmona- González et al., 2021; 260 eyes [24] | Small sample size | MAE | 0.30 | 0.24 | ||||||
| ±0.5 D | 80.8 | 90.4 | ||||||||
| ±1.0 D | 100 | 100 | ||||||||
| Zhang et al., 2021; 211 eyes [45] | Only vitrectomized eyes (relatively worse visual acuity) | MAE | 0.55 | 0.57 | ||||||
| ±0.5 D | 65.9 | 64.5 | ||||||||
| ±1.0 D | 85.8 | 85.3 | ||||||||
| Hipólito- Fernandes et al., 2021; 220 eyes [47] | Retrospective design of the study | MAE | 0.36 | 0.38 | ||||||
| ±0.5 D | 71.6 | 74.1 | ||||||||
| ±1.0 D | 95.7 | 95.7 | ||||||||
| Taroni et al., 2023; 1259 eyes [25] | Lack of LT data does not show the full capabilities of formulas that can utilize this parameter, such as Kane and Hill-RBF Retrospective design of the study | MAE | 0.38 | 0.36 | 0.36 | |||||
| ±0.5 D | 74.7 | 76.3 | 76.3 | |||||||
| ±1.0 D | 95.0 | 96.0 | 96.7 | |||||||
| Li et al., 2023; 6893 eyes [27] | No validation on a data set from a different institution Single IOL model, i.e., SN60WF (Alcon, Fort Worth, TX, USA) Small range of AL (no extremely long or extremely short eyes) | MAE | 0.31 | 0.33 | ||||||
| ±0.5 D | 80.2 | 77.7 | ||||||||
| ±1.0 D | 97.6 | 97.4 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stopyra, W.; Cooke, D.L.; Grzybowski, A. A Review of Intraocular Lens Power Calculation Formulas Based on Artificial Intelligence. J. Clin. Med. 2024, 13, 498. https://doi.org/10.3390/jcm13020498
Stopyra W, Cooke DL, Grzybowski A. A Review of Intraocular Lens Power Calculation Formulas Based on Artificial Intelligence. Journal of Clinical Medicine. 2024; 13(2):498. https://doi.org/10.3390/jcm13020498
Chicago/Turabian StyleStopyra, Wiktor, David L. Cooke, and Andrzej Grzybowski. 2024. "A Review of Intraocular Lens Power Calculation Formulas Based on Artificial Intelligence" Journal of Clinical Medicine 13, no. 2: 498. https://doi.org/10.3390/jcm13020498
APA StyleStopyra, W., Cooke, D. L., & Grzybowski, A. (2024). A Review of Intraocular Lens Power Calculation Formulas Based on Artificial Intelligence. Journal of Clinical Medicine, 13(2), 498. https://doi.org/10.3390/jcm13020498






