Concordance of LDL-C Estimating Equations with Direct Enzymatic Measurement in Diabetic and Prediabetic Subjects
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Participants
2.2. Biochemical Analyses
2.3. Lipid Estimations
2.4. Statistical Analysis
3. Results
3.1. Patient Characteristics
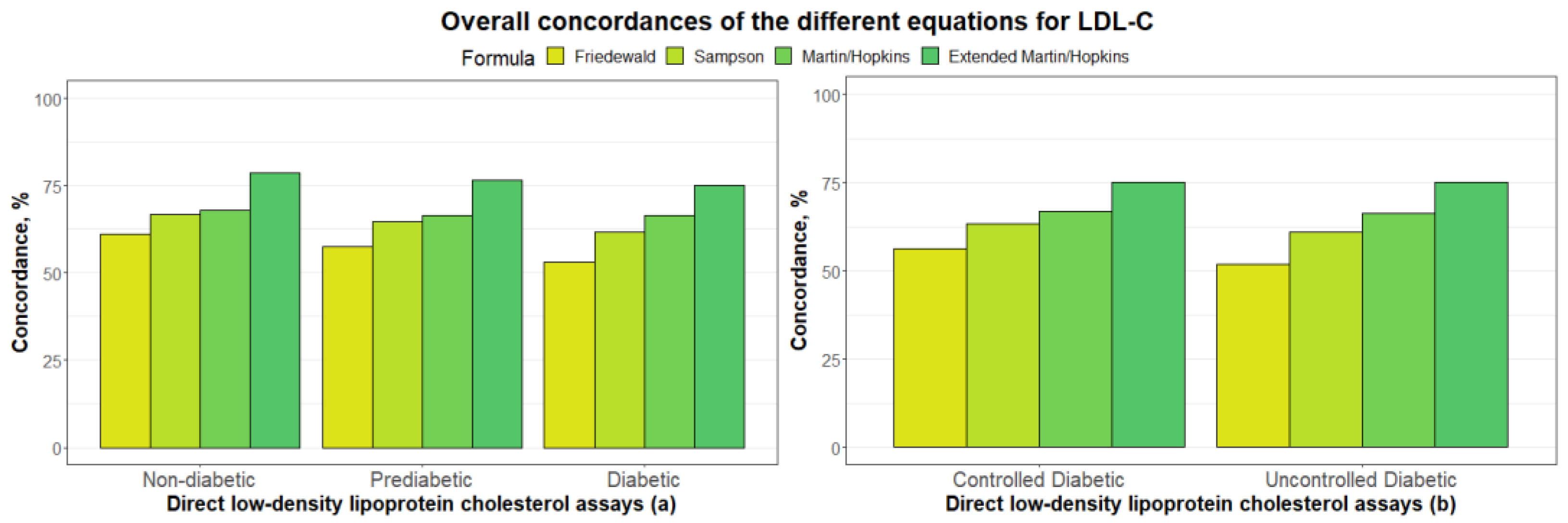
3.2. Overall Concordances of the Various LDL-C Estimating Equations
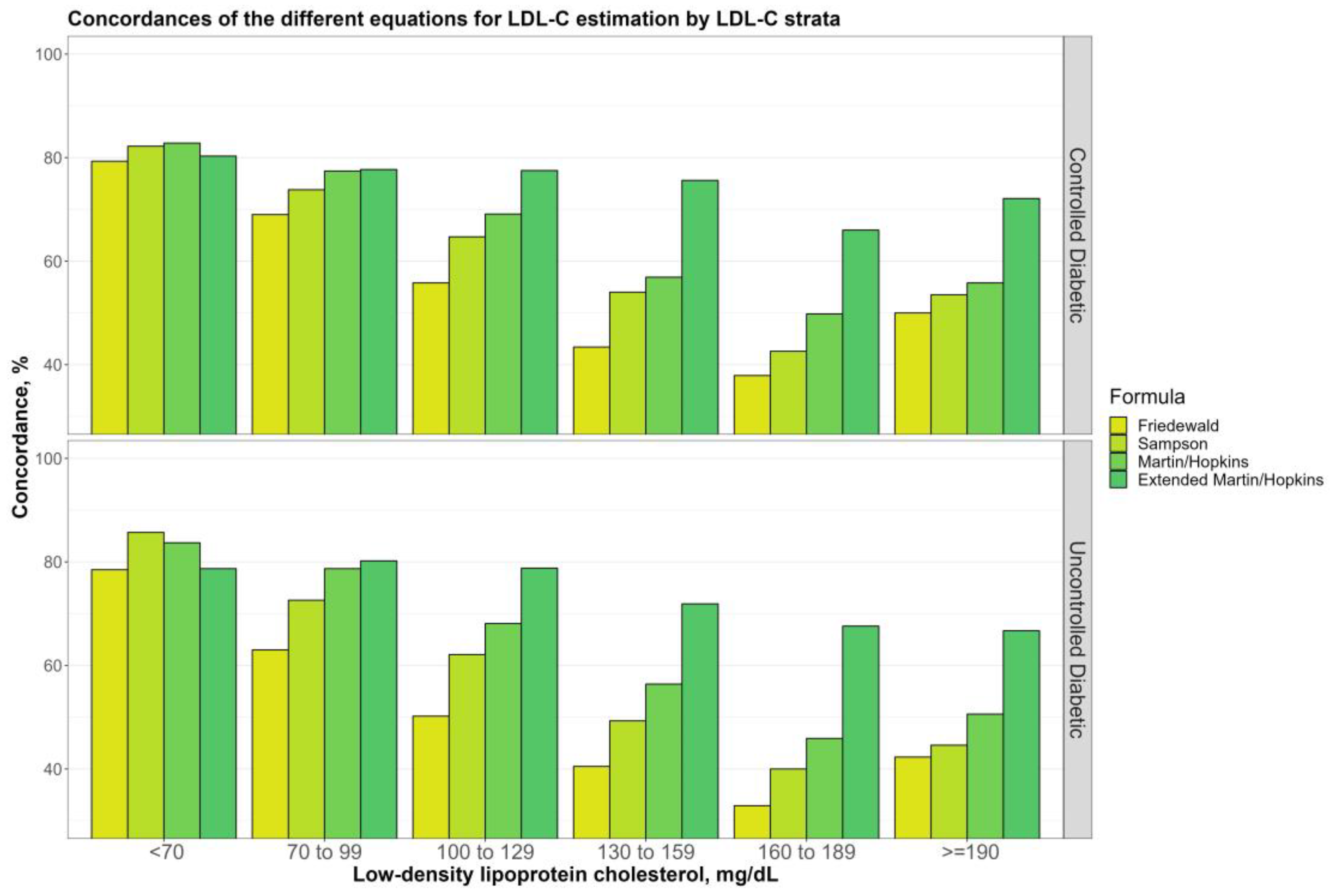
3.3. Overall Concordances of the Various LDL-C Estimating Equations by LDL-C Sublevels
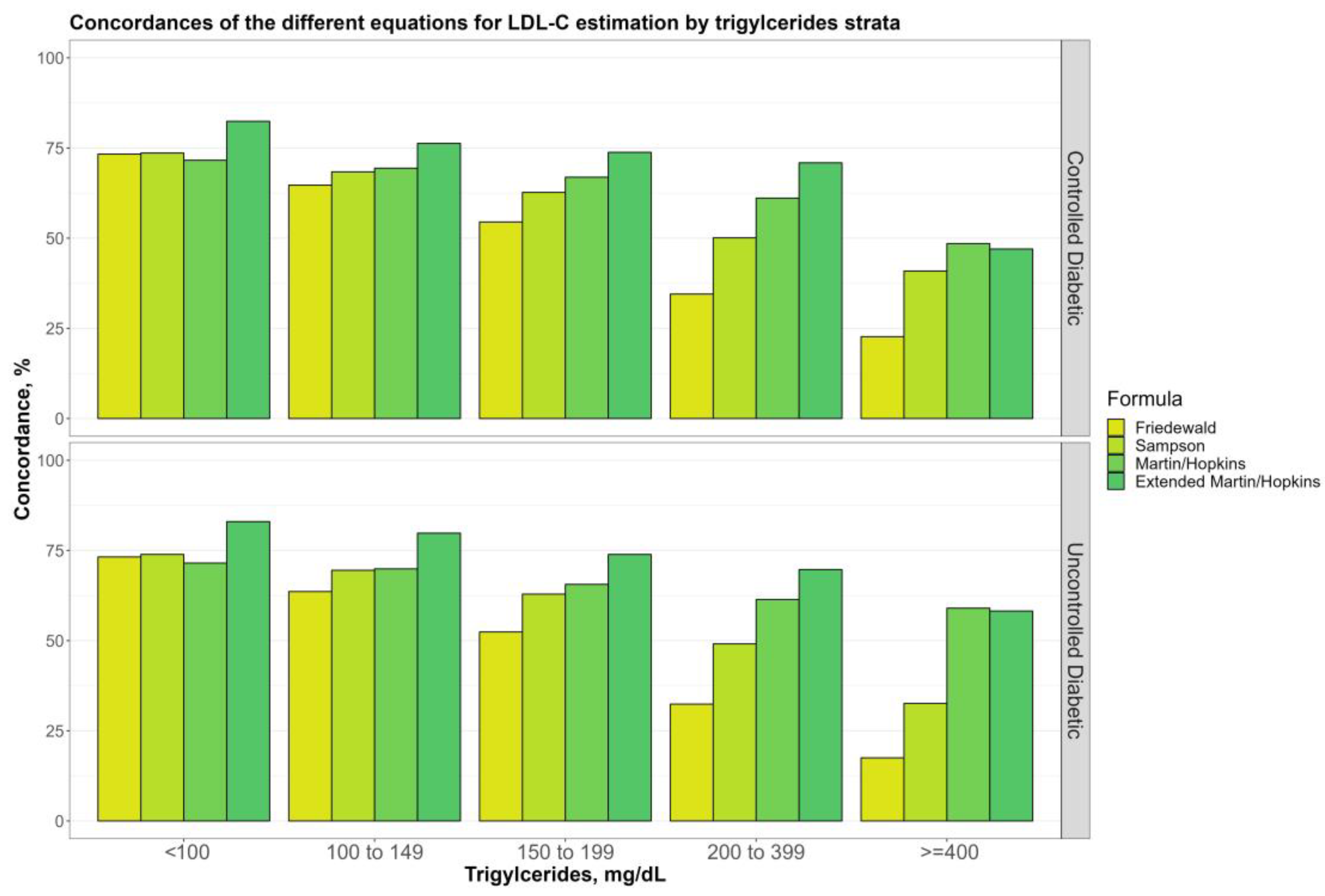
3.4. Overall Concordances of the Various LDL-C Estimating Equations by TG Sublevels
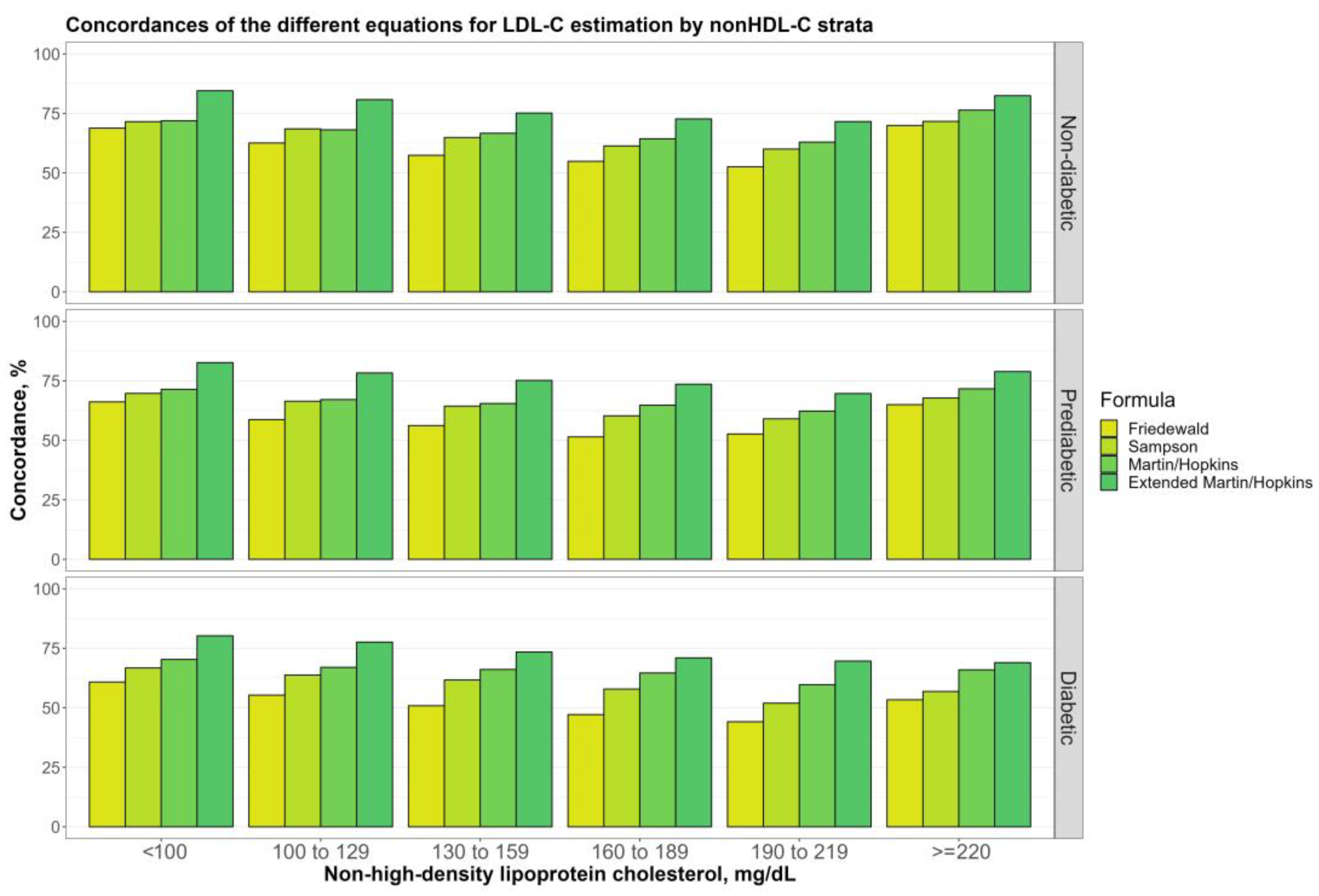
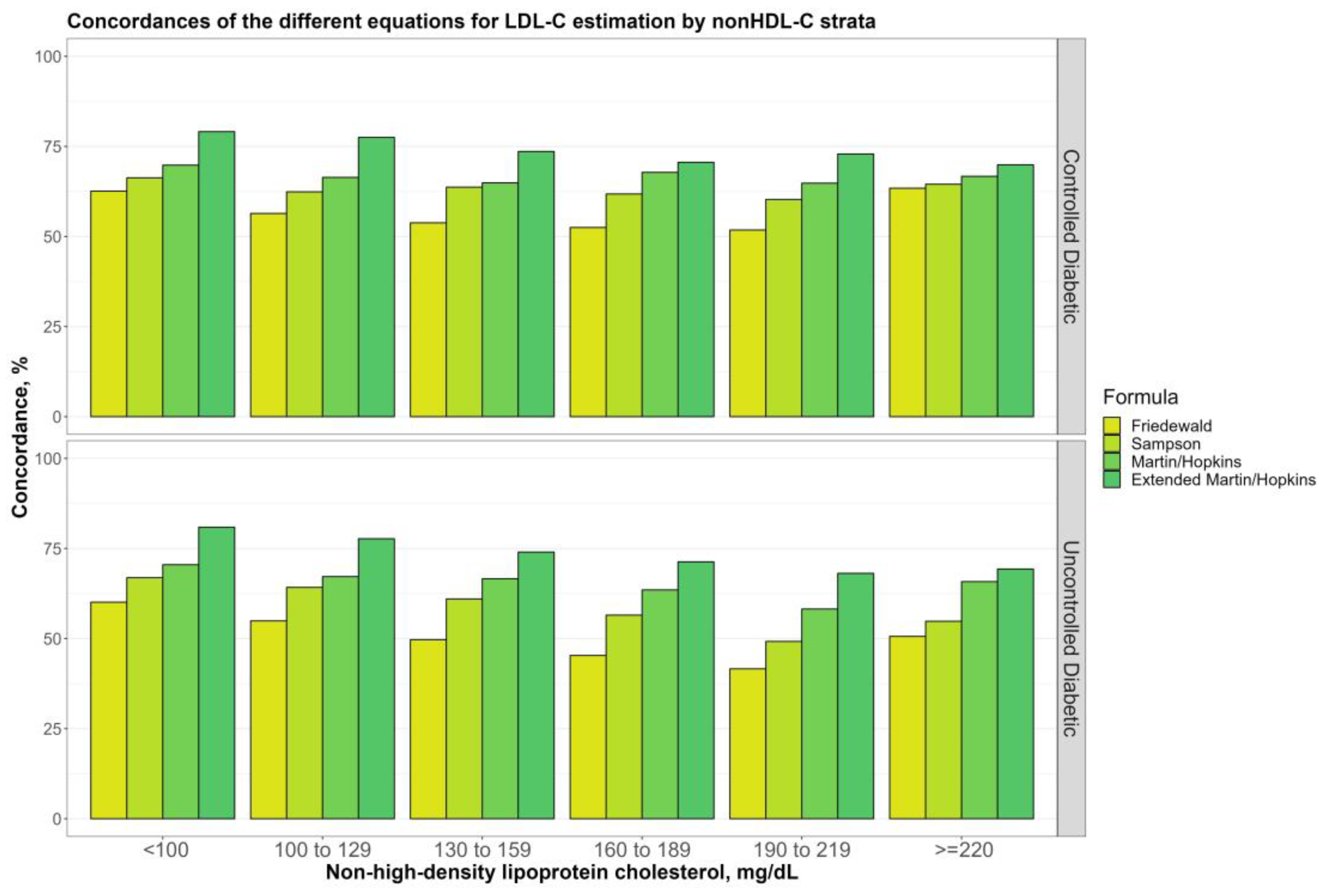
3.5. Overall Concordances of the Various LDL-C Estimating Equations by Non-HDL-C Sublevels
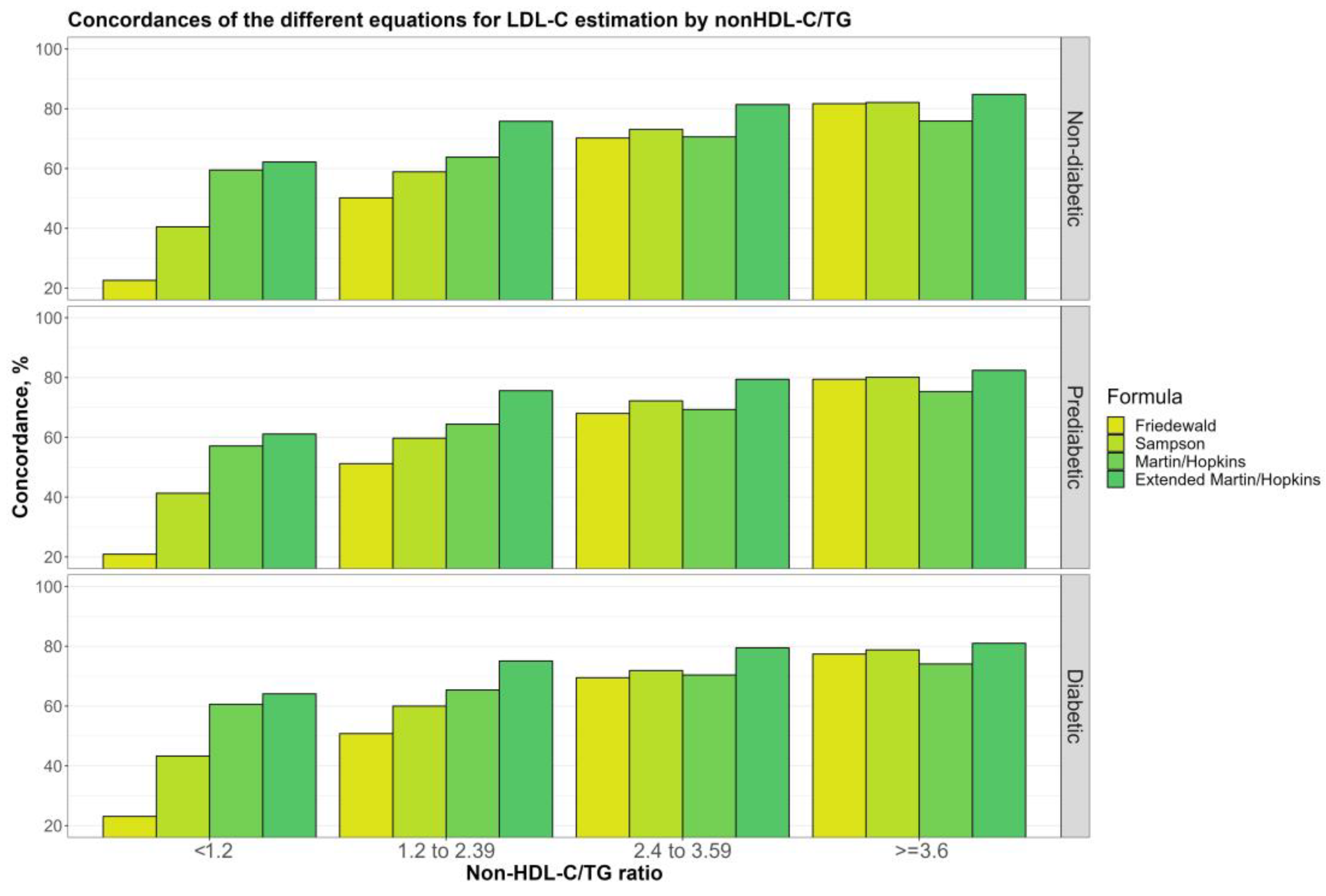
3.6. Overall Concordances of the Various LDL-C Estimating Equations by Non-HDL-C/TG Sublevels
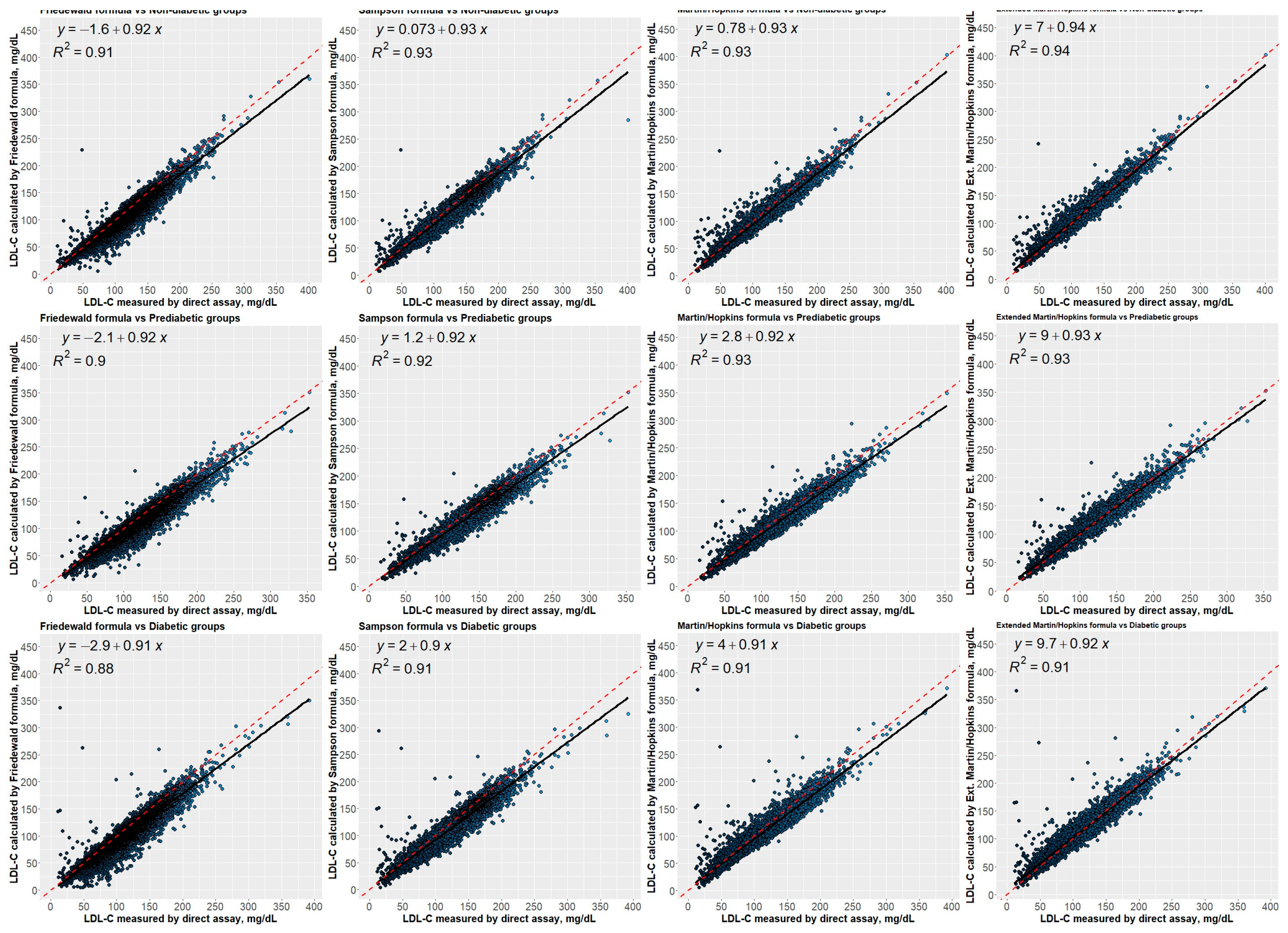
3.7. Correlation between Estimated LDL-C Levels Using Different Equations and Directly Measured LDL-C Levels
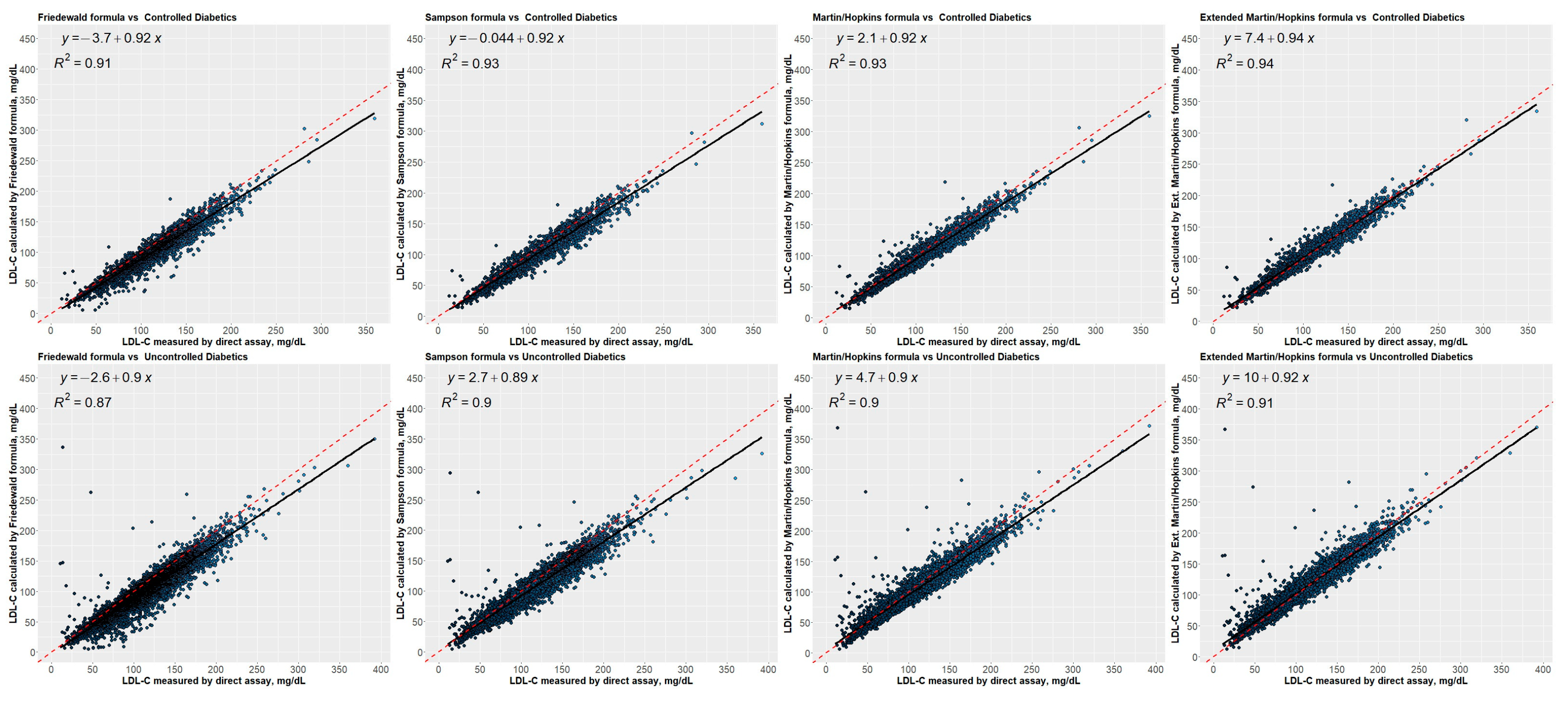
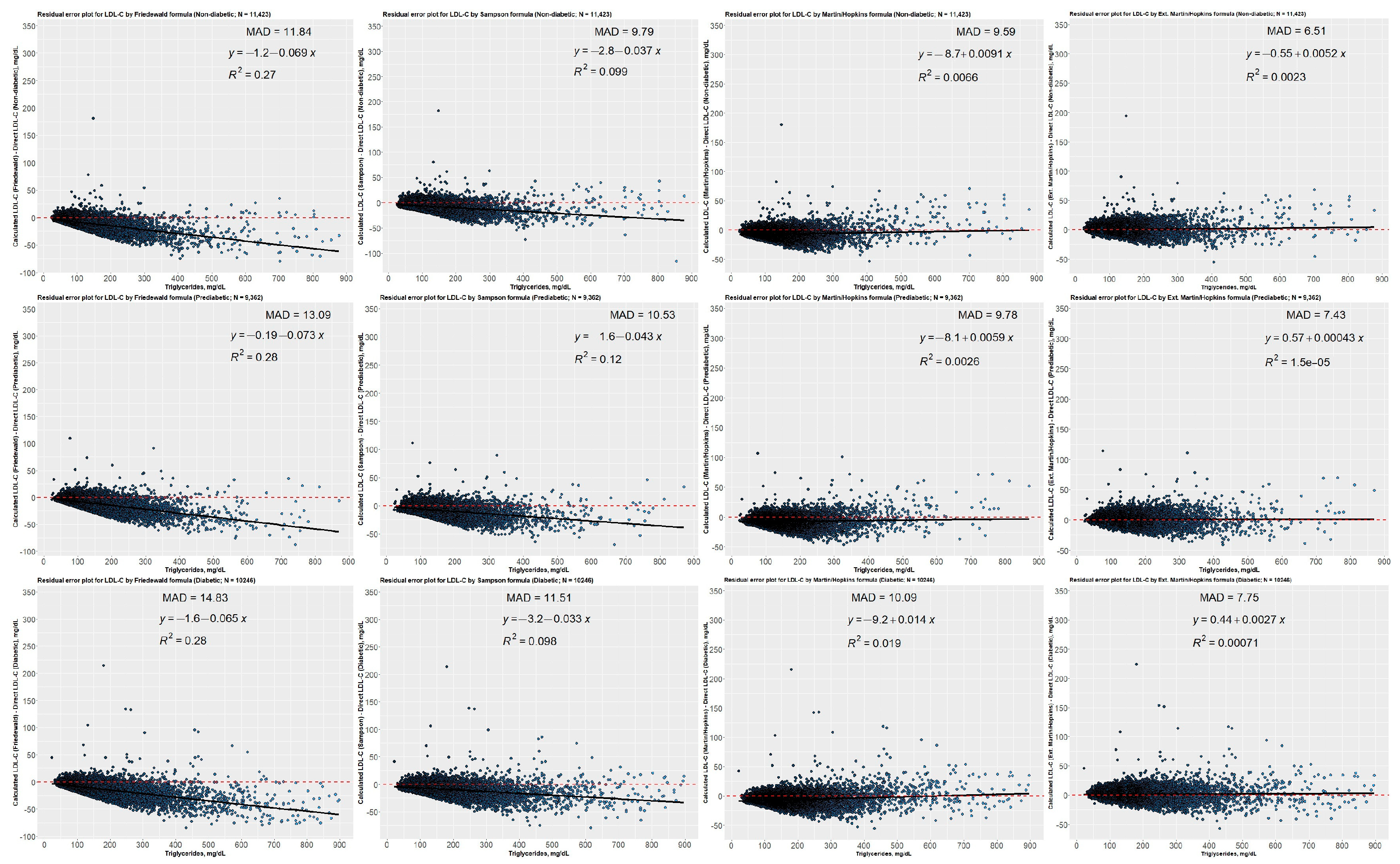
3.8. Residual Error Plots for LDL-C Concentrations Estimated by Different Equations concerning Direct Assay
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- American Diabetes Association. 2. Classification and Diagnosis of Diabetes: Standards of Medical Care in Diabetes—2021. Diabetes Care 2021, 44 (Suppl. S1), S15–S33. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Saeedi, P.; Karuranga, S.; Pinkepank, M.; Ogurtsova, K.; Duncan, B.B.; Stein, C.; Basit, A.; Chan, J.C.N.; Mbanya, J.C.; et al. IDF Diabetes Atlas: Global, Regional and Country-Level Diabetes Prevalence Estimates for 2021 and Projections for 2045. Diabetes Res. Clin. Pract. 2022, 183, 109119. [Google Scholar] [CrossRef] [PubMed]
- Toth, P.P. Effects of Combination Lipid Therapy in Type 2 Diabetes Mellitus. Yearb. Endocrinol. 2010, 2010, 50–52. [Google Scholar] [CrossRef]
- Forbes, J.M.; Cooper, M.E. Mechanisms of Diabetic Complications. Physiol. Rev. 2013, 93, 137–188. [Google Scholar] [CrossRef] [PubMed]
- American Diabetes Association. 10. Cardiovascular Disease and Risk Management: Standards of Medical Care in Diabetes—2022. Diabetes Care 2022, 45 (Suppl. S1), S144–S174. [Google Scholar] [CrossRef] [PubMed]
- Feingold, K.; Siperstein, M.D. Diabetic Vascular Disease. Adv. Intern. Med. 1986, 31, 309–340. [Google Scholar]
- Regensteiner, J.G.; Golden, S.; Anton, B.; Barrett-Connor, E.; Chang, A.Y.; Chyun, D.; Fox, C.S.; Huebschmann, A.G.; Kim, C.; Mehta, N.; et al. Sex Differences in the Cardiovascular Consequences of Diabetes Mellitus a Scientific Statement from the American Heart Association. Circulation 2015, 132, 2424–2447. [Google Scholar] [CrossRef]
- Fox, C.S.; Golden, S.H.; Anderson, C.; Bray, G.A.; Burke, L.E.; De Boer, I.H.; Deedwania, P.; Eckel, R.H.; Ershow, A.G.; Fradkin, J.; et al. Update on Prevention of Cardiovascular Disease in Adults with Type 2 Diabetes Mellitus in Light of Recent Evidence: A Scientific Statement from the American Heart Association and the American Diabetes Association. Circulation 2015, 132, 691–718. [Google Scholar] [CrossRef]
- Low Wang, C.C.; Hess, C.N.; Hiatt, W.R.; Goldfine, A.B. Clinical Update: Cardiovascular Disease in Diabetes Mellitus. Circulation 2016, 133, 2459–2502. [Google Scholar] [CrossRef]
- Milicevic, Z.; Raz, I.; Beattie, S.D.; Campaigne, B.N.; Sarwat, S.; Gromniak, E.; Kowalska, I.; Galic, E.; Tan, M.; Hanefeld, M. Natural History of Cardiovascular Disease in Patients with Diabetes: Role of Hyperglycemia. Diabetes Care 2008, 31 (Suppl. S2), S155–S160. [Google Scholar] [CrossRef]
- Rosengren, A.; Dikaiou, P. Cardiovascular Outcomes in Type 1 and Type 2 Diabetes. Diabetologia 2023, 66, 425–437. [Google Scholar] [CrossRef] [PubMed]
- Newman, C.; Bostrom, J.A.; Buysschaert, M.; Newman, J.D.; Goldberg, I.J.; Bergman, M. Diabetes Research and Clinical Practice Management of Dyslipidemia and Atherosclerotic Cardiovascular Risk in Prediabetes. Diabetes Res. Clin. Pract. 2022, 190, 109980. [Google Scholar] [CrossRef]
- Ertürk Zararsız, G.; Bolat, S.; Cephe, A.; Kochan, N.; Yerlitaş, S.İ.; Doğan, H.O.; Zararsız, G. Validation of Friedewald, Martin-Hopkins and Sampson Low-Density Lipoprotein Cholesterol Equations. PLoS ONE 2022, 17, e0263860. [Google Scholar] [CrossRef] [PubMed]
- Ginsberg, H.N.; Rosenson, R.S.; Kees Hovingh, G.; Letierce, A.; Samuel, R.; Poulouin, Y.; Cannon, C.P. LDL-C Calculated by Friedewald, Martin-Hopkins, or NIH Equation 2 versus Beta-Quantification: Pooled Alirocumab Trials. J. Lipid Res. 2022, 63, 100148. [Google Scholar] [CrossRef]
- Sampson, M.; Ling, C.; Sun, Q.; Harb, R.; Ashmaig, M.; Warnick, R.; Sethi, A.; Fleming, J.K.; Otvos, J.D.; Meeusen, J.W.; et al. A New Equation for Calculation of Low-Density Lipoprotein Cholesterol in Patients with Normolipidemia and/or Hypertriglyceridemia. JAMA Cardiol. 2020, 5, 540–548. [Google Scholar] [CrossRef]
- Van Deventer, H.E.; Miller, W.G.; Myers, G.L.; Sakurabayashi, I.; Bachmann, L.M.; Caudill, S.P.; Dziekonski, A.; Edwards, S.; Kimberly, M.M.; Korzun, W.J.; et al. Non-HDL Cholesterol Shows Improved Accuracy for Cardiovascular Risk Score Classification Compared to Direct or Calculated LDL Cholesterol in a Dyslipidemic Population. Clin. Chem. 2011, 57, 490–501. [Google Scholar] [CrossRef]
- Filippatos, T.; Tsimihodimos, V.; Pappa, E.; Elisaf, M. Pathophysiology of Diabetic Dyslipidaemia. Curr. Vasc. Pharmacol. 2017, 15, 566–575. [Google Scholar] [CrossRef]
- Glavinovic, T.; Thanassoulis, G.; de Graaf, J.; Couture, P.; Hegele, R.A.; Sniderman, A.D. Physiological Bases for the Superiority of Apolipoprotein B Over Low-Density Lipoprotein Cholesterol and Non–HighDensity Lipoprotein Cholesterol as a Marker of Cardiovascular Risk. J. Am. Heart Assoc. 2022, 11, e025858. [Google Scholar] [CrossRef]
- Srisurin, W. The Reliability of Calculated Low-Density Lipoprotein Cholesterol from Four Different Formulas in Thai Diabetic Patients. J. Med. Assoc. Thail. 2014, 97, 97. [Google Scholar]
- Chaen, H.; Kinchiku, S.; Miyata, M.; Kajiya, S.; Uenomachi, H.; Yuasa, T.; Takasaki, K.; Ohishi, M. Validity of a Novel Method for Estimation of Low-Density Lipoprotein Cholesterol Levels in Diabetic Patients. J. Atheroscler. Thromb. 2016, 23, 1355–1364. [Google Scholar] [CrossRef]
- Kurniawan, L.B.; Windarwati, W.; Mulyono, B. Analysis of Ldl-C Measurement Using Direct and Friedewald Formula in Type 2 Diabetes Mellitus Patients. Indones. J. Clin. Pathol. Med. Lab. 2018, 24, 255. [Google Scholar] [CrossRef]
- Razi, F.; Forouzanfar, K.; Bandarian, F.; Nasli-Esfahani, E. LDL-Cholesterol Measurement in Diabetic Type 2 Patients: A Comparison between Direct Assay and Popular Equations. J. Diabetes Metab. Disord. 2017, 16, 43. [Google Scholar] [CrossRef] [PubMed]
- Sibal, L.; Neely, R.D.G.; Jones, A.; Home, P.D. Friedewald Equation Underestimates Low-Density Lipoprotein Cholesterol at Low Concentrations in Young People with and without Type 1 Diabetes. Diabet. Med. 2010, 27, 37–45. [Google Scholar] [CrossRef]
- Naser, A.; Isgandarov, K.; Güvenç, T.S.; Güvenç, R.Ç. Original Article Comparison of Novel Martin/Hopkins and Sampson Equations for Calculation of Low-Density Lipoprotein Cholesterol in Diabetic Patients. Arq. Bras. Cardiol. 2022, 119, 225–233. [Google Scholar]
- Friedewald, W.T.; Levy, R.I.; Fredrickson, D.S. Estimation of the Concentration of Low-Density Lipoprotein Cholesterol in Plasma, without Use of the Preparative Ultracentrifuge. Clin. Chem. 1972, 18, 499–502. [Google Scholar] [CrossRef]
- Martin, S.S.; Blaha, M.J.; Elshazly, M.B.; Toth, P.P.; Kwiterovich, P.O.; Blumenthal, R.S.; Jones, S.R. Comparison of a Novel Method vs the Friedewald Equation for Estimating Low-Density Lipoprotein Cholesterol Levels from the Standard Lipid Profile. JAMA J. Am. Med. Assoc. 2013, 310, 2061–2068. [Google Scholar] [CrossRef]
- Sajja, A.; Park, J.; Sathiyakumar, V.; Varghese, B.; Pallazola, V.A.; Marvel, F.A.; Kulkarni, K.; Muthukumar, A.; Joshi, P.H.; Gianos, E.; et al. Comparison of Methods to Estimate Low-Density Lipoprotein Cholesterol in Patients with High Triglyceride Levels. JAMA Netw. Open 2021, 4, e2128817. [Google Scholar] [CrossRef]
- Esawy, M.M.; Shabana, M.A.; Magdy, M.M. Evaluation of Martin’s Equation for LDL-C Estimation in Type 2 Diabetes Mellitus Egyptian Patients. Clin. Chim. Acta 2019, 495, 487–492. [Google Scholar] [CrossRef]
- Tomo, S.; Sankanagoudar, S.; Shukla, R.; Sharma, P. Validation of a Novel Method for Determination of Low-Density Lipoprotein Cholesterol Levels in Indian Patients with Type 2 Diabetes. Diabetes Metab. Syndr. Clin. Res. Rev. 2022, 16, 102448. [Google Scholar] [CrossRef]
- Masson, W.; Huerín, M.; Lobo, M.; Masson, G.; Webmaster, D.; Fernández, N.; Micali, G.; Nemec, M.; Romero, C.; Molinero, G.; et al. Lipid Goals in Diabetic Patients. Clinical Implications after Application of a New Formula for Ldl-Cholesterol Calculation. Rev. Argent. Cardiol. 2020, 88, 39–45. [Google Scholar] [CrossRef]
- Choi, S.Y.; Park, H.E.; Kim, M.K.; Shin, C.S.; Cho, S.H.; Oh, B.H. Difference between Calculated and Direct-Measured Low-Density Lipoprotein Cholesterol in Subjects with Diabetes Mellitus or Taking Lipid-Lowering Medications. J. Clin. Lipidol. 2012, 6, 114–120. [Google Scholar] [CrossRef] [PubMed]
- Hirany, S.; Li, D.; Jialal, I. A More Valid Measurement of Low-Density Lipoprotein Cholesterol in Diabetic Patients. Am. J. Med. 1997, 102, 48–53. [Google Scholar] [CrossRef] [PubMed]
- Wägner, A.M.; Sánchez_quesada, J.L.; Pérez, A.; Rigla, M.; Cortés, M.; Blanco-Vaca, F.; Ordóñez-Llanos, J. Diabetes: Consequences for Patient Risk Classification. Clin. Chem. 2000, 46, 1830–1832. [Google Scholar] [CrossRef] [PubMed]
- Rubiés-Prat, J.; Reverter, J.L.; Sentí, M.; Pedro-Botet, J.; Salinas, I.; Lucas, A.; Nogués, X.; Sanmartí, A. Calculated low-density lipoprotein cholesterol should not be used for management of lipoprotein abnormalities in patients with diabetes mellitus. Diabetes Care 1993, 16, 1081–1086. [Google Scholar] [CrossRef]
- Whiting, L.J.; Shephard, M.D.S.; Tallis, G.A. Measurement of Plasma LDL Cholesterol in Patients with Diabetes. Diabetes Care 1997, 20, 12–14. [Google Scholar] [CrossRef] [PubMed]
- American Diabetes Association. 6. Glycemic Targets: Standards of Medical Care in Diabetesd—2019. Diabetes Care 2019, 42, S61–S70. [Google Scholar] [CrossRef]
- Gagel, A.; Zghyer, F.; Samuel, C.; Martin, S.S. What Is the Optimal Low-Density Lipoprotein Cholesterol? Med. Clin. N. Am. 2022, 106, 285–298. [Google Scholar] [CrossRef]
- Watts, G.F.; Barrett, P.H.R.; Ji, J.; Serone, A.P.; Chan, D.C.; Croft, K.D.; Loehrer, F.; Johnson, A.G. Differential Regulation of Lipoprotein Kinetics by Atorvastatin and Fenofibrate in Subjects with the Metabolic Syndrome. Diabetes 2003, 52, 803–811. [Google Scholar] [CrossRef]
- Chan, D.C.; Watts, G.F.; Redgrave, T.G.; Mori, T.A.; Barrett, P.H.R. Apolipoprotein B-100 Kinetics in Visceral Obesity: Associations with Plasma Apolipoprotein C-III Concentration. Metabolism 2002, 51, 1041–1046. [Google Scholar] [CrossRef]
- Riches, F.M.; Watts, G.F.; Naoumova, R.P.; Kelly, J.M.; Croft, K.D.; Thompson, G.R. Hepatic Secretion of Very-Low-Density Lipoprotein Apolipoprotein B-100 Studied with a Stable Isotope Technique in Men with Visceral Obesity. Int. J. Obes. 1998, 22, 414–423. [Google Scholar] [CrossRef]
- Ćwiklińska, A.; Wieczorek, E.; Gliwińska, A.; Marcinkowska, M.; Czaplińska, M.; Mickiewicz, A.; Kuchta, A.; Kortas-Stempak, B.; Gruchała, M.; Dȩbska-Ślizień, A.; et al. Non-HDL-C/TG Ratio Indicates Significant Underestimation of Calculated Low-Density Lipoprotein Cholesterol (LDL-C) Better than TG Level: A Study on the Reliability of Mathematical Formulas Used for LDL-C Estimation. Clin. Chem. Lab. Med. 2021, 59, 857–867. [Google Scholar] [CrossRef] [PubMed]
- Cicero, A.F.G.; Fogacci, F.; Patrono, D.; Mancini, R.; Ramazzotti, E.; Borghi, C.; D’Addato, S.; Bove, M.; Piani, F.; Giovannini, M.; et al. Application of the Sampson Equation to Estimate LDL-C in Children: Comparison with LDL Direct Measurement and Friedewald Equation in the BLIP Study. Nutr. Metab. Cardiovasc. Dis. 2021, 31, P1911–P1915. [Google Scholar] [CrossRef] [PubMed]
- Piani, F.; Cicero, A.F.G.; Ventura, F.; Dormi, A.; Fogacci, F.; Patrono, D.; Mancini, R.; Ramazzotti, E.; Borghi, C.; D’Addato, S.; et al. Evaluation of Twelve Formulas for LDL-C Estimation in a Large, Blinded, Random Italian Population. Int. J. Cardiol. 2021, 330, 221–227. [Google Scholar] [CrossRef] [PubMed]



| TG Levels (mg/dL) | Non-HDL-C (mg/dL) | |||||
|---|---|---|---|---|---|---|
| <100 | 100–129 | 130–159 | 160–189 | 190–219 | ≥220 | |
| 7–49 | 8.17 | 6.62 | 5.00 | 4.36 | - | 14.67 |
| 50–56 | 9.00 | 7.00 | 5.58 | 3.50 | - | 3.53 |
| 57–61 | 8.50 | 8.14 | 6.33 | 5.45 | 6.56 | - |
| 62–66 | 8.13 | 7.33 | 7.33 | 5.13 | 4.14 | - |
| 67–71 | 9.57 | 7.67 | 6.18 | 5.65 | 4.38 | 17.00 |
| 72–75 | 9.25 | 8.00 | 7.40 | 7.40 | 7.90 | 18.25 |
| 76–69 | 9.50 | 7.80 | 5.57 | 7.18 | 12.61 | 8.53 |
| 80–83 | 9.22 | 8.20 | 7.55 | 8.15 | 4.78 | 4.21 |
| 84–87 | 8.70 | 8.70 | 7.08 | 5.73 | 4.63 | 8.07 |
| 88–92 | 8.80 | 8.80 | 7.08 | 5.75 | 5.80 | 10.49 |
| 93–96 | 8.73 | 8.64 | 8.00 | 6.00 | 5.00 | 5.00 |
| 97–100 | 9.00 | 8.82 | 8.25 | 6.39 | 5.50 | 28.58 |
| 101–105 | 8.58 | 8.58 | 8.67 | 6.80 | 6.59 | 20.20 |
| 106–110 | 9.00 | 8.38 | 8.46 | 8.04 | 5.43 | 4.98 |
| 111–115 | 8.85 | 8.77 | 8.62 | 7.60 | 6.53 | 5.81 |
| 116–120 | 9.45 | 8.54 | 8.54 | 7.44 | 6.16 | 5.02 |
| 121–126 | 9.38 | 9.00 | 8.23 | 7.41 | 7.24 | 6.78 |
| 127–132 | 8.60 | 9.21 | 8.19 | 7.17 | 6.07 | 5.74 |
| 133–138 | 8.50 | 9.20 | 8.53 | 8.38 | 6.14 | 5.52 |
| 139–146 | 8.75 | 9.00 | 8.59 | 8.24 | 6.64 | 6.67 |
| 147–154 | 9.34 | 9.06 | 8.65 | 8.05 | 6.61 | 8.82 |
| 155–163 | 9.38 | 9.35 | 8.72 | 8.00 | 7.62 | 7.11 |
| 164–173 | 9.56 | 9.36 | 8.45 | 7.59 | 7.64 | 6.59 |
| 174–185 | 8.70 | 9.50 | 8.71 | 7.96 | 6.96 | 6.81 |
| 186–201 | 9.75 | 9.07 | 8.88 | 8.28 | 7.14 | 7.11 |
| 202–220 | 8.87 | 9.32 | 8.90 | 8.23 | 7.77 | 6.79 |
| 221–247 | 8.54 | 9.40 | 8.77 | 8.54 | 8.18 | 7.59 |
| 248–292 | 8.93 | 9.18 | 8.69 | 8.39 | 7.61 | 7.30 |
| 293–399 | 8.59 | 9.11 | 8.68 | 8.11 | 7.65 | 7.15 |
| ≥400 | 9.80 | 9.08 | 8.69 | 7.99 | 7.32 | 6.57 |
| Characteristic | Group | Diabetic Group | |||||
|---|---|---|---|---|---|---|---|
| Non-Diabetic (N = 11,423) | Prediabetic (N = 9362) | Diabetic (N = 10,246) | p | Uncontrolled (N = 7452) | Controlled (N = 2794) | p | |
| Age (years) | 43.57 ± 16.48 a | 56.97 ± 14.19 b | 61.12 ± 12.43 c | <0.001 | 60.78 ± 12.45 | 61.99 ± 12.34 | <0.001 |
| Sex | |||||||
| Female | 7276 (63.7) a | 5583 (59.6) b | 5768 (56.3) c | <0.001 | 4174 (56.0) | 1594 (57.1) | 0.892 |
| Male | 4147 (36.3) a | 3779 (40.4) b | 4478 (43.7) c | 3278 (44.0) | 1200 (42.9) | ||
| Lipid values | |||||||
| TC (mg/dL) | 176.00 (152.00–204.00) a | 186.00 (157.00–215.00) b | 178.00 (149.00–210.00) c | <0.001 | 178.00 (149.00–210.00) | 178.00 (148.00–208.00) | 0.164 |
| TG (mg/dL) | 116.00 (83.00–165.00) a | 139.00 (100.00–193.00) b | 155.00 (111.00–221.00) c | <0.001 | 159.00 (113.00–229.00) | 146.00 (107.00–201.25) | <0.001 |
| HDL-C (mg/dL) | 46.00 (39.00–56.00) a | 44.00 (37.00–52.00) b | 41.00 (34.75–49.00) c | <0.001 | 41.00 (34.00–49.00) | 42.00 (36.00–50.00) | <0.001 |
| Non-HDL-C (mg/dL) | 127.00 (103.00–155.00) a | 140.00 (113.00–169.00) b | 134.00 (107.00–166.00) c | <0.001 | 135.00 (107.00–167.00) | 134.00 (104.00–162.25) | 0.002 |
| TG-TC ratio | 0.66 (0.50–0.93) a | 0.76 (0.58–1.02) b | 0.89 (0.67–1.22) c | <0.001 | 0.92 (0.68–1.25) | 0.85 (0.64–1.12) | <0.001 |
| LDL-C(D) (mg/dL) | 112.00 (90.00–136.00) a | 121.00 (96.00–146.00) b | 113.00 (87.00–139.00) a | <0.001 | 113.00 (88.00–140.00) | 113.00 (86.00–138.00) | 0.467 |
| LDL-C(F) (mg/dL) | 101.00 (79.80–124.40) a | 108.60 (84.60–132.60) b | 99.00 (75.00–124.80) c | <0.001 | 98.60 (74.80–124.60) | 100.20 (75.40–125.25) | 0.306 |
| LDL-C(S) (mg/dL) | 103.79 (82.60–127.19) a | 112.24 (88.37–135.85) b | 103.41 (79.62–128.60) a | <0.001 | 103.07 (79.72–128.49) | 104.20 (79.29–129.06) | 0.717 |
| LDL-C(M) (mg/dL) | 104.13 (82.92–127.55) a | 113.30 (90.07–137.13) b | 105.98 (82.08–131.14) c | <0.001 | 105.85 (82.67–131.37) | 106.23 (80.70–130.52) | 0.385 |
| LDL-C(E) (mg/dL) | 112.00 (90.33–135.68) a | 121.17 (97.62–145.78) b | 113.95 (89.36–139.42) c | <0.001 | 113.58 (89.44–139.25) | 114.01 (87.93–138.58) | 0.612 |
| Non-HDL-C-TG ratio | 2.46 (1.82–3.23) a | 2.24 (1.70–2.92) b | 1.91 (1.43–2.52) c | <0.001 | - | - | - |
| Remnant-C(D) (mg/dL) | 14.00 (8.00–22.00) a | 17.00 (10.00–26.00) b | 19.00 (11.00–29.00) c | <0.001 | - | - | - |
| LDL-C | LDL-C Estimating Equations | |||
|---|---|---|---|---|
| Friedewald | Sampson | Martin–Hopkins | Extended Martin–Hopkins | |
| LDL-C | ||||
| <70 mg/dL | 78.7 | 84.7 | 83.5 | 77.8 |
| ≥70 mg/dL | 89.9 | 93.5 | 95.7 | 98.7 |
| LDL-C | ||||
| <100 mg/dL | 92.5 | 94.4 | 93.6 | 88.3 |
| ≥100 mg/dL | 76.0 | 83.0 | 86.5 | 95.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolat, S.; Ertürk Zararsız, G.; Doğan, K.; Kochan, N.; Yerlitaş, S.I.; Cephe, A.; Zararsız, G.; Cicero, A.F.G. Concordance of LDL-C Estimating Equations with Direct Enzymatic Measurement in Diabetic and Prediabetic Subjects. J. Clin. Med. 2023, 12, 3570. https://doi.org/10.3390/jcm12103570
Bolat S, Ertürk Zararsız G, Doğan K, Kochan N, Yerlitaş SI, Cephe A, Zararsız G, Cicero AFG. Concordance of LDL-C Estimating Equations with Direct Enzymatic Measurement in Diabetic and Prediabetic Subjects. Journal of Clinical Medicine. 2023; 12(10):3570. https://doi.org/10.3390/jcm12103570
Chicago/Turabian StyleBolat, Serkan, Gözde Ertürk Zararsız, Kübra Doğan, Necla Kochan, Serra I. Yerlitaş, Ahu Cephe, Gökmen Zararsız, and Arrigo F. G. Cicero. 2023. "Concordance of LDL-C Estimating Equations with Direct Enzymatic Measurement in Diabetic and Prediabetic Subjects" Journal of Clinical Medicine 12, no. 10: 3570. https://doi.org/10.3390/jcm12103570
APA StyleBolat, S., Ertürk Zararsız, G., Doğan, K., Kochan, N., Yerlitaş, S. I., Cephe, A., Zararsız, G., & Cicero, A. F. G. (2023). Concordance of LDL-C Estimating Equations with Direct Enzymatic Measurement in Diabetic and Prediabetic Subjects. Journal of Clinical Medicine, 12(10), 3570. https://doi.org/10.3390/jcm12103570







