Dynamic Properties of Water Confined in Graphene-Based Membrane: A Classical Molecular Dynamics Simulation Study
Abstract
1. Introduction
2. Computational Details
2.1. Force Field Parameters
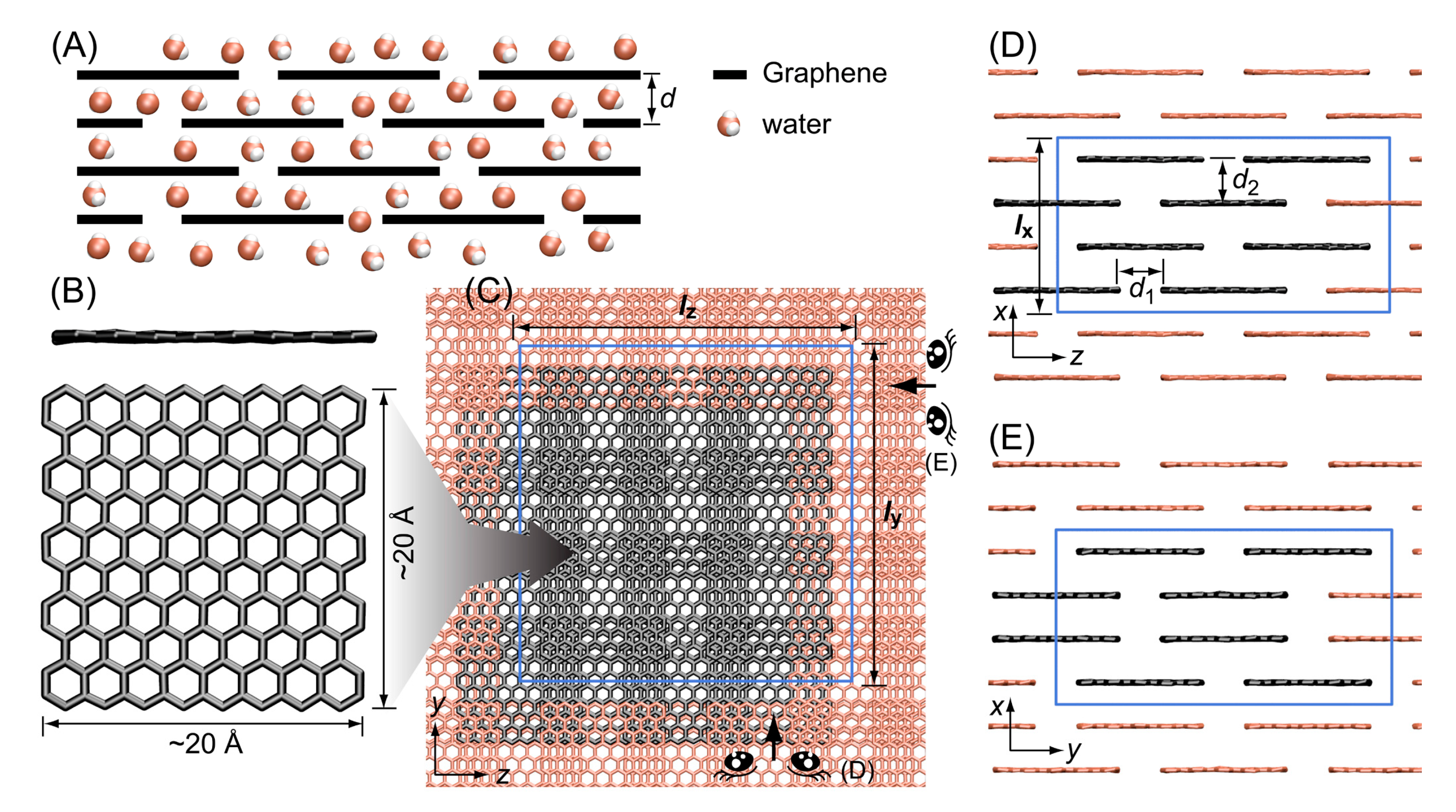
2.2. Molecular Dynamics Simulations
3. Results and Discussion
3.1. Stacked Graphene Membrane
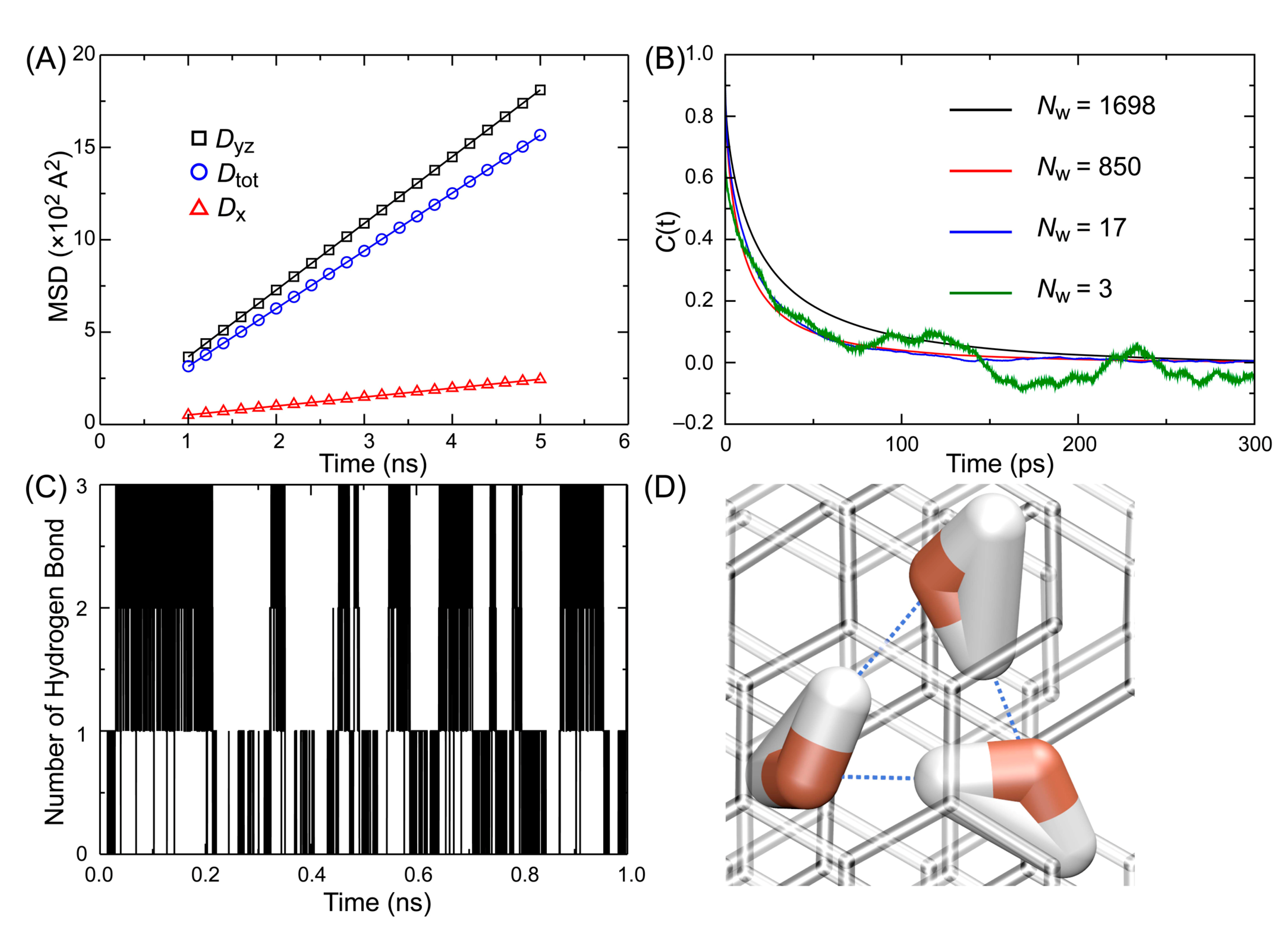
3.2. Diffusion of Water
3.3. Reorientation Correlation Time
3.4. Hydrogen Bond Lifetime
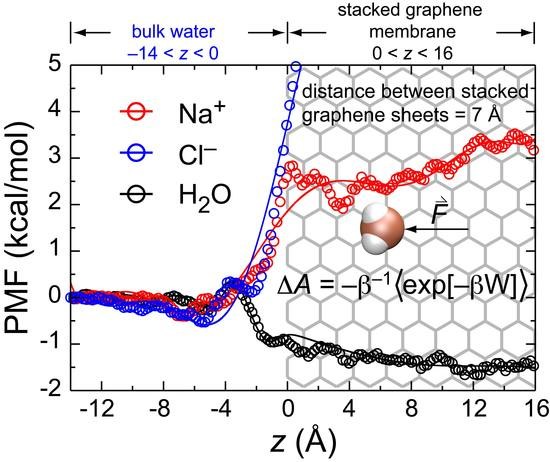
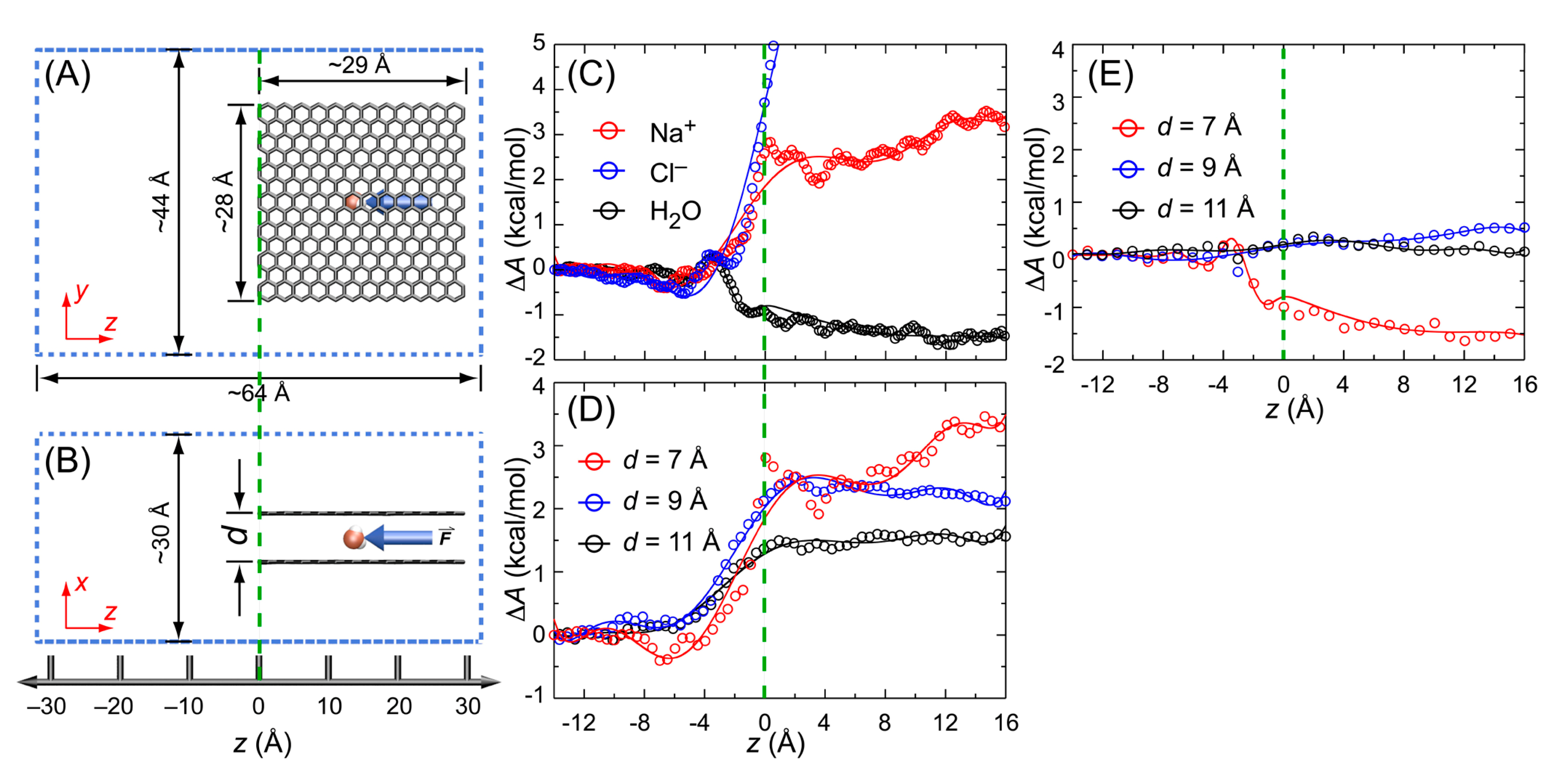
3.5. Potential of Mean Force (PMF)
Funding
Acknowledgments
Conflicts of Interest
References
- Nair, R.R.; Wu, H.A.; Jayaram, P.N.; Grigorieva, I.V.; Geim, A.K. Unimpeded Permeation of Water through Helium-Leak-Tight Graphene-Based Membranes. Science 2012, 335, 442–444. [Google Scholar] [CrossRef] [PubMed]
- Joshi, R.K.; Carbone, P.; Wang, F.C.; Kravets, V.G.; Su, Y.; Grigorieva, I.V.; Wu, H.A.; Geim, A.K.; Nair, R.R. Precise and Ultrafast Molecular Sieving through Graphene Oxide Membranes. Science 2014, 343, 752–754. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.; Vasu, K.S.; Williams, C.D.; Gopinadhan, K.; Su, Y.; Cherian, C.T.; Dix, J.; Prestat, E.; Haigh, S.J.; Grigorieva, I.V.; et al. Tunable Sieving of Ions Using Graphene Oxide Membranes. Nat. Nanotechnol. 2017, 12, 546. [Google Scholar] [CrossRef] [PubMed]
- Cohen-Tanugi, D.; Grossman, J.C. Water Desalination across Nanoporous Graphene. Nano Lett. 2012, 12, 3602–3608. [Google Scholar] [CrossRef]
- Cicero, G.; Grossman, J.C.; Schwegler, E.; Gygi, F.; Galli, G. Water Confined in Nanotubes and between Graphene Sheets: A First Principle Study. J. Am. Chem. Soc. 2008, 130, 1871–1878. [Google Scholar] [CrossRef]
- Boukhvalov, D.W.; Katsnelson, M.I.; Son, Y.W. Origin of Anomalous Water Permeation through Graphene Oxide Membrane. Nano Lett. 2013, 13, 3930–3935. [Google Scholar] [CrossRef]
- Choudhury, N.; Pettitt, B.M. Dynamics of Water Trapped between Hydrophobic Solutes. J. Phys. Chem. B 2005, 109, 6422–6429. [Google Scholar] [CrossRef]
- Cohen-Tanugi, D.; Grossman, J.C. Water Permeability of Nanoporous Graphene at Realistic Pressures for Reverse Osmosis Desalination. J. Chem. Phys. 2014, 141, 074704. [Google Scholar] [CrossRef]
- Cohen-Tanugi, D.; Lin, L.C.; Grossman, J.C. Multilayer Nanoporous Graphene Membranes for Water Desalination. Nano Lett. 2016, 16, 1027–1033. [Google Scholar] [CrossRef]
- Dai, H.W.; Xu, Z.J.; Yang, X.N. Water Permeation and Ion Rejection in Layer-by-Layer Stacked Graphene Oxide Nanochannels: A Molecular Dynamics Simulation. J. Phys. Chem. C 2016, 120, 22585–22596. [Google Scholar] [CrossRef]
- Muscatello, J.; Jaeger, F.; Matar, O.K.; Muller, E.A. Optimizing Water Transport through Graphene-Based Membranes: Insights from Nonequilibrium Molecular Dynamics. ACS Appl. Mater. Interfaces 2016, 8, 12330–12336. [Google Scholar] [CrossRef] [PubMed]
- Sint, K.; Wang, B.; Kral, P. Selective Ion Passage through Functionalized Graphene Nanopores. J. Am. Chem. Soc. 2008, 130, 16448–16449. [Google Scholar] [CrossRef] [PubMed]
- Willcox, J.A.L.; Kim, H.J. Molecular Dynamics Study of Water Flow across Multiple Layers of Pristine, Oxidized, and Mixed Regions of Graphene Oxide: Effect of Graphene Oxide Layer-to-Layer Distance. J. Phys. Chem. C 2017, 121, 23659–23668. [Google Scholar] [CrossRef]
- Willcox, J.K.L.; Kim, H.J. Molecular Dynamics Study of Water Flow across Multiple Layers of Pristine, Oxidized, and Mixed Regions of Graphene Oxide. ACS Nano 2017, 11, 2187–2193. [Google Scholar] [CrossRef]
- Haile, J.M. Molecular Dynamics Simulations: Elementary Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1992. [Google Scholar]
- Hwang, S.; Lee, O.S.; Chung, D.S. Free Energy Perturbation Studies on Enantiomeric Discrimination of Pyridino-18-Crown-6 Ethers. Chem. Lett. 2000, 29, 1002–1003. [Google Scholar] [CrossRef]
- Lee, K.H.; Lee, D.H.; Hwang, S.; Lee, O.S.; Chung, D.S.; Hong, J.I. Bowl-Shaped C-3-Symmetric Receptor with Concave Phosphine Oxide with a Remarkable Selectivity for Asparagine Derivatives. Org. Lett. 2003, 5, 1431–1433. [Google Scholar] [CrossRef]
- Lee, O.S.; Hwang, S.; Chung, D.S. Free Energy Perturbation and Molecular Dynamics Simulation Studies on the Enantiomeric Discrimination of Amines by Dimethyldiketopyridino-18-Crown-6. Supramol. Chem. 2000, 12, 255–272. [Google Scholar] [CrossRef]
- Lee, O.S.; Hwang, S.; Chung, D.S. Comparison of Computational Methods for Enthalpic and Entropic Contributions in the Enantiomeric Discrimination by Dimethyldiketopyridino-18-Crown-6 Ether. Chem. Lett. 2002, 31, 942–943. [Google Scholar] [CrossRef]
- Lee, O.S.; Jang, Y.H.; Cho, Y.G.; Hyun, M.H.; Kim, H.J.; Chung, D.S. Theoretical and Experimental Studies of Chiral Recognition in Charged Pirkle Phases. Chem. Lett. 2001, 30, 232–233. [Google Scholar] [CrossRef]
- Mark, P.; Nilsson, L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. [Google Scholar] [CrossRef]
- Vega, C.; de Miguel, E. Surface Tension of the Most Popular Models of Water by Using the Test-Area Simulation Method. J. Chem. Phys. 2007, 126, 154707. [Google Scholar] [CrossRef] [PubMed]
- Pi, H.L.; Aragones, J.L.; Vega, C.; Noya, E.G.; Abascal, J.L.F.; Gonzalez, M.A.; McBride, C. Anomalies in Water as Obtained from Computer Simulations of the TIP4P/2005 Model: Density Maxima, and Density, Isothermal Compressibility and Heat Capacity Minima. Mol. Phys. 2009, 107, 365–374. [Google Scholar] [CrossRef]
- Aragones, J.L.; MacDowell, L.G.; Vega, C. Dielectric Constant of Ices and Water: A Lesson About Water Interactions. J. Phys. Chem. A 2011, 115, 5745–5758. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Gygi, F.; Galli, G. Strongly Anisotropic Dielectric Relaxation of Water at the Nanoscale. J. Phys. Chem. Lett. 2013, 4, 2477–2481. [Google Scholar] [CrossRef]
- Wu, Y.B.; Aluru, N.R. Graphitic Carbon-Water Nonbonded Interaction Parameters. J. Phys. Chem. B 2013, 117, 8802–8813. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.H.; Pastor, R.W.; Brooks, B.R. Constant-Pressure Molecular-Dynamics Simulation—the Langevin Piston Method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant-Pressure Molecular-Dynamics Algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N·Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Andersen, H.C. Rattle: A Velocity Version of the Shake Algorithm for Molecular-Dynamics Calculations. J. Comput. Phys. 1983, 52, 24–34. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Marti, J.; Calero, C.; Franzese, G. Structure and Dynamics of Water at Carbon-Based Interfaces. Entropy 2017, 19, 135. [Google Scholar] [CrossRef]
- Einstein, A. Über Die Von Der Molekularkinetischen Theorie Der Wärme Geforderte Bewegung Von in Ruhenden Flüssigkeiten Suspendierten Teilchen. Ann. Phys. 1905, 322, 549. [Google Scholar] [CrossRef]
- Bampoulis, P.; Sotthewes, K.; Dollekamp, E.; Poelsema, B. Water Confined in Two-Dimensions: Fundamentals and Applications. Surf. Sci. Rep. 2018, 73, 233–264. [Google Scholar] [CrossRef]
- Zangi, R. Water Confined to a Slab Geometry: A Review of Recent Computer Simulation Studies. J. Phys. Condens. Matter 2004, 16, S5371–S5388. [Google Scholar] [CrossRef]
- Striolo, A. The Mechanism of Water Diffusion in Narrow Carbon Nanotubes. Nano Lett. 2006, 6, 633–639. [Google Scholar] [CrossRef]
- Fumagalli, L.; Esfandiar, A.; Fabregas, R.; Hu, S.; Ares, P.; Janardanan, A.; Yang, Q.; Radha, B.; Taniguchi, T.; Watanabe, K.; et al. Anomalously Low Dielectric Constant of Confined Water. Science 2018, 360, 1339–1342. [Google Scholar] [CrossRef]
- Marti, J.; Sala, J.; Guardia, E. Molecular Dynamics Simulations of Water Confined in Graphene Nanochannels: From Ambient to Supercritical Environments. J. Mol. Liq. 2010, 153, 72–78. [Google Scholar] [CrossRef]
- Sansom, M.S.P.; Kerr, I.D.; Breed, J.; Sankararamakrishnan, R. Water in Channel-Like Cavities: Structure and Dynamics. Biophys. J. 1996, 70, 693–702. [Google Scholar] [CrossRef]
- Halle, B.; Wennerstrom, H. Interpretation of Magnetic-Resonance Data from Water Nuclei in Heterogeneous Systems. J. Chem. Phys. 1981, 75, 1928–1943. [Google Scholar] [CrossRef]
- Krynicki, K. Proton Spin-Lattice Relaxation in Pure Water between Zero Degress C and 100 Degress C. Physica 1966, 32, 167–178. [Google Scholar] [CrossRef]
- Ludwig, R. NMR Relaxation Studies in Water-Alcohol Mixtures–the Water-Rich Region. Chem. Phys. 1995, 195, 329–337. [Google Scholar] [CrossRef]
- Struis, R.; de Bleijser, J.; Leyte, J.C. Dynamic Behavior and Some of the Molecular-Properties of Water-Molecules in Pure Water and in MgCl2 Solutions. J. Phys. Chem. 1987, 91, 1639–1645. [Google Scholar] [CrossRef]
- van der Maarel, J.R.C.; Lankhorst, D.; de Bleijser, J.; Leyte, J.C. On the Single-Molecule Dynamics of Water from Proton, Deuterium and O-17 Nuclear Magnetic-Relaxation. Chem. Phys. Lett. 1985, 122, 541–544. [Google Scholar] [CrossRef]
- Luzar, A. Resolving the Hydrogen Bond Dynamics Conundrum. J. Chem. Phys. 2000, 113, 10663–10675. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Structure and Hydrogen-Bond Dynamics of Water-Dimethyl Sulfoxide Mixtures by Computer-Simulations. J. Chem. Phys. 1993, 98, 8160–8173. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Hydrogen-Bond Kinetics in Liquid Water. Nature 1996, 379, 55–57. [Google Scholar] [CrossRef]
- Kumar, R.; Schmidt, J.R.; Skinner, J.L. Hydrogen Bonding Definitions and Dynamics in Liquid Water. J. Chem. Phys. 2007, 126, 05B611. [Google Scholar] [CrossRef]
- Conde, O.; Teixeira, J. Depolarized Light-Scattering of Heavy-Water, and Hydrogen-Bond Dynamics. Mol. Phys. 1984, 53, 951–959. [Google Scholar] [CrossRef]
- Teixeira, J.; Bellissentfunel, M.C.; Chen, S.H. Dynamics of Water Studied by Neutron-Scattering. J. Phys. Condes. Matter 1990, 2, SA105–SA108. [Google Scholar] [CrossRef]
- Antipova, M.L.; Petrenko, V.E. Hydrogen Bond Lifetime for Water in Classic and Quantum Molecular Dynamics. Russ. J. Phys. Chem. A 2013, 87, 1170–1174. [Google Scholar] [CrossRef]
- Voloshin, V.P.; Naberukhin, Y.I. Hydrogen Bond Lifetime Distributions in Computer-Simulated Water. J. Struct. Chem. 2009, 50, 78–89. [Google Scholar] [CrossRef]
- Hess, B.; Holm, C.; van der Vegt, N. Osmotic Coefficients of Atomistic Nacl (Aq) Force Fields. J. Chem. Phys. 2006, 124, 164509. [Google Scholar] [CrossRef] [PubMed]
- Weerasinghe, S.; Smith, P.E. A Kirkwood-Buff Derived Force Field for Sodium Chloride in Water. J. Chem. Phys. 2003, 119, 11342–11349. [Google Scholar] [CrossRef]
- Lee, O.S.; Carignano, M.A. Exfoliation of Electrolyte-Intercalated Graphene: Molecular Dynamics Simulation Study. J. Phys. Chem. C 2015, 119, 19415–19422. [Google Scholar] [CrossRef]
| Number of Water Molecules (Nw) | 1698 | 850 | 17 | 3 | ∞ * | ∞ ** |
|---|---|---|---|---|---|---|
| Dtot (×10−5 cm2/sec) | 0.60 | 1.19 | 1.20 | 5.44 | 2.39 | 2.3 |
| Dyz (×10−5 cm2/sec) | 0.78 | 1.77 | 1.82 | 5.41 | - | - |
| Dx (×10−5 cm2/sec) | 0.24 | 0.01 | 0.05 | 4.37 | - | - |
| Density of water (H2O/Å3) | 0.037 | 0.019 | 3.7 × 10−4 | 6.6 × 10−7 | 0.033 | 0.033 |
| d (Å) | 7 | ∞ * | ∞ ** |
|---|---|---|---|
| 6.66 | 4.28 | - | |
| 13.86 | 4.71 | 4.76 [40] | |
| 5.44 | 2.88 | - | |
| 8.94 | 4.45 | - | |
| 12.95 | 2.01 | 2.0 [41] | |
| 22.84 | 1.57 | 1.92 [40,42] | |
| 53.28 | 1.17 | - | |
| 15.12 | 1.81 | 1.95 [43,44,45] |
| Number of Water Molecules (Nw) | 1698 | 850 | 17 | 3 | Bulk Water * | Bulk Water |
|---|---|---|---|---|---|---|
| τHB (ps) | 11.0 | 15.0 | 18.6 | 31.7 | 3.2 | ~1.0 ** [50,51] 3–10 *** [52,53] |
| Density of water (H2O/Å3) | 0.037 | 0.019 | 3.7 × 10−4 | 6.6 × 10−7 | 0.033 | 0.033 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, O.-S. Dynamic Properties of Water Confined in Graphene-Based Membrane: A Classical Molecular Dynamics Simulation Study. Membranes 2019, 9, 165. https://doi.org/10.3390/membranes9120165
Lee O-S. Dynamic Properties of Water Confined in Graphene-Based Membrane: A Classical Molecular Dynamics Simulation Study. Membranes. 2019; 9(12):165. https://doi.org/10.3390/membranes9120165
Chicago/Turabian StyleLee, One-Sun. 2019. "Dynamic Properties of Water Confined in Graphene-Based Membrane: A Classical Molecular Dynamics Simulation Study" Membranes 9, no. 12: 165. https://doi.org/10.3390/membranes9120165
APA StyleLee, O.-S. (2019). Dynamic Properties of Water Confined in Graphene-Based Membrane: A Classical Molecular Dynamics Simulation Study. Membranes, 9(12), 165. https://doi.org/10.3390/membranes9120165