Molecular Dynamics Simulation Study of Solid Vibration Permeation in Microporous Amorphous Silica Network Voids
Abstract
1. Introduction
2. Simulation Method
2.1. Modeling of Thermally Vibrated Amorphous SiO2 Membranes
2.2. Non-Equilibrium Gas Permetion Molecular Dynamics Simulation
3. Results and Discussion
3.1. Verification of Silica Models
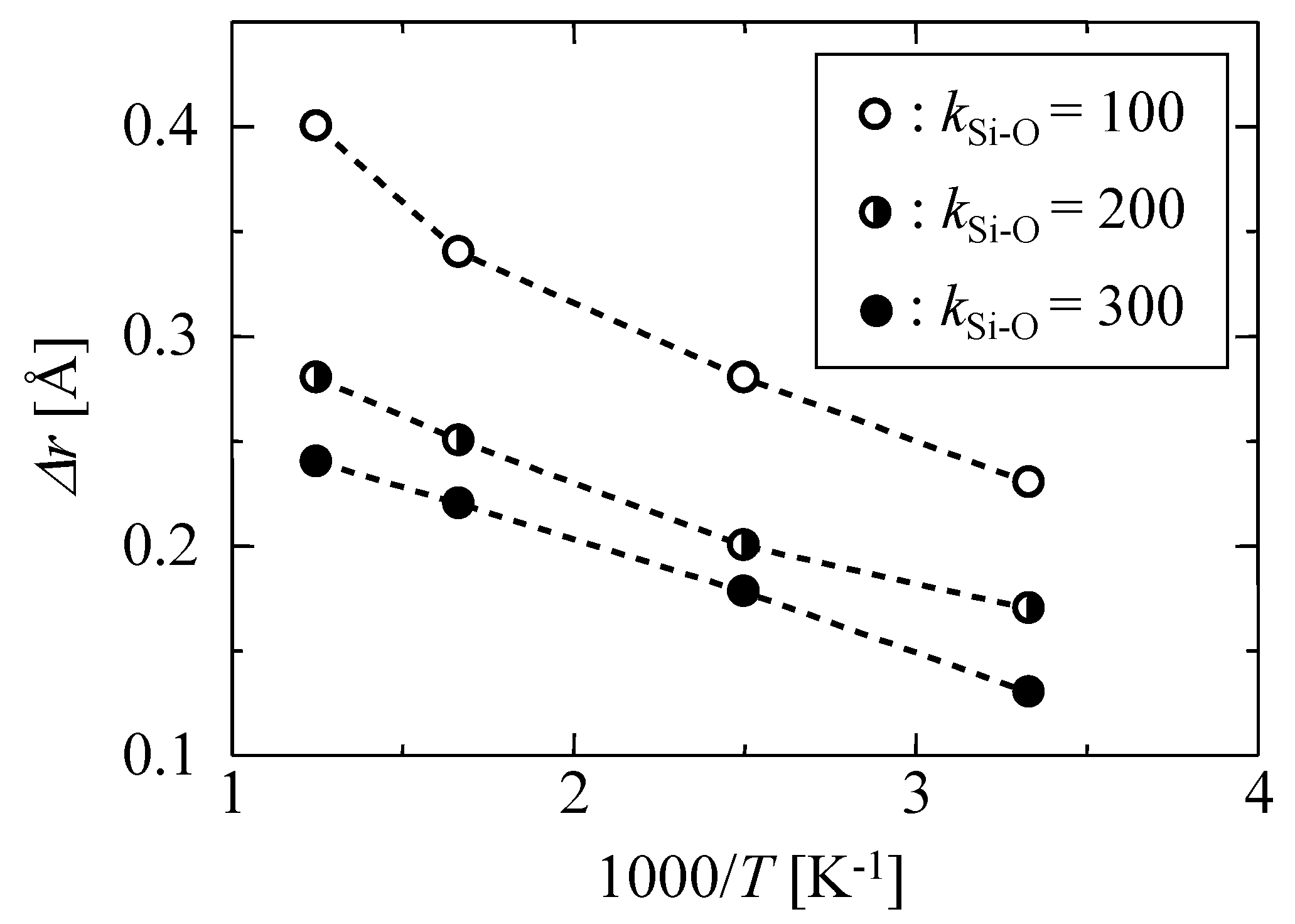
3.1.1. Harmonic Oscillation Properties
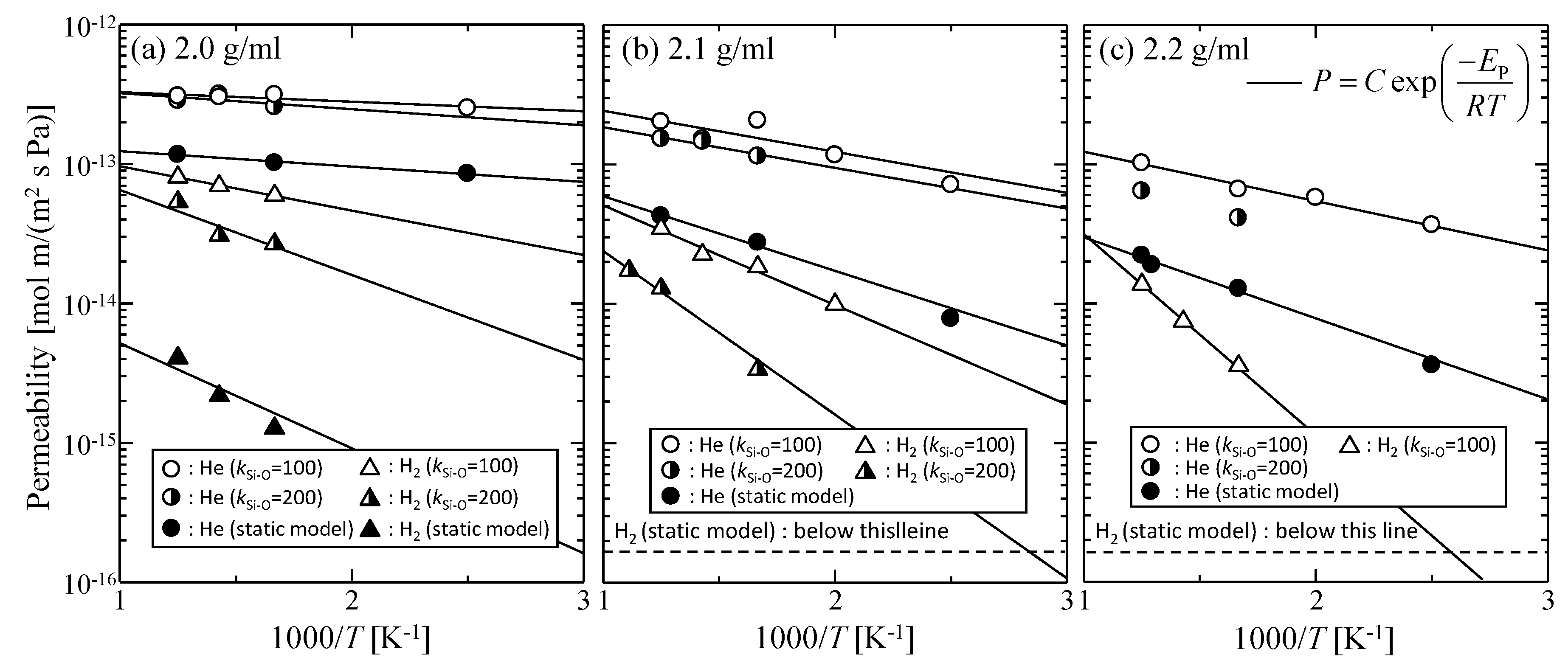
3.1.2. Effect of the Thermal Motion of Membrane Oxygen Atoms on Gas Permeation Properties
3.1.3. Validation of the Silica Membrane Model
3.2. Gas Diffusion and Permeation Models
3.3. Gas Diffusion and Permeation Characteristics for Silica Membranes
3.3.1. Characterization of a Silica Membrane Structure
3.3.2. Gas Diffusivity in a Silica Membrane Model
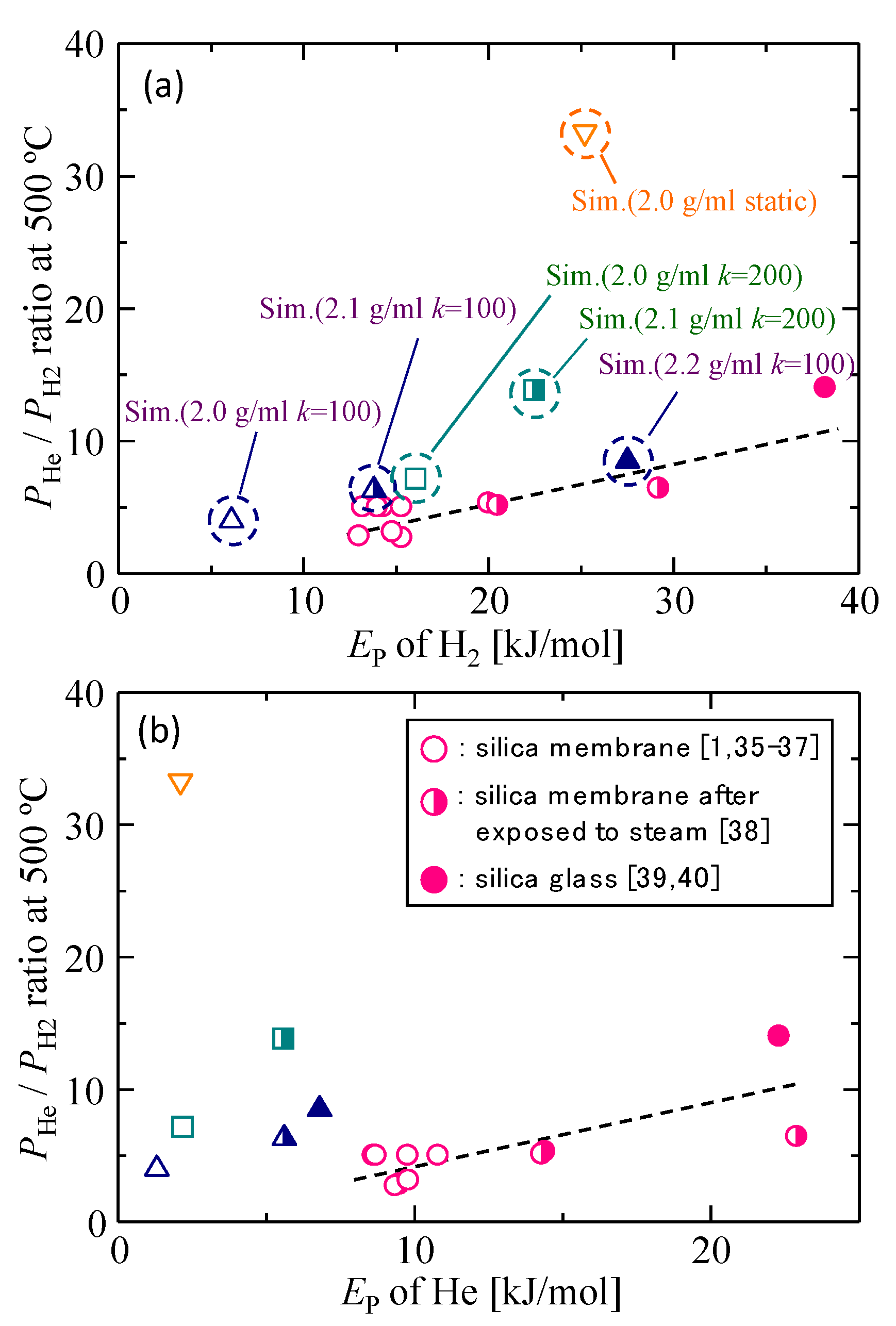
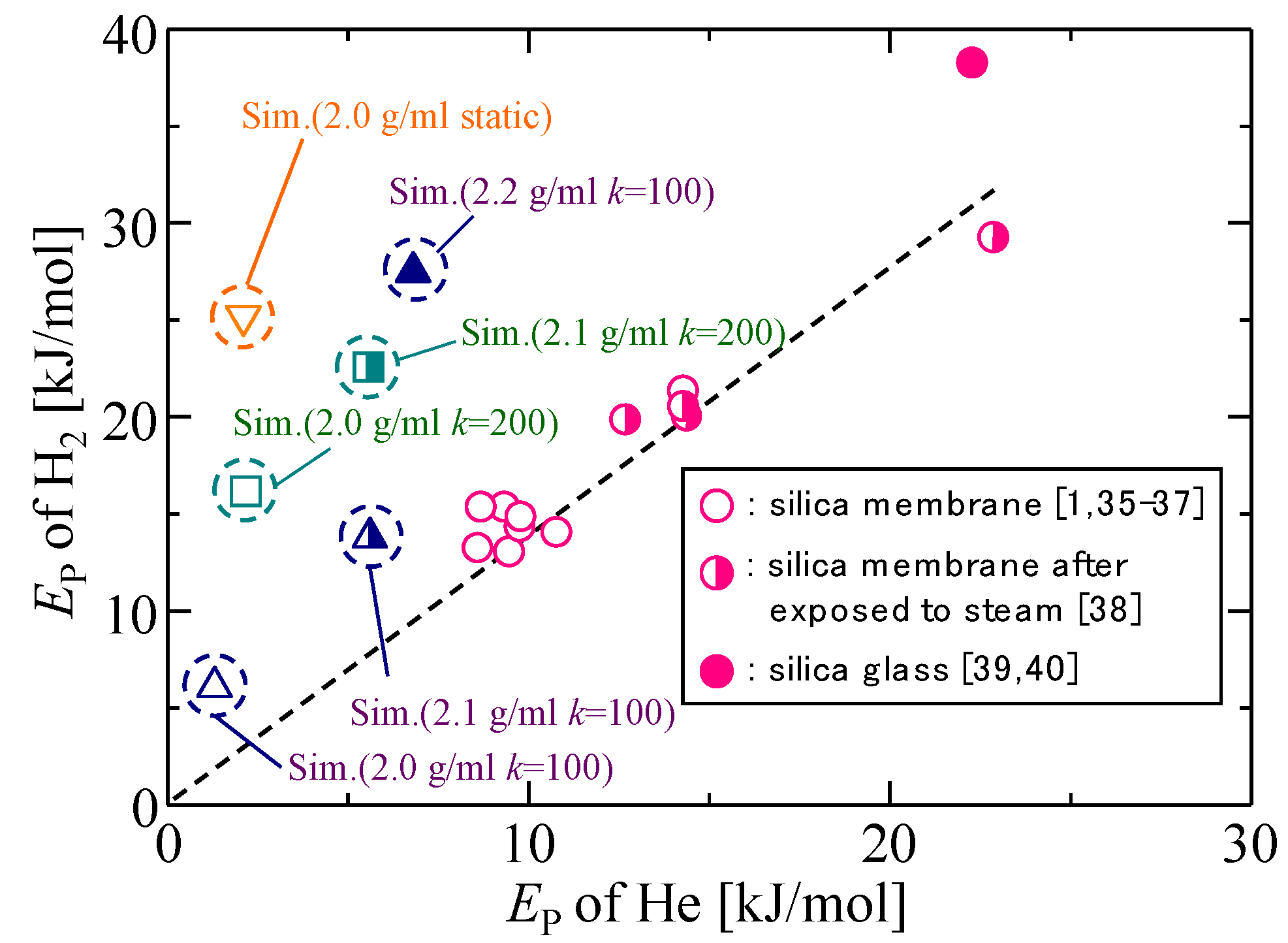
3.4. Gas Diffusion and Permeation Characteristics
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kanezashi, M.; Asaeda, M. Hydrogen permeation characteristics and stability of Ni-doped silica membranes in steam at high temperature. J. Membr. Sci. 2006, 271, 86–93. [Google Scholar] [CrossRef]
- Kanezashi, M.; Yada, K.; Yoshioka, T.; Tsuru, T. Design of silica networks for development of highly permeable hydrogen separation membranes with hydrothermal stability. J. Am. Chem. Soc. 2009, 131, 414–415. [Google Scholar] [CrossRef] [PubMed]
- Kanezashi, M.; Yada, K.; Yoshioka, T.; Tsuru, T. Organic–inorganic hybrid silica membranes with controlled silica network size: Preparation and gas permeation characteristics. J. Membr. Sci. 2010, 348, 310–318. [Google Scholar] [CrossRef]
- Benfer, S.; Arki, P.; Tomandl, G. Ceramic membranes for filtration applications—Preparation and characterization. Adv. Eng. Mater. 2004, 6, 495–500. [Google Scholar] [CrossRef]
- Nwogu, N.C.; Kajama, M.; Gobina, E. A study of gas diffusion characteristics on a micro porous composite silica ceramic membrane. Compos. Struct. 2015, 134, 1044–1050. [Google Scholar] [CrossRef]
- De Lange, R.S.A.; Keizer, K.; Burggraaf, A.J. Aging and stability of microporous sol-gel-modified ceramic membranes. Ind. Eng. Chem. Res. 1995, 34, 3838–3847. [Google Scholar] [CrossRef]
- Shelekhin, A.B.; Dixon, A.G.; Ma, Y.H. Theory of gas diffusion and permeation in inorganic molecular-sieve membranes. AIChE J. 1995, 41, 58–67. [Google Scholar] [CrossRef]
- Burggraaf, A.J. Single gas permeation of thin zeolite (MFI) membranes: Theory and analysis of experimental observations. J. Membr. Sci. 1999, 155, 45–65. [Google Scholar] [CrossRef]
- Yoshioka, T.; Nakanishi, E.; Tsuru, T.; Asaeda, M. Experimental study of gas permeation through microporous silica membranes. AIChE J. 2001, 47, 2052–2063. [Google Scholar] [CrossRef]
- Lee, H.R.; Kanezashi, M.; Shimomura, Y.; Yoshioka, T.; Tsuru, T. Evaluation and fabrication of pore-size-tuned silica membranes with tetraethoxydimethyl disiloxane for gas separation. AIChE J. 2011, 57, 2755–2765. [Google Scholar] [CrossRef]
- Yoshioka, T.; Kanezashi, M.; Tsuru, T. Micropore size estimation on gas separation membranes: A study in experimental and molecular dynamics. AIChE J. 2013, 59, 2179–2194. [Google Scholar] [CrossRef]
- Li, G.; Lee, H.R.; Nagasawa, H.; Kanezashi, M.; Yoshioka, T.; Tsuru, T. Pore-size evaluation and gas transport behaviors of microporous membranes: An experimental and theoretical study. AIChE J. 2015, 61, 2268–2279. [Google Scholar] [CrossRef]
- Wang, X.; Chi, C.; Zhang, K.; Qian, Y.; Gupta, K.M.; Kang, Z.; Jiang, J.; Zhao, D. Reversed thermo-switchable molecular sieving membranes composed of two-dimensional metal-organic nanosheets for gas separation. Nat. Commun. 2017, 8, 14460. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Kanezashi, M.; Nagasawa, H.; Ohshita, J.; Naka, A.; Tsuru, T. Fabrication and microstructure tuning of a pyrimidine-bridged organoalkoxysilane membrane for CO2 separation. Ind. Eng. Chem. Res. 2017, 56, 1316–1326. [Google Scholar] [CrossRef]
- Yoshioka, T.; Tsuru, T.; Asaeda, M. Molecular dynamics study of gas permeation through amorphous silica network and inter-particle pores on microporous silica membranes. Mol. Phys. 2004, 102, 191–202. [Google Scholar] [CrossRef]
- Yoshioka, T.; Yasumoto, A.; Kishi, K.; Tsuru, T.; Asaeda, M. MD simulation studies for effect of membrane structures and dynamics on gas permeation properties through microporous amorphous silica membranes. Desalination 2008, 233, 333–341. [Google Scholar] [CrossRef]
- Chang, K.; Yoshioka, T.; Kanezashi, M.; Tsuru, T.; Tung, K. A molecular dynamics simulation of a homogeneous organic–inorganic hybrid silica membrane. Chem. Commun. 2010, 46, 9140–9142. [Google Scholar] [CrossRef]
- Chang, K.; Yoshioka, T.; Kanezashi, M.; Tsuru, T.; Tung, K. Molecular simulation of micro-structures and gas diffusion behavior of organic–inorganic hybrid amorphous silica membranes. J. Membr. Sci. 2011, 381, 90–101. [Google Scholar] [CrossRef]
- Hacarlioglu, P.; Lee, D.; Gibbs, G.V.; Oyama, S.T. Activation energies for permeation of He and H2 through silica membranes: An ab initio calculation study. J. Membr. Sci. 2008, 313, 277–283. [Google Scholar] [CrossRef]
- Oyama, S.T.; Lee, D.; Hacarlioglu, P.; Saraf, R.F. Theory of hydrogen permeability in nonporous silica membranes. J. Membr. Sci. 2004, 244, 45–53. [Google Scholar] [CrossRef]
- Masaryk, J.S.; Fulrath, R.M. Diffusivity of helium in fused silica. J. Chem. Phys. 1973, 59, 1198–1202. [Google Scholar] [CrossRef]
- Xiao, J.; Wei, J. Diffusion mechanism of hydrocarbons in zeolites—I. Theory. Chem. Eng. Sci. 1992, 47, 1123–1141. [Google Scholar] [CrossRef]
- Feuston, B.P.; Garofalini, S.H. Empirical three-body potential for vitreous silica. J. Chem. Phys. 1988, 89, 5818–5824. [Google Scholar] [CrossRef]
- Yoshioka, T.; Asaeda, M.; Tsuru, T. A molecular dynamics simulation of pressure-driven gas permeation in a micropore potential field on silica membranes. J. Membr. Sci. 2007, 293, 81–93. [Google Scholar] [CrossRef]
- Pohl, P.I.; Heffelfinger, G.S. Massively parallel molecular dynamics simulation of gas permeation across porous silica membranes. J. Membr. Sci. 1999, 155, 1–7. [Google Scholar] [CrossRef]
- Valle, R.G.D.; Venuti, E. A molecular dynamics study of the vibrational properties of silica glass. Chem. Phys. 1994, 179, 411–419. [Google Scholar] [CrossRef]
- Bertoluzza, A. Raman and infrared spectra on silica gel evolving toward glass. J. Non-Cryst. Solid 1982, 48, 117–128. [Google Scholar] [CrossRef]
- Xu, L.; Sedigh, M.G.; Tsotsis, T.T.; Sahimi, M. Nonequilibrium molecular dynamics simulation of transport and separation of gases in carbon nanopores. II. Binary and ternary mixtures and comparison with the experimental data. J. Chem. Phys. 2000, 112, 910–922. [Google Scholar] [CrossRef]
- Brodka, A.; Zerda, T.W. Molecular dynamics of SF6 in porous silica. J. Chem. Phys. 1991, 95, 3710–3718. [Google Scholar] [CrossRef]
- Hofmann, D.; Fritz, L.; Ulbrich, J.; Paul, D. Molecular simulation of small molecule diffusion and solution in dense amorphous polysiloxanes and polyimides. Comput. Theor. Polym. Sci. 2000, 10, 419–436. [Google Scholar] [CrossRef]
- Benoit, M.; Ispas, S.; Jund, P.; Jullien, R. Model of silica glass from combined classical and ab initio molecular-dynamics simulations. Eur. Phys. J. B 2000, 13, 631–636. [Google Scholar] [CrossRef]
- Guillot, B.; Guissani, Y. Boson peak and high frequency modes in amorphous silica. Phys. Rev. Lett. 1997, 78, 2401–2404. [Google Scholar] [CrossRef]
- Girifalco, L.A. Statistical Physics of Materials; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 5th ed.; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Araki, S.; Mohri, N.; Yoshimitsu, Y.; Miyake, Y. Synthesis, characterization and gas permeation properties of a silica membrane prepared by high-pressure chemical vapor deposition. J. Membr. Sci. 2007, 290, 138–145. [Google Scholar] [CrossRef]
- Hwang, G.; Onuki, K.; Shimizu, S.; Ohya, H. Hydrogen separation in H2-H2O-HI gaseous mixture using the silica membrane prepared by chemical vapor deposition. J. Membr. Sci. 1999, 162, 83–90. [Google Scholar] [CrossRef]
- Lee, D.; Oyama, S.T. Gas permeation characteristics of a hydrogen selective supported silica membrane. J. Membr. Sci. 2002, 210, 291–306. [Google Scholar] [CrossRef]
- Kanezashi, M.; Asaeda, M. Stability of H2-permeselective Ni-doped silica membranes in steam at high temperature. J. Chem. Eng. Jpn. 2005, 38, 908–912. [Google Scholar] [CrossRef]
- Shelby, J.E. Pressure dependence of helium and neon solubility in vitreous silica. J. Appl. Phys. 1976, 47, 135–139. [Google Scholar] [CrossRef]
- Lee, R.W.; Frank, R.C.; Swets, D.E. Diffusion of hydrogen and deuterium in fused quartz. J. Chem. Phys. 1962, 36, 1062–1071. [Google Scholar] [CrossRef]
- Miller, C.C. The Stokes-Einstein law for diffusion in solution. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1924, 106, 724–749. [Google Scholar] [CrossRef]
- Shelekhin, A.B.; Dixon, A.G.; Ma, Y.H. Adsorption, diffusion and permeation of gases in microporous membranes. III. Application of percolation theory to interpretation of porosity, tortuosity, and surface area in microporous glass membranes. J. Membr. Sci. 1993, 83, 181–198. [Google Scholar] [CrossRef]

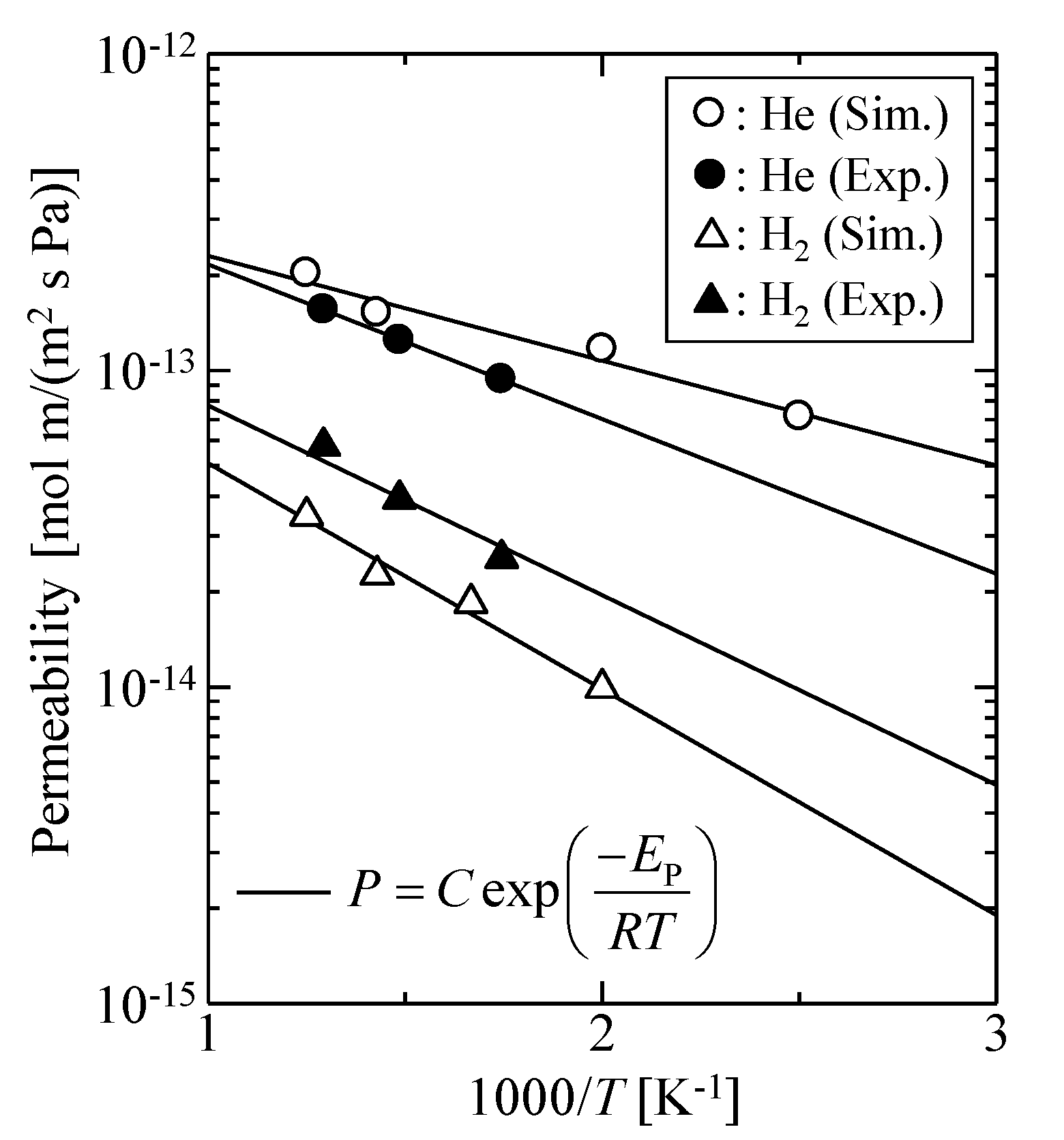
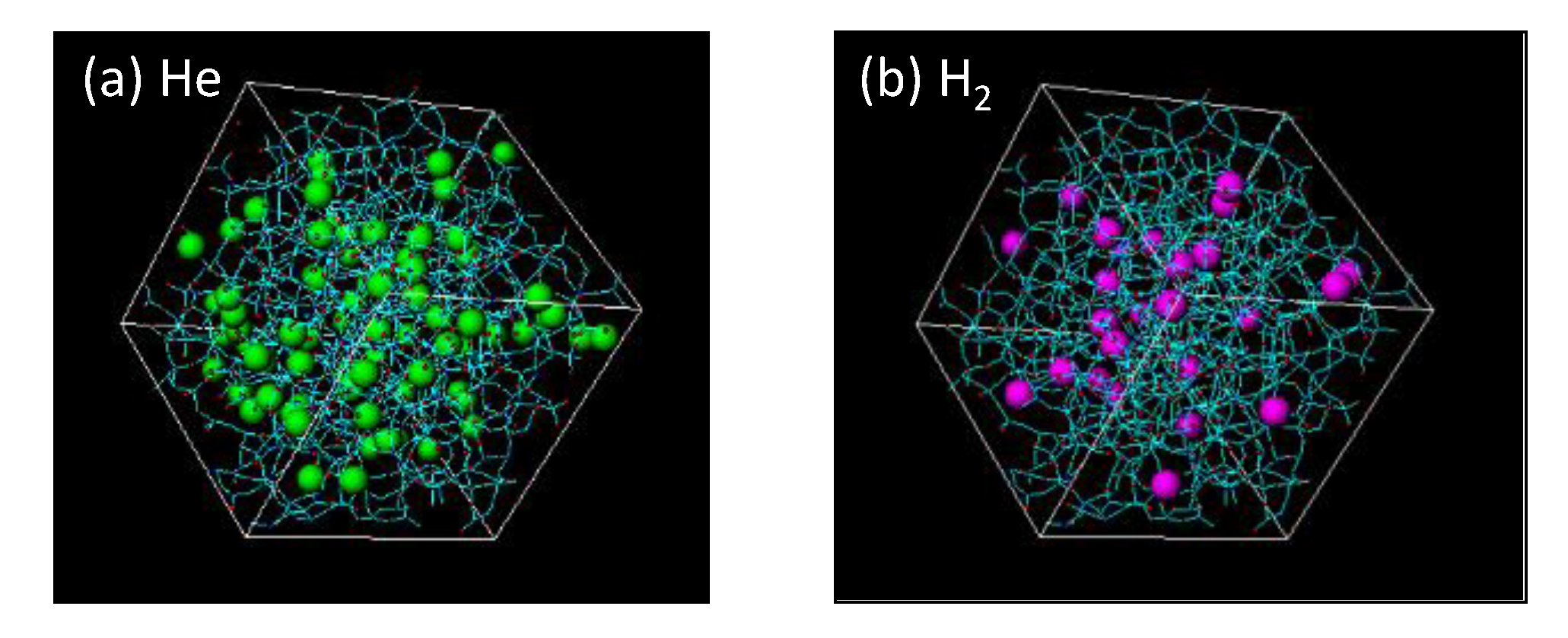
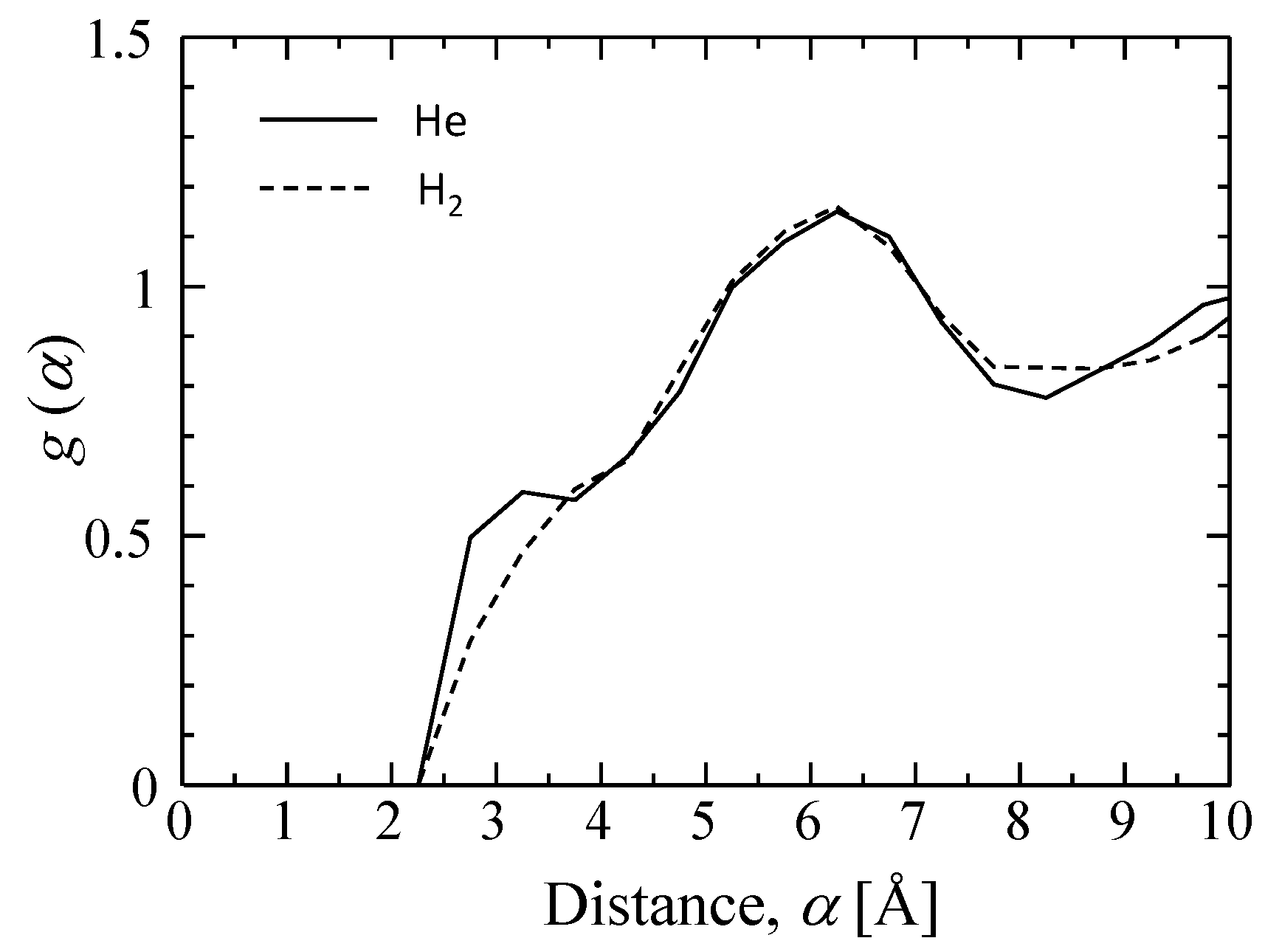


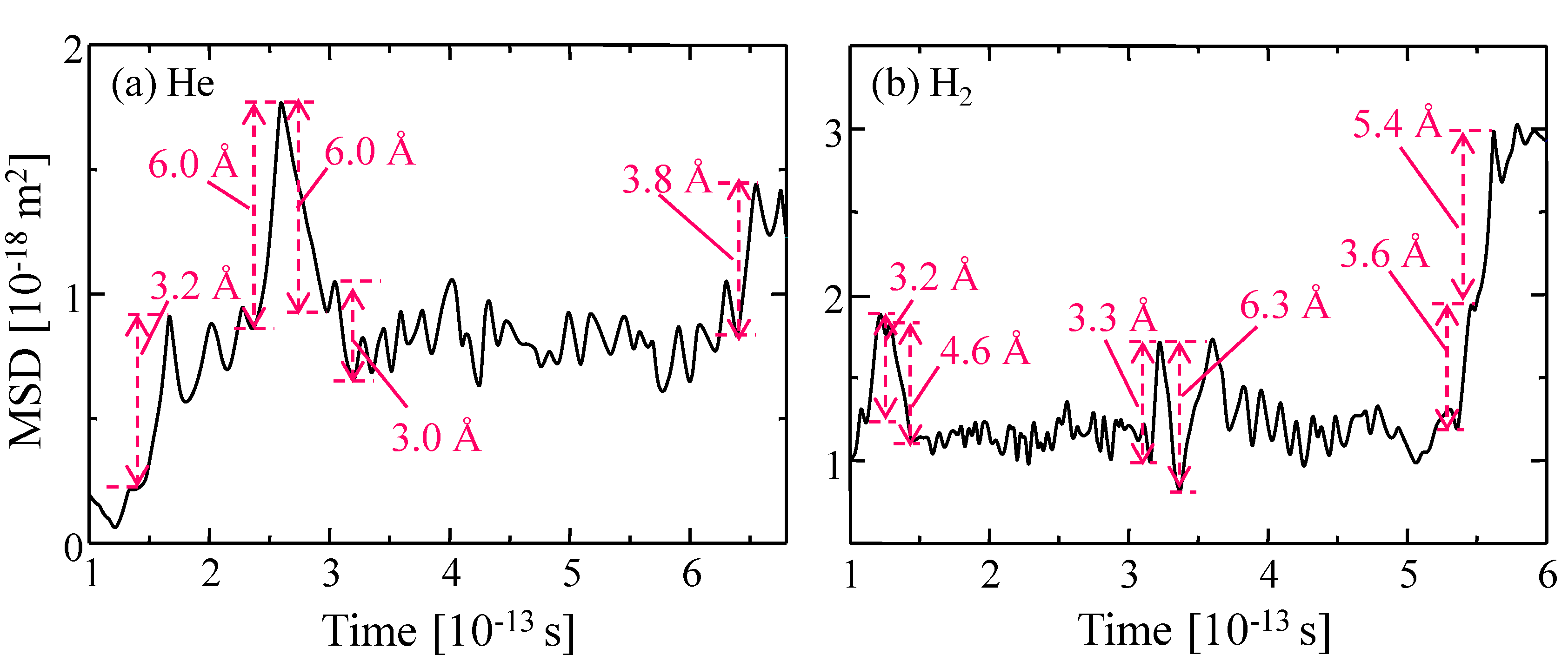
| - | [nm] | |
|---|---|---|
| Helium [7] | 10.22 | 0.26 |
| Hydrogen [28] | 38.00 | 0.289 |
| Oxygen in SiO2 [29] | 230 | 0.27 |
| (a) This Work | |
|---|---|
| kSi–O [J m−3] | Δr [Å] |
| 100 | 0.23 |
| 200 | 0.17 |
| 300 | 0.15 |
| (b) Reference | |
| Material | Δr [Å] |
| Polyimide [30] | 1.0 |
| Silica glass [31] | 0.28 |
| Silica glass [32] | 0.20 |
| T [K] | PHe/PH2 | Knudsen (MH2/MHe)0.5 | ||||||
|---|---|---|---|---|---|---|---|---|
| Density | 2.2 g/mL | 2.1 g/mL | 2.1 g/mL | 2.0 g/mL | 2.0 g/mL | 2.0 g/mL | ||
| kSi–O | 100 | 100 | 100 | 200 | 100 | (Static) | ||
| 800 | - | 7.4 | 11.8 | 5.8 | 5.3 | 3.8 | 28.8 | 0.71 |
| 700 | - | - | - | 6.7 | 10.3 | 4.3 | 46.7 | |
| 600 | - | 18.6 | 33.8 | 11.8 | 9.6 | 5.3 | 67.0 | |
| - | EP [kJ mol−1] | |||
|---|---|---|---|---|
| kSi–O = 200 [J m−3] | kSi–O = 100 [J m−3] | Static Model | ||
| 2.2 g/mL | He | - | 6.8 | 11.1 |
| H2 | - | 27.6 | - | |
| 2.1 g/mL | He | 5.6 | 5.6 | 10.2 |
| H2 | 22.5 | 13.7 | - | |
| 2.0 g/mL | He | 2.2 | 1.3 | 2.1 |
| H2 | 16.1 | 6.1 | 25.2 | |
| - | Volume [nm3] | ε [-] |
|---|---|---|
| Whole unit cell | 19.1 | - |
| Total voids | 11.2 | 0.59 |
| Voids greater than He | 3.3 | 0.17 |
| Voids greater than H2 | 2.5 | 0.13 |
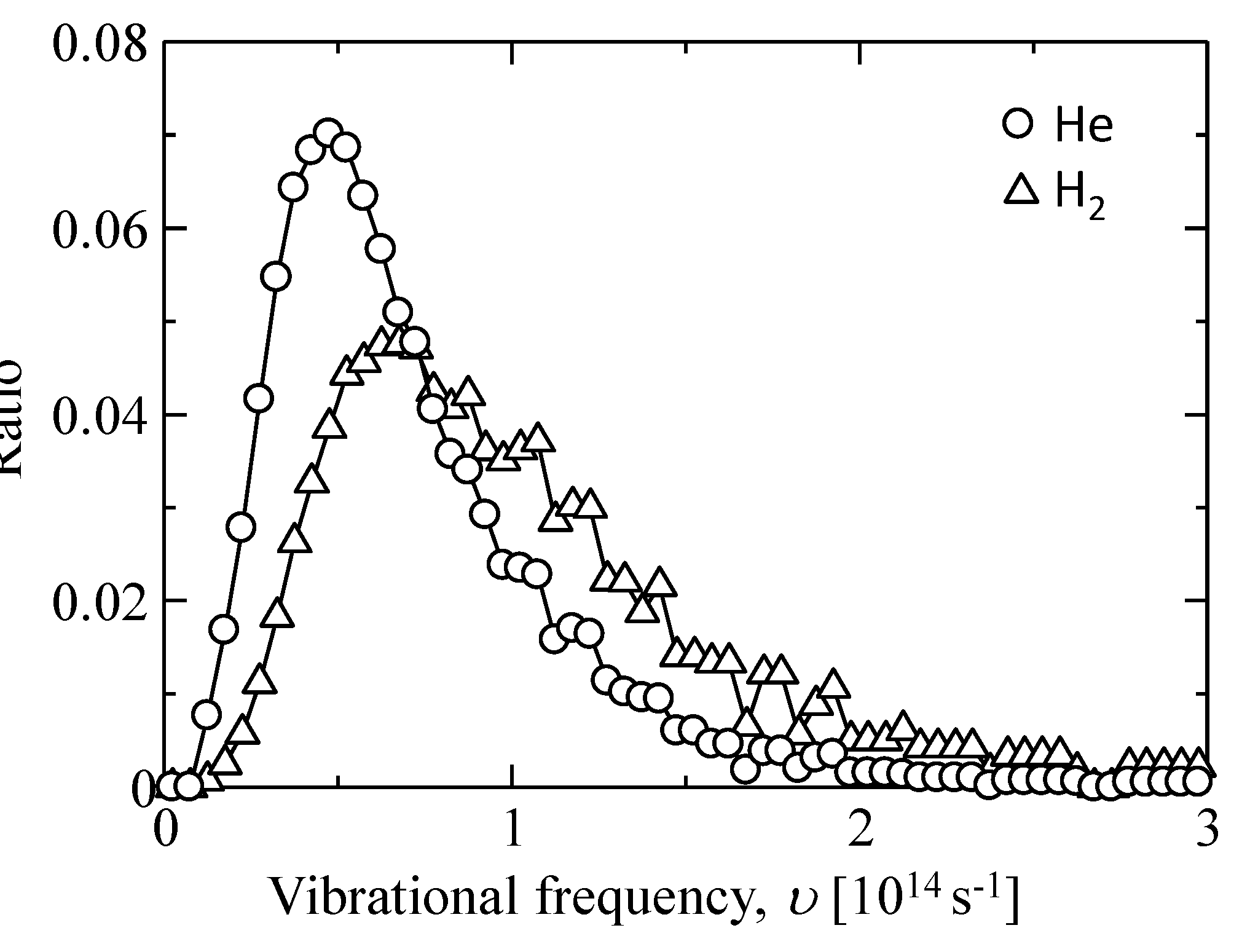
| - | υ [1013 s−1] | α [Å] |
|---|---|---|
| He | 4.75 ± 2.00 | 6.25 ± 1.00 |
| H2 | 6.75 ± 2.00 |
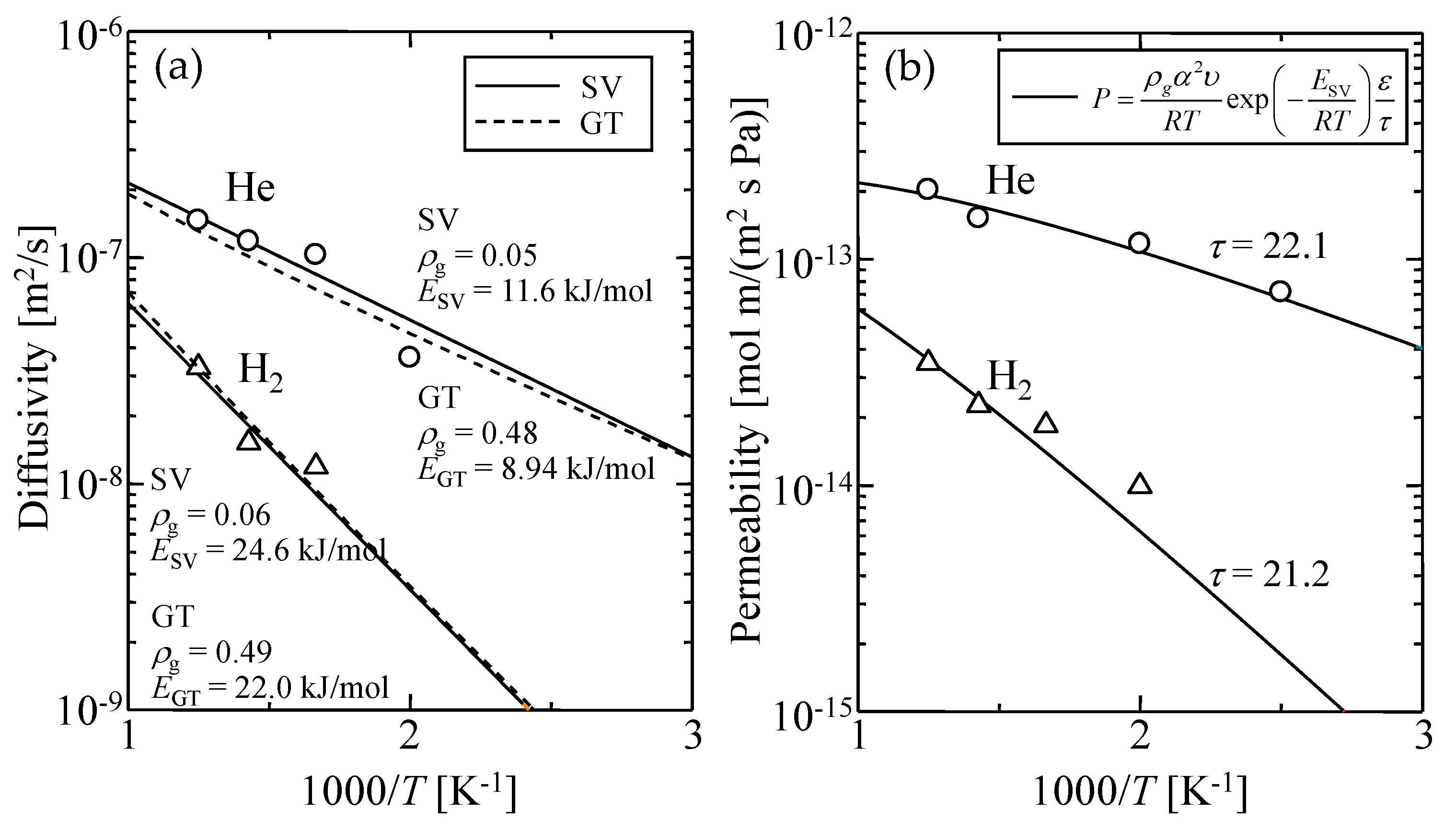
| - | - | ρg [-] | E [kJ/mol] |
|---|---|---|---|
| GT | He | 0.48 ± 0.10 | 8.94 |
| H2 | 0.49 ± 0.08 | 22.0 | |
| SV | He | 0.05 ± 0.03 | 11.6 |
| H2 | 0.06 ± 0.03 | 24.6 |
| - | ε [-] | τ [-] |
|---|---|---|
| He (This work) | 0.17 | 22.1 |
| H2 (This work) | 0.13 | 21.2 |
| Ref. [30] | 0.22 | 25 ± 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshioka, T.; Nakata, A.; Tung, K.-L.; Kanezashi, M.; Tsuru, T. Molecular Dynamics Simulation Study of Solid Vibration Permeation in Microporous Amorphous Silica Network Voids. Membranes 2019, 9, 132. https://doi.org/10.3390/membranes9100132
Yoshioka T, Nakata A, Tung K-L, Kanezashi M, Tsuru T. Molecular Dynamics Simulation Study of Solid Vibration Permeation in Microporous Amorphous Silica Network Voids. Membranes. 2019; 9(10):132. https://doi.org/10.3390/membranes9100132
Chicago/Turabian StyleYoshioka, Tomohisa, Akihiro Nakata, Kuo-Lun Tung, Masakoto Kanezashi, and Toshinori Tsuru. 2019. "Molecular Dynamics Simulation Study of Solid Vibration Permeation in Microporous Amorphous Silica Network Voids" Membranes 9, no. 10: 132. https://doi.org/10.3390/membranes9100132
APA StyleYoshioka, T., Nakata, A., Tung, K.-L., Kanezashi, M., & Tsuru, T. (2019). Molecular Dynamics Simulation Study of Solid Vibration Permeation in Microporous Amorphous Silica Network Voids. Membranes, 9(10), 132. https://doi.org/10.3390/membranes9100132








