Concentration Polarization in Ultrafiltration/Nanofiltration for the Recovery of Polyphenols from Winery Wastewaters
Abstract
1. Introduction
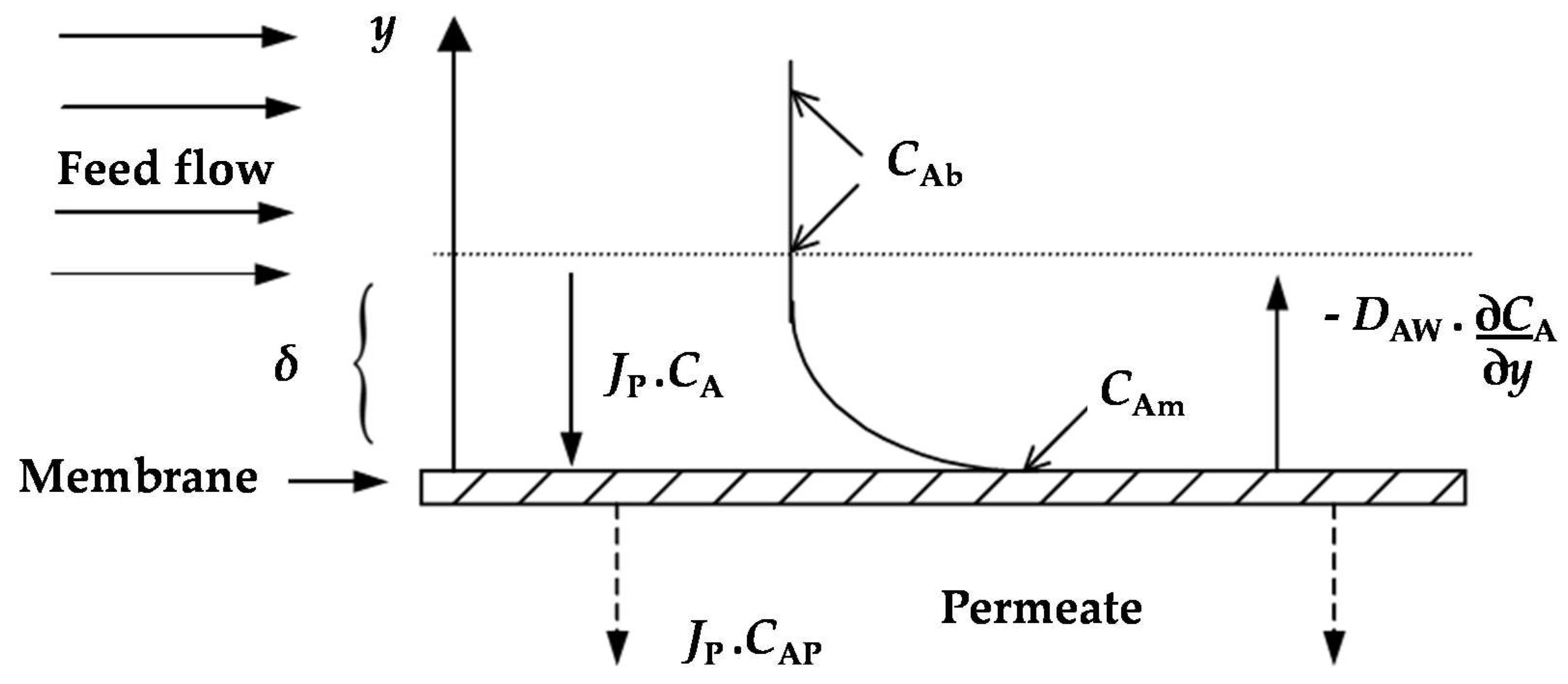
2. Theory
3. Materials and Methods
3.1. Winery Wastewater
3.2. Membranes
3.3. UF/NF Permeation Experiments
4. Results and Discussion
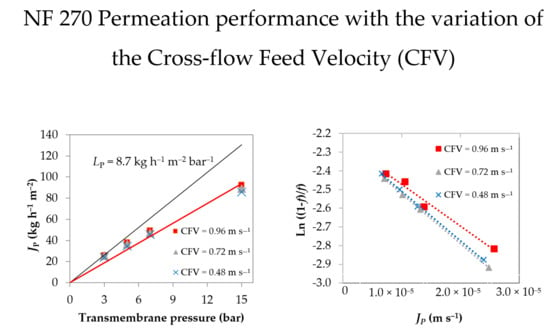
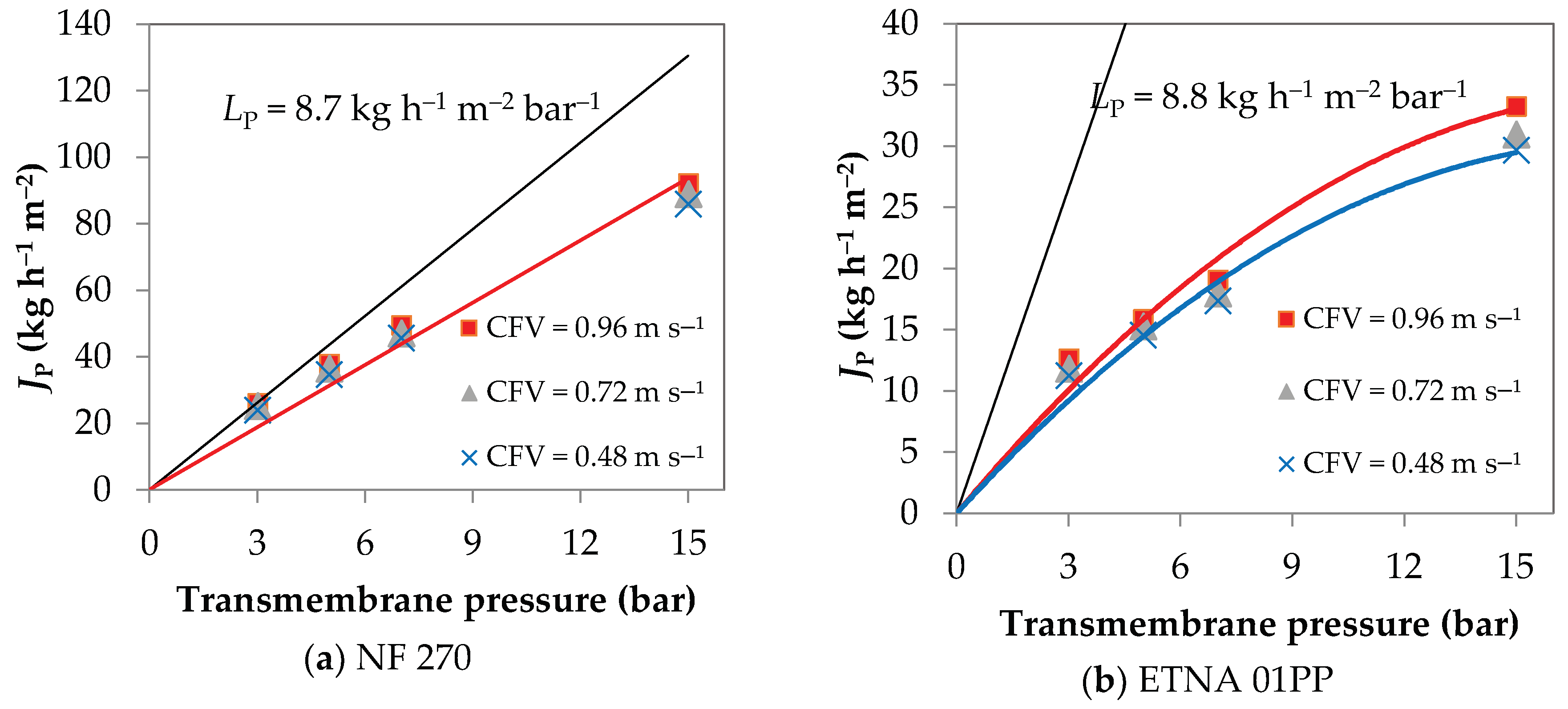
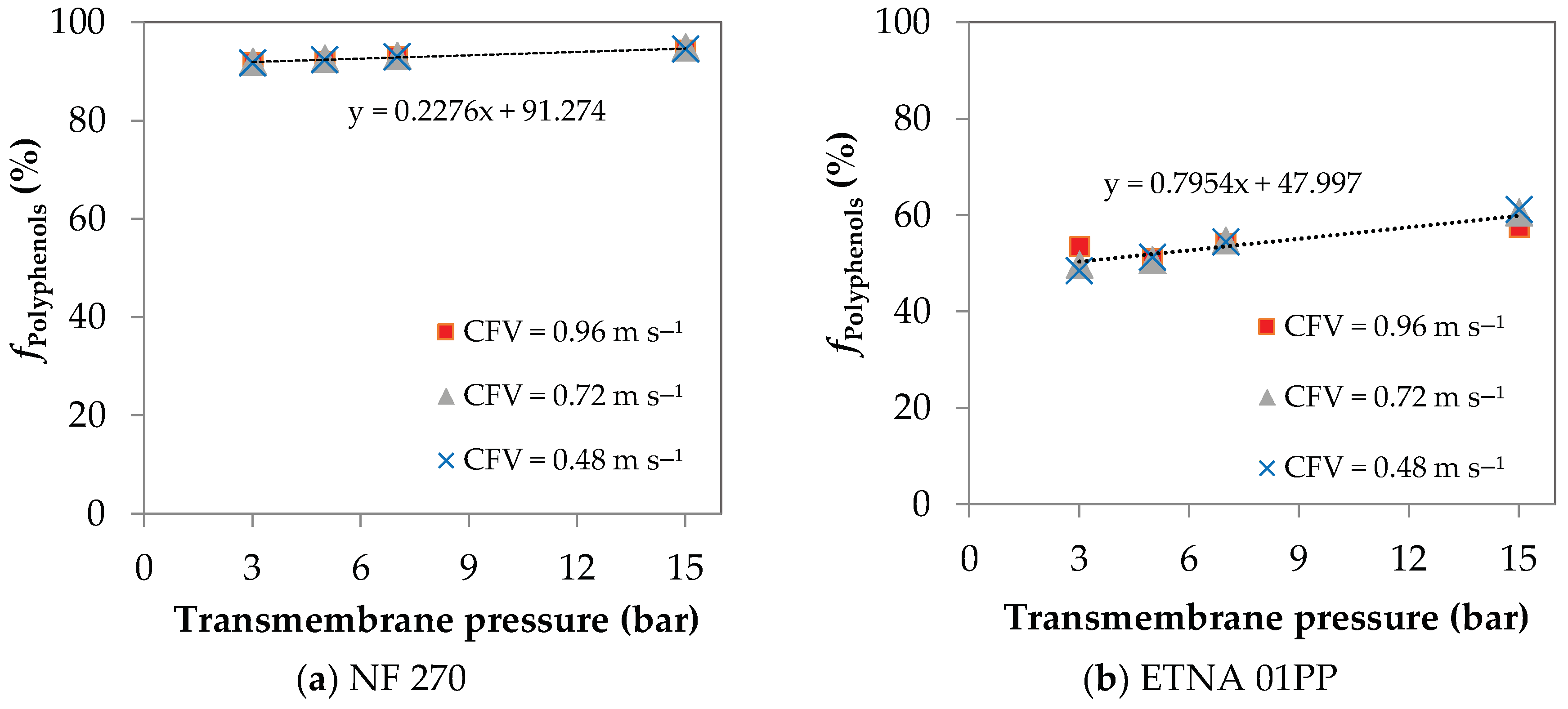
4.1. UF/NF Permeation Experiments
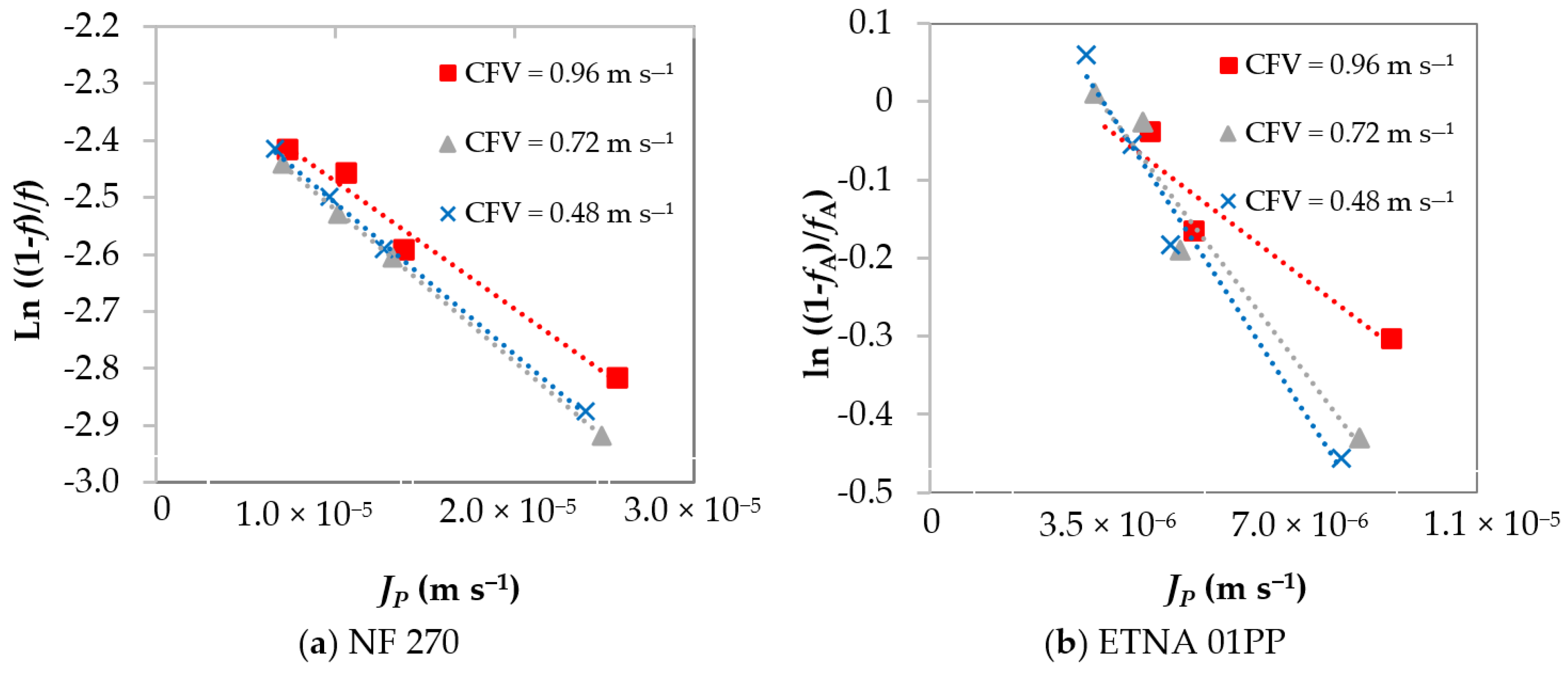
4.2. Concentration Polarization Quantification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- OIV—Organization Internationale de la Vigne et du Vin. 2017 World Vitiviniculture Situation. OIV Statistical Report on World Vitiviniculture. Available online: http://www.oiv.int/public/medias/5479/oiv-en-bilan-2017.pdf (accessed on 16 April 2018).
- Pirra, A.J.D. Caracterização e Tratamento de Efluentes Vinícolas da Região Demarcada do Douro. Ph.D. Thesis, Universidade de Trás-os-Montes e Alto Douro, Vila Real, Portugal, 2005. [Google Scholar]
- Bustamante, M.A.; Moral, R.; Paredes, C.; Pérez-Espinosa, A.; Moreno-Caselles, J.; Pérez-Murcia, M.D. Agrochemical characterisation of the solid by-products and residues from the winery and distillery industry. Waste Manag. 2008, 28, 372–380. [Google Scholar] [CrossRef] [PubMed]
- Anastasiadi, M.; Pratsinis, H.; Kletsas, D.; Skaltsounis, A.-L.; Haroutounian, S.A. Bioactive non-coloured polyphenols content of grapes, wines and vinification by-products: Evaluation of the antioxidant activities of their extracts. Food Res. Int. 2010, 43, 805–813. [Google Scholar] [CrossRef]
- Bhise, S.; Kaur, A.; Gandhi, N.; Gupta, R. Antioxidant property and health benefits of grape byproducts. J. Postharvest Technol. 2014, 2, 1–11. [Google Scholar]
- Ky, I.; Lorrain, B.; Kolbas, N.; Crozier, A.; Teissedre, P.-L. Wine by-Products: Phenolic Characterization and Antioxidant Activity Evaluation of Grapes and Grape Pomaces from Six Different French Grape Varieties. Molecules 2014, 19, 482–506. [Google Scholar] [CrossRef] [PubMed]
- Giacobbo, A.; Bernardes, A.M.; De Pinho, M.N. Nanofiltration for the Recovery of Low Molecular Weight Polysaccharides and Polyphenols from Winery Effluents. Sep. Sci. Technol. 2013, 48, 2524–2530. [Google Scholar] [CrossRef]
- Giacobbo, A.; Bernardes, A.M.; De Pinho, M.N. Sequential pressure-driven membrane operations to recover and fractionate polyphenols and polysaccharides from second racking wine lees. Sep. Purif. Technol. 2017, 173 (Suppl. C), 49–54. [Google Scholar] [CrossRef]
- Cassano, A.; Conidi, C.; Ruby-Figueroa, R.; Castro-Muñoz, R. Nanofiltration and Tight Ultrafiltration Membranes for the Recovery of Polyphenols from Agro-Food By-Products. Int. J. Mol. Sci. 2018, 19. [Google Scholar] [CrossRef] [PubMed]
- Chaabane, T.; Taha, S.; Taleb Ahmed, M.; Maachi, R.; Dorange, G. Coupled model of film theory and the Nernst–Planck equation in nanofiltration. Desalination 2007, 206, 424–432. [Google Scholar] [CrossRef]
- Díaz-Reinoso, B.; Moure, A.; Domínguez, H.; Parajó, J.C. Membrane concentration of antioxidants from Castanea sativa leaves aqueous extracts. Chem. Eng. J. 2011, 175, 95–102. [Google Scholar] [CrossRef]
- Giacobbo, A.; Do Prado, J.M.; Meneguzzi, A.; Bernardes, A.M.; De Pinho, M.N. Microfiltration for the recovery of polyphenols from winery effluents. Sep. Purif. Technol. 2015, 143, 12–18. [Google Scholar] [CrossRef]
- Porter, M.C. Concentration polarization in reverse osmosis and ultrafiltration. In Synthetic Membranes: Science, Engineering and Applications; Bungay, P.M., Lonsdale, H.K., De Pinho, M.N., Eds.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1986; pp. 267–388. ISBN 978-94-010-8596-0. [Google Scholar]
- De Pinho, M.N.; Prazeres, D.M. Fundamentos de Transferência de Massa; IST Press: Lisbon, Portugal, 2008; p. 204. ISBN 978–972-8469-56-6. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 1st ed.; John Wiley & Sons: New York, NY, USA, 1960; p. 780. ISBN 047107392X. [Google Scholar]
- Rosa, M.J.F. Separação Selectiva de Compostos Orgânicos de Correntes Aquosas por Ultrafiltração e Nanofiltração. Ph.D. Thesis, Instituto Supeior Técnico, Technical University of Lisbon, Lisbon, Portugal, 1995. [Google Scholar]
- Rosa, M.J.; De Pinho, M.N. Separation of organic solutes by membrane pressure-driven processes. J. Membr. Sci. 1994, 89, 235–243. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G.; Wiley, D.E. Spacer characterization and pressure drop modelling in spacer-filled channels for ultrafiltration. J. Membr. Sci. 1994, 87, 79–98. [Google Scholar] [CrossRef]
- Dubois, M.; Gilles, K.A.; Hamilton, J.K.; Rebers, P.A.; Smith, F. Colorimetric Method for Determination of Sugars and Related Substances. Anal. Chem. 1956, 28, 350–356. [Google Scholar] [CrossRef]
- Giusti, M.M.; Wrolstad, R.E. Characterization and Measurement of Anthocyanins by UV-Visible Spectroscopy. In Current Protocols in Food Analytical Chemistry; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001; ISBN 9780471142911. [Google Scholar]
- Librán, C.M.; Mayor, L.; Garcia-Castello, E.M.; Vidal-Brotons, D. Polyphenol extraction from grape wastes: Solvent and pH effect. Agric. Sci. 2013, 4, 56–62. [Google Scholar] [CrossRef]
- Curvelo-Garcia, A.S. Controlo de Qualidade dos Vinhos: Química Enológica, Métodos Analíticos; Instituto da Vinha e do Vinho: Lisbon, Portugal, 1988; p. 420.
- Rosa Santos, F.; Catarino, I.; Geraldes, V.; Pinho, M.N. Concentration and Rectification of Grape Must by Nanofiltration. Am. J. Enol. Viticult. 2008, 59, 446–450. [Google Scholar]
- Giacobbo, A.; Meneguzzi, A.; Bernardes, A.M.; De Pinho, M.N. Pressure-driven membrane processes for the recovery of antioxidant compounds from winery effluents. J. Clean. Prod. 2017, 155 Pt 1, 172–178. [Google Scholar] [CrossRef]
- Bacchin, P.; Aimar, P.; Field, R.W. Critical and sustainable fluxes: Theory, experiments and applications. J. Membr. Sci. 2006, 281, 42–69. [Google Scholar] [CrossRef]
- Lipnizki, F. Cross-flow membrane applications in the food industry. In Membranes for Food Applications; Peinemann, K.-V., Nunes, S.P., Giorno, L., Eds.; Willey-VCH: Weinheim, Germany, 2010; pp. 1–24. [Google Scholar]
- Mänttäri, M.; Nyström, M. Critical flux in NF of high molar mass polysaccharides and effluents from the paper industry. J. Membr. Sci. 2000, 170, 257–273. [Google Scholar] [CrossRef]
- Field, R.W.; Wu, D.; Howell, J.A.; Gupta, B.B. Critical flux concept for microfiltration fouling. J. Membr. Sci. 1995, 100, 259–272. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Dammak, I.; Neves, M.A.; Nabetani, H.; Isoda, H.; Sayadi, S.; Nakajima, M. Transport properties of oleuropein through nanofiltration membranes. Food Bioprod. Process. 2015, 94, 342–353. [Google Scholar] [CrossRef]
- Todisco, S.; Tallarico, P.; Gupta, B.B. Mass transfer and polyphenols retention in the clarification of black tea with ceramic membranes. Innov. Food Sci. Emerg. Technol. 2002, 3, 255–262. [Google Scholar] [CrossRef]
| Parameter | Feed Solution |
|---|---|
| TOC (mg L−1 C) | 716 ± 10.8 |
| Turbidity (NTU) | <1.0 |
| Conductivity (µS cm−1) | 241 ± 2.0 |
| Total Polysaccharides (mg L−1 Glucose) | 10.1 ± 0.4 |
| Total Polyphenols (mg L−1 GAE) | 26.6 ± 0.1 |
| Monomeric Anthocyanins (mg L−1 Mv3g) | 4.20 ± 0.1 |
| CFV (m s−1) | NF 270 | ETNA 01PP | ||
|---|---|---|---|---|
| k × 10−5 (m s−1) | k × 10−5 (m s−1) | |||
| 0.48 | 0.90 | 3.77 | 0.42 | 1.02 |
| 0.72 | 0.91 | 3.75 | 0.43 | 1.18 |
| 0.96 | 0.90 | 4.47 | 0.47 | 2.06 |
| CFV (m s−1) | k × 10−5 (m s−1) | |
|---|---|---|
| NF 270 | ETNA 01PP | |
| 0.48 | 2.92 | 1.63 |
| 0.72 | 3.54 | 2.00 |
| 0.96 | 4.05 | 2.31 |
| CFV (m s−1) | ΔP (bar) | NF 270 | ETNA 01PP | ||||
|---|---|---|---|---|---|---|---|
| CAP (mg L−1) | CAm (mg L−1) | CAP (mg L−1) | CAm (mg L−1) | ||||
| 0.48 | 3.0 | 2.18 | 31.30 | 1.19 | 13.68 | 31.22 | 1.36 |
| 5.0 | 2.02 | 33.73 | 1.29 | 12.92 | 33.25 | 1.49 | |
| 7.0 | 1.85 | 36.49 | 1.40 | 12.07 | 35.39 | 1.61 | |
| 15 | 1.42 | 48.93 | 1.89 | 10.30 | 46.92 | 2.25 | |
| 0.72 | 3.0 | 2.13 | 31.62 | 1.21 | 13.35 | 30.81 | 1.32 |
| 5.0 | 1.96 | 34.23 | 1.31 | 13.11 | 32.41 | 1.43 | |
| 7.0 | 1.83 | 36.95 | 1.42 | 12.02 | 34.25 | 1.53 | |
| 15 | 1.36 | 50.23 | 1.94 | 10.46 | 43.86 | 2.07 | |
| 0.96 | 3.0 | 2.18 | 30.87 | 1.18 | 12.34 | 29.22 | 1.19 |
| 5.0 | 2.10 | 33.08 | 1.27 | 13.02 | 29.81 | 1.24 | |
| 7.0 | 1.85 | 35.50 | 1.36 | 12.18 | 30.80 | 1.30 | |
| 15 | 1.50 | 46.01 | 1.78 | 11.28 | 35.26 | 1.57 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giacobbo, A.; Moura Bernardes, A.; Filipe Rosa, M.J.; De Pinho, M.N. Concentration Polarization in Ultrafiltration/Nanofiltration for the Recovery of Polyphenols from Winery Wastewaters. Membranes 2018, 8, 46. https://doi.org/10.3390/membranes8030046
Giacobbo A, Moura Bernardes A, Filipe Rosa MJ, De Pinho MN. Concentration Polarization in Ultrafiltration/Nanofiltration for the Recovery of Polyphenols from Winery Wastewaters. Membranes. 2018; 8(3):46. https://doi.org/10.3390/membranes8030046
Chicago/Turabian StyleGiacobbo, Alexandre, Andréa Moura Bernardes, Maria João Filipe Rosa, and Maria Norberta De Pinho. 2018. "Concentration Polarization in Ultrafiltration/Nanofiltration for the Recovery of Polyphenols from Winery Wastewaters" Membranes 8, no. 3: 46. https://doi.org/10.3390/membranes8030046
APA StyleGiacobbo, A., Moura Bernardes, A., Filipe Rosa, M. J., & De Pinho, M. N. (2018). Concentration Polarization in Ultrafiltration/Nanofiltration for the Recovery of Polyphenols from Winery Wastewaters. Membranes, 8(3), 46. https://doi.org/10.3390/membranes8030046