Theoretical and Experimental Investigations of the Potential of Osmotic Energy for Power Production †
Abstract
:1. Introduction
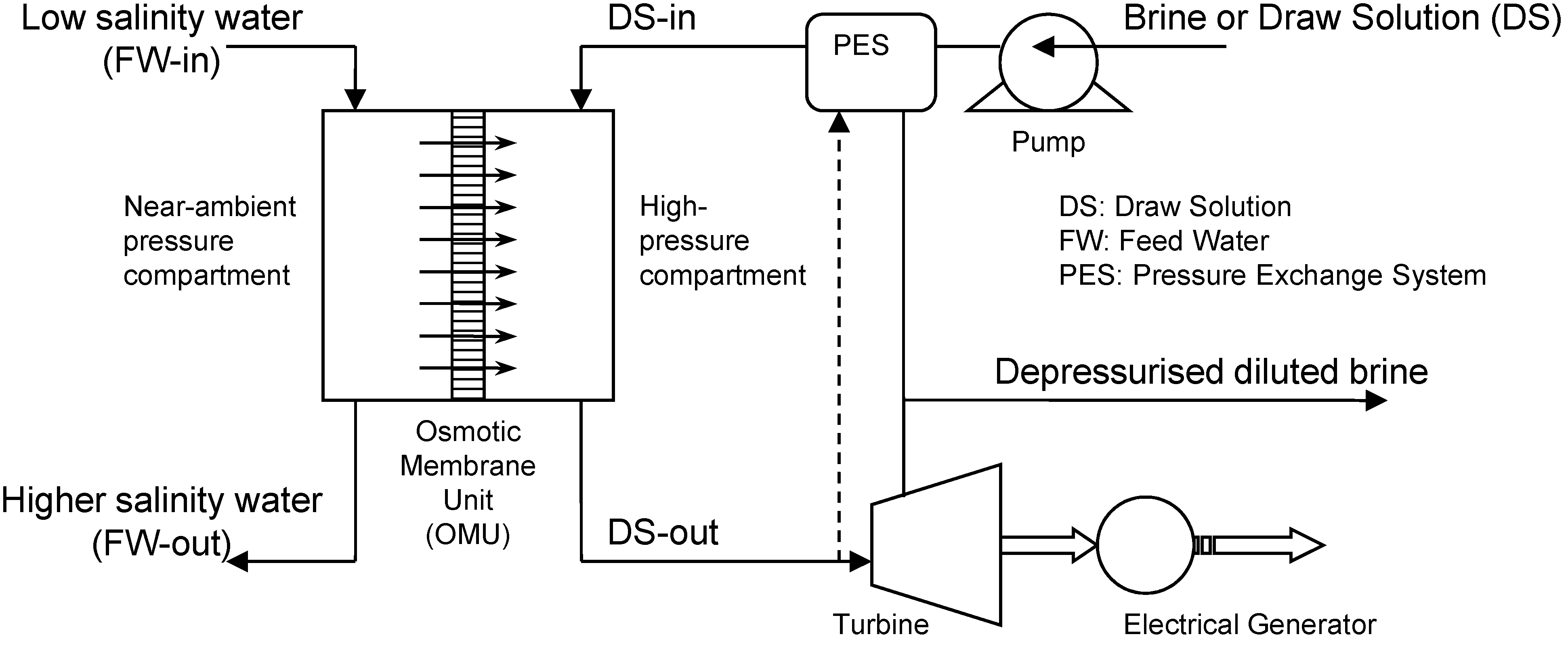
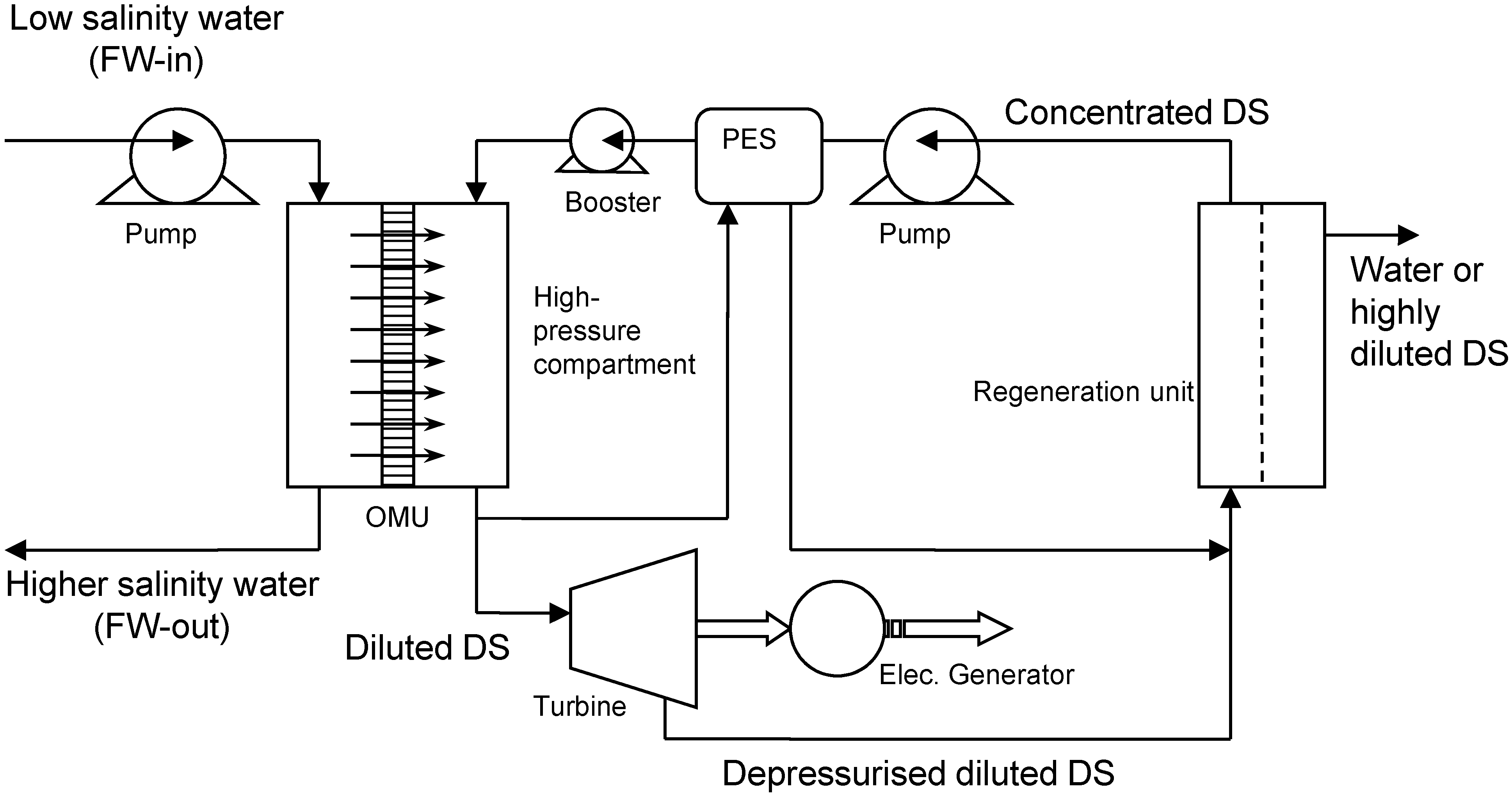
| Researcher (Year) | Feed/Draw Solution | Membrane | Hydraulic Pressure (bar) | Power Density (W/m2) | Ref. |
|---|---|---|---|---|---|
| Loeb et al. (1976) | Freshwater/Seawater | Hollow Fibre seawater RO | 12 | 0.35 | [11] |
| Mehta (1978) | Freshwater/Brine | Hollow Fibre seawater RO | 40 | 3.27 | [12] |
| Loeb & Mehta (1979) | Freshwater/Brine | FRL Composite seawater RO | 19 | 1.56 | [13] |
| Mehta & Loeb (1979) | Freshwater/Brine | Hollow Fibre seawater RO | 40 | 3.12 | [14] |
| Lee et al. (1980) | Freshwater/Brine (3.5%) | CA& PA& PBIL flat sheet seawater RO | 12.5 | 1.55 | [15] |
| Jellinek & Masuda (1981) | Freshwater/Brine | seawater spiral wound RO | 11–16 | 1.6 | [16] |
| Gerstandt et al. (2008) | Freshwater/Seawater | Lab TFC (flat sheet/hollow fibre) and CA | 10–13 | 1.3–3.5 | [17] |
| Skilhagen et al. (2008) | Freshwater/Seawater | Modified TFC for PRO | 11–15 | 1.0 | [7] |
| Achilli et al. (2009) | DI water/Brine (3.5%–6%) | CTA flat sheet seawater FO (HTI) | 9.7 | 2.7–5.1 | [18] |
| Thorsen & Holt (2009) | Freshwater/Seawater | TFC & CTA commercial FO flat sheet seawater | 7–12 | 1.6–2.7 | [19] |
| Chou et al. (2011) | River water & waste water/Brine (3.5%–6%) | TFC Hollow Fibre seawater FO | 8–9.1 | 8.4–11 | [20] |
| Yip & Elimelech (2011) | River water/Seawater (3.5%) | Modified TFC membrane, Hollow Fibre | 10–15 | 6.1–10 | [21] |
| She et al. (2012) | Freshwater/Brine (2 M NaCl) | CTA commercial flat sheet seawater FO(HTI) | 13 | 6.7 | [22] |
| Kim & Elimelech (2012) | NaCl solution (0.5–1 M)/Brine (2 M) | CTA commercial FO flat sheet | 12.5 | 4.7 | [23] |
| Wang et al. (2012) | River & Wastewater (0.5 M)/Seawater | TFC hollow fibre commercial FO | 5–8.9 | 4.1–5.7 | [24] |
| Schiestel et al. (2012) | Freshwater/Seawater | CTA commercial FO flat sheet | 8 | 2.25 | [25] |
| Saito et al. (2012) | Waste water/RO Brine (2–2.5 M) | commercial FO hollow fibre | 25 | 7.7 | [26] |
| Efraty (2012) | Freshwater/Seawater | Modified TFC membrane | 9.6 | 7.4 | [27] |
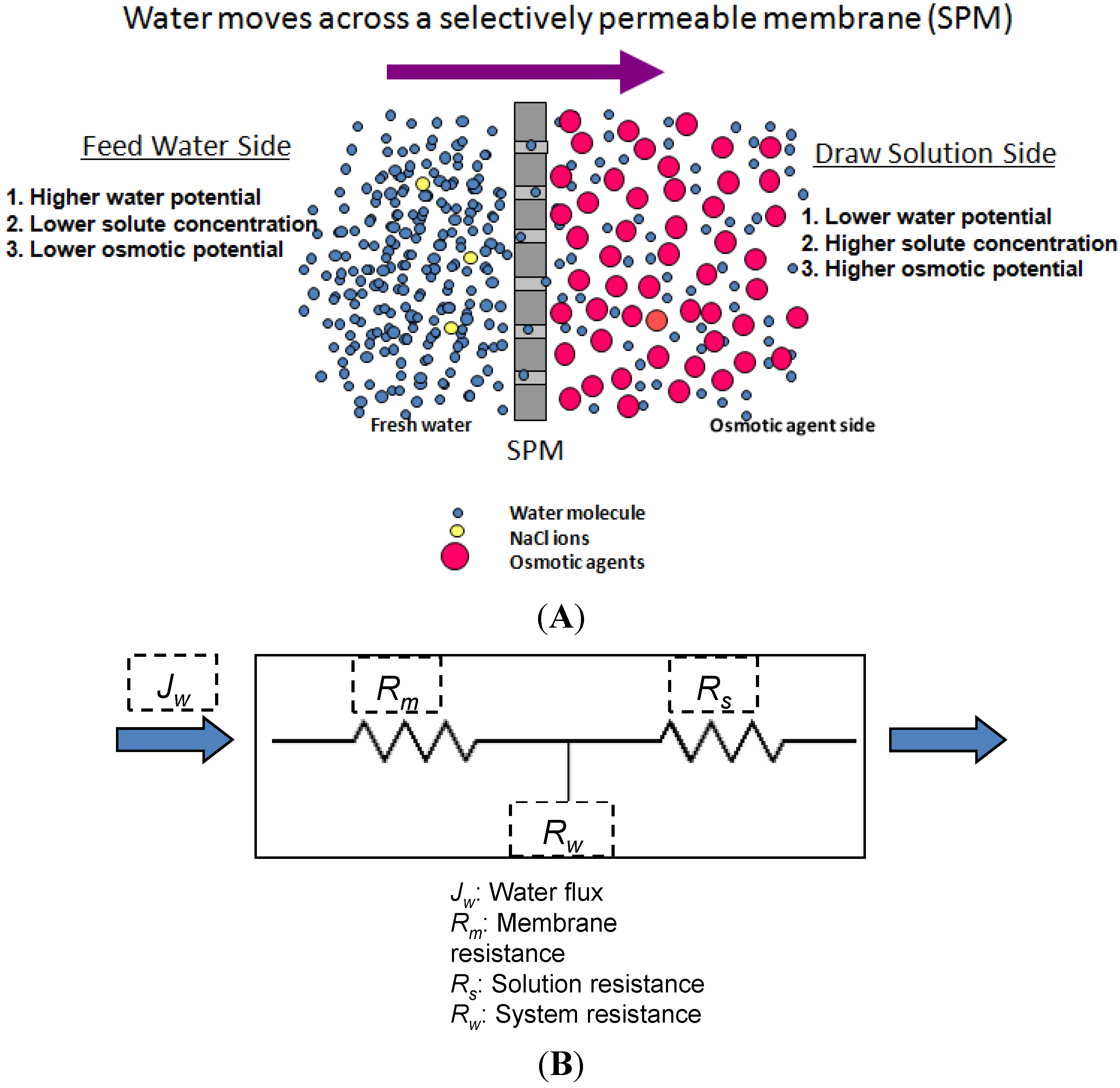
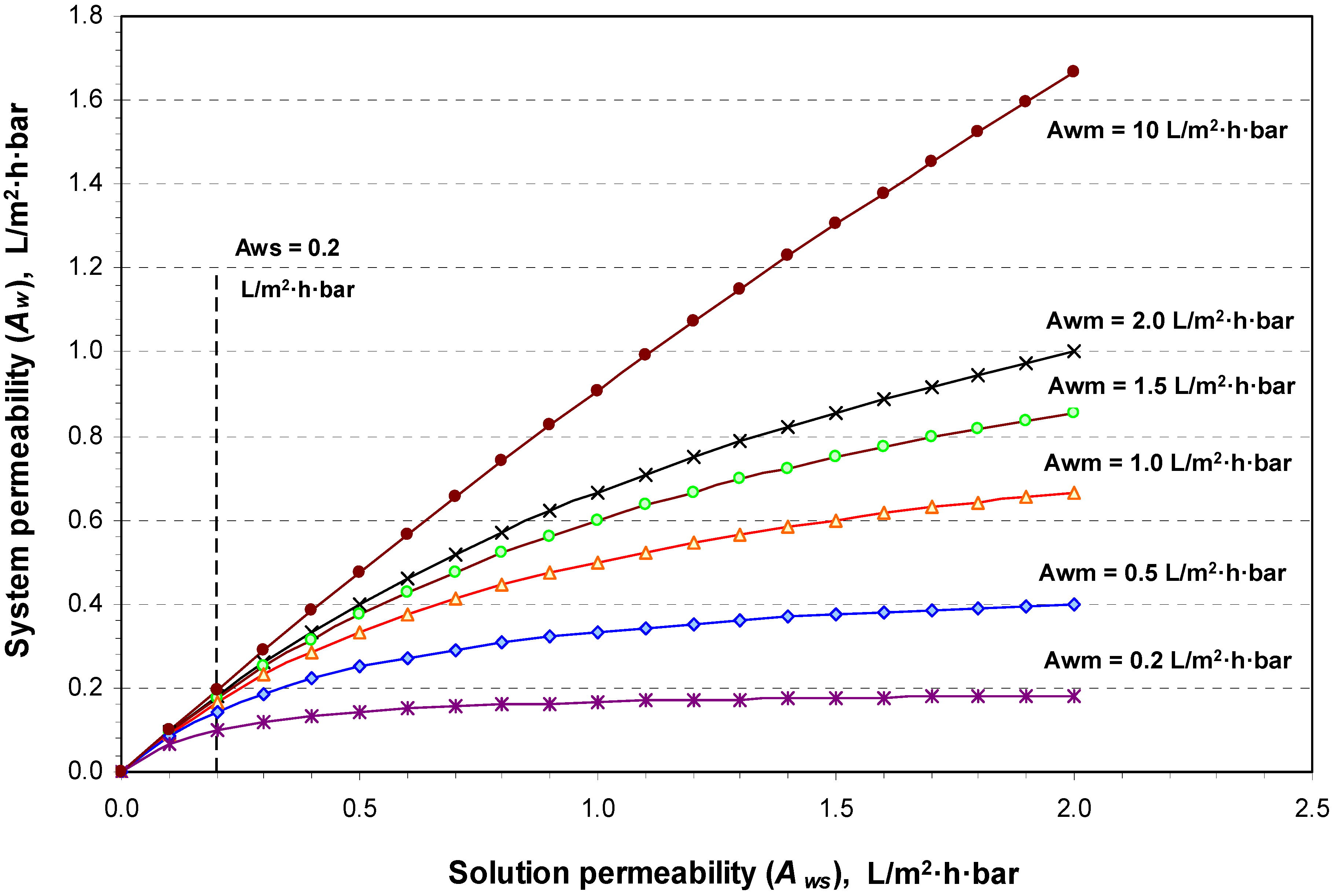
2. Basic Theory










3. Experimental Setup
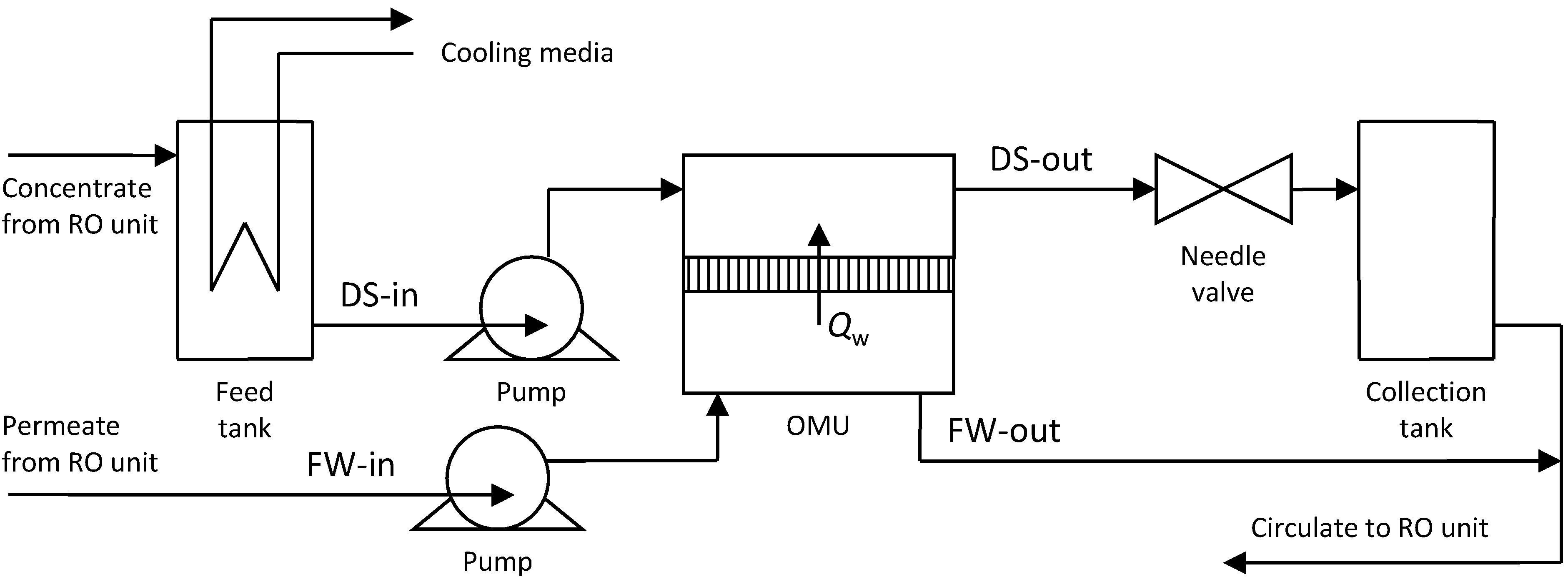
| Experiment No. | FW-in | DS-in | Osmotic pressure difference ∆Πf, bar | ||
|---|---|---|---|---|---|
| Concentration, ppm | Flow Rate, L/min | Concentration, ppm | Flow Rate, L/min | ||
| 1 | 240 | 11.1 | 34,560 | 9.8 | 27.4 |
| 2 | 6900 | 10.9 | 145,000 | 5.5 | 87.3 |
| 3 | 6900 | 9.5 | 34,690 | 5.5 | 22.1 |
4. Results and Discussion
4.1. Theoretical Calculation Results
| Osmotic membrane unit (OMU) | Value |
| Inlet (concentrated) DS hydraulic pressure (bar) | 15.0 |
| DS side hydraulic pressure drop (%) | 10 |
| Membrane element area (m2) | 100.8 |
| DS dilution rate (%) | 100 |
| Freshwater inlet hydraulic pressure (bar) | 0.4 |
| Freshwater inlet osmotic pressure (bar) | 0.0 |
| Discharged freshwater hydraulic pressure (bar) | 0.1 |
| Freshwater recovery rate (%) | 95 |
| Regeneration unit (RU) (FO unit) | Value |
| Brine inlet maximum osmotic pressure (bar) | 250 |
| Brine inlet hydraulic pressure (bar) | 2.0 |
| Discharged (diluted) brine hydraulic pressure (bar) | 0.1 |
| DS side hydraulic pressure drop (%) | 30 |
| DS recovery rate (%) | 50 |
| Brine dilution rate (%) | 100 |
| Membrane element area (m2) | 100 |
| Efficiencies | Value |
| Pumps and booster (%) | 80 |
| Turbine and generator (%) | 80 |
| PES (%) | 95 |
| Diluted DS (PES/Turbine) input flowrate ratio | 1.5 |
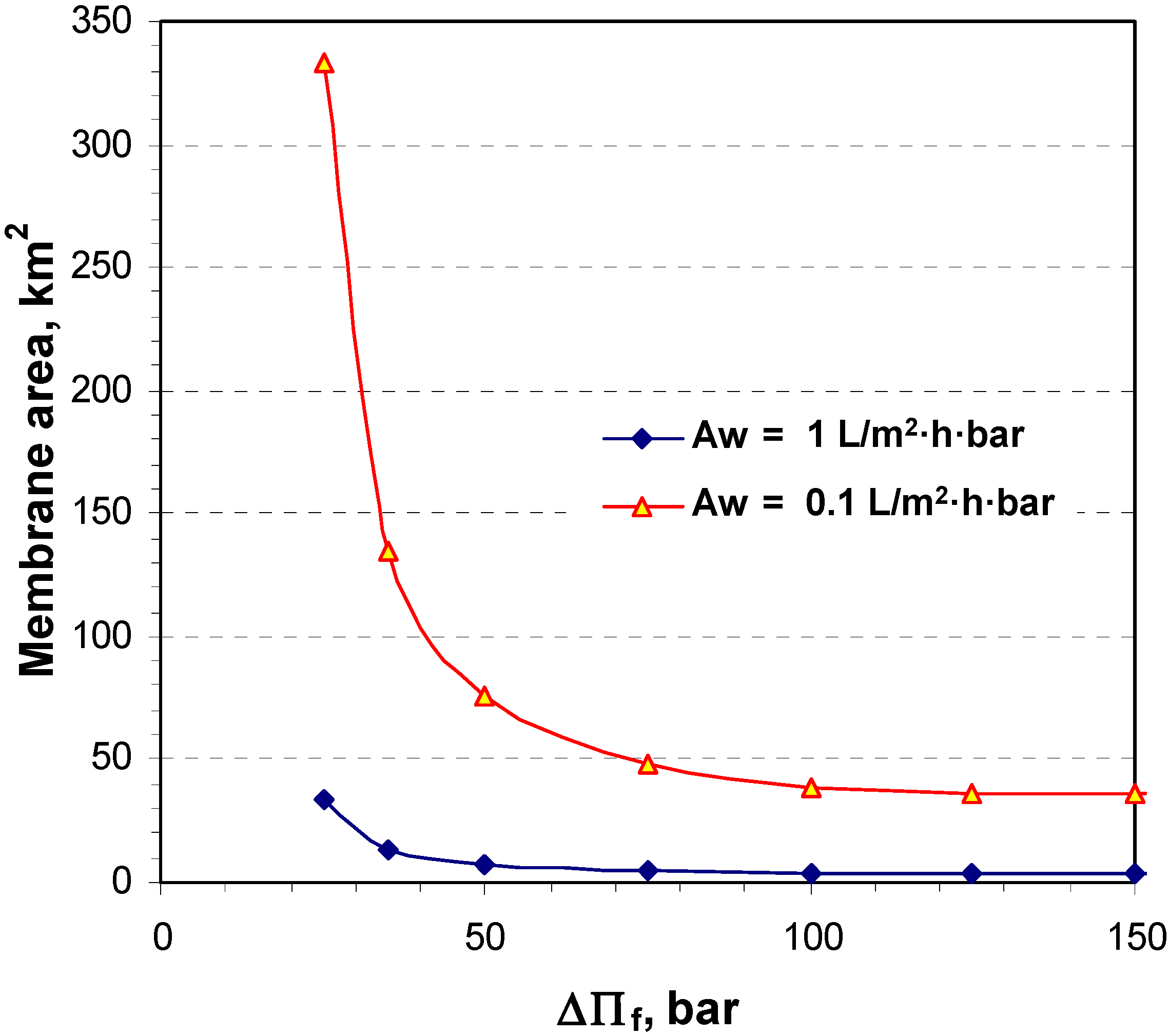
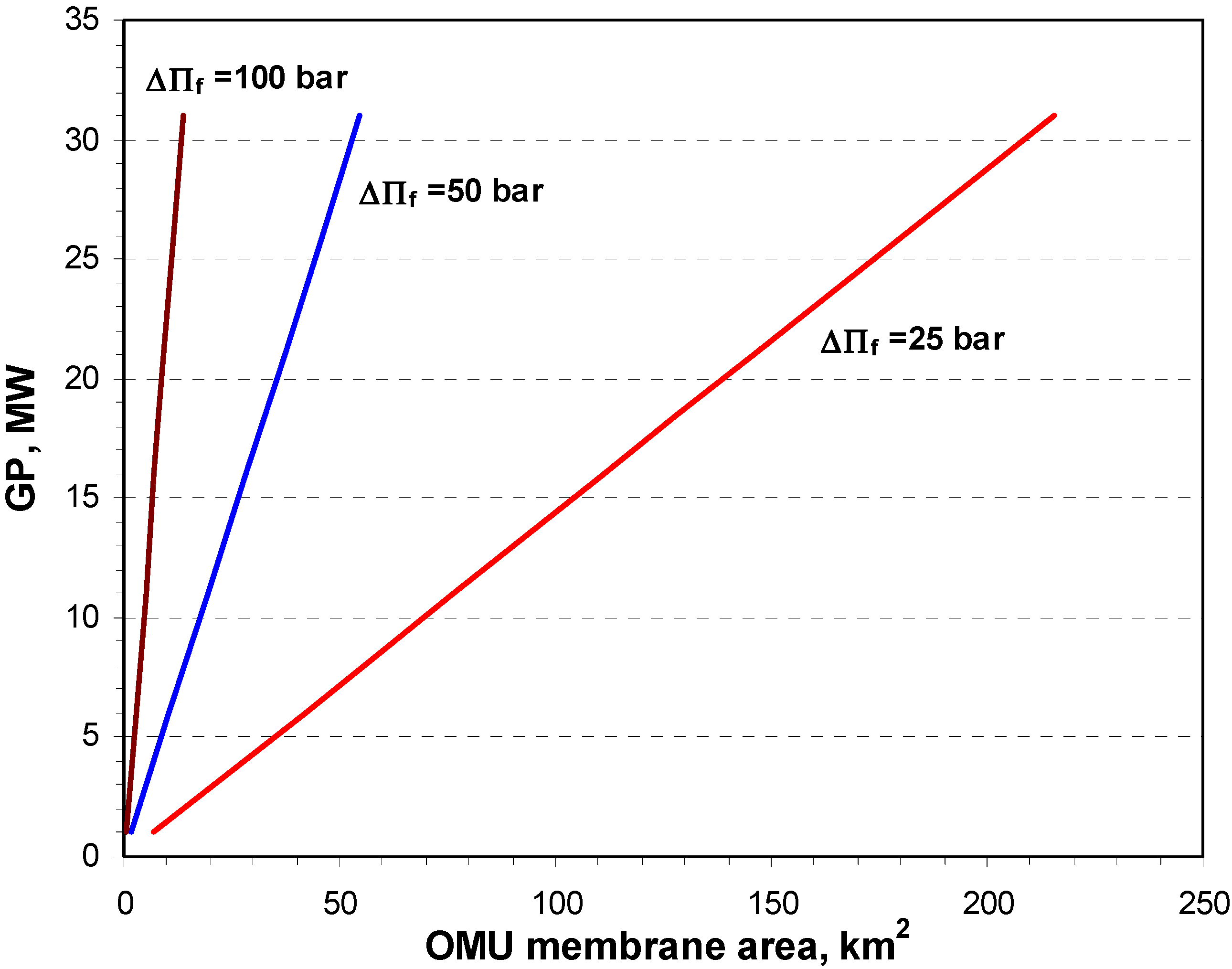
4.2. Pilot Plan Performance Test Results
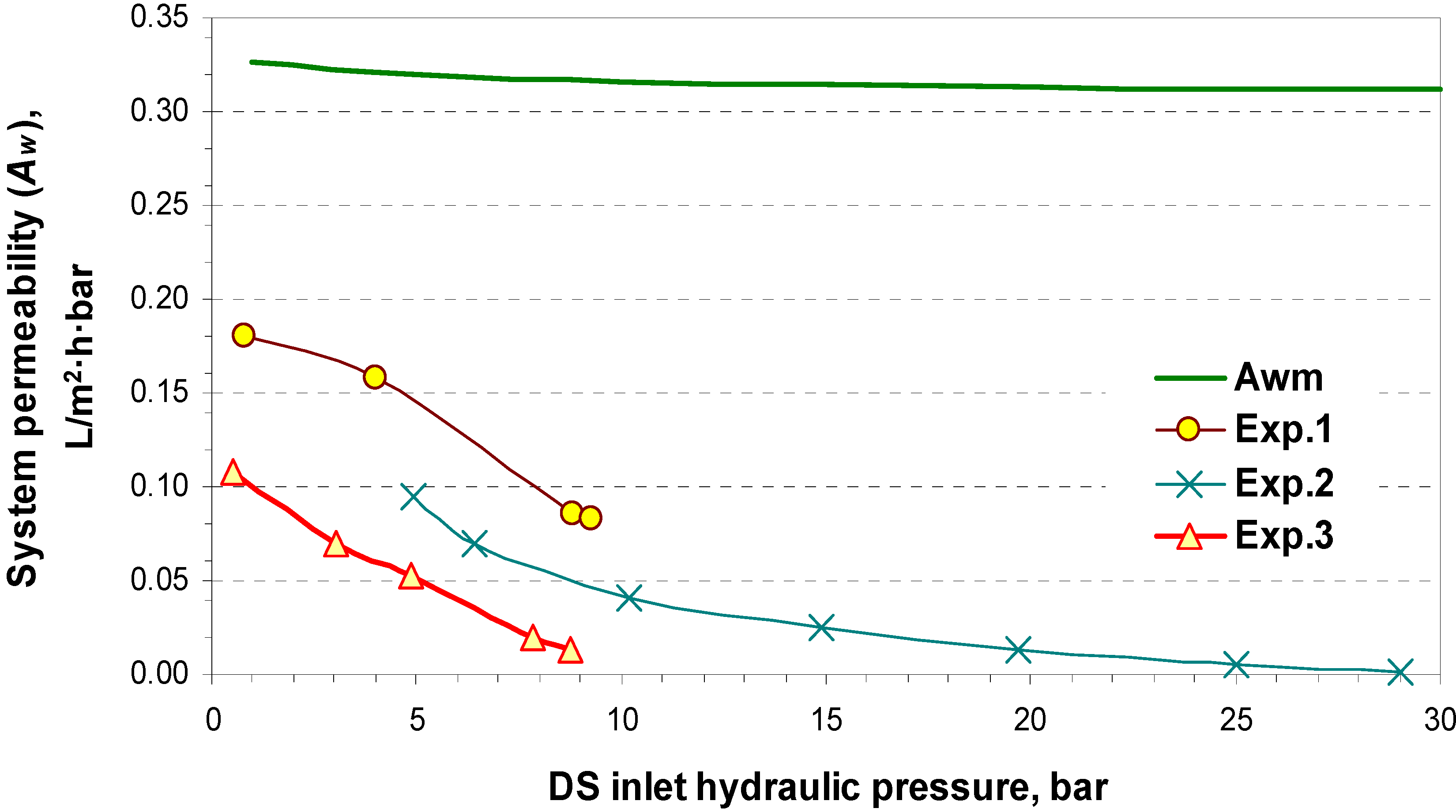
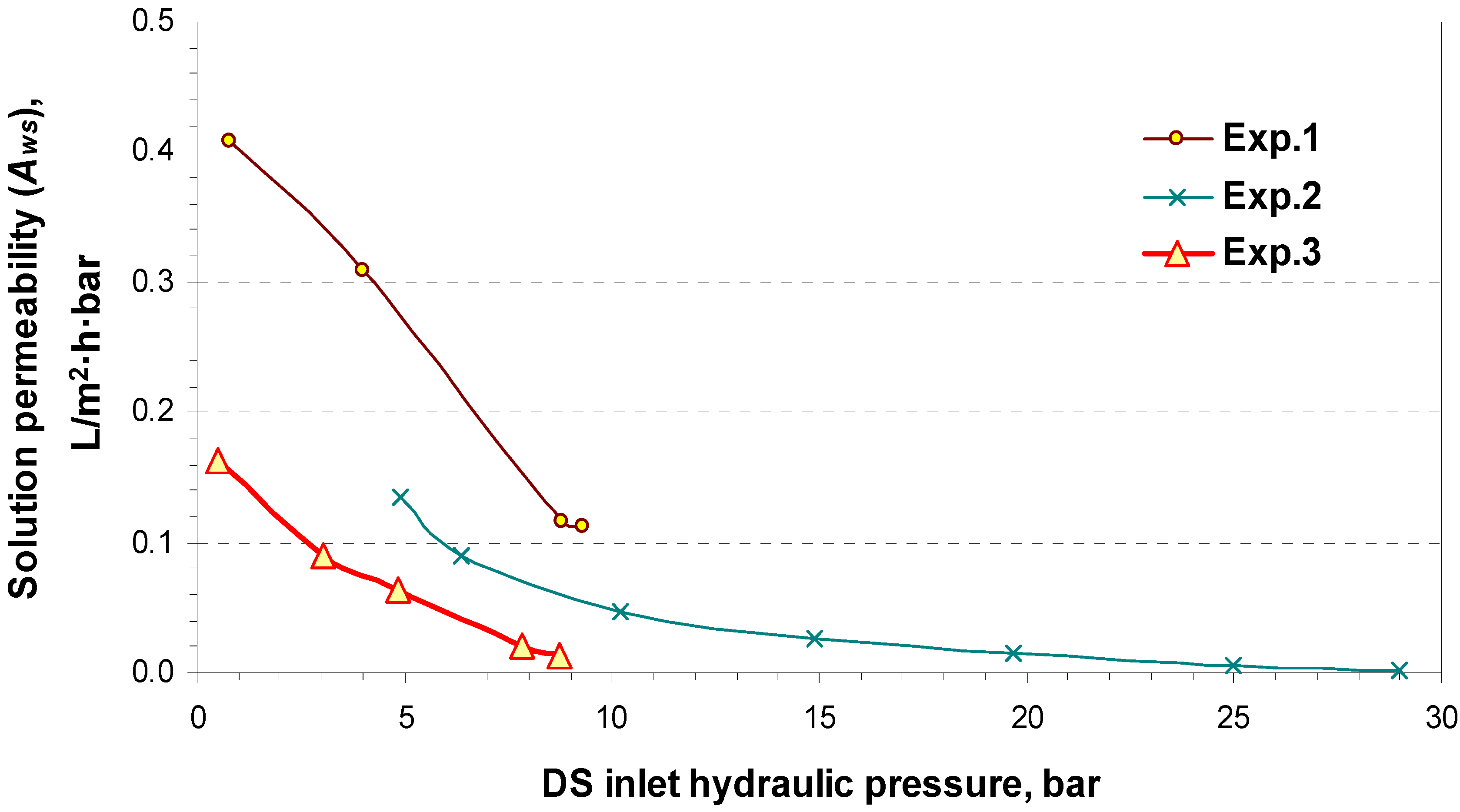
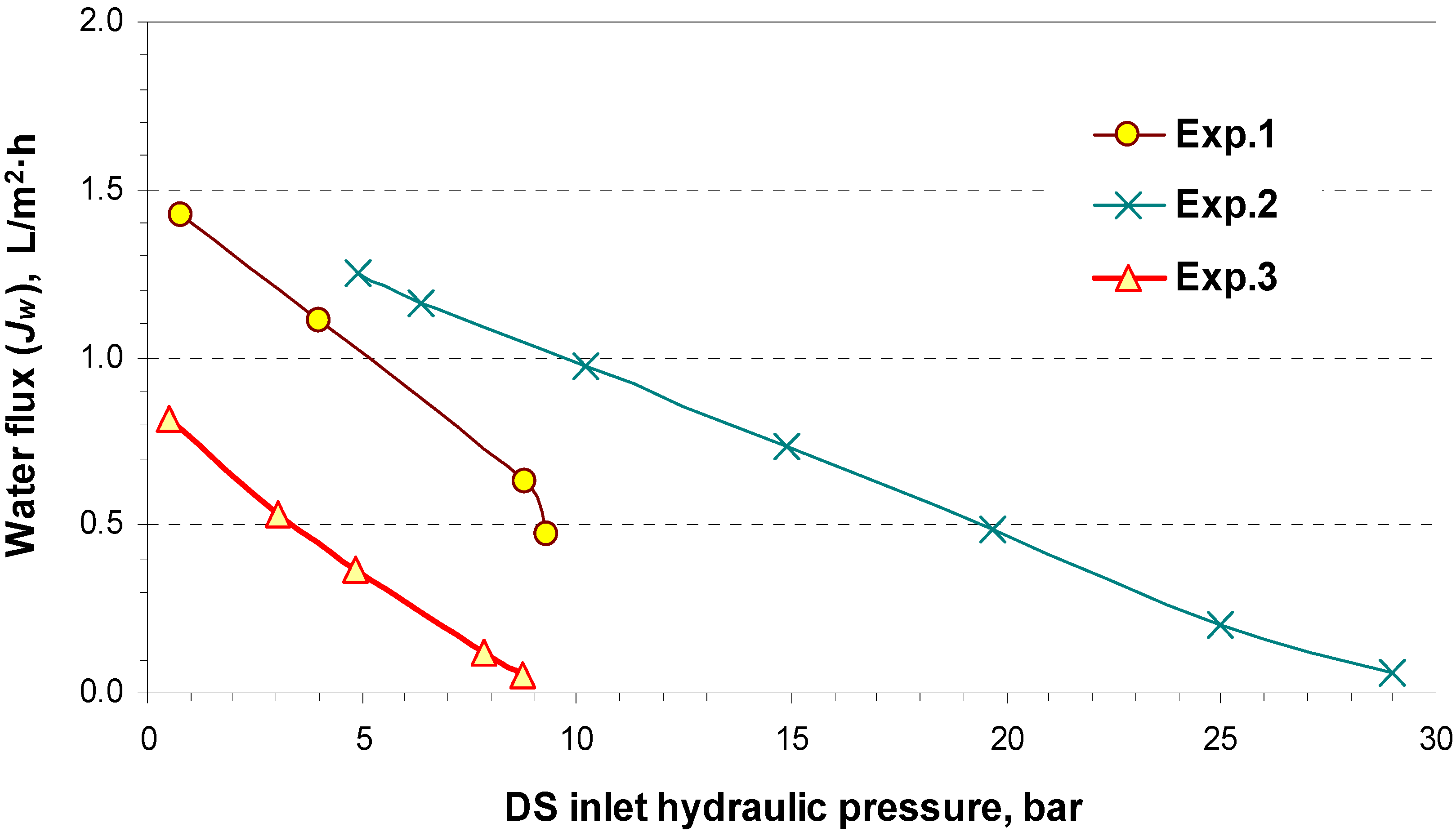
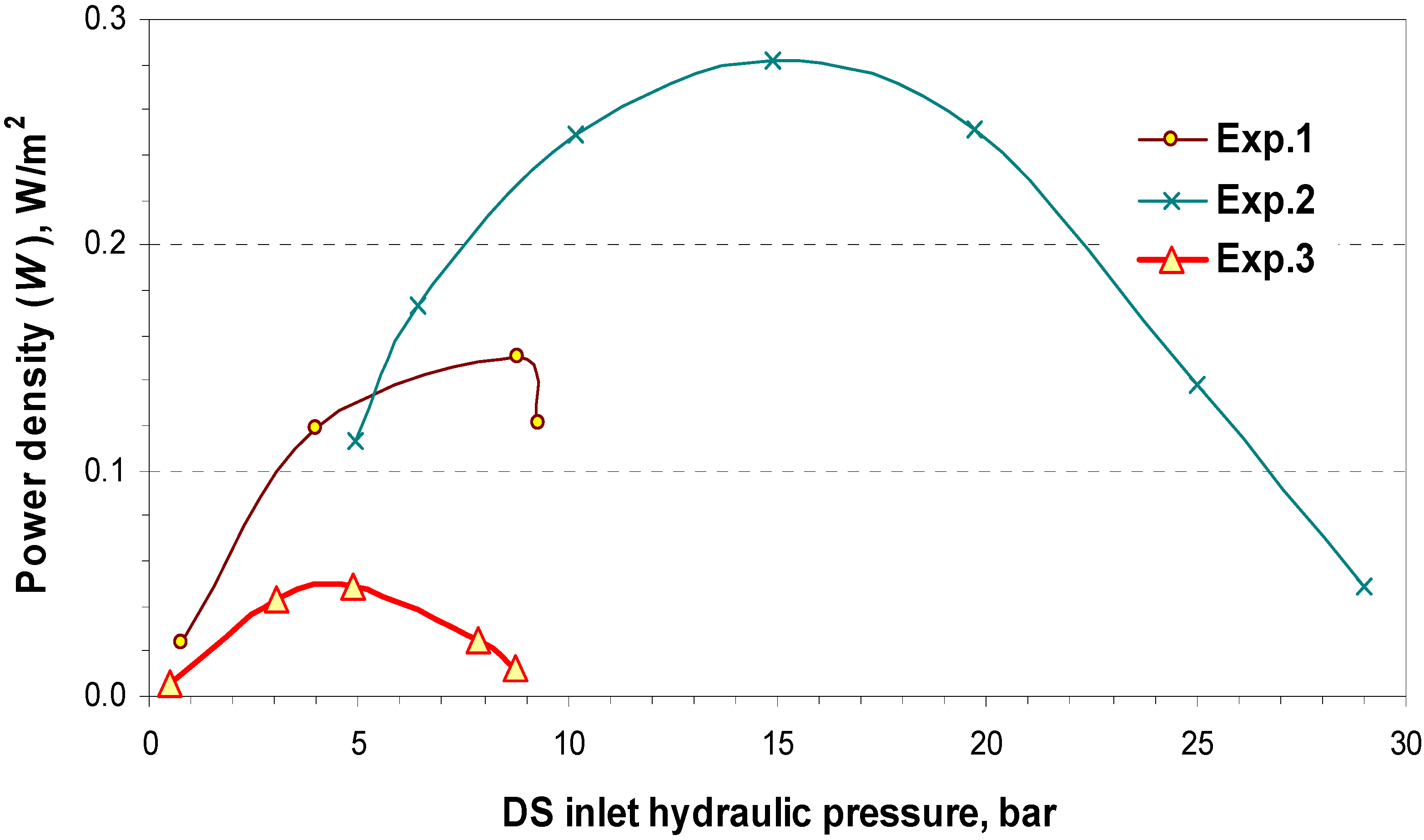
5. Commercial Potential and Cost Estimation
| Renewable/Non-Renewable Energy Sources | Estimated Energy Cost (€/MWh) Forecast 2030 |
|---|---|
| Nuclear | 45 |
| Gas CCGT | 85 |
| Oil CC | 125 |
| Coal PCC | 80 |
| Hydro dam | 85 |
| Hydro running | 48 |
| Biomass | 88 |
| Wind Offshore | 115 |
| Wind Onshore | 90 |
| Solar | 160 |
| Osmotic Energy | 50–100 |
| Plant Economic Performance | Value |
| Discount Rate (%) | 6 |
| Plant Lifetime (year) | 15 |
| Energy | Value |
| Industrial Electricity Price (£/kWh) | 0.05 |
| Turbine and Generator | Value |
| Specific Investment Cost (£/MWe) | 200,000 |
| O&M (% capital) | 3 |
| Life time (year) | 15 |
| Maximum Unit Capacity (MWe) | 100 |
| Low pressure pumps | Value |
| Specific Investment Cost (£/MWe) | 10,000 |
| Life time (year) | 15 |
| O & M (% capital) | 2.5 |
| Maximum Pump Unit Capacity (MWe) | 100 |
| Pressure exchanger system (PES) | Value |
| Specific Investment Cost (£/MW) | 50,000 |
| O&M costs (% capital) | 2.5 |
| Life time (year) | 15 |
| Maximum Unit Capacity (MWe) | 5 |
| Membranes (for both OMU and RU) | Value |
| Specific Investment Cost (£/module) | 70 |
| Life time (year) | 7 |
| Max Module Area (m2) | 100.8 |
| Pipes and valves | Value |
| Specific Cost (£/km) | 100,000 |
| Life time (year) | 15 |
| O&M costs (% capital) | 2.5 |
| Specific inv. Cost of Brine pre-treatment (% plant capital) | 4 |
| control system (£/MWe) | 10,000 |
| Specific cost of Draw Solution(£/m3) | 10 |
| Plant Availability (%) | 90 |
| Yearly Salary of Personnel (£/year) | 25,000 |
| No. of Personnel | 66 |
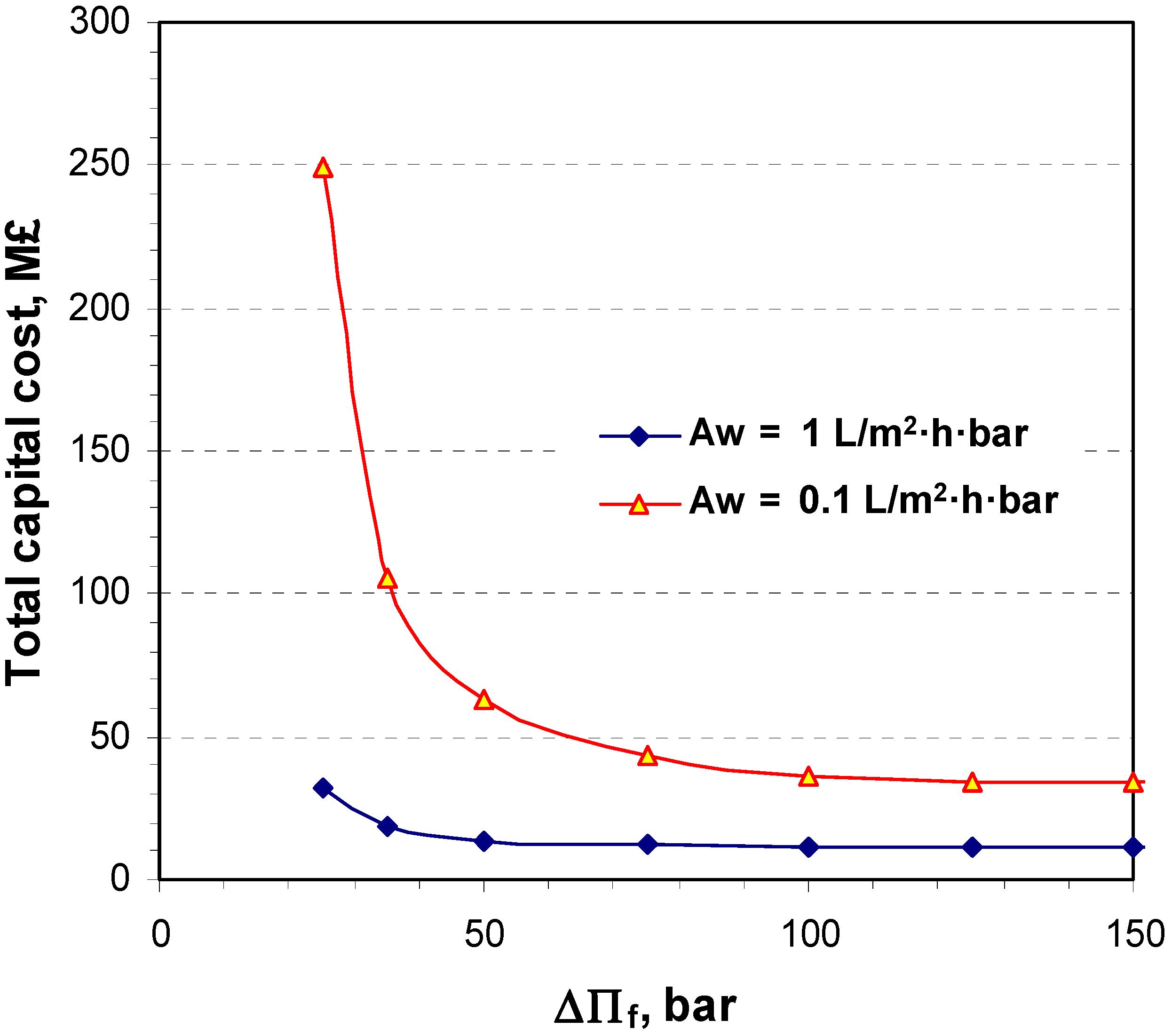

6. Conclusions
Nomenclature
Abbreviations
| HOP | Hydro-Osmotic Power |
| RE | Renewable Energy |
| RO | Reverse Osmosis |
| SEC | Specific Energy Consumption |
| ERS | Energy Recovery System |
| PRO | Pressure Retarded Osmosis |
| PES | Pressure Exchange System |
| OE | osmotic energy |
| FO | Forward Osmosis |
| DS | Draw Solution |
| CTA | Cellulose Triacetate |
| R&D | Research & Development |
| MW | Modern Water |
| CORA | Centre for Osmosis Research and Applications |
| OMU | Osmotic Membrane Unit |
| FW | Feed Water |
| RU | Regeneration Unit |
| OHE | Osmotic Heat Engine |
| SDPFFR | Solution-Diffusion Pore-Flow Fluid-Resistance |
| ASDPF | Analytical Solution-Diffusion Pore-Flow |
Symbols
| Jw | Water flux (L/m2·h) |
| AW | System permeability to water (L/m2·h·bar) |
| ∆П | Net osmotic pressure difference across membrane |
| ∆P | Net hydraulic pressure difference |
| W | Density of power (W/m2) |
| Awm | The membrane phase permeability (L/m2·h·bar) |
| Aws | The solution phase, the DS and the FW, permeability (L/m2·h·bar) |
| δmo | Membrane thickness |
| εo | Membrane porosity |
| τo | Membrane tortuosity |
| dmo | Membrane mean pore diameter |
| Dwo | Self-diffusivity |
| ρwo | Density |
| μo | Viscosity |
| Mw | Molecular weight of pure water at the reference temperature (To = 298.15 K) |
| Rg | Universal gas constant |
| T, Y, K, H | Constant values |
| П | Osmotic pressure (bar) |
| P | Hydraulic pressure (bar) |
| Q | The volumetric flow rate (m3/s) |
| Qw | The permeated water flow rate across the membrane (m3/s) |
| PG | The gross power production (MW) |
| ρE | The energy density (kWh/m3) |
| ES | The specific energy production (kWh/m3) |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Herzog, A.V.; Lipman, T.E.; Kammen, D.M. Renewable Energy Sources. Available online: https://rael.berkeley.edu/sites/default/files/old-site-files/2001/Herzog-Lipman-Kammen-RenewableEnergy-2001.pdf (accessed on 28 July 2001).
- Loeb, S. Large-scale power production by pressure-retarded osmosis using river water and seawater passing through spiral modules. Desalination 2002, 143, 115–122. [Google Scholar] [CrossRef]
- Loeb, S. Method and Apparatus for Generating Power Utilizing Pressure-Retarded-Osmosis. U.S. Patent US4193267 A, 18 March 1980. [Google Scholar]
- Reali, M. Submarine hydro-electro-osmotic power plants for an efficient exploitation of salinity gradients. Energy 1981, 6, 227–231. [Google Scholar] [CrossRef]
- Sharif, A.O.; Rahal, Z.; Merdaw, A.A. Power from salt water- is water going to be the World’s new oil? Arab Water World XXXIV 2010, 2, 6–9. [Google Scholar]
- Logan, B.E.; Elimelech, M. Membrane-based processes for sustainable power generation using water. Nature 2012, 488, 313–319. [Google Scholar] [CrossRef]
- Skilhagen, S.E.; Dugstad, J.E.; Aaberg, R.J. Osmotic power-Power production based on the osmotic pressure difference between waters with varying salt gradients. Desalination 2008, 220, 476–482. [Google Scholar] [CrossRef]
- Al-Mayahi, A.; Sharif, A.O. Energy Generation Method (Osmotic Energy). European Patent 1660772, 27 June 2007. [Google Scholar]
- McGinnis, R.L.; McCutcheon, J.R.; Elimelech, M. A novel ammonia-carbon dioxide osmotic heat engine for power generation. J. Membr. Sci. 2007, 305, 13–19. [Google Scholar] [CrossRef]
- Helfer, F.; Lemckert, Ch.; Anissimov, Y.G. Osmotic power with Pressure Retarded Osmosis: Theory, performance and trends—A review. J. Membr. Sci. 2014, 453, 337–358. [Google Scholar] [CrossRef]
- Loeb, S.; Hessen, F.V.; Shahaf, D. Production of energy from concentrated brines by pressure-retarded osmosis II Experimental results and projected energy costs. J. Membr. Sci. 1976, 1, 249–269. [Google Scholar] [CrossRef]
- Mehta, G.D. Further results on the performance of present-day osmotic membranes in various osmotic regions. J. Membr. Sci. 1982, 10, 3–19. [Google Scholar] [CrossRef]
- Loeb, S.; Mehta, G.D. A two coefficient water transport equation for pressure retarded osmosis. J. Membr. Sci. 1979, 4, 351–362. [Google Scholar] [CrossRef]
- Mehta, G.D.; Loeb, S. Performance of permasep B-9 and B-10 membranes in various osmotic regions and at high osmotic pressures. J. Membr. Sci. 1979, 4, 335–349. [Google Scholar] [CrossRef]
- Lee, K.L.; Baker, R.W.; Lonsdale, H.K. Membrane for power generation by pressure retarded osmosis. J. Membr. Sci. 1981, 8, 141–171. [Google Scholar] [CrossRef]
- Jellinek, H.H.; Masuda, H. Osmo-power, theory and performance of an osmo-power pilot plant. Ocean Eng. 1981, 8, 103–128. [Google Scholar] [CrossRef]
- Gerstandt, K.; Peinemann, K.V.; Skilhagen, S.E.; Thorsen, T.; Holt, T. Membrane processes in energy supply for an osmotic power plant. Desalination 2008, 224, 64–70. [Google Scholar] [CrossRef]
- Achilli, A.; Cath, T.; Childress, A. Power generation with pressure retarded osmosis: An experimental and theoretical investigation. J. Membr. Sci. 2009, 343, 42–52. [Google Scholar] [CrossRef]
- Thorsen, T.; Holt, T. The potential for power production from salinity gradients by pressure retarded osmosis. J. Membr. Sci. 2009, 335, 103–110. [Google Scholar] [CrossRef]
- Chou, S.; Wang, R.; Shi, L.; She, Q.; Tang, C.; Fane, A.G. Thin-film composite hollow fibre membranes for pressure retarded osmosis (PRO) process with high power density. J. Membr. Sci. 2012, 389, 25–33. [Google Scholar] [CrossRef]
- Yip, N.; Elimelech, M. Thermodynamic and energy efficiency analysis of power generation from natural salinity gradients by pressure retarded osmosis. Energy Environ. Sci. 2012, 46, 5230–5239. [Google Scholar]
- She, Q.; Jin, X.; Tang, C. Osmotic power production from salinity gradient resource by pressure retarded osmosis: Effect of operating conditions and reverse solute diffusion. J. Membr. Sci. 2012, 401–402, 262–273. [Google Scholar] [CrossRef]
- Kim, Y.; Elimelech, M. Potential of osmotic power generation by pressure retarded osmosis using seawater as feed solution: Analysis and experiments. J. Membr. Sci. 2013, 429, 330–337. [Google Scholar] [CrossRef]
- Wang, R.; Tang, C.; Fane, A.G. Development of pressure retarded osmosis (PRO) membranes with high power density for osmotic power harvesting. In Proceedings of the 3rd Osmosis Membrane Summit, Statkraft, Barcelona, Spain, 26–27 April 2012.
- Schiestel, T.; Hänel, C.; Öxler, L.; Roelofs, K.; Walitza, E. Cellulose acetate membranes with an optimized internal structure for pressure retarded osmosis. In Proceedings of the 3rd Osmosis Membrane Summit, Statkraft, Barcelona, Spain, 26–27 April 2012.
- Saito, K.; Irie, M.; Zaitsu, S.; Sakai, H.; Hayashi, H.; Tanioka, A. Power generation with salinity gradient by pressure retarded osmosis using concentrated brine from SWRO system and treated sewage as pure water. Desalin. Water Treat. 2012, 41, 114–121. [Google Scholar] [CrossRef]
- Efraty, A. Pressure retarded osmosis in closed circuit without need of energy recovery. In Proceedings of the 3rd Osmosis Membrane Summit, Statkraft, Barcelona, Spain, 26–27 April 2012.
- Spiegler, K.S.; E1-Sayed, Y.M. The energetics of desalination processes. Desalination 2001, 134, 109–128. [Google Scholar] [CrossRef]
- Loeb, S. Energy production at the Dead Sea by pressure-retarded osmosis: Challenge or chimera? Desalination 1998, 120, 247–262. [Google Scholar] [CrossRef]
- Lachish, U. Osmosis and thermodynamics. Am. J. Phys. 2007, 75, 997–998. [Google Scholar] [CrossRef]
- Merdaw, A.A.; Sharif, A.O.; Derwish, G.A.W. Water permeability in polymeric membranes, Part II. Desalination 2010, 257, 184–194. [Google Scholar] [CrossRef]
- Toffoletto, M.; Merdaw, A.A.; Sharif, A.O.; Bertucco, A. Experimental approaches to feed solution permeability in pressure-driven membrane separation processes. J. Membr. Sci. 2010, 364, 27–33. [Google Scholar] [CrossRef]
- Merdaw, A.A.; Sharif, A.O.; Derwish, G.A.W. Mass transfer in pressure-driven membrane separation processes, Part I. Chem. Eng. J. 2011, 168, 215–228. [Google Scholar] [CrossRef]
- Merdaw, A.A.; Sharif, A.O.; Derwish, G.A.W. Water permeability in polymeric membranes, Part I. Desalination 2010, 260, 180–192. [Google Scholar] [CrossRef]
- Skilhagen, S. Osmotic power a new renewable energy source. Desalination 2010, 15, 271–278. [Google Scholar] [CrossRef]
- Sharif, A.O. Separation Process. UK Patent Application No. WO 2008/050087, September 2008. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sharif, A.O.; Merdaw, A.A.; Aryafar, M.; Nicoll, P. Theoretical and Experimental Investigations of the Potential of Osmotic Energy for Power Production. Membranes 2014, 4, 447-468. https://doi.org/10.3390/membranes4030447
Sharif AO, Merdaw AA, Aryafar M, Nicoll P. Theoretical and Experimental Investigations of the Potential of Osmotic Energy for Power Production. Membranes. 2014; 4(3):447-468. https://doi.org/10.3390/membranes4030447
Chicago/Turabian StyleSharif, Adel O., Ali A. Merdaw, Maryam Aryafar, and Peter Nicoll. 2014. "Theoretical and Experimental Investigations of the Potential of Osmotic Energy for Power Production" Membranes 4, no. 3: 447-468. https://doi.org/10.3390/membranes4030447
APA StyleSharif, A. O., Merdaw, A. A., Aryafar, M., & Nicoll, P. (2014). Theoretical and Experimental Investigations of the Potential of Osmotic Energy for Power Production. Membranes, 4(3), 447-468. https://doi.org/10.3390/membranes4030447




