Membrane Charge Effects on Solute Transport in Nanofiltration: Experiments and Molecular Dynamics Simulations
Abstract
1. Introduction
2. Methods
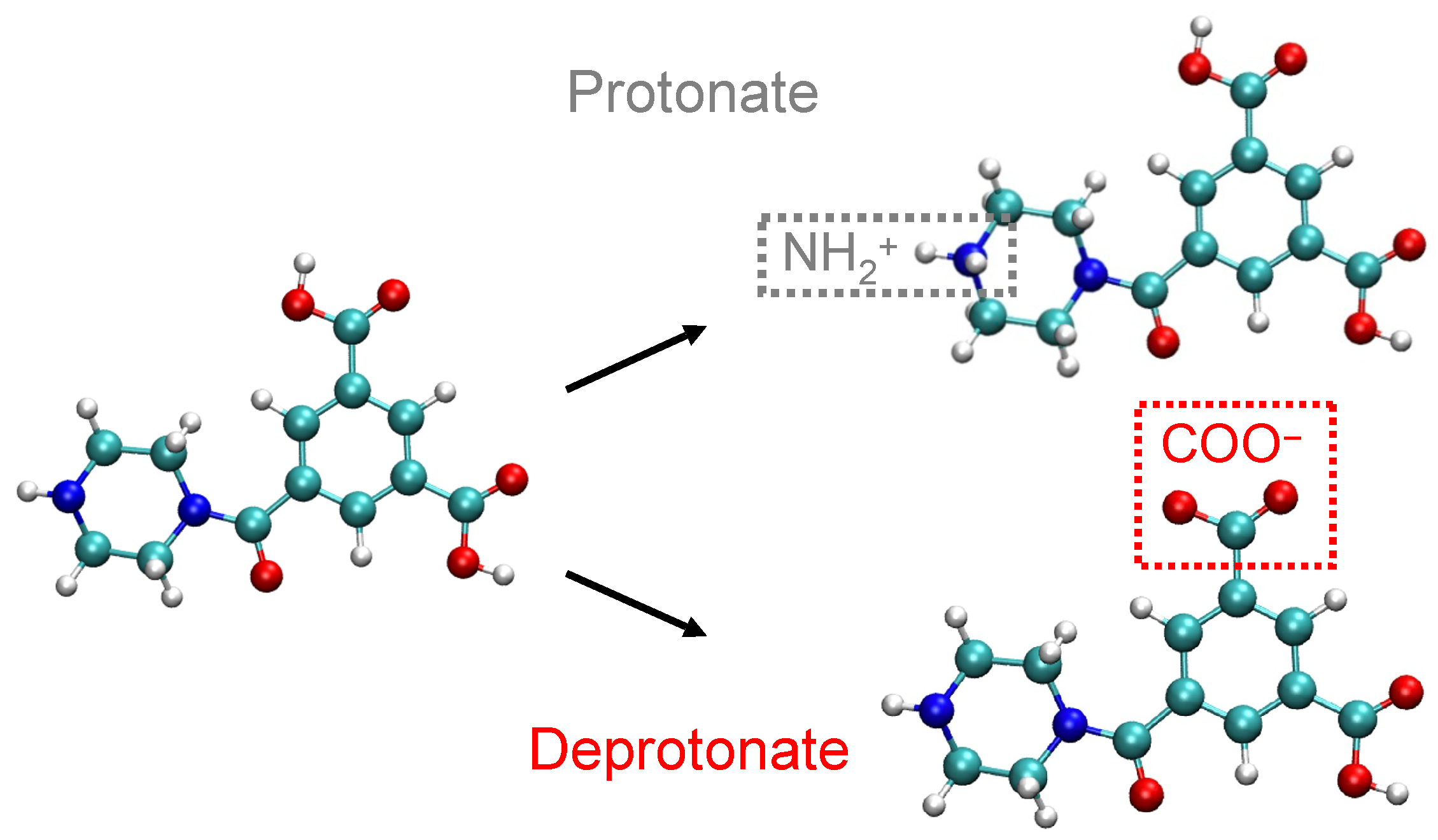
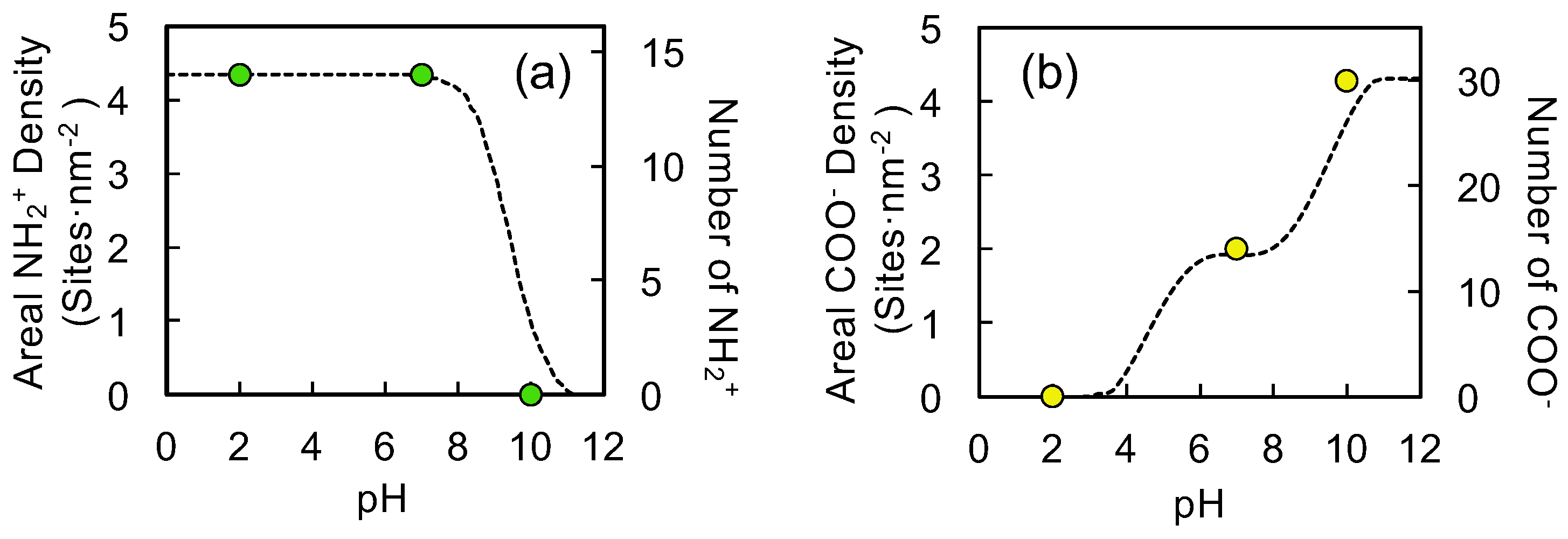
2.1. Membrane Model Preparation
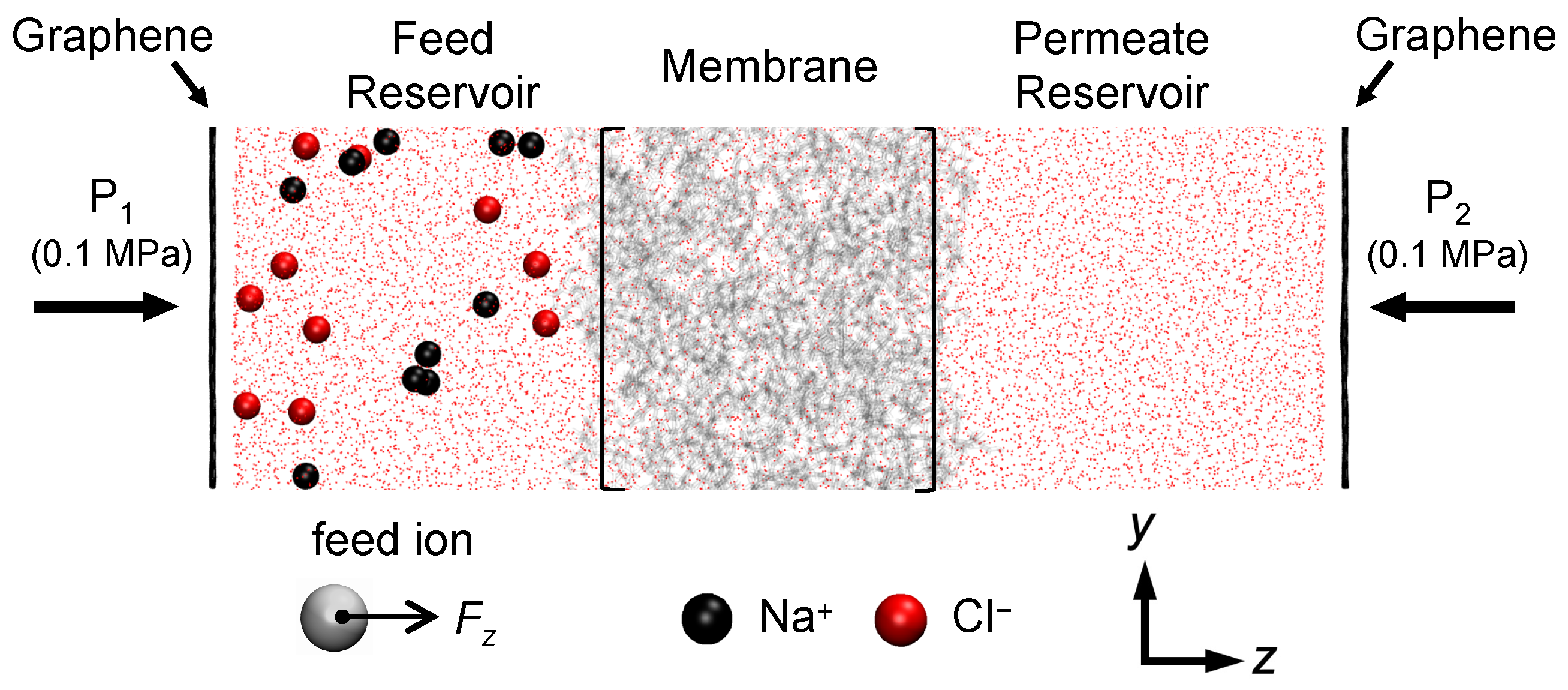
2.2. Solute Transport Simulations
2.3. Experiment Design
3. Results and Discussion
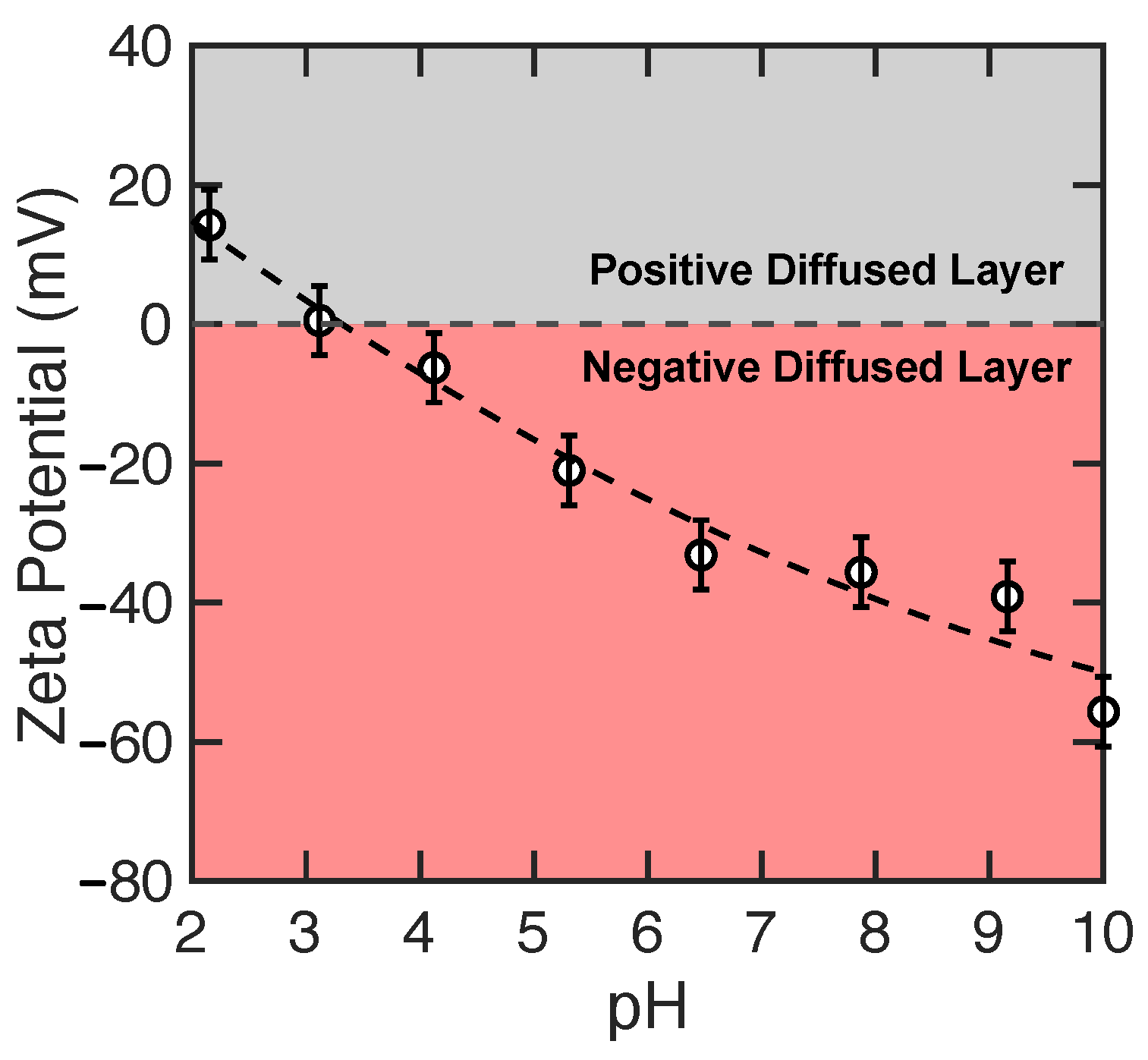
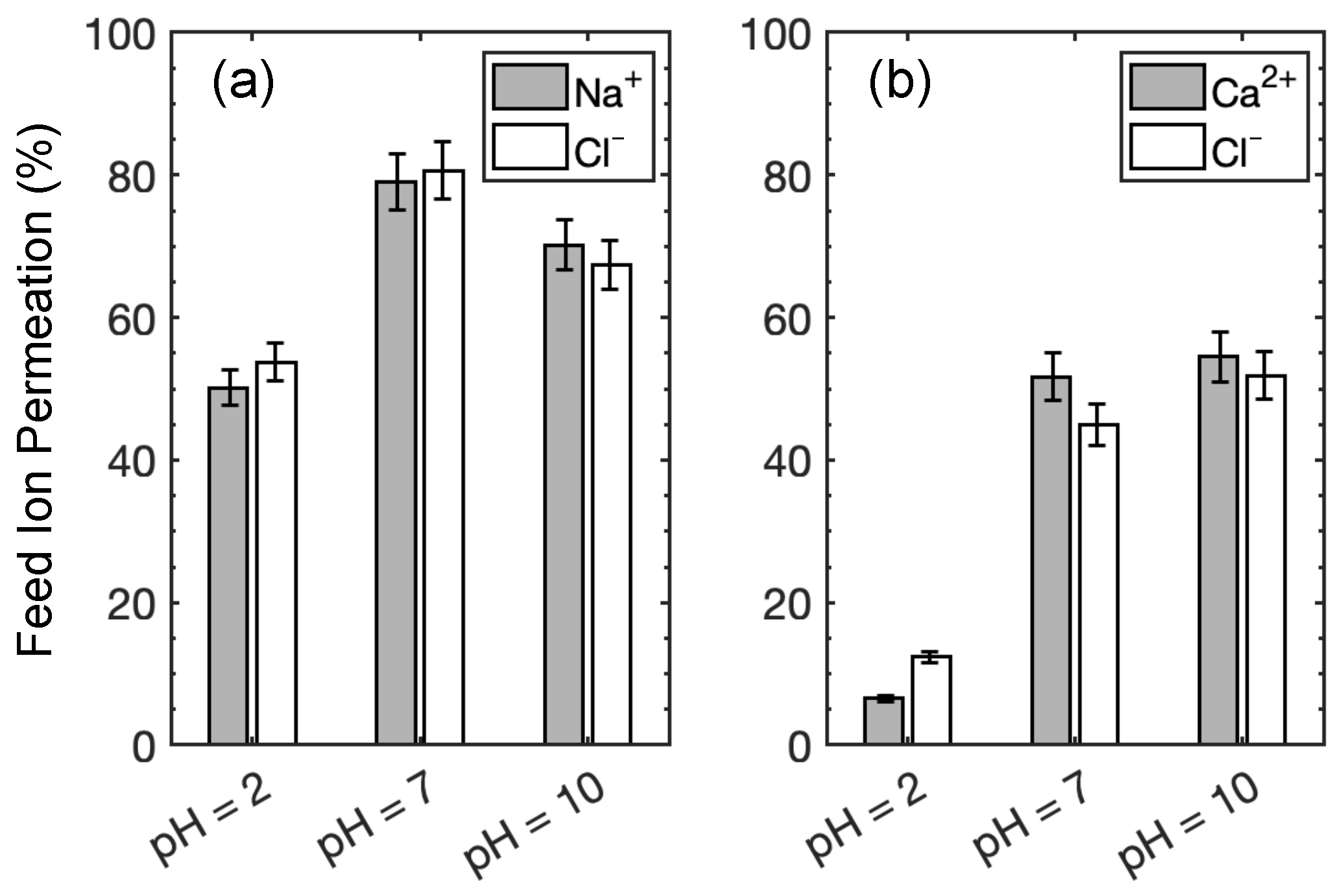
3.1. Experimental Results
3.2. Solute Transport Simulations
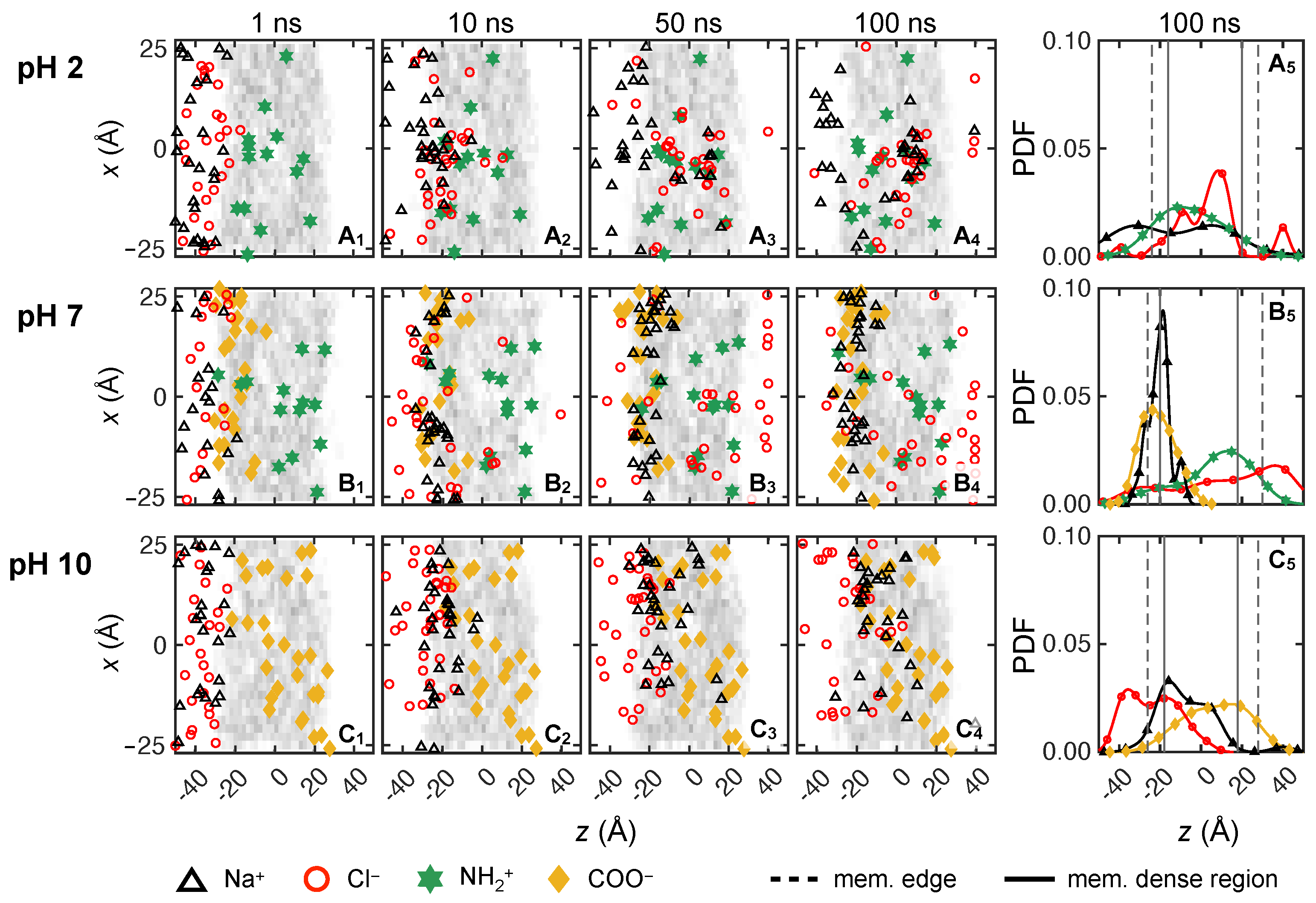
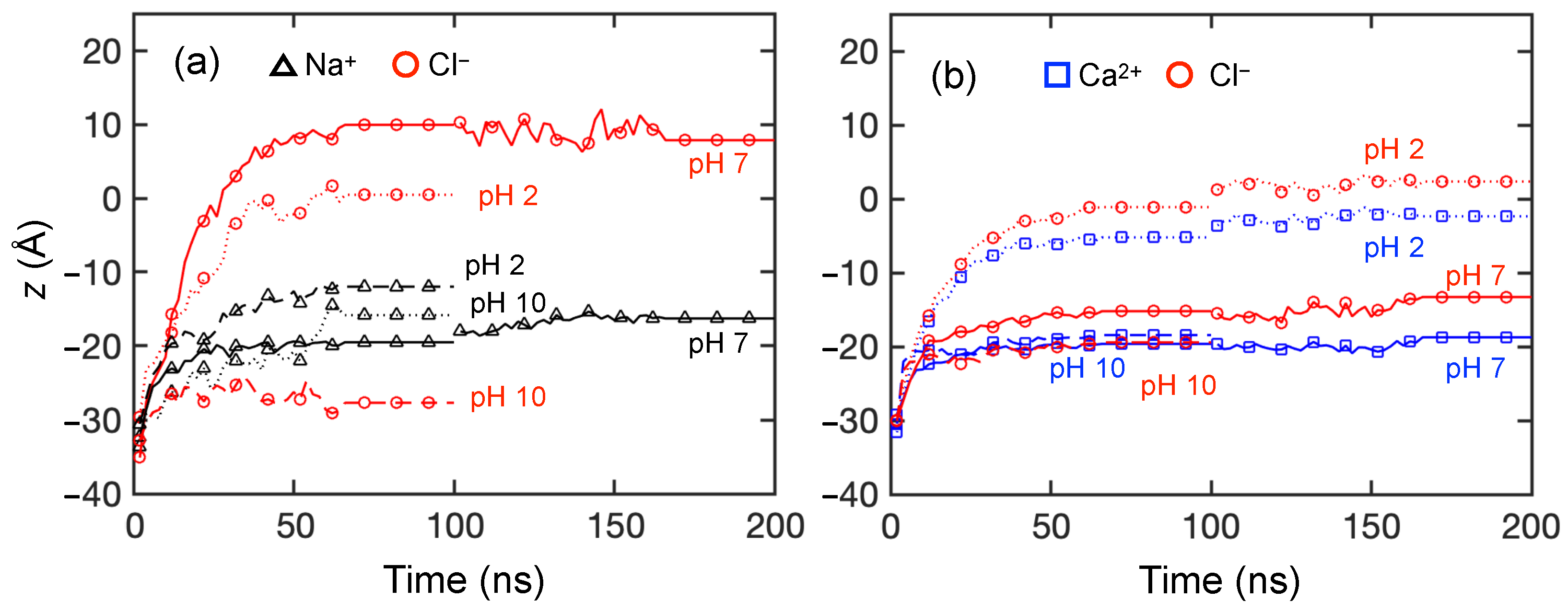
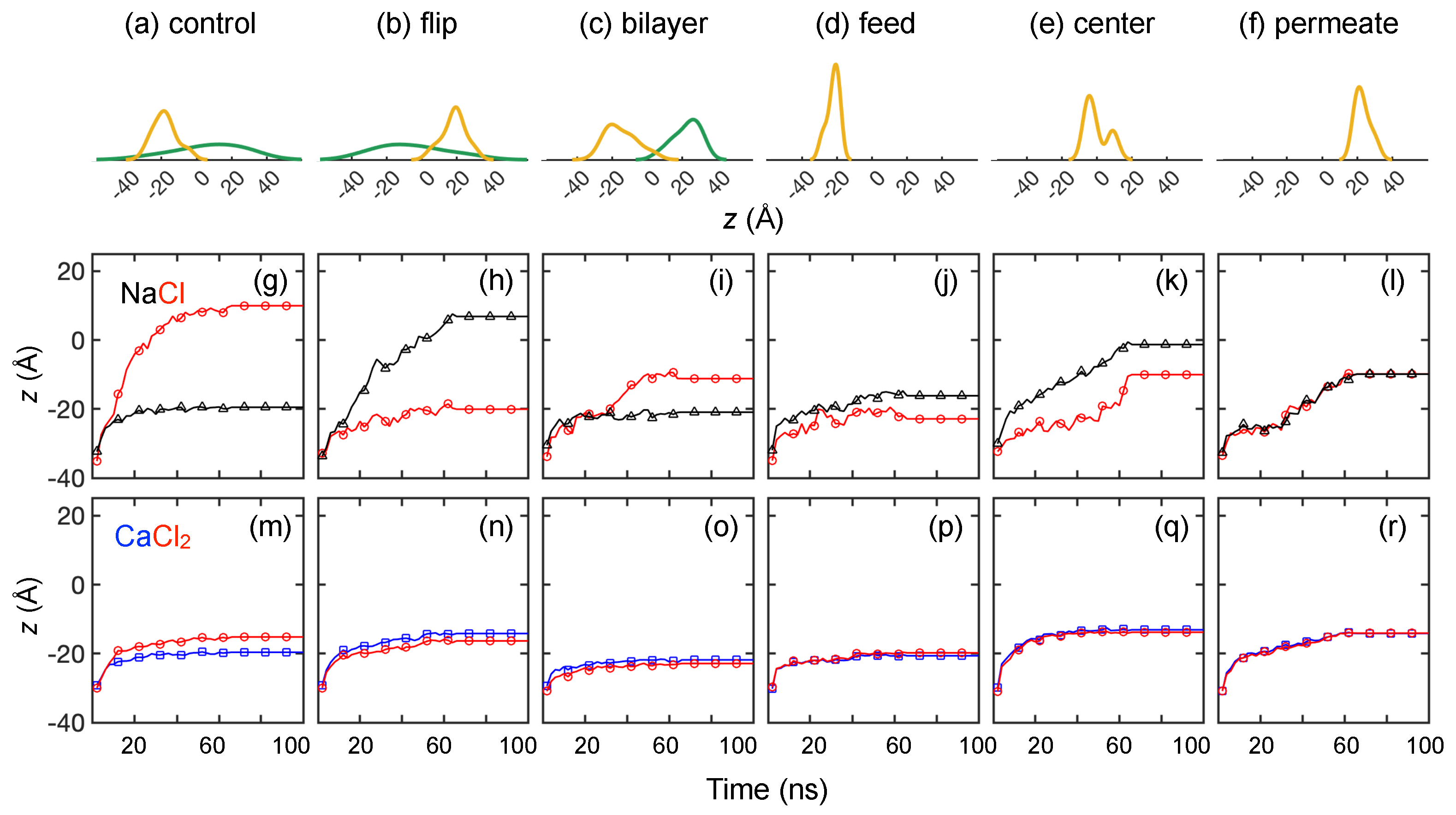
3.2.1. Monovalent Solute Transport
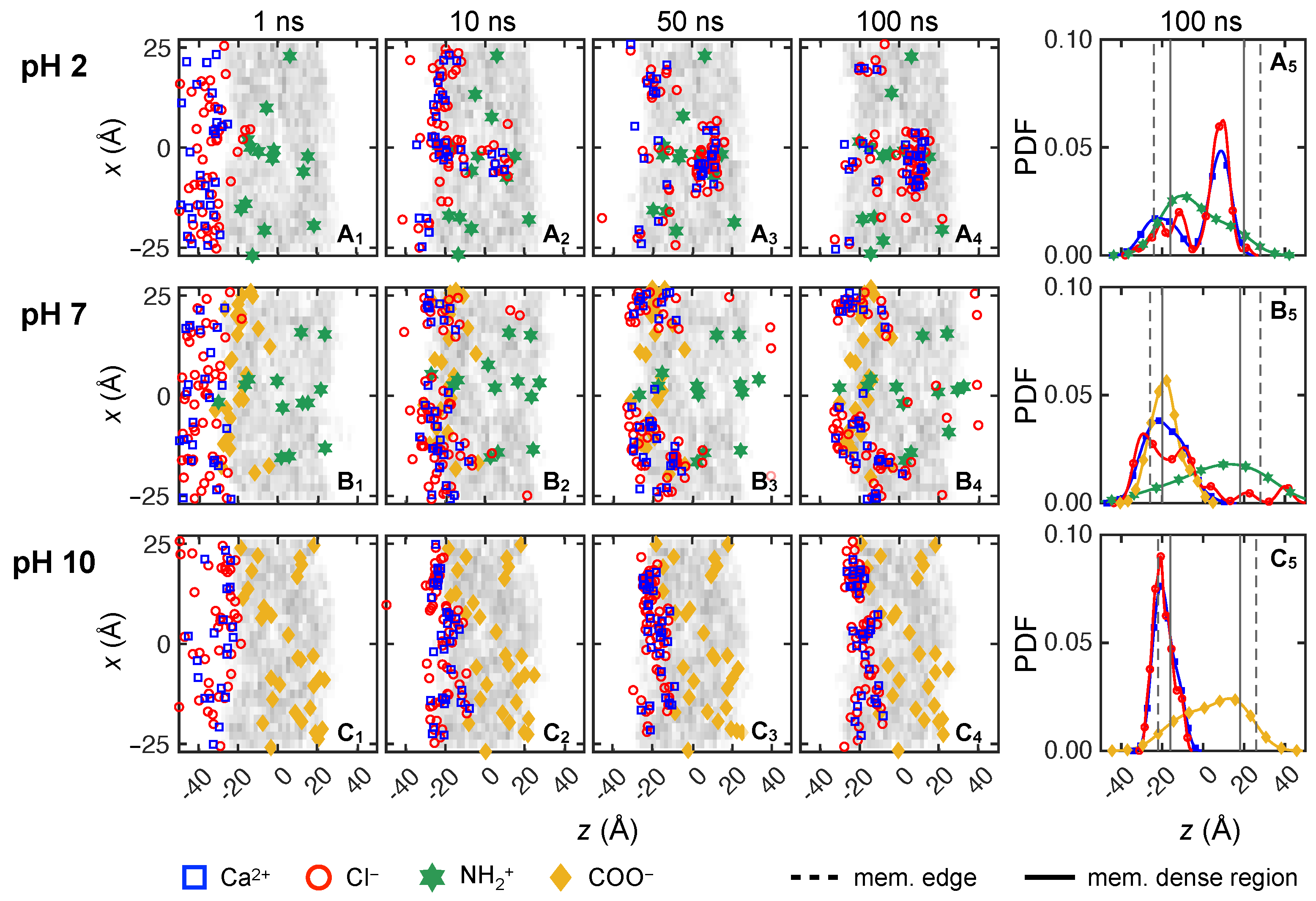
3.2.2. Divalent Solute Transport
3.2.3. Comparing Mono- and Di-Valent Solute Transport
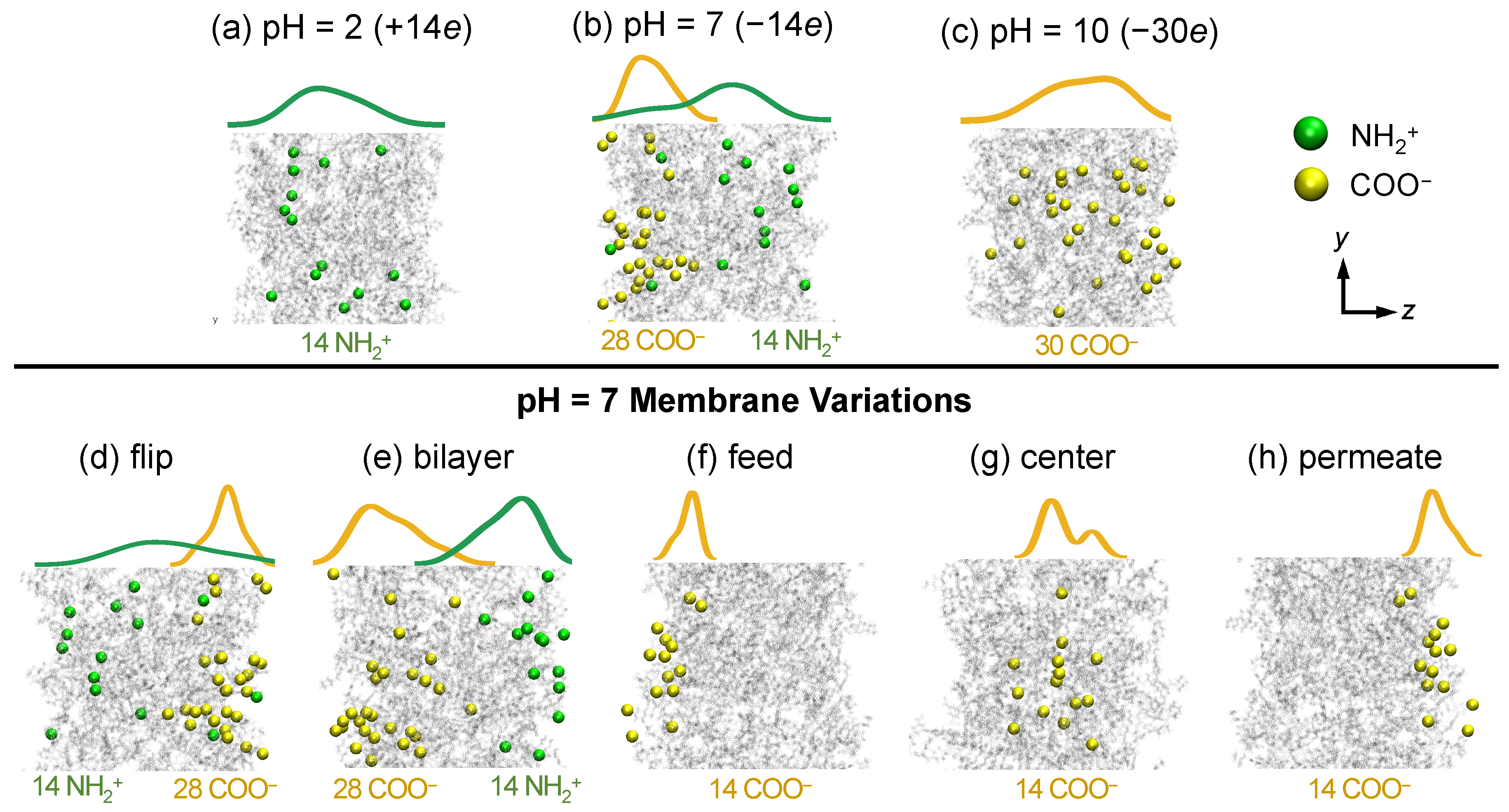
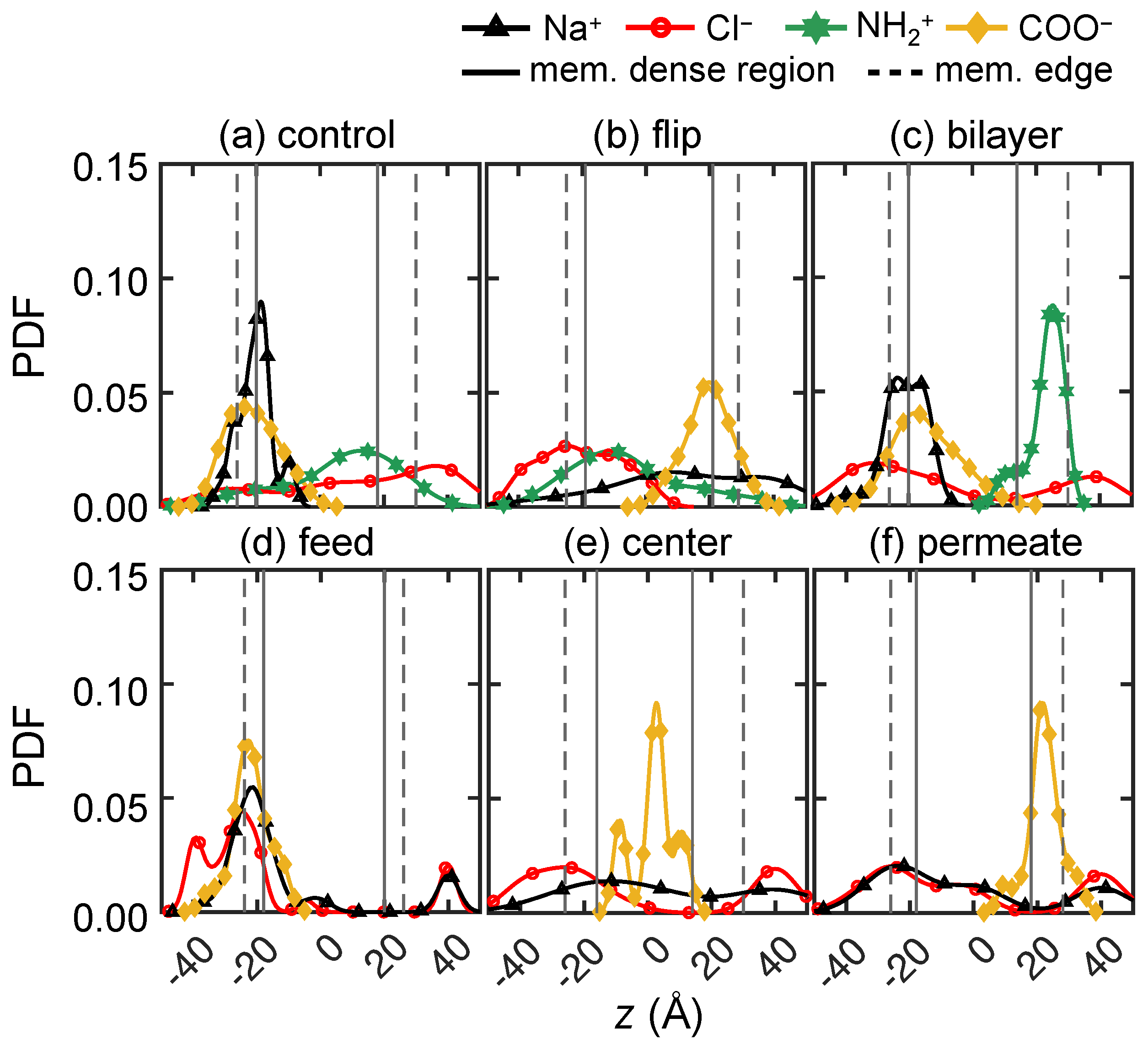
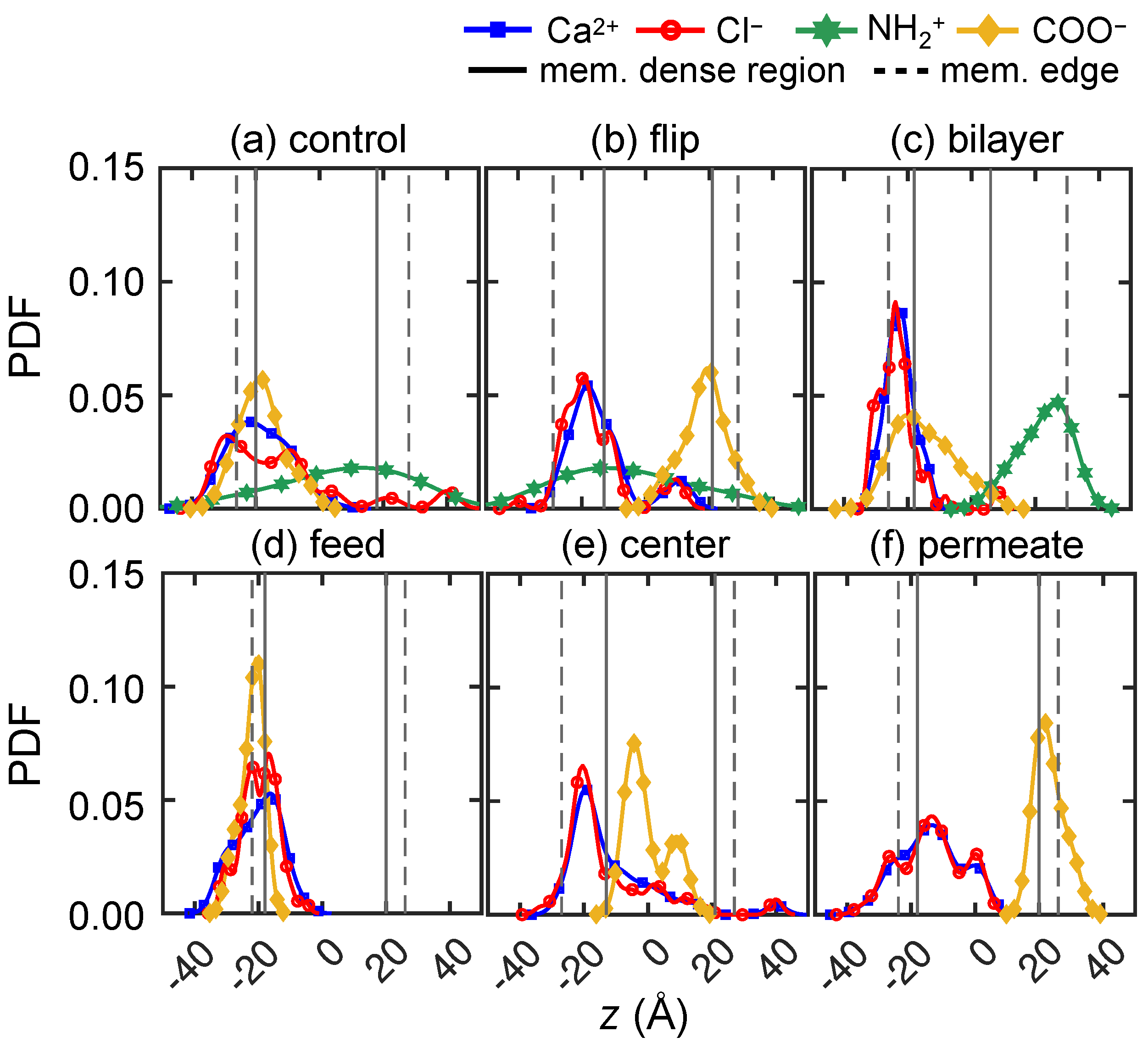
3.2.4. Solute Transport Dependence on Charge Distribution
3.3. Solute–Membrane Dynamics and Interactions
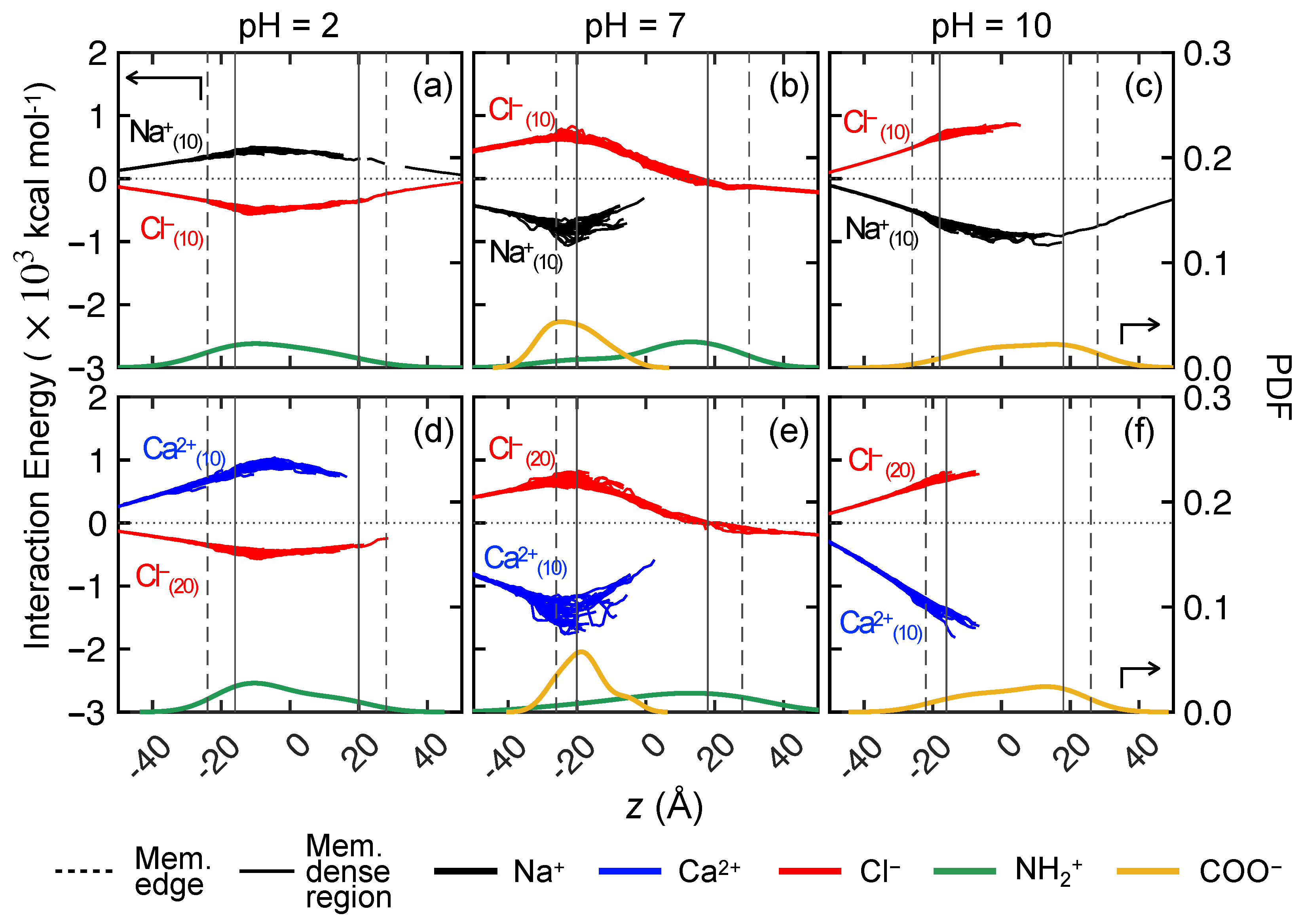
3.3.1. Ion–Membrane Interaction Energy
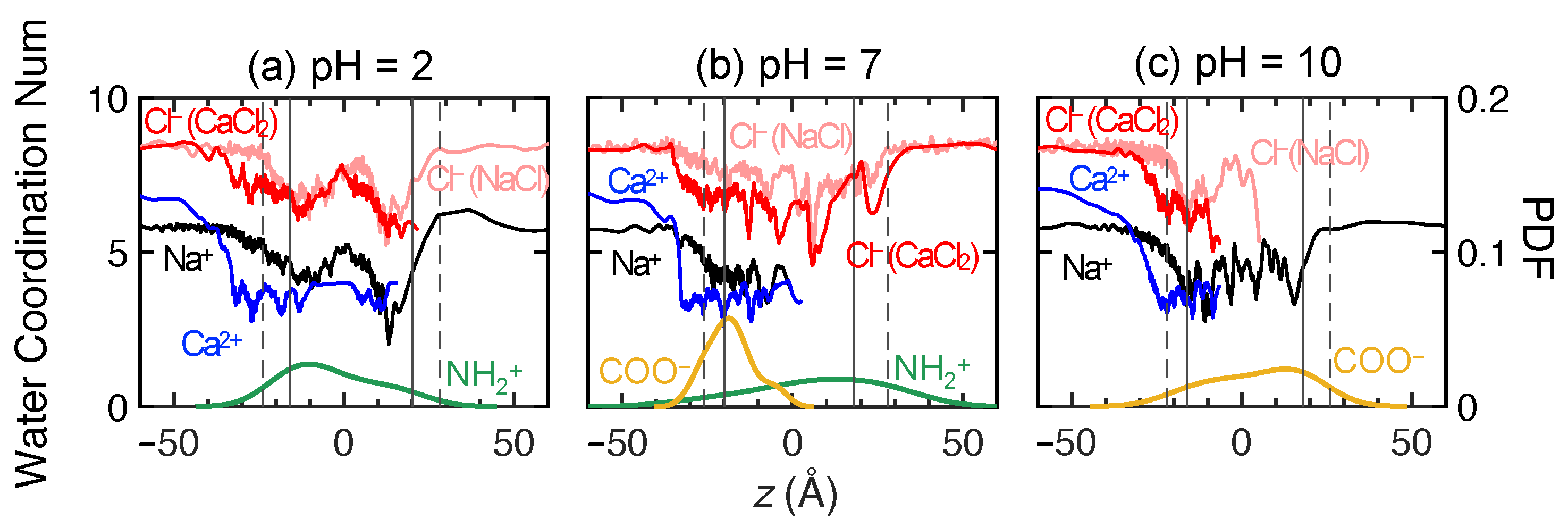
3.3.2. Ion Hydration in Membranes
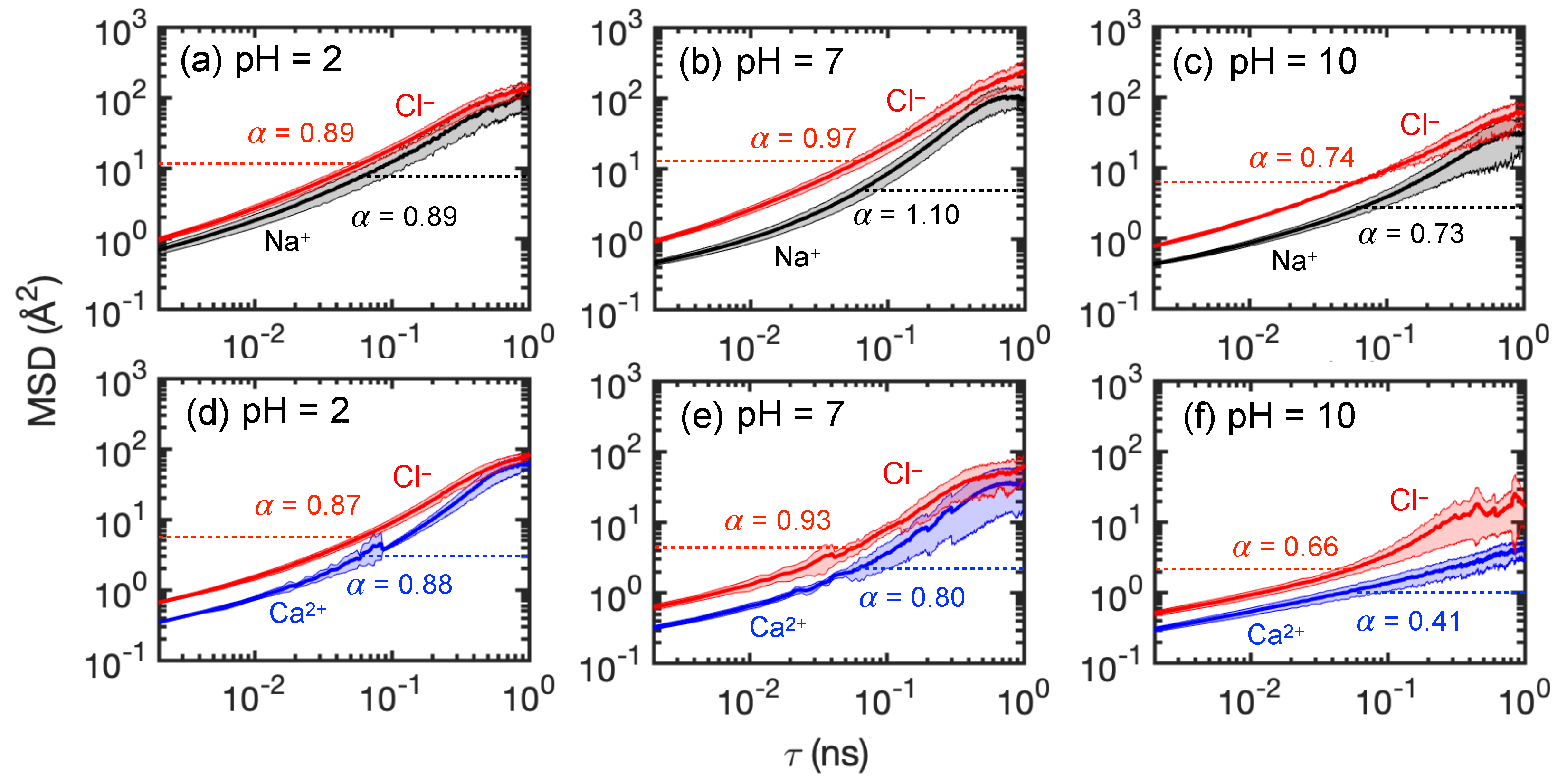
3.3.3. Ion Diffusivity in Membranes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RO | Reverse Osmosis |
| NF | Nanofiltration |
| MD | Molecular Dynamics |
| TMC | Trimesoyl Chloride |
| MPD | m-Phenylene Diamine |
| PIP | Piperazine |
| IEP | Isoelectric Point |
| AMBER | Assisted Model Building with Energy Refinement |
| GaFF | General AMBER Force Field |
| AM1-BCC | Austin Model 1-Bond Charge Correction |
| NAMD | Nanoscale Molecular Dynamics |
| TIP4P | Transferable Intermolecular Potential with 4 Points |
| PME | Particle Mesh Ewald |
| ICP-MS | Inductively Coupled Plasma Mass Spectrometry |
| ICP-OES | Inductively Coupled Plasma Optical Emission Spectroscopy |
| OPLS | Optimized Potentials for Liquid Simulations |
| RDF | Radial Distribution Function |
| WCN | Water Coordination Number |
| Probability Density Function | |
| MSD | Mean Square Displacement |
| Ion Permeance |
References
- Kiso, Y.; Nishimura, Y.; Kitao, T.; Nishimura, K. Rejection properties of non-phenylic pesticides with nanofiltration membranes. J. Membr. Sci. 2000, 171, 229–237. [Google Scholar] [CrossRef]
- Schäfer, A.; Nghiem, L.; Waite, T. Removal of the natural hormone estrone from aqueous solutions using nanofiltration and reverse osmosis. Environ. Sci. Technol. 2003, 37, 182–188. [Google Scholar] [CrossRef] [PubMed]
- Kiso, Y.; Sugiura, Y.; Kitao, T.; Nishimura, K. Effects of hydrophobicity and molecular size on rejection of aromatic pesticides with nanofiltration membranes. J. Membr. Sci. 2001, 192, 1–10. [Google Scholar] [CrossRef]
- Foo, Z.H.; Liu, S.; Kanias, L.; Lee, T.R.; Heath, S.M.; Tomi, Y.; Miyabe, T.; Keten, S.; Lueptow, R.M.; Lienhard, J.H. Positively-Coated Nanofiltration Membranes for Lithium Recovery from Battery Leachates and Salt-Lakes: Ion Transport Fundamentals and Module Performance. Adv. Funct. Mater. 2024, 34, 2408685. [Google Scholar] [CrossRef]
- Charcosset, C. A review of membrane processes and renewable energies for desalination. Desalination 2009, 245, 214–231. [Google Scholar] [CrossRef]
- Pontié, M.; Dach, H.; Leparc, J.; Hafsi, M.; Lhassani, A. Novel approach combining physico-chemical characterizations and mass transfer modelling of nanofiltration and low pressure reverse osmosis membranes for brackish water desalination intensification. Desalination 2008, 221, 174–191. [Google Scholar] [CrossRef]
- Yoon, Y.; Lueptow, R.M. Removal of organic contaminants by RO and NF membranes. J. Membr. Sci. 2005, 261, 76–86. [Google Scholar] [CrossRef] [PubMed]
- Uemura, T.; Henmi, M. Thin-film composite membranes for reverse osmosis. In Advanced Membrane Technology and Applications; Li, N.N., Fane, A.G., Ho, W.S.W., Matsuura, T., Eds.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lee, S.; Lueptow, R.M. Membrane rejection of nitrogen compounds. Environ. Sci. Technol. 2001, 35, 3008–3018. [Google Scholar] [CrossRef]
- Geise, G.M.; Lee, H.S.; Miller, D.J.; Freeman, B.D.; McGrath, J.E.; Paul, D.R. Water purification by membranes: The role of polymer science. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 1685–1718. [Google Scholar] [CrossRef]
- Bellona, C.; Drewes, J.E.; Xu, P.; Amy, G. Factors affecting the rejection of organic solutes during NF/RO treatment—A literature review. Water Res. 2004, 38, 2795–2809. [Google Scholar] [CrossRef]
- Schaep, J.; Van der Bruggen, B.; Vandecasteele, C.; Wilms, D. Influence of ion size and charge in nanofiltration. Sep. Purif. Technol. 1998, 14, 155–162. [Google Scholar] [CrossRef]
- Van der Bruggen, B.; Vandecasteele, C.; Van Gestel, T.; Doyen, W.; Leysen, R. A review of pressure-driven membrane processes in wastewater treatment and drinking water production. Environ. Prog. 2003, 22, 46–56. [Google Scholar] [CrossRef]
- Ng, L.Y.; Mohammad, A.W.; Ng, C.Y.; Leo, C.P.; Rohani, R. Development of nanofiltration membrane with high salt selectivity and performance stability using polyelectrolyte multilayers. Desalination 2014, 351, 19–26. [Google Scholar] [CrossRef]
- Labban, O.; Liu, C.; Chong, T.H.; Lienhard, J.H. Relating transport modeling to nanofiltration membrane fabrication: Navigating the permeability-selectivity trade-off in desalination pretreatment. J. Membr. Sci. 2018, 554, 26–38. [Google Scholar] [CrossRef]
- Le, N.L.; Nunes, S.P. Materials and membrane technologies for water and energy sustainability. Sustain. Mater. Technol. 2016, 7, 1–28. [Google Scholar] [CrossRef]
- Coronell, O.; González, M.I.; Mariñas, B.J.; Cahill, D.G. Ionization behavior, stoichiometry of association, and accessibility of functional groups in the active layers of reverse osmosis and nanofiltration membranes. Environ. Sci. Technol. 2010, 44, 6808–6814. [Google Scholar] [CrossRef]
- Ritt, C.L.; Werber, J.R.; Wang, M.; Yang, Z.; Zhao, Y.; Kulik, H.J.; Elimelech, M. Ionization behavior of nanoporous polyamide membranes. Proc. Natl. Acad. Sci. USA 2020, 117, 30191–30200. [Google Scholar] [CrossRef]
- Pontié, M.; Derauw, J.; Plantier, S.; Edouard, L.; Bailly, L. Seawater desalination: Nanofiltration—A substitute for reverse osmosis? Desalin. Water Treat. 2013, 51, 485–494. [Google Scholar] [CrossRef]
- Abdel-Fatah, M.A. Nanofiltration systems and applications in wastewater treatment. Ain Shams Eng. J. 2018, 9, 3077–3092. [Google Scholar] [CrossRef]
- Meihong, L.; Sanchuan, Y.; Yong, Z.; Congjie, G. Study on the thin-film composite nanofiltration membrane for the removal of sulfate from concentrated salt aqueous: Preparation and performance. J. Membr. Sci. 2008, 310, 289–295. [Google Scholar] [CrossRef]
- Zhao, D.; Yu, S. A review of recent advance in fouling mitigation of NF/RO membranes in water treatment: Pretreatment, membrane modification, and chemical cleaning. Desalin. Water Treat. 2015, 55, 870–891. [Google Scholar] [CrossRef]
- Xu, R.; Qin, W.; Zhang, B.; Wang, X.; Li, T.; Zhang, Y.; Wen, X. Nanofiltration in pilot scale for wastewater reclamation: Long-term performance and membrane biofouling characteristics. Chem. Eng. J. 2020, 395, 125087. [Google Scholar] [CrossRef]
- Foo, Z.H.; Rehman, D.; Bouma, A.T.; Monsalvo, S.; Lienhard, J.H. Lithium Concentration from Salt-Lake Brine by Donnan-Enhanced Nanofiltration. Environ. Sci. Technol. 2023, 57, 6320–6330. [Google Scholar] [CrossRef]
- Kamcev, J.; Freeman, B.D. Charged polymer membranes for environmental/energy applications. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 111–133. [Google Scholar] [CrossRef]
- Rivas, B.L.; Pereira, E.D.; Palencia, M.; Sánchez, J. Water-soluble functional polymers in conjunction with membranes to remove pollutant ions from aqueous solutions. Prog. Polym. Sci. 2011, 36, 294–322. [Google Scholar] [CrossRef]
- Wang, X.L.; Shang, W.J.; Wang, D.X.; Wu, L.; Tu, C.H. Characterization and applications of nanofiltration membranes: State of the art. Desalination 2009, 236, 316–326. [Google Scholar] [CrossRef]
- Mohammad, A.W.; Teow, Y.; Ang, W.; Chung, Y.; Oatley-Radcliffe, D.; Hilal, N. Nanofiltration membranes review: Recent advances and future prospects. Desalination 2015, 356, 226–254. [Google Scholar] [CrossRef]
- Mansourpanah, Y.; Madaeni, S.; Rahimpour, A. Fabrication and development of interfacial polymerized thin-film composite nanofiltration membrane using different surfactants in organic phase; study of morphology and performance. J. Membr. Sci. 2009, 343, 219–228. [Google Scholar] [CrossRef]
- Lu, D.; Yao, Z.; Jiao, L.; Waheed, M.; Sun, Z.; Zhang, L. Separation mechanism, selectivity enhancement strategies and advanced materials for mono-/multivalent ion-selective nanofiltration membrane. Adv. Membr. 2022, 2, 100032. [Google Scholar] [CrossRef]
- Paul, M.; Jons, S.D. Chemistry and fabrication of polymeric nanofiltration membranes: A review. Polymer 2016, 103, 417–456. [Google Scholar] [CrossRef]
- Bowen, W.R.; Jenner, F. Theoretical descriptions of membrane filtration of colloids and fine particles: An assessment and review. Adv. Colloid Interface Sci. 1995, 56, 141–200. [Google Scholar] [CrossRef]
- Mason, E.; Lonsdale, H. Statistical-mechanical theory of membrane transport. J. Membr. Sci. 1990, 51, 1–81. [Google Scholar] [CrossRef]
- Ghidossi, R.; Veyret, D.; Moulin, P. Computational fluid dynamics applied to membranes: State of the art and opportunities. Chem. Eng. Process. Process Intensif. 2006, 45, 437–454. [Google Scholar] [CrossRef]
- Ridgway, H.F.; Orbell, J.; Gray, S. Molecular simulations of polyamide membrane materials used in desalination and water reuse applications: Recent developments and future prospects. J. Membr. Sci. 2017, 524, 436–448. [Google Scholar] [CrossRef]
- Heiranian, M.; DuChanois, R.M.; Ritt, C.L.; Violet, C.; Elimelech, M. Molecular simulations to elucidate transport phenomena in polymeric membranes. Environ. Sci. Technol. 2022, 56, 3313–3323. [Google Scholar] [CrossRef]
- Shen, M.; Keten, S.; Lueptow, R.M. Dynamics of water and solute transport in polymeric reverse osmosis membranes via molecular dynamics simulations. J. Membr. Sci. 2016, 506, 95–108. [Google Scholar] [CrossRef]
- Shen, M.; Keten, S.; Lueptow, R.M. Rejection mechanisms for contaminants in polyamide reverse osmosis membranes. J. Membr. Sci. 2016, 509, 36–47. [Google Scholar] [CrossRef]
- Luo, Y.; Harder, E.; Faibish, R.S.; Roux, B. Computer simulations of water flux and salt permeability of the reverse osmosis FT-30 aromatic polyamide membrane. J. Membr. Sci. 2011, 384, 1–9. [Google Scholar] [CrossRef]
- Wang, R.; Lin, S. Pore model for nanofiltration: History, theoretical framework, key predictions, limitations, and prospects. J. Membr. Sci. 2021, 620, 118809. [Google Scholar] [CrossRef]
- Jung, O.; Saravia, F.; Wagner, M.; Heissler, S.; Horn, H. Quantifying concentration polarization—Raman microspectroscopy for in-situ measurement in a flat sheet cross-flow nanofiltration membrane unit. Sci. Rep. 2019, 9, 15885. [Google Scholar] [CrossRef]
- Kitto, D.; Kamcev, J. Manning condensation in ion exchange membranes: A review on ion partitioning and diffusion models. J. Polym. Sci. 2022, 60, 2929–2973. [Google Scholar] [CrossRef]
- Varol, S.; Kaya, D.; Contini, E.; Gualandi, C.; Genovese, D. Fluorescence methods to probe mass transport and sensing in solid-state nanoporous membranes. Mater. Adv. 2024, 5, 8351–8383. [Google Scholar] [CrossRef]
- Ali, M.; Nasir, S.; Ramirez, P.; Cervera, J.; Mafe, S.; Ensinger, W. Calcium binding and ionic conduction in single conical nanopores with polyacid chains: Model and experiments. ACS Nano 2012, 6, 9247–9257. [Google Scholar] [CrossRef]
- Varol, H.S.; Förster, C.; Andrieu-Brunsen, A. Ligand-Binding Mediated Gradual Ionic Transport in Nanopores. Adv. Mater. Interfaces 2023, 10, 2201902. [Google Scholar] [CrossRef]
- Dong, B.; Mansour, N.; Huang, T.X.; Huang, W.; Fang, N. Single molecule fluorescence imaging of nanoconfinement in porous materials. Chem. Soc. Rev. 2021, 50, 6483–6506. [Google Scholar] [CrossRef]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. Modeling chemical reactions in classical molecular dynamics simulations. Polymer 2017, 128, 211–217. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Liu, S.; Ganti-Agrawal, S.; Keten, S.; Lueptow, R.M. Molecular insights into charged nanofiltration membranes: Structure, water transport, and water diffusion. J. Membr. Sci. 2022, 644, 120057. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Jons, S.D.; Stutts, K.J.; Ferritto, M.S.; Mickols, W.E. Treatment of Composite Polyamide Membranes to Improve Performance. U.S. Patent 5,876,602, 1999. [Google Scholar]
- Zhu, H.; Szymczyk, A.; Balannec, B. On the salt rejection properties of nanofiltration polyamide membranes formed by interfacial polymerization. J. Membr. Sci. 2011, 379, 215–223. [Google Scholar] [CrossRef]
- Freger, V. Nanoscale heterogeneity of polyamide membranes formed by interfacial polymerization. Langmuir 2003, 19, 4791–4797. [Google Scholar] [CrossRef]
- Sarkisov, L.; Bueno-Perez, R.; Sutharson, M.; Fairen-Jimenez, D. Materials Informatics with PoreBlazer v4.0 and the CSD MOF Database. Chem. Mater. 2020, 32, 9849–9867. [Google Scholar] [CrossRef]
- Kim, S.H.; Kwak, S.Y.; Suzuki, T. Positron annihilation spectroscopic evidence to demonstrate the flux-enhancement mechanism in morphology-controlled thin-film-composite (TFC) membrane. Environ. Sci. Technol. 2005, 39, 1764–1770. [Google Scholar] [CrossRef]
- Zhang, W.; Chu, R.; Shi, W.; Hu, Y. Quantitively unveiling the activity-structure relationship of polyamide membrane: A molecular dynamics simulation study. Desalination 2022, 528, 115640. [Google Scholar] [CrossRef]
- Ding, M.; Szymczyk, A.; Ghoufi, A. On the structure and rejection of ions by a polyamide membrane in pressure-driven molecular dynamics simulations. Desalination 2015, 368, 76–80. [Google Scholar] [CrossRef]
- Leung, K.; Rempe, S.B. Ion rejection by nanoporous membranes in pressure-driven molecular dynamics simulations. J. Comput. Theor. Nanosci. 2009, 6, 1948–1955. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Beglov, D.; Roux, B. Finite representation of an infinite bulk system: Solvent boundary potential for computer simulations. J. Chem. Phys. 1994, 100, 9050–9063. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the Cartesian equations of motion of a system with constraints: Molecular Dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Liu, S.; Keten, S.; Lueptow, R.M. Effect of molecular dynamics water models on flux, diffusivity, and ion dynamics for polyamide membrane simulations. J. Membr. Sci. 2023, 678, 121630. [Google Scholar] [CrossRef]
- Elimelech, M.; Chen, W.H.; Waypa, J.J. Measuring the zeta (electrokinetic) potential of reverse osmosis membranes by a streaming potential analyzer. Desalination 1994, 95, 269–286. [Google Scholar] [CrossRef]
- Xie, H.; Saito, T.; Hickner, M.A. Zeta potential of ion-conductive membranes by streaming current measurements. Langmuir 2011, 27, 4721–4727. [Google Scholar] [CrossRef]
- Luo, J.; Wan, Y. Effects of pH and salt on nanofiltration—A critical review. J. Membr. Sci. 2013, 438, 18–28. [Google Scholar] [CrossRef]
- Teixeira, M.R.; Rosa, M.J.; Nyström, M. The role of membrane charge on nanofiltration performance. J. Membr. Sci. 2005, 265, 160–166. [Google Scholar] [CrossRef]
- Foo, Z.H.; Rehman, D.; Coombs, O.Z.; Deshmukh, A.; Lienhard, J.H. Multicomponent Fickian solution-diffusion model for osmotic transport through membranes. J. Membr. Sci. 2021, 640, 119819. [Google Scholar] [CrossRef]
- Bowman, A.W.; Azzalini, A. Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations; Oxford Academic: Oxford, UK, 1997; Volume 18. [Google Scholar]
- Peter, D.H. Kernel estimation of a distribution function. Commun. Stat. Theory Methods 1985, 14, 605–620. [Google Scholar] [CrossRef]
- Jones, M.C. Simple boundary correction for kernel density estimation. Stat. Comput. 1993, 3, 135–146. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis, 1st ed.; CRC Press: London, UK, 2018. [Google Scholar]
- Donnan, F.G. Theory of membrane equilibria and membrane potentials in the presence of non-dialysing electrolytes. A contribution to physical-chemical physiology. J. Membr. Sci. 1995, 100, 45–55. [Google Scholar] [CrossRef]
- Epsztein, R.; Shaulsky, E.; Dizge, N.; Warsinger, D.M.; Elimelech, M. Role of ionic charge density in donnan exclusion of monovalent anions by nanofiltration. Environ. Sci. Technol. 2018, 52, 4108–4116. [Google Scholar] [CrossRef]
- Aydogan Gokturk, P.; Sujanani, R.; Qian, J.; Wang, Y.; Katz, L.E.; Freeman, B.D.; Crumlin, E.J. The Donnan potential revealed. Nat. Commun. 2022, 13, 5880. [Google Scholar] [CrossRef] [PubMed]
- Fridman-Bishop, N.; Tankus, K.A.; Freger, V. Permeation mechanism and interplay between ions in nanofiltration. J. Membr. Sci. 2018, 548, 449–458. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Tirado-Rives, J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [Google Scholar] [CrossRef]
- Roux, B.; Simonson, T. Implicit solvent models. Biophys. Chem. 1999, 78, 1–20. [Google Scholar] [CrossRef]
- Honig, B.; Nicholls, A. Classical electrostatics in biology and chemistry. Science 1995, 268, 1144–1149. [Google Scholar] [CrossRef]
- Rashin, A.A.; Honig, B. Reevaluation of the Born model of ion hydration. J. Phys. Chem. 1985, 89, 5588–5593. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Belch, A.C.; Berkowitz, M.; McCammon, J. Solvation structure of a sodium chloride ion pair in water. J. Am. Chem. Soc. 1986, 108, 1755–1761. [Google Scholar] [CrossRef]
- Bruni, F.; Imberti, S.; Mancinelli, R.; Ricci, M. Aqueous solutions of divalent chlorides: Ions hydration shell and water structure. J. Chem. Phys. 2012, 136, 064520. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A. On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat. Ann. Der. Phys. 1905, 17, 208. [Google Scholar]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Kepten, E.; Weron, A.; Sikora, G.; Burnecki, K.; Garini, Y. Guidelines for the fitting of anomalous diffusion mean square displacement graphs from single particle tracking experiments. PLoS ONE 2015, 10, e0117722. [Google Scholar] [CrossRef]
- Bargeman, G.; Vollenbroek, J.; Straatsma, J.; Schroën, C.; Boom, R. Nanofiltration of multi-component feeds. Interactions between neutral and charged components and their effect on retention. J. Membr. Sci. 2005, 247, 11–20. [Google Scholar] [CrossRef]
- Pages, N.; Yaroshchuk, A.; Gibert, O.; Cortina, J.L. Rejection of trace ionic solutes in nanofiltration: Influence of aqueous phase composition. Chem. Eng. Sci. 2013, 104, 1107–1115. [Google Scholar] [CrossRef]
- Feder, T.J.; Brust-Mascher, I.; Slattery, J.P.; Baird, B.; Webb, W.W. Constrained diffusion or immobile fraction on cell surfaces: A new interpretation. Biophys. J. 1996, 70, 2767–2773. [Google Scholar] [CrossRef]
- Elvati, P.; Violi, A. Free energy calculation of Permeant–membrane interactions using molecular dynamics simulations. Nanotoxicity Methods Protoc. 2012, 926, 189–202. [Google Scholar]
- Lemaalem, M.; Hadrioui, N.; El Fassi, S.; Derouiche, A.; Ridouane, H. An efficient approach to study membrane nano-inclusions: From the complex biological world to a simple representation. RSC Adv. 2021, 11, 10962–10974. [Google Scholar] [CrossRef]
- He, J.; Arbaugh, T.; Nguyen, D.; Xian, W.; Hoek, E.M.; McCutcheon, J.R.; Li, Y. Molecular mechanisms of thickness-dependent water desalination in polyamide reverse-osmosis membranes. J. Membr. Sci. 2023, 674, 121498. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Foo, Z.; Lienhard, J.H.; Keten, S.; Lueptow, R.M. Membrane Charge Effects on Solute Transport in Nanofiltration: Experiments and Molecular Dynamics Simulations. Membranes 2025, 15, 184. https://doi.org/10.3390/membranes15060184
Liu S, Foo Z, Lienhard JH, Keten S, Lueptow RM. Membrane Charge Effects on Solute Transport in Nanofiltration: Experiments and Molecular Dynamics Simulations. Membranes. 2025; 15(6):184. https://doi.org/10.3390/membranes15060184
Chicago/Turabian StyleLiu, Suwei, Zihao Foo, John H. Lienhard, Sinan Keten, and Richard M. Lueptow. 2025. "Membrane Charge Effects on Solute Transport in Nanofiltration: Experiments and Molecular Dynamics Simulations" Membranes 15, no. 6: 184. https://doi.org/10.3390/membranes15060184
APA StyleLiu, S., Foo, Z., Lienhard, J. H., Keten, S., & Lueptow, R. M. (2025). Membrane Charge Effects on Solute Transport in Nanofiltration: Experiments and Molecular Dynamics Simulations. Membranes, 15(6), 184. https://doi.org/10.3390/membranes15060184





