Design of Mixed Ionic-Electronic Materials for Permselective Membranes and Solid Oxide Fuel Cells Based on Their Oxygen and Hydrogen Mobility
Abstract
1. Introduction
2. Importance of Oxygen and Hydrogen Transport Properties for the Performance of Membranes and SOFCs
2.1. Oxygen Separation Membranes
2.2. Hydrogen Separation Membranes
- Some proton transport mechanisms being mediated by the oxygen transport as will be mentioned in Section 3.2 [90,91,92];
- n = 0.5, when protons are minority defects, then ;
- n = 0.25, when protons are majority defects compensated by electrons, then
2.3. Solid Oxide Fuel Cells
3. Oxygen and Hydrogen Diffusion in MIEC Materials
3.1. Self-Diffusion, Tracer Diffusion and Chemical Diffusion
- “Direct” coefficients corresponding to the effect of the gradient on the flux ;
- “Indirect” coefficients corresponding to the effective diffusion coefficients of i-th species under the effect of the driving force when , i.e., they correspond to the effect of the gradient on the flux when ;
- The coefficients with three different indices correspond to the effective diffusion coefficients of i-th species when is a driven force and .
3.2. Oxygen and Hydrogen Diffusion Mechanisms
3.3. Surface Exchange of Oxygen and Hydrogen
- Physical adsorption;
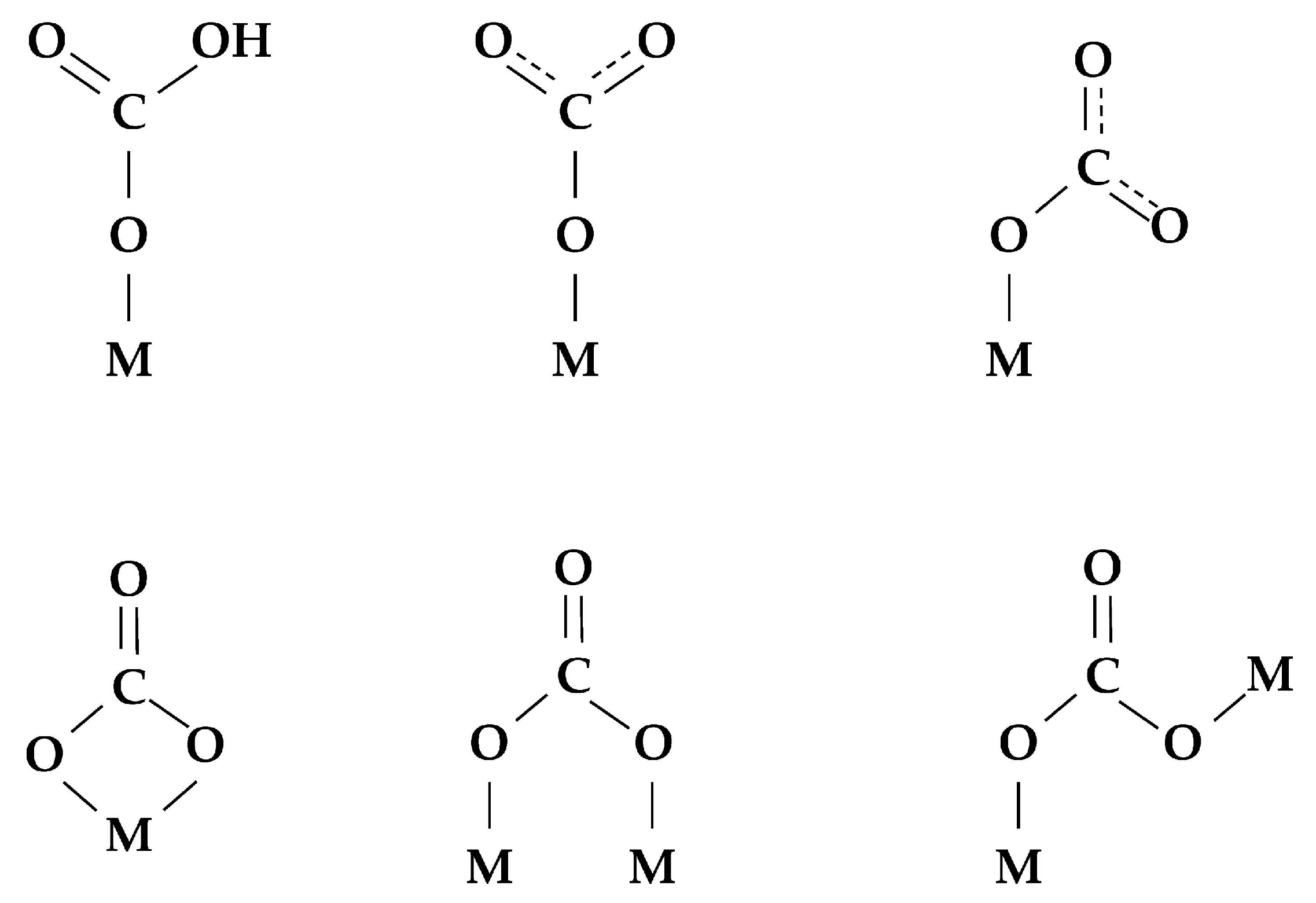
- Dissociative chemisorption (Equations (29)–(31)):
- 3.
- Embedding (the exchange itself) (Equation (32)):
4. Isotope Exchange of Oxygen and Hydrogen
- Homoexchange:
- o
- R0-type (0-atomic type, I type):
- Heteroexchange:
- o
- R1-type (1-atomic type, II type):X2 + (Y)S = XY + (X)S,
- o
- R2-type (2-atomic type, III type):
- Uniform 1D model (e.g., simple oxides) (Figure 11a);
- Non-uniform 1D model with a single diffusion channel involving the weakest bound oxygen form and an exchange with the neighboring strongly bound oxygen forms (complex oxides) (Figure 11b);
- Non-uniform 1D model with several parallel diffusion channels involving different oxygen forms (composites) (Figure 11c);
- Non-uniform 2D model with a single fast diffusion channel along grain boundaries followed by diffusion of the isotope tracer within the grain bulk (monocrystalline) (Figure 11d);
- Non-uniform 2D model with a single fast diffusion channel along grain boundaries with subsequent diffusion of the isotope tracer within the balk of different grains (polycrystalline) (Figure 11e).
5. Relaxation Techniques
- The infinite plane sheet (Equations (56)–(62)):
- The infinite cylinder (Equations (61)–(64)):
- The short cylinder (Equations (65)–(67)):
- The sphere (Equations (68)–(71)):
- The rectangular bar (Equations (72)–(75)):
6. Oxygen and Hydrogen Mobility of Materials for Membranes and SOFC
6.1. Fluorites, Bixbyites and Rhombohedral Phases
- La2Ce2O7 (50% CeO2 + 50% La2O3) fluorite, a proton conductor below 450 °C and an oxygen ion conductor at high temperatures [190]; and
6.2. Pyrochlores
6.3. Perovskites
6.4. Ruddlesden–Popper Phases
6.5. Composites
6.6. Other Materials
7. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rahman, A.; Farrok, O.; Haque, M.M. Environmental Impact of Renewable Energy Source Based Electrical Power Plants: Solar, Wind, Hydroelectric, Biomass, Geothermal, Tidal, Ocean, and Osmotic. Renew. Sustain. Energy Rev. 2022, 161, 112279. [Google Scholar] [CrossRef]
- Abanades, S.; Abbaspour, H.; Ahmadi, A.; Das, B.; Ehyaei, M.A.; Esmaeilion, F.; Assad, M.E.H.; Hajilounezhad, T.; Hmida, A.; Rosen, M.A.; et al. A Conceptual Review of Sustainable Electrical Power Generation from Biogas. Energy Sci. Eng. 2022, 10, 630–655. [Google Scholar] [CrossRef]
- Ang, T.-Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A.; Prabaharan, N. A Comprehensive Study of Renewable Energy Sources: Classifications, Challenges and Suggestions. Energy Strat. Rev. 2022, 43, 100939. [Google Scholar] [CrossRef]
- Tian, X.; An, C.; Chen, Z. The Role of Clean Energy in Achieving Decarbonization of Electricity Generation, Transportation, and Heating Sectors by 2050: A Meta-Analysis Review. Renew. Sustain. Energy Rev. 2023, 182, 113404. [Google Scholar] [CrossRef]
- Isazadeh, A.; Ziviani, D.; Claridge, D.E. Global Trends, Performance Metrics, and Energy Reduction Measures in Datacom Facilities. Renew. Sustain. Energy Rev. 2023, 174, 113149. [Google Scholar] [CrossRef]
- Sayed, E.T.; Olabi, A.G.; Alami, A.H.; Radwan, A.; Mdallal, A.; Rezk, A.; Abdelkareem, M.A. Renewable Energy and Energy Storage Systems. Energies 2023, 16, 1415. [Google Scholar] [CrossRef]
- Wimalaratna, Y.P.; Afrouzi, H.N.; Mehranzamir, K.; Siddique, M.B.M.; Liew, S.C.; Ahmed, J. Analysing Wind Power Penetration in Hybrid Energy Systems Based on Techno-Economic Assessments. Sustain. Energy Technol. Assess. 2022, 53, 102538. [Google Scholar] [CrossRef]
- Kamal, M.M.; Ashraf, I. Evaluation of a Hybrid Power System Based on Renewable and Energy Storage for Reliable Rural Electrification. Renew. Energy Focus 2023, 45, 179–191. [Google Scholar] [CrossRef]
- Das, P.; Chandramohan, V.P. A Review on Recent Advances in Hybrid Solar Updraft Tower Plants: Challenges and Future Aspects. Sustain. Energy Technol. Assess. 2023, 55, 102978. [Google Scholar] [CrossRef]
- Gomaa, M.R.; Al-Bawwat, A.K.; Al-Dhaifallah, M.; Rezk, H.; Ahmed, M. Optimal Design and Economic Analysis of a Hybrid Renewable Energy System for Powering and Desalinating Seawater. Energy Rep. 2023, 9, 2473–2493. [Google Scholar] [CrossRef]
- Ileberi, G.R.; Li, P. Integrating Hydrokinetic Energy into Hybrid Renewable Energy System: Optimal Design and Comparative Analysis. Energies 2023, 16, 3403. [Google Scholar] [CrossRef]
- Shokri, A.; Fard, M.S. Water-Energy Nexus: Cutting Edge Water Desalination Technologies and Hybridized Renewable-Assisted Systems; Challenges and Future Roadmaps. Sustain. Energy Technol. Assess. 2023, 57, 103173. [Google Scholar] [CrossRef]
- Kuterbekov, K.A.; Nikonov, A.V.; Bekmyrza, K.Z.; Pavzderin, N.B.; Kabyshev, A.M.; Kubenova, M.M.; Kabdrakhimova, G.D.; Aidarbekov, N. Classification of Solid Oxide Fuel Cells. Nanomaterials 2022, 12, 1059. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Liu, B.; Jia, L.; Yan, D.; Li, J. Liquid Biofuels for Solid Oxide Fuel Cells: A Review. J. Power Sources 2023, 556, 232437. [Google Scholar] [CrossRef]
- Kazula, S.; de Graaf, S.; Enghardt, L. Review of Fuel Cell Technologies and Evaluation of Their Potential and Challenges for Electrified Propulsion Systems in Commercial Aviation. J. Glob. Power Propuls. Soc. 2023, 7, 43–57. [Google Scholar] [CrossRef]
- Peng, J.; Zhao, D.; Xu, Y.; Wu, X.; Li, X. Comprehensive Analysis of Solid Oxide Fuel Cell Performance Degradation Mechanism, Prediction, and Optimization Studies. Energies 2023, 16, 788. [Google Scholar] [CrossRef]
- Damo, U.M.; Ferrari, M.L.; Turan, A.; Massardo, A.F. Solid Oxide Fuel Cell Hybrid System: A Detailed Review of an Environmentally Clean and Efficient Source of Energy. Energy 2019, 168, 235–246. [Google Scholar] [CrossRef]
- Ma, S.; Lin, M.; Lin, T.-E.; Lan, T.; Liao, X.; Maréchal, F.; Van Herle, J.; Yang, Y.; Dong, C.; Wang, L. Fuel Cell-Battery Hybrid Systems for Mobility and off-Grid Applications: A Review. Renew. Sustain. Energy Rev. 2021, 135, 110119. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, O. A Review of Solid Oxide Fuel Cell Based Hybrid Cycles. Int. J. Energy Res. 2022, 46, 8560–8589. [Google Scholar] [CrossRef]
- Sinha, A.A.; Sanjay; Ansari, M.Z.; Shukla, A.K.; Choudhary, T. Comprehensive Review on Integration Strategies and Numerical Modeling of Fuel Cell Hybrid System for Power & Heat Production. Int. J. Hydrogen Energy, 2023; in press. [Google Scholar] [CrossRef]
- Iliev, I.K.; Filimonova, A.A.; Chichirov, A.A.; Chichirova, N.D.; Pechenkin, A.V.; Vinogradov, A.S. Theoretical and Experimental Studies of Combined Heat and Power Systems with SOFCs. Energies 2023, 16, 1898. [Google Scholar] [CrossRef]
- He, V.; Gaffuri, M.; Van Herle, J.; Schiffmann, J. Readiness Evaluation of SOFC-MGT Hybrid Systems with Carbon Capture for Distributed Combined Heat and Power. Energy Convers. Manag. 2023, 278, 116728. [Google Scholar] [CrossRef]
- Rahimi-Ahar, Z.; Hatamipour, M.S. Exergy Analysis of Thermal Desalination Processes: A Review. Clean. Technol. Environ. Policy, 2023; in press. [Google Scholar] [CrossRef]
- Qin, X.; Cao, J.; Geng, G.; Li, Y.; Zheng, Y.; Zhang, W.; Yu, B. Solid Oxide Fuel Cell System for Automobiles. Int. J. Green Energy 2022, 9, 75–86. [Google Scholar] [CrossRef]
- Abuadala, A.; Dincer, I. A Review on Biomass-Based Hydrogen Production and Potential Applications: A Review on Biomass-Based Hydrogen Production and Applications. Int. J. Energy Res. 2012, 36, 415–455. [Google Scholar] [CrossRef]
- Lee, J.; Lin, K.-Y.A.; Jung, S.; Kwon, E.E. Hybrid Renewable Energy Systems Involving Thermochemical Conversion Process for Waste-to-Energy Strategy. Chem. Eng. J. 2023, 452, 139218. [Google Scholar] [CrossRef]
- Salimi, M.; Hosseinpour, M.; Mansouri, S.; Borhani, T.N. Environmental Aspects of the Combined Cooling, Heating, and Power (CCHP) Systems: A Review. Processes 2022, 10, 711. [Google Scholar] [CrossRef]
- Tarancón, A. Strategies for Lowering Solid Oxide Fuel Cells Operating Temperature. Energies 2009, 2, 1130–1150. [Google Scholar] [CrossRef]
- Skutina, L.; Filonova, E.; Medvedev, D.; Maignan, A. Undoped Sr2MMoO6 Double Perovskite Molybdates (M = Ni, Mg, Fe) as Promising Anode Materials for Solid Oxide Fuel Cells. Materials 2021, 14, 1715. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, M.; Zhu, Z. Perovskite Cathode Materials for Low-Temperature Solid Oxide Fuel Cells: Fundamentals to Optimization. Electrochem. Energy Rev. 2022, 5, 263–311. [Google Scholar] [CrossRef]
- Kumar, R.V.; Khandale, A.P. A Review on Recent Progress and Selection of Cobalt-Based Cathode Materials for Low Temperature-Solid Oxide Fuel Cells. Renew. Sustain. Energy Rev. 2022, 156, 111985. [Google Scholar] [CrossRef]
- Ahmad, M.Z.; Ahmad, S.H.; Chen, R.S.; Ismail, A.F.; Hazan, R.; Baharuddin, N.A. Review on Recent Advancement in Cathode Material for Lower and Intermediate Temperature Solid Oxide Fuel Cells Application. Int. J. Hydrogen Energy 2022, 47, 1103–1120. [Google Scholar] [CrossRef]
- Pikalova, E.Y.; Kalinina, E.G.; Pikalova, N.S.; Filonova, E.A. High-Entropy Materials in SOFC Technology: Theoretical Foundations for Their Creation, Features of Synthesis, and Recent Achievements. Materials 2022, 15, 8783. [Google Scholar] [CrossRef] [PubMed]
- Tarutin, A.P.; Filonova, E.A.; Ricote, S.; Medvedev, D.A.; Shao, Z. Chemical Design of Oxygen Electrodes for Solid Oxide Electrochemical Cells: A Guide. Sustain. Energy Technol. Assess. 2023, 57, 103185. [Google Scholar] [CrossRef]
- Filonova, E.; Pikalova, E. Overview of Approaches to Increase the Electrochemical Activity of Conventional Perovskite Air Electrodes. Materials 2023, 16, 4967. [Google Scholar] [CrossRef]
- Mathur, L.; Namgung, Y.; Kim, H.; Song, S.-J. Recent Progress in Electrolyte-Supported Solid Oxide Fuel Cells: A Review. J. Korean Ceram. Soc. 2023, 60, 614–636. [Google Scholar] [CrossRef]
- Hanif, M.B.; Rauf, S.; Motola, M.; Babar, Z.U.D.; Li, C.-J.; Li, C.-X. Recent Progress of Perovskite-Based Electrolyte Materials for Solid Oxide Fuel Cells and Performance Optimizing Strategies for Energy Storage Applications. Mater. Res. Bull. 2022, 146, 111612. [Google Scholar] [CrossRef]
- Kim, D.; Jeong, I.; Kim, K.J.; Bae, K.T.; Kim, D.; Koo, J.; Yu, H.; Lee, K.T. A Brief Review of Heterostructure Electrolytes for High-Performance Solid Oxide Fuel Cells at Reduced Temperatures. J. Korean Ceram. Soc. 2022, 59, 131–152. [Google Scholar] [CrossRef]
- Maiti, T.K.; Majhi, J.; Maiti, S.K.; Singh, J.; Dixit, P.; Rohilla, T.; Ghosh, S.; Bhushan, S.; Chattopadhyay, S. Zirconia- and Ceria-Based Electrolytes for Fuel Cell Applications: Critical Advancements toward Sustainable and Clean Energy Production. Environ. Sci. Pollut. Res. 2022, 29, 64489–64512. [Google Scholar] [CrossRef]
- Choudhary, B.; Besra, L.; Anwar, S.; Anwar, S. La2Ce2O7 Based Materials for next Generation Proton Conducting Solid Oxide Cells: Progress, Opportunity and Future Prospects. Int. J. Hydrogen Energy 2023, 42, S0360319923015604. [Google Scholar] [CrossRef]
- Filonova, E.; Medvedev, D. Recent Progress in the Design, Characterisation and Application of LaAlO3- and LaGaO3-Based Solid Oxide Fuel Cell Electrolytes. Nanomaterials 2022, 12, 1991. [Google Scholar] [CrossRef]
- Yin, H.; Yip, A.C.K. A Review on the Production and Purification of Biomass-Derived Hydrogen Using Emerging Membrane Technologies. Catalysts 2017, 7, 297. [Google Scholar] [CrossRef]
- Sun, C.; Alonso, J.A.; Bian, J. Recent Advances in Perovskite-Type Oxides for Energy Conversion and Storage Applications. Adv. Energy Mater. 2021, 11, 2000459. [Google Scholar] [CrossRef]
- Acharya, D.; Ng, D.; Xie, Z. Recent Advances in Catalysts and Membranes for MCH Dehydrogenation: A Mini Review. Membranes 2021, 11, 955. [Google Scholar] [CrossRef] [PubMed]
- Al-Rowaili, F.N.; Khaled, M.; Jamal, A.; Zahid, U. Mixed Matrix Membranes for H2/CO2 Gas Separation- a Critical Review. Fuel 2023, 333, 126285. [Google Scholar] [CrossRef]
- Han, N.; Shen, Z.; Zhao, X.; Chen, R.; Thakur, V.K. Perovskite Oxides for Oxygen Transport: Chemistry and Material Horizons. Sci. Total Environ. 2022, 806, 151213. [Google Scholar] [CrossRef] [PubMed]
- Meulenberg, W.A.; Schulze-Küppers, F.; Deibert, W.; Gestel, T.V.; Baumann, S. Ceramic Membranes: Materials—Components—Potential Applications. ChemBioEng Rev. 2019, 6, 198–208. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, T.; Dewangan, N.; Li, Z.; Das, S.; Pati, S.; Li, Z.; Lin, J.Y.S.; Kawi, S. Catalytic Mixed Conducting Ceramic Membrane Reactors for Methane Conversion. React. Chem. Eng. 2020, 5, 1868–1891. [Google Scholar] [CrossRef]
- Algieri, C.; Coppola, G.; Mukherjee, D.; Shammas, M.I.; Calabro, V.; Curcio, S.; Chakraborty, S. Catalytic Membrane Reactors: The Industrial Applications Perspective. Catalysts 2021, 11, 691. [Google Scholar] [CrossRef]
- Leo, A.; Liu, S.; Costa, J.C.D.D. Development of Mixed Conducting Membranes for Clean Coal Energy Delivery. Int. J. Greenh. Gas Control 2009, 3, 357–367. [Google Scholar] [CrossRef]
- Gupta, S.; Mahapatra, M.K.; Singh, P. Lanthanum Chromite Based Perovskites for Oxygen Transport Membrane. Mater. Sci. Eng. Rep. 2015, 90, 1–36. [Google Scholar] [CrossRef]
- Deibert, W.; Ivanova, M.E.; Baumann, S.; Guillon, O.; Meulenberg, W.A. Ion-Conducting Ceramic Membrane Reactors for High-Temperature Applications. J. Membr. Sci. 2017, 543, 79–97. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Sadovskaya, E.M.; Eremeev, N.F.; Pikalova, E.Y.; Bogdanovich, N.M.; Filonova, E.A.; Krieger, T.A.; Fedorova, Y.E.; Krasnov, A.V.; Skriabin, P.I.; et al. Novel Materials for Solid Oxide Fuel Cells Cathodes and Oxygen Separation Membranes: Fundamentals of Oxygen Transport and Performance. Carbon Resour, Convers. 2020, 3, 112–121. [Google Scholar] [CrossRef]
- Pikalova, E.Y.; Kalinina, E.G. Solid Oxide Fuel Cells Based on Ceramic Membranes with Mixed Conductivity: Improving Efficiency. Russ. Chem. Rev. 2021, 90, 703–749. [Google Scholar] [CrossRef]
- Sadykov, V.; Eremeev, N.; Sadovskaya, E.; Bespalko, Y.; Simonov, M.; Arapova, M.; Smal, E. Nanomaterials with Oxygen Mobility for Catalysts of Biofuels Transformation into Syngas, SOFC and Oxygen/Hydrogen Separation Membranes: Design and Performance. Catal. Today 2022, 113936. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Eremeev, N.F.; Sadovskaya, E.M.; Shlyakhtina, A.V.; Pikalova, E.Y.; Osinkin, D.A.; Yaremchenko, A.A. Design of Materials for Solid Oxide Fuel Cells, Permselective Membranes, and Catalysts for Biofuel Transformation into Syngas and Hydrogen Based on Fundamental Studies of Their Real Structure, Transport Properties, and Surface Reactivity. Curr. Opin. Green Sustain. Chem. 2022, 33, 100558. [Google Scholar] [CrossRef]
- Adler, S.B. Factors Governing Oxygen Reduction in Solid Oxide Fuel Cell Cathodes. Chem. Rev. 2004, 104, 4791–4844. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Sadovskaya, E.M.; Eremeev, N.F.; Skriabin, P.I.; Krasnov, A.V.; Bespalko, Y.N.; Pavlova, S.N.; Fedorova, Y.E.; Pikalova, E.Y.; Shlyakhtina, A.V. Oxygen Mobility in the Materials for Solid Oxide Fuel Cells and Catalytic Membranes (Review). Russ. J. Electrochem. 2019, 55, 701–718. [Google Scholar] [CrossRef]
- Adler, S.B.; Lane, J.A.; Steele, B.C.H. Electrode Kinetics of Porous Mixed-Conducting Oxygen Electrodes. J. Electrochem. Soc. 1996, 143, 3554–3564. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Muzykantov, V.S.; Yeremeev, N.F.; Pelipenko, V.V.; Sadovskaya, E.M.; Bobin, A.S.; Fedorova, Y.E.; Amanbaeva, D.G.; Smirnova, A.L. Solid Oxide Fuel Cell Cathodes: Importance of Chemical Composition and Morphology. Catal. Sustain. Energy 2015, 2, 57–70. [Google Scholar] [CrossRef]
- He, S.; Jiang, S.P. Electrode/Electrolyte Interface and Interface Reactions of Solid Oxide Cells: Recent Development and Advances. Progr. Nat. Sci. Mater. Int. 2021, 31, 341–372. [Google Scholar] [CrossRef]
- Mori, T.; Wepf, R.; Jiang, S.P. Future Prospects for the Design of ‘State-of-the-Art’ Solid Oxide Fuel Cells. J. Phys. Energy 2020, 2, 031001. [Google Scholar] [CrossRef]
- Manthiram, A.; Kim, J.-H.; Kim, Y.N.; Lee, K.-T. Crystal Chemistry and Properties of Mixed Ionic-Electronic Conductors. J. Electroceram. 2011, 27, 93–107. [Google Scholar] [CrossRef]
- van Eck, N.J.; Waltman, L. Software Survey: VOSviewer, a Computer Program for Bibliometric Mapping. Scientometrics 2010, 84, 523–538. [Google Scholar] [CrossRef]
- Zhu, W.Z.; Deevi, S.C. A Review on the Status of Anode Materials for Solid Oxide Fuel Cells. Mater. Sci. Eng. A 2003, 362, 228–239. [Google Scholar] [CrossRef]
- Shaikh, S.P.S.; Muchtar, A.; Somalu, M.R. A Review on the Selection of Anode Materials for Solid-Oxide Fuel Cells. Renew. Sustain. Energy Rev. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Tarancón, A.; Burriel, M.; Santiso, J.; Skinner, S.J.; Kilner, J.A. Advances in Layered Oxide Cathodes for Intermediate Temperature Solid Oxide Fuel Cells. J. Mater. Chem. 2010, 20, 3799–3813. [Google Scholar] [CrossRef]
- Pelosato, R.; Cordaro, G.; Stucchi, D.; Cristiani, C.; Dotelli, G. Cobalt Based Layered Perovskites as Cathode Material for Intermediate Temperature Solid Oxide Fuel Cells: A Brief Review. J. Power Sources 2015, 298, 46–67. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Mezentseva, N.V.; Bobrova, L.N.; Smorygo, O.L.; Eremeev, N.F.; Fedorova, Y.E.; Bespalko, Y.N.; Skriabin, P.I.; Krasnov, A.V.; Lukashevich, A.I.; et al. Advanced Materials for Solid Oxide Fuel Cells and Membrane Catalytic Reactors. In Advanced Nanomaterials for Catalysis and Energy; Elsevier: Amsterdam, The Netherlands, 2019; pp. 435–514. ISBN 978-0-12-814807-5. [Google Scholar]
- Zhu, X.; Yang, W.; Kharton, V.V. Mixed Conducting Ceramic Membranes. In Green Chemistry and Sustainable Technology; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-662-53532-5. [Google Scholar]
- Zhao, J.; Pang, Y.; Su, C.; Jiang, S.; Ge, L. Toward High Performance Mixed Ionic and Electronic Conducting Perovskite-Based Oxygen Permeable Membranes: An Overview of Strategies and Rationales. Energy Fuels 2023, 37, 7042–7061. [Google Scholar] [CrossRef]
- Athayde, D.D.; Motuzas, J.; Vasconcelos, W. Perovskite Membranes for Oxygen Separation. In Perovskite Ceramics; Elsevier: Amsterdam, The Netherlands, 2023; pp. 263–294. ISBN 978-0-323-90586-2. [Google Scholar]
- Ahmad, F.N.; Sazali, N.; Shalbi, S.; Ngadiman, N.H.A.; Othman, M.H.D. Oxygen Separation Process Using Ceramic-Based Membrane: A Review. J. Adv. Res. Fluid Mechan. Therm. Sci. 2019, 62, 1–9. [Google Scholar]
- Xue, J.; Weng, G.; Chen, L.; Suo, Y.; Wei, Y.; Feldhoff, A.; Wang, H. Various Influence of Surface Modification on Permeability and Phase Stability through an Oxygen Permeable Membrane. J. Membr. Sci. 2019, 573, 588–594. [Google Scholar] [CrossRef]
- Li, C.; Li, W.; Chew, J.J.; Liu, S.; Zhu, X.; Sunarso, J. Rate Determining Step in SDC-SSAF Dual-Phase Oxygen Permeation Membrane. J. Membr. Sci. 2019, 573, 628–638. [Google Scholar] [CrossRef]
- Li, C.; Li, W.; Chew, J.J.; Liu, S.; Zhu, X.; Sunarso, J. Oxygen Permeation through Single-Phase Perovskite Membrane: Modeling Study and Comparison with the Dual-Phase Membrane. Sep. Purif. Technol. 2020, 235, 116224. [Google Scholar] [CrossRef]
- Xu, S.J.; Thomson, W.J. Oxygen Permeation Rates through Ion-Conducting Perovskite Membranes. Chem. Eng. Sci. 1999, 54, 3839–3850. [Google Scholar] [CrossRef]
- Bouwmeester, H.J.M.; Burggraaf, A.J. Chapter 10 Dense Ceramic Membranes for Oxygen Separation. In Membrane Science and Technology; Elsevier: Amsterdam, The Netherlands, 1996; Volume 4, pp. 435–528. ISBN 978-0-444-81877-5. [Google Scholar]
- Shelepova, E.; Vedyagin, A.; Sadykov, V.; Mezentseva, N.; Fedorova, Y.; Smorygo, O.; Klenov, O.; Mishakov, I. Theoretical and Experimental Study of Methane Partial Oxidation to Syngas in Catalytic Membrane Reactor with Asymmetric Oxygen-Permeable Membrane. Catal. Today 2016, 268, 103–110. [Google Scholar] [CrossRef]
- Wilkner, K.; Mücke, R.; Baumann, S.; Meulenberg, W.A.; Guillon, O. Sensitivity of Material, Microstructure and Operational Parameters on the Performance of Asymmetric Oxygen Transport Membranes: Guidance from Modeling. Membranes 2022, 12, 614. [Google Scholar] [CrossRef]
- Qadir, S.; Ahsan, M.; Hussain, A. Computational Fluid Dynamics Analysis of a Hollow Fiber Membrane Module for Binary Gas Mixture. Gases 2023, 3, 77–91. [Google Scholar] [CrossRef]
- Magrasó, A.; Haugsrud, R. Effects of the La/W Ratio and Doping on the Structure, Defect Structure, Stability and Functional Properties of Proton-Conducting Lanthanum Tungstate La28−xW4+xO54+δ. A Review. J. Mater. Chem. A 2014, 2, 12630–12641. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Shcherbakova, L.G. New Solid Electrolytes of the Pyrochlore Family. Russ. J. Electrochem. 2012, 48, 3. [Google Scholar] [CrossRef]
- Manohar. Development & Characterization of Ceramic Membranes. Int. J. Modern Eng. Res. 2012, 2, 1492–1506. [Google Scholar]
- Habib, M.A.; Harale, A.; Paglieri, S.; Alrashed, F.S.; Al-Sayoud, A.; Rao, M.V.; Nemitallah, M.A.; Hossain, S.; Hussien, M.; Ali, A.; et al. Palladium-Alloy Membrane Reactors for Fuel Reforming and Hydrogen Production: A Review. Energy Fuels 2021, 35, 5558–5593. [Google Scholar] [CrossRef]
- Cheng, H. Dual-Phase Mixed Protonic-Electronic Conducting Hydrogen Separation Membranes: A Review. Membranes 2022, 12, 647. [Google Scholar] [CrossRef] [PubMed]
- Vermaak, L.; Neomagus, H.W.J.P.; Bessarabov, D.G. Recent Advances in Membrane-Based Electrochemical Hydrogen Separation: A Review. Membranes 2021, 11, 127. [Google Scholar] [CrossRef]
- Suzuki, A.; Yukawa, H. A Review for Consistent Analysis of Hydrogen Permeability through Dense Metallic Membranes. Membranes 2020, 10, 120. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Zhang, Y.; Hu, T.; Jiang, H. Enhanced H2 Production by Using La5.5WO11.25-δ-La0.8Sr0.2FeO3-δ Mixed Oxygen Ion-Proton-Electron Triple-Conducting Membrane. Int. J. Hydrogen Energy 2021, 46, 33143–33151. [Google Scholar] [CrossRef]
- Del-Pozo, A.; Villalobos, J.C.; Serna, S. A General Overview of Hydrogen Embrittlement. In Current Trends and Future Developments on (Bio-) Membranes; Elsevier: Amsterdam, The Netherlands, 2020; pp. 139–168. ISBN 978-0-12-818332-8. [Google Scholar]
- Hegde, R.M.; Kurkuri, M.D.; Kigga, M. Current Scenario of Nanocomposite Materials for Fuel Cell Applications. In Sustainable Polymer Composites and Nanocomposites; Inamuddin, Thomas, S., Kumar Mishra, R., Asiri, A.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 557–592. ISBN 978-3-030-05398-7. [Google Scholar]
- Animitsa, I.; Neiman, A.; Sharafutdinov, A.; Nochrin, S. Strontium Tantalates with Perovskite-Related Structure. Solid State Ion. 2000, 136–137, 265–271. [Google Scholar] [CrossRef]
- Sunarso, J.; Hashim, S.S.; Zhu, N.; Zhou, W. Perovskite Oxides Applications in High Temperature Oxygen Separation, Solid Oxide Fuel Cell and Membrane Reactor: A Review. Progr. Energy Combust. Sci. 2017, 61, 57–77. [Google Scholar] [CrossRef]
- Escolástico, S.; Solís, C.; Haugsrud, R.; Magrasó, A.; Serra, J.M. On the Ionic Character of H2 Separation through Mixed Conducting Nd5.5W0.5Mo0.5O11.25−δ Membrane. Int. J. Hydrogen Energy 2017, 42, 11392–11399. [Google Scholar] [CrossRef]
- Papac, M.; Stevanović, V.; Zakutayev, A.; O’Hayre, R. Triple Ionic–Electronic Conducting Oxides for next-Generation Electrochemical Devices. Nat. Mater. 2021, 20, 301–313. [Google Scholar] [CrossRef]
- Virkar, A. Transport of H2, O2 and H2O through Single-Phase, Two-Phase and Multi-Phase Mixed Proton, Oxygen Ion, and Electron Hole Conductors. Solid State Ion. 2001, 140, 275–283. [Google Scholar] [CrossRef]
- Sanders, M.D.; O’Hayre, R.P. Coupled Transport and Uphill Permeation of Steam and Oxygen in a Dense Ceramic Membrane. J. Membr. Sci. 2011, 376, 96–101. [Google Scholar] [CrossRef]
- Liu, L.C.; Gong, H.R.; Zhou, S.F.; Gong, X. Adsorption, Diffusion, and Permeation of Hydrogen at PdCu Surfaces. J. Membr. Sci. 2019, 588, 117206. [Google Scholar] [CrossRef]
- Cardoso, S.P.; Azenha, I.S.; Lin, Z.; Portugal, I.; Rodrigues, A.E.; Silva, C.M. Inorganic Membranes for Hydrogen Separation. Sep. Purif. Rev. 2018, 47, 229–266. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Q.-Y.; Liao, Q.; Chen, Y.; Yan, X.; Guo, X.-J.; Lang, W.-Z. Influence of Cr Doping on Hydrogen Permeation Performance of Lanthanum Tungstate Membrane. Sep. Purif. Technol. 2021, 262, 118333. [Google Scholar] [CrossRef]
- Norby, T.; Haugsrud, R. Dense Ceramic Membranes for Hydrogen Separation. In Nonporous Inorganic Membranes; Sammells, A.F., Mundschau, M.V., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2006; pp. 1–48. ISBN 978-3-527-60879-9. [Google Scholar]
- Kreuer, K. On the Complexity of Proton Conduction Phenomena. Solid State Ion. 2000, 136–137, 149–160. [Google Scholar] [CrossRef]
- Fontaine, M.; Norby, T.; Larring, Y.; Grande, T.; Bredesen, R. Oxygen and Hydrogen Separation Membranes Based on Dense Ceramic Conductors. In Membrane Science and Technology; Elsevier: Amsterdam, The Netherlands, 2008; Volume 13, pp. 401–458. ISBN 978-0-444-53070-7. [Google Scholar]
- Bobrova, L.; Vernikovskaya, N.; Eremeev, N.; Sadykov, V. Model-Based Performance Analysis of Membrane Reactor with Ethanol Steam Reforming over a Monolith. Membranes 2022, 12, 741. [Google Scholar] [CrossRef] [PubMed]
- Bobrova, L.; Eremeev, N.; Vernikovskaya, N.; Sadykov, V.; Smorygo, O. Effect of Asymmetric Membrane Structure on Hydrogen Transport Resistance and Performance of a Catalytic Membrane Reactor for Ethanol Steam Reforming. Membranes 2021, 11, 332. [Google Scholar] [CrossRef] [PubMed]
- Eremeev, N.; Krasnov, A.; Bespalko, Y.; Bobrova, L.; Smorygo, O.; Sadykov, V. An Experimental Performance Study of a Catalytic Membrane Reactor for Ethanol Steam Reforming over a Metal Honeycomb Catalyst. Membranes 2021, 11, 790. [Google Scholar] [CrossRef]
- Malavasi, L.; Fisher, C.A.J.; Islam, M.S. Oxide-Ion and Proton Conducting Electrolyte Materials for Clean Energy Applications: Structural and Mechanistic Features. Chem. Soc. Rev. 2010, 39, 4370–4387. [Google Scholar] [CrossRef]
- Zhang, L.; Yao, F.; Meng, J.; Zhang, W.; Wang, H.; Liu, X.; Meng, J.; Zhang, H. Oxygen Migration and Proton Diffusivity in Transition-Metal (Mn, Fe, Co, and Cu) Doped Ruddlesden–Popper Oxides. J. Mater. Chem. A 2019, 7, 18558–18567. [Google Scholar] [CrossRef]
- Shi, H.; Su, C.; Ran, R.; Cao, J.; Shao, Z. Electrolyte Materials for Intermediate-Temperature Solid Oxide Fuel Cells. Progr. Nat. Sci. Mater. Int. 2020, 30, 764–774. [Google Scholar] [CrossRef]
- Yang, G.; Jung, W.; Ahn, S.-J.; Lee, D. Controlling the Oxygen Electrocatalysis on Perovskite and Layered Oxide Thin Films for Solid Oxide Fuel Cell Cathodes. Appl. Sci. 2019, 9, 1030. [Google Scholar] [CrossRef]
- Poetzsch, D.; Merkle, R.; Maier, J. Proton Conductivity in Mixed-Conducting BSFZ Perovskite from Thermogravimetric Relaxation. Phys. Chem. Chem. Phys. 2014, 16, 16446–16453. [Google Scholar] [CrossRef]
- Poetzsch, D.; Merkle, R.; Maier, J. Stoichiometry Variation in Materials with Three Mobile Carriers-Thermodynamics and Transport Kinetics Exemplified for Protons, Oxygen Vacancies, and Holes. Adv. Funct. Mater. 2015, 25, 1542–1557. [Google Scholar] [CrossRef]
- Poetzsch, D.; Merkle, R.; Maier, J. Proton Uptake in the H+-SOFC Cathode Material Ba0.5Sr0.5Fe0.8Zn0.2O3−δ: Transition from Hydration to Hydrogenation with Increasing Oxygen Partial Pressure. Faraday Discuss. 2015, 182, 129–143. [Google Scholar] [CrossRef]
- Salrin, T.C.; Johnson, L.; White, S.; Kilpatrick, G.; Weber, E.; Bragatto, C. Using LAMMPS to Shed Light on Haven’s Ratio: Calculation of Haven’s Ratio in Alkali Silicate Glasses Using Molecular Dynamics. Front. Mater. 2023, 10, 1123213. [Google Scholar] [CrossRef]
- Murch, G.E. The Nernst-Einstein Equation in High-Defect-Content Solids. Philos. Magaz A 1982, 45, 685–692. [Google Scholar] [CrossRef]
- Akbar, S.A. A Generalized View of the Correlation Factor in Solid-state Diffusion. J. Appl. Phys. 1994, 75, 2851–2856. [Google Scholar] [CrossRef]
- Poirier, D.R.; Geiger, G.H. Fick’s Law and Diffusivity of Materials. In Transport Phenomena in Materials Processing; Springer International Publishing: Cham, Switzerland, 2016; pp. 419–461. ISBN 978-3-319-48565-2. [Google Scholar]
- Goldberg, E.; Nemudry, A.; Boldyrev, V.; Schöllhorn, R. Model for Anomalous Transport of Oxygen in Nonstoichiometric Perovskites: 1. General Formulation of the Problem. Solid State Ion. 1998, 110, 223–233. [Google Scholar] [CrossRef]
- Goldberg, E.; Nemudry, A.; Boldyrev, V.; Schöllhorn, R. Model for Anomalous Transport of Oxygen in Nonstoichiometric Perovskites Analytical and Numerical Solutions. Solid State Ion. 1999, 122, 17–22. [Google Scholar] [CrossRef]
- Nemudry, A.; Rogatchev, A.; Gainutdinov, I.; Schöllhorn, R. Reactivity of the Perovskite System Ca1−xSrxFeO2.5 in Topotactic Electrochemical Oxidation at Ambient Temperature. J. Solid State Electrochem. 2001, 5, 450–458. [Google Scholar] [CrossRef]
- Nemudry, A.; Goldberg, E.L.; Aguirre, M.; Alario-Franco, M.Á. Electrochemical Topotactic Oxidation of Nonstoichiometric Perovskites at Ambient Temperature. Solid State Sci. 2002, 4, 677–690. [Google Scholar] [CrossRef]
- Nemudry, A.; Uvarov, N. Nanostructuring in Composites and Grossly Nonstoichiometric or Heavily Doped Oxides. Solid State Ion. 2006, 177, 2491–2494. [Google Scholar] [CrossRef]
- Zhogin, I.L.; Nemudry, A.P.; Glyanenko, P.V.; Kamenetsky, Y.M.; Bouwmeester, H.J.M.; Ismagilov, Z.R. Oxygen Diffusion in Nanostructured Perovskites. Catal. Today 2006, 118, 151–157. [Google Scholar] [CrossRef][Green Version]
- Jin, X.; White, R.E.; Huang, K. Simulating Charge Transport in Solid Oxide Mixed Ionic and Electronic Conductors: Nernst-Planck Theory vs Modified Fick’s Law. J. Electrochem. Soc. 2016, 163, A2702–A2719. [Google Scholar] [CrossRef]
- Mebane, D.S.; Liu, Y.; Liu, M. A Two-Dimensional Model and Numerical Treatment for Mixed Conducting Thin Films. J. Electrochem. Soc. 2007, 154, A421–A426. [Google Scholar] [CrossRef]
- Lynch, M.E.; Liu, M. Investigation of Sheet Resistance in Thin-Film Mixed-Conducting Solid Oxide Fuel Cell Cathode Test Cells. J. Power Sources 2010, 195, 5155–5166. [Google Scholar] [CrossRef]
- Liu, M. Distributions of Charged Defects in Mixed Ionic-Electronic Conductors: I. General Equations for Homogeneous Mixed Ionic-Electronic Conductors. J. Electrochem. Soc. 1997, 144, 1813–1834. [Google Scholar] [CrossRef]
- Lane, J.; Benson, S.; Waller, D.; Kilner, J. Oxygen Transport in La0.6Sr0.4Co0.2Fe0.8O3−δ. Solid State Ion. 1999, 121, 201–208. [Google Scholar] [CrossRef]
- Kilner, J.; De Souza, R.; Fullarton, I. Surface Exchange of Oxygen in Mixed Conducting Perovskite Oxides. Solid State Ion. 1996, 86–88, 703–709. [Google Scholar] [CrossRef]
- Honders, A.; Derkinderen, J.; Vanheeren, A.; Dewit, J.; Broers, G. Bounded Diffusion in Solid Solution Electrode Powder Compacts. Part II. The Simultaneous Measurement of the Chemical Diffusion Coefficient and the Thermodynamic Factor in LixTiS2 and LixCoO2. Solid State Ion. 1985, 15, 265–276. [Google Scholar] [CrossRef]
- Ishihara, T. Perovskite Oxide for Solid Oxide Fuel Cells; Springer Science + Business Media, LLC: Dordrecht, The Netherlands, 2009; 302p. [Google Scholar] [CrossRef]
- Wimmer, E.; Wolf, W.; Sticht, J.; Saxe, P.; Geller, C.B.; Najafabadi, R.; Young, G.A. Temperature-Dependent Diffusion Coefficients from Ab Initio Computations: Hydrogen, Deuterium, and Tritium in Nickel. Phys. Rev. B 2008, 77, 134305. [Google Scholar] [CrossRef]
- De Larramendi, I.R.; Ortiz-Vitoriano, N.; Dzul-Bautista, I.B.; Rojo, T. Designing Perovskite Oxides for Solid Oxide Fuel Cells. In Perovskite Materials Synthesis, Characterisation, Properties, and Applications; Pan, L., Zhu, G., Eds.; InTech: Nappanee, IN, USA, 2016; ISBN 978-953-51-2245-6. [Google Scholar]
- Chroneos, A.; Yildiz, B.; Tarancón, A.; Parfitt, D.; Kilner, J.A. Oxygen Diffusion in Solid Oxide Fuel Cell Cathode and Electrolyte Materials: Mechanistic Insights from Atomistic Simulations. Energy Environ. Sci. 2011, 4, 2774–2789. [Google Scholar] [CrossRef]
- Traqueia, L.S.M.; Marques, F.M.B.; Kharton, V.V. Oxygen ion conduction in oxide materials: Selected examples and basic mechanisms. Bol. Soc. Cerám. 2006, 45, 115–121. [Google Scholar] [CrossRef]
- Hosono, H.; Hayashi, K.; Kajihara, K.; Sushko, P.V.; Shluger, A.L. Oxygen Ion Conduction in 12CaO·7Al2O3: O2− Conduction Mechanism and Possibility of O− Fast Conduction. Solid State Ion. 2009, 180, 550–555. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Belov, D.A.; Knotko, A.V.; Avdeev, M.; Kolbanev, I.V.; Vorobieva, G.A.; Karyagina, O.K.; Shcherbakova, L.G. Oxide Ion Transport in (Nd2−xZrx)Zr2O7+δ Electrolytes by an Interstitial Mechanism. J. Alloys Compd. 2014, 603, 274–281. [Google Scholar] [CrossRef]
- Jacobson, A.J. Materials for Solid Oxide Fuel Cells. Chem. Mater. 2010, 22, 660–674. [Google Scholar] [CrossRef]
- Lundin, S.T.B.; Patki, N.S.; Fuerst, T.S.; Ricote, S.; Wolden, S.A.; Way, J.D. Dense Inorganic Membranes for Hydrogen Separation. In Membranes for Gas Separations; Carreon, M.A., Ed.; World Scientific Publishing: Hackensack, NJ, USA, 2017; pp. 271–363. [Google Scholar]
- Ueki, T.; Watanabe, M. Macromolecules in Ionic Liquids: Progress, Challenges, and Opportunities. Macromolecules 2008, 41, 3739–3749. [Google Scholar] [CrossRef]
- Colomban, P. Vibrational Characterization of the Various Forms of (Solvated or Unsolvated) Mobile Proton in the Solid State. Advantages, Limitations and Open Questions. Solid State Ion. 2023, 393, 116187. [Google Scholar] [CrossRef]
- Boreskov, G.K.; Muzykantov, V.S. Investigation of oxide-type oxidation catalysts by reactions of oxygen isotopic exchange. Ann. N. Y. Acad. Sci. 1973, 213, 137–170. [Google Scholar] [CrossRef]
- Muzykantov, V.S. Isotopic Studies of Dioxygen Activation on Oxide Catalysts for Oxidation: Problems, Results and Perspectives. React. Kinet. Catal. Lett. 1987, 35, 437–447. [Google Scholar] [CrossRef]
- Busca, G.; Lorenzelli, V. Infrared Spectroscopic Identification of Species Arising from Reactive Adsorption of Carbon Oxides on Metal Oxide Surfaces. Mater. Chem. 1982, 7, 89–126. [Google Scholar] [CrossRef]
- Boreskov, G.K.; Kasatkina, L.A.; Amerikov, V.G. Homomolecular Isotope Exchange of CO2 on Metal Oxides of the IV Period. Kinet. Catal. 1969, 10, 102–112. [Google Scholar]
- Muzykantov, V.S.; Cheshkova, K.T.; Boreskov, G.K. Heteroexchange and Self-Diffusion of Oxygen in the O2–CO2–MoO3 System. Kinet. Catal. 1973, 14, 432–439. [Google Scholar]
- Gorelov, V.P.; Kurumchin, E.K. Investigation of the Exchange of Cerium Dioxide by Isotopic Exchange with Molecular Oxygen. Kinet. Catal. 1986, 27, 1346–1351. [Google Scholar]
- Gorelov, V.P.; Kurumchin, E.K. Investigation of the Exchange of Cerium Dioxide by Isotopic Exchange with Carbon Dioxide. In Solid State Ionics.; UIF “Nauka”: Yekaterinburg, Russia, 1993; pp. 46–53. [Google Scholar]
- Amerikov, V.G.; Boreskov, G.K.; Kasatkina, L.A. Catalytic Activity of Iron, Cobalt and Nickel Oxides with Respect to the Reaction of Isotope Exchange of Carbon Dioxide Molecules. Kinet. Catal. 1967, 8, 646–653. [Google Scholar]
- Uxa, D.; Dörrer, L.; Schulz, M.; Knoblauch, N.; Fielitz, P.; Roeb, M.; Schmücker, M.; Borchardt, G. Investigation of CO2 Splitting on Ceria-Based Redox Materials for Low-Temperature Solar Thermochemical Cycling with Oxygen Isotope Exchange Experiments. Processes 2022, 11, 109. [Google Scholar] [CrossRef]
- Kasatkina, L.A.; Nekipelov, V.N.; Zhivotenko, N.N. Reaction of Isotope Exchange of Carbon Monoxide on Fe3O4. Kinet. Catal. 1973, 14, 363–371. [Google Scholar]
- Tenelshof, J.; Bouwmeester, H.; Verweij, H. Oxygen Transport through La1−xSrxFeO3−δ Membranes II. Permeation in Air/CO, CO Gradients. Solid State Ion. 1996, 89, 81–92. [Google Scholar] [CrossRef]
- Xu, X.; Mace, B.; Enriquez, E.; Bao, S.; Harrell, Z.; Chen, C.; Whangbo, M.-H. Roles of Reaction Kinetics of CO2 on a PrBaCo2O5.5+δ Surfaces. RSC Adv. 2017, 7, 40558–40562. [Google Scholar] [CrossRef]
- Bachiller-Baeza, B.; Rodriguez-Ramos, I.; Guerrero-Ruiz, A. Interaction of Carbon Dioxide with the Surface of Zirconia Polymorphs. Langmuir 1998, 14, 3556–3564. [Google Scholar] [CrossRef]
- Bonhoeffer, K.F.; Farkas, A. On Adsorption and Reflection Processes in the Interaction of Hydrogen and Metals. Trans. Faraday Soc. 1932, 28, 242–247. [Google Scholar] [CrossRef]
- Rideal, E.K. A Note on a Simple Molecular Mechanism for Heterogeneous Catalytic Reactions. Math. Proc. Camb. Philos. Soc. 1939, 35, 130–132. [Google Scholar] [CrossRef]
- Eley, D.D. The Absolute Rate of Conversion of Parahydrogen by Metallic Catalysts. Trans. Faraday Soc. 1948, 44, 216–226. [Google Scholar] [CrossRef]
- Kim, S.; Wang, S.; Chen, X.; Yang, Y.L.; Wu, N.; Ignatiev, A.; Jacobson, A.J.; Abeles, B. Oxygen Surface Exchange in Mixed Ionic Electronic Conductors: Application to La0.5Sr0.5Fe0.8Ga0.2O3−δ. J. Electrochem. Soc. 2000, 147, 2398. [Google Scholar] [CrossRef]
- Burriel, M.; Garcia, G.; Santiso, J.; Kilner, J.A.; Chater, R.J.; Skinner, S.J. Anisotropic Oxygen Diffusion Properties in Epitaxial Thin Films of La2NiO4+δ. J. Mater. Chem. 2008, 18, 416–422. [Google Scholar] [CrossRef]
- Porotnikova, N.M.; Khodimchuk, A.V.; Zakharov, D.M.; Bogdanovich, N.M.; Osinkin, D.A. Enhancement of Surface Exchange and Oxygen Diffusion of Sr1.95Fe1.4Ni0.1Mo0.5O6–δ Oxide Determined by Two Independent Isotope Exchange Methods. App. Surf. Sci. 2023, 613, 156015. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Sadovskaya, E.M.; Uvarov, N.F. Methods of Isotopic Relaxations for Estimation of Oxygen Diffusion Coefficients in Solid Electrolytes and Materials with Mixed Ionic-Electronic Conductivity. Russ. J. Electrochem. 2015, 51, 458–467. [Google Scholar] [CrossRef]
- Pikalova, E.; Sadykov, V.; Sadovskaya, E.; Yeremeev, N.; Kolchugin, A.; Shmakov, A.; Vinokurov, Z.; Mishchenko, D.; Filonova, E.; Belyaev, V. Correlation between Structural and Transport Properties of Ca-Doped La Nickelates and Their Electrochemical Performance. Crystals 2021, 11, 297. [Google Scholar] [CrossRef]
- Sadykov, V.; Shlyakhtina, A.; Sadovskaya, E.; Eremeev, N.; Skazka, V.; Goncharov, V. 2D Diffusion of Oxygen in Ln10Mo2O21 (Ln = Nd, Ho) Oxides. Solid State Ion. 2020, 346, 115229. [Google Scholar] [CrossRef]
- Sadykov, V.; Shlyakhtina, A.; Lyskov, N.; Sadovskaya, E.; Cherepanova, S.; Eremeev, N.; Skazka, V.; Goncharov, V.; Kharitonova, E. Oxygen Diffusion in Mg-Doped Sm and Gd Zirconates with Pyrochlore Structure. Ionics 2020, 26, 4621–4633. [Google Scholar] [CrossRef]
- Muzykantov, V.S.; Popovskii, V.V.; Boreskov, G.K. Kinetics of Isotope Exchange in a Molecular Oxygen—Solid Oxide System. Kinet. Catal. 1964, 5, 624–629. [Google Scholar]
- Ananyev, M.V.; Zakharov, D.M. H/D Isotopic Exchange between Methane and a Proton-Conducting Oxide: Theory and Experiment. Catal. Sci. Technol. 2020, 10, 3561–3571. [Google Scholar] [CrossRef]
- Zakharov, D.M.; Zhuravlev, N.A.; Denisova, T.A.; Belozerov, A.S.; Stroeva, A.Y.; Vovkotrub, E.G.; Farlenkov, A.S.; Ananyev, M.V. Catalytic Methane Activation over La1−xSrxScO3−α Proton-Conducting Oxide Surface: A Comprehensive Study. J. Catal. 2021, 394, 67–82. [Google Scholar] [CrossRef]
- Huang, Y.; Qiu, R.; Lian, W.; Lei, L.; Liu, T.; Zhang, J.; Wang, Y.; Liu, J.; Huang, J.; Chen, F. Review: Measurement of Partial Electrical Conductivities and Transport Numbers of Mixed Ionic-Electronic Conducting Oxides. J. Power Sources 2022, 528, 231201. [Google Scholar] [CrossRef]
- Zhao, L.; Dou, B.; Zhang, H.; Wang, Z. Oxygen Carriers for Chemical-Looping Water Splitting to Hydrogen Production: A Critical Review. Carbon Capture Sci. Technol. 2021, 1, 100006. [Google Scholar] [CrossRef]
- Zhang, C.; Sunarso, J.; Liu, S. Designing CO2-Resistant Oxygen-Selective Mixed Ionic–Electronic Conducting Membranes: Guidelines, Recent Advances, and Forward Directions. Chem. Soc. Rev. 2017, 46, 2941–3005. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Wang, Y.; Zhu, Z.; Xia, C.; Bouwmeester, H.J.M. Measuring Oxygen Surface Exchange Kinetics on Mixed-Conducting Composites by Electrical Conductivity Relaxation. J. Mater. Chem. A 2015, 3, 10296–10302. [Google Scholar] [CrossRef]
- He, F.; Jin, X.; Tian, T.; Ding, H.; Green, R.D.; Xue, X. Determination of Electrochemical Kinetic Property for Mixed Ionic Electronic Conductors from Electrical Conductivity Relaxation Measurements. J. Electrochem. Soc. 2015, 162, F951–F958. [Google Scholar] [CrossRef]
- Søgaard, M.; Hendriksen, P.V.; Mogensen, M. Oxygen Nonstoichiometry and Transport Properties of Strontium Substituted Lanthanum Ferrite. J. Solid State Chem. 2007, 180, 1489–1503. [Google Scholar] [CrossRef]
- Ovtar, S.; Søgaard, M.; Norrman, K.; Hendriksen, P.V. Oxygen Exchange and Transport in (La0.6Sr0.4)0.98FeO3−d–Ce0.9Gd0.1O1.95 Dual-Phase Composites. J. Electrochem. Soc. 2018, 165, F220–F231. [Google Scholar] [CrossRef]
- He, F.; Jiang, Y.; Ren, C.; Dong, G.; Gan, Y.; Lee, M.; Green, R.D.; Xue, X. Generalized Electrical Conductivity Relaxation Approach to Determine Electrochemical Kinetic Properties for MIECs. Solid State Ion. 2016, 297, 82–92. [Google Scholar] [CrossRef]
- Seo, H.G.; Tuller, H.L. Surface Oxygen Exchange Kinetics of Mixed Conducting Oxides: Dilatometric vs Electrical Conductivity Relaxation Study. Scr. Mater. 2023, 228, 115314. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Sadovskaya, E.M.; Filonova, E.A.; Eremeev, N.F.; Belyaev, V.D.; Tsvinkinberg, V.A.; Pikalova, E.Y. Oxide Ionic Transport Features in Gd-Doped La Nickelates. Solid State Ion. 2020, 357, 115462. [Google Scholar] [CrossRef]
- Seong, A.; Jeong, D.; Kim, M.; Choi, S.; Kim, G. Performance Comparison of Composite Cathode: Mixed Ionic and Electronic Conductor and Triple Ionic and Electronic Conductor with BaZr0.1Ce0.7Y0.1Yb0.1O3-δ for Highly Efficient Protonic Ceramic Fuel Cells. J. Power Sources 2022, 530, 231241. [Google Scholar] [CrossRef]
- Sadykov, V.; Okhlupin, Y.; Yeremeev, N.; Vinokurov, Z.; Shmakov, A.; Belyaev, V.; Uvarov, N.; Mertens, J. In Situ X-Ray Diffraction Studies of Pr2−xNiO4+δ Crystal Structure Relaxation Caused by Oxygen Loss. Solid State Ion. 2014, 262, 918–922. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Bristol, UK, 1975; p. 414. [Google Scholar]
- Otter, M.D.; van der Haar, L.; Bouwmeester, H. Numerical Evaluation of Eigenvalues of the Sheet Diffusion Problem in the Surface/Diffusion Mixed Regime. Solid State Ion. 2000, 134, 259–264. [Google Scholar] [CrossRef]
- Otter, M.W.D.; Bouwmeester, H.J.M.; Boukamp, B.A.; Verweij, H. Reactor Flush Time Correction in Relaxation Experiments. J. Electrochem. Soc. 2001, 148, J1. [Google Scholar] [CrossRef]
- Sun, Z.; Fabbri, E.; Bi, L.; Traversa, E. Lowering Grain Boundary Resistance of BaZr0.8Y0.2O3−δ with LiNO3 Sintering-Aid Improves Proton Conductivity for Fuel Cell Operation. Phys. Chem. Chem. Phys. 2011, 13, 7692–7700. [Google Scholar] [CrossRef]
- Sun, W.; Liu, M.; Liu, W. Chemically Stable Yttrium and Tin Co-Doped Barium Zirconate Electrolyte for Next Generation High Performance Proton-Conducting Solid Oxide Fuel Cells. Adv. Energy Mater. 2013, 3, 1041–1050. [Google Scholar] [CrossRef]
- Fabbri, E.; Bi, L.; Tanaka, H.; Pergolesi, D.; Traversa, E. Chemically Stable Pr and Y Co-Doped Barium Zirconate Electrolytes with High Proton Conductivity for Intermediate-Temperature Solid Oxide Fuel Cells. Adv. Funct. Mater. 2011, 21, 158–166. [Google Scholar] [CrossRef]
- Zvonareva, I.; Fu, X.-Z.; Medvedev, D.; Shao, Z. Electrochemistry and Energy Conversion Features of Protonic Ceramic Cells with Mixed Ionic-Electronic Electrolytes. Energy Environ. Sci. 2022, 15, 439–465. [Google Scholar] [CrossRef]
- Danilov, N.; Pikalova, E.; Lyagaeva, J.; Antonov, B.; Medvedev, D.; Demin, A.; Tsiakaras, P. Grain and Grain Boundary Transport in BaCe0.5Zr0.3Ln0.2O3−δ (Ln–Y or Lanthanide) Electrolytes Attractive for Protonic Ceramic Fuel Cells Application. J. Power Sources 2017, 366, 161–168. [Google Scholar] [CrossRef]
- Omata, T.; Otsuka-Yao-Matsuo, S. Electrical Properties of Proton-Conducting Ca2+-Doped La2Zr2O7 with a Pyrochlore-Type Structure. J. Electrochem. Soc. 2001, 148, E252–E261. [Google Scholar] [CrossRef]
- Labrincha, J.A.; Frade, J.R.; Marques, F.M.B. Protonic Conduction in La2Zr2O7-Based Pyrochlore Materials. Solid State Ion. 1997, 99, 33–40. [Google Scholar] [CrossRef]
- Besikiotis, V.; Knee, C.S.; Ahmed, I.; Haugsrud, R.; Norby, T. Crystal Structure, Hydration and Ionic Conductivity of the Inherently Oxygen-Deficient La2Ce2O7. Solid State Ion. 2012, 228, 1–7. [Google Scholar] [CrossRef]
- Shimura, T.; Fujimoto, S.; Iwahara, H. Proton Conduction in Non-Perovskite-Type Oxides at Elevated Temperatures. Solid State Ion. 2001, 143, 117–123. [Google Scholar] [CrossRef]
- Seeger, J.; Ivanova, M.E.; Meulenberg, W.A.; Sebold, D.; Stöver, D.; Scherb, T.; Schumacher, G.; Escolástico, S.; Solís, C.; Serra, J.M. Synthesis and Characterization of Nonsubstituted and Substituted Proton-Conducting La6–xWO12–y. Inorg. Chem. 2013, 52, 10375–10386. [Google Scholar] [CrossRef]
- Escolástico, S.; Vert, V.B.; Serra, J.M. Preparation and Characterization of Nanocrystalline Mixed Proton−Electronic Conducting Materials Based on the System Ln6WO12. Chem. Mater. 2009, 21, 3079–3089. [Google Scholar] [CrossRef]
- Fantin, A.; Scherb, T.; Seeger, J.; Schumacher, G.; Gerhards, U.; Ivanova, M.E.; Meulenberg, W.A.; Dittmeyer, R.; Banhart, J. Relation between Composition and Vacant Oxygen Sites in the Mixed Ionic-Electronic Conductors La5.4W1−yMyO12−δ (M= Mo, Re; 0 ≤ y ≤ 0.2) and Their Mother Compound La6−xWO12−δ (0.4 ≤ x ≤ 0.8). Solid State Ion. 2017, 306, 104–111. [Google Scholar] [CrossRef]
- Marcano, D.; Ivanova, M.E.; Mauer, G.; Sohn, Y.J.; Schwedt, A.; Bram, M.; Menzler, N.H.; Vaßen, R. PS-PVD Processing of Single-Phase Lanthanum Tungstate Layers for Hydrogen-Related Applications. J. Therm. Spray Technol. 2019, 28, 1554–1564. [Google Scholar] [CrossRef]
- Partin, G.S.; Korona, D.V.; Neiman, A.Y.; Belova, K.G. Conductivity and Hydration of Fluorite-Type La6−xWO12−1.5x Phases (x = 0.4; 0.6; 0.8; 1). Russ. J. Electrochem. 2015, 51, 381–390. [Google Scholar] [CrossRef]
- Savvin, S.N.; Shlyakhtina, A.V.; Kolbanev, I.V.; Knotko, A.V.; Belov, D.A.; Shcherbakova, L.G.; Nuñez, P. Zr-Doped Samarium Molybdates—Potential Mixed Electron–Proton Conductors. Solid State Ion. 2014, 262, 713–718. [Google Scholar] [CrossRef]
- Savvin, S.N.; Shlyakhtina, A.V.; Borunova, A.B.; Shcherbakova, L.G.; Ruiz-Morales, J.C.; Núñez, P. Crystal Structure and Proton Conductivity of Some Zr-Doped Rare-Earth Molybdates. Solid State Ion. 2015, 271, 91–97. [Google Scholar] [CrossRef]
- López-Vergara, A.; Porras-Vázquez, J.M.; Vøllestad, E.; Canales-Vazquez, J.; Losilla, E.R.; Marrero-López, D. Metal-Doping of La5.4MoO11.1 Proton Conductors: Impact on the Structure and Electrical Properties. Inorg. Chem. 2018, 57, 12811–12819. [Google Scholar] [CrossRef]
- López-Vergara, A.; Bergillos-Ruiz, M.; Zamudio-García, J.; Porras-Vázquez, J.M.; Canales-Vazquez, J.; Marrero-López, D.; Losilla, E.R. Synergic Effect of Metal and Fluorine Doping on the Structural and Electrical Properties of La5.4MoO11.1 -Based Materials. Inorg. Chem. 2020, 59, 1444–1452. [Google Scholar] [CrossRef] [PubMed]
- Shlyakhtina, A.V.; Savvin, S.N.; Lyskov, N.V.; Belov, D.A.; Shchegolikhin, A.N.; Kolbanev, I.V.; Karyagina, O.K.; Chernyak, S.A.; Shcherbakova, L.G.; Núñez, P. Sm6−xMoO12-δ (x = 0, 0.5) and Sm6WO12—Mixed Electron-Proton Conducting Materials. Solid State Ion. 2017, 302, 143–151. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Savvin, S.N.; Lyskov, N.V.; Kolbanev, I.V.; Karyagina, O.K.; Chernyak, S.A.; Shcherbakova, L.G.; Núñez, P. Polymorphism in the Family of Ln6−xMoO12−δ (Ln = La, Gd–Lu; x = 0, 0.5) Oxygen Ion- and Proton-Conducting Materials. J. Mater. Chem. A 2017, 5, 7618–7630. [Google Scholar] [CrossRef]
- López-Vergara, A.; Porras-Vázquez, J.M.; Infantes-Molina, A.; Canales-Vázquez, J.; Cabeza, A.; Losilla, E.R.; Marrero-López, D. Effect of Preparation Conditions on the Polymorphism and Transport Properties of La6–xMoO12−δ (0 ≤ x ≤ 0.8). Chem. Mater. 2017, 29, 6966–6975. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Kolbanev, I.V.; Degtyarev, E.N.; Lyskov, N.V.; Karyagina, O.K.; Chernyak, S.A.; Shcherbakova, L.G. Kinetic Aspects of the Synthesis of Ln6−хMoO12−δ (Ln = Sm, Ho -Yb; x = 0, 0.5) Rare-Earth Molybdates Using Mechanical Activation of Oxides. Solid State Ion. 2018, 320, 272–282. [Google Scholar] [CrossRef]
- Savvin, S.N.; Avdeev, M.; Kolbanev, I.V.; Kharitonova, E.P.; Shcherbakova, L.G.; Shlyakhtina, A.V.; Nuñez, P. Stability against Reduction of Fluorite-like Rhombohedral La5.5MoO11.25 and Ho5.4Zr0.6MoO12.3 Fluorite: Conductivity and Neutron Diffraction Study. Solid State Ion. 2018, 319, 148–155. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Lyskov, N.V.; Avdeev, M.; Goffman, V.G.; Gorshkov, N.V.; Knotko, A.V.; Kolbanev, I.V.; Karyagina, O.K.; Maslakov, K.I.; Shcherbakova, L.G.; et al. Comparative Study of Electrical Conduction and Oxygen Diffusion in the Rhombohedral and Bixbyite Ln6MoO12 (Ln = Er, Tm, Yb) Polymorphs. Inorg. Chem. 2019, 58, 4275–4288. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Avdeev, M.; Abrantes, J.C.C.; Gomes, E.; Lyskov, N.V.; Kharitonova, E.P.; Kolbanev, I.V.; Shcherbakova, L.G. Structure and Conductivity of Nd6MoO12-Based Potential Electron–Proton Conductors under Dry and Wet Redox Conditions. Inorg. Chem. Front. 2019, 6, 566–575. [Google Scholar] [CrossRef]
- Denisova, K.; Shlyakhtina, A.; Yumashev, O.; Avdeev, M.; Abdel-Hafiez, M.; Volkova, O.; Vasiliev, A. Low Temperature Thermodynamics of Yb6MoO12 and Lu6MoO12. J. Alloys Compd. 2019, 778, 756–760. [Google Scholar] [CrossRef]
- López-Vergara, A.; Vizcaíno-Anaya, L.; Porras-Vázquez, J.M.; Baldinozzi, G.; Santos-Gómez, L.D.; Canales-Vazquez, J.; Marrero-López, D.; Losilla, E.R. Unravelling Crystal Superstructures and Transformations in the La6−xMoO12−δ (0.6 ≤ x ≤ 3.0) Series: A System with Tailored Ionic/Electronic Conductivity. Chem. Mater. 2020, 32, 7052–7062. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Avdeev, M.; Lyskov, N.V.; Abrantes, J.C.C.; Gomes, E.; Denisova, K.N.; Kolbanev, I.V.; Chernyak, S.A.; Volkova, O.S.; Vasiliev, A.N. Structure, Conductivity and Magnetism of Orthorhombic and Fluorite Polymorphs in MoO3–Ln2O3 (Ln = Gd, Dy, Ho) Systems. Dalton Trans. 2020, 49, 2833–2842. [Google Scholar] [CrossRef] [PubMed]
- Shlyakhtina, A.V.; Lyskov, N.V.; Kolbanev, I.V.; Shchegolikhin, A.N.; Karyagina, O.K.; Shcherbakova, L.G. Key Trends in the Proton Conductivity of Ln6−xMoO12−δ (Ln = La, Nd, Sm, Gd -Yb; x = 0, 0.5, 0.6, 0.7, 1) Rare-Earth Molybdates. Int. J. Hydrogen Energy 2021, 46, 16989–16998. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Lyskov, N.V.; Šalkus, T.; Kežionis, A.; Patrakeev, M.V.; Leonidov, I.A.; Shcherbakova, L.G.; Chernyak, S.A.; Shefer, K.I.; Sadovskaya, E.M.; et al. Conductivity and Oxygen Diffusion in Bixbyites and Fluorites Ln6−xMoO12−δ (Ln = Er, Tm; x = 0, 0.5). Int. J. Hydrogen Energy 2021, 46, 16965–16976. [Google Scholar] [CrossRef]
- Bartram, S.F. Crystal Structure of the Rhombohedral MO3.3R2O3 Compounds (M = U, W, or Mo) and Their Relation to Ordered R7O12 Phases. Inorg. Chem. 1966, 5, 749–754. [Google Scholar] [CrossRef]
- Czeskleba-Kerner, H.; Cros, B.; Tourne, G. Phase Equilibria and Compound Formation in the Nd-Mo-O System between 1273 and 1673°K. J. Solid State Chem. 1981, 37, 294–301. [Google Scholar] [CrossRef]
- Polfus, J.M.; Li, Z.; Xing, W.; Sunding, M.F.; Walmsley, J.C.; Fontaine, M.-L.; Henriksen, P.P.; Bredesen, R. Chemical Stability and H2 Flux Degradation of Cercer Membranes Based on Lanthanum Tungstate and Lanthanum Chromite. J. Membr. Sci. 2016, 503, 42–47. [Google Scholar] [CrossRef]
- Eremeev, N.F.; Bespalko, Y.N.; Sadovskaya, E.M.; Skriabin, P.I.; Krieger, T.A.; Ishchenko, A.V.; Sadykov, V.A. Structural and Transport Properties of Nd Tungstates and Their Composites with Ni0.5Cu0.5O Obtained by Mechanical Activation. Dalton Trans. 2022, 51, 7705–7714. [Google Scholar] [CrossRef]
- Voronkova, V.I.; Leonidov, I.A.; Kharitonova, E.P.; Belov, D.A.; Patrakeev, M.V.; Leonidova, O.N.; Kozhevnikov, V.L. Oxygen Ion and Electron Conductivity in Fluorite-like Molybdates Nd5Mo3O16 and Pr5Mo3O16. J. Alloys Compd. 2014, 615, 395–400. [Google Scholar] [CrossRef]
- Chambrier, M.-H. Analyse Structurale Au Sein Du Diagramme de Phase La2O3-WO3 et Exploration Des Proprietes de Conduction Ionique. Ph.D. Thesis, Extended Abstract of Doct. Sci. (Chem.). L’Université du Maine, Maine, France, 2009. [Google Scholar]
- Chambrier, M.-H.; Le Bail, A.; Giovannelli, F.; Redjaïmia, A.; Florian, P.; Massiot, D.; Suard, E.; Goutenoire, F. La10W2O21: An Anion-Deficient Fluorite-Related Superstructure with Oxide Ion Conduction. Inorg. Chem. 2014, 53, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Balaguer, M.; Yoo, C.-Y.; Bouwmeester, H.J.M.; Serra, J.M. Bulk Transport and Oxygen Surface Exchange of the Mixed Ionic–Electronic Conductor Ce1−xTbxO2−δ (x = 0.1, 0.2, 0.5). J. Mater. Chem. A 2013, 1, 10234–10242. [Google Scholar] [CrossRef]
- Kumari, N.; Anjum, U.; Haider, M.A.; Basu, S. Oxygen Anion Diffusion in Doped Ceria MxCe1−xO2-0.5x (M=Gd, Sm and Pr): A Molecular Dynamics Simulation Study. MRS Adv. 2019, 4, 783–792. [Google Scholar] [CrossRef]
- Schaube, M.; Merkle, R.; Maier, J. Oxygen Exchange Kinetics on Systematically Doped Ceria: A Pulsed Isotope Exchange Study. J. Mater. Chem. A 2019, 7, 21854–21866. [Google Scholar] [CrossRef]
- Fernández-García, M.; Martínez-Arias, A.; Hanson, J.C.; Rodriguez, J.A. Nanostructured Oxides in Chemistry: Characterization and Properties. Chem. Rev. 2004, 104, 4063–4104. [Google Scholar] [CrossRef]
- Hungría, A.B.; Martínez-Arias, A.; Fernández-García, M.; Iglesias-Juez, A.; Guerrero-Ruiz, A.; Calvino, J.J.; Conesa, J.C.; Soria, J. Structural, Morphological, and Oxygen Handling Properties of Nanosized Cerium−Terbium Mixed Oxides Prepared by Microemulsion. Chem. Mater. 2003, 15, 4309–4316. [Google Scholar] [CrossRef]
- Zhong, F.; Yang, S.; Chen, C.; Fang, H.; Chen, K.; Zhou, C.; Lin, L.; Luo, Y.; Au, C.; Jiang, L. Defect-Induced Pyrochlore Pr2Zr2O7 Cathode Rich in Oxygen Vacancies for Direct Ammonia Solid Oxide Fuel Cells. J. Power Sources 2022, 520, 230847. [Google Scholar] [CrossRef]
- Anantharaman, A.P.; Dasari, H.P. Potential of Pyrochlore Structure Materials in Solid Oxide Fuel Cell Applications. Ceram. Int. 2021, 47, 4367–4388. [Google Scholar] [CrossRef]
- Julbe, A.; Farrusseng, D.; Guizard, C. Limitations and Potentials of Oxygen Transport Dense and Porous Ceramic Membranes for Oxidation Reactions. Catal. Today 2005, 104, 102–113. [Google Scholar] [CrossRef]
- Bespalko, Y.; Eremeev, N.; Sadovskaya, E.; Krieger, T.; Bulavchenko, O.; Suprun, E.; Mikhailenko, M.; Korobeynikov, M.; Sadykov, V. Synthesis and Oxygen Mobility of Bismuth Cerates and Titanates with Pyrochlore Structure. Membranes 2023, 13, 598. [Google Scholar] [CrossRef]
- Phair, J.W.; Badwal, S.P.S. Materials for Separation Membranes in Hydrogen and Oxygen Production and Future Power Generation. Sci. Technol. Adv. Mater. 2006, 7, 792–805. [Google Scholar] [CrossRef]
- Phair, J.W.; Badwal, S.P.S. Review of Proton Conductors for Hydrogen Separation. Ionics 2006, 12, 103–115. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Koroleva, M.S.; Piir, I.V.; Chezhina, N.V.; Korolev, D.A.; Skriabin, P.I.; Krasnov, A.V.; Sadovskaya, E.M.; Eremeev, N.F.; Nekipelov, S.V.; et al. Structural and Transport Properties of Doped Bismuth Titanates and Niobates. Solid State Ion. 2018, 315, 33–39. [Google Scholar] [CrossRef]
- Krasnov, A.G.; Piir, I.V.; Koroleva, M.S.; Sekushin, N.A.; Ryabkov, Y.I.; Piskaykina, M.M.; Sadykov, V.A.; Sadovskaya, E.M.; Pelipenko, V.V.; Eremeev, N.F. The Conductivity and Ionic Transport of Doped Bismuth Titanate Pyrochlore Bi1.6MxTi2O7−δ (M–Mg, Sc, Cu). Solid State Ion. 2017, 302, 118–125. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Pigalskiy, K.S.; Belov, D.A.; Lyskov, N.V.; Kharitonova, E.P.; Kolbanev, I.V.; Borunova, A.B.; Karyagina, O.K.; Sadovskaya, E.M.; Sadykov, V.A.; et al. Proton and Oxygen Ion Conductivity in the Pyrochlore/Fluorite Family of Ln2−xCaxScMO7−δ (Ln = La, Sm, Ho, Yb; M = Nb, Ta; x = 0, 0.05, 0.1) Niobates and Tantalates. Dalton Trans. 2018, 47, 2376–2392. [Google Scholar] [CrossRef]
- Shimura, T.; Komori, M.; Iwahara, H. Ionic Conduction in Pyrochlore-Type Oxides Containing Rare Earth Elements at High Temperature. Solid State Ion. 1996, 86–88, 685–689. [Google Scholar] [CrossRef]
- Omata, T.; Ikeda, K.; Tokashiki, R.; Otsuka-Yao-Matsuo, S. Proton Solubility for La2Zr2O7 with a Pyrochlore Structure Doped with a Series of Alkaline-Earth Ions. Solid State Ion. 2004, 167, 389–397. [Google Scholar] [CrossRef]
- Eurenius, K.E.J.; Ahlberg, E.; Knee, C.S. Proton Conductivity in Ln1.96Ca0.04Sn2O7-δ (Ln=La, Sm, Yb) Pyrochlores as a Function of the Lanthanide Size. Solid State Ion. 2010, 181, 1258–1263. [Google Scholar] [CrossRef]
- Eurenius, K.E.J.; Ahlberg, E.; Ahmed, I.; Eriksson, S.G.; Knee, C.S. Investigation of Proton Conductivity in Sm1.92Ca0.08Ti2O7−δ and Sm2Ti1.92Y0.08O7−δ Pyrochlores. Solid State Ion. 2010, 181, 148–153. [Google Scholar] [CrossRef]
- Antonova, E.P.; Farlenkov, A.S.; Tropin, E.S.; Eremin, V.A.; Khodimchuk, A.V.; Ananyev, M.V. Oxygen Isotope Exchange, Water Uptake and Electrical Conductivity of Ca-Doped Lanthanum Zirconate. Solid State Ion. 2017, 306, 112–117. [Google Scholar] [CrossRef]
- Huo, D.; Gosset, D.; Siméone, D.; Baldinozzi, G.; Khodja, H.; Villeroy, B.; Surblé, S. Influence of Sintering Methods on Microstructure and Ionic Conductivity of La1.95Sr0.05Zr2O6.975 Synthesized by Co-Precipitation. Solid State Ion. 2015, 278, 181–185. [Google Scholar] [CrossRef][Green Version]
- Huo, D.; Baldinozzi, G.; Siméone, D.; Khodja, H.; Surblé, S. Grain Size-Dependent Electrical Properties of La1.95Sr0.05Zr2O7-δ as Potential Proton Ceramic Fuel Cell Electrolyte. Solid State Ion. 2016, 298, 35–43. [Google Scholar] [CrossRef]
- Shlyakhtina, A.V.; Abrantes, J.C.C.; Gomes, E.; Lyskov, N.V.; Konysheva, E.Y.; Chernyak, S.A.; Kharitonova, E.P.; Karyagina, O.K.; Kolbanev, I.V.; Shcherbakova, L.G. Evolution of Oxygen–Ion and Proton Conductivity in Ca-Doped Ln2Zr2O7 (Ln = Sm, Gd), Located Near Pyrochlore–Fluorite Phase Boundary. Materials 2019, 12, 2452. [Google Scholar] [CrossRef] [PubMed]
- Shlyakhtina, A.V.; Lyskov, N.V.; Konysheva, E.Y.; Chernyak, S.A.; Kolbanev, I.V.; Vorobieva, G.A.; Shcherbakova, L.G. Gas-Tight Proton-Conducting Nd2−xCaxZr2O7−δ (x = 0, 0.05) Ceramics. J. Solid State Electrochem. 2020, 24, 1475–1486. [Google Scholar] [CrossRef]
- Kaur, P.; Singh, K. Review of Perovskite-Structure Related Cathode Materials for Solid Oxide Fuel Cells. Ceram. Int. 2020, 46, 5521–5535. [Google Scholar] [CrossRef]
- Ndubuisi, A.; Abouali, S.; Singh, K.; Thangadurai, V. Recent Advances, Practical Challenges, and Perspectives of Intermediate Temperature Solid Oxide Fuel Cell Cathodes. J. Mater. Chem. A 2022, 10, 2196–2227. [Google Scholar] [CrossRef]
- Farlenkov, A.S.; Vlasov, M.I.; Porotnikova, N.M.; Bobrikov, I.A.; Khodimchuk, A.V.; Ananyev, M.V. Hydrogen Diffusivity in the Sr-Doped LaScO3 Proton-Conducting Oxides. Int. J. Hydrogen Energy 2020, 45, 23455–23468. [Google Scholar] [CrossRef]
- Ji, Q.; Bi, L.; Zhang, J.; Cao, H.; Zhao, X.S. The Role of Oxygen Vacancies of ABO3 Perovskite Oxides in the Oxygen Reduction Reaction. Energy Environ. Sci. 2020, 13, 1408–1428. [Google Scholar] [CrossRef]
- Swierczek, K.; Marzec, J.; Palubiak, D.; Zajac, W.; Molenda, J. LFN and LSCFN Perovskites—Structure and Transport Properties. Solid State Ion. 2006, 177, 1811–1817. [Google Scholar] [CrossRef]
- De Souza, R.A.; Kilner, J.A.; Walker, J.F. A SIMS Study of Oxygen Tracer Diffusion and Surface Exchange in La0.8Sr0.2MnO3+δ. Mater. Lett. 2000, 43, 43–52. [Google Scholar] [CrossRef]
- Balaguer, M.; Vert, V.B.; Navarrete, L.; Serra, J.M. SOFC Composite Cathodes Based on LSM and Co-Doped Cerias (Ce0.8Gd0.1X0.1O2–δ, X = Gd, Cr, Mg, Bi, Ce). J. Power Sources 2013, 223, 214–220. [Google Scholar] [CrossRef]
- Chen, M.; Cheng, Y.; He, S.; Ai, N.; Veder, J.-P.; Rickard, W.D.A.; Saunders, M.; Chen, K.; Zhang, T.; Jiang, S.P. Active, Durable Bismuth Oxide-Manganite Composite Oxygen Electrodes: Interface Formation Induced by Cathodic Polarization. J. Power Sources 2018, 397, 16–24. [Google Scholar] [CrossRef]
- Wang, X.; Tang, B.; Wen, P.; Dong, W.; Wang, L.; Wang, D. YSZ/LSM Composite Cathode Deposited by Solution Precursor Plasma Spraying. Coatings 2022, 12, 321. [Google Scholar] [CrossRef]
- Budiman, R.A.; Miyazaki, T.; Hashimoto, S.; Yashiro, K.; Kawada, T. Determination of Oxygen Surface Exchange Constant of LaNi0.6Fe0.4O3−δ Coated with Ce0.9Gd0.1O1.95 by Isotope Exchange Technique. Solid State Ion. 2016, 286, 19–23. [Google Scholar] [CrossRef]
- Chen, J.; Vashook, V.; Trots, D.M.; Wang, S.; Guth, U. Chemical Diffusion and Oxygen Exchange of LaNi0.4Fe0.6O3−δ Ceramics. J. Adv. Ceram. 2014, 3, 240–249. [Google Scholar] [CrossRef]
- Chen, J.Y.; Rebello, J.; Vashook, V.; Trots, D.M.; Wang, S.R.; Wen, T.L.; Zosel, J.; Guth, U. Thermal Stability, Oxygen Non-Stoichiometry and Transport Properties of LaNi0.6Fe0.4O3. Solid State Ion. 2011, 192, 424–430. [Google Scholar] [CrossRef]
- Kharton, V.V.; Viskup, A.P.; Naumovich, E.N.; Tikhonovich, V.N. Oxygen Permeability of LaFe1−xNixO3−δ Solid Solutions. Mater. Res. Bull. 1999, 34, 1311–1317. [Google Scholar] [CrossRef]
- Harrison, C.M.; Slater, P.R.; Steinberger-Wilckens, R. Lanthanum Nickelates and Their Application in Solid Oxide Cells—The LaNi1−xFexO3 System and Other ABO3-Type Nickelates. Solid State Ion. 2021, 373, 115799. [Google Scholar] [CrossRef]
- Khoshkalam, M.; Faghihi-Sani, M.A.; Tong, X.; Chen, M.; Hendriksen, P.V. Enhanced Activity of Pr6O11 and CuO Infiltrated Ce0.9Gd0.1O2 Based Composite Oxygen Electrodes. J. Electrochem. Soc. 2020, 167, 024505. [Google Scholar] [CrossRef]
- Pikalova, E.; Bogdanovich, N.; Kolchugin, A.; Shubin, K.; Ermakova, L.; Eremeev, N.; Farlenkov, A.; Khrustov, A.; Filonova, E.; Sadykov, V. Development of Composite LaNi0.6Fe0.4O3-δ-Based Air Electrodes for Solid Oxide Fuel Cells with a Thin-Film Bilayer Electrolyte. Int. J. Hydrogen Energy 2021, 46, 16947–16964. [Google Scholar] [CrossRef]
- Hou, J.; Qian, J.; Bi, L.; Gong, Z.; Peng, R.; Liu, W. The Effect of Oxygen Transfer Mechanism on the Cathode Performance Based on Proton-Conducting Solid Oxide Fuel Cells. J. Mater. Chem. A 2015, 3, 2207–2215. [Google Scholar] [CrossRef]
- Pikalova, E.; Bogdanovich, N.; Kolchugin, A.; Ermakova, L.; Khrustov, A.; Farlenkov, A.; Bronin, D. Methods to Increase Electrochemical Activity of Lanthanum Nickelate-Ferrite Electrodes for Intermediate and Low Temperature SOFCs. Int. J. Hydrogen Energy 2021, 46, 35923–35937. [Google Scholar] [CrossRef]
- Basu, R.N.; Tietz, F.; Teller, O.; Wessel, E.; Buchkremer, H.P.; Stöver, D. LaNi0.6Fe0.4O3 as a Cathode Contact Material for Solid Oxide Fuel Cells. J. Solid State Electrochem. 2003, 7, 416–420. [Google Scholar] [CrossRef]
- Osinkin, D.; Bogdanovich, N. Sintering Aid Strategy for Promoting Oxygen Reduction Reaction on High-Performance Double-Layer LaNi0.6Fe0.4O3–δ Composite Electrode for Devices Based on Solid-State Membranes. Membranes 2023, 13, 603. [Google Scholar] [CrossRef] [PubMed]
- Tai, L.; Nasrallah, M.; Anderson, H.; Sparlin, D.; Sehlin, S.-W. Structure and Electrical Properties of La1−xSrxCo1−yFeyO3. Part 1. The System La0.8Sr0.2Co1−yFeyO3. Solid State Ion. 1995, 76, 259–271. [Google Scholar] [CrossRef]
- Acosta, M.; Baiutti, F.; Tarancón, A.; MacManus-Driscoll, J.L. Nanostructured Materials and Interfaces for Advanced Ionic Electronic Conducting Oxides. Adv. Mater. Interfaces 2019, 6, 1900462. [Google Scholar] [CrossRef]
- Vibhu, V.; Yildiz, S.; Vinke, I.C.; Eichel, R.-A.; Bassat, J.-M.; De Haart, L.G.J. High Performance LSC Infiltrated LSCF Oxygen Electrode for High Temperature Steam Electrolysis Application. J. Electrochem. Soc. 2019, 166, F102–F108. [Google Scholar] [CrossRef]
- Budiman, R.A.; Hong, H.J.; Hashimoto, S.; Yashiro, K.; Bagarinao, K.D.; Kishimoto, H.; Yamaji, K.; Kawada, T. Determination of Relevant Factors Affecting the Surface Oxygen Exchange Coefficient of Solid Oxide Fuel Cell Cathode with Ionic Conducting Oxide Coating. Solid State Ion. 2020, 353, 115372. [Google Scholar] [CrossRef]
- Christy, M.; Rajan, H.; Yang, H.; Kim, Y.-B. Optimizing the Surface Characteristics of La0.6Sr0.4CoO3−δ Perovskite Oxide by Rapid Flash Sintering Technology for Easy Fabrication and Fast Reaction Kinetics in Alkaline Medium. Energy Fuels 2020, 34, 16838–16846. [Google Scholar] [CrossRef]
- Wolf, S.E.; Vibhu, V.; Tröster, E.; Vinke, I.C.; Eichel, R.-A.; De Haart, L.G.J. Steam Electrolysis vs. Co-Electrolysis: Mechanistic Studies of Long-Term Solid Oxide Electrolysis Cells. Energies 2022, 15, 5449. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Pavlova, S.N.; Vinokurov, Z.S.; Shmakov, A.N.; Eremeev, N.F.; Fedorova, Y.E.; Yakimchuk, E.P.; Kriventsov, V.V.; Bolotov, V.A.; Tanashev, Y.Y.; et al. Application of SR Methods for the Study of Nanocomposite Materials for Hydrogen Energy. Phys. Procedia 2016, 84, 397–406. [Google Scholar] [CrossRef]
- Aziz, A.J.A.; Baharuddin, N.A.; Somalu, M.R.; Muchtar, A. Review of Composite Cathodes for Intermediate-Temperature Solid Oxide Fuel Cell Applications. Ceram. Int. 2020, 46, 23314–23325. [Google Scholar] [CrossRef]
- Ren, R.; Wang, Z.; Xu, C.; Sun, W.; Qiao, J.; Rooney, D.W.; Sun, K. Tuning the Defects of the Triple Conducting Oxide BaCo0.4Fe0.4Zr0.1Y0.1O3−δ Perovskite toward Enhanced Cathode Activity of Protonic Ceramic Fuel Cells. J. Mater. Chem. A 2019, 7, 18365–18372. [Google Scholar] [CrossRef]
- Seong, A.; Kim, J.; Jeong, D.; Sengodan, S.; Liu, M.; Choi, S.; Kim, G. Electrokinetic Proton Transport in Triple (H+/O2−/e−) Conducting Oxides as a Key Descriptor for Highly Efficient Protonic Ceramic Fuel Cells. Adv. Sci. 2021, 8, 2004099. [Google Scholar] [CrossRef] [PubMed]
- Kasyanova, A.V.; Tarutina, L.R.; Rudenko, A.O.; Lyagaeva, J.G.; Medvedev, D.A. Ba(Ce,Zr)O3 -Based Electrodes for Protonic Ceramic Electrochemical Cells: Towards Highly Compatible Functionality and Triple-Conducting Behaviour. Russ. Chem. Rev. 2020, 89, 667–692. [Google Scholar] [CrossRef]
- Uchida, H.; Yoshikawa, H.; Esaka, T.; Ohtsu, S.; Iwahara, H. Formation of Protons in SrCeO3-Based Proton Conducting Oxides. Part II. Evaluation of Proton Concentration and Mobility in Yb-Doped SrCeO3. Solid State Ion. 1989, 36, 89–95. [Google Scholar] [CrossRef]
- Kreuer, K.; Schonherr, E.; Maier, J. Proton and Oxygen Diffusion in BaCeO3 Based Compounds: A Combined Thermal Gravimetric Analysis and Conductivity Study. Solid State Ion. 1994, 70–71, 278–284. [Google Scholar] [CrossRef]
- Kreuer, K.D.; Münch, W.; Traub, U.; Maier, J. On Proton Transport in Perovskite-Type Oxides and Plastic Hydroxides. Berichte Der Bunsenges. Für Phys. Chem. 1998, 102, 552–559. [Google Scholar] [CrossRef]
- Afroze, S.; Karim, A.; Cheok, Q.; Eriksson, S.; Azad, A.K. Latest Development of Double Perovskite Electrode Materials for Solid Oxide Fuel Cells: A Review. Front. Energy 2019, 13, 770–797. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, L.; Wang, Y.; Du, Z.; Zhang, B.; Ciucci, F.; Zhao, H. Correction: Enhanced Oxygen Reduction Kinetics of IT-SOFC Cathode with PrBaCo2O5+δ/Gd0.1Ce0.9O2−δ Coherent Interface. J. Mater. Chem. A 2022, 10, 7409. [Google Scholar] [CrossRef]
- Ivanov, I.L.; Zakiryanov, P.O.; Sereda, V.V.; Mazurin, M.O.; Malyshkin, D.A.; Zuev, A.Y.; Tsvetkov, D.S. Nonstoichiometry, Defect Chemistry and Oxygen Transport in Fe-Doped Layered Double Perovskite Cobaltite PrBaCo2−xFexO6−δ (x = 0–0.6) Membrane Materials. Membranes 2022, 12, 1200. [Google Scholar] [CrossRef] [PubMed]
- Ananyev, M.V.; Eremin, V.A.; Tsvetkov, D.S.; Porotnikova, N.M.; Farlenkov, A.S.; Zuev, A.Y.; Fetisov, A.V.; Kurumchin, E.K. Oxygen Isotope Exchange and Diffusion in LnBaCo2O6−δ (Ln = Pr, Sm, Gd) with Double Perovskite Structure. Solid State Ion. 2017, 304, 96–106. [Google Scholar] [CrossRef]
- Li, K.; Niemczyk, A.; Świerczek, K.; Stępień, A.; Naumovich, Y.; Dąbrowa, J.; Zajusz, M.; Zheng, K.; Dabrowski, B. Co-Free Triple Perovskite La1.5Ba1.5Cu3O7±δ as a Promising Air Electrode Material for Solid Oxide Fuel Cells. J. Power Sources 2022, 532, 231371. [Google Scholar] [CrossRef]
- Lee, J.-I.; Park, K.-Y.; Park, H.; Bae, H.; Saqib, M.; Park, K.; Shin, J.-S.; Jo, M.; Kim, J.; Song, S.-J.; et al. Triple Perovskite Structured Nd1.5Ba1.5CoFeMnO9−δ Oxygen Electrode Materials for Highly Efficient and Stable Reversible Protonic Ceramic Cells. J. Power Sources 2021, 510, 230409. [Google Scholar] [CrossRef]
- Belik, A.A.; Johnson, R.D.; Khalyavin, D.D. The Rich Physics of A-Site-Ordered Quadruple Perovskite Manganites AMn7O12. Dalton Trans. 2021, 50, 15458–15472. [Google Scholar] [CrossRef] [PubMed]
- Moazzam, M.; Li, C.; Cordaro, G.; Dezanneau, G. Effect of A-Site Cation Ordering on Oxygen Diffusion in NdBa2Fe3O8 through Molecular Dynamics. J. Solid State Chem. 2023, 325, 124148. [Google Scholar] [CrossRef]
- Morales-Zapata, M.A.; Larrea, A.; Laguna-Bercero, M.A. Lanthanide Nickelates for Their Application on Solid Oxide Cells. Electrochim. Acta 2023, 444, 141970. [Google Scholar] [CrossRef]
- Boehm, E.; Bassat, J.-M.; Steil, M.C.; Dordor, P.; Mauvy, F.; Grenier, J.-C. Oxygen Transport Properties of La2Ni1−xCuxO4+δ Mixed Conducting Oxides. Solid State Sci. 2003, 5, 973–981. [Google Scholar] [CrossRef]
- Tropin, E.; Ananyev, M.; Porotnikova, N.; Khodimchuk, A.; Saher, S.; Farlenkov, A.; Kurumchin, E.; Shepel, D.; Antipov, E.; Istomin, S.; et al. Oxygen Surface Exchange and Diffusion in Pr1.75Sr0.25Ni0.75Co0.25O4±δ. Phys. Chem. Chem. Phys. 2019, 21, 4779–4790. [Google Scholar] [CrossRef]
- Yatoo, M.A.; Skinner, S.J. Ruddlesden-Popper Phase Materials for Solid Oxide Fuel Cell Cathodes: A Short Review. Mater. Today Proc. 2022, 56, 3747–3754. [Google Scholar] [CrossRef]
- Pikalov, S.M.; Vedmid’, L.B.; Filonova, E.A.; Pikalova, E.Y.; Lyagaeva, J.G.; Danilov, N.A.; Murashkina, A.A. High-Temperature Behavior of Calcium Substituted Layered Neodymium Nickelates. J. Alloys Compd. 2019, 801, 558–567. [Google Scholar] [CrossRef]
- Tsvinkinberg, V.A.; Tolkacheva, A.S.; Filonova, E.A.; Gyrdasova, O.I.; Pikalov, S.M.; Vorotnikov, V.A.; Vylkov, A.I.; Moskalenko, N.I.; Pikalova, E.Y. Structure, Thermal Expansion and Electrical Conductivity of La2−xGdxNiO4+δ (0.0 ≤x≤ 0.6) Cathode Materials for SOFC Applications. J. Alloys Compd. 2021, 853, 156728. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Sadovskaya, E.M.; Pikalova, E.Y.; Kolchugin, A.A.; Filonova, E.A.; Pikalov, S.M.; Eremeev, N.F.; Ishchenko, A.V.; Lukashevich, A.I.; Bassat, J.M. Transport Features in Layered Nickelates: Correlation between Structure, Oxygen Diffusion, Electrical and Electrochemical Properties. Ionics 2018, 24, 1181–1193. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Sadovskaya, E.M.; Filonova, E.A.; Eremeev, N.F.; Bogdanovich, N.M.; Pikalov, S.M.; Vylkov, A.I.; Pikalova, E.Y. Mixed Ionic-Electronic Conductivity Features of A-Site Deficient Nd Nickelates. Ceram. Int. 2020, 46, 25527–25535. [Google Scholar] [CrossRef]
- Boehm, E.; Bassat, J.; Dordor, P.; Mauvy, F.; Grenier, J.; Stevens, P. Oxygen Diffusion and Transport Properties in Non-Stoichiometric Ln2−xNiO4+δ Oxides. Solid State Ion. 2005, 176, 2717–2725. [Google Scholar] [CrossRef]
- Minervini, L.; Grimes, R.W.; Kilner, J.A.; Sickafus, K.E. Oxygen Migration in La2NiO4+δ. J. Mater. Chem. 2000, 10, 2349–2354. [Google Scholar] [CrossRef]
- Chroneos, A.; Parfitt, D.; Kilner, J.A.; Grimes, R.W. A molecular dynamics study of anisotropic oxygen diffusion in La2NiO4+δ. Open-Access J. Basic Princip. Diff. Theory Exp. Appl. 2009, 101, 1–2. [Google Scholar]
- Li, X.; Benedek, N.A. Enhancement of Ionic Transport in Complex Oxides through Soft Lattice Modes and Epitaxial Strain. Chem. Mater. 2015, 27, 2647–2652. [Google Scholar] [CrossRef]
- Lee, D.; Lee, H. Controlling Oxygen Mobility in Ruddlesden–Popper Oxides. Materials 2017, 10, 368. [Google Scholar] [CrossRef]
- Xu, S.; Jacobs, R.; Morgan, D. Factors Controlling Oxygen Interstitial Diffusion in the Ruddlesden–Popper Oxide La2–xSrxNiO4+δ. Chem. Mater. 2018, 30, 7166–7177. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Pikalova, E.Y.; Vinokurov, Z.S.; Shmakov, A.N.; Eremeev, N.F.; Sadovskaya, E.M.; Lyagaeva, J.G.; Medvedev, D.A.; Belyaev, V.D. Tailoring the Structural, Thermal and Transport Properties of Pr2NiO4+δ through Ca-Doping Strategy. Solid State Ion. 2019, 333, 30–37. [Google Scholar] [CrossRef]
- Pikalova, E.Y.; Sadykov, V.A.; Filonova, E.A.; Eremeev, N.F.; Sadovskaya, E.M.; Pikalov, S.M.; Bogdanovich, N.M.; Lyagaeva, J.G.; Kolchugin, A.A.; Vedmid’, L.B.; et al. Structure, Oxygen Transport Properties and Electrode Performance of Ca-Substituted Nd2NiO4. Solid State Ion. 2019, 335, 53–60. [Google Scholar] [CrossRef]
- Filonova, E.A.; Pikalova, E.Y.; Maksimchuk, T.Y.; Vylkov, A.I.; Pikalov, S.M.; Maignan, A. Crystal Structure and Functional Properties of Nd1.6Ca0.4Ni1-yCuyO4+δ as Prospective Cathode Materials for Intermediate Temperature Solid Oxide Fuel Cells. Int. J. Hydrogen Energy 2021, 46, 17037–17050. [Google Scholar] [CrossRef]
- Xue, J.; Liao, Q.; Chen, W.; Bouwmeester, H.J.M.; Wang, H.; Feldhoff, A. A New CO2-Resistant Ruddlesden–Popper Oxide with Superior Oxygen Transport: A-Site Deficient (Pr0.9La0.1)1.9(Ni0.74Cu0.21Ga0.05)O4+δ. J. Mater. Chem. A 2015, 3, 19107–19114. [Google Scholar] [CrossRef]
- Pikalova, E.; Eremeev, N.; Sadovskaya, E.; Sadykov, V.; Tsvinkinberg, V.; Pikalova, N.; Kolchugin, A.; Vylkov, A.; Baynov, I.; Filonova, E. Influence of the Substitution with Rare Earth Elements on the Properties of Layered Lanthanum Nickelate—Part 1: Structure, Oxygen Transport and Electrochemistry Evaluation. Solid State Ion. 2022, 379, 115903. [Google Scholar] [CrossRef]
- Ishihara, T.; Sirikanda, N.; Nakashima, K.; Miyoshi, S.; Matsumoto, H. Mixed Oxide Ion and Hole Conductivity in Pr2−αNi0.76−xCu0.24GaxO4+δ Membrane. J. Electrochem. Soc. 2010, 157, B141. [Google Scholar] [CrossRef]
- Yashima, M.; Sirikanda, N.; Ishihara, T. Crystal Structure, Diffusion Path, and Oxygen Permeability of a Pr2NiO4 -Based Mixed Conductor (Pr0.9La0.1)2(Ni0.74Cu0.21Ga0.05)O4+δ. J. Am. Chem. Soc. 2010, 132, 2385–2392. [Google Scholar] [CrossRef] [PubMed]
- Adler, S. Limitations of Charge-Transfer Models for Mixed-Conducting Oxygen Electrodes. Solid State Ion. 2000, 135, 603–612. [Google Scholar] [CrossRef]
- Yashima, M.; Yamada, H.; Nuansaeng, S.; Ishihara, T. Role of Ga3+ and Cu2+ in the High Interstitial Oxide-Ion Diffusivity of Pr2NiO4 -Based Oxides: Design Concept of Interstitial Ion Conductors through the Higher-Valence d10 Dopant and Jahn–Teller Effect. Chem. Mater. 2012, 24, 4100–4113. [Google Scholar] [CrossRef]
- Maksimchuk, T.; Filonova, E.; Mishchenko, D.; Eremeev, N.; Sadovskaya, E.; Bobrikov, I.; Fetisov, A.; Pikalova, N.; Kolchugin, A.; Shmakov, A.; et al. High-Temperature Behavior, Oxygen Transport Properties, and Electrochemical Performance of Cu-Substituted Nd1.6Ca0.4NiO4+δ Electrode Materials. Appl. Sci. 2022, 12, 3747. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Sadovskaya, E.M.; Eremeev, N.F.; Maksimchuk, T.Y.; Pikalov, S.M.; Filonova, E.A.; Pikalova, N.S.; Gilev, A.R.; Pikalova, E.Y. Structure, Oxygen Mobility, and Electrochemical Characteristics of La1.7Ca0.3Ni1−xCuxO4+δ Materials. Russ. J. Electrochem. 2023, 59, 37–48. [Google Scholar] [CrossRef]
- Miyoshi, S.; Furuno, T.; Sangoanruang, O.; Matsumoto, H.; Ishihara, T. Mixed Conductivity and Oxygen Permeability of Doped Pr2NiO4-Based Oxides. J. Electrochem. Soc. 2007, 154, B57. [Google Scholar] [CrossRef]
- Song, J.; Ning, D.; Boukamp, B.; Bassat, J.-M.; Bouwmeester, H.J.M. Structure, Electrical Conductivity and Oxygen Transport Properties of Ruddlesden–Popper Phases Lnn+1NinO3n+1 (Ln = La, Pr and Nd; n = 1, 2 and 3). J. Mater. Chem. A 2020, 8, 22206–22221. [Google Scholar] [CrossRef]
- Yatoo, M.A.; Seymour, I.D.; Skinner, S.J. Neutron Diffraction and DFT Studies of Oxygen Defect and Transport in Higher-Order Ruddlesden–Popper Phase Materials. RSC Adv. 2023, 13, 13786–13797. [Google Scholar] [CrossRef]
- Ota, T.; Alaydrus, M.; Kizaki, H.; Morikawa, Y. Analysis of Atomic Structure, Magnetic Ordering, and Oxygen Diffusion in Oxygen Deficient Sr3Fe2O7−δ Perovskite: Toward Rational Catalysts Design. Phys. Rev. Mater. 2022, 6, 015801. [Google Scholar] [CrossRef]
- Yatoo, M.A.; Skinner, S.J. Oxygen Transport in Higher-Order Ruddlesden-Popper Phase Materials. ECS Trans. 2023, 111, 2405–2412. [Google Scholar] [CrossRef]
- Kuo, J.H.; Anderson, H.U.; Sparlin, D.M. Oxidation-Reduction Behavior of Undoped and Sr-Doped LaMnO3: Defect Structure, Electrical Conductivity, and Thermoelectric Power. J. Solid State Chem. 1990, 87, 55–63. [Google Scholar] [CrossRef]
- Cao, J.; Su, C.; Ji, Y.; Yang, G.; Shao, Z. Recent Advances and Perspectives of Fluorite and Perovskite-Based Dual-Ion Conducting Solid Oxide Fuel Cells. J. Energy Chem. 2021, 57, 406–427. [Google Scholar] [CrossRef]
- Ananyev, M.V.; Porotnikova, N.M.; Eremin, V.A.; Kurumchin, E.K. Interaction of O2 with LSM–YSZ Composite Materials and Oxygen Spillover Effect. ACS Catal. 2021, 11, 4247–4262. [Google Scholar] [CrossRef]
- Wang, M.; Su, C.; Zhu, Z.; Wang, H.; Ge, L. Composite Cathodes for Protonic Ceramic Fuel Cells: Rationales and Materials. Compos. Part B Eng. 2022, 238, 109881. [Google Scholar] [CrossRef]
- Tan, K.H.; Hamimah, A.R.; Nor, M.R. Addition of Sm0.2Ce0.8O1.9 carbonate into perovskite Cathode materials for low-temperature solid oxide fuel cell: Short review. J. Innov. Technol. 2022, 4, 1–10. [Google Scholar]
- Esquirol, A.; Kilner, J.; Brandon, N. Oxygen Transport in La0.6Sr0.4Co0.2Fe0.8O3-δ/Ce0.8Ge0.2O2−x Composite Cathode for IT-SOFCs. Solid State Ion. 2004, 175, 63–67. [Google Scholar] [CrossRef]
- Eremeev, N.F. Structural Studies of Pr Nickelate-Cobaltite—Y-Doped Ceria Nanocomposite. J. Ceram. Sci. Tech. 2017, 8, 129–140. [Google Scholar] [CrossRef]
- Xin, X.; Liu, L.; Liu, Y.; Zhu, Q. Novel Perovskite-Spinel Composite Conductive Ceramics for SOFC Cathode Contact Layer. Int. J. Hydrogen Energy 2018, 43, 23036–23040. [Google Scholar] [CrossRef]
- Cheng, J.; Qian, W.; Wang, P.; Tian, C. A High Activity Cathode of Sm0.2Ce0.8O1.9 Decorated Mn1.5Co1.5O4 Using Ion Impregnation Technique within a Solid Oxide Fuel Cell System. SSRN J. 2022, 131, 106962. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Y.; Mushtaq, N.; Shah, M.A.K.Y.; Rauf, S.; Lund, P.D.; Asghar, M.I. Novel LaFe2O4 Spinel Structure with a Large Oxygen Reduction Response towards Protonic Ceramic Fuel Cell Cathode. J. Rare Earths 2023, 41, 413–421. [Google Scholar] [CrossRef]
- Ogura, Y.; Yokoi, T.; Toyoura, K.; Matsunaga, K. First-Principles Analysis of Oxide-Ion Conduction Mechanism in Neodymium Silicate. Solid State Ion. 2020, 355, 115367. [Google Scholar] [CrossRef]
- Kendrick, E.; Kendrick, J.; Knight, K.S.; Islam, M.S.; Slater, P.R. Cooperative Mechanisms of Fast-Ion Conduction in Gallium-Based Oxides with Tetrahedral Moieties. Nat. Mater. 2007, 6, 871–875. [Google Scholar] [CrossRef]
- Thabet, K.; Salle, A.L.G.L.; Quarez, E.; Joubert, O. Protonic-Based Ceramics for Fuel Cells and Electrolyzers. In Solid Oxide-Based Electrochemical Devices; Elsevier: Amsterdam, The Netherlands, 2020; pp. 91–122. ISBN 978-0-12-818285-7. [Google Scholar]
- Mitra, C.; Meyer, T.; Lee, H.N.; Reboredo, F.A. Oxygen Diffusion Pathways in Brownmillerite SrCoO2.5: Influence of Structure and Chemical Potential. J. Chem. Phys. 2014, 141, 084710. [Google Scholar] [CrossRef]
- Zhang, W.; Yashima, M. Recent Developments in Oxide Ion Conductors: Focusing on Dion–Jacobson Phases. Chem. Commun. 2023, 59, 134–152. [Google Scholar] [CrossRef] [PubMed]
- Thangadurai, V.; Weppner, W. Determination of the Sodium Ion Transference Number of the Dion−Jacobson-Type Layered Perovskite NaCa2Nb3O10 Using Ac Impedance and Dc Methods. Chem. Mater. 2002, 14, 1136–1143. [Google Scholar] [CrossRef]
- Shi, J.; Han, C.; Niu, H.; Zhu, Y.; Yun, S. Theoretical Investigation of Proton Diffusion in Dion–Jacobson Layered Perovskite RbBiNb2O7. Nanomaterials 2021, 11, 1953. [Google Scholar] [CrossRef] [PubMed]
- Teusner, M.; De Souza, R.A.; Krause, H.; Ebbinghaus, S.G.; Martin, M. Oxygen Transport in Undoped and Doped Mayenite. Solid State Ion. 2016, 284, 25–27. [Google Scholar] [CrossRef]
- Phaneuf, V.N. Synthesis, Characterization and Application of Mayenite. Ph.D. Thesis, Clemson University, Clemson, SC, USA, 2021. [Google Scholar]
- Orera, A.; Slater, P.R. Water Incorporation Studies in Apatite-Type Rare Earth Silicates/Germanates. Solid State Ion. 2010, 181, 110–114. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, Q.; Ragipani, R.; Wang, B. Formation and Transport Mechanisms of Hydrogenous Species in Mayenite. J. Phys. Chem. C 2020, 124, 11150–11157. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, Y.; Bu, F.; Yang, F.; Wang, M.; Li, Y. Preparation and Properties of Low Thermal Expansion Coefficient (Y0.5Ca0.5)1−xInxBaCo3ZnO7+δ (X=0, 0.1, 0.2, 0.3) Solid Oxide Fuel Cell Cathode Materials. SSRN J. 2021. [Google Scholar] [CrossRef]
- Shin, J.-S.; Park, H.; Park, K.; Saqib, M.; Jo, M.; Kim, J.H.; Lim, H.-T.; Kim, M.; Kim, J.; Park, J.-Y. Activity of Layered Swedenborgite Structured Y0.8Er0.2BaCo3.2Ga0.8O7+δ for Oxygen Electrode Reactions in at Intermediate Temperature Reversible Ceramic Cells. J. Mater. Chem. A 2021, 9, 607–621. [Google Scholar] [CrossRef]
- Kirichenko, V.G.; Kovalenko, O.V. Study of Element Composition and Component Diffusion of Yttrium Iron Garnet Thin Films. Vopr. At. Nauk. I Tekhnik 2014, 89, 133–140. [Google Scholar]
- Zhang, X.; Tian, Y.; Nie, Z.; Wu, X.; Li, Y.; Ding, L. Electrochemical Characteristics of Ca3Co4O9+δ Oxygen Electrode for Reversible Solid Oxide Cells. J. Electroanal. Chem. 2022, 922, 116708. [Google Scholar] [CrossRef]
- Urusova, A.; Bryuzgina, A.; Solomakhina, E.; Kolchugin, A.; Malyshkin, D.; Pikalova, E.; Filonova, E. Assessment of the Y-Doped Ca3Co4O9+δ as Cathode Material for Proton-Conducting Fuel Cells. Int. J. Hydrogen Energy 2023, 48, 22656–22670. [Google Scholar] [CrossRef]
- Yue, X.; Huang, X.; Li, J.; Su, C.; Zhang, Y.; Zhang, Y.; Wei, B.; Lv, Z. In-Situ Surface Reconstruction Induced-Significant Performance Promotion of Ca3Co4O9+δ Cathode for Solid Oxide Fuel Cells. J. Power Sources 2022, 528, 231203. [Google Scholar] [CrossRef]
- Zhu, X.; Lusi, A.; Zhu, C.; Wang, Y.; Jin, J. Performance Evaluation of Ca3Co4O9-δ Cathode on Sm0.075Nd0.075Ce0.85O2-δ Electrolyte for Solid Oxide Fuel Cells. J. Alloys Compd. 2017, 694, 877–883. [Google Scholar] [CrossRef]
- Pikalova, E.; Kolchugin, A.; Koroleva, M.; Vdovin, G.; Farlenkov, A.; Medvedev, D. Functionality of an Oxygen Ca3Co4O9+δ Electrode for Reversible Solid Oxide Electrochemical Cells Based on Proton-Conducting Electrolytes. J. Power Sources 2019, 438, 226996. [Google Scholar] [CrossRef]
- Rolle, A.; Mohamed, H.A.A.; Huo, D.; Capoen, E.; Mentré, O.; Vannier, R.-N.; Daviero-Minaud, S.; Boukamp, B.A. Ca3Co4O9+δ, a Growing Potential SOFC Cathode Material: Impact of the Layer Composition and Thickness on the Electrochemical Properties. Solid State Ion. 2016, 294, 21–30. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, W.; Chen, Y.; Shao, Z. An Aurivillius Oxide Based Cathode with Excellent CO2 Tolerance for Intermediate-Temperature Solid Oxide Fuel Cells. Angew. Chem. Int. Ed. 2016, 55, 8988–8993. [Google Scholar] [CrossRef] [PubMed]
- Villegas, M.; Moure, C.; Fernandez, J.F.; Duran, P. Low-Temperature Sintering of Submicronic Randomly Oriented Bi4Ti3O12 Materials. Ceram. Int. 1996, 22, 15–22. [Google Scholar] [CrossRef]
- Thoréton, V.; Hu, Y.; Pirovano, C.; Capoen, E.; Nuns, N.; Mamede, A.S.; Dezanneau, G.; Yoo, C.Y.; Bouwmeester, H.J.M.; Vannier, R.N. Oxygen Transport Kinetics of the Misfit Layered Oxide Ca3Co4O9+δ. J. Mater. Chem. A 2014, 2, 19717–19725. [Google Scholar] [CrossRef]
- Filonova, E.A.; Tokareva, E.S.; Pikalova, N.S.; Vylkov, A.I.; Bogdanovich, N.M.; Pikalova, E.Y. Assessment of Prospective Cathodes Based on (1−x)Ca3Co4O9+δ-xBaCe0.5Zr0.3Y0.1Yb0.1O3-δ Composites for Protonic Ceramic Electrochemical Cells. J. Solid State Electrochem. 2020, 24, 1509–1521. [Google Scholar] [CrossRef]
- Boukamp, B.A.; Rolle, A.; Vannier, R.N.; Sharma, R.K.; Djurado, E. Electrostatic Spray Deposited Ca3Co4O9+δ and Ca3Co4O9+δ/Ce0.9Gd0.1O1.95 Cathodes for SOFC. Electrochim. Acta 2020, 362, 137142. [Google Scholar] [CrossRef]
- Yurchenko, M.V.; Antonova, E.P.; Tropin, E.S.; Suntsov, A.Y. Adjusting Electrochemical Properties of PrBaCo2O6–δ as SOFC Cathode by Controllable Ca3Co4O9 Additions. Ceram. Int. 2023, 49, 21485–21491. [Google Scholar] [CrossRef]
- Xing, W.; Syvertsen, G.E.; Grande, T.; Li, Z.; Haugsrud, R. Hydrogen Permeation, Transport Properties and Microstructure of Ca-Doped LaNbO4 and LaNb3O9 Composites. J. Membr. Sci. 2012, 415–416, 878–885. [Google Scholar] [CrossRef]
- Syvertsen, G.E.; Estournès, C.; Fjeld, H.; Haugsrud, R.; Einarsrud, M.-A.; Grande, T. Spark Plasma Sintering and Hot Pressing of Hetero-Doped LaNbO4. J. Am. Ceram. Soc. 2012, 95, 1563–1571. [Google Scholar] [CrossRef]
- Haugsrud, R.; Norby, T. Proton Conduction in Rare-Earth Ortho-Niobates and Ortho-Tantalates. Nat. Mater. 2006, 5, 193–196. [Google Scholar] [CrossRef]
- Wood, J.R. Defects and Conductivity in Sr-Doped LaNb3O9. Master’s Thesis, University of Oslo, Oslo, Norway, 2007. [Google Scholar]
- Haugsrud, R.; Norby, T. High-Temperature Proton Conductivity in Acceptor-Doped LaNbO4. Solid State Ion. 2006, 177, 1129–1135. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Bespalko, Y.N.; Krasnov, A.V.; Skriabin, P.I.; Lukashevich, A.I.; Fedorova, Y.E.; Sadovskaya, E.M.; Eremeev, N.F.; Krieger, T.A.; Ishchenko, A.V.; et al. Novel Proton-Conducting Nanocomposites for Hydrogen Separation Membranes. Solid State Ion. 2018, 322, 69–78. [Google Scholar] [CrossRef]
- Altynbekova, D.; Bespalko, Y.; Valeev, K.; Eremeev, N.; Sadovskaya, E.; Krieger, T.; Ulihin, A.; Uhina, A.; Massalimova, B.; Simonov, M.; et al. Simple Approach to the Fabrication of Lanthanum Orthoniobates and Nanocomposites with Ni, Cu, and Co Metal Nanoparticles Using Supercritical Isopropanol. J. Compos. Sci. 2022, 6, 243. [Google Scholar] [CrossRef]
- Colognesi, D.; Demmel, F.; Filabozzi, A.; Pietropaolo, A.; Pozio, A.; Romanelli, G.; Santucci, A.; Tosti, S. Proton Dynamics in Palladium–Silver: An Inelastic Neutron Scattering Investigation. Molecules 2020, 25, 5587. [Google Scholar] [CrossRef]
- Huang, F.; Li, X.; Shan, X.; Guo, J.; Gallucci, F.; Annaland, M.V.S.; Liu, D. Hydrogen Transport through the V-Cr-Al Alloys: Hydrogen Solution, Permeation and Thermal-Stability. Separ. Purif. Technol. 2020, 240, 116654. [Google Scholar] [CrossRef]
- Sidorov, N.I.; Estemirova, S.K.; Kurbanova, E.D.; Polukhin, V.A. Hydrogen Kinetics in Membrane Alloys Based on Fe–Ni, Nb–Ni, and V–Ni. Russ. Met. Met. 2022, 2022, 887–897. [Google Scholar] [CrossRef]
- Alimov, V.N.; Bobylev, I.V.; Busnyuk, A.O.; Kolgatin, S.N.; Peredistov, E.Y.; Livshits, A.I. Fuel Processor with Vanadium Alloy Membranes for Converting CH4 into Ultrapure Hydrogen to Generate Electricity via Fuel Cell. Appl. Energy 2020, 269, 115148. [Google Scholar] [CrossRef]
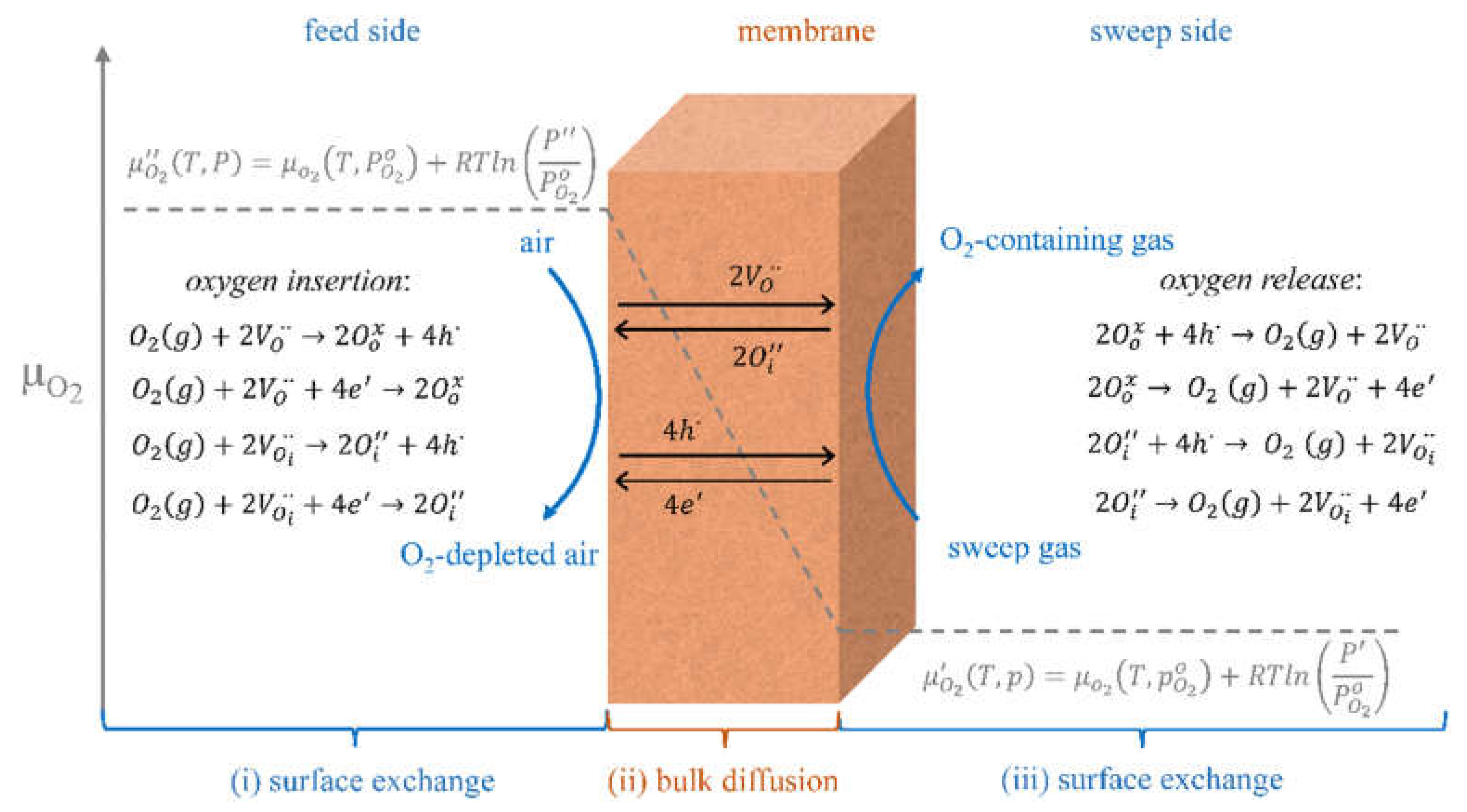
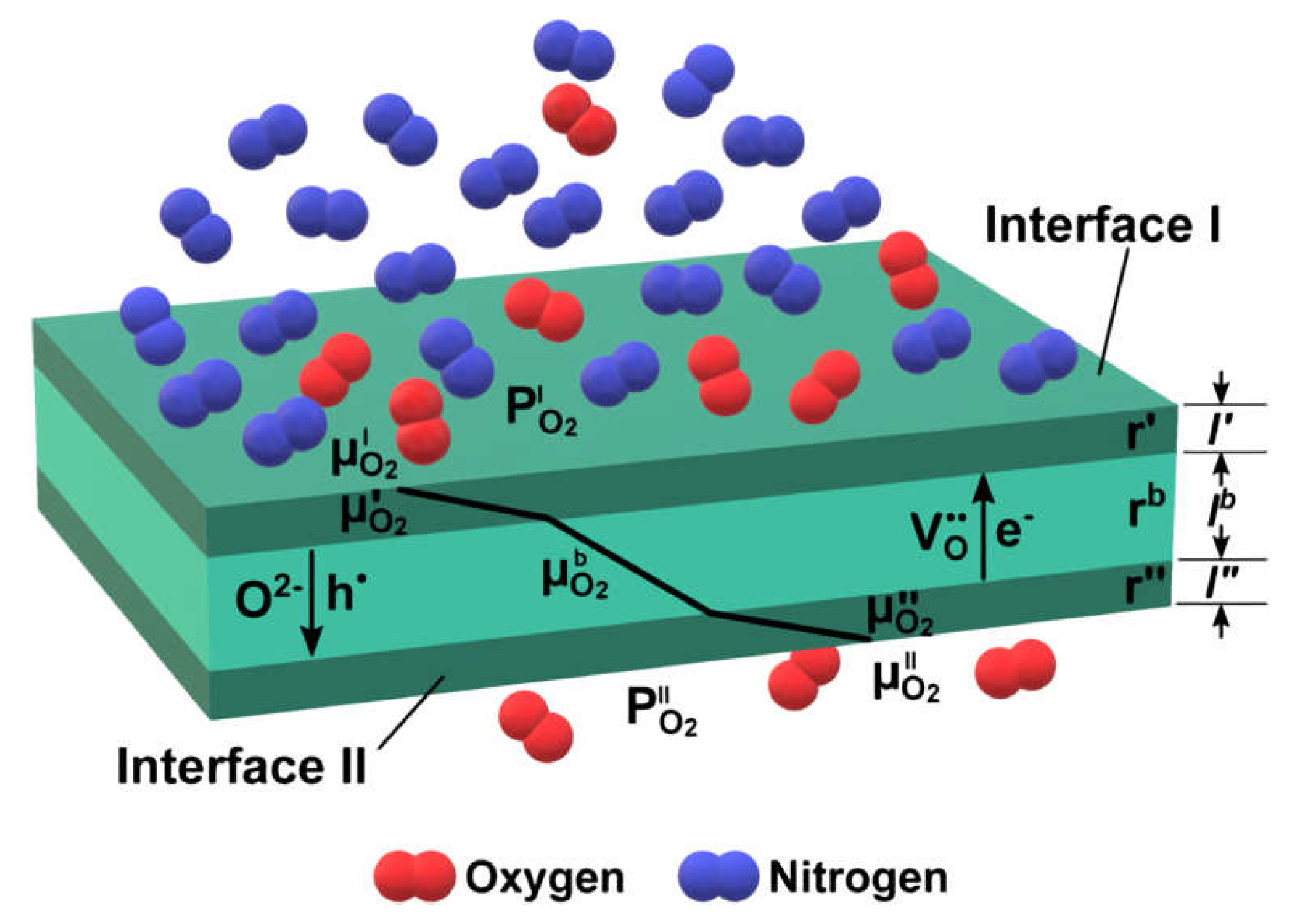
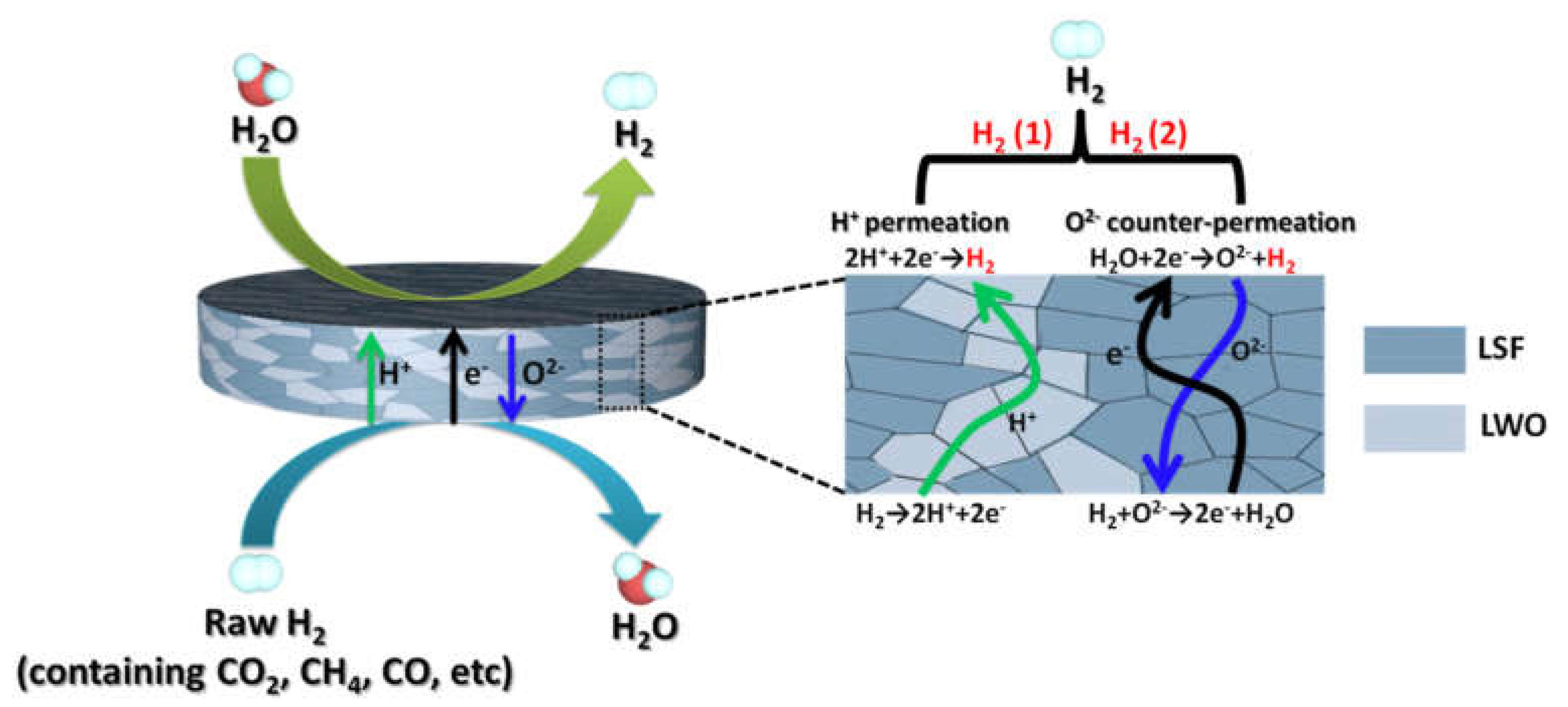
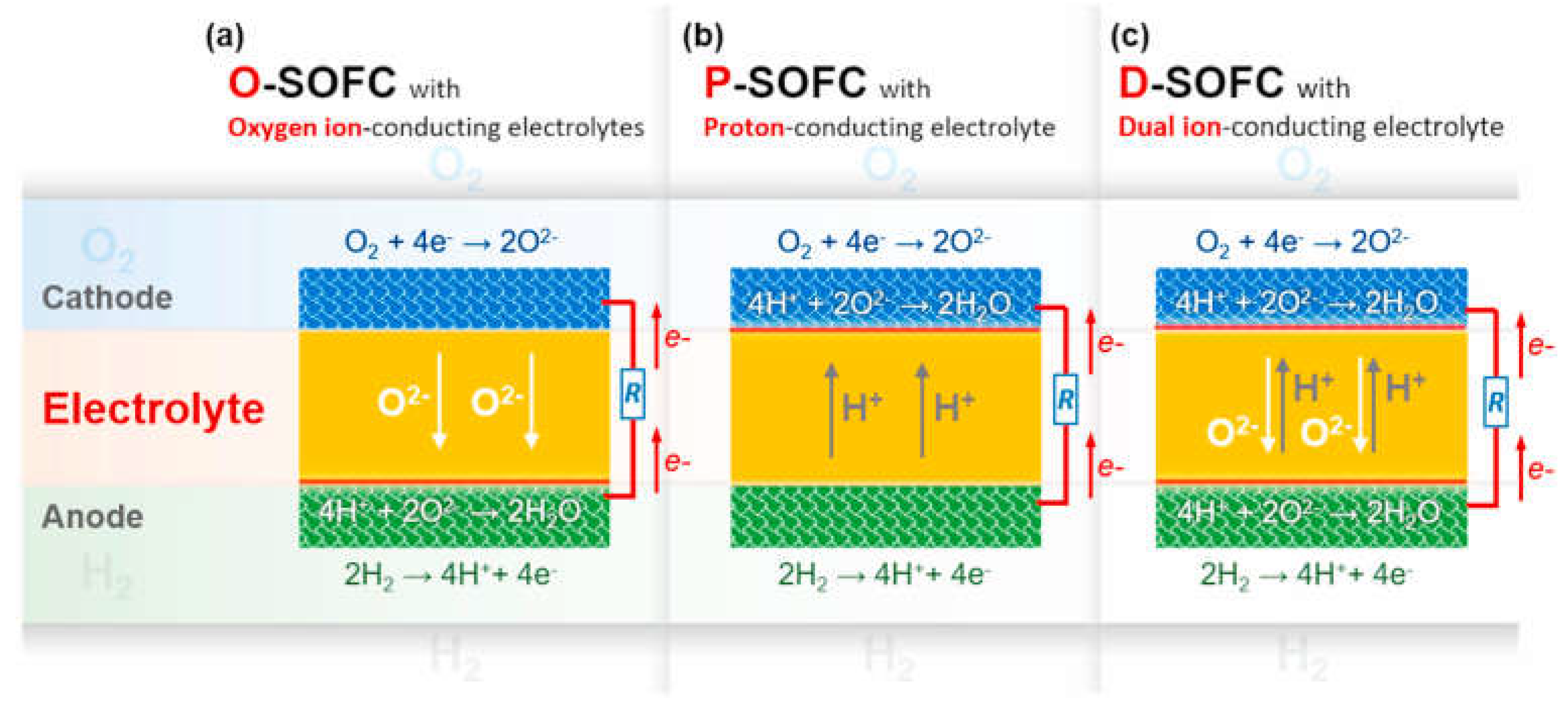
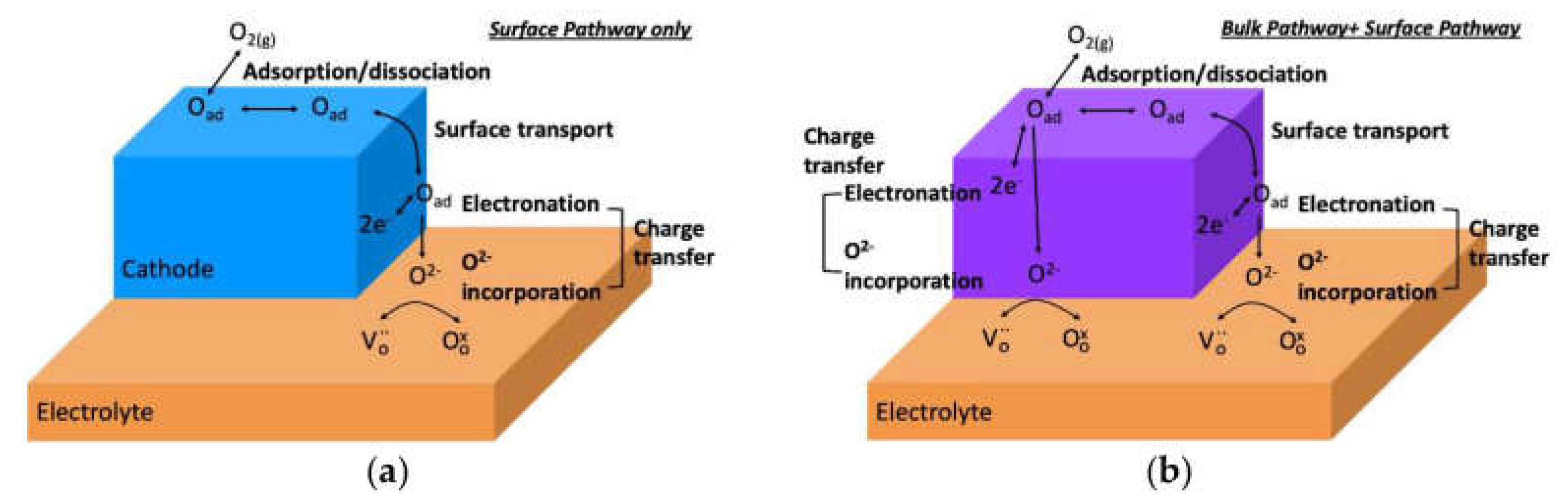
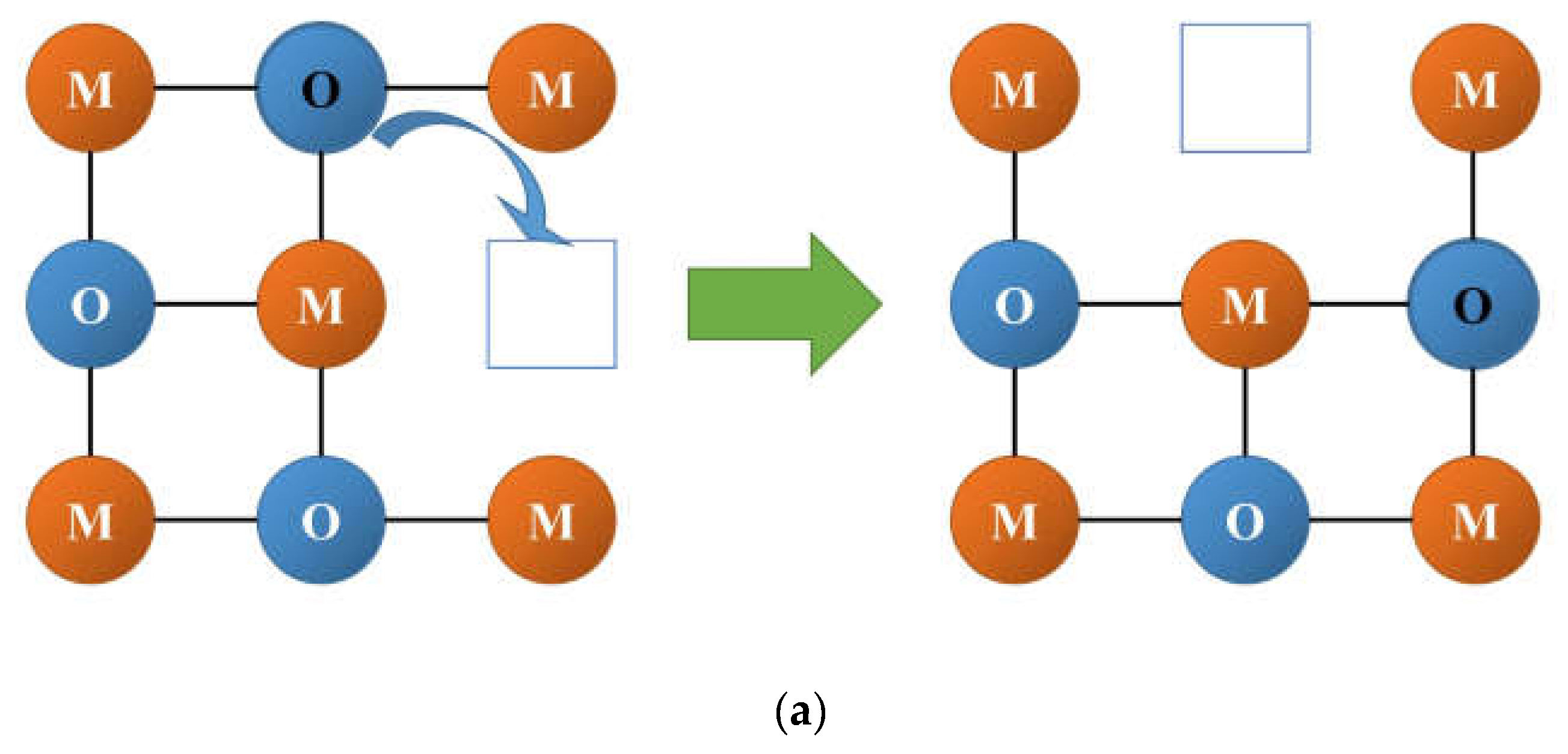
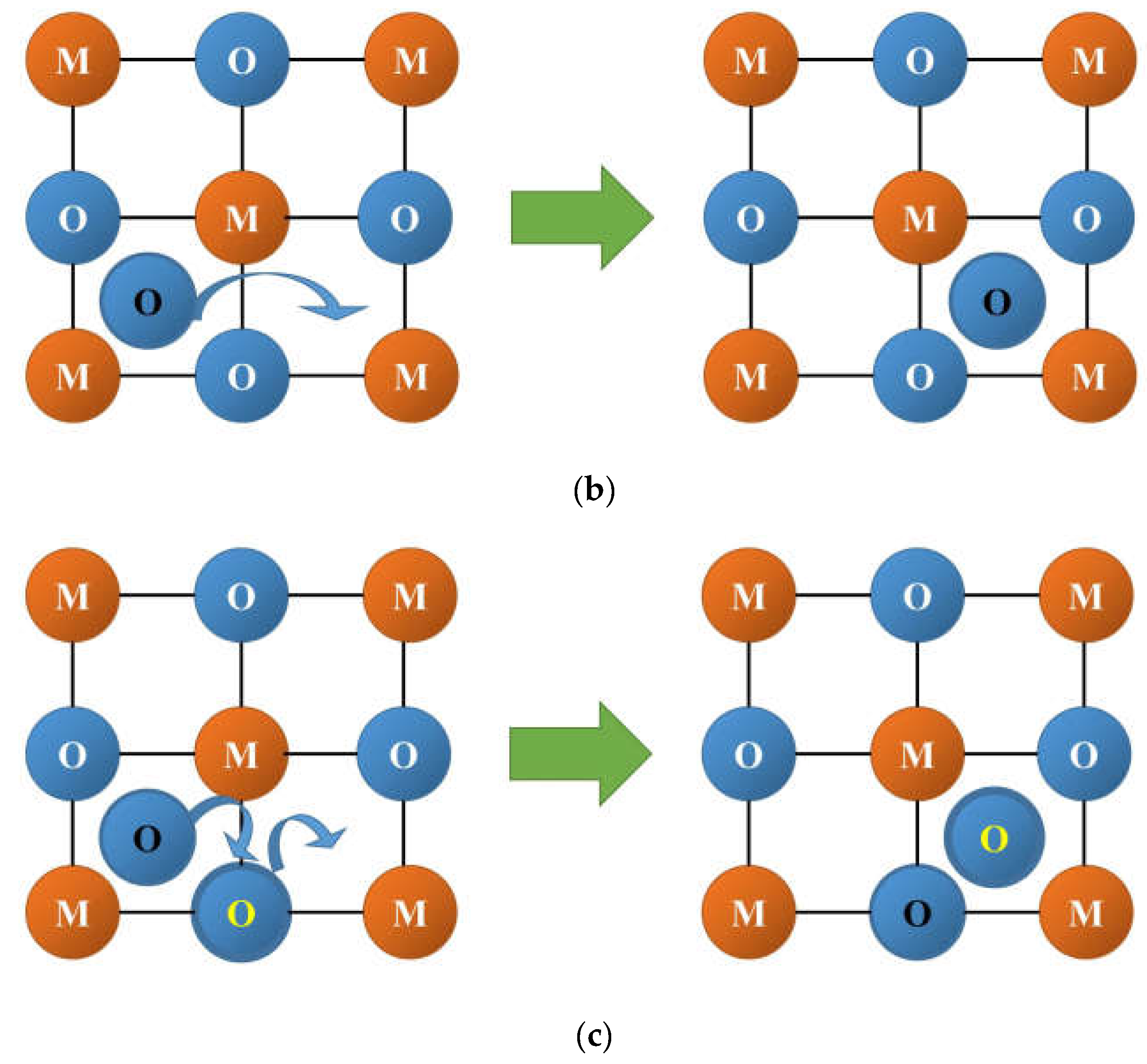
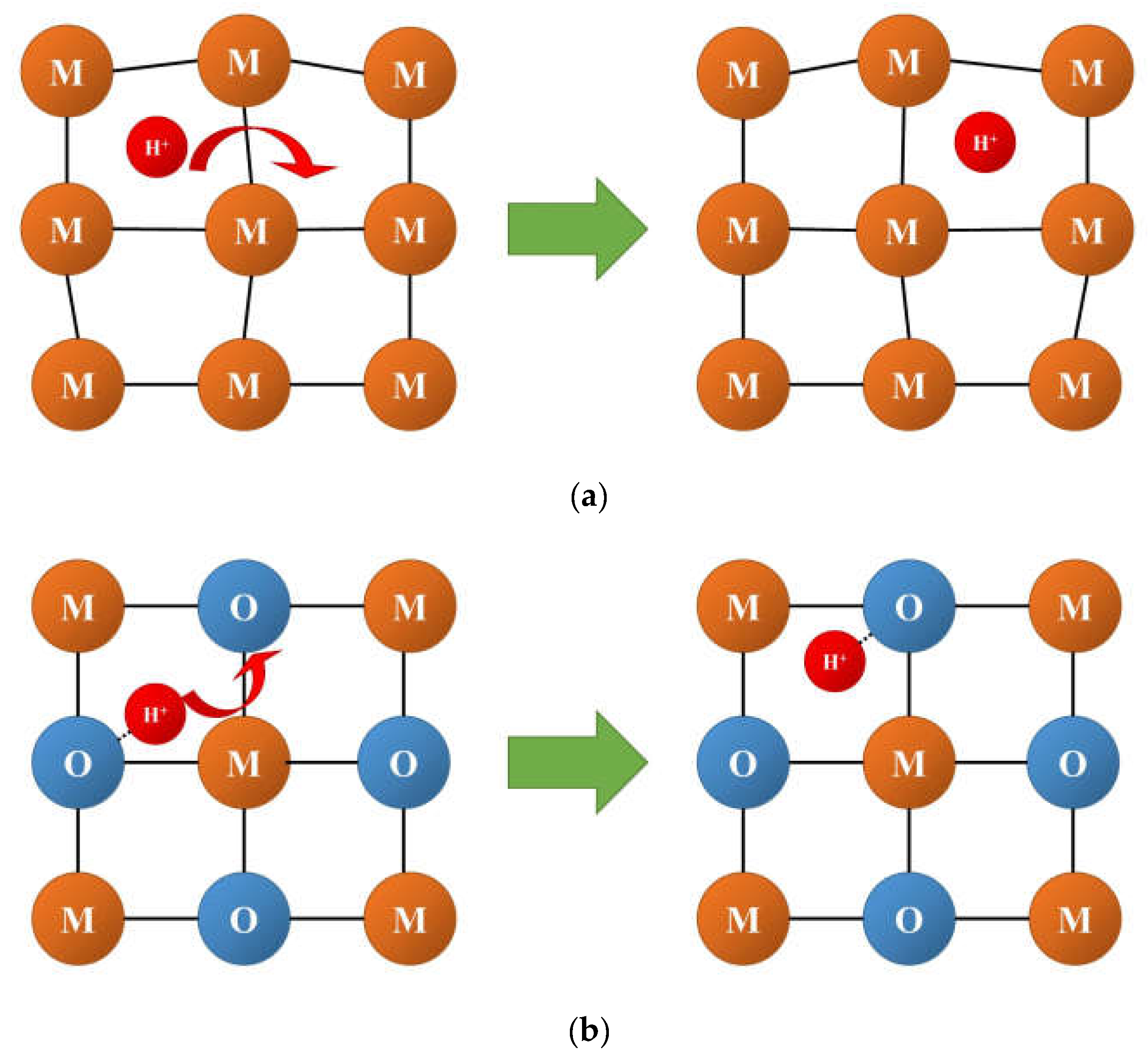
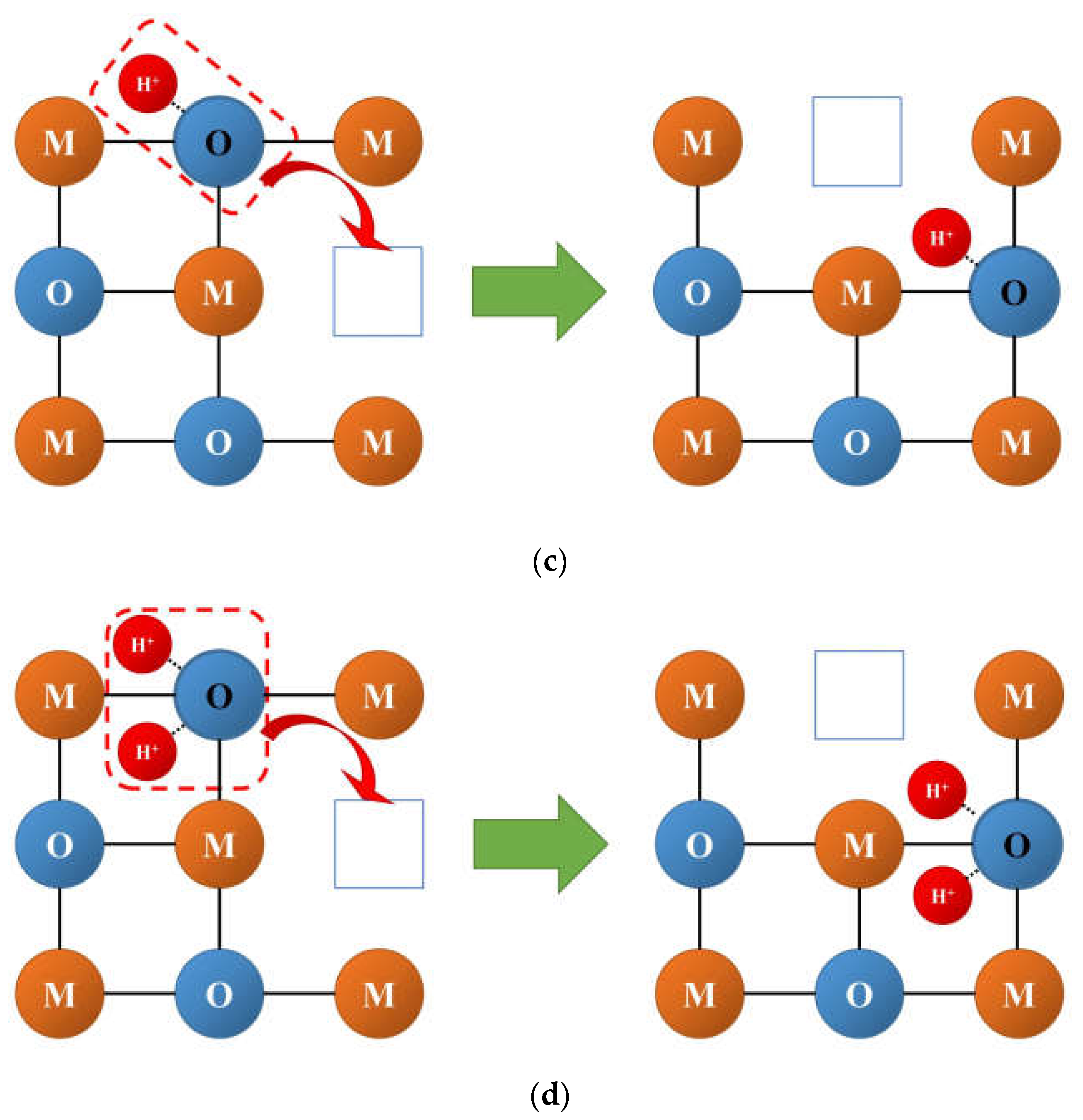
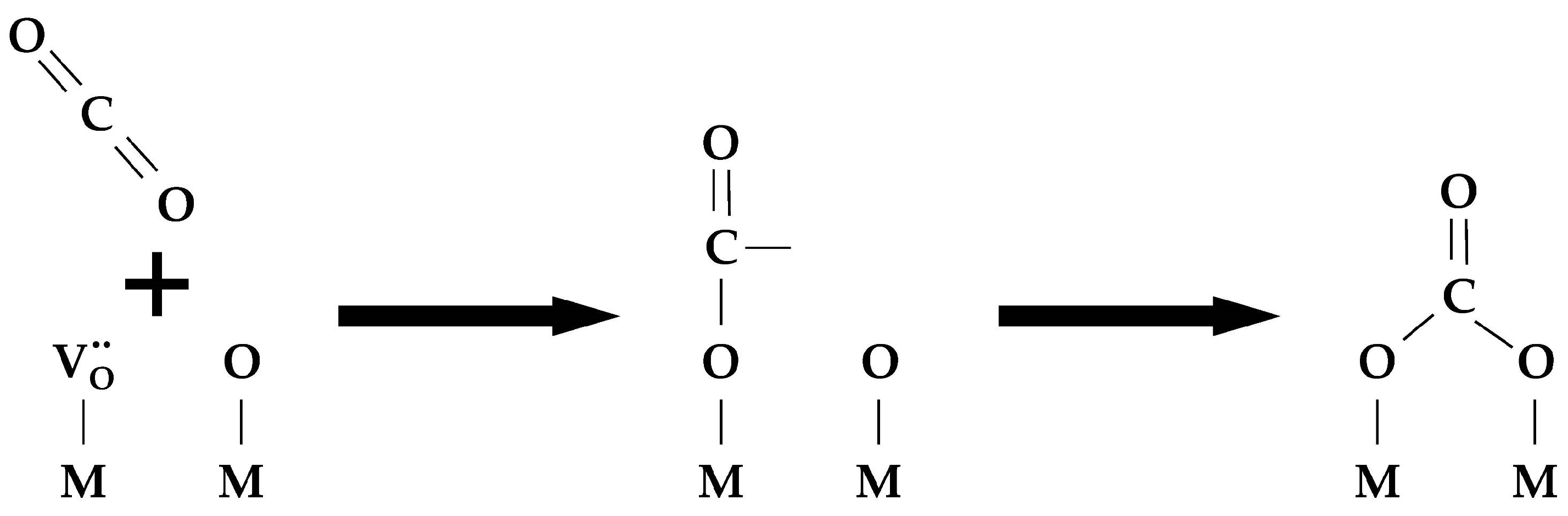
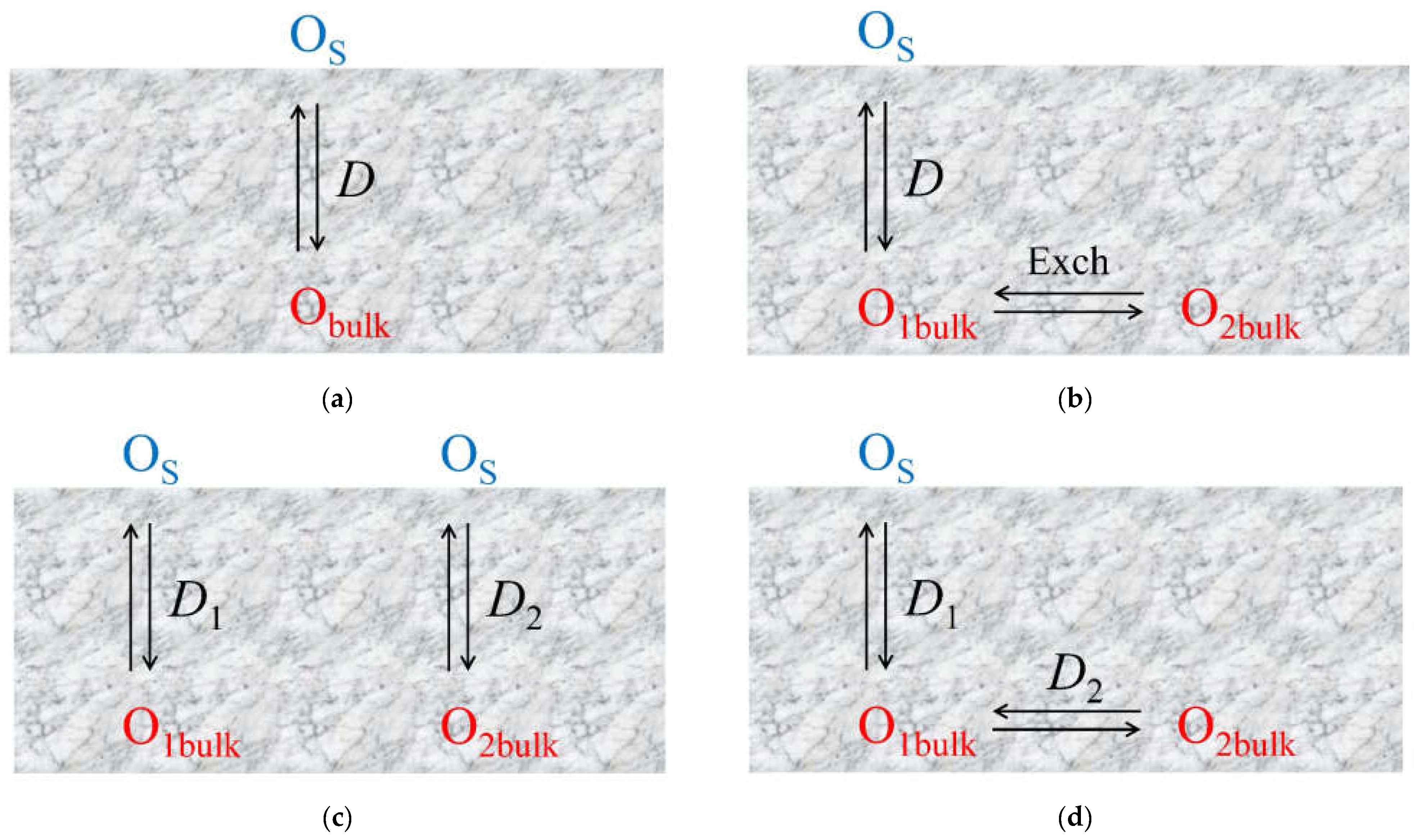
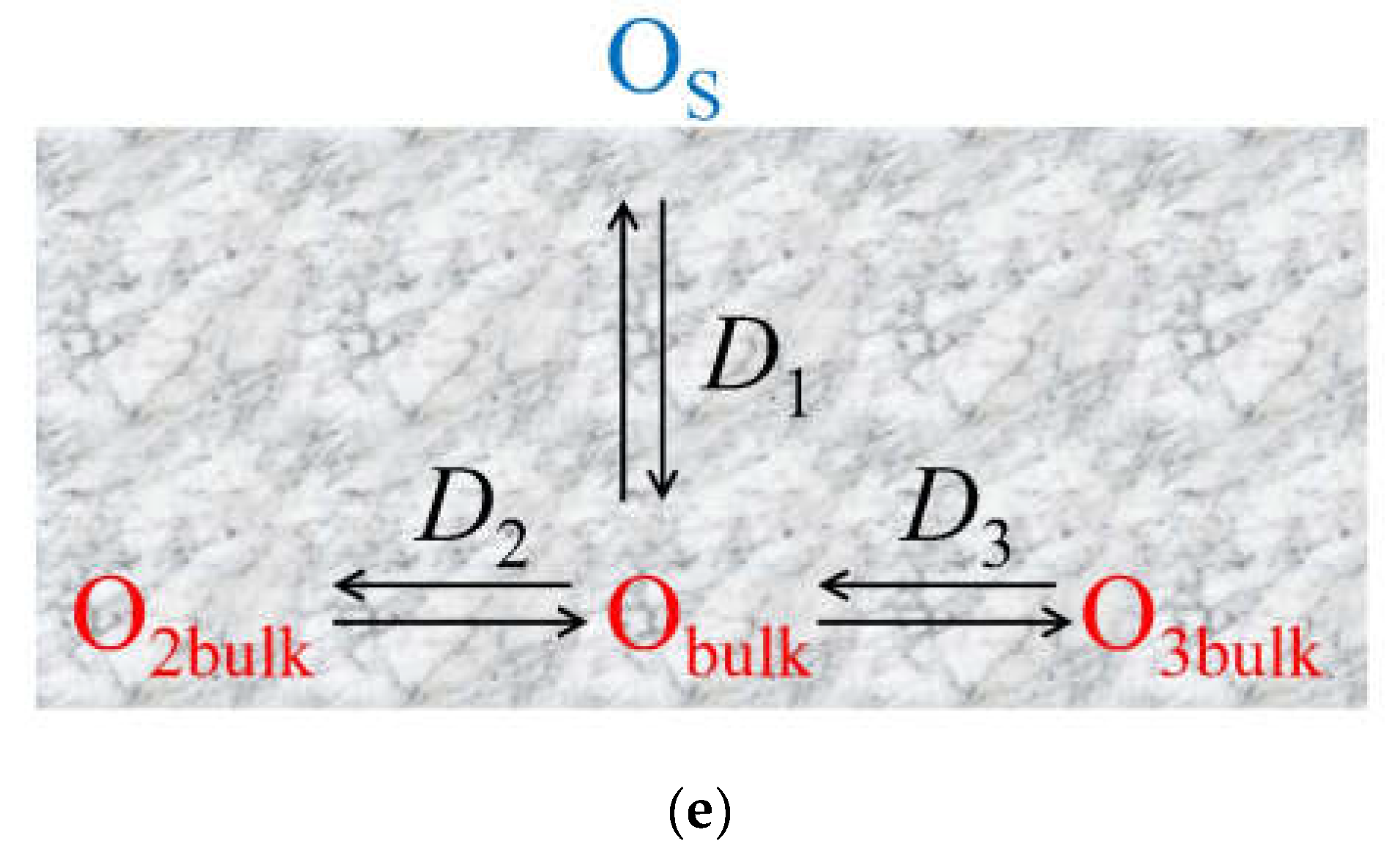
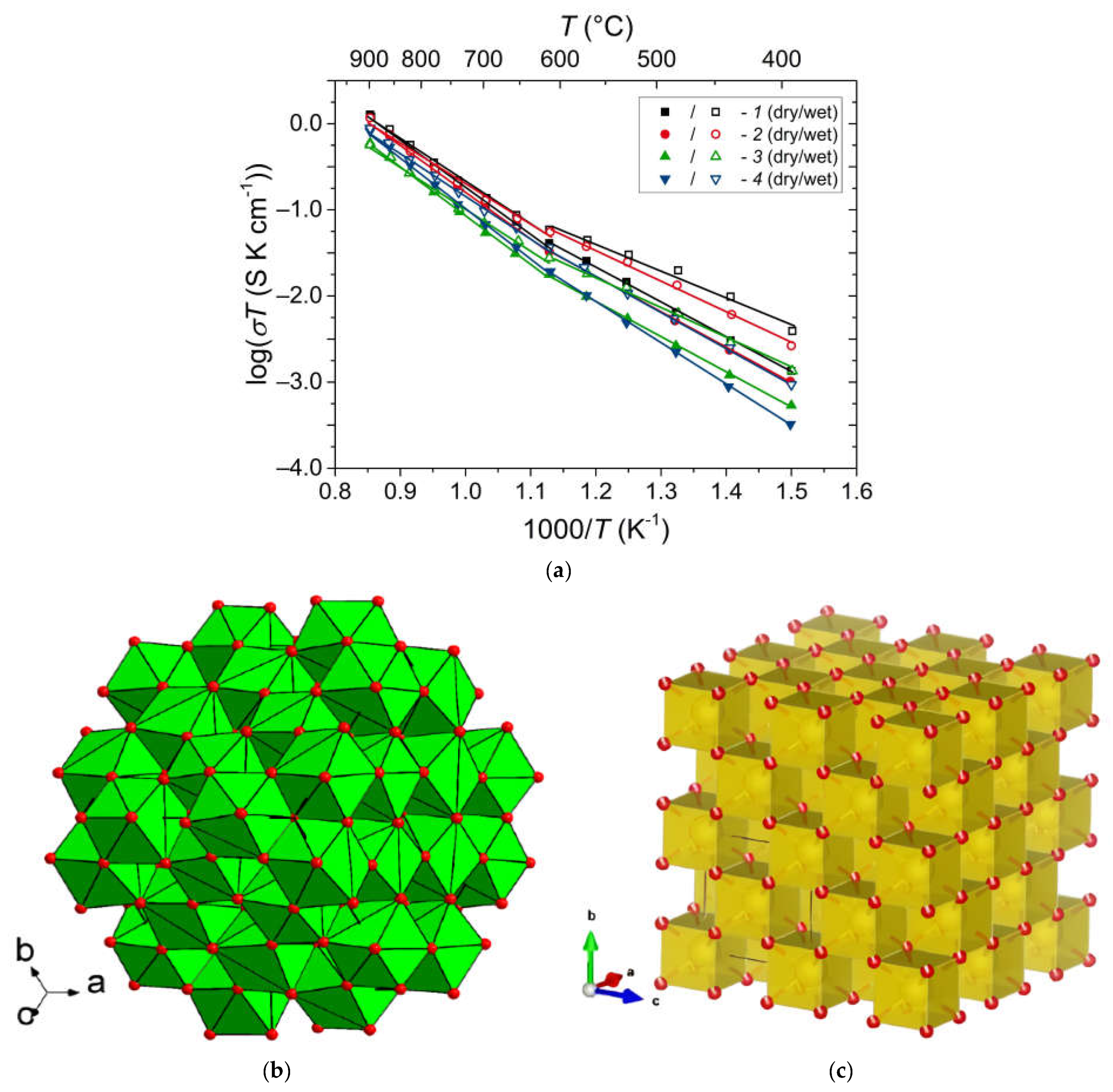
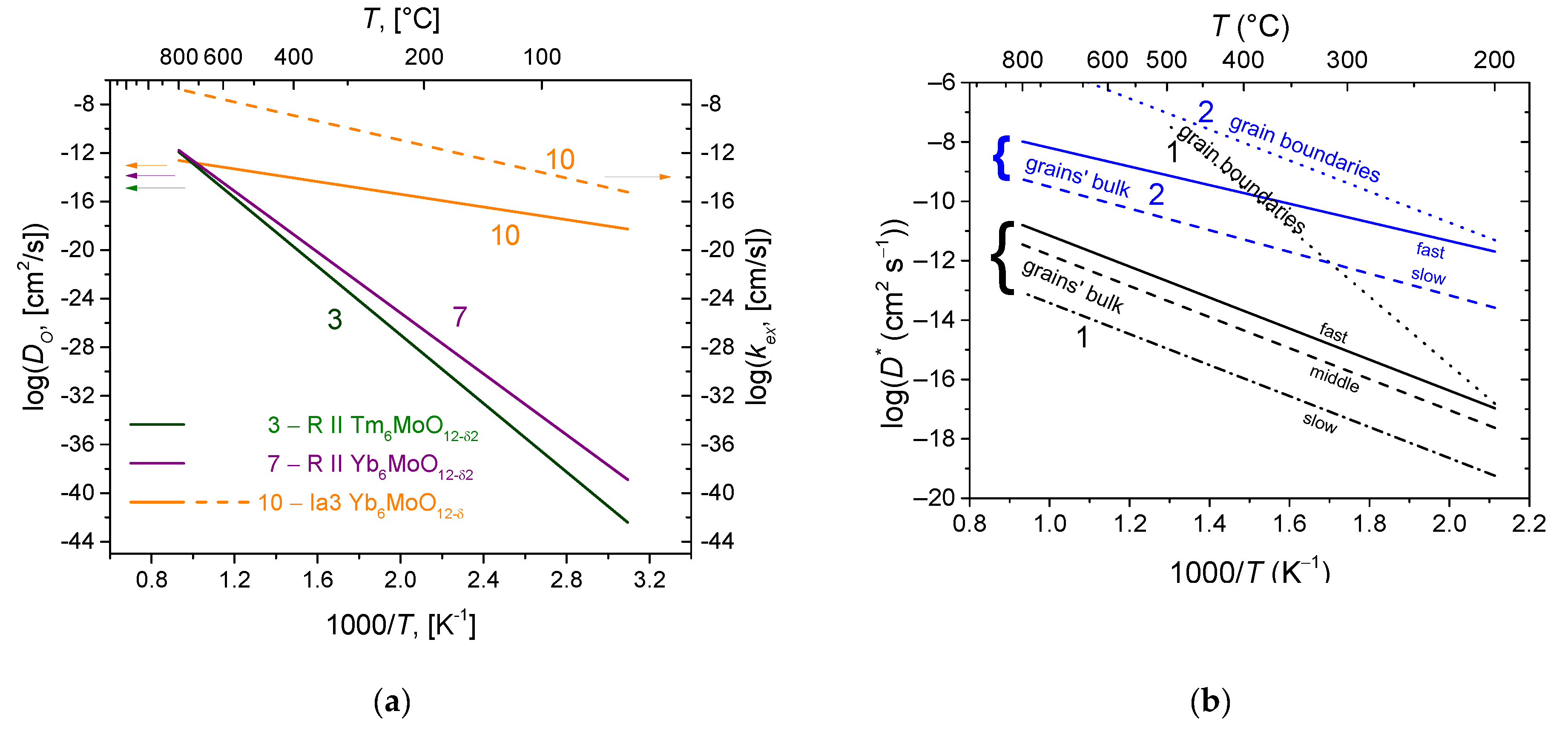
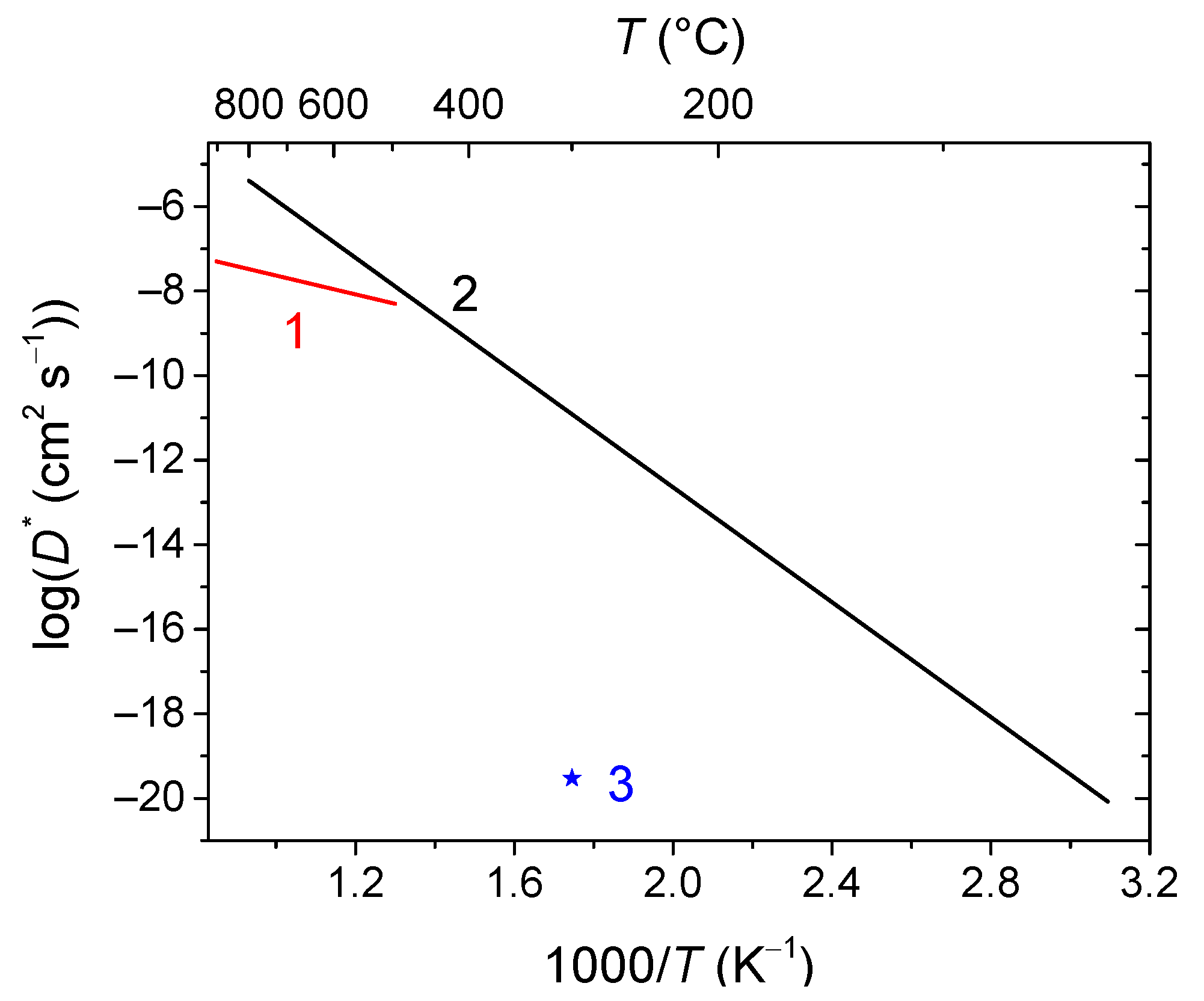
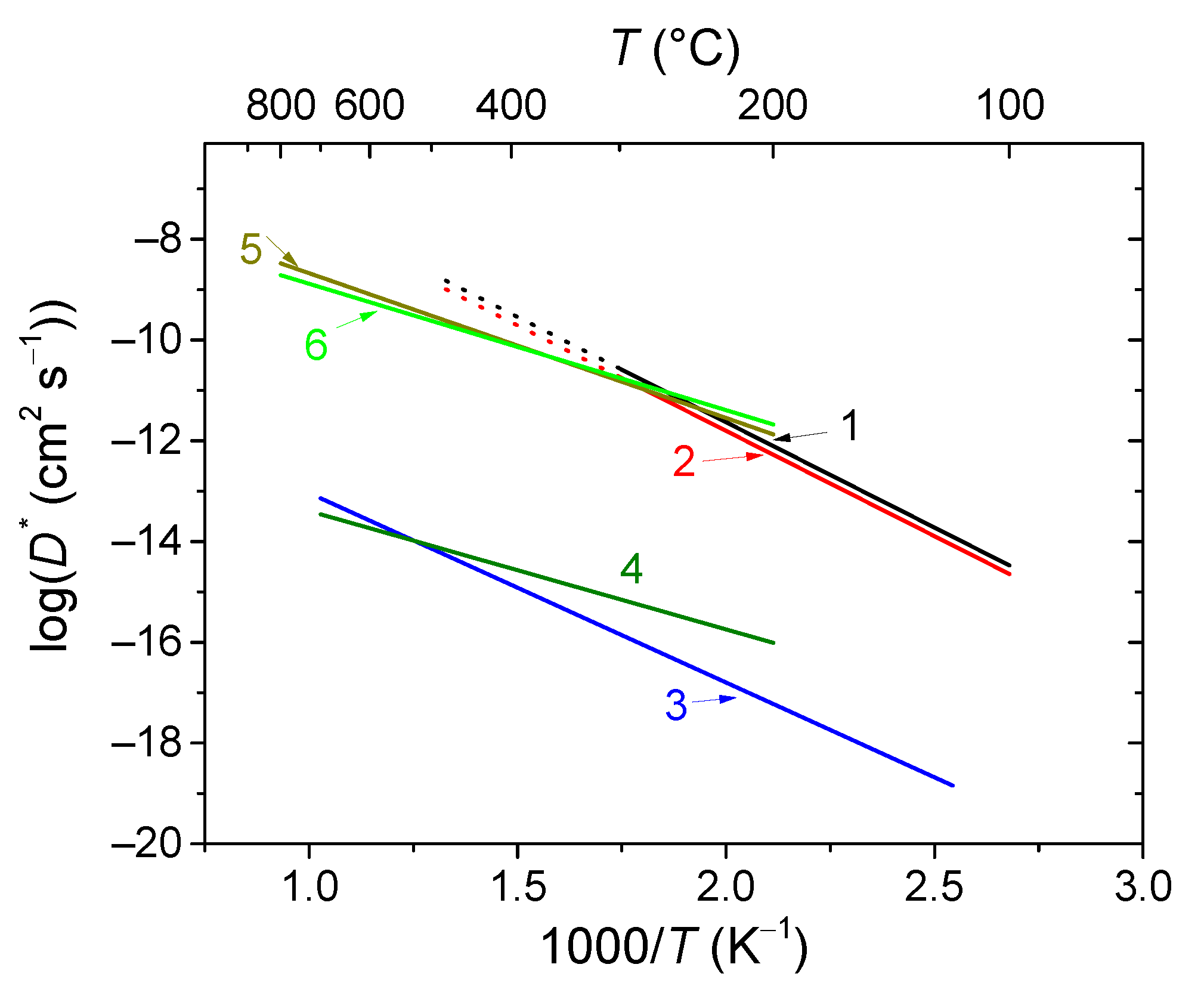
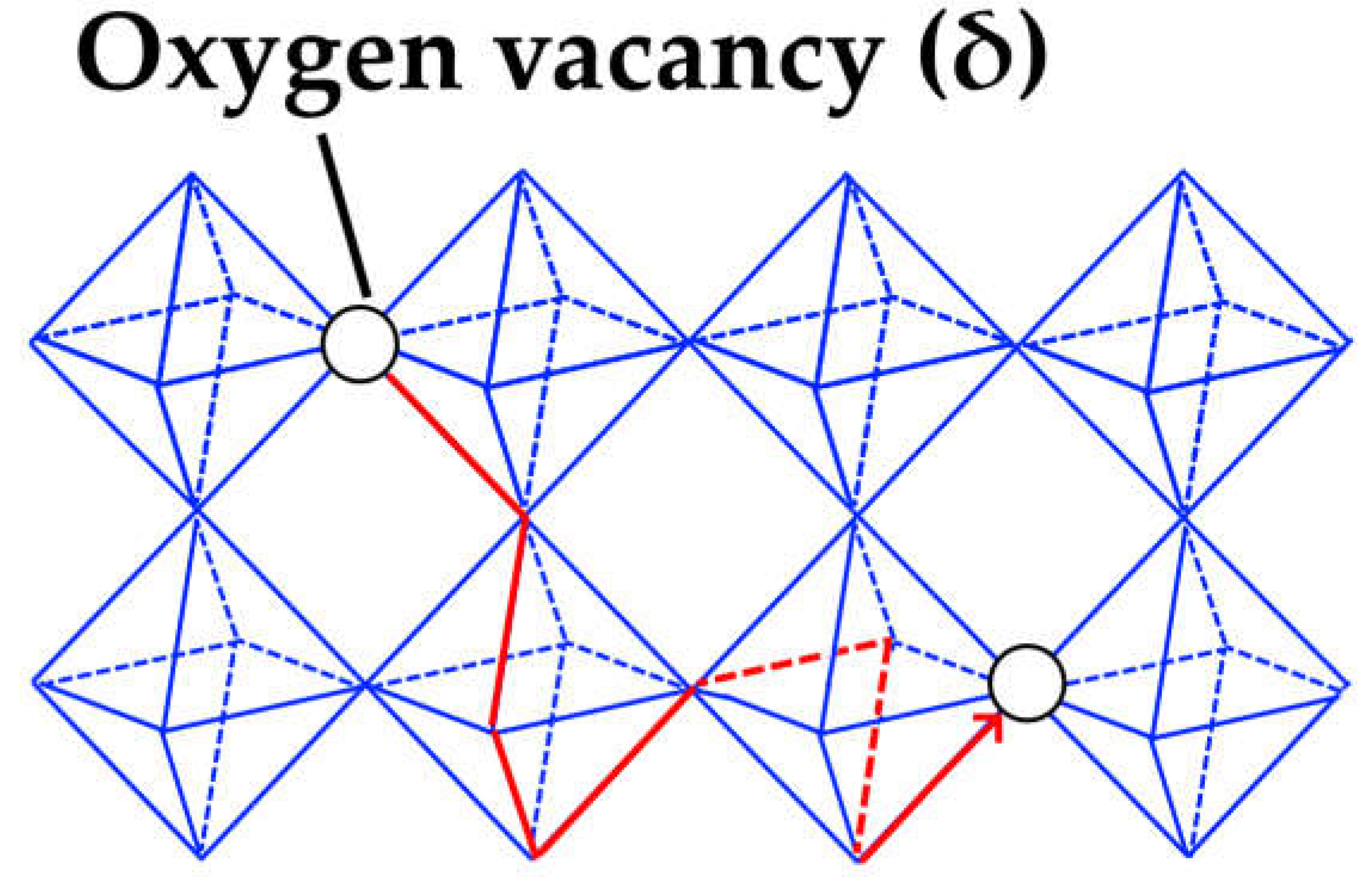
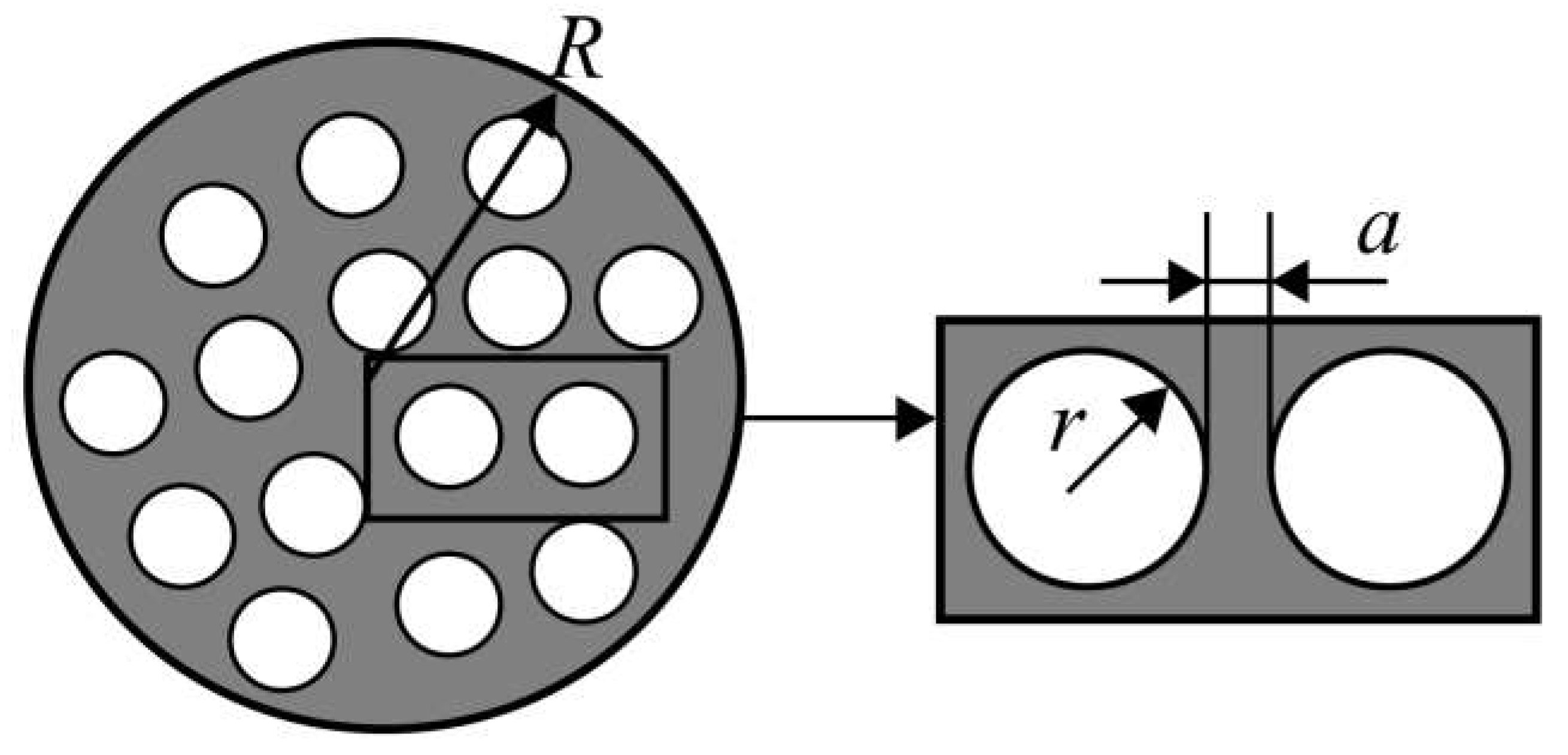
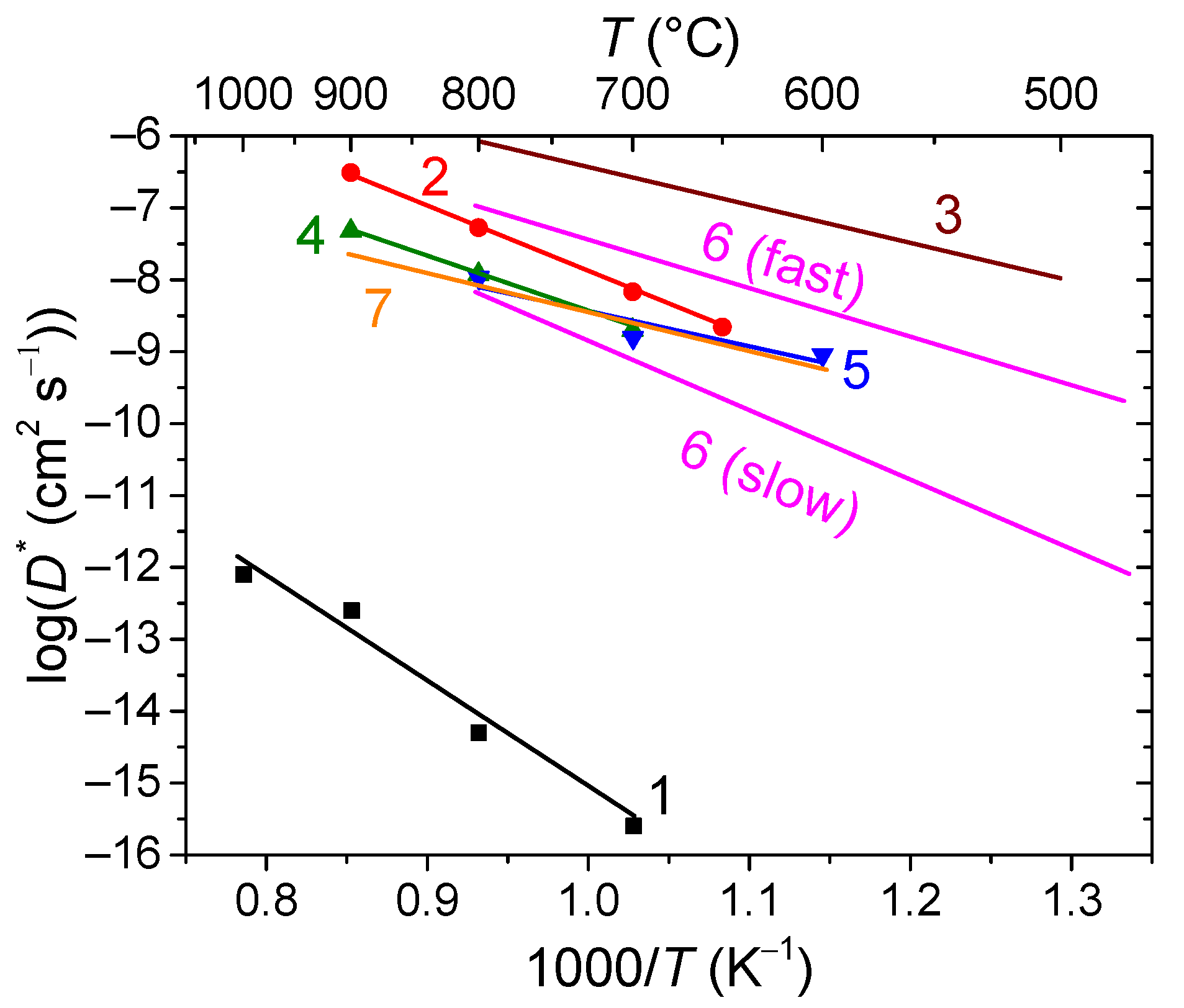
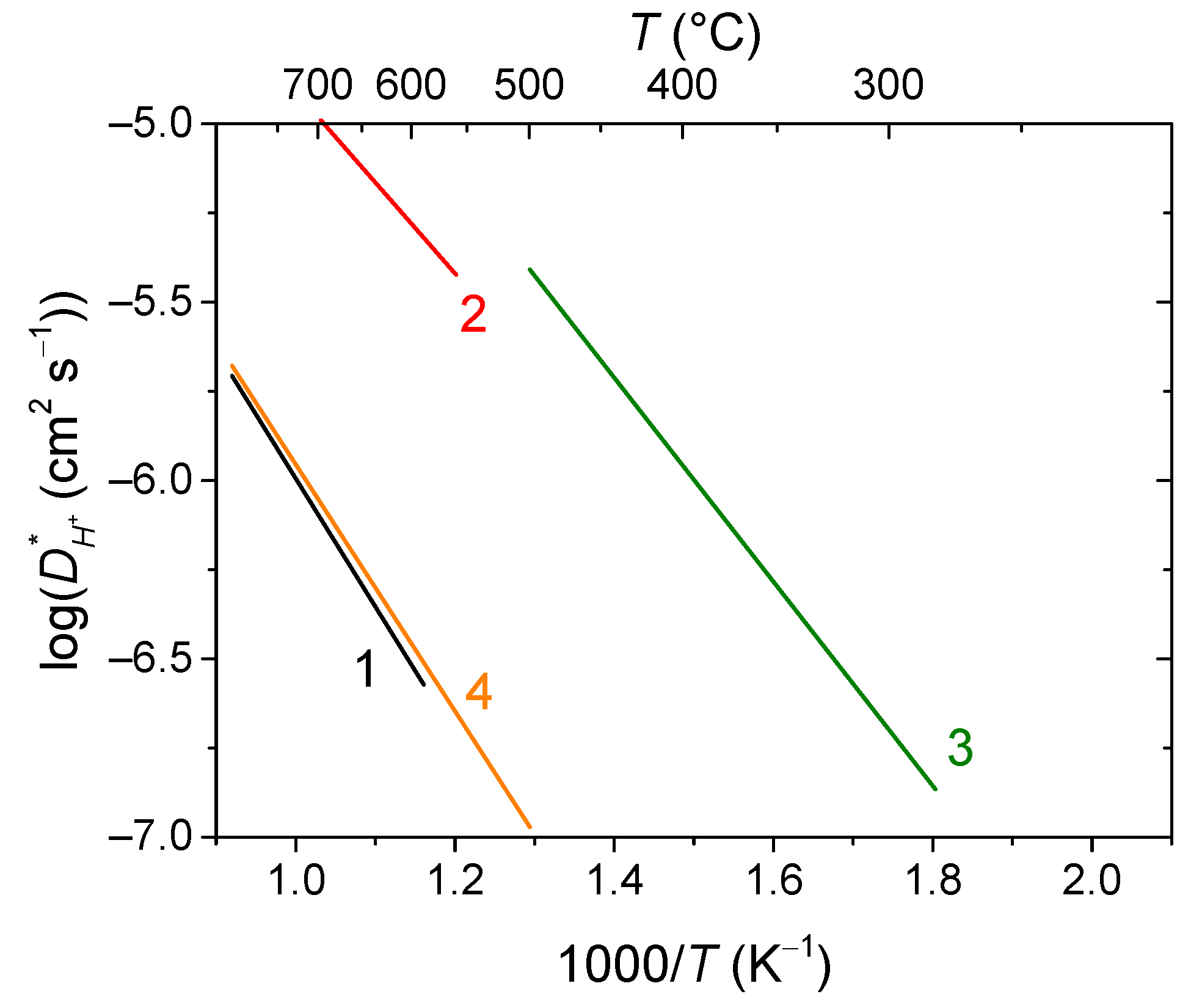
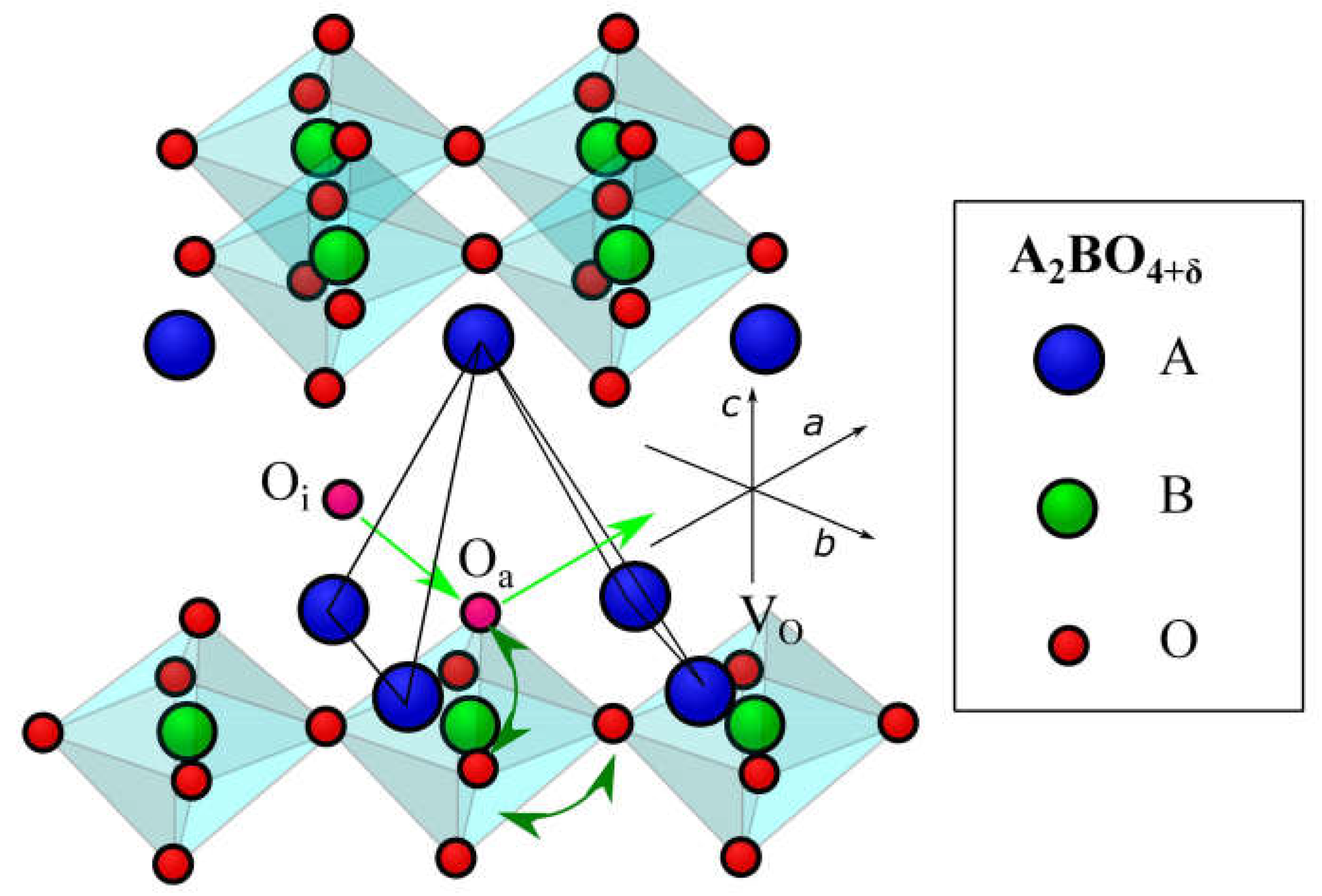
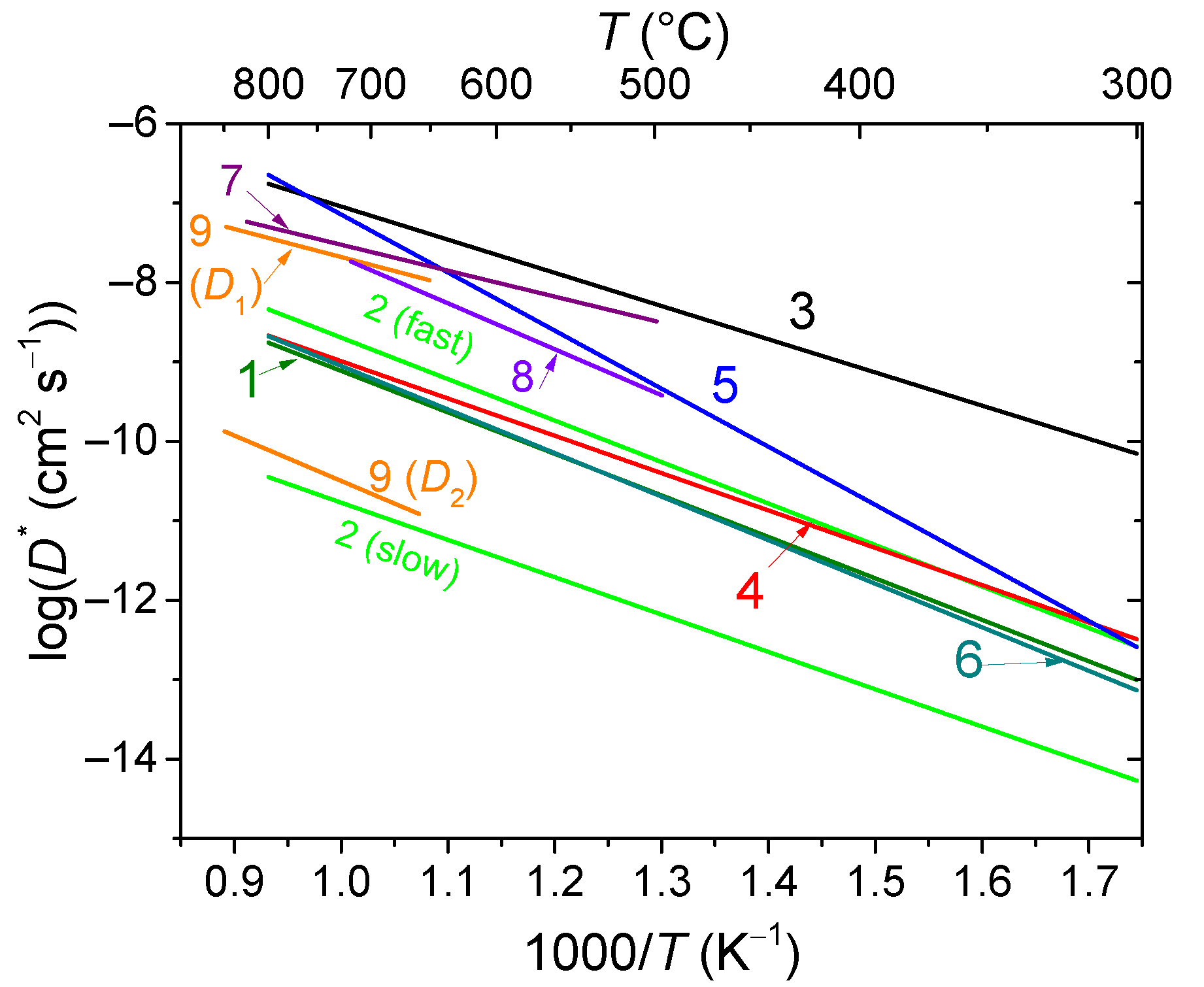
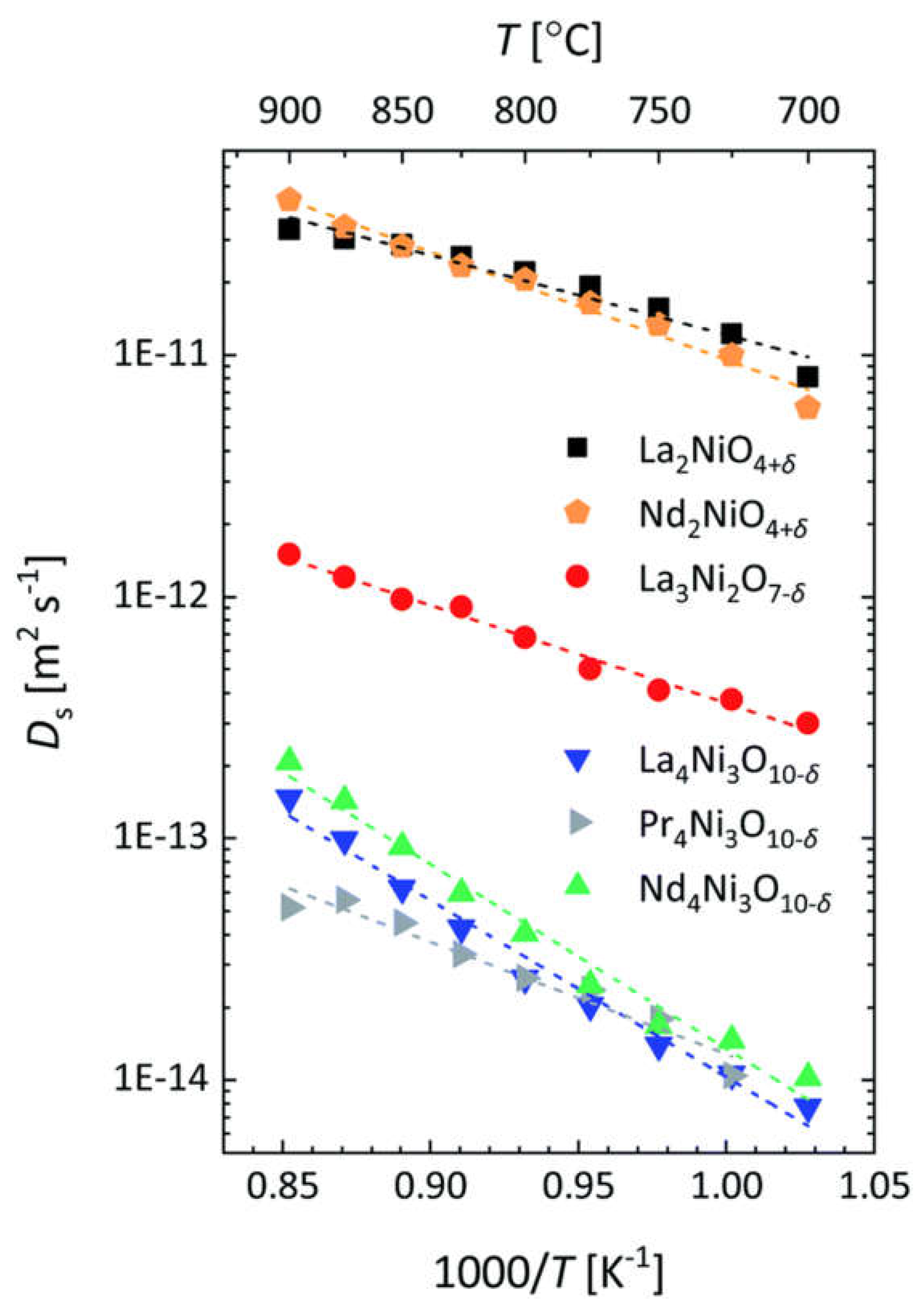
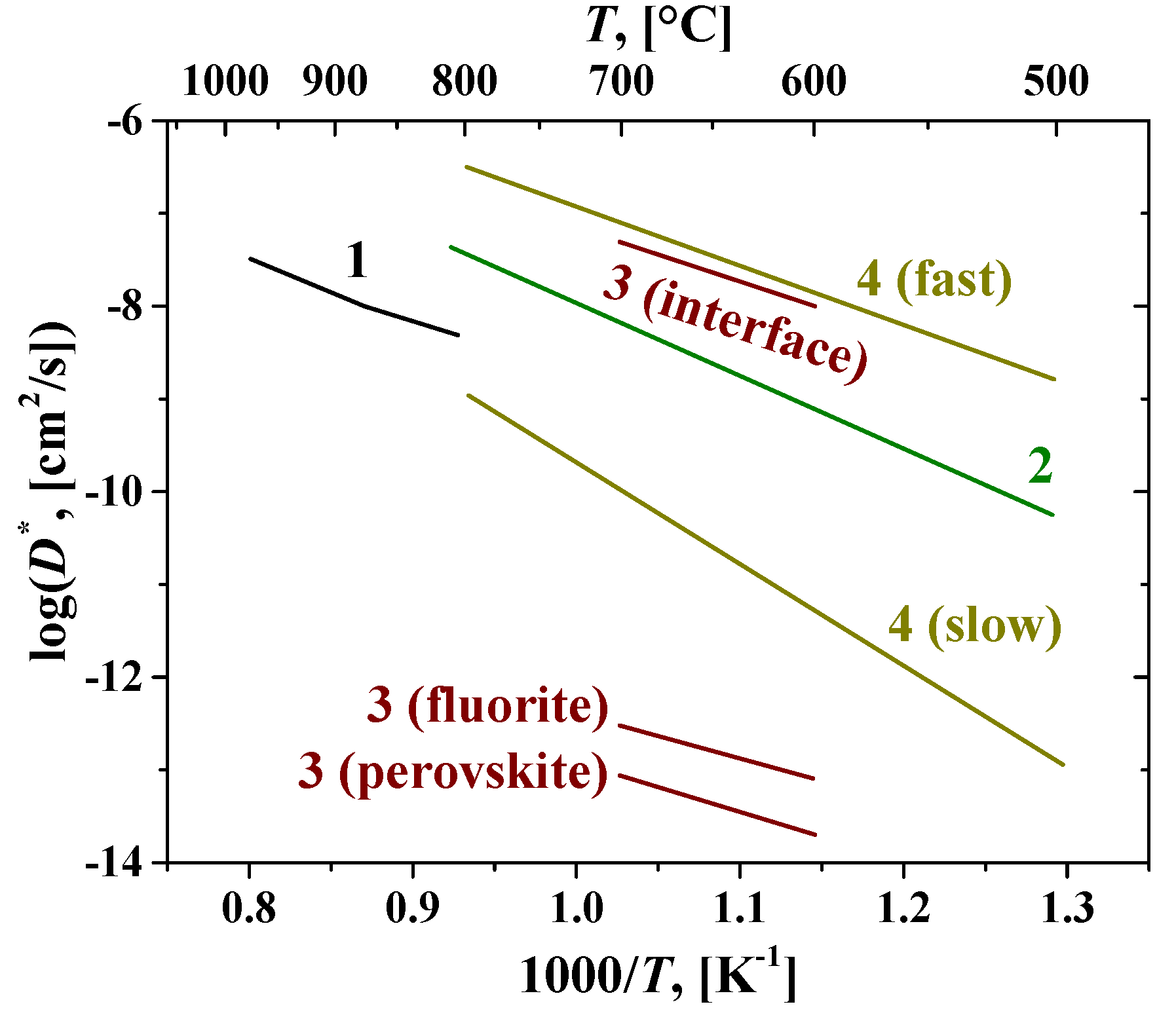
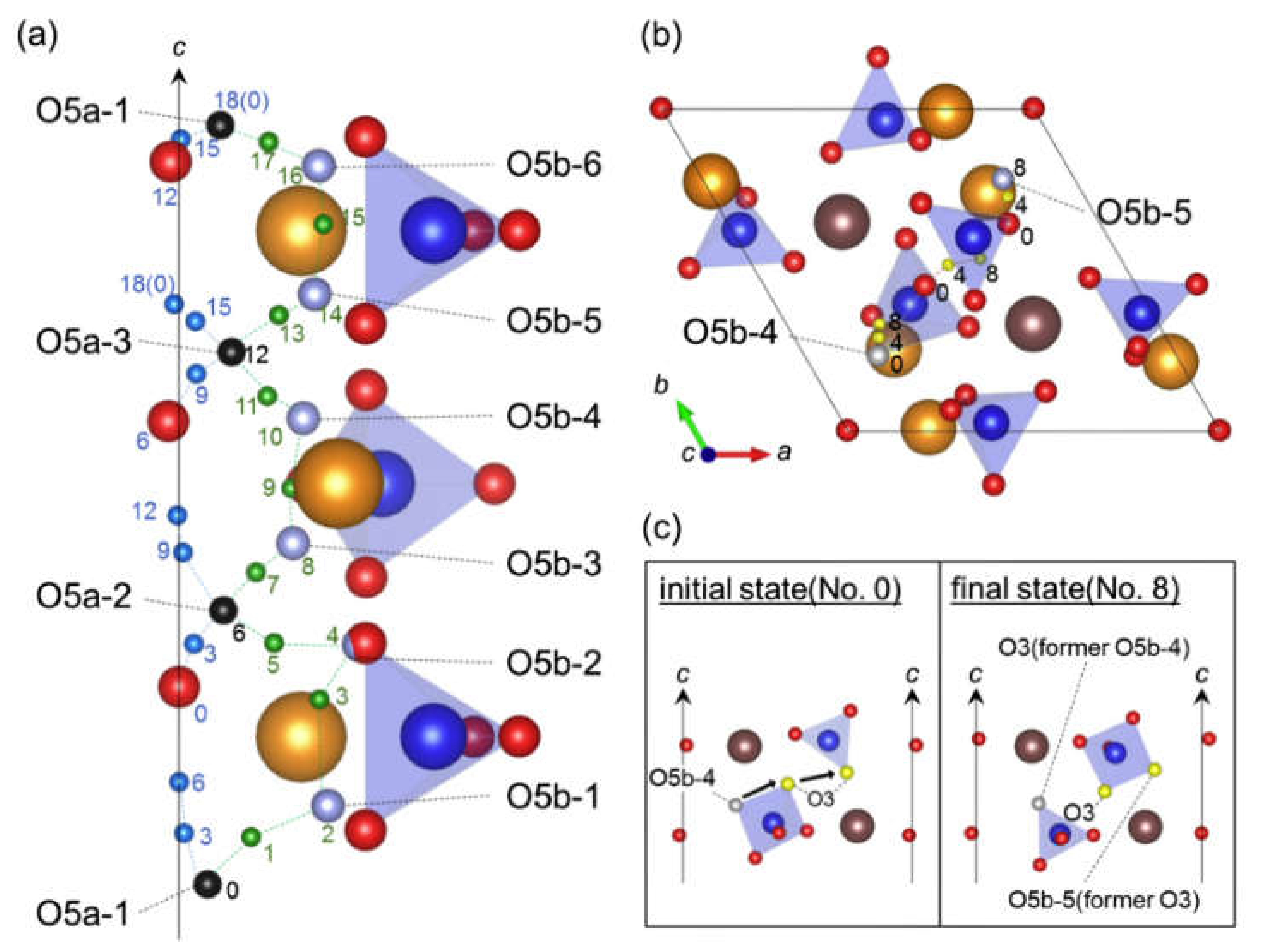
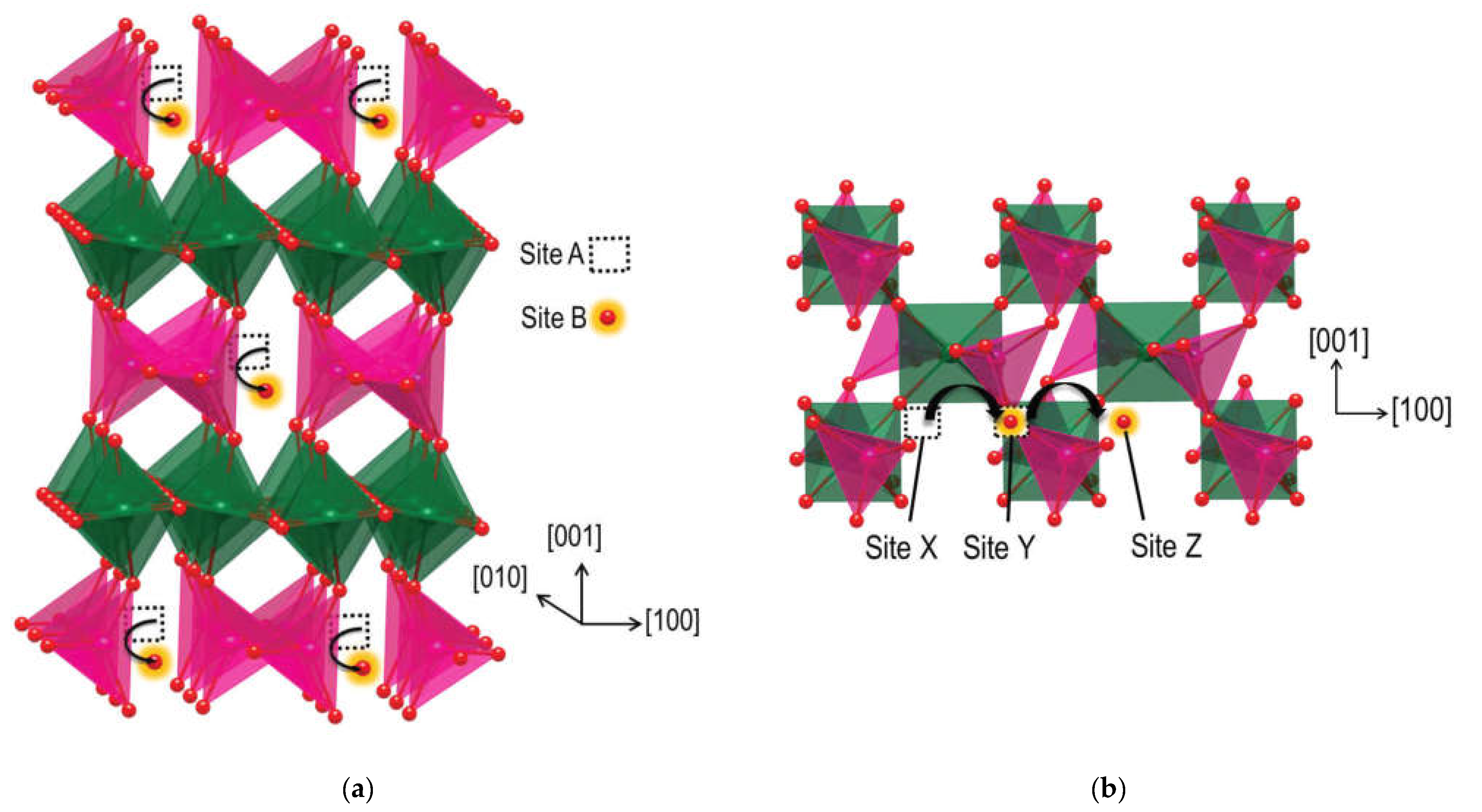
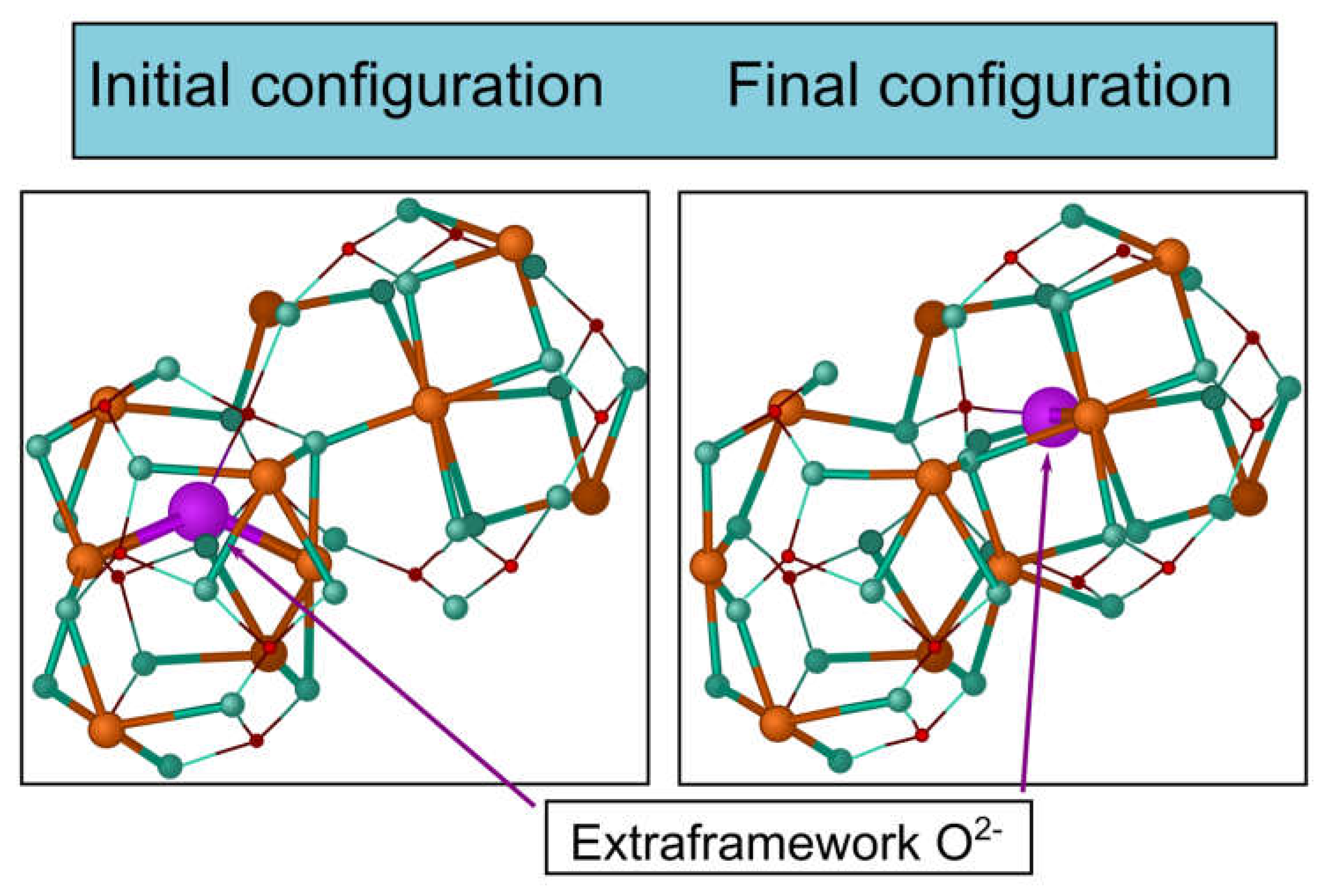
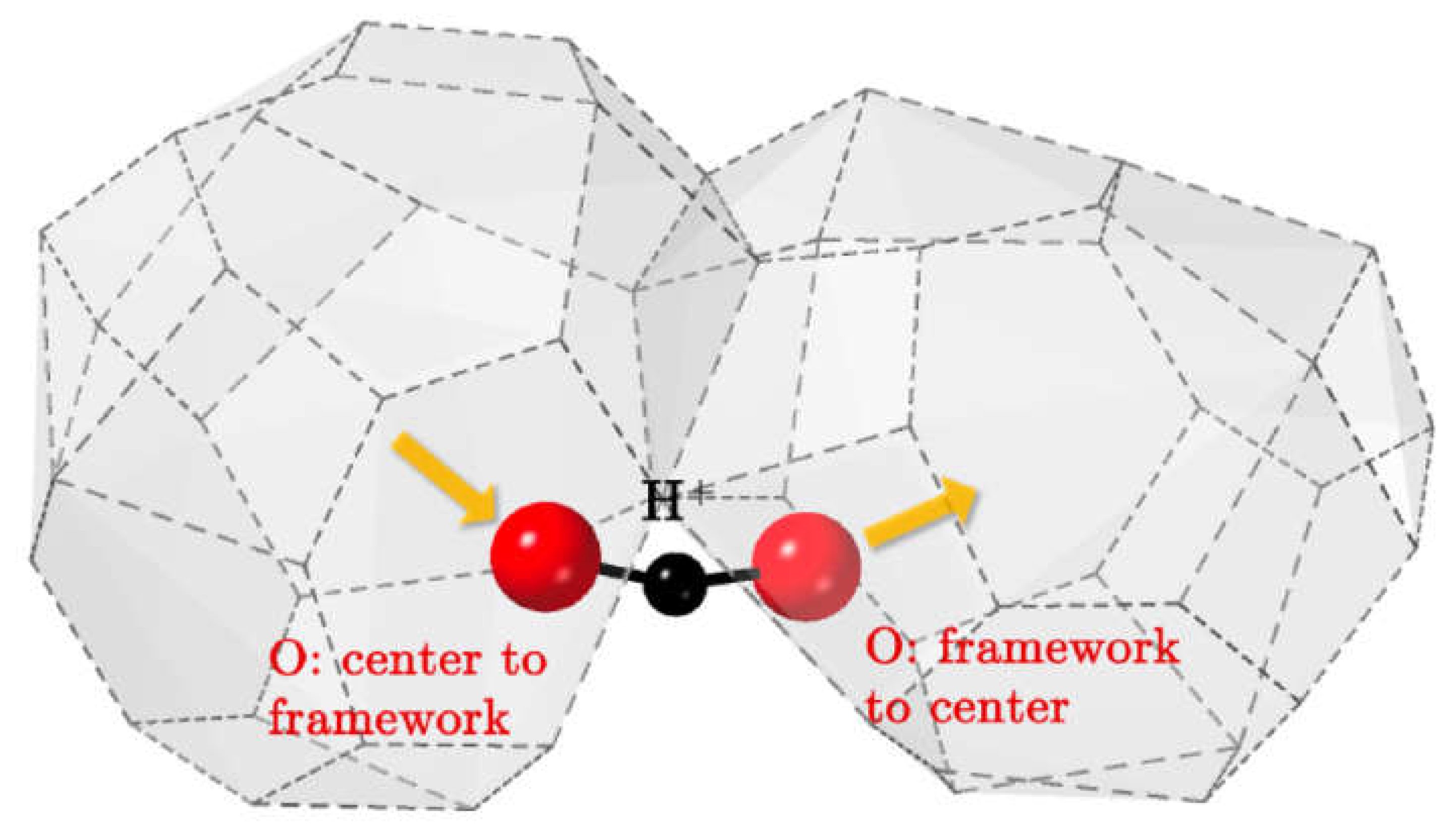
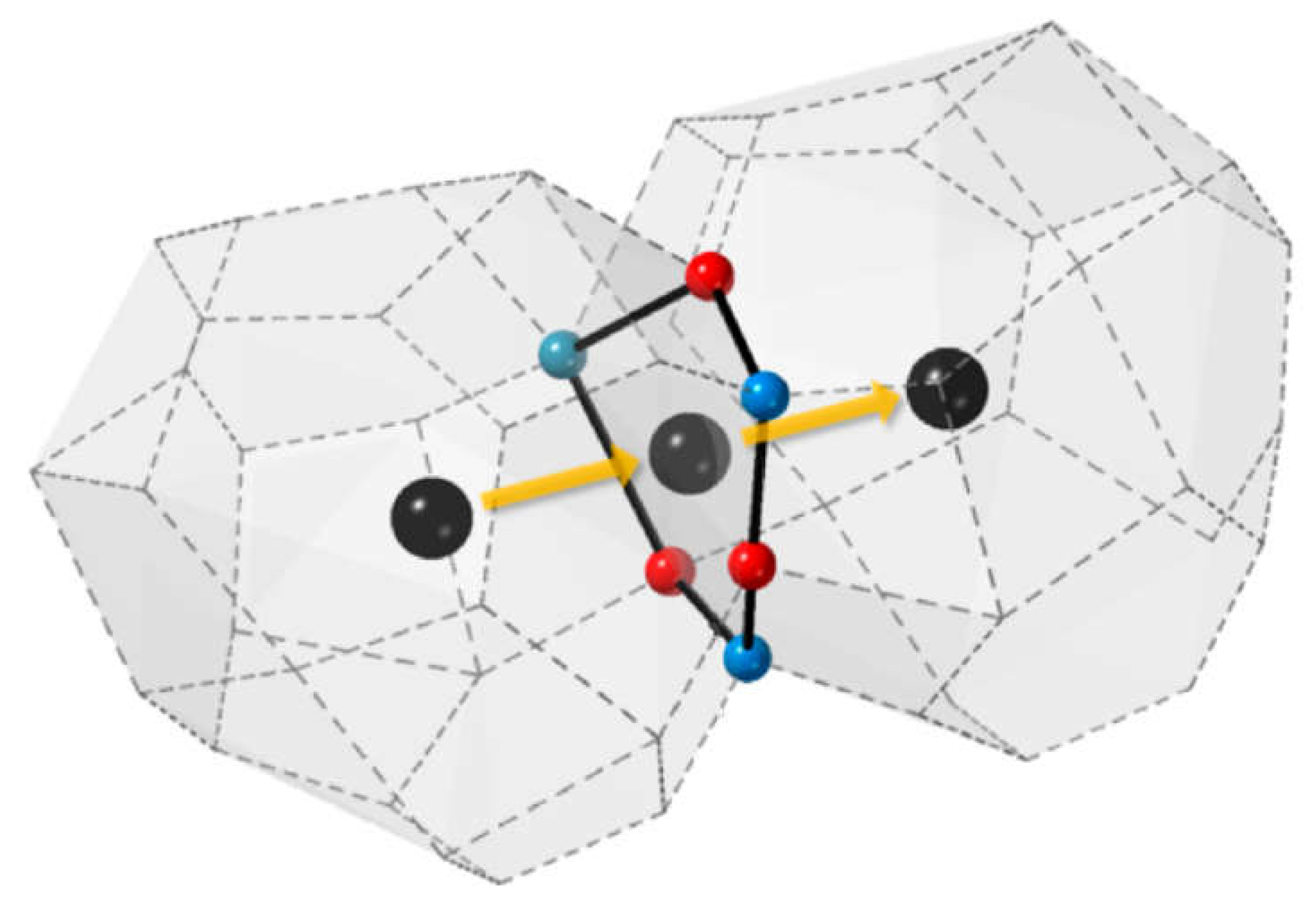
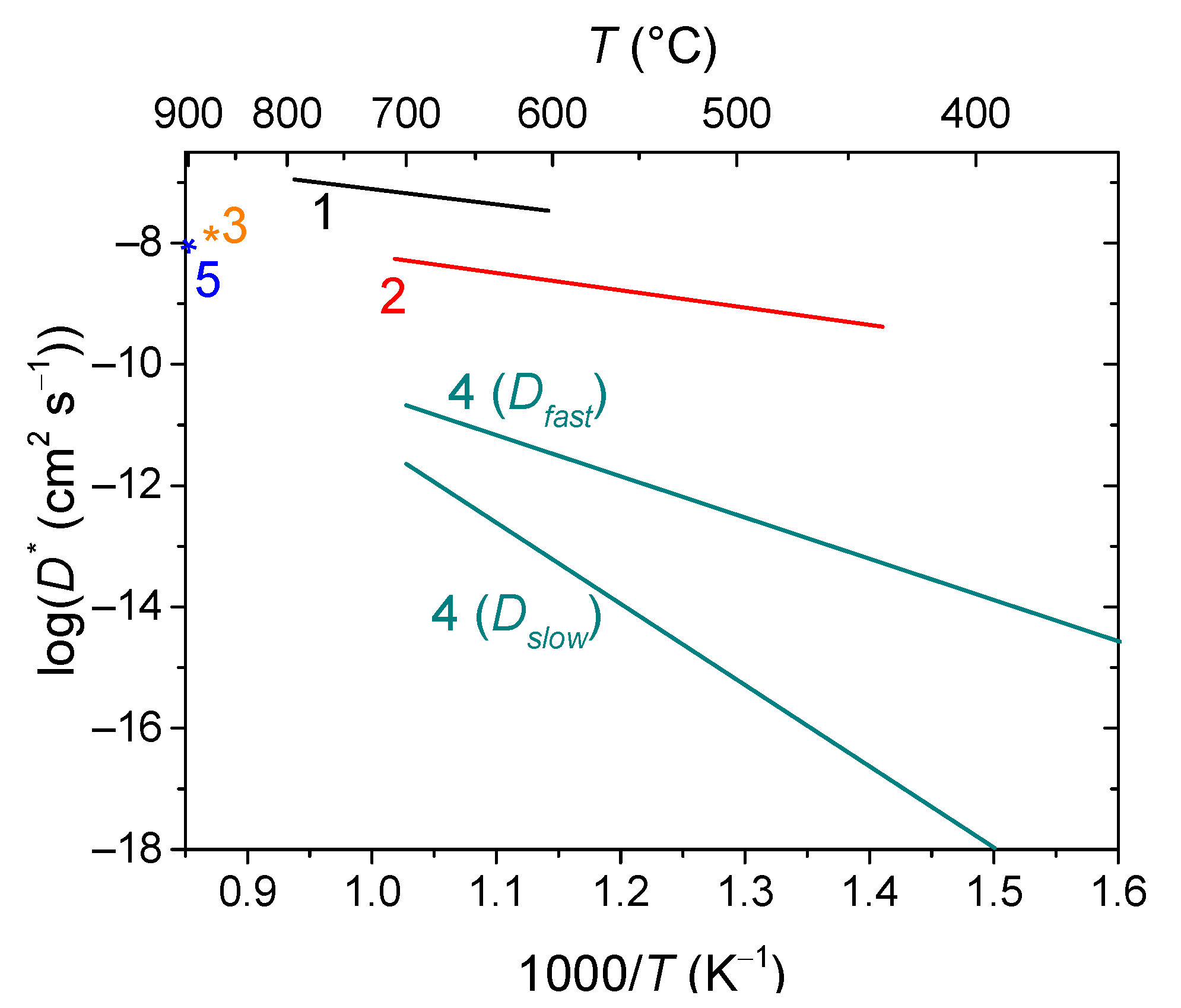
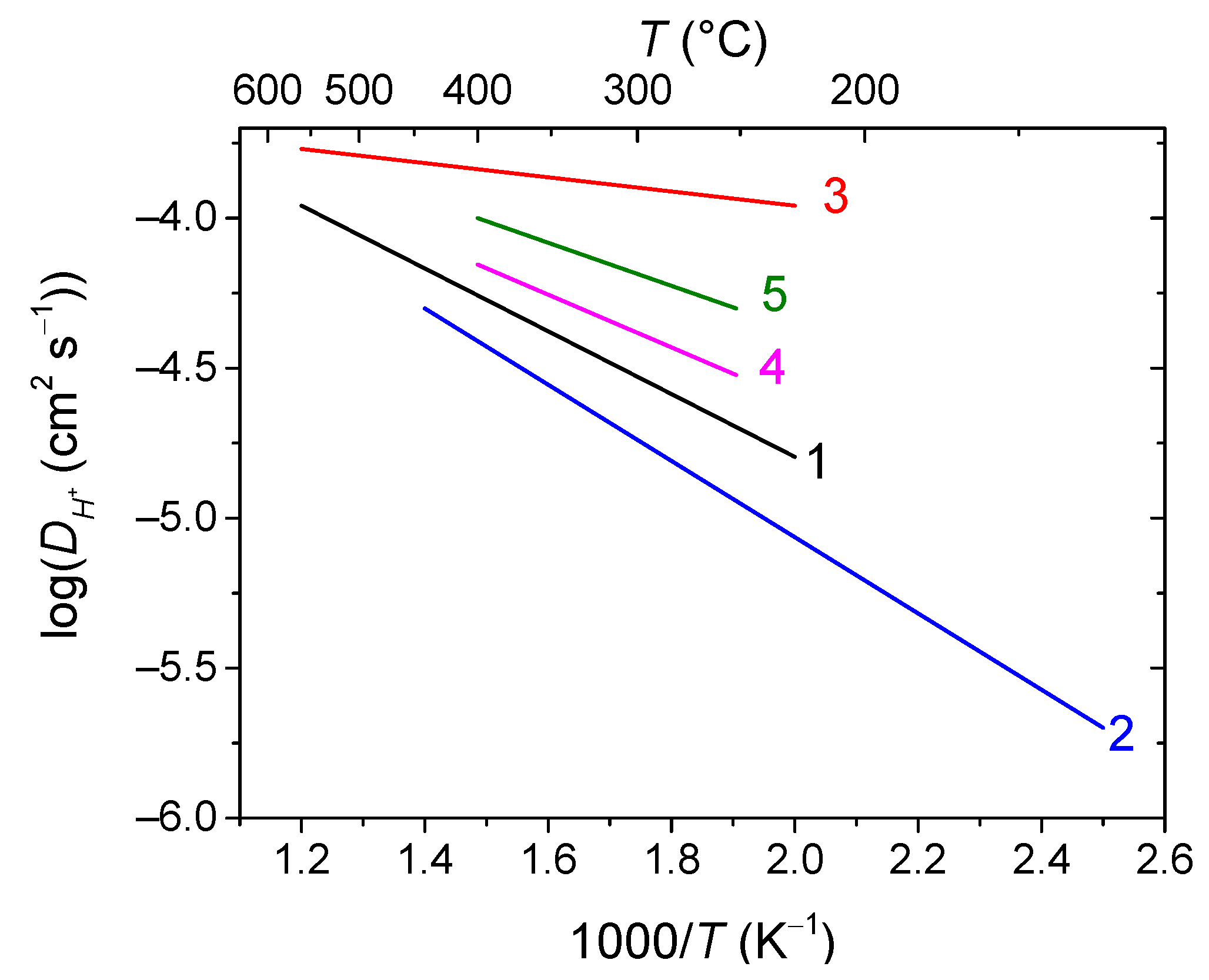
| Reactor Type | ||
|---|---|---|
| Static | Flow | |
| Oxygen exchanged in the oxide | <10% | up to ≅100% |
| Sensitivity to the diffusion rate | No | Yes |
| Low isotope consumption | Yes | No |
| Simple reactor construction | No | Yes |
| Exchangeable gas-phase reagent | ||
| 18O2 | C18O2 | |
| Sensitivity to the diffusion rate | No | Yes |
| Sensitivity to the kinetics of interaction with the oxide surface | Yes | No |
| Temperature mode | ||
| Isothermal | Temperature-programmed | |
| Sensitivity to the oxygen non-uniformity in the oxide bulk | No | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadykov, V.; Pikalova, E.; Sadovskaya, E.; Shlyakhtina, A.; Filonova, E.; Eremeev, N. Design of Mixed Ionic-Electronic Materials for Permselective Membranes and Solid Oxide Fuel Cells Based on Their Oxygen and Hydrogen Mobility. Membranes 2023, 13, 698. https://doi.org/10.3390/membranes13080698
Sadykov V, Pikalova E, Sadovskaya E, Shlyakhtina A, Filonova E, Eremeev N. Design of Mixed Ionic-Electronic Materials for Permselective Membranes and Solid Oxide Fuel Cells Based on Their Oxygen and Hydrogen Mobility. Membranes. 2023; 13(8):698. https://doi.org/10.3390/membranes13080698
Chicago/Turabian StyleSadykov, Vladislav, Elena Pikalova, Ekaterina Sadovskaya, Anna Shlyakhtina, Elena Filonova, and Nikita Eremeev. 2023. "Design of Mixed Ionic-Electronic Materials for Permselective Membranes and Solid Oxide Fuel Cells Based on Their Oxygen and Hydrogen Mobility" Membranes 13, no. 8: 698. https://doi.org/10.3390/membranes13080698
APA StyleSadykov, V., Pikalova, E., Sadovskaya, E., Shlyakhtina, A., Filonova, E., & Eremeev, N. (2023). Design of Mixed Ionic-Electronic Materials for Permselective Membranes and Solid Oxide Fuel Cells Based on Their Oxygen and Hydrogen Mobility. Membranes, 13(8), 698. https://doi.org/10.3390/membranes13080698