1. Introduction
Helium is a unique and valuable chemically inert gas because of its low boiling point (−269 °C), low solubility, and excellent diffusivity [
1]. It is widely utilized in various fields such as the military, aerospace, semiconductor, deep-sea diving, and medical applications. Due to the extremely low concentration of helium gas in the air, which is only 0.0005 mol% [
2], the extraction of helium from natural gas is currently almost the sole industrial source of helium [
3].
Helium is typically produced as a byproduct of liquefied natural gas (LNG) production. The off gas from the nitrogen rejection unit (NRU) in LNG plants contains approximately 1–4% helium [
3,
4]. The helium in the off gas is recovered and purified through a cryogenic distillation process, but this conventional helium recovery method requires high investment and energy consumption [
5,
6]. Due to the similar molecular size and similar boiling points of hydrogen and helium, membrane processes and adsorption processes widely used in hydrogen separation [
7,
8] can also be applied to helium recovery and purification processes [
9]. These processes offer alternative options for helium recovery that are more cost-effective and energy-efficient [
10,
11,
12,
13]. Hamedi et al. [
14] proposed a helium recovery process based on highly selective silicon dioxide membranes. Their research indicates that, compared to conventional multistage polymer membranes, single-stage silicon dioxide membranes are more economical because of the elimination of interstage compression. Scholes et al. [
15] conducted a techno-economic study on the membrane separation process for helium recovery from natural gas and NRU off gas. The results indicate that membrane separation becomes economically competitive when the helium concentration in natural gas is ≥0.3 mol%. For the recovery and purification of helium from the NRU off gas, a combined membrane-pressure swing adsorption (PSA) process is more cost-effective compared to the conventional cryogenic distillation process.
However, the similar molecular sizes and similar boiling points of hydrogen and helium make it challenging to achieve their separation using conventional gas separation methods, such as membrane, cryogenic distillation, and PSA. Currently, the industrial removal of hydrogen is primarily achieved through catalytic oxidation—converting hydrogen into water, which is then separated [
16]. However, this process inevitably introduces new impurities such as O
2, leading to increased energy consumption and a waste of hydrogen resources. Electrochemical hydrogen pump (EHP) technology, driven by electrical energy, offers an effective solution to overcome the challenge posed by the similar properties of hydrogen and helium [
17,
18]. Hydrogen is selectively transported as protons through the membrane electrode assembly, allowing for the one-step separation of hydrogen and helium. Onda et al. [
19] used the EHP to recover hydrogen from H
2/CO
2 or H
2/N
2 mixed gases. After processing, the released anode gas had a hydrogen concentration of <50 ppm. Nordio et al. [
20] successfully used the EHP to recover hydrogen from the H
2/He mixture. When the feed gas had a helium content of 20%, the H
2 purity of cathode was 99.97%. The EHP caused almost no loss of helium. However, the application of the EHP for hydrogen–helium separation is currently limited to the laboratory stage. For real gases with complex components, such as NRU off gas, it is hoped that novel technologies, such as the EHP, could be widely implemented in engineering practice to achieve efficient hydrogen–helium separation.
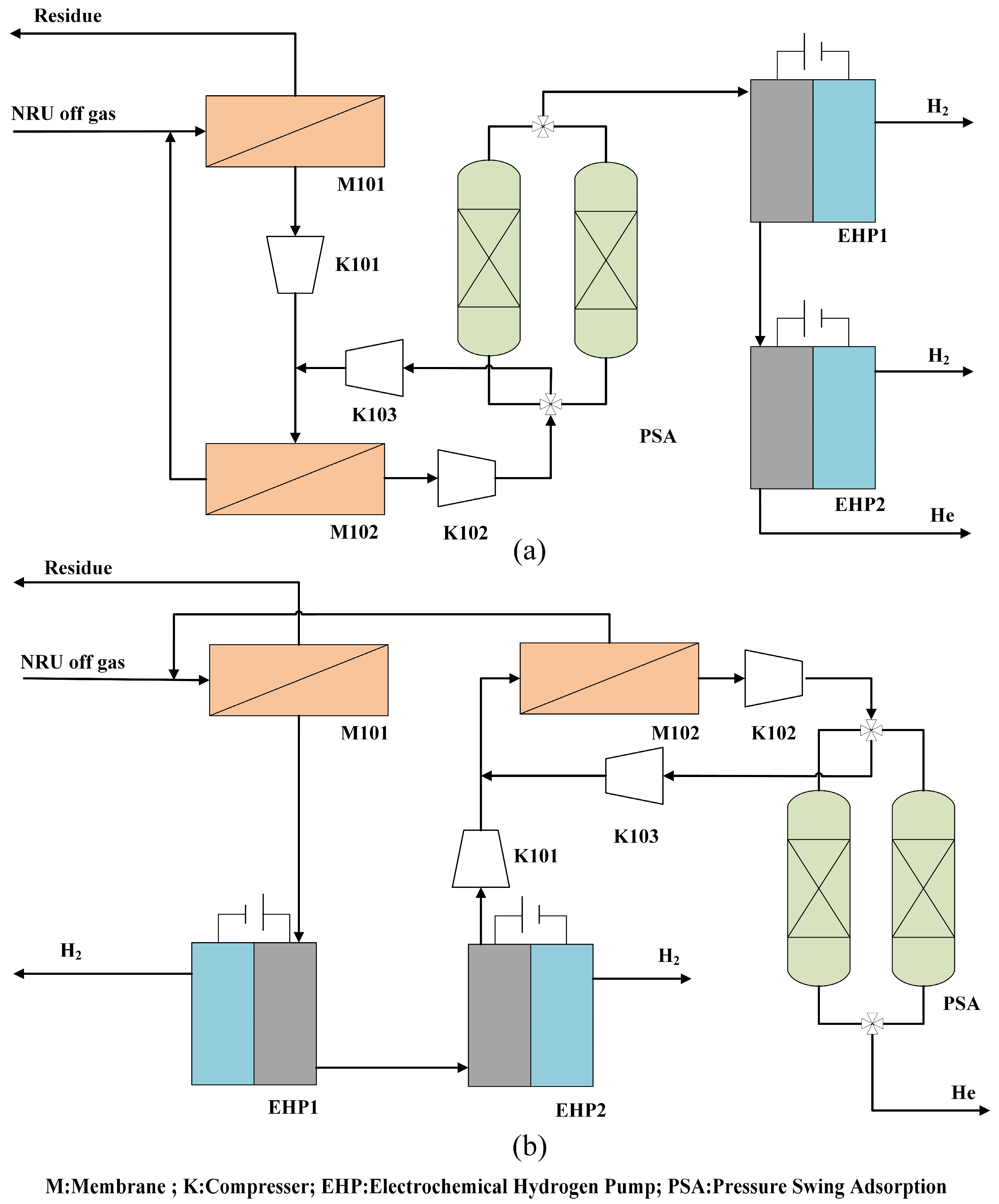
In this work, our objective is to design a novel process for helium recovery from the NRU off gas by combining membranes, PSA, and EHP. We designed two different coupling separation processes based on different sequences of hydrogen gas removal. A sensitivity analysis was conducted for the optimization of both two processes to achieve the production target of an 80% recovery fraction. The preferred process was determined through an economic assessment. Additionally, the key operational parameters of the preferred process, such as the membrane area and membrane permeate pressure, were optimized using response surface methodology (RSM).
4. Optimization of Flowsheet #2 Based on Response Surface Methodology
In complex process simulations, there is often a trade-off relationship between the quality of the target product and the production cost. For example, increasing the membrane area improves the separation performance but also increases the investment cost of the membrane module. In addition, there are strong interactions between operating parameters in the process. For instance, the membrane area of M101 determines the feed flow rate and composition of M102, thereby affecting the M102 area under the same separation requirement. At the same time, because the residue of M102 returns to the inlet of M101 to recycle helium, the area of M101 is affected by the area of M102. The interactions cause the variables in the coupled system to affect each other.
Response surface methodology (RSM) has been used to explore, optimize, and model the performance of complex systems. RSM is a combination of mathematical and statistical methods. By modeling the relationship between variables and responses, it can effectively optimize multiple variables at the same time [
28,
29,
30]. This method is actually a polynomial approximation of the effective variables and their interactions in an unknown complex model. Based on the results of the sensitivity analysis, the optimal range of influential parameters was determined, and then the statistical method RSM was used for experimental design and process optimization.
For preferred flowsheet #2, multiobjective optimization was performed to achieve the maximum helium recovery fraction and the minimum production cost. Based on sensitivity analysis of
Section 3.1 and
Section 3.2, three significant variables were selected, the membrane area of M101, the permeate pressure of M101, and the membrane area of M102, which serve as response functions for the helium recovery fraction and cost of helium production. The ranges of optimization variables are shown in
Table 5. A quadratic regression model was fitted using the Box–Behnken Design (BBD) and then optimized.
Table 6 represents the 17 experiments designed based on the BBD method using Design Expert, including four repeated experiments. According to the simulation results from
Table 6, the quadratic polynomial regression equation models, expressed in terms of coded factors, are as follows:
where
is the recovery fraction of helium;
is the cost of helium production (
$/kg He)
is the membrane area of M101 (m
2);
is the permeate pressure of M101 (kPa); and
is the membrane area of M102 (m
2).
The analysis of variance (ANOVA) of the data was applied to analyze the fitness and adequacy of the experimental model, as shown in
Table 7.
As can be seen from
Table 7, whether it is for
or
, the F-values of 654.80 and 115.24 imply that the models are significant. There is only a 0.01% chance that a “Model F-value” could occur because of noise. Both
p-values are less than 0.0001, indicating that the models are statistically significant at the 95% confidence level. The regression model’s coefficients
of the regression model are 0.9988 and 0.9933, respectively. The closer
is to 1, the better the data fit the model. The predicted correlation coefficients
are basically consistent with the adjusted correlation coefficients
The differences are less than 0.2. Additionally, the variation coefficients are only 1.20% and 1.95%, indicating a sufficiently high level of reliability. In summary, the response surface correlation model is in good agreement with the actual situation, can effectively predict and analyze the process, and is suitable for the optimization of key variables.
The model validation results are shown in
Figure 6. From the comparison between the model’s predicted value and the actual value, it can be seen that the model’s predicted value is reasonably consistent with the actual value, and the predicted value falls on a straight line as much as possible. The reliability and accuracy of the regression model are verified again, and it can be used for the prediction and analysis of key parameter optimization.
According to the fitted response surface model, the corresponding three-dimensional response plots were generated, as shown in
Figure 7,
Figure 8 and
Figure 9.
Figure 7 shows the responses of the helium recovery fraction and production cost to the area of M101 and area of M102. It can be observed that as the area of M101 and the area of M102 increase, both the helium recovery fraction and production cost also increase. However, their increasing trends are not exactly the same. When the M102 area is relatively large, such as 30 m
2, the recovery fraction increases rapidly with the increase in the M101 area, but the production cost does not increase significantly. On the other hand, when the M102 area is small, such as 15 m
2, the recovery fraction does not increase significantly with the increase in the M101 area, but the production cost increases sharply. Based on this response surface graph, it can be concluded that in order to achieve a higher recovery fraction and lower production cost, the area of M102 should be larger than 30 m
2.
Figure 8 shows the responses of the helium recovery fraction and production cost to the permeate pressure and area of M101. It can be observed that as the area of M101 increases, both the helium recovery fraction and production cost increase. However, with the increase in the permeation pressure, the helium recovery fraction continuously decreases, while the production cost sharply increases. This is mainly due to the increase in the permeation pressure, which leads to a decrease in the pressure ratio on both sides of the membrane. The decrease in the driving force of the gas membrane separation process leads to a reduction in helium gas production, resulting in an increase in the production cost. Based on this response surface graph, it can be concluded that in order to achieve a higher recovery fraction and lower production cost, the permeate pressure of M101 should be as low as possible, such as 100 kPa.
Figure 9 shows the responses of the helium recovery fraction and production cost to the permeate pressure of M101 and area of M102. It can be observed that the responses to the permeate pressure of M101 in
Figure 9 are similar to those in
Figure 8, and the responses to the area of M102 in
Figure 9 are similar to those in
Figure 7.
According to the quadratic response surface regression models, the optimal solution was obtained using Design Expert software, as shown in
Table 8. The optimized variables were simulated and calculated again in UniSim Design. the MEA areas of EHP1 and EHP2 were adjusted to 5 and 2 m
2 to remove all hydrogen. It was found that the maximum He recovery fraction and minimum production cost were 90.66% and 2.21
$/kg He, respectively. Compared to the production cost of 1.92
$/kg mentioned in
Section 3.5, despite the increase in cost of 0.29
$/kg, the helium recovery fraction increased by 10.66%. Helium was successfully recovered to a greater extent.