Phosphates Transfer in Pristine and Modified CJMA-2 Membrane during Electrodialysis Processing of NaxH(3−x)PO4 Solutions with pH from 4.5 to 9.9
Abstract
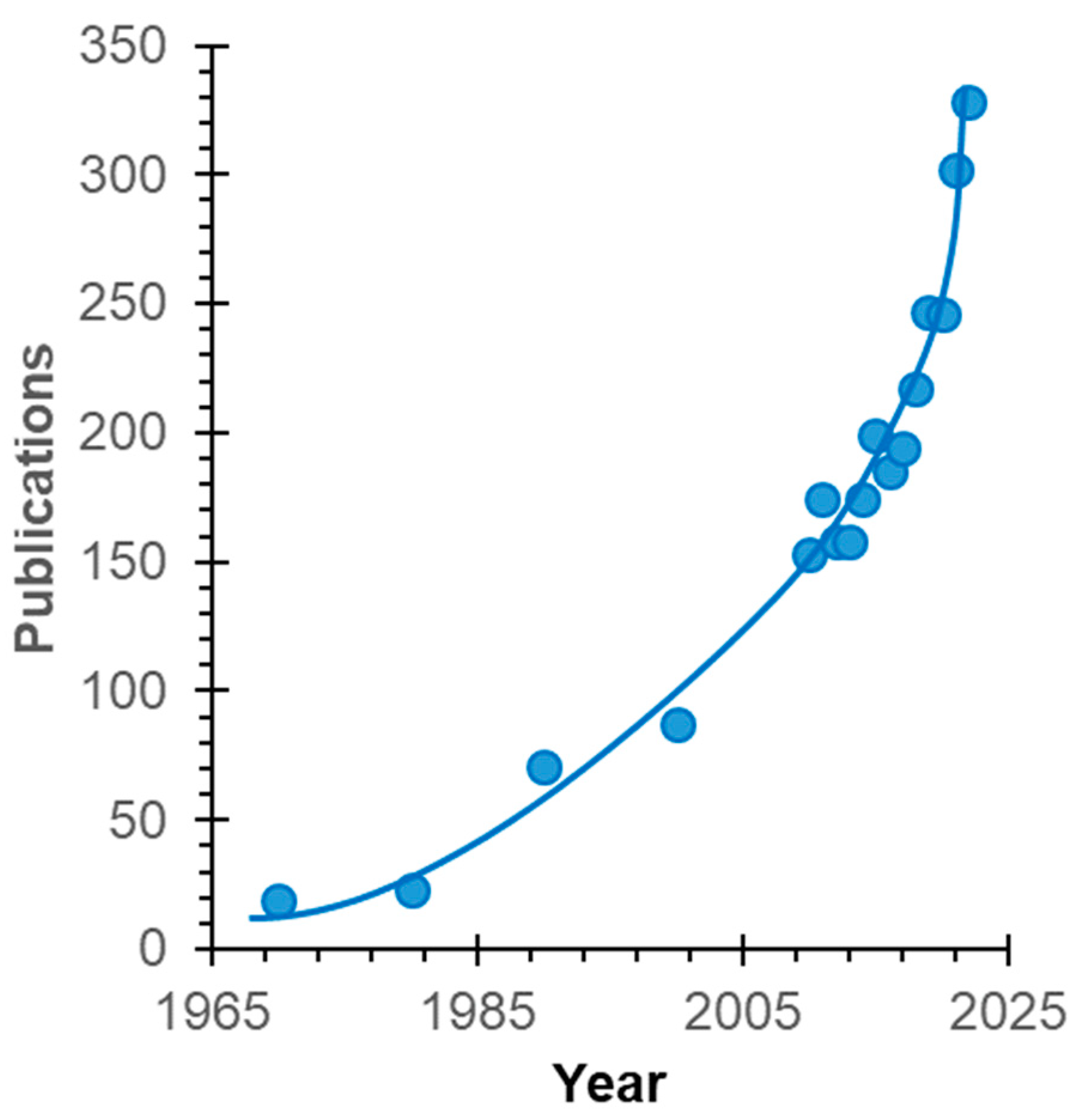
1. Introduction
2. Materials and Methods
2.1. Membranes and Solutions
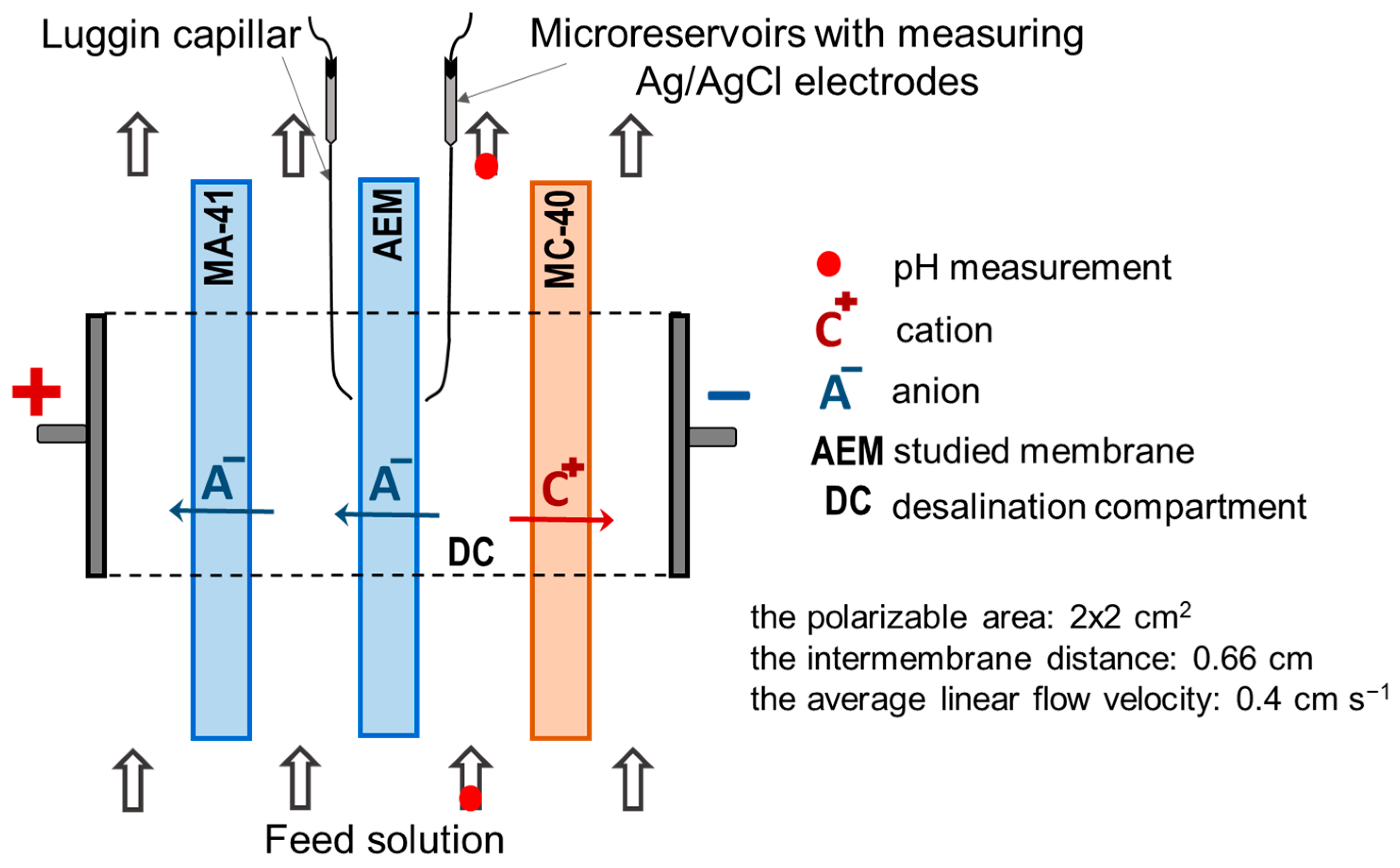
2.2. Methods
2.3. Calculations
3. Results
3.1. Membranes Characterization
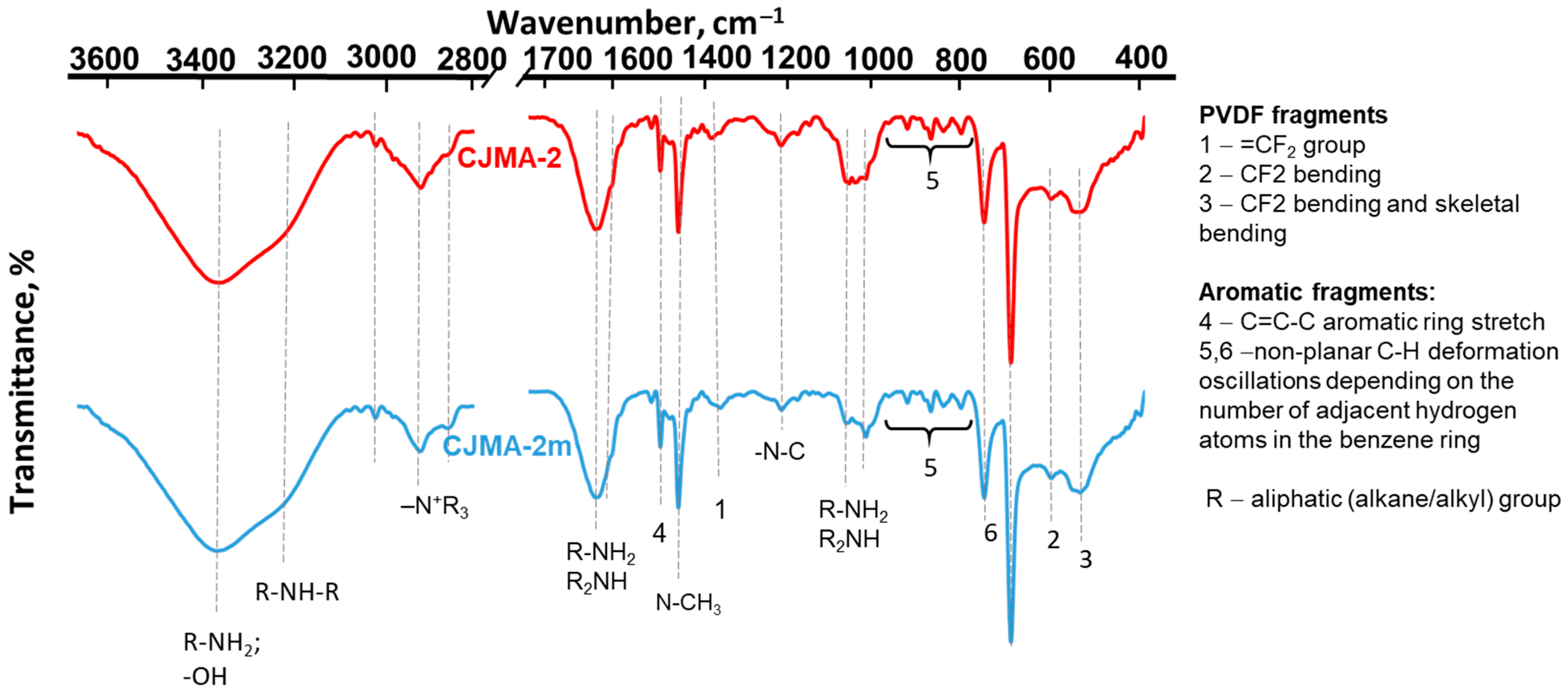
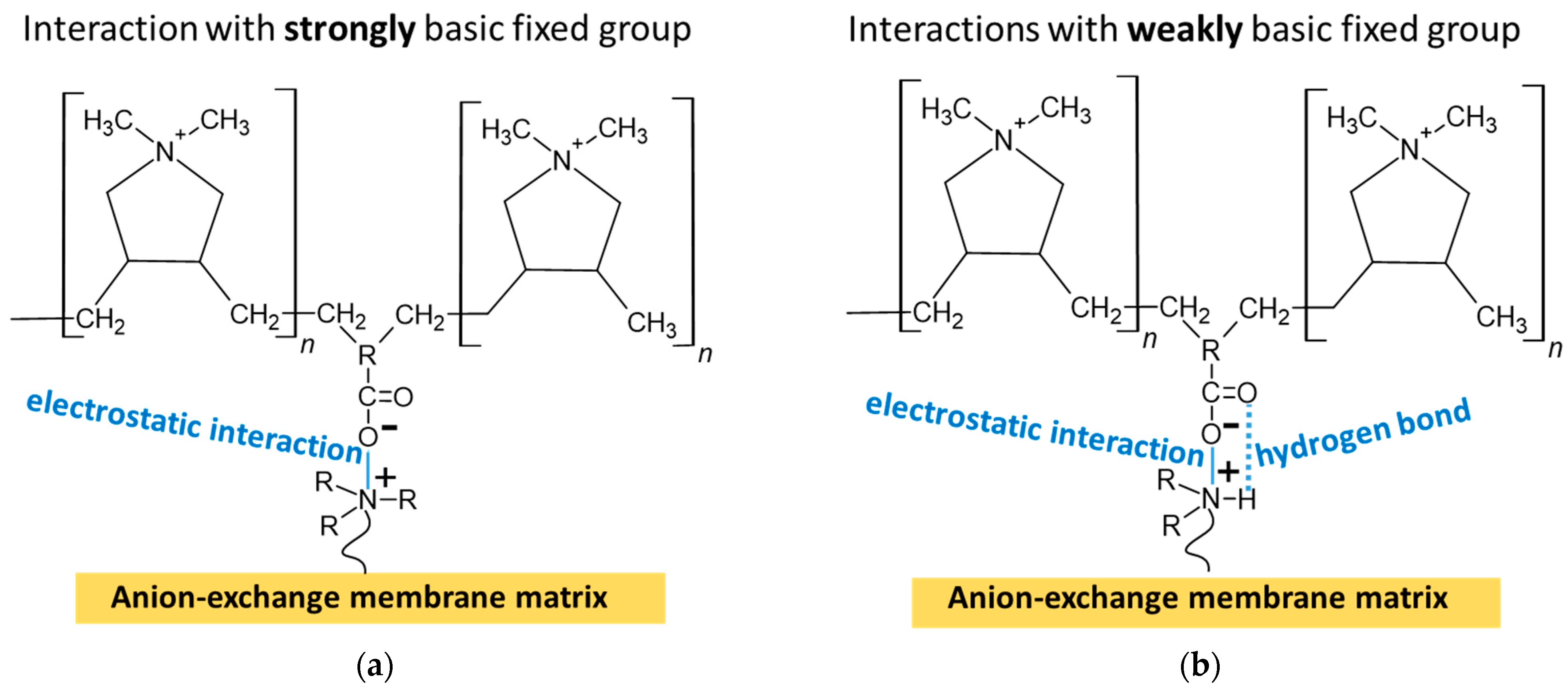
3.1.1. IR Spectra
3.1.2. Surface Geometry and Hydrophilicity
3.1.3. Ion-Exchange Capacity, Water Uptake, Conductivity
3.2. Electrochemical Characteristics of the Studied Membranes in NaCl Solutions
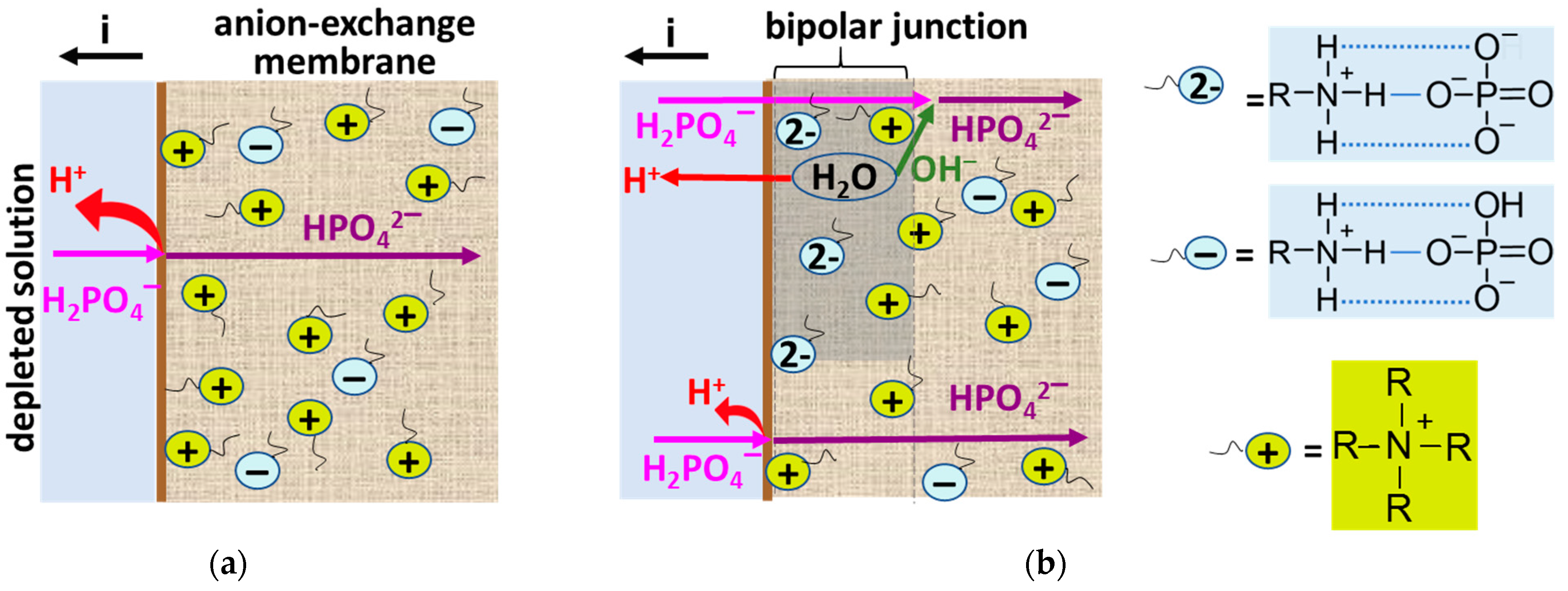
3.3. Electrochemical Characteristics of the Studied Membranes in NaxH(3−x)PO4 Solutions

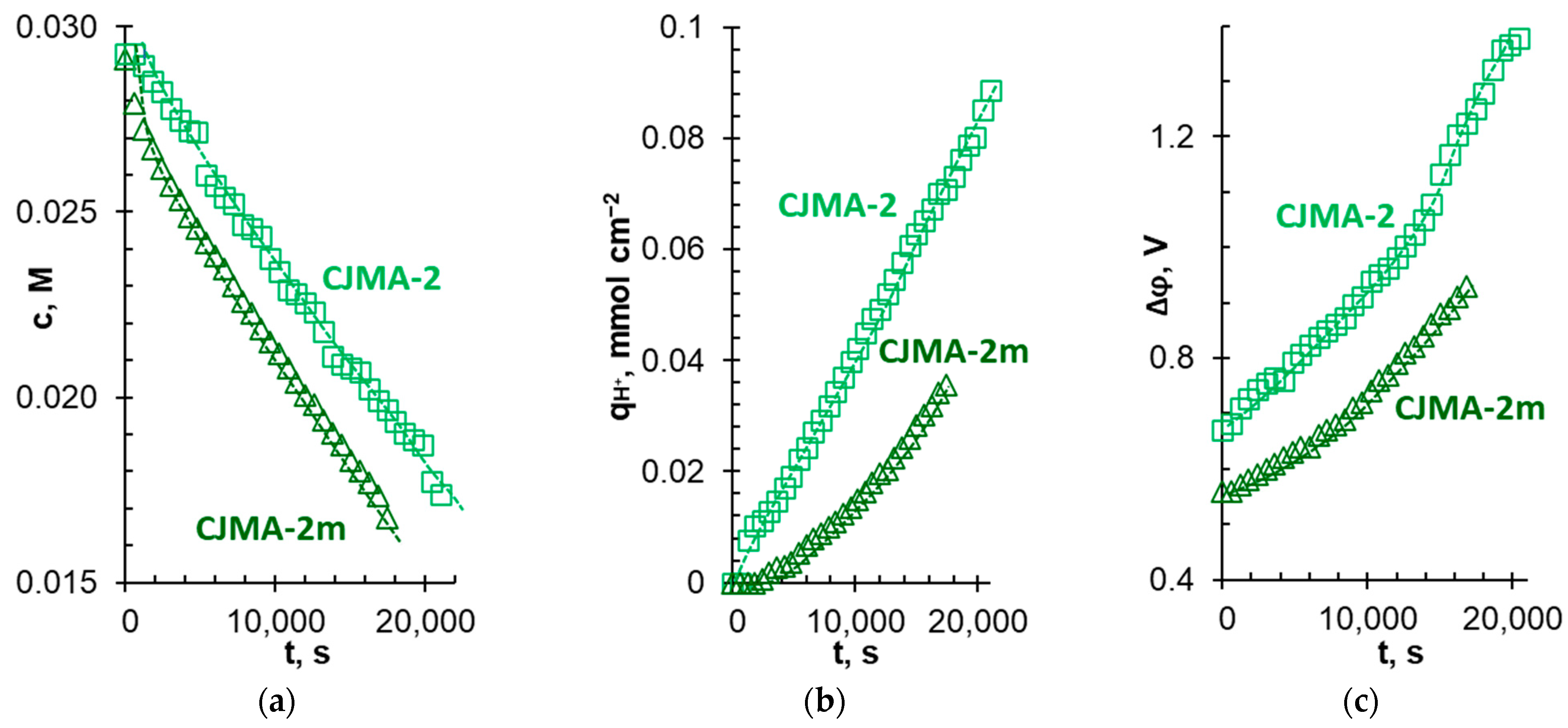
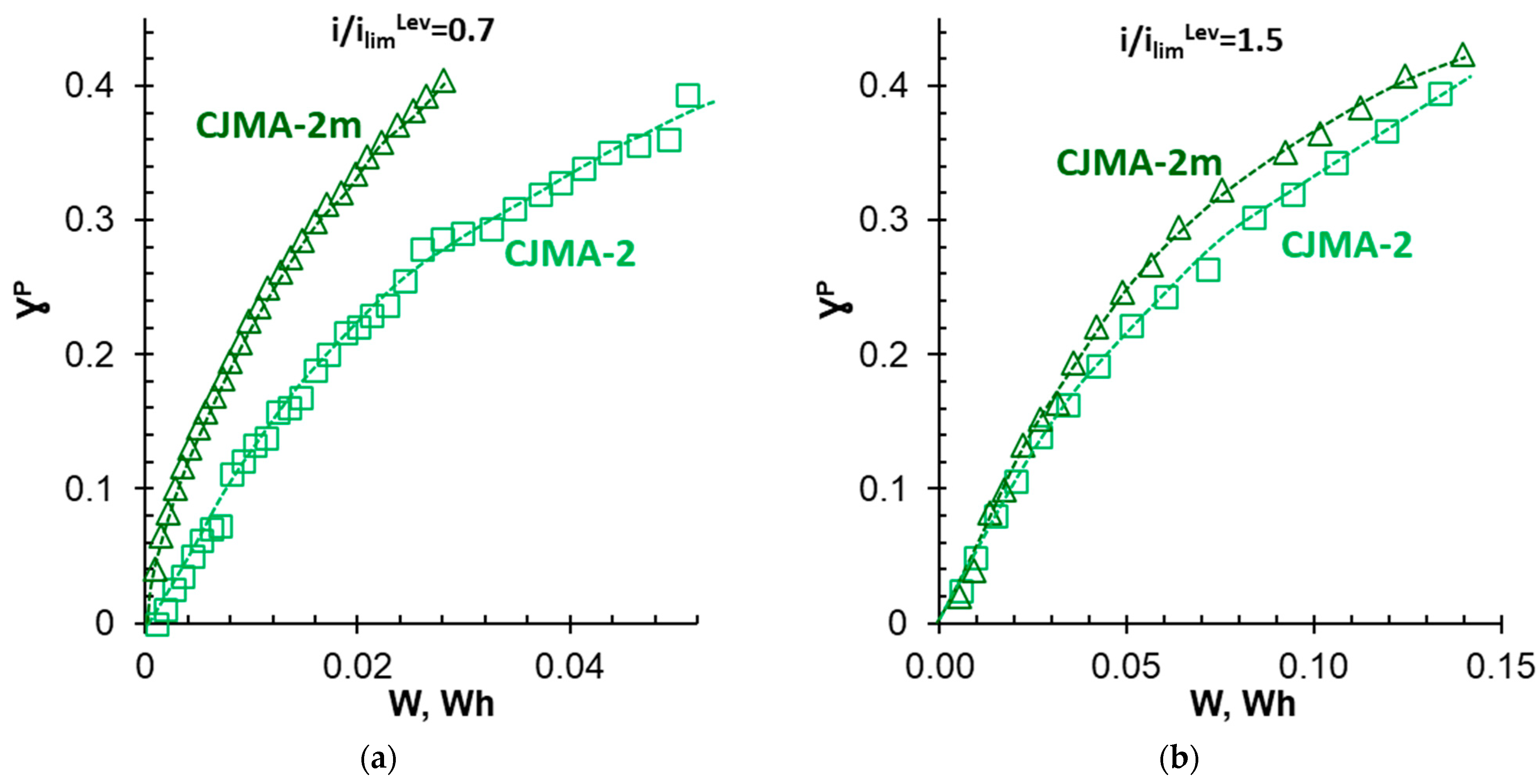
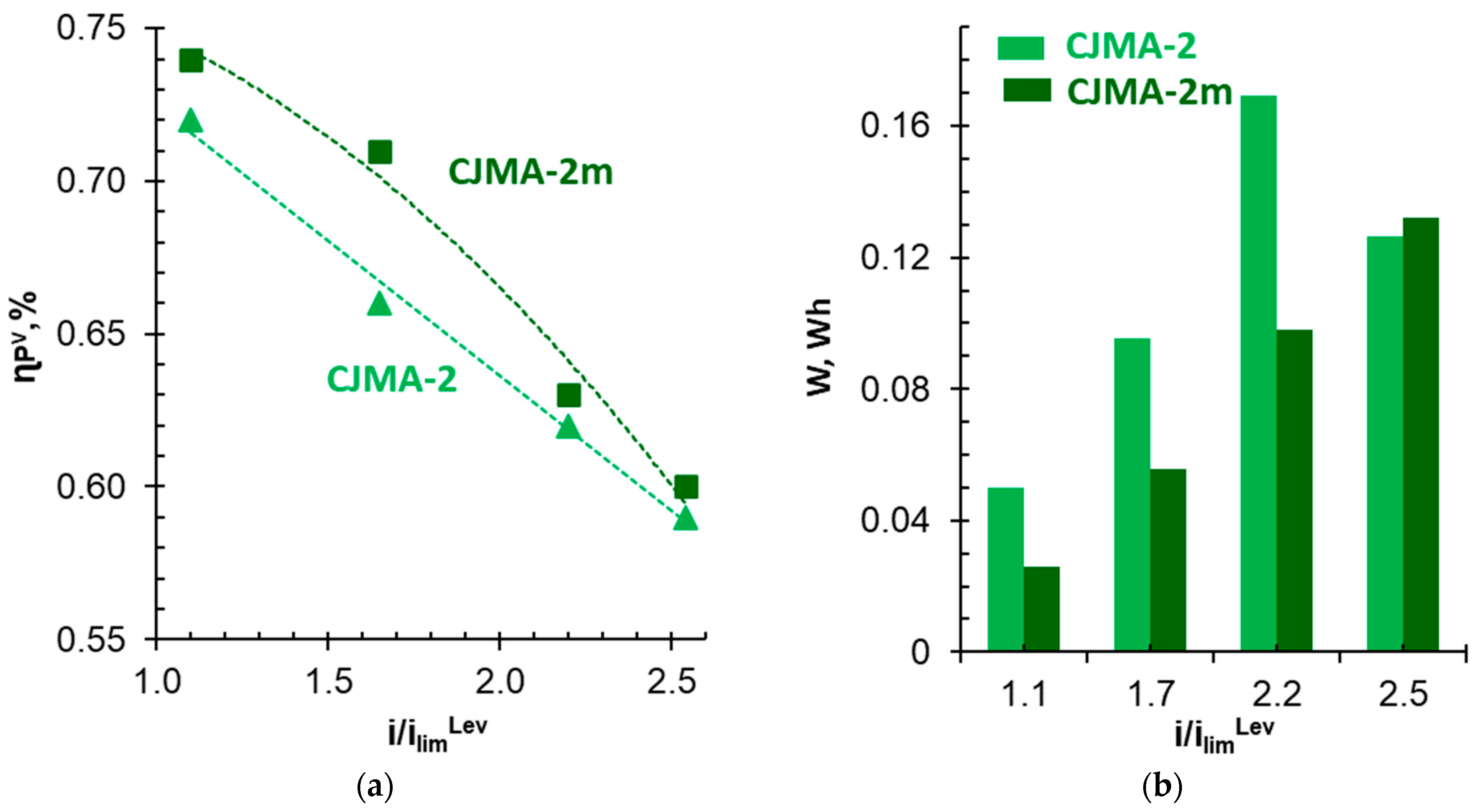
3.4. Batch Electrodialysis of NaxH(3−x)PO4 Solution
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knežević, K.; Saracevic, E.; Krampe, J.; Kreuzinger, N. Comparison of ion removal from waste fermentation effluent by nanofiltration, electrodialysis and ion exchange for a subsequent sulfuric acid recovery. J. Environ. Chem. Eng. 2022, 10, 108423. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, G.Q.; Lin, L.; Li, X.; Kentish, S.E. Purification of organic acids using electrodialysis with bipolar membranes (EDBM) combined with monovalent anion selective membranes. Sep. Purif. Technol. 2021, 279, 119739. [Google Scholar] [CrossRef]
- Hülber-Beyer, É.; Bélafi-Bakó, K.; Nemestóthy, N. Low-waste fermentation-derived organic acid production by bipolar membrane electrodialysis—An overview. Chem. Pap. 2021, 75, 5223–5234. [Google Scholar] [CrossRef]
- Wang, Z.; He, P.; Zhang, H.; Zhang, N.; Lü, F. Desalination, nutrients recovery, or products extraction: Is electrodialysis an effective way to achieve high-value utilization of liquid digestate? Chem. Eng. J. 2022, 446, 136996. [Google Scholar] [CrossRef]
- Grushevenko, E.; Bazhenov, S.; Vasilevsky, V.; Novitsky, E.; Shalygin, M.; Volkov, A. Effect of Carbon Dioxide Loading on Removal of Heat Stable Salts from Amine Solvent by Electrodialysis. Membranes 2019, 9, 152. [Google Scholar] [CrossRef] [PubMed]
- Rizzioli, F.; Bertasini, D.; Bolzonella, D.; Frison, N.; Battista, F. A critical review on the techno-economic feasibility of nutrients recovery from anaerobic digestate in the agricultural sector. Sep. Purif. Technol. 2023, 306, 122690. [Google Scholar] [CrossRef]
- Zhou, H.; Ju, P.; Hu, S.; Shi, L.; Yuan, W.; Chen, D.; Wang, Y.; Shi, S. Separation of Hydrochloric Acid and Oxalic Acid from Rare Earth Oxalic Acid Precipitation Mother Liquor by Electrodialysis. Membranes 2023, 13, 162. [Google Scholar] [CrossRef]
- Sniatala, B.; Kurniawan, T.A.; Sobotka, D.; Makinia, J.; Othman, M.H.D. Macro-nutrients recovery from liquid waste as a sustainable resource for production of recovered mineral fertilizer: Uncovering alternative options to sustain global food security cost-effectively. Sci. Total Environ. 2023, 856, 159283. [Google Scholar] [CrossRef]
- Sedneva, T.A.; Ivanenko, V.I.; Belikov, M.L. Special Features of Electro-Membrane Recovery of Acids and Alkalis from the Water-Soluble Wastes of Nuclear Power Plants. Russ. J. Electrochem. 2022, 58, 216–225. [Google Scholar] [CrossRef]
- Karpenko, T.V.; Kovalev, N.V.; Kirillova, K.R.; Achoh, A.R.; Melnikov, S.S.; Sheldeshov, N.V.; Zabolotsky, V.I. Competing Transport of Malonic and Acetic acids across Commercial and Modified RALEX AMH Anion-Exchange Membranes. Membr. Membr. Technol. 2022, 4, 118–126. [Google Scholar] [CrossRef]
- Fidaleo, M.; Ventriglia, G. Application of Design of Experiments to the Analysis of Fruit Juice Deacidification Using Electrodialysis with Monopolar Membranes. Foods 2022, 11, 1770. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Zhou, R.; Dong, Z.; Yan, J.; Ma, X.; Liu, W.; Sun, L.; Li, C.; Yan, H.; Wang, Y.; et al. Bipolar Membrane Electrodialysis for Cleaner Production of Diprotic Malic Acid: Separation Mechanism and Performance Evaluation. Membranes 2023, 13, 197. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Wu, D.; Chen, G.; Halim, R.; Liu, J.; Deng, H. Comparative study on tartaric acid production by two-chamber and three-chamber electro-electrodialysis. Sep. Purif. Technol. 2021, 263, 118403. [Google Scholar] [CrossRef]
- Chandra, A.; E, B.; Chattopadhyay, S. A critical analysis on ion transport of organic acid mixture through an anion-exchange membrane during electrodialysis. Chem. Eng. Res. Des. 2022, 178, 13–24. [Google Scholar] [CrossRef]
- Mandal, P.; Mondal, R.; Goel, P.; E, B.; Chatterjee, U.; Chattopadhyay, S. Selective recovery of carboxylic acid through PVDF blended anion exchange membranes using electrodialysis. Sep. Purif. Technol. 2022, 292, 121069. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, H.; Liu, Y.; Chen, R.; Qian, Q.; Van der Bruggen, B. Cr(III) recovery in form of Na2CrO4 from aqueous solution using improved bipolar membrane electrodialysis. J. Membr. Sci. 2020, 604, 118097. [Google Scholar] [CrossRef]
- Wang, B.; Yan, J.; Wang, H.; Li, R.; Fu, R.; Jiang, C.; Nikonenko, V.; Pismenskaya, N.; Wang, Y.; Xu, T. Ionic liquid-based pore-filling anion-exchange membranes enable fast large-sized metallic anion migration in electrodialysis. J. Membr. Sci. 2023, 670, 121348. [Google Scholar] [CrossRef]
- Fang, Q.; Wei, X.; Yan, H.; Jiang, C.; Wang, Y.; Xu, T. A Sustainable Electrochemical Method for the Production of Vanadium Pentoxide Using Bipolar Membrane Electrodialysis. Ind. Eng. Chem. Res. 2022, 61, 8233–8241. [Google Scholar] [CrossRef]
- Rotta, E.H.; Marder, L.; Pérez-Herranz, V.; Bernardes, A.M. Characterization of an anion-exchange membrane subjected to phosphate and sulfate separation by electrodialysis at overlimiting current density condition. J. Membr. Sci. 2021, 635, 119510. [Google Scholar] [CrossRef]
- Monat, L.; Zhang, W.; Jarošíková, A.; Haung, H.; Bernstein, R.; Nir, O. Circular Process for Phosphoric Acid Plant Wastewater Facilitated by Selective Electrodialysis. ACS Sustain. Chem. Eng. 2022, 10, 11567–11576. [Google Scholar] [CrossRef]
- Zheng, Y.; Wan, Y.; Zhang, Y.; Huang, J.; Yang, Y.; Tsang, D.C.W.; Wang, H.; Chen, H.; Gao, B. Recovery of phosphorus from wastewater: A review based on current phosphorous removal technologies. Crit. Rev. Environ. Sci. Technol. 2023, 53, 1148–1172. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Wang, Y.; Wu, G.; Luo, J.; Wang, S. Development of a selective electrodialysis for nutrient recovery and desalination during secondary effluent treatment. Chem. Eng. J. 2017, 322, 224–233. [Google Scholar] [CrossRef]
- Vecino, X.; Reig, M.; Gibert, O.; Valderrama, C.; Cortina, J.L. Integration of liquid-liquid membrane contactors and electrodialysis for ammonium recovery and concentration as a liquid fertilizer. Chemosphere 2020, 245, 125606. [Google Scholar] [CrossRef] [PubMed]
- Hussain, A.; Wang, H.; Fu, R.; Afsar, N.U.; Wang, B.; Jiang, C.; Wang, Y.; Xu, T. Ion Transport Behavior in Bipolar Membrane Electrodialysis: Role of Anions. Ind. Eng. Chem. Res. 2023, 62, 698–707. [Google Scholar] [CrossRef]
- Chandra, A.; Chattopadhyay, S. Chain length and acidity of carboxylic acids influencing adsorption/desorption mechanism and kinetics over anion exchange membrane. Colloids Surf. A Physicochem. Eng. Asp. 2020, 589, 124395. [Google Scholar] [CrossRef]
- Yang, X.; Merenda, A.; AL-Attabi, R.; Dumée, L.F.; Zhang, X.; Thang, S.H.; Pham, H.; Kong, L. Towards next generation high throughput ion exchange membranes for downstream bioprocessing: A review. J. Membr. Sci. 2022, 647, 120325. [Google Scholar] [CrossRef]
- Zhang, S.; Tanioka, A.; Matsumoto, H. De Novo Ion-Exchange Membranes Based on Nanofibers. Membranes 2021, 11, 652. [Google Scholar] [CrossRef]
- Sedighi, M.; Behvand Usefi, M.M.; Ismail, A.F.; Ghasemi, M. Environmental sustainability and ions removal through electrodialysis desalination: Operating conditions and process parameters. Desalination 2023, 549, 116319. [Google Scholar] [CrossRef]
- Iddya, A.; Zarzycki, P.; Kingsbury, R.; Khor, C.M.; Ma, S.; Wang, J.; Wheeldon, I.; Ren, Z.J.; Hoek, E.M.; Jassby, D. A reverse-selective ion exchange membrane for the selective transport of phosphates via an outer-sphere complexation–diffusion pathway. Nat. Nanotechnol. 2022, 17, 1222–1228. [Google Scholar] [CrossRef]
- Babiak, P.; Schaffer-Harris, G.; Kainuma, M.; Fedorovich, V.; Goryanin, I. Development of a New Hydrogel Anion Exchange Membrane for Swine Wastewater Treatment. Membranes 2022, 12, 984. [Google Scholar] [CrossRef]
- Rybalkina, O.A.; Sharafan, M.V.; Nikonenko, V.V.; Pismenskaya, N.D. Two mechanisms of H+/OH− ion generation in anion-exchange membrane systems with polybasic acid salt solutions. J. Membr. Sci. 2022, 651, 120449. [Google Scholar] [CrossRef]
- Rotta, E.H.; Martí-Calatayud, M.C.; Pérez-Herranz, V.; Bernardes, A.M. Evaluation by Means of Electrochemical Impedance Spectroscopy of the Transport of Phosphate Ions through a Heterogeneous Anion-Exchange Membrane at Different pH and Electrolyte Concentration. Water 2022, 15, 9. [Google Scholar] [CrossRef]
- Barros, K.S.; Martí-Calatayud, M.C.; Ortega, E.M.; Pérez-Herranz, V.; Espinosa, D.C.R. Chronopotentiometric study on the simultaneous transport of EDTA ionic species and hydroxyl ions through an anion-exchange membrane for electrodialysis applications. J. Electroanal. Chem. 2020, 879, 114782. [Google Scholar] [CrossRef]
- Pismenskaya, N.; Rybalkina, O.; Moroz, I.; Mareev, S.; Nikonenko, V. Influence of Electroconvection on Chronopotentiograms of an Anion-Exchange Membrane in Solutions of Weak Polybasic Acid Salts. Int. J. Mol. Sci. 2021, 22, 13518. [Google Scholar] [CrossRef]
- Martí-Calatayud, M.C.; Evdochenko, E.; Bär, J.; García-Gabaldón, M.; Wessling, M.; Pérez-Herranz, V. Tracking homogeneous reactions during electrodialysis of organic acids via EIS. J. Membr. Sci. 2020, 595, 117592. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Rybalkina, O.A.; Kozmai, A.E.; Tsygurina, K.A.; Melnikova, E.D.; Nikonenko, V.V. Generation of H+ and OH− ions in anion-exchange membrane/ampholyte-containing solution systems: A study using electrochemical impedance spectroscopy. J. Membr. Sci. 2020, 601, 117920. [Google Scholar] [CrossRef]
- Melnikov, S.; Kolot, D.; Nosova, E.; Zabolotskiy, V. Peculiarities of transport-structural parameters of ion-exchange membranes in solutions containing anions of carboxylic acids. J. Membr. Sci. 2018, 557, 1–12. [Google Scholar] [CrossRef]
- Chandra, A.; Bhuvanesh, E.; Chattopadhyay, S. Physicochemical interactions of organic acids influencing microstructure and permselectivity of anion exchange membrane. Colloids Surf. A Physicochem. Eng. Asp. 2019, 560, 260–269. [Google Scholar] [CrossRef]
- D’Agostino, L.; Di Luccia, A. Polyamines interact with DNA as molecular aggregates. Eur. J. Biochem. 2002, 269, 4317–4325. [Google Scholar] [CrossRef]
- Marmisollé, W.A.; Irigoyen, J.; Gregurec, D.; Moya, S.; Azzaroni, O. Supramolecular Surface Chemistry: Substrate-Independent, Phosphate-Driven Growth of Polyamine-Based Multifunctional Thin Films. Adv. Funct. Mater. 2015, 25, 4144–4152. [Google Scholar] [CrossRef]
- Dressick, W.J.; Wahl, K.J.; Bassim, N.D.; Stroud, R.M.; Petrovykh, D.Y. Divalent–Anion Salt Effects in Polyelectrolyte Multilayer Depositions. Langmuir 2012, 28, 15831–15843. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Yaroshchuk, A.; Bruening, M.L. Moderate pH changes alter the fluxes, selectivities and limiting currents in ion transport through polyelectrolyte multilayers deposited on membranes. J. Membr. Sci. 2020, 616, 118570. [Google Scholar] [CrossRef]
- Pérez-Mitta, G.; Marmisollé, W.A.; Albesa, A.G.; Toimil-Molares, M.E.; Trautmann, C.; Azzaroni, O. Phosphate-Responsive Biomimetic Nanofluidic Diodes Regulated by Polyamine-Phosphate Interactions: Insights into Their Functional Behavior from Theory and Experiment. Small 2018, 14, 1702131. [Google Scholar] [CrossRef] [PubMed]
- Fenoy, G.E.; Piccinini, E.; Knoll, W.; Marmisollé, W.A.; Azzaroni, O. The Effect of Amino–Phosphate Interactions on the Biosensing Performance of Enzymatic Graphene Field-Effect Transistors. Anal. Chem. 2022, 94, 13820–13828. [Google Scholar] [CrossRef]
- Kooijman, E.E.; Tieleman, D.P.; Testerink, C.; Munnik, T.; Rijkers, D.T.S.; Burger, K.N.J.; de Kruijff, B. An Electrostatic/Hydrogen Bond Switch as the Basis for the Specific Interaction of Phosphatidic Acid with Proteins. J. Biol. Chem. 2007, 282, 11356–11364. [Google Scholar] [CrossRef]
- Laucirica, G.; Marmisollé, W.A.; Azzaroni, O. Dangerous liaisons: Anion-induced protonation in phosphate–polyamine interactions and their implications for the charge states of biologically relevant surfaces. Phys. Chem. Chem. Phys. 2017, 19, 8612–8620. [Google Scholar] [CrossRef] [PubMed]
- Butylskii, D.Y.; Troitskiy, V.A.; Ponomar, M.A.; Moroz, I.A.; Sabbatovskiy, K.G.; Sharafan, M.V. Efficient Anion-Exchange Membranes with Anti-Scaling Properties Obtained by Surface Modification of Commercial Membranes Using a Polyquaternium-22. Membranes 2022, 12, 1065. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nikonenko, V.V.; Pokhidnya, E.V.; Butylsky, D.Y. Method of Modifying Anion-Exchange Membranes. Patent of Russia No RU2699646C1, 6 September 2019. [Google Scholar]
- Sarapulova, V.V.; Titorova, V.D.; Nikonenko, V.V.; Pismenskaya, N.D. Transport Characteristics of Homogeneous and Heterogeneous Ion-Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions. Membr. Membr. Technol. 2019, 1, 168–182. [Google Scholar] [CrossRef]
- Ponomar, M.; Krasnyuk, E.; Butylskii, D.; Nikonenko, V.; Wang, Y.; Jiang, C.; Xu, T.; Pismenskaya, N. Sessile Drop Method: Critical Analysis and Optimization for Measuring the Contact Angle of an Ion-Exchange Membrane Surface. Membranes 2022, 12, 765. [Google Scholar] [CrossRef] [PubMed]
- Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A.; Gnusin, N.P. Characterization of ion-exchange membrane materials: Properties vs structure. Adv. Colloid Interface Sci. 2008, 139, 3–28. [Google Scholar] [CrossRef]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Titorova, V.D.; Mareev, S.A.; Gorobchenko, A.D.; Gil, V.V.; Nikonenko, V.V.; Sabbatovskii, K.G.; Pismenskaya, N.D. Effect of current-induced coion transfer on the shape of chronopotentiograms of cation-exchange membranes. J. Membr. Sci. 2021, 624, 119036. [Google Scholar] [CrossRef]
- Kniaginicheva, E.; Pismenskaya, N.; Melnikov, S.; Belashova, E.; Sistat, P.; Cretin, M.; Nikonenko, V. Water splitting at an anion-exchange membrane as studied by impedance spectroscopy. J. Membr. Sci. 2015, 496, 78–83. [Google Scholar] [CrossRef]
- Danilczuk, M.; Lin, L.; Schlick, S.; Hamrock, S.J.; Schaberg, M.S. Understanding the fingerprint region in the infra-red spectra of perfluorinated ionomer membranes and corresponding model compounds: Experiments and theoretical calculations. J. Power Sources 2011, 196, 8216–8224. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Li, J.; Zhai, M. PVDF based ion exchange membrane prepared by radiation grafting of ethyl styrenesulfonate and sequent hydrolysis. Radiat. Phys. Chem. 2017, 130, 252–258. [Google Scholar] [CrossRef]
- Bormashenko, Y.; Pogreb, R.; Stanevsky, O.; Bormashenko, E. Vibrational spectrum of PVDF and its interpretation. Polym. Test. 2004, 23, 791–796. [Google Scholar] [CrossRef]
- Tarasevich, B.N. Infrared Spectrum of Basic Classes of Organic Compounds. IR Spectra of General Classes of Organic Compounds: Handbook; Mosk. Gos. Univ.: Moscow, Russia, 2012. [Google Scholar]
- Nakanishi, K. Infrared spectra and structure of organic compounds/K. Nakanishi. Per. English. M. Mir 1965, 216. (In Russian) [Google Scholar]
- Garcia-Vasquez, W.; Ghalloussi, R.; Dammak, L.; Larchet, C.; Nikonenko, V.; Grande, D. Structure and properties of heterogeneous and homogeneous ion-exchange membranes subjected to ageing in sodium hypochlorite. J. Membr. Sci. 2014, 452, 104–116. [Google Scholar] [CrossRef]
- Zhu, S.; Kingsbury, R.S.; Call, D.F.; Coronell, O. Impact of solution composition on the resistance of ion exchange membranes. J. Membr. Sci. 2018, 554, 39–47. [Google Scholar] [CrossRef]
- Huang, Y.; Fan, H.; Yip, N.Y. Influence of electrolyte on concentration-induced conductivity-permselectivity tradeoff of ion-exchange membranes. J. Memb. Sci. 2023, 668, 121184. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics 86TH Edition 2005–2006; CRC Press: Boca Raton, FL, USA, 2005; ISBN 0849304792. [Google Scholar]
- Kim, J.; Seidler, P.; Wan, L.S.; Fill, C. Formation, structure, and reactivity of amino-terminated organic films on silicon substrates. J. Colloid Interface Sci. 2009, 329, 114–119. [Google Scholar] [CrossRef]
- Díaz, J.C.; Kamcev, J. Ionic conductivity of ion-exchange membranes: Measurement techniques and salt concentration dependence. J. Membr. Sci. 2021, 618, 118718. [Google Scholar] [CrossRef]
- Belloň, T.; Slouka, Z. Overlimiting behavior of surface-modified heterogeneous anion-exchange membranes. J. Membr. Sci. 2020, 610, 118291. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Concentration polarization of interface and non-linear electrokinetic phenomena. Adv. Colloid Interface Sci. 2010, 160, 16–39. [Google Scholar] [CrossRef] [PubMed]
- Coates, J. Interpretation of Infrared Spectra, A Practical Approach. In Encyclopedia of Analytical Chemistry; John Wiley & Sons, Ltd.: Chichester, UK, 2006. [Google Scholar]
- Cao, Y.-C.; Wang, X.; Mamlouk, M.; Scott, K. Preparation of alkaline anion exchange polymer membrane from methylated melamine grafted poly(vinylbenzyl chloride) and its fuel cell performance. J. Mater. Chem. 2011, 21, 12910. [Google Scholar] [CrossRef]
- Sultana, S.; Rahman, N.; Razzak, M.; Sardar, M.N. Diallyl Dimethyl Ammonium Chloride (DADMAC) and Acrylic Acid (AAc) Embedded Nonwoven Irradiated Polyethylene Fabric as Efficient Adsorbent to Separate U(VI) from Aqueous Solution. Environ. Res. Technol. 2023, 6, 21–34. [Google Scholar] [CrossRef]
- Jareansin, S.; Sukaam, P.; Kusuktham, B. Preparation and characterization of modified cotton fabrics with responsive pH. Polym. Bull. 2019, 76, 4507–4520. [Google Scholar] [CrossRef]
- Popov, Y.V.; Mikhailovich, M.V.; Budko, I.I. Method of Producing Carboxylic Acid Amides. RU2565059C1, 20 October 2015. [Google Scholar]
- Wei, X.; Wang, Y.; Yan, H.; Jiang, C.; Xu, T. A sustainable valorization of neopentyl glycol salt waste containing sodium formate via bipolar membrane electrodialysis. Sep. Purif. Technol. 2021, 254, 117563. [Google Scholar] [CrossRef]
- Misra, A.; Tyagi, P.; Rai, P.; Misra, D.S. FTIR Spectroscopy of Multiwalled Carbon Nanotubes: A Simple Approachto Study the Nitrogen Doping. J. Nanosci. Nanotechnol. 2007, 7, 1820–1823. [Google Scholar] [CrossRef] [PubMed]
- Yurchenko, V.E.; Polovko, N.P.; Kovaleva, T.N. Razrabotka tekhnologii krema Metroksal. Vestn. Farmatsii 2013, 62, 5–11. [Google Scholar]
- Kollman, P.A.; Allen, L.C. Theory of the hydrogen bond. Chem. Rev. 1972, 72, 283–303. [Google Scholar] [CrossRef]
- Butylskii, D.Y.; Troitskiy, V.A.; Sharafan, M.V.; Pismenskaya, N.D.; Nikonenko, V.V. Scaling-resistant anion-exchange membrane prepared by in situ modification with a bifunctional polymer containing quaternary amino groups. Desalination 2022, 537, 115821. [Google Scholar] [CrossRef]
- Dzyura, V.; Maruschak, P.; Slavov, S.; Dimitrov, D.; Semehen, V.; Markov, O. Evaluating Some Functional Properties of Surfaces with Partially Regular Microreliefs Formed by Ball-Burnishing. Machines 2023, 11, 633. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Equilibrium electro-osmotic instability in concentration polarization at a perfectly charge-selective interface. Phys. Rev. Fluids 2017, 2, 093702. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Polarization of systems with complex geometry. Curr. Opin. Colloid Interface Sci. 2013, 18, 137–148. [Google Scholar] [CrossRef]
- Lee, H. Electroconvective Instability on Undulated Ion-selective Surface. Korean Chem. Eng. Res. 2019, 57, 735–742. [Google Scholar]
- Choi, J.-H.; Moon, S.-H. Structural change of ion-exchange membrane surfaces under high electric fields and its effects on membrane properties. J. Colloid Interface Sci. 2003, 265, 93–100. [Google Scholar] [CrossRef]
- Pismenskaya, N.; Rybalkina, O.; Solonchenko, K.; Pasechnaya, E.; Sarapulova, V.; Wang, Y.; Jiang, C.; Xu, T.; Nikonenko, V. How Chemical Nature of Fixed Groups of Anion-Exchange Membranes Affects the Performance of Electrodialysis of Phosphate-Containing Solutions? Polymers 2023, 15, 2288. [Google Scholar] [CrossRef]
- Krol, J. Concentration polarization with monopolar ion exchange membranes: Current–voltage curves and water dissociation. J. Membr. Sci. 1999, 162, 145–154. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of electroconvection and its use in intensifying the mass transfer in electrodialysis (Review). Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Equilibrium Electroconvective Instability. Phys. Rev. Lett. 2015, 114, 114502. [Google Scholar] [CrossRef]
- Nebavskaya, K.A.; Sarapulova, V.V.; Sabbatovskiy, K.G.; Sobolev, V.D.; Pismenskaya, N.D.; Sistat, P.; Cretin, M.; Nikonenko, V.V. Impact of ion exchange membrane surface charge and hydrophobicity on electroconvection at underlimiting and overlimiting currents. J. Membr. Sci. 2017, 523, 36–44. [Google Scholar] [CrossRef]
- Simons, R. Electric field effects on proton transfer between ionizable groups and water in ion exchange membranes. Electrochim. Acta 1984, 29, 151–158. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Sharafan, M.V.; Shel’deshov, N.V. The dissociation rate of water molecules in systems with cation- and anion-exchange membranes. Russ. J. Electrochem. 2012, 48, 550–555. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Chermit, R.K.; Sharafan, M.V. Mass transfer mechanism and chemical stability of strongly basic anion-exchange membranes under overlimiting current conditions. Russ. J. Electrochem. 2014, 50, 38–45. [Google Scholar] [CrossRef]
- Helfferich, F.G. Ion Exchange; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Slavinskaya, G.V.; Kurenkova, O.V. On the multifunctional character of strong basic anion-exchange resin. Sorpt. Chromatogr. Process. 2019, 19, 101–110. [Google Scholar] [CrossRef]
- Kozmai, A.E.; Nikonenko, V.V.; Zyryanova, S.; Pismenskaya, N.D.; Dammak, L. A simple model for the response of an anion-exchange membrane to variation in concentration and pH of bathing solution. J. Membr. Sci. 2018, 567, 127–138. [Google Scholar] [CrossRef]
- Macdonald, J.R.; Barsoukov, E. Impedance spectroscopy: Theory, experiment, and applications; John Wiley: Hoboken, NJ, USA, 2005; ISBN 978-0-471-64749-2. [Google Scholar]
- Pärnamäe, R.; Mareev, S.; Nikonenko, V.; Melnikov, S.; Sheldeshov, N.; Zabolotskii, V.; Hamelers, H.V.M.; Tedesco, M. Bipolar membranes: A review on principles, latest developments, and applications. J. Membr. Sci. 2021, 617, 118538. [Google Scholar] [CrossRef]
- Nefedova, G.Z.; Klimova, Z.G.; Sapoznikova, G.S. Ion-Exchange Membranes, Granulates, Powders. Catalogue 1977. [Google Scholar]
- Simons, R. Water splitting in ion exchange membranes. Electrochim. Acta 1985, 30, 275–282. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Shel’deshov, N.V.; Gnusin, N.P. Dissociation of Water Molecules in Systems with Ion-exchange Membranes. Russ. Chem. Rev. 1988, 57, 801–808. [Google Scholar] [CrossRef]
- Belashova, E.D.; Melnik, N.A.; Pismenskaya, N.D.; Shevtsova, K.A.; Nebavsky, A.V.; Lebedev, K.A.; Nikonenko, V.V. Overlimiting mass transfer through cation-exchange membranes modified by Nafion film and carbon nanotubes. Electrochim. Acta 2012, 59, 412–423. [Google Scholar] [CrossRef]
- Lteif, R.; Dammak, L.; Larchet, C.; Auclair, B. Conductivitéélectrique membranaire: étude de l’effet de la concentration, de la nature de l’électrolyte et de la structure membranaire. Eur. Polym. J. 1999, 35, 1187–1195. [Google Scholar] [CrossRef]
- Kozmai, A.; Porozhnyy, M.; Ruleva, V.; Gorobchenko, A.; Pismenskaya, N.; Nikonenko, V. Is It Possible to Prepare a “Super” Anion-Exchange Membrane by a Polypyrrole-Based Modification? Membranes 2023, 13, 103. [Google Scholar] [CrossRef]
- Porozhnyy, M.; Huguet, P.; Cretin, M.; Safronova, E.; Nikonenko, V. Mathematical modeling of transport properties of proton-exchange membranes containing immobilized nanoparticles. Int. J. Hydrogen Energy 2016, 41, 15605–15614. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nevakshenova, E.E.; Nikonenko, V.V. Using a Single Set of Structural and Kinetic Parameters of the Microheterogeneous Model to Describe the Sorption and Kinetic Properties of Ion-Exchange Membranes. Pet. Chem. 2018, 58, 465–473. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Membr. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Titorova, V.; Sabbatovskiy, K.; Sarapulova, V.; Kirichenko, E.; Sobolev, V.; Kirichenko, K. Characterization of MK-40 Membrane Modified by Layers of Cation Exchange and Anion Exchange Polyelectrolytes. Membranes 2020, 10, 20. [Google Scholar] [CrossRef] [PubMed]
- Belova, E.I.; Lopatkova, G.Y.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Pourcelly, G. Effect of Anion-exchange Membrane Surface Properties on Mechanisms of Overlimiting Mass Transfer. J. Phys. Chem. B 2006, 110, 13458–13469. [Google Scholar] [CrossRef]
- Ślęzak, A.; Bryll, A.; Grzegorczyn, S. A Numerical Study of the Hydrodynamic Stable Concentration Boundary Layers in a Membrane System Under Microgravitational Conditions. J. Biol. Phys. 2006, 32, 553–562. [Google Scholar] [CrossRef]
- Moya, A.A.; Moleón, J.A. Study of the electrical properties of bi-layer ion-exchange membrane systems. J. Electroanal. Chem. 2010, 647, 53–59. [Google Scholar] [CrossRef]
- Moya, A.A. Electrochemical Impedance of Ion-Exchange Membranes in Ternary Solutions with Two Counterions. J. Phys. Chem. C 2014, 118, 2539–2553. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B.; Futerman, A.; Gitis, V.; Nikonenko, V. Reexamination of electrodiffusion time scales. Phys. Rev. E 2009, 79, 021506. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Kozmai, A.E. Electrical equivalent circuit of an ion-exchange membrane system. Electrochim. Acta 2011, 56, 1262–1269. [Google Scholar] [CrossRef]
- Vorotyntsev, M.A.; Badiali, J.-P.; Inzelt, G. Electrochemical impedance spectroscopy of thin films with two mobile charge carriers: Effects of the interfacial charging. J. Electroanal. Chem. 1999, 472, 7–19. [Google Scholar] [CrossRef]
- Vorotyntsev, M.A. Impedance of thin films with two mobile charge carriers. Interfacial exchange of both species with adjacent media. Effect of the double layer charges. Electrochim. Acta 2002, 47, 2071–2079. [Google Scholar] [CrossRef]
- Impedance Spectroscopy; Barsoukov, E., Macdonald, J.R., Eds.; Wiley: Hoboken, NJ, USA, 2005; ISBN 9780471647492. [Google Scholar]
- Sistat, P.; Kozmai, A.; Pismenskaya, N.; Larchet, C.; Pourcelly, G.; Nikonenko, V. Low-frequency impedance of an ion-exchange membrane system. Electrochim. Acta 2008, 53, 6380–6390. [Google Scholar] [CrossRef]
- Muralidharan, V.S. Warburg impedance—basics revisited. Anti-Corrosion Methods Mater. 1997, 44, 26–29. [Google Scholar] [CrossRef]
- Femmer, R.; Martí-Calatayud, M.C.; Wessling, M. Mechanistic modeling of the dielectric impedance of layered membrane architectures. J. Membr. Sci. 2016, 520, 29–36. [Google Scholar] [CrossRef]
- Moya, A.A. Harmonic analysis in ideal ion-exchange membrane systems. Electrochim. Acta 2013, 90, 1–11. [Google Scholar] [CrossRef]
- Lévêque, M.A. The laws of heat transmission by convection. Les Ann. des Mines Mem. 1928, 12, 201–299. [Google Scholar]
- Gnusin, N.P.; Zabolotskii, V.I.; Nikonenko, V.V.; Urtenov, M.K. Convective-Diffusion Model of Electrodialytic Desalination. Limiting Current and Diffusion Layer. Sov. Electrochem. 1986, 23, 273–278. [Google Scholar]
- La Cerva, M.; Gurreri, L.; Tedesco, M.; Cipollina, A.; Ciofalo, M.; Tamburini, A.; Micale, G. Determination of limiting current density and current efficiency in electrodialysis units. Desalination 2018, 445, 138–148. [Google Scholar] [CrossRef]
- Nikonenko, V.; Nebavsky, A.; Mareev, S.; Kovalenko, A.; Urtenov, M.; Pourcelly, G. Modelling of Ion Transport in Electromembrane Systems: Impacts of Membrane Bulk and Surface Heterogeneity. Appl. Sci. 2018, 9, 25. [Google Scholar] [CrossRef]
- Belashova, E.D.; Pismenskaya, N.D.; Nikonenko, V.V.; Sistat, P.; Pourcelly, G. Current-voltage characteristic of anion-exchange membrane in monosodium phosphate solution. Modelling and experiment. J. Membr. Sci. 2017, 542, 177–185. [Google Scholar] [CrossRef]
- Urtenov, M.A.K.; Kirillova, E.V.; Seidova, N.M.; Nikonenko, V.V. Decoupling of the Nernst-Planck and Poisson equations. Application to a membrane system at overlimiting currents. J. Phys. Chem. B 2007. [Google Scholar] [CrossRef]
- Kharkats, Y.I.; Sokirko, A.V. Theory of the effect of migration current exaltation taking into account dissociation-recombination reactions. J. Electroanal. Chem. 1991, 303, 27–44. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Jiang, C.; Xu, T. Recovery of gamma-aminobutyric acid (GABA) from reaction mixtures containing salt by electrodialysis. Sep. Purif. Technol. 2016, 170, 353–359. [Google Scholar] [CrossRef]
- Yan, H.; Wang, Y.; Xu, T. Developing Ion Exchange Membrane for Treating High Salinity Water Using Electrodialysis. In Proceedings of the 5th International Conference on Sustainable Chemical Production Process Engineering (SCPPE), Tianjin, China, 30 June–3 July 2019. [Google Scholar]
- Sarapulova, V.; Pismenskaya, N.; Titorova, V.; Sharafan, M.; Wang, Y.; Xu, T.; Zhang, Y.; Nikonenko, V. Transport Characteristics of CJMAEDTM Homogeneous Anion Exchange Membranes in Sodium Chloride and Sodium Sulfate Solutions. Int. J. Mol. Sci. 2021, 22, 1415. [Google Scholar] [CrossRef] [PubMed]
- Astom Detailed Specification of IEMs Produced Astom Corporation. Available online: http://www.astom-corp.jp/en/product/10.html (accessed on 22 May 2023).
- Chen, G.Q.; Wei, K.; Hassanvand, A.; Freeman, B.D.; Kentish, S.E. Single and binary ion sorption equilibria of monovalent and divalent ions in commercial ion exchange membranes. Water Res. 2020, 175, 115681. [Google Scholar] [CrossRef]
- Sugimoto, Y.; Ujike, R.; Higa, M.; Kakihana, Y.; Higa, M. Power Generation Performance of Reverse Electrodialysis (RED) Using Various Ion Exchange Membranes and Power Output Prediction for a Large RED Stack. Membranes 2022, 12, 1141. [Google Scholar] [CrossRef]
- Hernández-Pérez, L.; Martí-Calatayud, M.; Montañés, M.; Pérez-Herranz, V. Interplay between Forced Convection and Electroconvection during the Overlimiting Ion Transport through Anion-Exchange Membranes: A Fourier Transform Analysis of Membrane Voltage Drops. Membranes 2023, 13, 363. [Google Scholar] [CrossRef] [PubMed]
- Zabolotskiy, V.I.; But, A.Y.; Vasil’eva, V.I.; Akberova, E.M.; Melnikov, S.S. Ion transport and electrochemical stability of strongly basic anion-exchange membranes under high current electrodialysis conditions. J. Membr. Sci. 2017, 526, 60–72. [Google Scholar] [CrossRef]
- Pasechnaya, E.; Tsygurina, K.; Ponomar, M.; Chuprynina, D.; Nikonenko, V.; Pismenskaya, N. Comparison of the Electrodialysis Performance in Tartrate Stabilization of a Red Wine Using Aliphatic and Aromatic Commercial and Modified Ion-Exchange Membranes. Membranes 2023, 13, 84. [Google Scholar] [CrossRef] [PubMed]


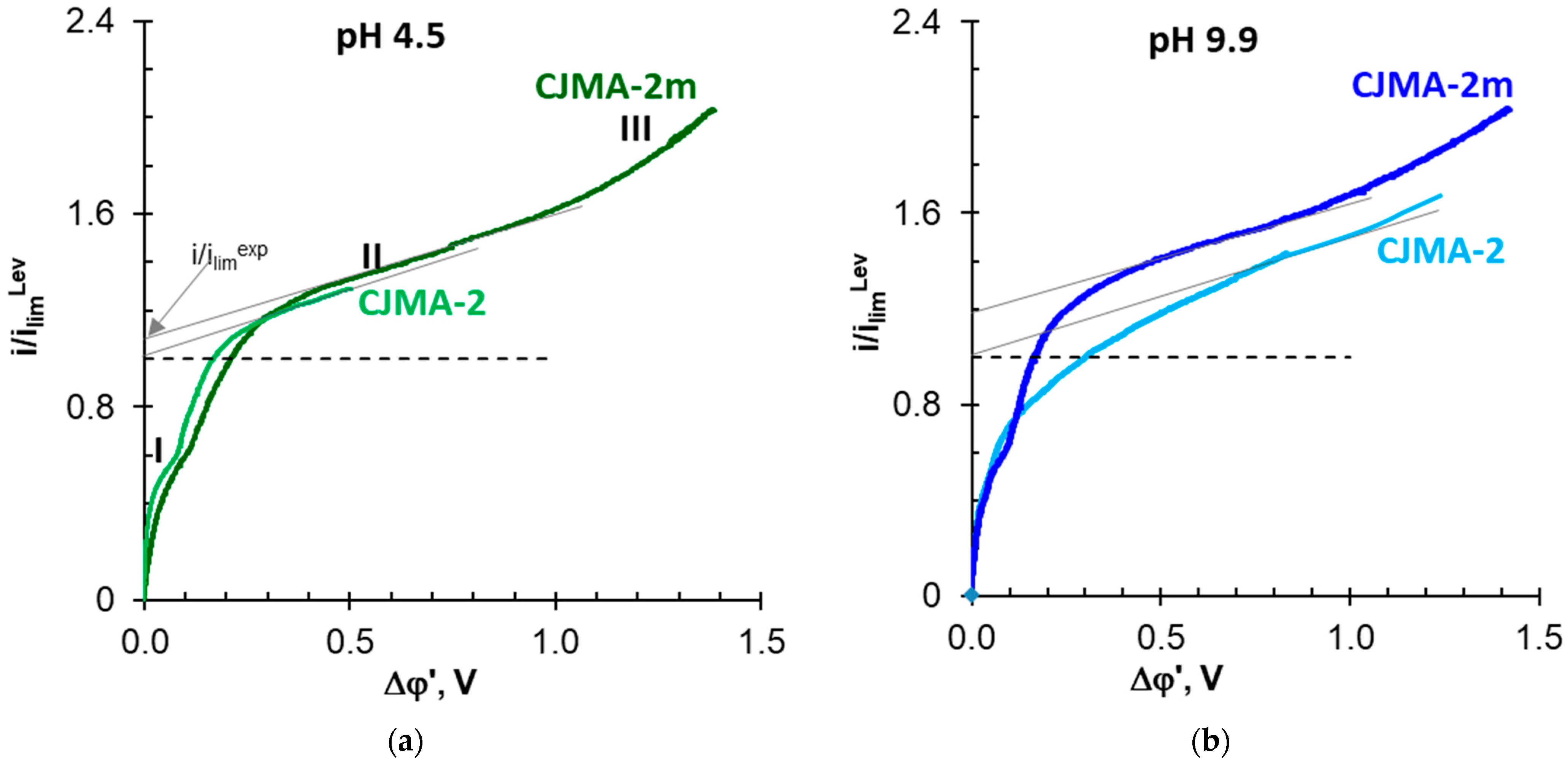
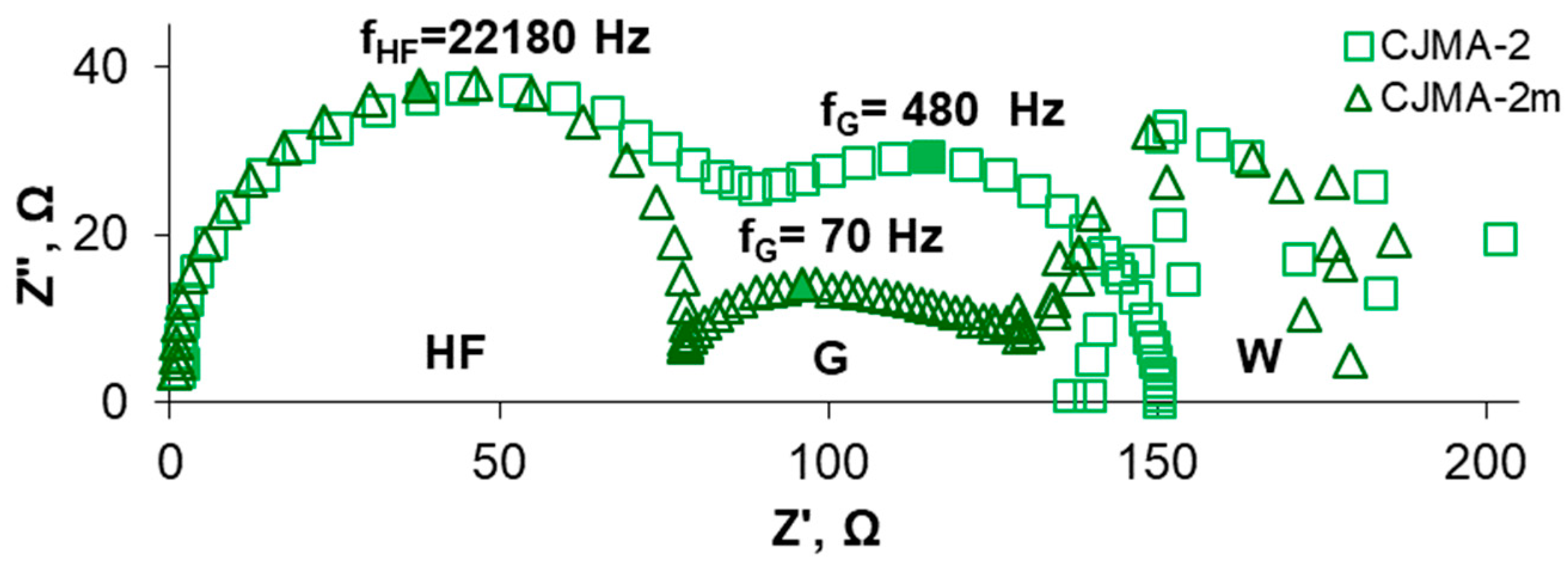


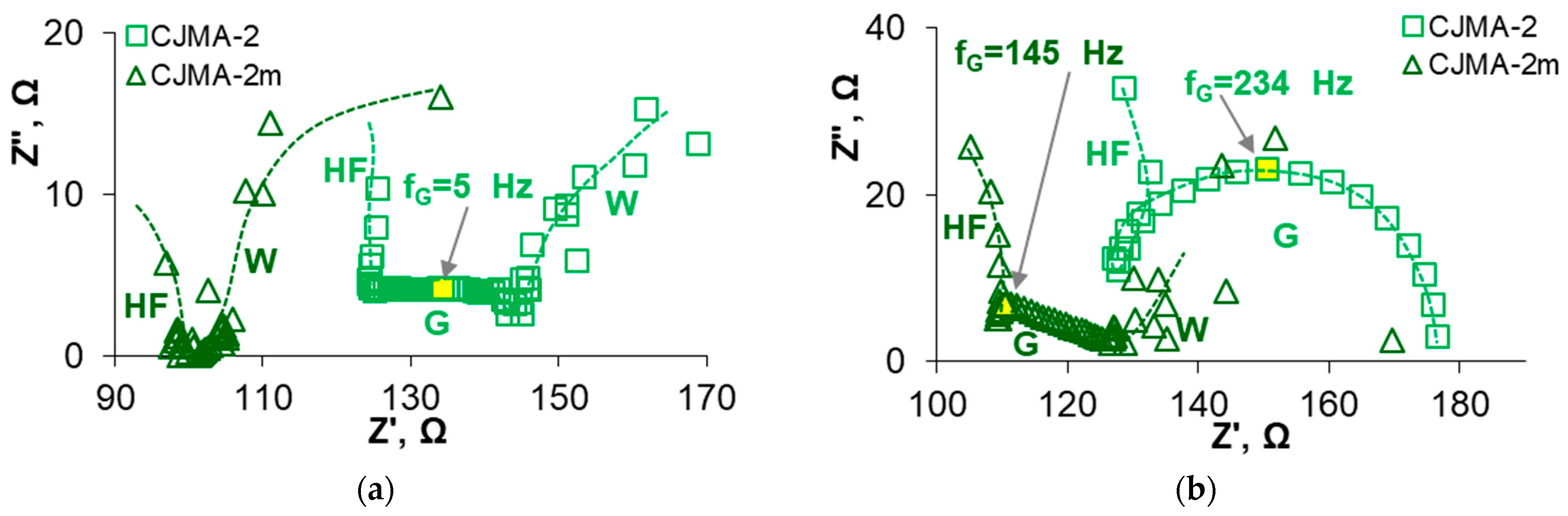
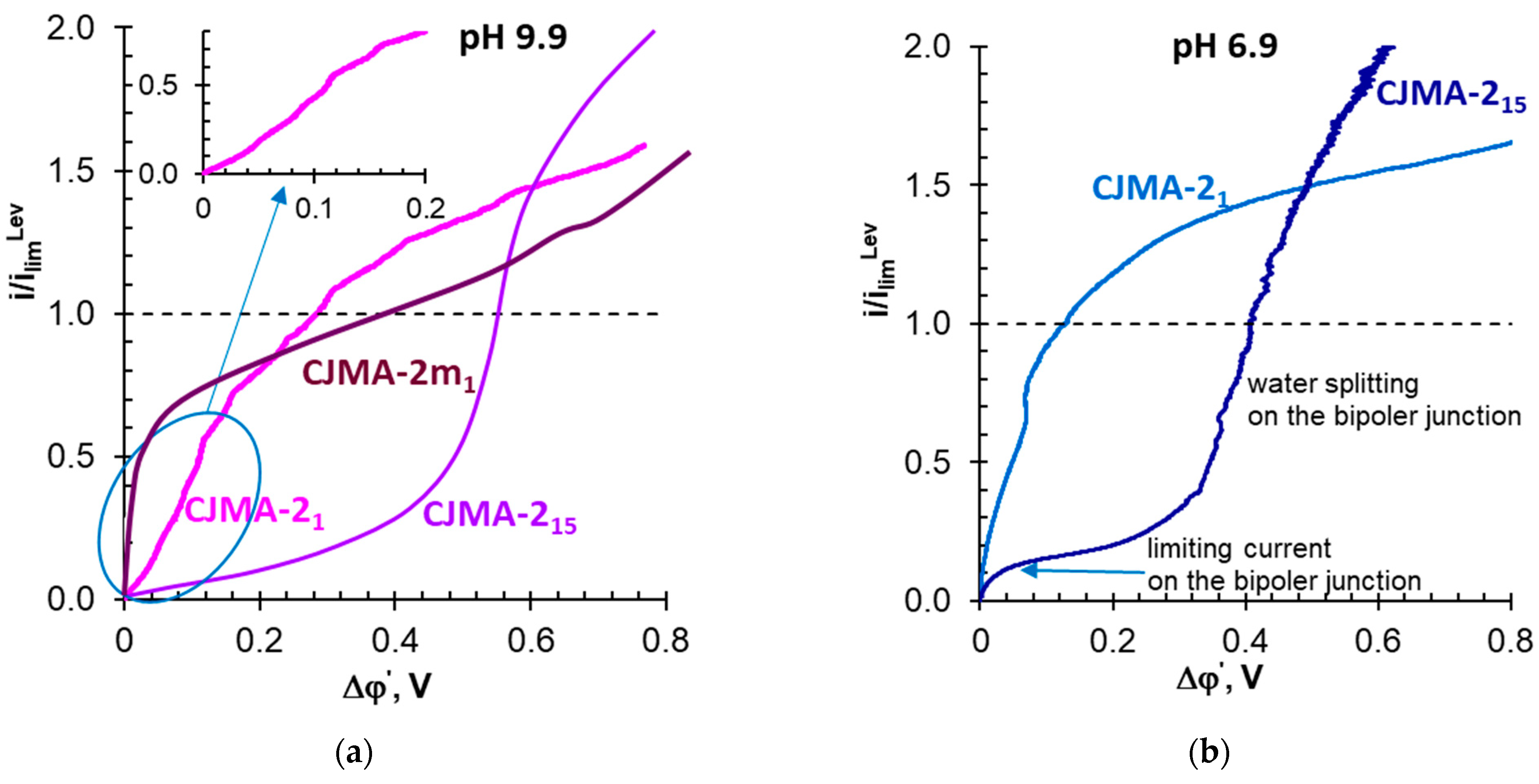
| pH of the Solution | Solution Composition in Mole Fractions, % | ||
|---|---|---|---|
| NaH2PO4 | Na2HPO4 | Na3PO4 | |
| 4.5 | 99.40 | 0.59 | 2.66 × 10−9 |
| 6.6 | 79.80 | 20.19 | 3.38 × 10−5 |
| 9.9 | 0.17 | 99.50 | 0.33 |
| Membrane | Ion-Exchange Capacity, mmol/gdry | Water Content, gH2O/gdry, % | * Conductivity, mS cm−1 in 0.5 M Solution | * t1 in 0.5 M NaCl Solution | |
|---|---|---|---|---|---|
| NaCl (pH 5.4) | NaH2PO4 (pH 4.5) | ||||
| CJMA-2 | 0.9 ± 0.1 [73] | 35 ± 5 [73] | 2.3 ± 0.1 | 0.8 ± 0.1 | 0.97 ± 0.1 |
| CJMA-2m | 1.0 ± 0.1 | 35 ± 5 | 3.0 ± 0.1 | 1.5 ± 0.1 | 0.97 ± 0.1 |
| i, mA cm−2 | i/ilimLev | Membrane | ED Duration, s | qH+, mol m−2 | Δφ, V | W 103, Wh | ||
|---|---|---|---|---|---|---|---|---|
| γP = 0% | γP = 40% | |||||||
| 1.63 | 0.66 | 1.10 | CJMA-2 | 20,000 | 0.83 | 1.38 | 0.72 | 50 |
| CJMA-2m | 15,600 | 0.30 | 0.93 | 0.74 | 26 | |||
| 2.46 | 1.00 | 1.65 | CJMA-2 | 14,100 | 0.90 | 2.56 | 0.66 | 95 |
| CJMA-2m | 13,500 | 0.82 | 1.60 | 0.71 | 56 | |||
| 3.25 | 1.30 | 2.20 | CJMA-2 | 12,300 | 1.25 | 3.65 | 0.62 | 169 |
| CJMA-2m | 11,400 | 0.10 | 2.54 | 0.63 | 98 | |||
| 3.75 | 1.52 | 2.54 | CJMA-2 | 9300 | 0.13 | 3.34 | 0.59 | 126 |
| CJMA-2m | 11,400 | 0.13 | 3.16 | 0.60 | 130 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pismenskaya, N.; Rybalkina, O.; Solonchenko, K.; Butylskii, D.; Nikonenko, V. Phosphates Transfer in Pristine and Modified CJMA-2 Membrane during Electrodialysis Processing of NaxH(3−x)PO4 Solutions with pH from 4.5 to 9.9. Membranes 2023, 13, 647. https://doi.org/10.3390/membranes13070647
Pismenskaya N, Rybalkina O, Solonchenko K, Butylskii D, Nikonenko V. Phosphates Transfer in Pristine and Modified CJMA-2 Membrane during Electrodialysis Processing of NaxH(3−x)PO4 Solutions with pH from 4.5 to 9.9. Membranes. 2023; 13(7):647. https://doi.org/10.3390/membranes13070647
Chicago/Turabian StylePismenskaya, Natalia, Olesya Rybalkina, Ksenia Solonchenko, Dmitrii Butylskii, and Victor Nikonenko. 2023. "Phosphates Transfer in Pristine and Modified CJMA-2 Membrane during Electrodialysis Processing of NaxH(3−x)PO4 Solutions with pH from 4.5 to 9.9" Membranes 13, no. 7: 647. https://doi.org/10.3390/membranes13070647
APA StylePismenskaya, N., Rybalkina, O., Solonchenko, K., Butylskii, D., & Nikonenko, V. (2023). Phosphates Transfer in Pristine and Modified CJMA-2 Membrane during Electrodialysis Processing of NaxH(3−x)PO4 Solutions with pH from 4.5 to 9.9. Membranes, 13(7), 647. https://doi.org/10.3390/membranes13070647









