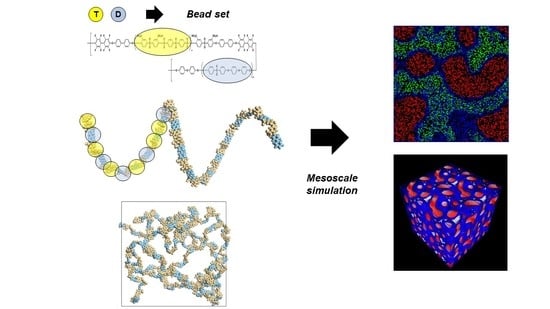
Mesoscale Simulation Based on the Dynamic Mean-Field Density Functional Method on Block-Copolymeric Ionomers for Polymer Electrolyte Membranes
Abstract
1. Introduction
2. Materials and Methods
2.1. MD Simulation for Solubility Parameter Calculation
2.2. Mesoscale Simulation
3. Results and Discussion
3.1. Sulfonated Polymer Models and Their Solubility Parameters
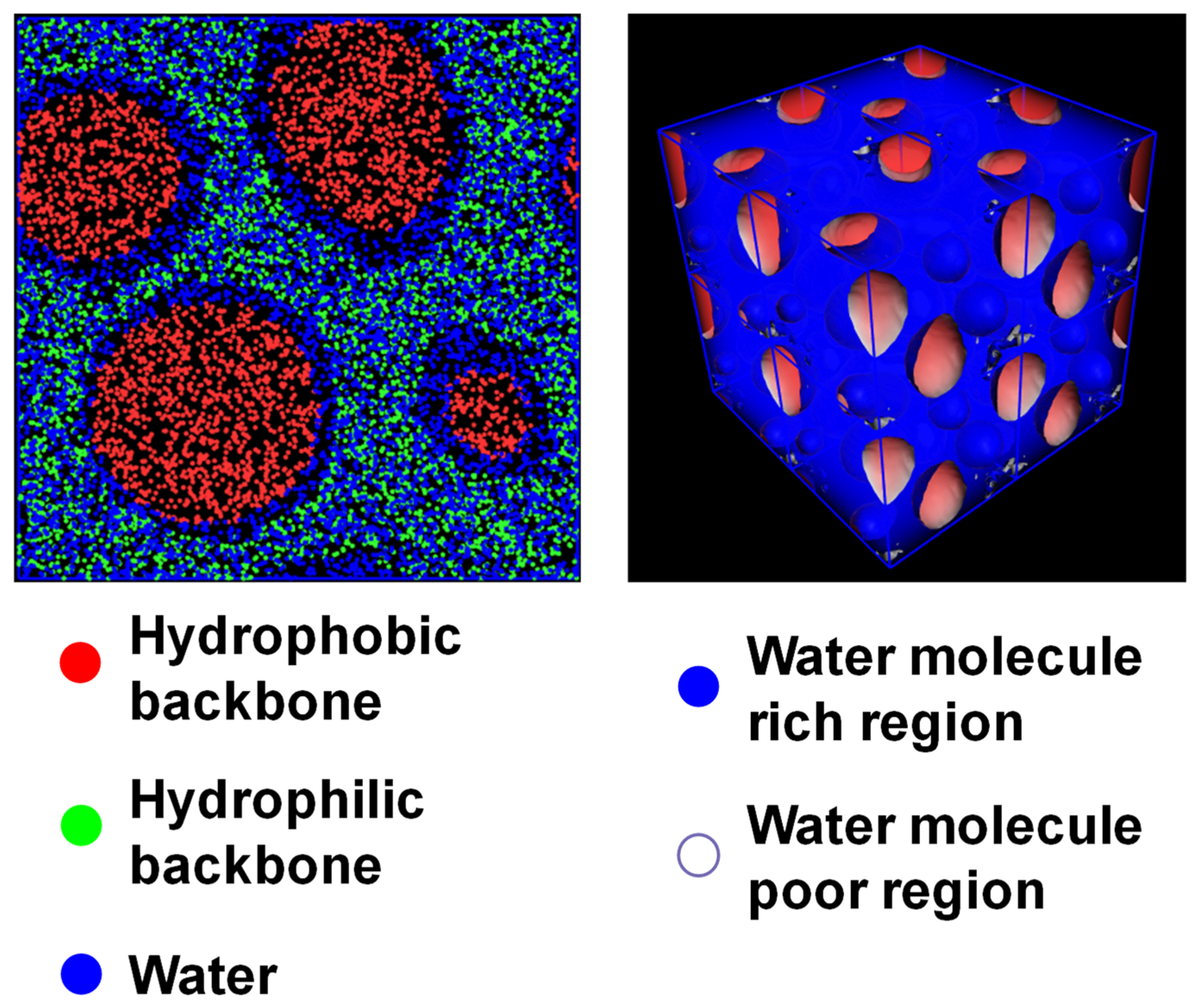
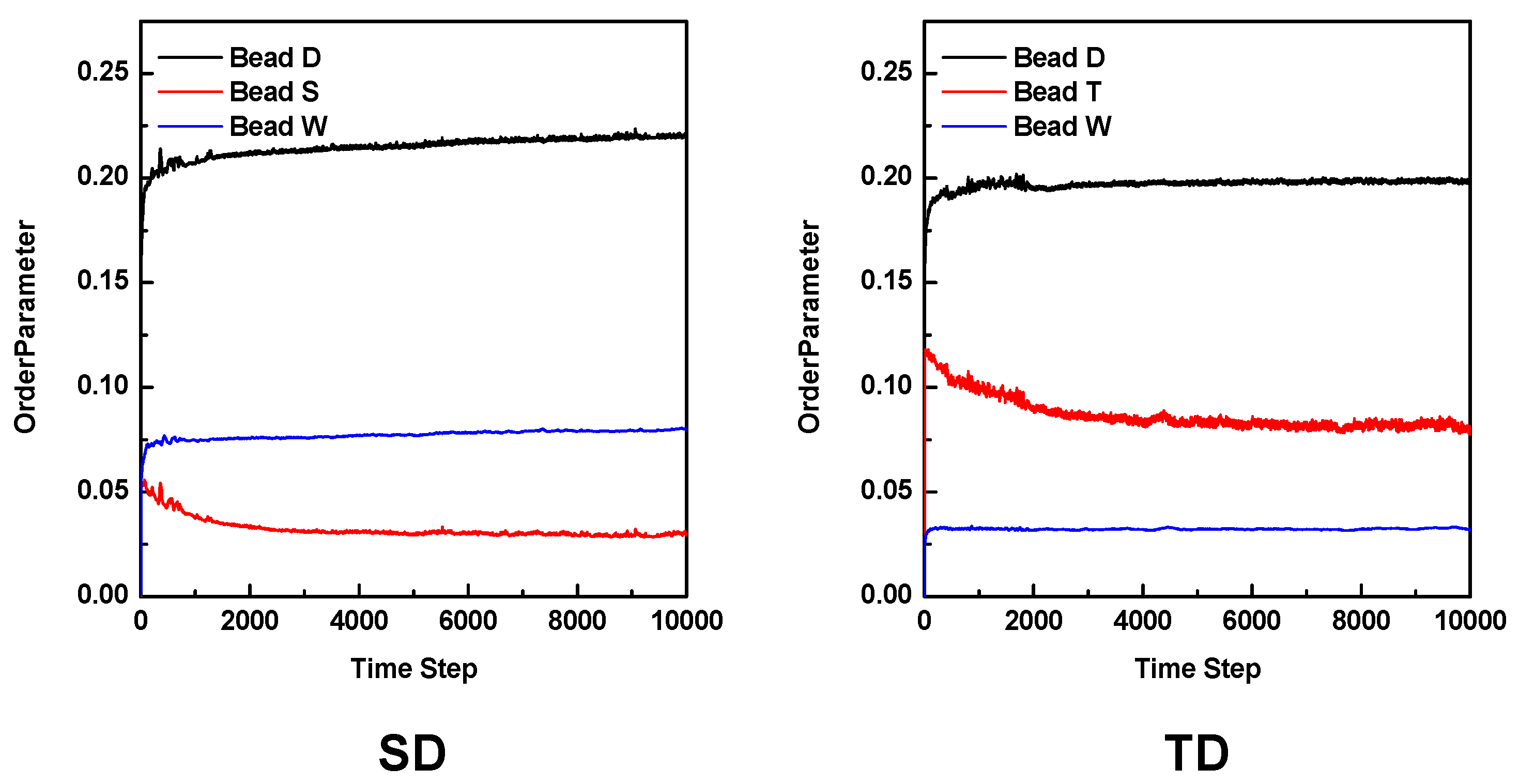
3.2. Mesoscale Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ruzette, A.V.; Leibler, L. Block copolymers in tomorrow’s plastics. Nat. Mater. 2005, 4, 19–31. [Google Scholar] [CrossRef]
- Ryan, A.J. Polymer scince: Designer polymer blends. Nat. Mater. 2002, 1, 8–10. [Google Scholar] [CrossRef]
- Bae, B.; Yoda, T.; Miyatake, K.; Uchida, H.; Watanabe, M. Proton-conductive aromatic ionomers containing highly sulfonated blocks for high-temperature-operable fuel cells. Angew. Chem. Int. Ed. 2010, 49, 317–320. [Google Scholar] [CrossRef]
- Asano, N.; Miyatake, K.; Watanabe, M. Sulfonated block polyimide copolymers as a proton-conductive membrane. J. Polym. Sci. Part A Polym. Chem. 2006, 44, 2744–2748. [Google Scholar] [CrossRef]
- Takamuku, S.; Takimoto, N.; Abe, M.; Shinohara, K. Investigation of through-plane morphologies of multiblock copolymers based on poly(arylene ether sulfone)s. J. Power Sources 2010, 195, 1095–1098. [Google Scholar] [CrossRef]
- Lee, H.-S.; Roy, A.; Lane, O.; Dunn, S.; McGrath, J.E. Hydrophilic-hydrophobic multiblock copolymers based on poly(arylene ether sulfone) via low-temperature coupling reactions for proton exchange membrane fuel cells. Polymer 2008, 49, 715–723. [Google Scholar] [CrossRef]
- Meier-Haack, J.; Taeger, A.; Vogel, C.; Schlenstedt, K.; Lenk, W.; Lehmann, D. Membranes from sulfonated block copolymers for use in fuel cells. Sep. Purif. Technol. 2005, 41, 207–220. [Google Scholar] [CrossRef]
- Kreuer, K.D. Proton conductivity: Materials and applications. Chem. Mater. 1996, 8, 610–641. [Google Scholar] [CrossRef]
- Kreuer, K.-D.; Paddison, S.J.; Spohr, E.; Schuster, M. Transport in proton conductors for fuel-cell applications: Simulations, elementary reactions, and phenomenology. Chem. Rev. 2004, 104, 4637–4678. [Google Scholar] [CrossRef]
- Park, C.H.; Lee, C.H.; Guiver, M.D.; Lee, Y.M. Sulfonated hydrocarbon membranes for medium-temperature and low-humidity proton exchange membrane fuel cells (pemfcs). Prog. Polym. Sci. 2011, 36, 1443–1498. [Google Scholar] [CrossRef]
- Shin, D.W.; Guiver, M.D.; Lee, Y.M. Hydrocarbon-based polymer electrolyte membranes: Importance of morphology on ion transport and membrane stability. Chem. Rev. 2017, 117, 4759–4805. [Google Scholar] [CrossRef] [PubMed]
- Park, C.H.; Lee, C.H.; Sohn, J.-Y.; Park, H.B.; Guiver, M.D.; Lee, Y.M. Phase separation and water channel formation in sulfonated block copolyimide. J. Phys. Chem. B 2010, 114, 12036–12045. [Google Scholar] [CrossRef] [PubMed]
- Peckham, T.J.; Schmeisser, J.; Rodgers, M.; Holdcroft, S. Main-chain, statistically sulfonated proton exchange membranes: The relationships of acid concentration and proton mobility to water content and their effect upon proton conductivity. J. Mater. Chem. 2007, 17, 3255–3268. [Google Scholar] [CrossRef]
- Park, C.H.; Nam, S.Y. Mesoscale simulation of polymeric membranes for energy and environmental application. Membr. J. 2017, 27, 121–128. [Google Scholar] [CrossRef]
- Park, C.H.; Nam, S.Y.; Hong, Y.T. Molecular dynamics (md) study of proton exchange membranes for fuel cells. Membr. J. 2016, 26, 329–336. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Y.; Li, W.; Wang, S.; Liu, X.; Xie, X.; Chen, J.; Li, Q.; Jensen, J.O. Molecular dynamics simulation of radiation grafted fep films as proton exchange membranes: Effects of the side chain length. Int. J. Hydrogen Energy 2017, 42, 29977–29987. [Google Scholar] [CrossRef]
- Sengupta, S.; Pant, R.; Komarov, P.; Venkatnathan, A.; Lyulin, A.V. Atomistic simulation study of the hydrated structure and transport dynamics of a novel multi acid side chain polyelectrolyte membrane. Int. J. Hydrogen Energy 2017, 42, 27254–27268. [Google Scholar] [CrossRef]
- Tai, C.C.; Chen, C.L.; Liu, C.W. Computer simulation to investigate proton transport and conductivity in perfluorosulfonate ionomeric membrane. Int. J. Hydrogen Energy 2017, 42, 3981–3986. [Google Scholar] [CrossRef]
- Park, C.H.; Lee, S.Y.; Lee, C.H. Investigation of water channel formation in sulfonated polyimides via mesoscale simulation. Membr. J. 2017, 27, 389–398. [Google Scholar] [CrossRef]
- Van Vlimmeren, B.A.C.; Maurits, N.M.; Zvelindovsky, A.V.; Sevink, G.J.A.; Fraaije, J.G.E.M. Simulation of 3D mesoscale structure formation in concentrated aqueous solution of the triblock polymer surfactants (ethylene oxide)13(propylene oxide)30(ethylene oxide)13 and (propylene oxide)19(ethylene oxide)33(propylene oxide)19. Application of dynamic mean-field density functional theory. Macromolecules 1999, 32, 646–656. [Google Scholar] [CrossRef]
- Guo, S.L.; Hou, T.J.; Xu, X.J. Simulation of the phase behavior of the (EO)13(PO)30(EO)13(Pluronic L64)/water/p-xylene system using mesodyn. J. Phys. Chem. B 2002, 106, 11397–11403. [Google Scholar] [CrossRef]
- Knoll, A.; Lyakhova, K.S.; Horvat, A.; Krausch, G.; Sevink, G.J.A.; Zvelindovsky, A.V.; Magerle, R. Direct imaging and mesoscale modelling of phse transitions in a nanostructured fluid. Nat. Mater. 2004, 3, 886–891. [Google Scholar] [CrossRef]
- Wescott, J.T.; Qi, Y.; Subramanian, L.; Capehart, T.W. Mesoscale simulation of morphology in hydrated perfluorosulfonic acid membranes. J. Chem. Phys. 2006, 124, 134702. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yuan, S.; Wu, J. Mesoscopic simulation on phase behavior of ternary copolymeric solution in the absence and presence of shear. Macromolecules 2006, 39, 6631–6642. [Google Scholar] [CrossRef]
- Park, C.H.; Kim, D.J.; Nam, S.Y. Molecular dynamics (MD) study of polymeric membranes for gas separation. Membr. J. 2014, 24, 341–349. [Google Scholar] [CrossRef]
- Jung, C.-Y.; Park, C.-H.; Lee, Y.-M.; Kim, W.-J.; Yi, S.-C. Numerical analysis of catalyst agglomerates and liquid water transport in proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2010, 35, 8433–8445. [Google Scholar] [CrossRef]
- Shimpalee, S.; Ohashi, M.; Van Zee, J.W.; Ziegler, C.; Stoeckmann, C.; Sadeler, C.; Hebling, C. Experimental and numerical studies of portable pemfc stack. Electrochim. Acta 2009, 54, 2899–2911. [Google Scholar] [CrossRef]
- Hildebrand, J.; Prausnitz, J.M.; Scott, R.L. Regular and Related Solutions: The Solubility of Gases, Liquids, and Solids; Van Nostrand Reinhold Co.: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Jung, M.; Kim, T.-H.; Yoon, Y.J.; Kang, C.G.; Yu, D.M.; Lee, J.Y.; Kim, H.-J.; Hong, Y.T. Sulfonated poly(arylene sulfone) multiblock copolymers for proton exchange membrane fuel cells. J. Membr. Sci. 2014, 459, 72–85. [Google Scholar] [CrossRef]
- Hildebrand, J.; Scott, R.L. The Solubility of Nonelectrolytes, 3rd ed.; Reinhold: New York, NY, USA, 1950. [Google Scholar]
- Hildebrand, J.; Scott, R.L. Regular Solutions; Prentice-Hall: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Lee, K.; Lim, H.J.; Yang, S.J.; Kim, Y.S.; Park, C.R. Determination of solubility parameters of single-walled and double-walled carbon nanotubes using a finite-length model. RSC Adv. 2013, 3, 4814–4820. [Google Scholar] [CrossRef]
- Maiti, A.; Wescott, J.; Kung, P. Nanotube–polymer composites: Insights from flory–huggins theory and mesoscale simulations. Mol. Simul. 2005, 31, 143–149. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Van Krevelen, D.W.; Te Nijenhuis, K. Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applicationsoverview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Yang, J.; Ren, Y.; Tian, A.; Sun, H. COMPASS force field for 14 inorganic molecules, He, Ne, Ar, Kr, Xe, H2, O2, N2, NO, CO, CO2, NO2, CS2, and SO2, in liquid phases. J. Phys. Chem. B 2000, 104, 4951–4957. [Google Scholar] [CrossRef]
- Material Studio Online Help; Accelrys Software Inc.: San Diego, CA, USA, 2008.
- Lee, J.H.; Park, C.H. Effect of force-field types on the proton diffusivity calculation in molecular dynamics (MD) simulation. Membr. J. 2017, 27, 358–366. [Google Scholar] [CrossRef]
- Tang, Y.-H.; He, Y.-D.; Wang, X.-L. Three-dimensional analysis of membrane formation via thermally induced phase separation by dissipative particle dynamics simulation. J. Membr. Sci. 2013, 437, 40–48. [Google Scholar] [CrossRef]
- Jorn, R.; Voth, G.A. Mesoscale simulation of proton transport in proton exchange membranes. J. Phys. Chem. C 2012, 116, 10476–10489. [Google Scholar] [CrossRef]
- Park, C.H.; Tocci, E.; Fontananova, E.; Bahattab, M.A.; Aljlil, S.A.; Drioli, E. Mixed matrix membranes containing functionalized multiwalled carbon nanotubes: Mesoscale simulation and experimental approach for optimizing dispersion. J. Membr. Sci. 2016, 514, 195–209. [Google Scholar] [CrossRef]
- Zhang, Z.; Sass, J.; Krajniak, J.; Ganesan, V. Ion correlations and partial ionicities in the lamellar phases of block copolymeric ionic liquids. ACS Macro Lett. 2022, 11, 1265–1271. [Google Scholar] [CrossRef]
- Zhang, Z.; Krajniak, J.; Ganesan, V. A multiscale simulation study of influence of morphology on ion transport in block copolymeric ionic liquids. Macromolecules 2021, 54, 4997–5010. [Google Scholar] [CrossRef]
- Zhang, Z.; Krajniak, J.; Keith, J.R.; Ganesan, V. Mechanisms of ion transport in block copolymeric polymerized ionic liquids. ACS Macro Lett. 2019, 8, 1096–1101. [Google Scholar] [CrossRef]
- Krajniak, J.; Zhang, Z.; Pandiyan, S.; Nies, E.; Samaey, G. Coarse-grained molecular dynamics simulations of polymerization with forward and backward reactions. J. Comput. Chem. 2018, 39, 1764–1778. [Google Scholar] [CrossRef]
- Zhang, Z.; Krajniak, J.; Samaey, G.; Nies, E. A parallel multiscale simulation framework for complex polymerization: Ab2-type monomer hyperbranched polymerization as an example. Adv. Theory Simul. 2019, 2, 1800102. [Google Scholar] [CrossRef]
- Mauritz, K.A.; Moore, R.B. State of understanding of nafion. Chem. Rev. 2004, 104, 4535–4585. [Google Scholar] [CrossRef] [PubMed]



| PEM Samples (hydrophilic Mn/hydrophobic Mn) | IECtheoretical (meq/g) | Water Uptake (%) | Topology of PEM Model |
|---|---|---|---|
| TD (12 K/5 K) | 1.88 | 35.18 | T 17 D 12 |
| SD (10 K/8 K) | 2.47 | 77.52 | S 12 D 19 |
| PEM Model | Bead Name | Predicted by Synthia | Calculated by MD | Molecular Weight (g/mol) | Topology of PEM Model | ||
|---|---|---|---|---|---|---|---|
| Vbead-mol (cm3/mol) | δ (MPa1/2) | Vbead-mol (cm3/mol) | δ (MPa1/2) | ||||
| TD | T | 436.9 | 28.42 | 450.9 | 26.66 | 873 | T 17 D 12 |
| D | 318.9 | 22.69 | 327.2 | 19.62 | 419 | ||
| SD | S | 238.9 | 27.84 | 244.1 | 26.69 | 410 | S 12 D 19 |
| D | 318.9 | 22.69 | 327.2 | 19.62 | 419 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, H.; Cheon, M.; Lee, C.H.; Kim, T.-H.; Hong, Y.T.; Nam, S.Y.; Park, C.H. Mesoscale Simulation Based on the Dynamic Mean-Field Density Functional Method on Block-Copolymeric Ionomers for Polymer Electrolyte Membranes. Membranes 2023, 13, 258. https://doi.org/10.3390/membranes13030258
Kang H, Cheon M, Lee CH, Kim T-H, Hong YT, Nam SY, Park CH. Mesoscale Simulation Based on the Dynamic Mean-Field Density Functional Method on Block-Copolymeric Ionomers for Polymer Electrolyte Membranes. Membranes. 2023; 13(3):258. https://doi.org/10.3390/membranes13030258
Chicago/Turabian StyleKang, Hoseong, Muyeong Cheon, Chang Hyun Lee, Tae-Ho Kim, Young Taik Hong, Sang Yong Nam, and Chi Hoon Park. 2023. "Mesoscale Simulation Based on the Dynamic Mean-Field Density Functional Method on Block-Copolymeric Ionomers for Polymer Electrolyte Membranes" Membranes 13, no. 3: 258. https://doi.org/10.3390/membranes13030258
APA StyleKang, H., Cheon, M., Lee, C. H., Kim, T.-H., Hong, Y. T., Nam, S. Y., & Park, C. H. (2023). Mesoscale Simulation Based on the Dynamic Mean-Field Density Functional Method on Block-Copolymeric Ionomers for Polymer Electrolyte Membranes. Membranes, 13(3), 258. https://doi.org/10.3390/membranes13030258