An Isotonic Model of Neuron Swelling Based on Co-Transport of Salt and Water
Abstract
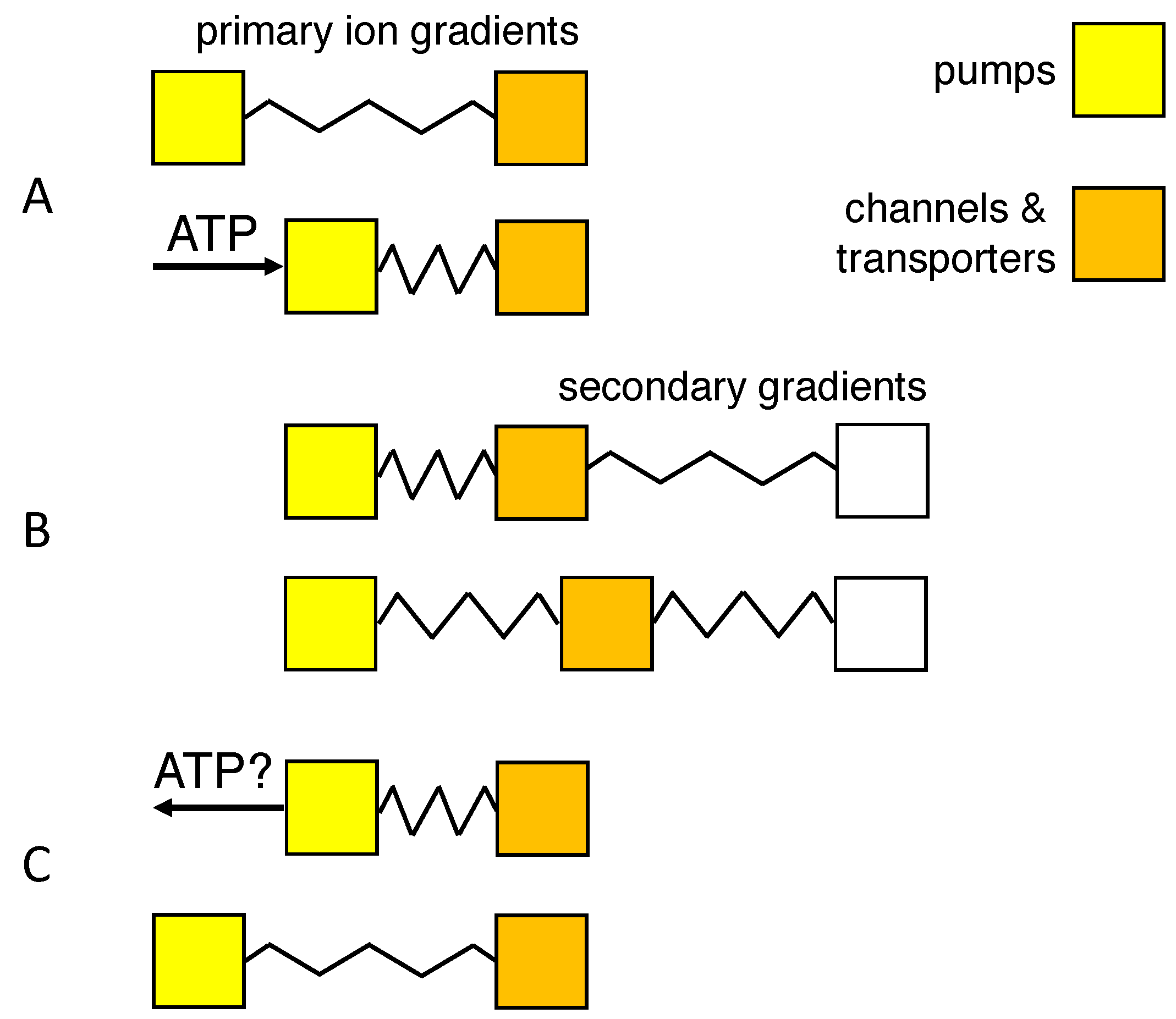
1. Introduction
| Ion Species | Physiological ( = 0.25) a | Full Equilibrium () | Transport | |
|---|---|---|---|---|
| Outside (mM) | Inside (mM) | Outside = Inside (mM) | Outside → Inside (mM) | |
| 148 | 12 | 46 | 159.0 | |
| 4 | 140 | 106 | −7.0 | |
| 113 | 8 | 34.25 | 121.5 | |
| 29 | 10 | 14.75 | 30.5 | |
| b | 10 c | 134 | 103 | 0 |
| Total | 304 | 304 | 304 | 304 |
2. Materials and Methods
3. Results
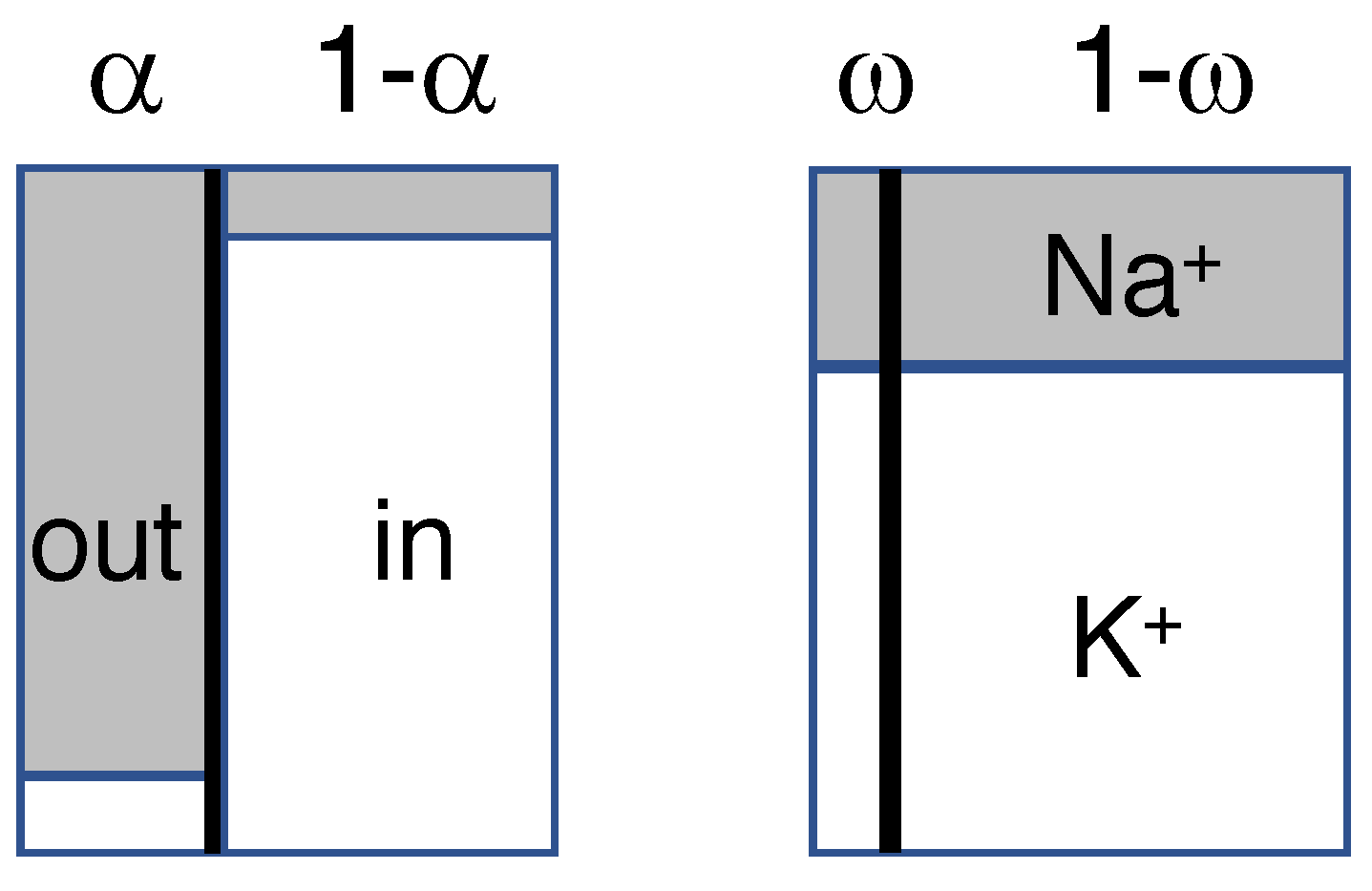
3.1. Construction of the Isotonic Path
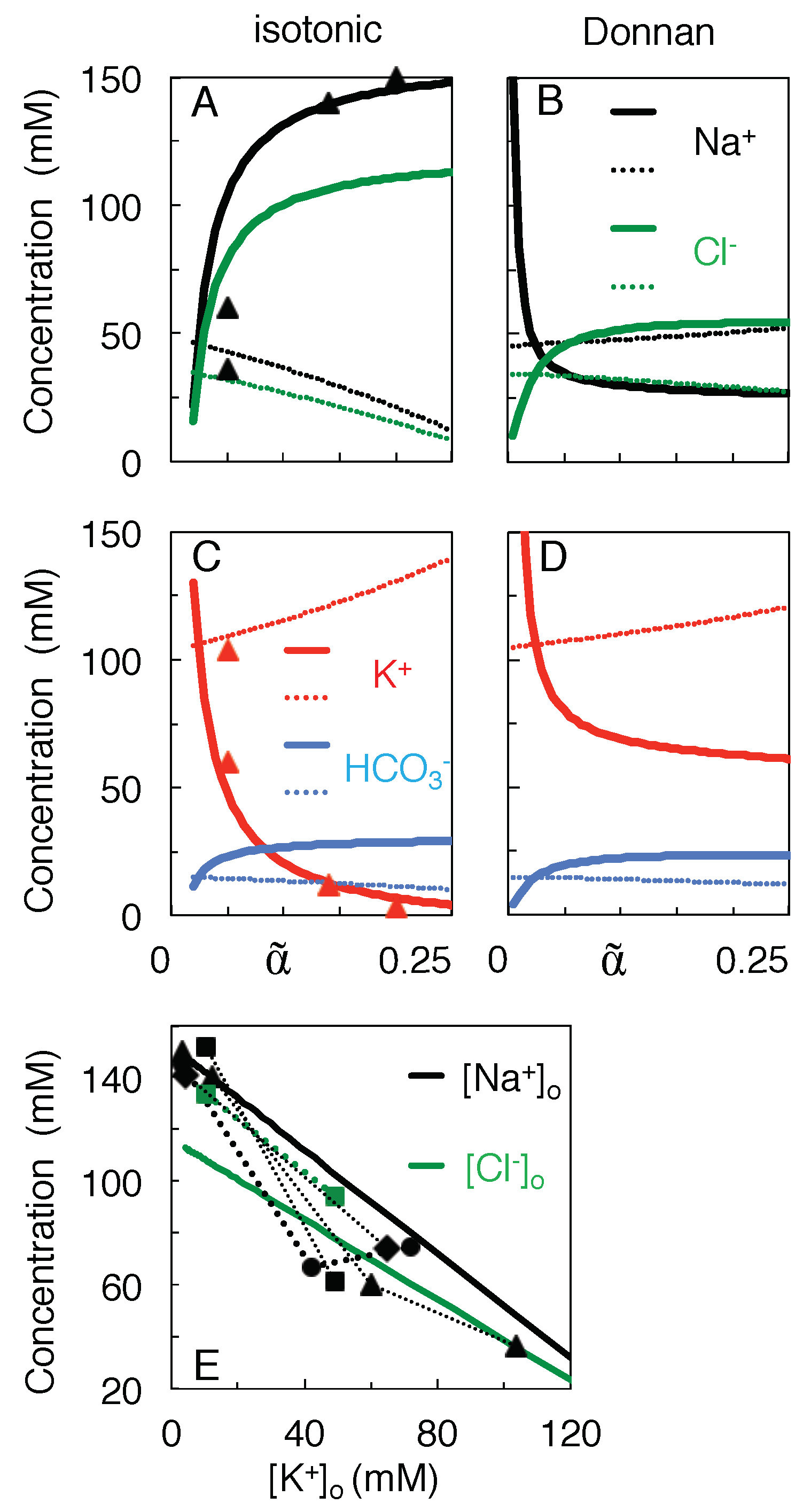
3.2. Qualitative Comparison of the Isotonic Path and the Donnan Equilibria
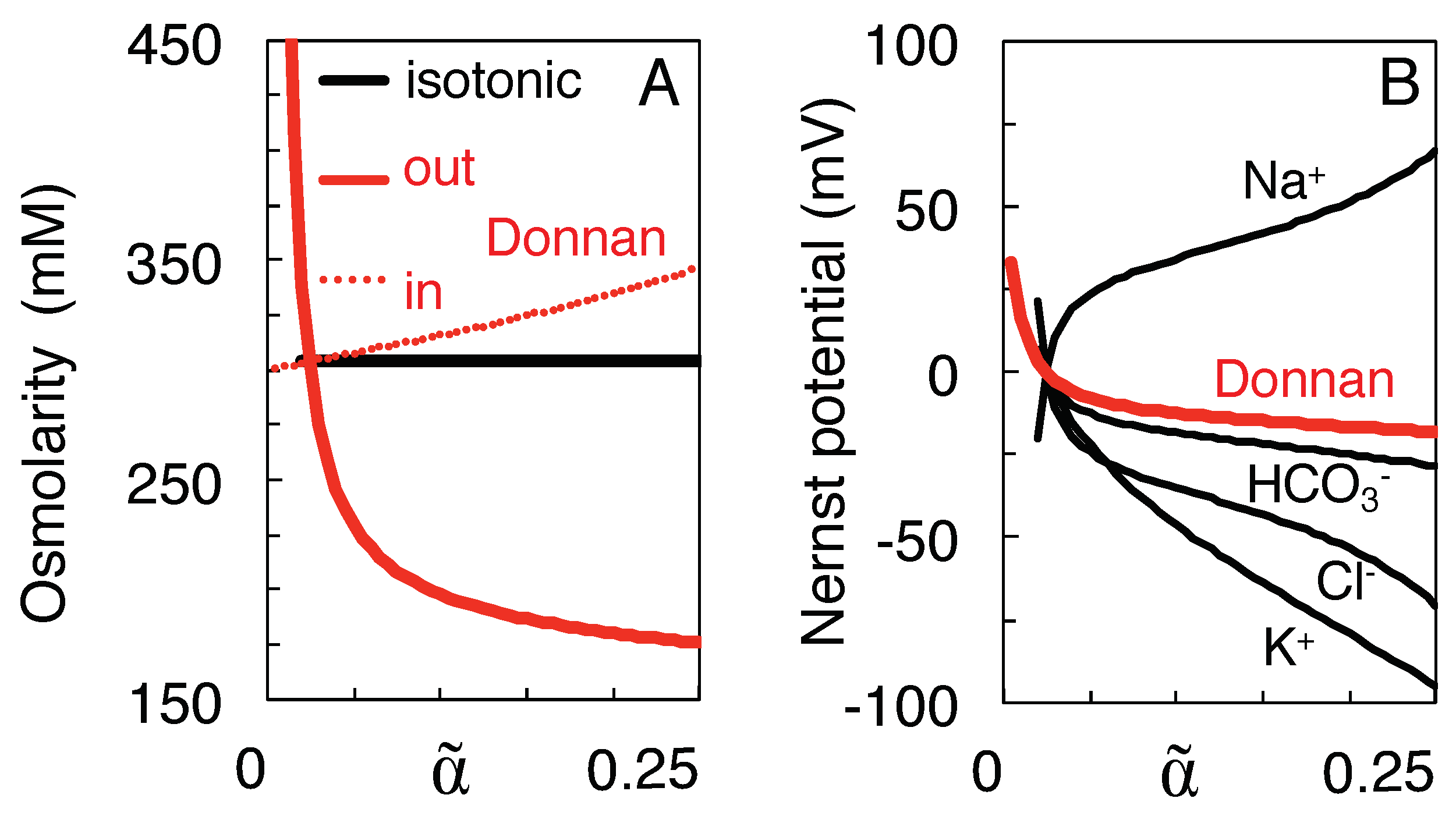
3.3. Variation of Ion Concentration with Extracellular Volume
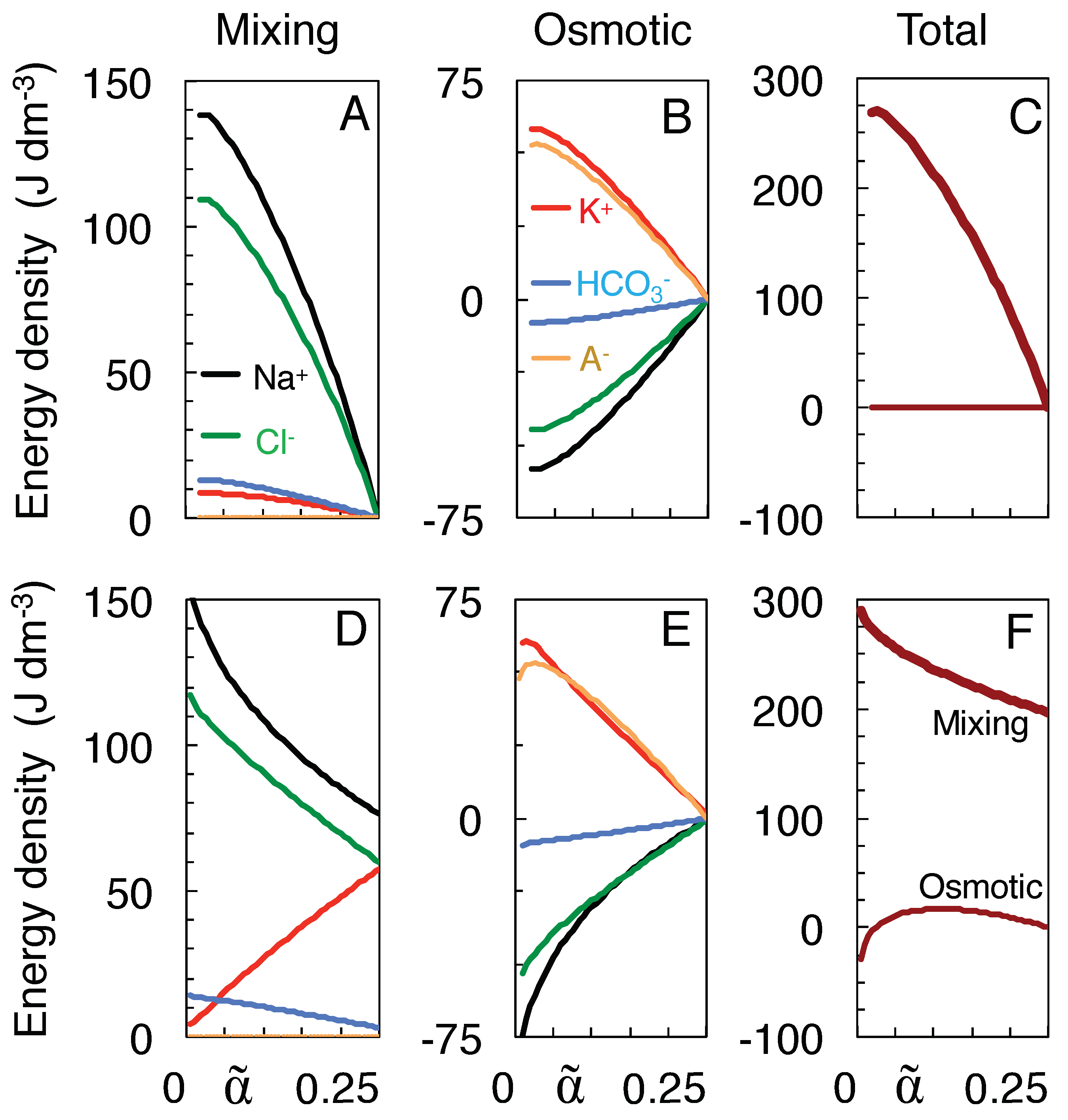
3.4. Work of Mixing versus Osmotic Work
4. Discussion
- (1)
- An isotonic path was chosen to conform to the observation that neurons lack aquaporins that can transduce osmotic forces [11,12,36], and isotonicity was preserved by the flow of water through co-transporters. Another, indistinguishable way of implementing isotonic swelling would be to have water permeate the lipid-bilayer membrane in response to each infinitesimal change in tonicity, using a model of coupled transport of water and solute [49,50].
- (2)
- The choice for the KCC2 co-transporter was motivated by its expression in neurons [30], and the repeated observation that swelling, or water transport, is strongly reduced or delayed in the absence of extracellular Cl ions [5,11,28,49]. Nevertheless, blockade of the KCC2 co-transporter reduced dendritic beading by only 36% in pyramidal cells [11], and Cl ions have also been observed to enter neurons through voltage- and ligand-gated channels [5].
- (3)
- Mixing was assumed to follow a path to the full equilibration of all ion species (Table 1), without requiring, however, that neurons travel the entire trajectory to equilibrium, a state they probably never reach in their lifetime.This state of full equilibrium is also the state of least energy (at constant entropy) or maximum entropy (at constant energy) [6], and thus being the state to which the system must evolve in the absence of energy supply, it allows components of the system to be ignored which can influence the speed of evolution but not its final state (such as the membrane potential, see below).Of course, other isotonic paths can be constructed, but they reduce the work of mixing. For instance, incrementing and decrementing and by 20 mM, respectively, to values of 179.0 and −27.0 mM, would preserve isotonicity and electro-neutrality but reduce the work of mixing from 269.8 to 263.2 J/l. Furthermore, the increased Na transport would deplete the extracellular Na store before the impermeant anions can equilibrate (more precisely, after shrinkage of extracellular space to a volume fraction of 0.05 as compared to 0.024 for mixing to full equilibrium).
- (4)
- Reversibility of the path requires that the direction of transport through the KCC2 co-transporter can be reversed [10,33,37]. Payne [33] reports that the driving force for K-Cl co-transport at physiological concentrations is close to thermodynamic equilibrium, the transport reversing from efflux to influx when ]o exceeds 5 mM. Backward operation of the Na/K pump, on the other hand, has been described experimentally only under extreme ionic and ATP potentials [52,53,54]. Although it would provide a clear example of how ions might do work for the cell’s survival, recent experimental support for pump reversal is lacking, and the rate of the reverse reaction and the pump capacity may be too low for it to be of relevance in acute ischemic brain injury.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Superscripts | ||
| * | initial condition | |
| ∘ | final condition | |
| Subscripts | ||
| e | equilibrium | |
| i | inner (intracellular) | |
| o | outer (extracellular) | |
| Constants | ||
| physiological volume fraction taken by extracellular space | 0.25 | |
| R | universal gas constant | 8.3145 J mol K |
| T | absolute temperature | 310 K |
| C | integration constant (Equation (9a)) | |
| D | integration constant (Equation (9b)) | |
| Variables | ||
| fractional volume of extracellular space | ||
| fractional volume of extracellular space at equilibrium | ||
| ratio of solvent to solute transport or (mM) | ||
| concentration of membrane transport of ion species K (mM) | ||
| K | (compartmental concentration of) ion species K (mM) | |
| V | (compartmental) volume (m) | |
| w | relative shrinkage of extracellular space (ratio of to ) | |
| y | relative expansion of intracellular space |
Appendix A. Proof of Isotonicity and Electro-Neutrality of the Path of Neuron Swelling
References
- Ereciñska, M.; Silver, I.A. ATP and brain function. J. Cereb. Blood Flow Metab. 1989, 9, 2–19. [Google Scholar] [CrossRef] [PubMed]
- Skou, J.C. The influence of some cations on an adenosine triphosphatase from peripheral nerves. Biochim. Biophys. Acta 1957, 23, 394–401. [Google Scholar] [CrossRef] [PubMed]
- De Weer, P.; Gadsby, D.C.; Rakowski, R.F. Voltage dependence of the Na-K pump. Annu. Rev. Physiol. 1988, 50, 225–241. [Google Scholar] [CrossRef]
- Maex, R. Effect of extracellular volume on the energy stored in transmembrane concentration gradients. Phys. Rev. E 2021, 104, 044409. [Google Scholar] [CrossRef] [PubMed]
- Rungta, R.L.; Choi, H.B.; Tyson, J.R.; Malik, A.; Dissing-Olesen, L.; Lin, P.J.C.; Cain, S.M.; Cullis, P.R.; Snutch, T.P.; MacVicar, B.A. The cellular mechanisms of neuronal swelling underlying cytotoxic edema. Cell 2015, 161, 610–621. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Trans. Conn. Acad. Arts Sci. 1875, 3, 108–248. [Google Scholar] [CrossRef]
- Attwell, D.; Laughlin, S.B. An energy budget for signaling in the grey matter of the brain. J. Cereb. Blood Flow Metab. 2001, 21, 1133–1145. [Google Scholar] [CrossRef]
- Dietzel, I.; Heinemann, U. Dynamic variations of the brain cell microenvironment in relation to neuronal hyperactivity. Ann. N. Y. Acad. Sci. 1986, 481, 72–86. [Google Scholar] [CrossRef]
- Mori, K.; Miyazaki, M.; Iwase, H.; Maeda, M. Temporal profile of changes in brain tissue extracellular space and extracellular ion (Na+, K+) concentrations after cerebral ischemia and the effects of mild cerebral hypothermia. J. Neurotrauma 2002, 19, 1261–1270. [Google Scholar] [CrossRef]
- Larsen, B.R.; MacAulay, N. Activity-dependent astrocyte swelling is mediated by pH-regulating mechanisms. Glia 2017, 65, 1668–1681. [Google Scholar] [CrossRef]
- Steffensen, A.B.; Sword, J.; Croom, D.; Kirov, S.A.; MacAulay, N. Chloride cotransporters as a molecular mechanism underlying spreading depolarization-induced dendritic beading. J. Neurosci. 2015, 35, 12172–12187. [Google Scholar] [CrossRef] [PubMed]
- Andrew, R.D.; Labron, M.W.; Boehnke, S.E.; Carnduff, L.; Kirov, S.A. Physiological evidence that pyramidal neurons lack functional water channels. Cereb. Cortex 2007, 17, 787–802. [Google Scholar] [CrossRef] [PubMed]
- Voříšek, I.; Syková, E. Ischemia-induced changes in the extracellular space diffusion parameters, K+, and pH in the developing rat cortex and corpus callosum. J. Cereb. Blood Flow Metab. 1997, 17, 191–203. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, R.; O’Donnell, J.; Ding, F.; Nedergaard, M. Interstitial ions: A key regulator of state-dependent neural activity? Prog. Neurobiol. 2020, 193, 101802. [Google Scholar] [CrossRef]
- Ayata, C.; Lauritzen, M. Spreading depression, spreading depolarizations, and the cerebral vasculature. Physiol. Rev. 2015, 95, 953–993. [Google Scholar] [CrossRef]
- Lemale, C.L.; Lückl, J.; Horst, V.; Reiffurth, C.; Major, S.; Hecht, N.; Woitzik, J.; Dreier, J.P. Migraine aura, transient ischemic attacks, stroke, and dying of the brain share the same key pathophysiological process in neurons driven by Gibbs-Donnan forces, namely spreading depolarization. Front. Cell. Neurosci. 2022, 16, 837650. [Google Scholar] [CrossRef]
- Murphy, T.R.; Davila, D.; Cuvelier, N.; Young, L.R.; Lauderdale, K.; Binder, D.K.; Fiacco, T.A. Hippocampal and cortical pyramidal neurons swell in parallel with astrocytes during acute hypoosmolar stress. Front. Cell. Neurosci. 2017, 11, 275. [Google Scholar] [CrossRef]
- Xie, L.; Kang, H.; Xu, Q.; Chen, M.J.; Liao, Y.; Thiyagarajan, M.; O’Donnell, J.; Christensen, D.J.; Nicholson, C.; Iliff, J.J.; et al. Sleep drives metabolite clearance from the adult brain. Science 2013, 342, 373–377. [Google Scholar] [CrossRef]
- Armstrong, C.M. Packaging life: The origin of ion-selective channels. Biophys. J. 2015, 109, 173–177. [Google Scholar] [CrossRef]
- Delpire, E.; Staley, K.J. Novel determinants of the neuronal Cl− concentration. J. Physiol. 2014, 592, 4099–4114. [Google Scholar] [CrossRef]
- Park, J.O.; Rubin, S.A.; Xu, Y.F.; Amador-Noguez, D.; Fan, J.; Shlomi, T.; Rabinowitz, J.D. Metabolite concentrations, fluxes and free energies imply efficient enzyme usage. Nat. Chem. Biol. 2016, 12, 482–489. [Google Scholar] [CrossRef] [PubMed]
- Westheimer, F.H. Why nature chose phosphates. Science 1987, 235, 1173–1178. [Google Scholar] [CrossRef] [PubMed]
- Donnan, F.G. Theorie der Membrangleichgewichte und Membranpotentiale bei Vorhandensein von nicht dialysierenden Elektrolyten. Z. Elektrochem. 1911, 17, 572–581. [Google Scholar]
- Benedek, G.B.; Villars, F.M.H. Physics with Illustrative Examples from Medicine and Biology, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- MacAulay, N. Molecular mechanisms of brain water transport. Nat. Rev. Neurosci. 2021, 22, 326–344. [Google Scholar] [CrossRef]
- Kimelberg, H.K. Water homeostasis in the brain: Basic concepts. Neuroscience 2004, 129, 851–860. [Google Scholar] [CrossRef]
- Zhang, R.B.; Verkman, A.S. Water and urea permeability properties of Xenopus oocytes: Expression of mRNA from toad urinary bladder. Am. J. Physiol. 1991, 260, 26–34. [Google Scholar] [CrossRef]
- Zeuthen, T. Cotransport of K+, Cl− and H2O by membrane proteins from choroid plexus epithelium of Necturus maculosus. J. Physiol. 1994, 478 Pt 2, 203–219. [Google Scholar] [CrossRef]
- MacAulay, N.; Hamann, S.; Zeuthen, T. Water transport in the brain: Role of cotransporters. Neuroscience 2004, 129, 1031–1044. [Google Scholar] [CrossRef]
- Williams, J.R.; Sharp, J.W.; Kumari, V.G.; Wilson, M.; Payne, J.A. The neuron-specific K-Cl cotransporter, KCC2. Antibody development and initial characterization of the protein. J. Biol. Chem. 1999, 274, 12656–12664. [Google Scholar] [CrossRef]
- Delpire, E.; Mount, D.B. Human and murine phenotypes associated with defects in cation-chloride cotransport. Annu. Rev. Physiol. 2002, 64, 803–843. [Google Scholar] [CrossRef]
- Zeuthen, T.; Stein, W.D. Cotransport of salt and water in membrane proteins: Membrane proteins as osmotic engines. J. Membr. Biol. 1994, 137, 179–195. [Google Scholar] [CrossRef] [PubMed]
- Payne, J.A. Functional characterization of the neuronal-specific K-Cl cotransporter: Implications for [K+]o regulation. Am. J. Physiol. 1997, 273, C1516–C1525. [Google Scholar] [CrossRef] [PubMed]
- Simard, J.M.; Kent, T.A.; Chen, M.; Tarasov, K.V.; Gerzanich, V. Brain oedema in focal ischaemia: Molecular pathophysiology and theoretical implications. Lancet Neurol. 2007, 6, 258–268. [Google Scholar] [CrossRef] [PubMed]
- Du, T.; Mestre, H.; Kress, B.T.; Liu, G.; Sweeney, A.M.; Samson, A.J.; Rasmussen, M.K.; Mortensen, K.N.; Bork, P.A.R.; Peng, W.; et al. Cerebrospinal fluid is a significant fluid source for anoxic cerebral oedema. Brain 2022, 145, 787–797. [Google Scholar] [CrossRef]
- Hellas, J.A.; Andrew, R.D. Neuronal Swelling: A Non-osmotic Consequence of Spreading Depolarization. Neurocrit. Care 2021, 35, 112–134. [Google Scholar] [CrossRef]
- Jarolimek, W.; Lewen, A.; Misgeld, U. A furosemide-sensitive K+-Cl− cotransporter counteracts intracellular Cl− accumulation and depletion in cultured rat midbrain neurons. J. Neurosci. 1999, 19, 4695–4704. [Google Scholar] [CrossRef]
- Dijkstra, K.; Hofmeijer, J.; van Gils, S.A.; van Putten, M.J. A biophysical model for cytotoxic cell swelling. J. Neurosci. 2016, 36, 11881–11890. [Google Scholar] [CrossRef]
- El Hady, A.; Machta, B.B. Mechanical surface waves accompany action potential propagation. Nat. Commun. 2015, 6, 6697. [Google Scholar] [CrossRef]
- Sachs, F.; Sivaselvan, M.V. Cell volume control in three dimensions: Water movement without solute movement. J. Gen. Physiol. 2015, 145, 373–380. [Google Scholar] [CrossRef]
- Kraig, R.P.; Nicholson, C. Extracellular ionic variations during spreading depression. Neuroscience 1978, 3, 1045–1059. [Google Scholar] [CrossRef]
- Hansen, A.J.; Zeuthen, T. Extracellular ion concentrations during spreading depression and ischemia in the rat brain cortex. Acta Physiol. Scand. 1981, 113, 437–445. [Google Scholar] [CrossRef] [PubMed]
- Hansen, A.J. Effect of anoxia on ion distribution in the brain. Physiol. Rev. 1985, 65, 101–148. [Google Scholar] [CrossRef] [PubMed]
- Dreier, J.P.; Isele, T.; Reiffurth, C.; Offenhauser, N.; Kirov, S.A.; Dahlem, M.A.; Herreras, O. Is spreading depolarization characterized by an abrupt, massive release of Gibbs free energy from the human brain cortex? Neuroscientist 2013, 19, 25–42. [Google Scholar] [CrossRef] [PubMed]
- Windmüller, O.; Lindauer, U.; Foddis, M.; Einhäupl, K.M.; Dirnagl, U.; Heinemann, U.; Dreier, J.P. Ion changes in spreading ischaemia induce rat middle cerebral artery constriction in the absence of NO. Brain 2005, 128, 2042–2051. [Google Scholar] [CrossRef] [PubMed]
- Stiefel, M.F.; Marmarou, A. Cation dysfunction associated with cerebral ischemia followed by reperfusion: A comparison of microdialysis and ion-selective electrode methods. J. Neurosurg. 2002, 97, 97–103. [Google Scholar] [CrossRef]
- Dai, J.; Sheetz, M.P.; Wan, X.; Morris, C.E. Membrane tension in swelling and shrinking molluscan neurons. J. Neurosci. 1998, 18, 6681–6692. [Google Scholar] [CrossRef]
- Roffay, C.; Molinard, G.; Kim, K.; Urbanska, M.; Andrade, V.; Barbarasa, V.; Nowak, P.; Mercier, V.; García-Calvo, J.; Matile, S.; et al. Passive coupling of membrane tension and cell volume during active response of cells to osmosis. Proc. Natl. Acad. Sci. USA 2021, 118, e2103228118. [Google Scholar] [CrossRef]
- Tomita, M.; Gotoh, F. Cascade of cell swelling: Thermodynamic potential discharge of brain cells after membrane injury. Am. J. Physiol. 1992, 262, H603–H610. [Google Scholar] [CrossRef]
- Nagasawa, M.; Tasaka, M.; Tomita, M. Coupled transport of water and ions through membranes as a possible cause of cytotoxic edema. Neurosci. Lett. 1986, 66, 19–24. [Google Scholar] [CrossRef]
- Robertson, R.M.; Dawson-Scully, K.D.; Andrew, R.D. Neural shutdown under stress: An evolutionary perspective on spreading depolarization. J. Neurophysiol. 2020, 123, 885–895. [Google Scholar] [CrossRef]
- Garrahan, P.J.; Glynn, I.M. The incorporation of inorganic phosphate into adenosine triphosphate by reversal of the sodium pump. J. Physiol. 1967, 192, 237–256. [Google Scholar] [CrossRef] [PubMed]
- Chmouliovsky, M.; Straub, R.W. Increase in ATP by reversal of the Na-K-pump in mammalian non-myelinated nerve fibres. Pflügers Arch. 1974, 350, 309–320. [Google Scholar] [CrossRef] [PubMed]
- Lehninger, A.L. Biochemistry; Worth Publishers: New York, NY, USA, 1975. [Google Scholar]
- Kristián, T.; Siesjö, B.K. Calcium in ischemic cell death. Stroke 1998, 29, 705–718. [Google Scholar] [CrossRef] [PubMed]
- Hübel, N.; Ullah, G. Anions govern cell volume: A case study of relative astrocytic and neuronal swelling in spreading depolarization. PLoS ONE 2016, 11, e0147060. [Google Scholar] [CrossRef] [PubMed]
- Somjen, G.G.; Kager, H.; Wadman, W.J. Computer simulations of neuron-glia interactions mediated by ion flux. J. Comput. Neurosci. 2008, 25, 349–365. [Google Scholar] [CrossRef]
- Dmitriev, A.V.; Dmitriev, A.A.; Linsenmeier, R.A. The logic of ionic homeostasis: Cations are for voltage, but not for volume. PLoS Comput. Biol. 2019, 15, e1006894. [Google Scholar] [CrossRef]
- Dienel, G.A.; Rothman, D.L. Reevaluation of astrocyte-neuron energy metabolism with astrocyte volume fraction correction: Impact on cellular glucose oxidation rates, glutamate-glutamine cycle energetics, glycogen levels and utilization rates vs. exercising muscle, and Na+/K+ pumping rates. Neurochem. Res. 2020, 45, 2607–2630. [Google Scholar] [CrossRef]
- Masuda, T.; Dobson, G.P.; Veech, R.L. The Gibbs-Donnan near-equilibrium system of heart. J. Biol. Chem. 1990, 265, 20321–20334. [Google Scholar] [CrossRef]
- Zerangue, N.; Kavanaugh, M.P. Flux coupling in a neuronal glutamate transporter. Nature 1996, 383, 634–637. [Google Scholar] [CrossRef]
- Rossi, D.J.; Oshima, T.; Attwell, D. Glutamate release in severe brain ischaemia is mainly by reversed uptake. Nature 2000, 403, 316–321. [Google Scholar] [CrossRef]
- Chesler, M. Regulation and modulation of pH in the brain. Physiol. Rev. 2003, 83, 1183–1221. [Google Scholar] [CrossRef]
- Ruusuvuori, E.; Kaila, K. Carbonic anhydrases and brain pH in the control of neuronal excitability. Subcell. Biochem. 2014, 75, 271–290. [Google Scholar] [CrossRef] [PubMed]
- Alberty, R.A. Thermodynamics of the hydrolysis of adenosine triphosphate. J. Chem. Educ. 1969, 46, 713–719. [Google Scholar] [CrossRef]
- Mestre, H.; Du, T.; Sweeney, A.M.; Liu, G.; Samson, A.J.; Peng, W.; Mortensen, K.N.; Stæger, F.F.; Bork, P.A.R.; Bashford, L.; et al. Cerebrospinal fluid influx drives acute ischemic tissue swelling. Science 2020, 367, eaax7171. [Google Scholar] [CrossRef] [PubMed]
- Collewijn, H.; Schadé, J.P. Changes in the size of astrocytes and oligodendrocytes during anoxia, hypothermia and spreading depression. Prog. Brain Res. 1965, 15, 184–195. [Google Scholar]
| Ion Species | Outside (mM) | Inside (mM) |
|---|---|---|
| 26.6 | 52.5 | |
| 61.2 | 120.9 | |
| 54.4 | 27.5 | |
| 23.4 | 11.9 | |
| 10 | 134 | |
| Total | 175.6 | 346.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maex, R. An Isotonic Model of Neuron Swelling Based on Co-Transport of Salt and Water. Membranes 2023, 13, 206. https://doi.org/10.3390/membranes13020206
Maex R. An Isotonic Model of Neuron Swelling Based on Co-Transport of Salt and Water. Membranes. 2023; 13(2):206. https://doi.org/10.3390/membranes13020206
Chicago/Turabian StyleMaex, Reinoud. 2023. "An Isotonic Model of Neuron Swelling Based on Co-Transport of Salt and Water" Membranes 13, no. 2: 206. https://doi.org/10.3390/membranes13020206
APA StyleMaex, R. (2023). An Isotonic Model of Neuron Swelling Based on Co-Transport of Salt and Water. Membranes, 13(2), 206. https://doi.org/10.3390/membranes13020206






