Modeling and Validation of a LiOH Production Process by Bipolar Membrane Electrodialysis from Concentrated LiCl
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model Development
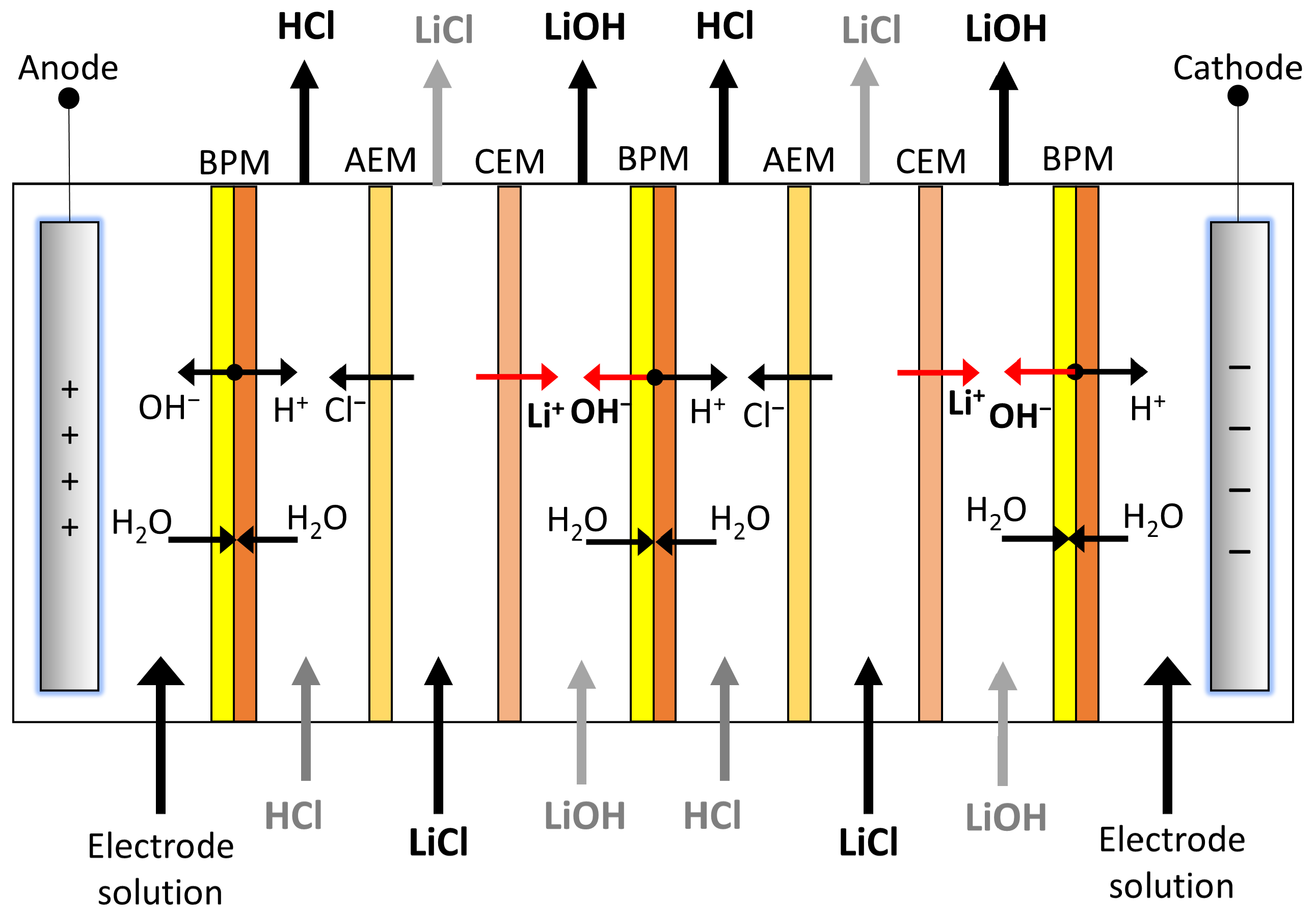
2.1.1. Lithium Transport across the Cation Exchange Membrane
- -
- Diffusion boundary layer effects are neglected.
- -
- Linear concentration profiles in the cation exchange membrane are considered.
- -
- Fixed charge density on membrane is determined by initial electrolyte concentrations and water content in membrane as input parameters.
- -
- Electric current through the cation exchange membrane is carried mainly by Li+ ions transport as a counterion and by undesired OH− transport as a co-ion.
- -
- Solutions volume remains constant with time.
2.1.2. OH− Production and Cl− Leakage in the Bipolar Membrane
- -
- A quasi-symmetric membrane is assumed, where Li+ and Cl− flux through the bipolar membrane are equivalent, but in opposite directions. Furthermore, thickness is same for both layers of the bipolar membrane .
- -
- Due to the continuity principle, chloride flux in the anionic layer of bipolar membrane is equal to chloride flux for the cationic layer. Same is true for lithium-ion flux.
- -
- Linear concentration profiles in bipolar membrane layers are considered.
- -
- Ion concentration in the intermediate catalytic region of the bipolar membrane is assumed to be zero.
- -
- Average diffusion coefficient , used for both transport of salts (co-ions and counterions) across anionic and cationic layers of the bipolar membrane, is defined.
2.1.3. Energy Parameters
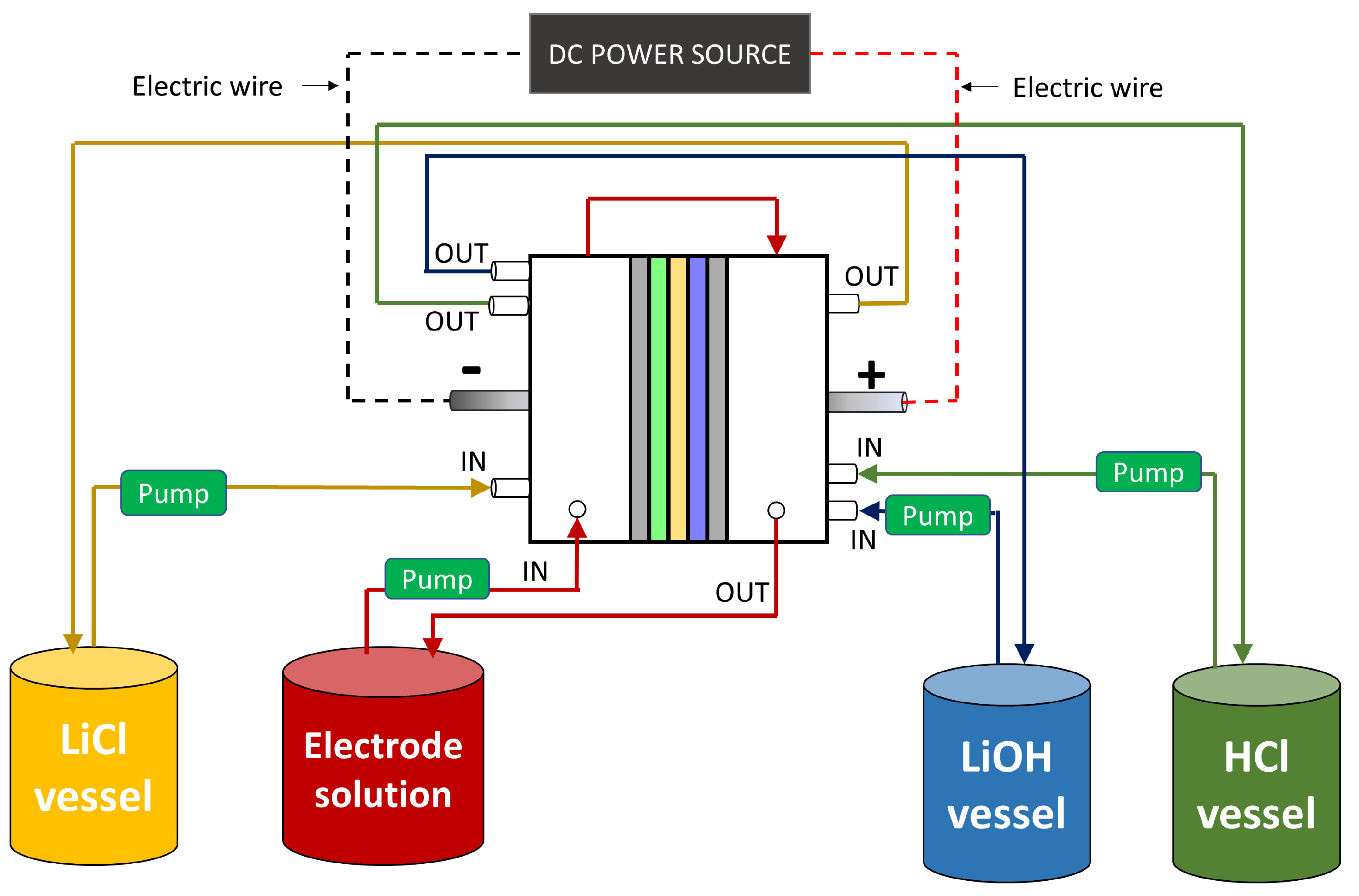
2.2. BMED Process Simulation
2.2.1. Validation
2.2.2. Parametric Study
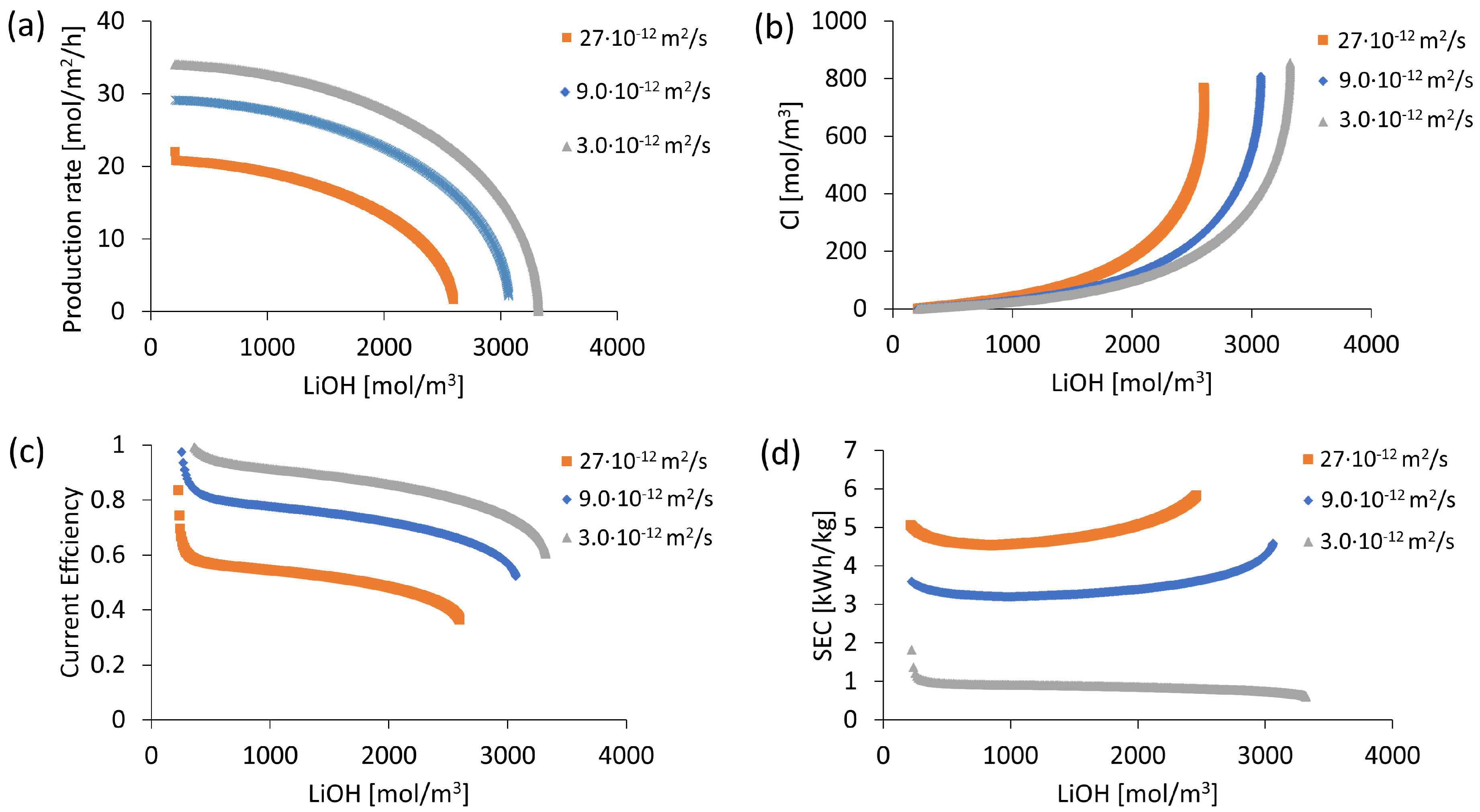
OH− Leakage in Cationic Membrane Evaluation
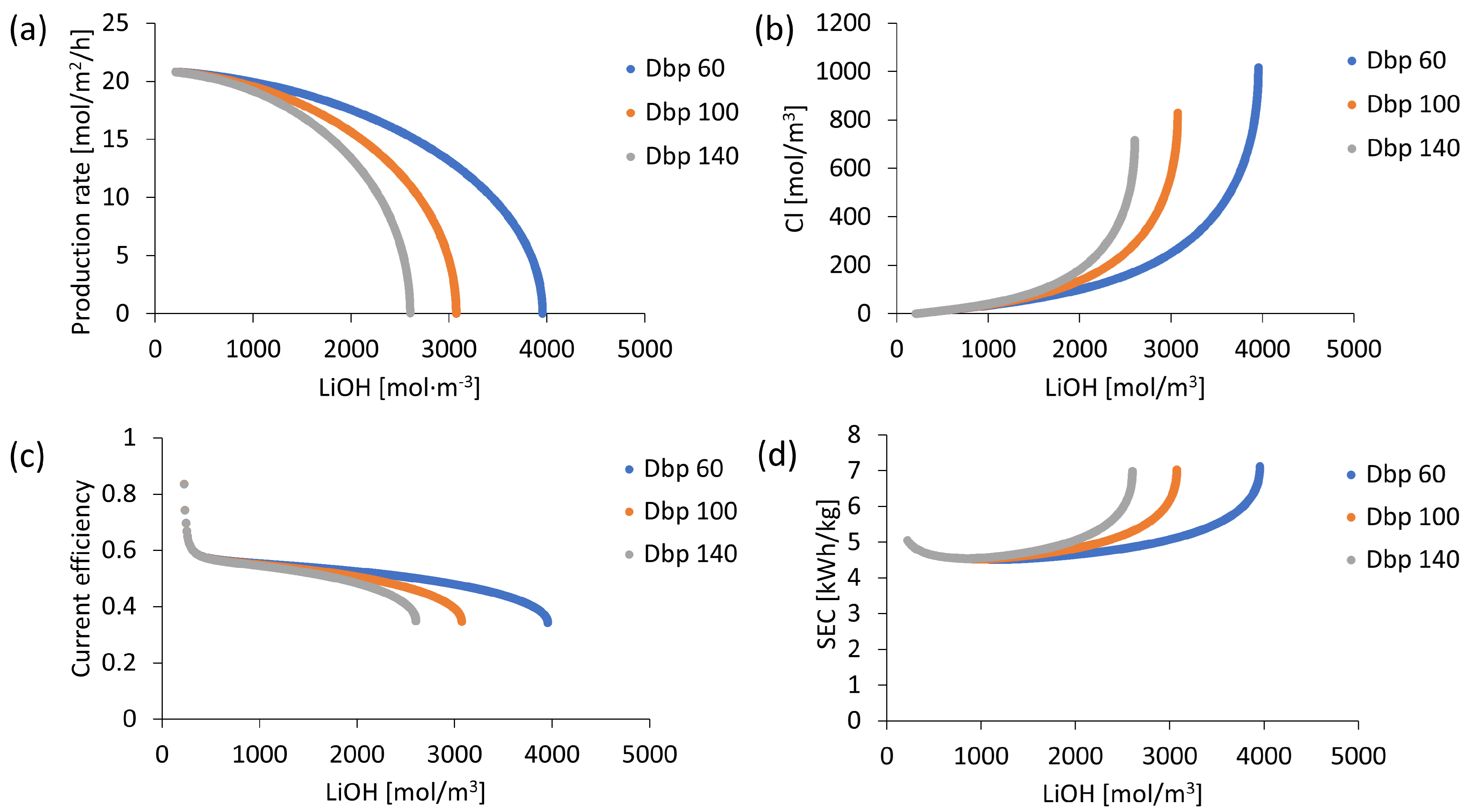
Bipolar Membrane Performance Evaluation
Sensitivity to Operating and Design Conditions
3. Results
3.1. OH− Leakage
3.2. Process Sensitivity to Bipolar Membrane Performance
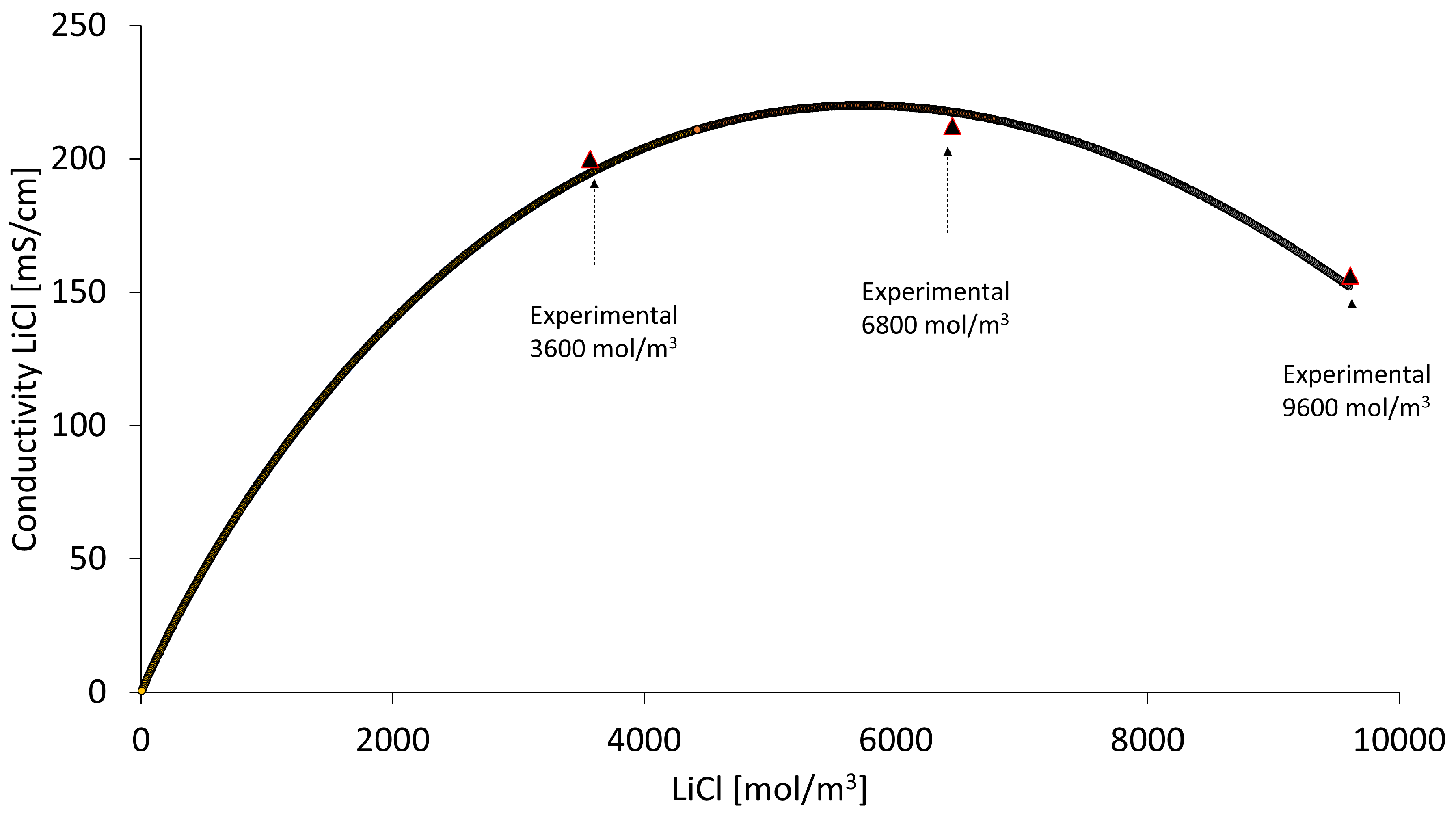
3.3. Model Validation
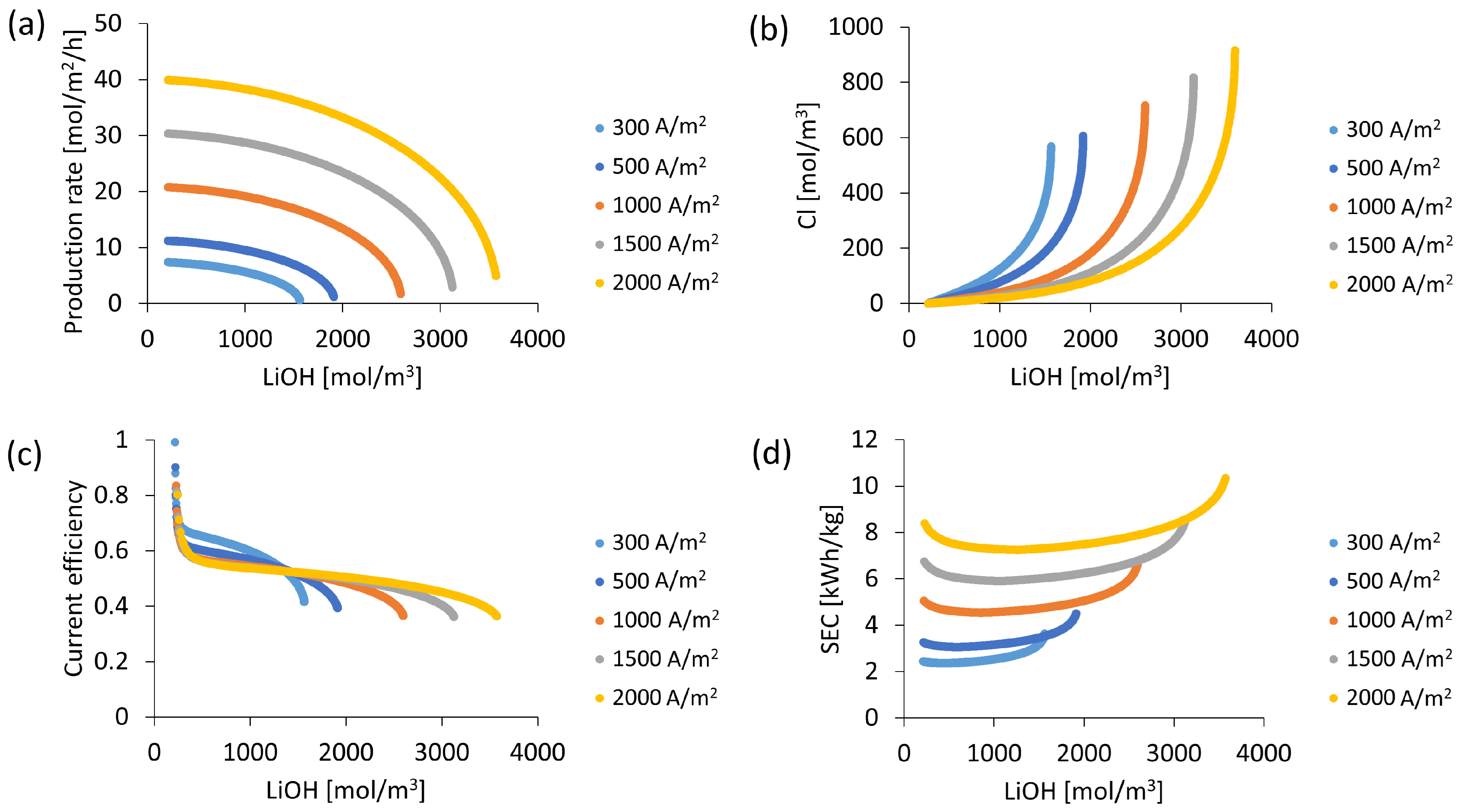
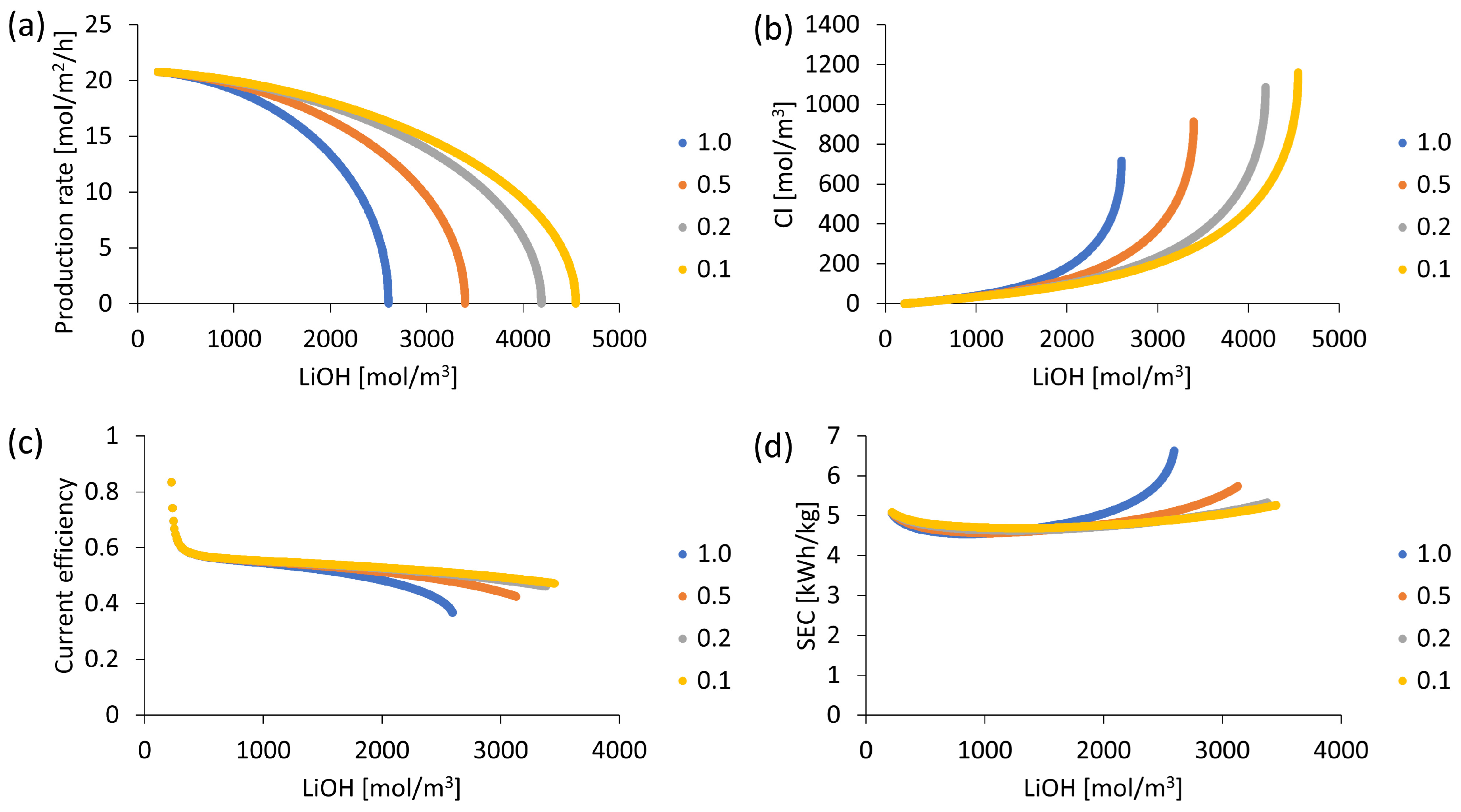
3.4. LiOH Production According to Electric Current Density
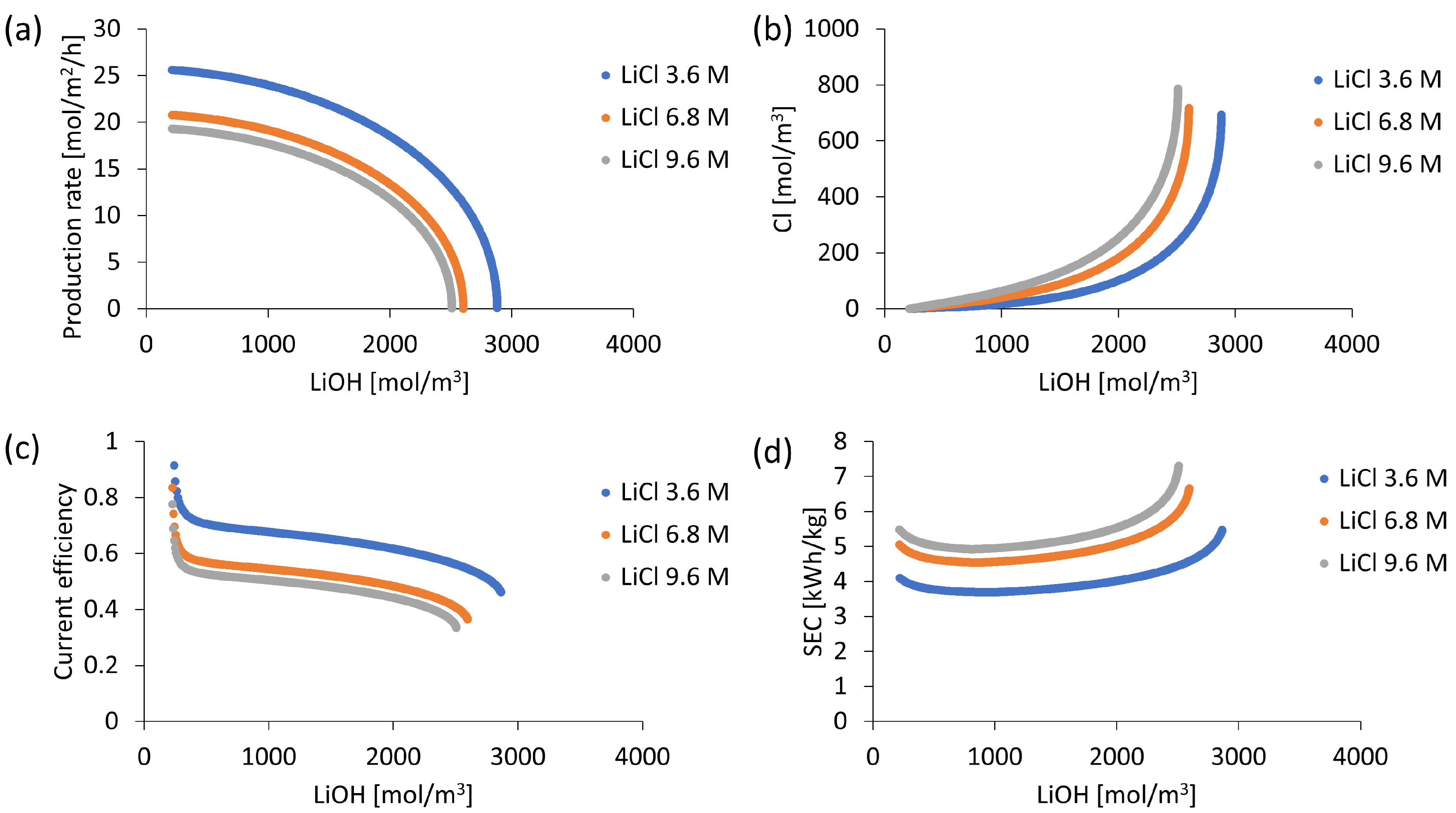
3.5. Initial Concentration Influence
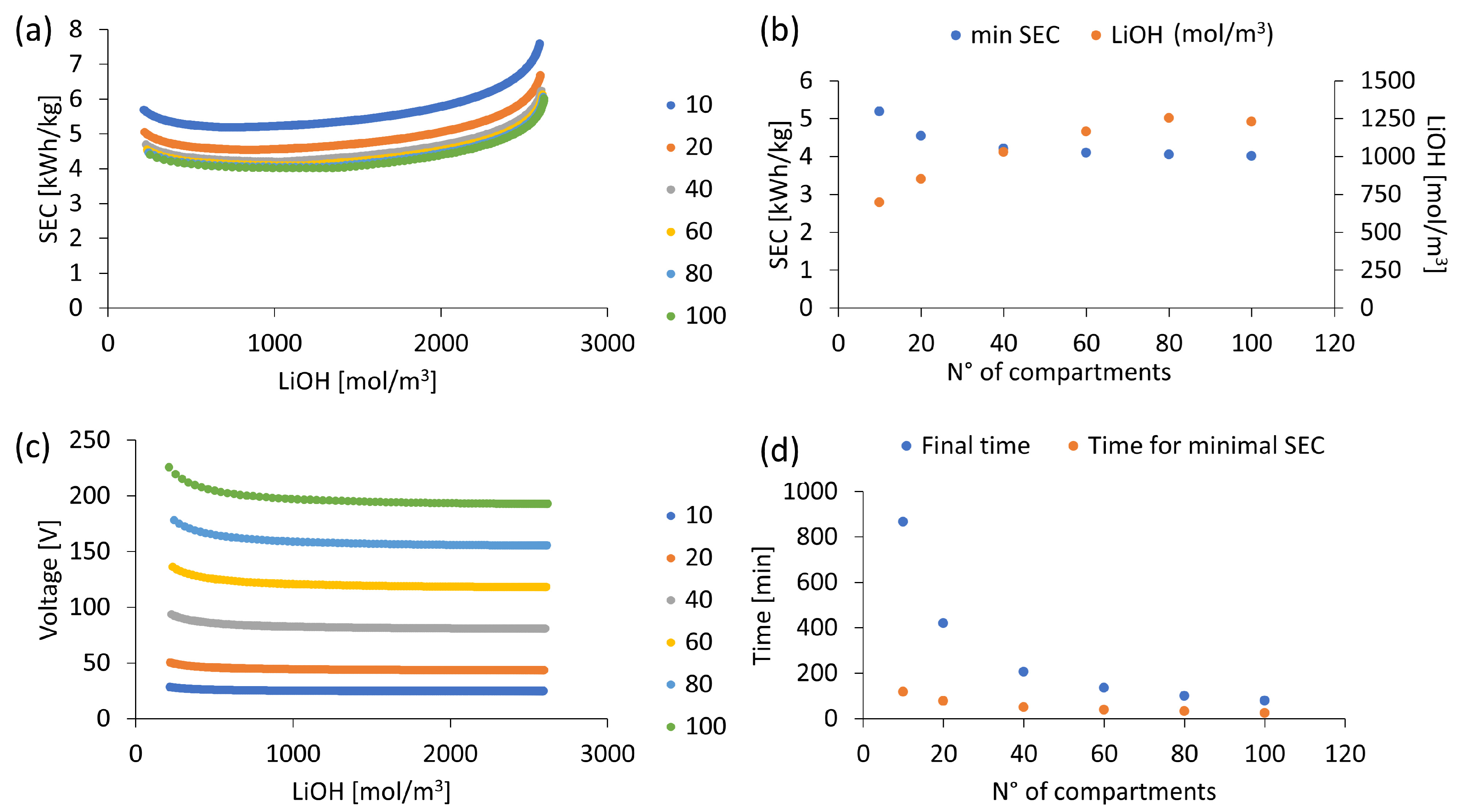
3.6. Influence of Number of Compartments
3.7. Initial Solution Volume Variation
4. Discussion and Application Potential
| Technology | Initial Concentration | Final LiOH Concentration | Final LiOH Solution Purity | SEC (kWh/kg of LiOH) | Current Efficiency | Ref. |
|---|---|---|---|---|---|---|
| Chlor-Alcali/Membrane electrolysis | 13.4% by mass LiCl | - | - | 7.25 | 70% | [11] |
| 19.1% by mass Li2SO4 | 3% by mass | - | 6.1–14.6 | 45–70% | [65] | |
| BMED | 14% by mass LiCl | 4.05–4.35% | 95.4% | 8.71–9.45 | 77–59% | [37] |
| 70–130 g/L LiCl (approx 6.7–12.0% by mass) | 1.50–1.75 M (approx 3.5–4.0% by mass) | - | Approx 3.4–4.0 | Approx 50–60% | [38] | |
| 1.5 M Li2SO4 | 2.2 M (approx 5.0% by mass) | - | 10 | 55% | [39] | |
| 0.05 M Li2SO4 | 0.9 M (approx 2.1% by mass) | 99.75% | 7 | 74% | ||
| 60–120 g/L LiCl (approx 5.8–11.3% by mass) | 1.73–2.69 M (approx 3.99–6.07% by mass) | - | 5.51–8.96 | 24.01–14.07% | [66] | |
| Simulated BMED | 14% by mass | Approx 4.0–4.5% by mass | >95% | 3.9–4.0 | 60–80% | This work |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ions molar flux | |
| Apparent diffusion coefficiente | |
| Mole concentration per unit volumen | |
| Cation exchange membrane thickness | |
| Number of electrons per ion | |
| Electric potential | |
| Ideal gas constant | |
| Temperature | |
| Electric current density | |
| Faraday Constant | |
| Number of compartments | |
| time | |
| Effective membrane area | |
| Molar conductivity | |
| Kohlraush constant | |
| Specific conductivity | |
| Electric resistance of solution | |
| Distance between membranes | |
| Electrode compartment thickness | |
| Cell potential | |
| overpotential | |
| Voltage | |
| mass produced | |
| Specific electrical energy consumption | |
| Current efficiency | |
| molality | |
| Molar mass | |
| Solution volume | |
| density | |
| Subscripts and Superscripts | |
| Cation membrane | |
| Cation membrane surface | |
| Fixed, associated with fixed charges of the cation exchange membrane or bipolar membrane | |
| Ionic or molecular species | |
| solution | |
| Initial time zero | |
| counterion | |
| Co-ion | |
| Production | |
| Related to limiting current density | |
| Bipolar membrane layer | |
| Anionic | |
| Cationic | |
| molar | |
| ° | standar |
| Membrane | |
| Bipolar membrane | |
| equilibrum | |
| cell | |
| Electrolyte solution | |
References
- Zybert, M.; Ronduda, H.; Szcesna, A.; Trzeciak, T.; Ostrowski, A.; Zero, E.; Wieczorek, W.; Rarog-Pilecka, W.; Marcinek, M. Different strategies of introduction of lithium ions into nickel-manganese-cobalt carbonate resulting in LiNi0.6Mn0.2Co0.2O2 (NMC622) cathode material for Li-ion batteries. Solid State Ionics 2020, 348, 115273. [Google Scholar] [CrossRef]
- Li, H.; Cormier, M.; Zhang, N.; Inglis, J.; Li, J.; Dahn, J.R. Is Cobalt Needed in Ni-Rich Positive Electrode Materials for Lithium Ion Batteries? J. Electrochem. Soc. 2019, 166, A429–A439. [Google Scholar] [CrossRef]
- Kim, J.-K.; Scheers, J.; Hwang, G.-C.; Zhao, X.; Kang, S.; Johansson, P.; Ahn, J.-H.; Jacobsson, P. Role of lithium precursor in the structure and electrochemical performance of LiFePO4. Scr. Mater. 2013, 69, 716–719. [Google Scholar] [CrossRef]
- Liu, A.; Liu, Y.; Hu, Z.; Gao, G.; Xu, Y.; Lei, L. Electrochemical performance of LiFePO4/C synthesized by solid state reaction using different lithium and iron sources. J. Phys. Chem. Solids 2011, 72, 831–835. [Google Scholar] [CrossRef]
- Fitch, B.; Yakovleva, M.; Meiere, S. Lithium Hydroxide Based Performance Improvements for nickel rich NCM layered cathode material. In Proceedings of the The Electrochemical Society, PRiME 2016/230th ECS Meeting. Honolulu, Hawaii, 2–7 October 2016; Volume MA2016-02 469. [Google Scholar] [CrossRef]
- Garrett, D.E. Handbook of Lithium and Natural Calcium Chloride, Their Deposits, Processing, Uses and Properties; Elsevier: Amsterdam, The Netherlands, 2004; pp. 1–235. [Google Scholar]
- Grágeda, M.; González, A.; Alavia, W.; Ushak, S. Development and optimization of a modified process for producing the battery grade LiOH: Optimization of energy and water consumption. Energy 2015, 89, 667–677. [Google Scholar] [CrossRef]
- Hou, M.; Chen, L.; Guo, Z.; Dong, X.; Wang, Y.; Xia, Y. A clean and membrane-free chlor-alkali process with decoupled Cl2 and H2/NaOH production. Nat. Commun. 2018, 9, 438. [Google Scholar] [CrossRef] [PubMed]
- Zhao, A.; Zhong, F.; Feng, X.; Chen, W.; Ai, X.; Yang, H.; Cao, Y. A membrane-free and energy-efficient three-step chlor-alkali electrolysis with higher-purity NaOH production. ACS Appl. Mater. Interfaces 2019, 11, 45126–45132. [Google Scholar] [CrossRef]
- Zhang, L.N.; Li, R.; Zang, H.Y.; Tan, H.Q.; Kang, Z.H.; Wang, Y.H.; Li, Y.G. Advanced hydrogen evolution electrocatalysts promising sustainable hydrogen and chlor-alkali co-production. Energy Environ. Sci. 2021, 14, 6191–6210. [Google Scholar]
- Grageda, M.; Gonzalez, A.; Quispe, A.; Ushak, S. Analysis of a Process for Producing Battery Grade Lithium Hydroxide by Membrane Electrodialysis. Membranes 2020, 10, 198. [Google Scholar] [CrossRef]
- Ryabtsev, A.; Kotsupalo, N.N.N.; Serikova, L. Preparation of High-Purity Lithium Hydroxide Monohydrate from Technical-Grade Lithium Carbonate by Membrane Electrolysis. Russ. J. Appl. Chem. 2004, 77, 1108–1116, Translated from Zhurnal Prikladnoi Khimii 2004, 77, 1123–1131. [Google Scholar] [CrossRef]
- Pourcelly, G. Electrodialysis with Bipolar membranes: Principles, Optimization, and Applications. Russ. J. Electrochem. 2002, 38, 919–926, From Elektrokhimiya 2002, 38, 1026–1033. [Google Scholar] [CrossRef]
- Koter, S.; Warszawski, A. A new model for characterization of bipolar membrane electrodialysis of brine. Desalination 2006, 198, 111–123. [Google Scholar] [CrossRef]
- Zabolotskii, V.; Sheldeshov, N.; Melnikov, S. Heterogeneous bipolar membranes and their application in electrodialysis. Desalination 2014, 341, 183–203. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, Y.; Shen, J.; Van der Bruggen, B. Application of bipolar membrane electrodialysis in environmental protection and resource recovery: A Review. Membranes 2022, 12, 829. [Google Scholar] [CrossRef] [PubMed]
- Ghyselbrecht, K.; Silva, A.; Van der Bruggen, B.; Boussu, K.; Meesschaert, B.; Pinoy, L. Desalination feasibility study of an industrial NaCl stream by bipolar membrane electrodialysis. J. Environ. Manag. 2014, 140, 69–75. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, C.; Wang, Y.; Fu, R.; Liu, Z.; Xu, T. Selectrodialysis with bipolar membrane for the reclamation of concentrated brine from RO plant. Desalination 2018, 442, 8–15. [Google Scholar] [CrossRef]
- Reig, M.; Casas, S.; Valderrama, C.; Gibert, O.; Cortina, J. Integration of monopolar and bipolar electrodialysis for valorization of seawater reverse osmosis desalination brines: Production of strong acid and base. Desalination 2016, 398, 87–97. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Y.; Zhang, X.; Xu, T. Comparative study on regenerating sodium hydroxide from the spent caustic bipolar membrane electrodialysis (BMED) and electro-electrodialysis (EED). Sep. Purificacion Technol. 2013, 118, 49–54. [Google Scholar] [CrossRef]
- Ye, W.; Huang, J.; Lin, J.; Zhang, X.; Shen, J.; Luis, P.; Van der Bruggen, B. Environmental evaluation of bipolar membrane electrodialysis for NaOH production from wastewater: Conditioning NaOH as a CO2 absorbent. Sep. Purif. Technol. 2015, 144, 206–214. [Google Scholar] [CrossRef]
- Fernandez-Gonzalez, C.; Dominguez-Ramos, A.; Ibañez, R.; Chen, Y.; Irabien, A. Valorization of desalination brines by electrodialysis with bipolar membranes using nanocomposite anion exchange membranes. Desalination 2016, 406, 16–24. [Google Scholar] [CrossRef]
- Hwang, C.W.; Jeong, M.H.; Kim, Y.J.; Son, W.K.; Kang, K.S.; Lee, C.S.; Hwang, T.S. Process design for lithium recovery using bipolar membrane electrodialysis system. Sep. Purif. Technol. 2016, 166, 34–40. [Google Scholar] [CrossRef]
- Sun, X.; Wang, J. Recovery of citric acid from fermented liquid by bipolar membrane electrodialysis. J. Clean. Prod. 2017, 143, 250–256. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, X.; Fan, A.; Fu, L.; Gao, C. An innovative beneficial reuse of seawater concentrate using bipolar membrane electrodialysis. J. Membr Sci. 2014, 449, 119–126. [Google Scholar] [CrossRef]
- Herrero-Gonzalez, M.; Diaz-Guridi, P.; Dominguez-Ramos, A.; Ibañez, R.; Irabien, A. Photovoltaic solar electrodialysis with bipolar membranes. Desalination 2018, 433, 155–163. [Google Scholar] [CrossRef]
- Zhong, C.; Lv, Y.; Wen, W.; Chen, Q.; Zhang, W. Sustainable Production of Lithium Acetate by Bipolar Membrane Electrodialysis Metathesis. ACS Sustain. Chem. Eng. 2022, 10, 6045–6056. [Google Scholar] [CrossRef]
- Sun, M.; Li, M.; Zhang, X.; Wu, C.; Wu, Y. Graphene oxide modified porous P84 co-polyimide membranes for boron recovery by bipolar membrane electrodialysis process. Sep. Purif. Technol. 2020, 232, 115963. [Google Scholar] [CrossRef]
- Parsa, N.; Moheb, A.; Mehrabani-Zeinabad, A.; Masigol, M.A. Recovery of lithium ions from sodium-contaminted lithium bromide solution by using electrodialysis process. Chem. Eng. Res. Des. 2015, 98, 81–88. [Google Scholar] [CrossRef]
- Iizuka, A.; Yamashita, Y.; Nagasawa, H.; Yamasaki, A.; Yanagisawa, Y. Separation of lithium and cobalt from waste lithium-ion batteries via bipolar membrane electrodialysis coupled with chelation. Sep. Purif. Technol. 2013, 113, 33–41. [Google Scholar] [CrossRef]
- Bunani, S.; Yoshizuka, K.; Nishihama, S.; Arda, M.; Kabay, N. Application of bipolar membrane electrodialysis (BMED) for simultaneous separation and recovery of boron and lithium from aqueous solutions. Desalination 2017, 424, 37–44. [Google Scholar] [CrossRef]
- Bunani, S.; Arda, M.; Kabay, N.; Yoshizuka, K.; Nishihama, S. Effect of process conditions on recovery of lithium and boron from water using bipolar membrane electrodialysis (BMED). Desalination 2017, 416, 10–15. [Google Scholar] [CrossRef]
- Kabay, N.; Kaya, T.Z.; Çermikli, E.; Jarma, Y.A.; Altiok, E.; İpekçi, D.; Arda, M. Effect of Operational Parameters on Recovery of Lithium from Brine with Bipolar Membrane Electrodialysis. J. Membr. Sci. Res. 2022. In Progress. [Google Scholar] [CrossRef]
- Wang, C.J.Y.; Wang, Q.; Feng, H.; Xu, T. Production of Lithium Hydroxide from Lake Brines through Electro-Electrodialysis with Bipolar Membranes (EEDBM). Ind. Eng. Chem. Res. 2014, 53, 6103–6112. [Google Scholar]
- Melnikov, S.; Sheldeshov, N.; Zabolotsky, V.; Loza, S.; Achoh, A. Pilot scale complex electrodialysis technology for processing a solution of lithium chloride containing organic solvents. Sep. Purif. Technol. 2017, 189, 74–81. [Google Scholar] [CrossRef]
- Cho, Y.; Kim, K.; Ahn, J.; Lee, J. A Study on Lithium Hydroxide Recovery Using Bipolar Membrane Electrodialysis. Korean J. Met. Mater. 2021, 59, 223–232. [Google Scholar] [CrossRef]
- González, A.; Grágeda, M.; Quispe, A.; Ushak, S.; Sistat, P.; Cretin, M. Application and Analysis of Bipolar Membrane Electrodialysis for LiOH Production at High Electrolyte Concentrations: Current Scope and Challenges. Membranes 2021, 11, 575. [Google Scholar] [CrossRef]
- Tian, H.; Yan, X.; Zhou, F.; Xu, C.; Li, C.; Chen, X.; He, X. Effect of process conditions on generation of hydrochloric acid and lithium hydroxide from simulated lithium chloride solution using bipolar membrane electrodialysis. SN Appl. Sci. 2022, 4, 47. [Google Scholar] [CrossRef]
- Chen, X.; Ruan, X.; Kentish, S.; Li, G.; Xu, T.; Chen, G. Production of lithium hydroxide by electrodialysis with bipolar membranes. Sep. Purif. Technol. 2021, 274, 119026. [Google Scholar] [CrossRef]
- Jaime-Ferrer, J.; Couallier, E.; Viers, P.; Durand, G.; Rakib, M. Three-compartment bipolar membrane electrodialys for splitting of sodium formate into formic acid and sodium hydroxide: Role of diffusion of molecular acid. J. Membr. Sci. 2008, 325, 528–536. [Google Scholar] [CrossRef]
- Fu, L.; Gao, X.; Yang, Y.; Aiyong, F.; Hao, H.; Gao, C. Preparation of succinic acid using bipolar membrane electrodialysis. Sep. Purif. Technol. 2014, 127, 212–218. [Google Scholar] [CrossRef]
- Wilhelm, F.; Pünt, I.; van der Vegt, N.; Wessling, M.; Strathmann, H. Optimisation strategies for the preparation of bipolar membranes with reduced salt ion leakage in acid-base electrodialysis. J. Membr. Sci. 2001, 182, 13–28. [Google Scholar] [CrossRef]
- Balster, J.; Sumbharaju, R.; Srikantharajah, S.; Pünt, I.; Stamatialis, D.F.; Jordan, V.; Wessling, M. Assymmetric bipolar membrane: A tool to improve product purity. J. Membr. Sci. 2007, 287, 246–256. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, A.; Zhang, X.; Xu, T. Simulation of Electrodialysis with Bipolar Membranes: Estimation of Process Performance and Energy Consumption. Ind. Eng. Chem. Res. 2011, 50, 13911–13921. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Shi, S.; Cao, H.; Yip, N.; Lin, S. Bipolar Membrane Electrodialysis for Ammonia Recovery from Synthetic Urine: Experiments, Modeling, and Performance Analysis. Environ. Sci. Technol. 2021, 55, 14886–14896. [Google Scholar] [CrossRef]
- Peng, Z.; Sun, Y.; Shi, P.; Wang, Y. A mathematical model of the external circuits in a bipolar membrane electrodialysis stack: Leakage currents and Joule heating effect. Sep. Purif. Technol. 2022, 290, 120816. [Google Scholar] [CrossRef]
- Culcasi, A.; Gurreri, L.; Cipollina, A.; Tamburini, A.; Micale, G. A comprehensive multi-scale model for bipolar membrane electrodialysis (BMED). Chem. Eng. J. 2022, 437, 135317. [Google Scholar] [CrossRef]
- Asadi, A.; Kang, B.; Harandi, H.B.; Jung, J.C.; Shen, Z.; Sui, P. Electrodialysis of Lithium Sulphate Solution: Model Development and validation. J. Electrochem. Soc. 2022, 169, 053508. [Google Scholar] [CrossRef]
- Gonzalez Panzo, I.J.; Cruz Díaz, M.R.; Rodríguez, P.F.A.; Rivero, M.E.P. Bipolar Membrane Modeling from the Chemical Equilibrium of Water Dissociation Approach. SSRN 2022, in press. [CrossRef]
- Avci, A.H.; Rijnaarts, T.; Fontananova, E.; Di Profio, G.; Vankelecom, I.F.V.; De Vos, W.M.; Curcio, E. Sulfonated polyethersulfone based cation exchange membranes for reverse electrodialysis under high salinity gradients. J. Membr. Sci. 2019, 595, 117585. [Google Scholar] [CrossRef]
- Izquierdo-Gil, M.; Barragán, V.; Villaluenga, J.; Godino, M. Water uptake and salt transport through Nafion cation-exchange membranes with different thicknesses. Chem. Eng. Sci. 2012, 71, 1–9. [Google Scholar] [CrossRef]
- Dammak, L.; Lteif, R.; Bulvestre, G.; Pourcelly, G.; Auclair, B. Determination of the diffusion coefficients of ions in cation-exchange membranes, supposed to be homogeneous, from the electrical membrane conductivity and the equilibrium quantity of absorbed electrolyte. Electrochim. Acta 2001, 47, 451–457. [Google Scholar] [CrossRef]
- Dlugolecki, P.; Gambier, A.; Nijmeijer, K.; Wessling, M. Practical potential of reverse electrodialysis as process for sustainable energy generation. Environ. Sci. Technol. 2009, 43, 6888. [Google Scholar] [CrossRef] [PubMed]
- Strathmann, H. Chapter 3—Preparation and Characterization of Ion-Exchange Membranes. Membrane Science and Technology 2004, 9, 89–146. [Google Scholar] [CrossRef]
- Liu, R.; Wu, L.; Pan, J.; Jiang, C.; Xu, T. Diffusion dialysis membranes with semi-interpenetrating network for alkali recovery. J. Membr. Sci. 2014, 451, 18–23. [Google Scholar] [CrossRef]
- Garcia-Vasquez, W.; Dammak, L.; Larchet, C.; Nikonenko, V.; Grande, D. Effectsof acid-base cleaning procedure on structure and properties of anion-exchangemembranes used in electrodialysis. J. Membr. Sci. 2016, 507, 12e23. [Google Scholar] [CrossRef]
- Davis, T.; Genders, J.D.; Pletcher, D. A First Course in Ion Permeable Membranes; The Electrochemical Consultancy: Romsey, UK, 1997; ISBN 0-9517307-8-9. [Google Scholar]
- Sosa-Fernandez, P.; Miedema, S.; Bruning, H.; Leermakers, F.; Post, J.; Rijnaarts, H. Effects of feed composition on the fouling on cation-exchange membranes desalinating polymer-flooding produced water. J. Colloid Interface Sci. 2021, 584, 634–646. [Google Scholar] [CrossRef]
- Hayes, T.D.; Severin, B.F. Electrodialysis of highly concentrated brines: Effects of calcium. Sep. Purif. Technol. 2017, 175, 443–453. [Google Scholar] [CrossRef]
- Grágeda, M.; González, A.; Grágeda, M.; Ushak, S. Purification of brines by chemical precipitation and ion-exchange processes for obtaining battery-grade lithium compounds. Int. J. Energy Res. 2018, 42, 2386–2399. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, H.; Wang, Y.; Sha, Z. Review on the electrochemical extraction of lithium from seawater/brine. J. Electroanal. Chem. 2019, 850, 113389. [Google Scholar] [CrossRef]
- Stringfellow, W.; Dobson, P. Technology for the Recovery of Lithium from Geothermal Brines. Energies 2021, 14, 6805. [Google Scholar] [CrossRef]
- Wang, Y.; Weinstock, I. Polyoxometalate-decorated nanoparticles. Chem. Soc. Rev. 2012, 41, 7479–7496. [Google Scholar] [CrossRef]
- Firdaous, L.; Maleriat, J.P.; Schlumpf, J.P. Transfer of Monovalent and Divalent Cations in Salt Solutions by Electrodialysis. Sep. Sci. Technol. 2007, 42, 931–948. [Google Scholar] [CrossRef]
- Turan, A.; Baloglu, H.; Ünveren, E.; Bulutcu, A. The behaviour of Nafion® 424 membrane in the electrochemical production of lithium hydroxide. J. Chem. Technol. Biotechnol. 2015, 91, 2529–2538. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, H.; Li, Y.; Wang, M.; Xiang, X. An integrated membrane process for preparation of lithium hydroxide from high Mg/Li ratio salt lake brine. Desalination 2020, 493, 114620. [Google Scholar] [CrossRef]


| Cation Exchange Membrane | ||
|---|---|---|
| Ion exchange capacity (meq/gr) | 1.6 | |
| Water content | 29.7–33.5% | |
| Thickness (mm) | 18 | |
| Apparent Li+ diffusion coefficient (10−12 m2/s) | 9.0 | |
| Apparent OH− diffusion coefficient (10−12 m2/s) | 3–27 | |
| Bipolar Membrane | ||
| Fixed charge density anion and cation layer (mol/m3) | 3500 to 6500 | |
| Anion layer thickness (mm) | 0.11 | |
| Cation layer thickness (mm) | 0.11 | |
| Diffusion coefficient (10−12 × m2/s) | 60 to 140 | |
| Electrodes Compartments | ||
| Standard electrode potential difference (V) | 2.06 | |
| Anode overpotential | 0.1 | |
| Cathode overpotential | 0.1 | |
| Configuration 1 | Configuration 2 | Configuration 3 | Configuration 4 | |
|---|---|---|---|---|
| Number of compartments | 2 | 2 | 2 | 4 |
| Current density | 1000 A/m2 | 500 A/m2 | 1000 A/m2 | 500 A/m2 |
| Inicial LiCl concentration | 3.56 mol/L (aprox 14 %mass) | 3.56 mol/L (aprox 14 %mass) | 6.77 mol/L (aprox 25 %mass) | 9.62 mol/L (aprox 34 %mass) |
| LiCl volumen solution | 450 mL | 450 mL | 300 mL | 450 mL |
| Design of Stack | ||
|---|---|---|
| Number of compartments | 20 | |
| Distance between membranes (m) | 0.001 | |
| Electrode compartment thickness (m) | 0.02 | |
| Effective membrane area (m2) | 0.03 | |
| Membrane electric resistance (Ω∙cm2) | 3.0 | |
| Operating conditions | ||
| Initial LiOH concentration (mol/m3) | 210 | |
| Initial LiCl concentration (mol/m3) | 3600 to 9600 | |
| Initial HCl concentration (mol/m3) | 137 | |
| Electrode solution concentration (mol/m3) | 1000 | |
| LiOH solution volume (m3) | 0.025 | |
| LiCl solution volume (m3) | 0.025 | |
| HCl solution volume (m3) | 0.025 | |
| Current density (A/m2) | 300 to 2000 | |
| Temperature (°C) | 25 | |
| Configuration | Parameter | (%) | (%) | CE (-) | SEC (kWh/kg) | Purity (%) | Voltage (V) |
|---|---|---|---|---|---|---|---|
| 1N | R2 | 99.883 | 93.116 | 99.993 | 98.147 | 94.344 | 97.634 |
| RMSE | 0.30 | 0.07 | 0.11 | 1.82 | 0.03 | 0.43 | |
| 1F | R2 | 99.925 | 95.407 | 99.990 | 99.9999 | 89.301 | 94.679 |
| RMSE | 0.11 | 0.08 | 0.06 | 1.04 | 0.06 | 0.49 | |
| 2 | R2 | 97.051 | 99.999 | 98.974 | 99.991 | 98.915 | 99.407 |
| RMSE | 0.19 | 0.27 | 0.01 | 2.00 | 0.03 | 1.29 | |
| 3X | R2 | 99.331 | 94.465 | 99.655 | 99.289 | 35.054 | 67.568 |
| RMSE | 0.43 | 0.06 | 0.04 | 0.89 | 0.03 | 0.89 | |
| 3B | R2 | 99.811 | 97.248 | 97.555 | 96.536 | 80.743 | 87.0971 |
| RMSE | 0.23 | 0.03 | 0.06 | 0.57 | 0.01 | 1.26 | |
| 4 | R2 | 99.311 | 97.562 | 99.857 | 99.921 | 99.978 | 59.405 |
| RMSE | 0.14 | 0.09 | 0.07 | 1.19 | 0.03 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, A.; Grágeda, M.; Ushak, S. Modeling and Validation of a LiOH Production Process by Bipolar Membrane Electrodialysis from Concentrated LiCl. Membranes 2023, 13, 187. https://doi.org/10.3390/membranes13020187
González A, Grágeda M, Ushak S. Modeling and Validation of a LiOH Production Process by Bipolar Membrane Electrodialysis from Concentrated LiCl. Membranes. 2023; 13(2):187. https://doi.org/10.3390/membranes13020187
Chicago/Turabian StyleGonzález, Alonso, Mario Grágeda, and Svetlana Ushak. 2023. "Modeling and Validation of a LiOH Production Process by Bipolar Membrane Electrodialysis from Concentrated LiCl" Membranes 13, no. 2: 187. https://doi.org/10.3390/membranes13020187
APA StyleGonzález, A., Grágeda, M., & Ushak, S. (2023). Modeling and Validation of a LiOH Production Process by Bipolar Membrane Electrodialysis from Concentrated LiCl. Membranes, 13(2), 187. https://doi.org/10.3390/membranes13020187







