Study on Static Characteristics of Aerostatic Bearing Based on Porous SiC Ceramic Membranes
Abstract
:1. Introduction
2. Preparation and Characterization of Aerostatic Bearing
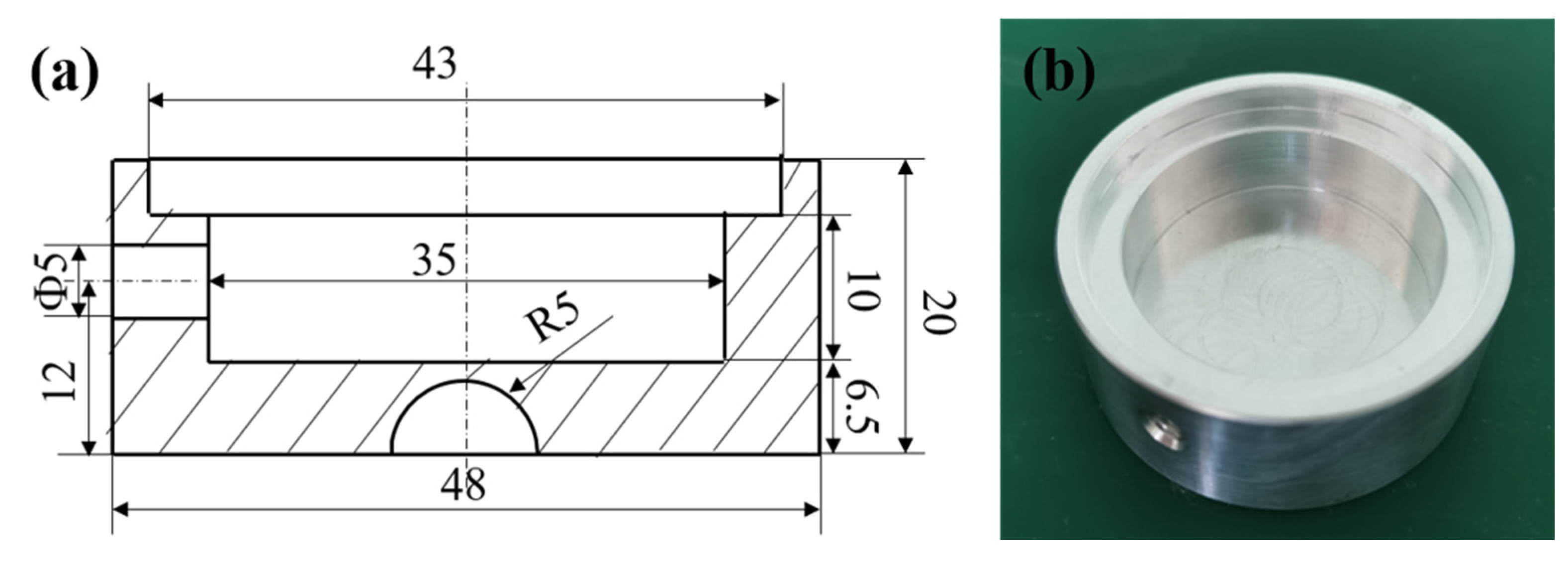
2.1. Structural Design and Preparation of Aerostatic Bearing Based on Porous SiC Ceramics
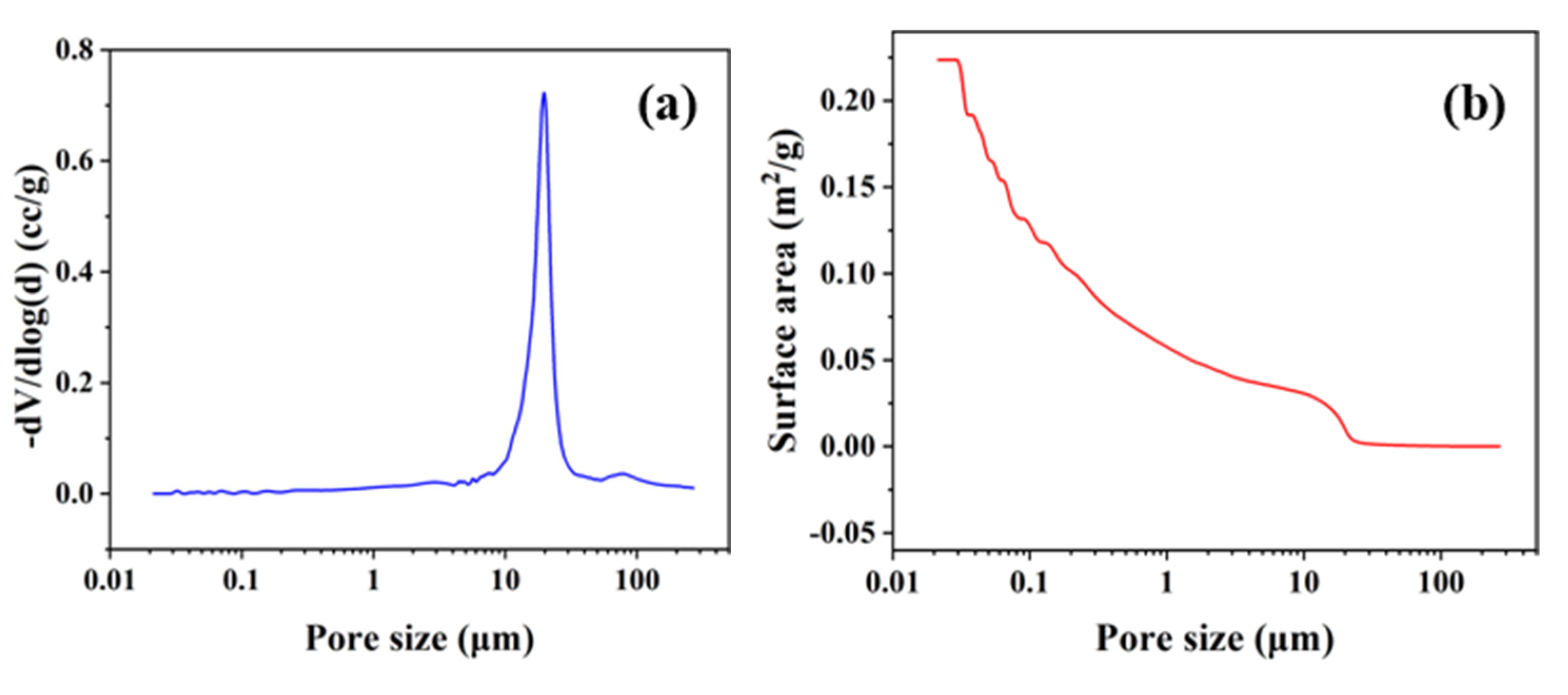
2.2. Pore Characteristics and Mechanical Properties
2.3. Permeability of Porous SiC Ceramic Membrane
3. Simulation of Static Characteristics of Aerostatic Bearing
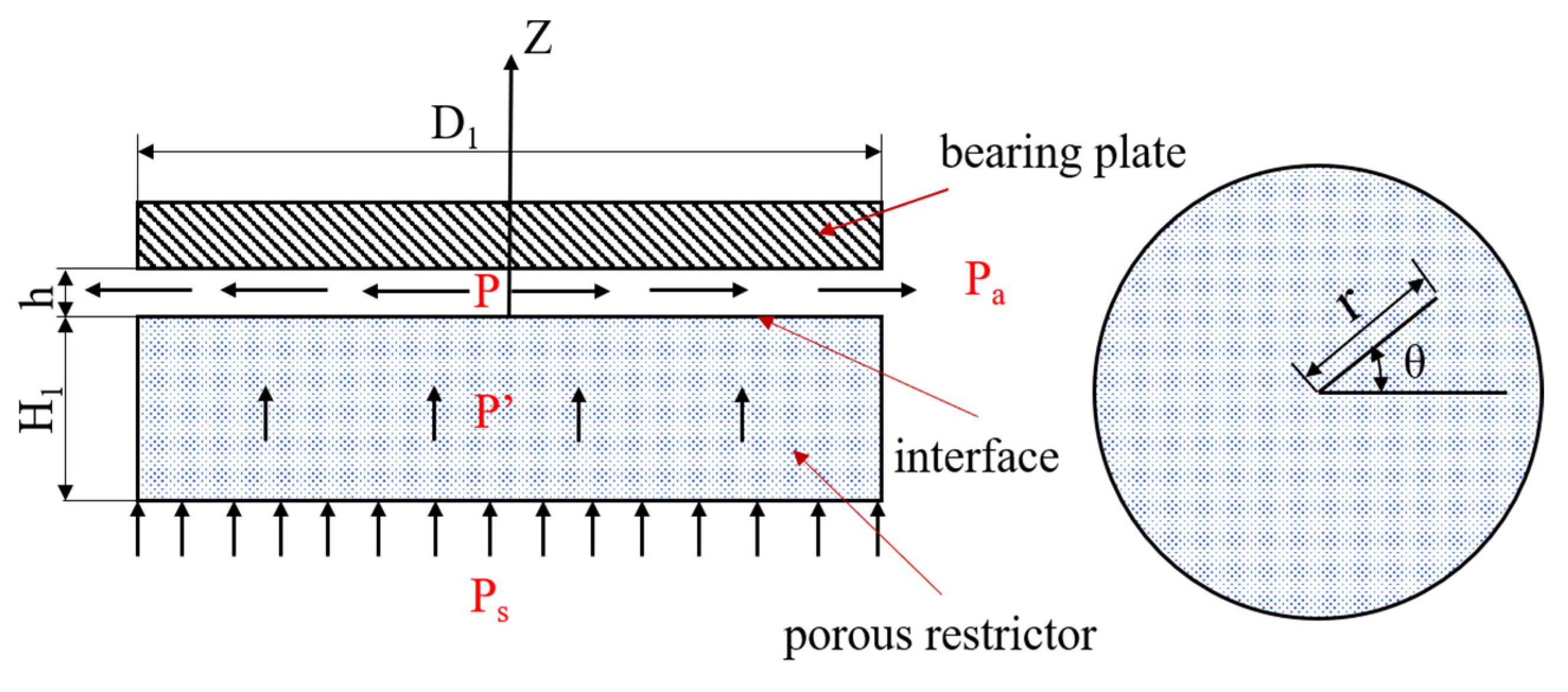
3.1. Establishment of Calculation Model
- (1)
- Gas inlet boundary: 0 ≤ θ ≤ 2π, 0 ≤ r ≤ R, z = −H, p′ = ps;
- (2)
- Continuous boundary: 0 ≤ θ ≤ 2π, 0 ≤ r ≤ R, z = 0, p′ = p;
- (3)
- Closed boundary: 0 ≤ θ ≤ 2π, r = R, −H ≤ z ≤ 0, ∂p′/∂r = 0;
- (4)
- Gas outlet boundary: 0 ≤ θ ≤ 2π, r = R, 0 ≤ z ≤ h, p′ = pa.
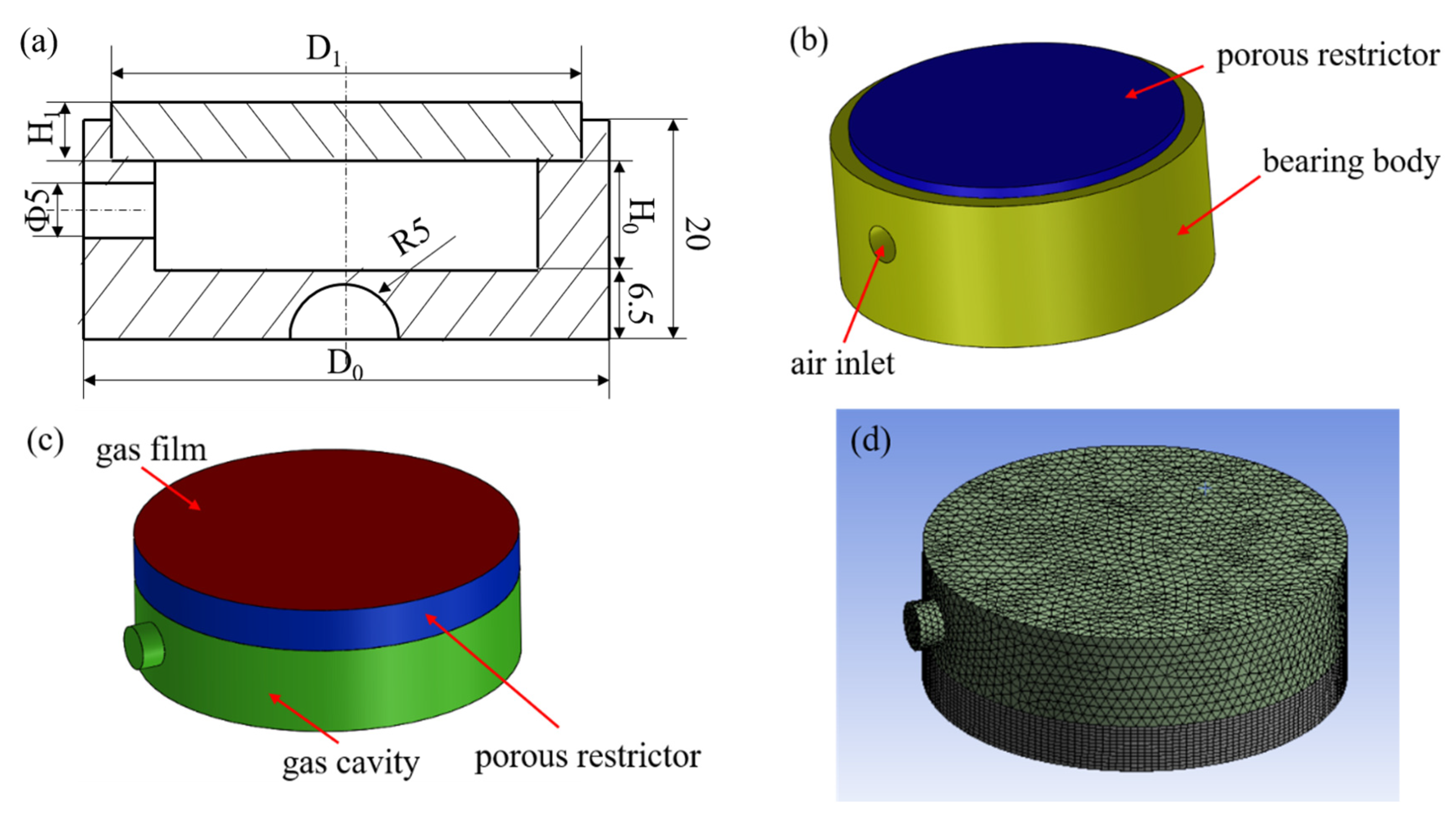
3.2. Establishment of Geometric Model and Grid Meshing
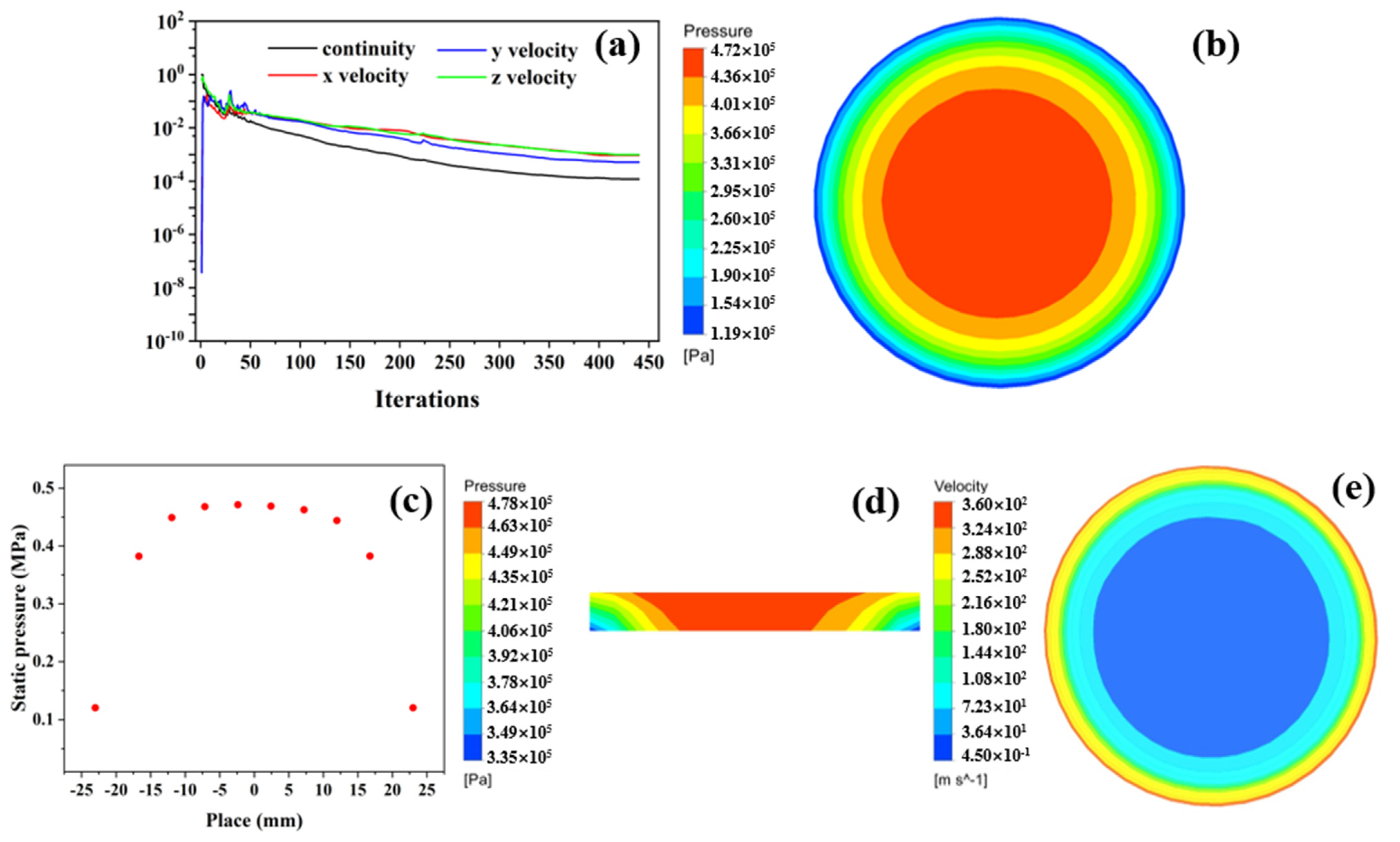
3.3. Simulation Analysis of Aerostatic Bearing
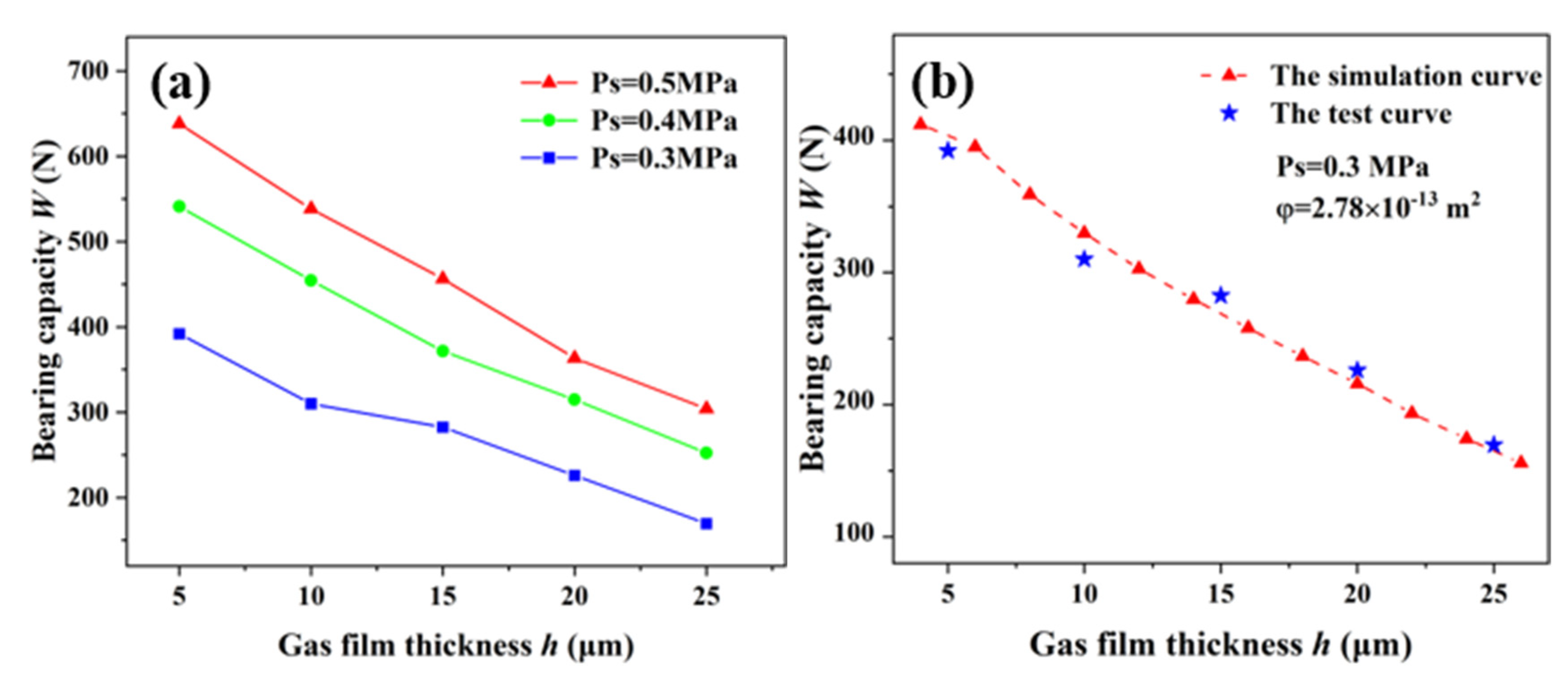
3.4. Static-Characteristic Analysis of Aerostatic Bearing
4. Experimental Research on Static Characteristics of Aerostatic Bearing
4.1. Construction and Test of Static-Characteristic-Measurement System for Aerostatic Bearing
4.2. Experimental Verification Results of Static Characteristics of Aerostatic Bearing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeng, C.; Wang, W.; Cheng, X.; Zhao, R.; Cui, H. Three-dimensional flow state analysis of microstructures of porous graphite restrictor in aerostatic bearings. Tribol. Int. 2021, 159, 106955. [Google Scholar] [CrossRef]
- Gao, Q.; Chen, W.; Lu, L.; Huo, D.; Cheng, K. Aerostatic bearings design and analysis with the application to precision engineering: State-of-the-art and future perspectives. Tribol. Int. 2019, 135, 1–17. [Google Scholar] [CrossRef]
- Zhang, P. Accuracy prediction model of an orifice-compensated aerostatic bearing. Precis. Eng. 2021, 72, 837–846. [Google Scholar] [CrossRef]
- Ishibashi, K.; Kondo, A.; Kawada, S.; Miyatake, M.; Yoshimoto, S.; Stolarski, T. Static and dynamic characteristics of a downsized aerostatic circular thrust bearing with a single feed hole. Precis. Eng. 2019, 60, 448–457. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, Z.; Sun, T.; Zhao, X.; Zhang, J.; Zong, W. Analysis of the static performance of a cableless aerostatic guideway. Machines 2022, 10, 308. [Google Scholar] [CrossRef]
- Shi, J.; Cao, H.; Jin, X. Investigation on the static and dynamic characteristics of 3-DOF aerostatic thrust bearings with orifice restrictor. Tribol. Int. 2019, 138, 435–449. [Google Scholar] [CrossRef]
- Ise, T.; Nakatsuka, M.; Nagao, K.; Matsubara, M.; Kawamura, S.; Asami, T.; Kinugawa, T.; Nishimura, K. Externally pressurized gas journal bearing with slot restrictors arranged in the axial direction. Precis. Eng. 2017, 50, 286–292. [Google Scholar] [CrossRef]
- Kodnyanko, V.; Shatokhin, S.; Kurzakov, A.; Pikalov, Y.; Brungardt, M.; Strok, L.; Pikalov, I. Theoretical investigation on performance characteristics of aerostatic journal bearings with active displacement compensator. Appl. Sci. 2021, 11, 2623. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, L.; Mao, X.; An, L.; Liu, Y.; Wang, S.; Zhang, J.; Feng, K. Preparation and properties of porous alumina ceramics for ultra-precision aerostatic bearings. Ceram. Int. 2022, 48, 13311–13318. [Google Scholar] [CrossRef]
- Cui, H.; Wang, Y.; Yue, X.; Huang, M.; Wang, W. Effects of manufacturing errors on the static characteristics of aerostatic journal bearings with porous restrictor. Tribol. Int. 2017, 115, 246–260. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, X.; Zhang, M.; Gong, W.; Cui, H. Effect of the deformation of porous materials on the performance of aerostatic bearings by fluid-solid interaction method. Tribol. Int. 2020, 150, 106391. [Google Scholar] [CrossRef]
- Gu, Y.; Cheng, J.; Xie, C.; Li, L.; Zheng, C. Theoretical and numerical investigations on static characteristics of aerostatic porous journal bearings. Machines 2022, 10, 171. [Google Scholar] [CrossRef]
- Zhang, P.; Zha, J. Dynamic accuracy model of porous journal air bearing considering rotational speed. Tribol. Int. 2021, 161, 107064. [Google Scholar] [CrossRef]
- Li, C.; Zhou, Z. Air permeability and tensile properties of novel micron-scale gradient porous plates fabricated by rolling and vacuum sintering. Powder Technol. 2022, 399, 117205. [Google Scholar] [CrossRef]
- Huang, L.; Qin, H.; Hu, T.; Xie, J.; Guo, W.; Gao, P.; Xiao, H. Fabrication of high permeability SiC ceramic membrane with gradient pore structure by one-step freeze-casting process. Ceram. Int. 2021, 47, 17597–17605. [Google Scholar] [CrossRef]
- Xu, X.; Liu, X.; Wu, J.; Zhang, C.; Tian, K.; Yu, J. Effect of preparation conditions on gas permeability parameters of porous SiC ceramics. J. Eur. Ceram. Soc. 2021, 41, 3252–3263. [Google Scholar] [CrossRef]
- Liu, D.; Li, Y.; Lv, C.; Chen, J.; Zhang, D.; Wu, Z.; Ding, D.; Xiao, G. Permeating behaviour of porous SiC ceramics fabricated with different SiC particle sizes. Ceram. Int. 2021, 47, 5610–5616. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Liu, D.; Chen, J.; Zhang, D.; Wu, Z. Permeability of the porous Al2O3 ceramic with bimodal pore size distribution. Ceram. Int. 2019, 45, 5952–5957. [Google Scholar] [CrossRef]
- Li, W.; Wang, G.; Feng, K.; Zhang, Y.; Wang, P. CFD-based investigation and experimental study on the performances of novel back-flow channel aerostatic bearings. Tribol. Int. 2022, 165, 107319. [Google Scholar] [CrossRef]
- Duan, L.; Xu, M. Study on static performance of gas-lubricated thrust bearing based on multi-microporous stainless steel plate. J. Braz. Soc. Mech. Sci. 2021, 43, 250. [Google Scholar]
- Nawaz, A.; Rani, S. Fabrication and evaluation of percent porosity and density reduction of aluminium alloy foam. Mater. Today Proc. 2021, 47, 6025–6029. [Google Scholar] [CrossRef]
- Caccia, M.; Narciso, J. Key parameters in the manufacture of SiC based composite materials by practive melt infiltration. Materials 2019, 12, 2425. [Google Scholar] [CrossRef]
- Molina, J.M.; Saravanan, R.A.; Arpo´n, R.; Garcıá-Cordovilla, C.; Louis, E.; Narciso, J. Pressure infiltration of liquid aluminium into packed SiC particulate with a bimodal size distribution. Acta Mater. 2002, 50, 247–257. [Google Scholar] [CrossRef]
- Garcia-Cordovilla, C.; Louis, E.; Narciso, J. Pressure infiltration of packed ceramic particulates by liquid metals. Acta Mater. 1999, 47, 4461–4479. [Google Scholar] [CrossRef]
- Xia, F.; Wu, X.; Liu, P. Method for determining aperture of porous materials. J. Clin. Reha. Tiss. Eng. Res. 2008, 41, 8183–8188. [Google Scholar]
- Calderon, N.; Martinez-Escandell, M.; Narciso, J.; Rodriguez-Reinoso, F. Manufacture of biomorphic SiC components with homogenous properties from sawdust by reactive infiltration with liquid Silicon. J. Am. Ceram. Soc. 2010, 93, 1003–1009. [Google Scholar] [CrossRef]
- Cui, H.; Wang, Y.; Zhang, M.; Wang, W.; Zhao, C. A fractal method to calculate the permeability for compressible gas flow through a porous restrictor in aerostatic bearings. Int. J. Heat Mass Tran. 2018, 121, 437–452. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Zhao, J.; Ai, L.; Yang, L. Variations in permeability along with interfacial tension in hydrate-bearing porous media. J. Nat. Gas Sci. Eng. 2018, 51, 141–146. [Google Scholar] [CrossRef]
- Yifei, L.; Yihui, Y.; Hong, Y.; Xinen, L.; Jun, M.; Hailong, C. Modeling for optimization of circular flat pad aerostatic bearing with a single central orifice-type restrictor based on CFD simulation. Tribol. Int. 2017, 109, 206–216. [Google Scholar] [CrossRef]
- Caccia, M.; Camarano, A.; Sergi, D.; Ortona, A.; Narciso, J. Wetting and Navier-Stokes Equation: The Manufacture of Composite materials, Wetting and Wettability; InTechOpen: London, UK, 2015. [Google Scholar]
- Bahraini, M.; Molina, J.M.; Kida, M.; Weber, L.; Narciso, J.; Mortensen, A. Measuring and tailoring capillary forces during liquid metal infiltration. Curr. Opin. Solid State Mater. Sci. 2005, 9, 196–201. [Google Scholar] [CrossRef]
- Rybus, T.; Seweryn, K. Planar air-bearing microgravity simulators: Review of applications, existing solutions and design parameters. Acta Astronaut. 2016, 120, 239–259. [Google Scholar] [CrossRef]
- Du, J.; Ai, D.; Xiao, X.; Song, J.; Li, Y.; Chen, Y.; Wang, L.; Zhu, K. Rational design and porosity of porous alumina ceramic membrane for air bearing. Membranes 2021, 11, 872. [Google Scholar] [CrossRef]






| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| Pressure drop (Δp) (MPa) | 0.02 | 0.03 | 0.04 | 0.05 |
| Volume flow rate (Q × 10−5 (m3/s)) | 8.633 | 13.283 | 18.583 | 23.267 |
| Parameter | Value |
|---|---|
| Bearing body diameter (D0) (mm) | 48 |
| Gas-capacity thickness (H0) (mm) | 10 |
| Porous medium diameter (D1) (mm) | 43 |
| Porous medium thickness (H1) (mm) | 5 |
| Gas-film thickness (h) (μm) | 4~26 |
| Gas-supply pressure (Ps) (MPa) | 0.5 |
| Environmental temperature (T) (K) | 298 |
| Environmental pressure (P0) (MPa) | 0.1 |
| Aerodynamic viscosity (μ) (N·s/m2) | 1.7894 × 10−5 |
| Permeability coefficient of porous medium (φ) (m2) | 2.78 × 10−13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Du, J.; Zhang, Y.; Yan, J.; Li, Y.; Zhu, K.; Wang, L. Study on Static Characteristics of Aerostatic Bearing Based on Porous SiC Ceramic Membranes. Membranes 2022, 12, 898. https://doi.org/10.3390/membranes12090898
Xiao X, Du J, Zhang Y, Yan J, Li Y, Zhu K, Wang L. Study on Static Characteristics of Aerostatic Bearing Based on Porous SiC Ceramic Membranes. Membranes. 2022; 12(9):898. https://doi.org/10.3390/membranes12090898
Chicago/Turabian StyleXiao, Xin, Jianzhou Du, Yu Zhang, Jingyi Yan, Yunping Li, Kongjun Zhu, and Luming Wang. 2022. "Study on Static Characteristics of Aerostatic Bearing Based on Porous SiC Ceramic Membranes" Membranes 12, no. 9: 898. https://doi.org/10.3390/membranes12090898
APA StyleXiao, X., Du, J., Zhang, Y., Yan, J., Li, Y., Zhu, K., & Wang, L. (2022). Study on Static Characteristics of Aerostatic Bearing Based on Porous SiC Ceramic Membranes. Membranes, 12(9), 898. https://doi.org/10.3390/membranes12090898









