Conversion Kinetics and Ionic Conductivity in Na-β”-Alumina + YSZ (Naβ”AY) Sodium Solid Electrolyte via Vapor Phase Conversion Process
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of α-Alumina + YSZ Samples
2.2. Formation of Na-β”-Alumina + YSZ Samples via Vapor Phase Conversion
2.3. Characterization
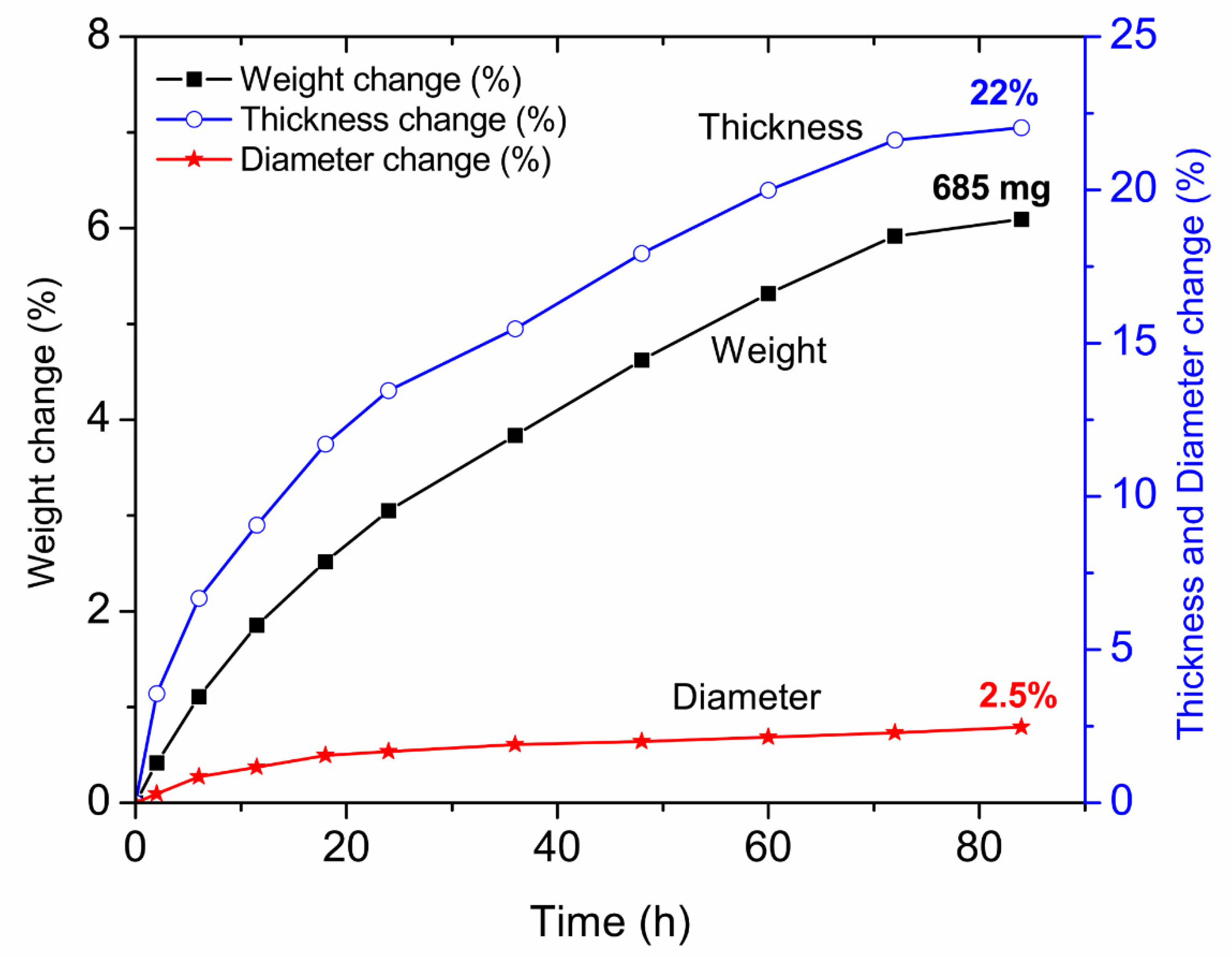
3. Results and Discussion
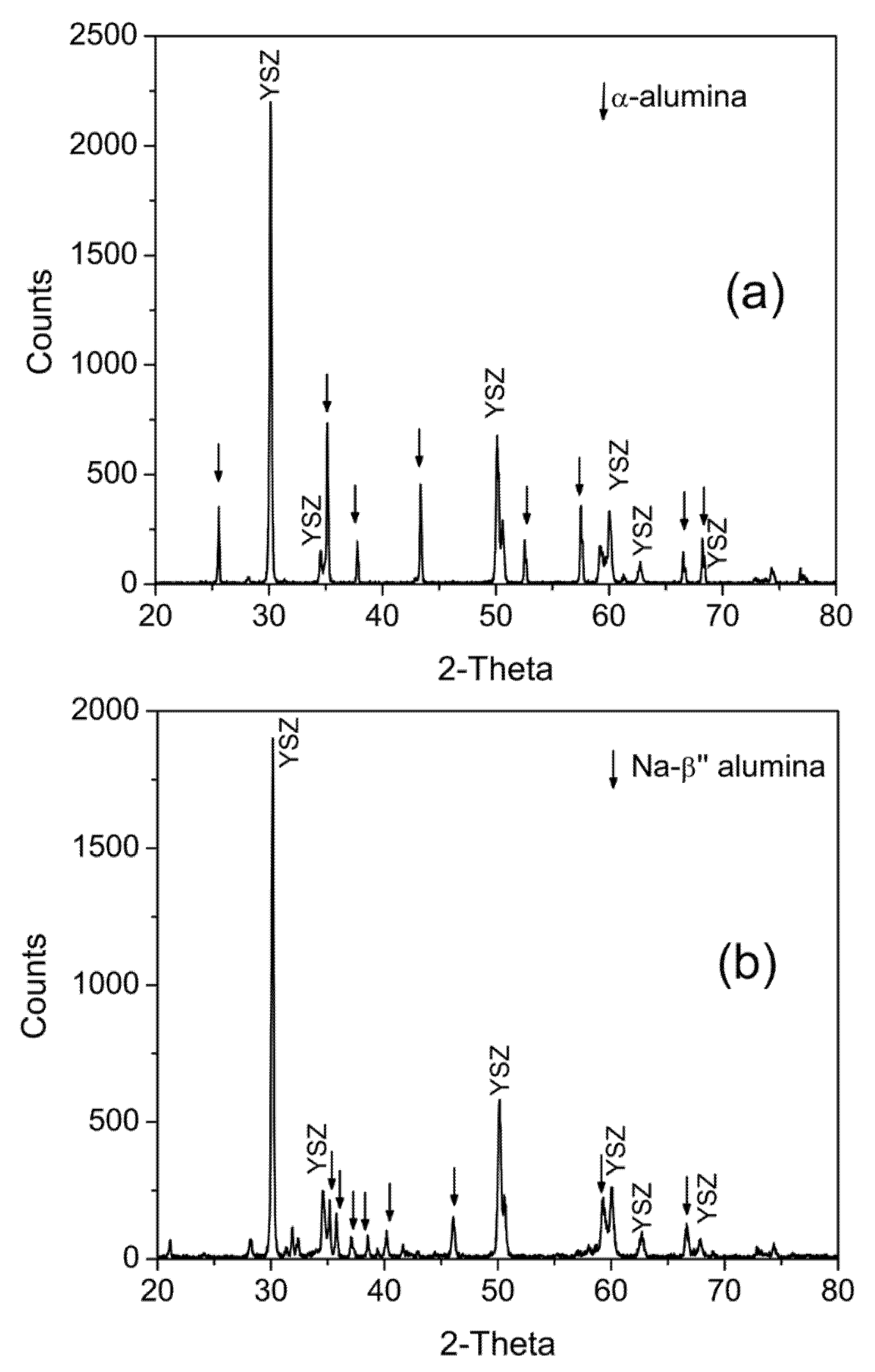
3.1. X-ray-Diffraction
3.2. SEM and EDS Analysis
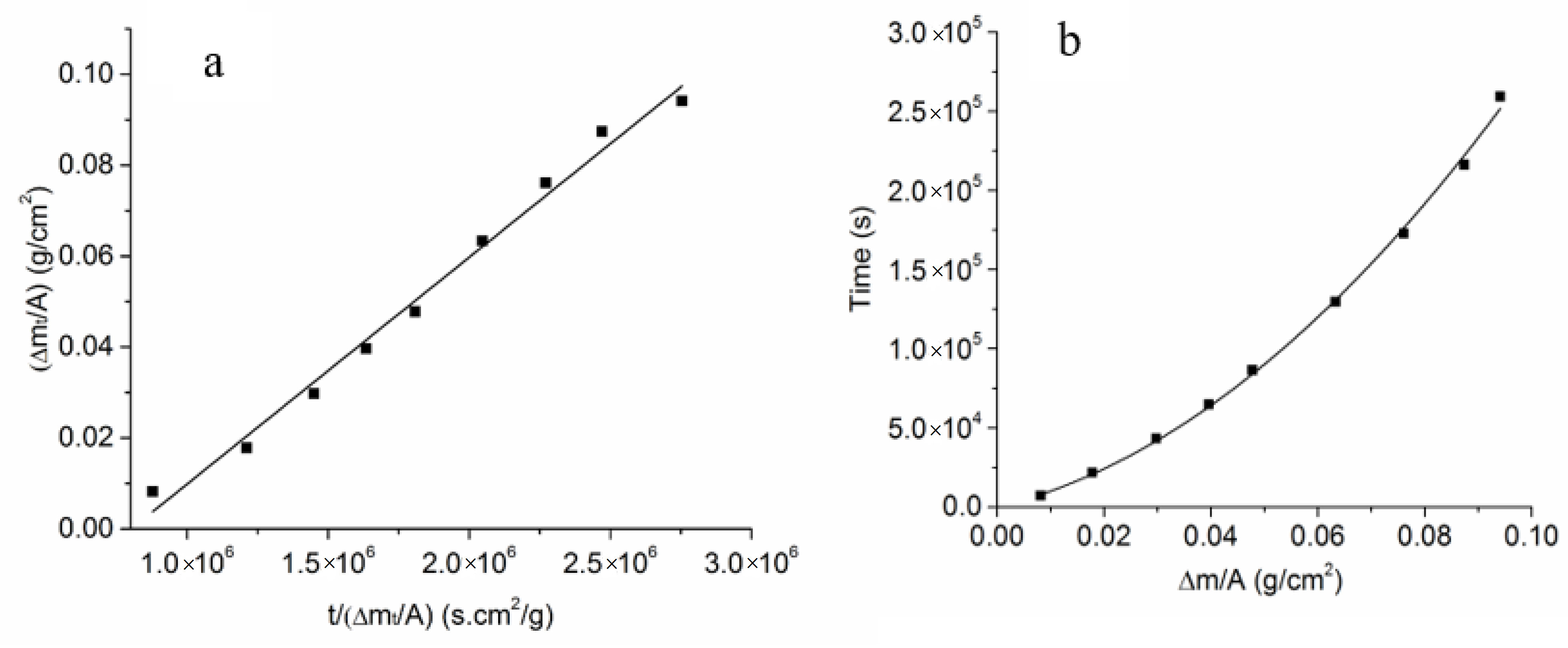
3.3. Estimation of the Kinetic Parameters on the Uncoated Samples
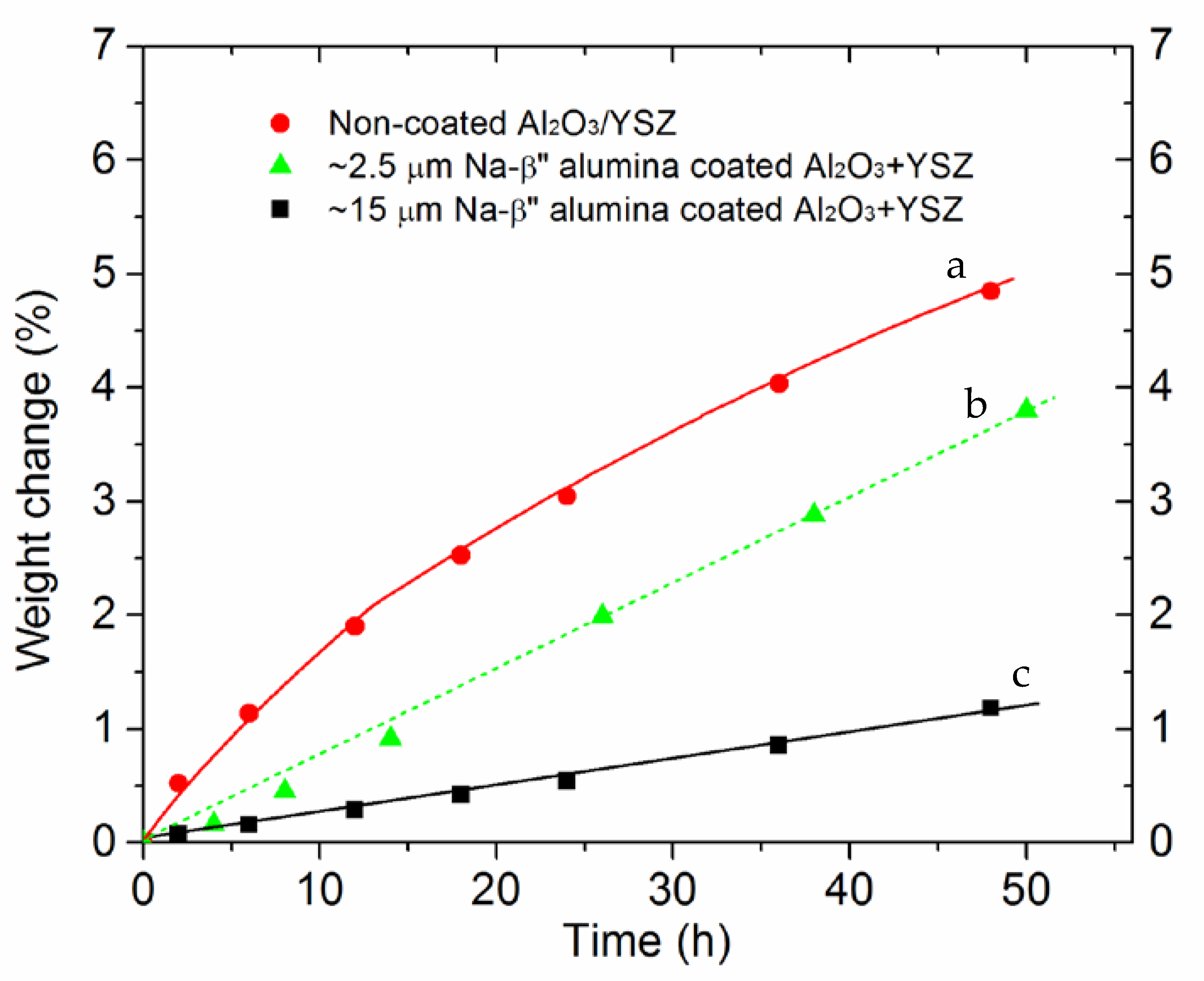
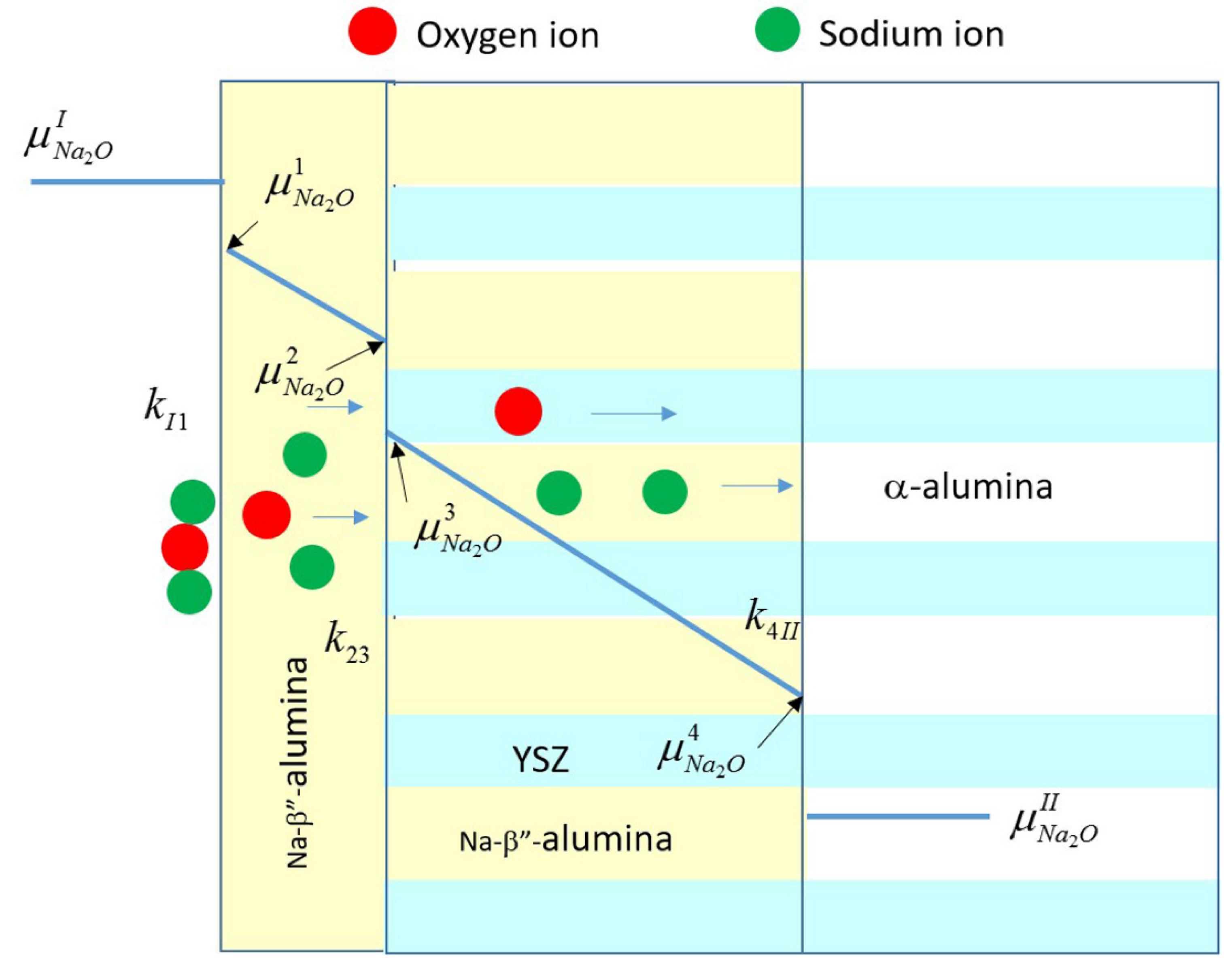
3.4. Effects of Na-β”-Alumina Coating on Conversion Kinetics
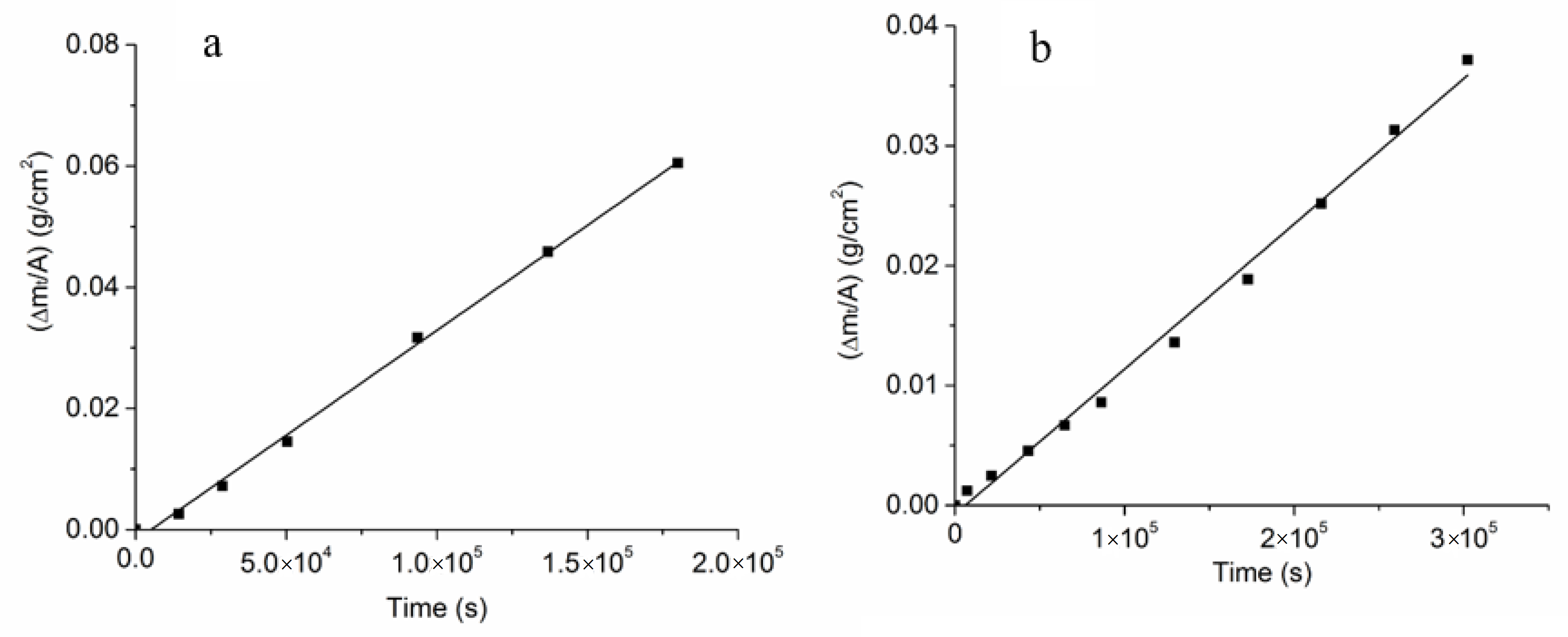
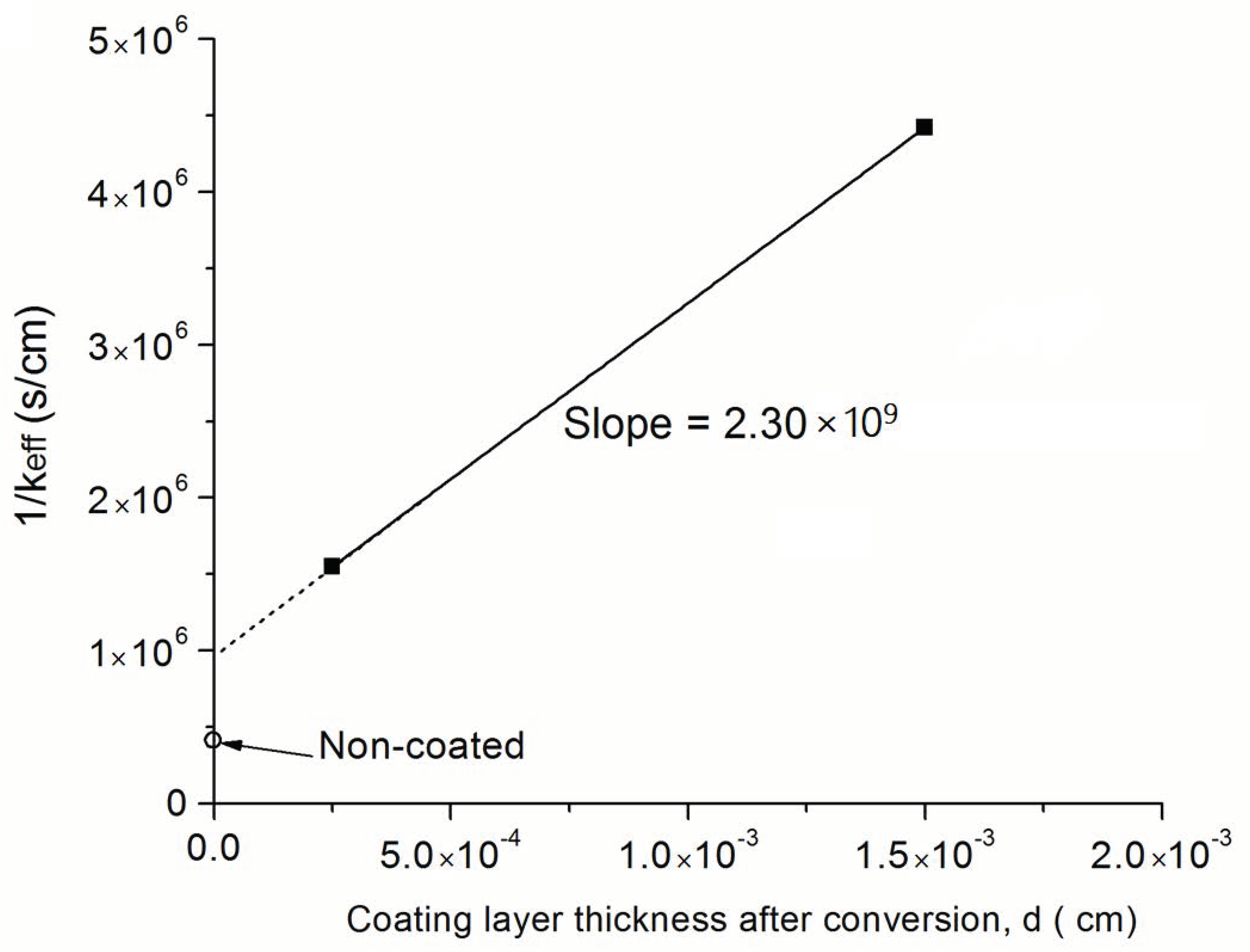
3.5. Estimation of the Kinetic Parameter for the Coated Samples
3.6. Measurement of Ionic Conductivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
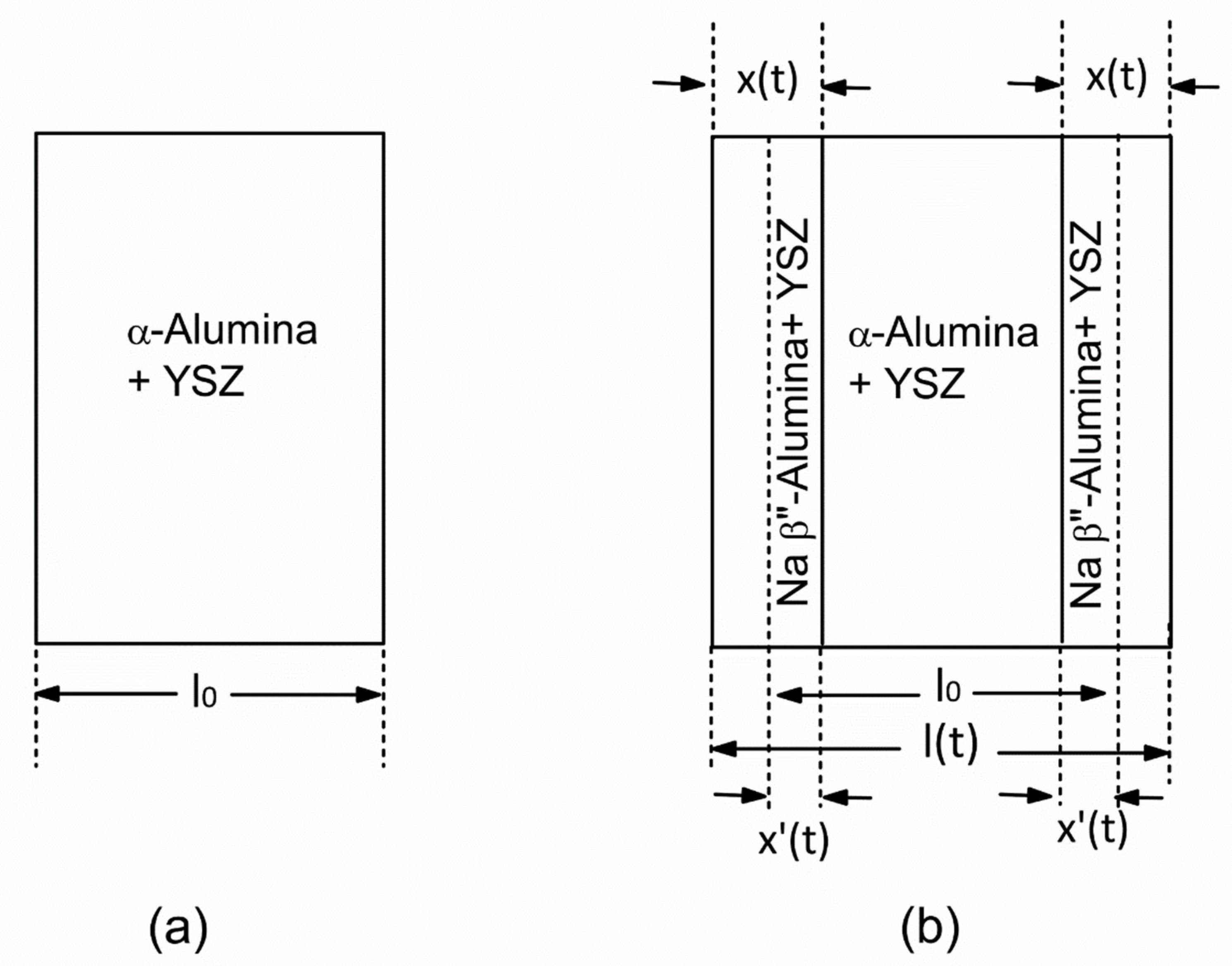
Appendix A. Vapor Phase Conversion Kinetics and Transport Parameters
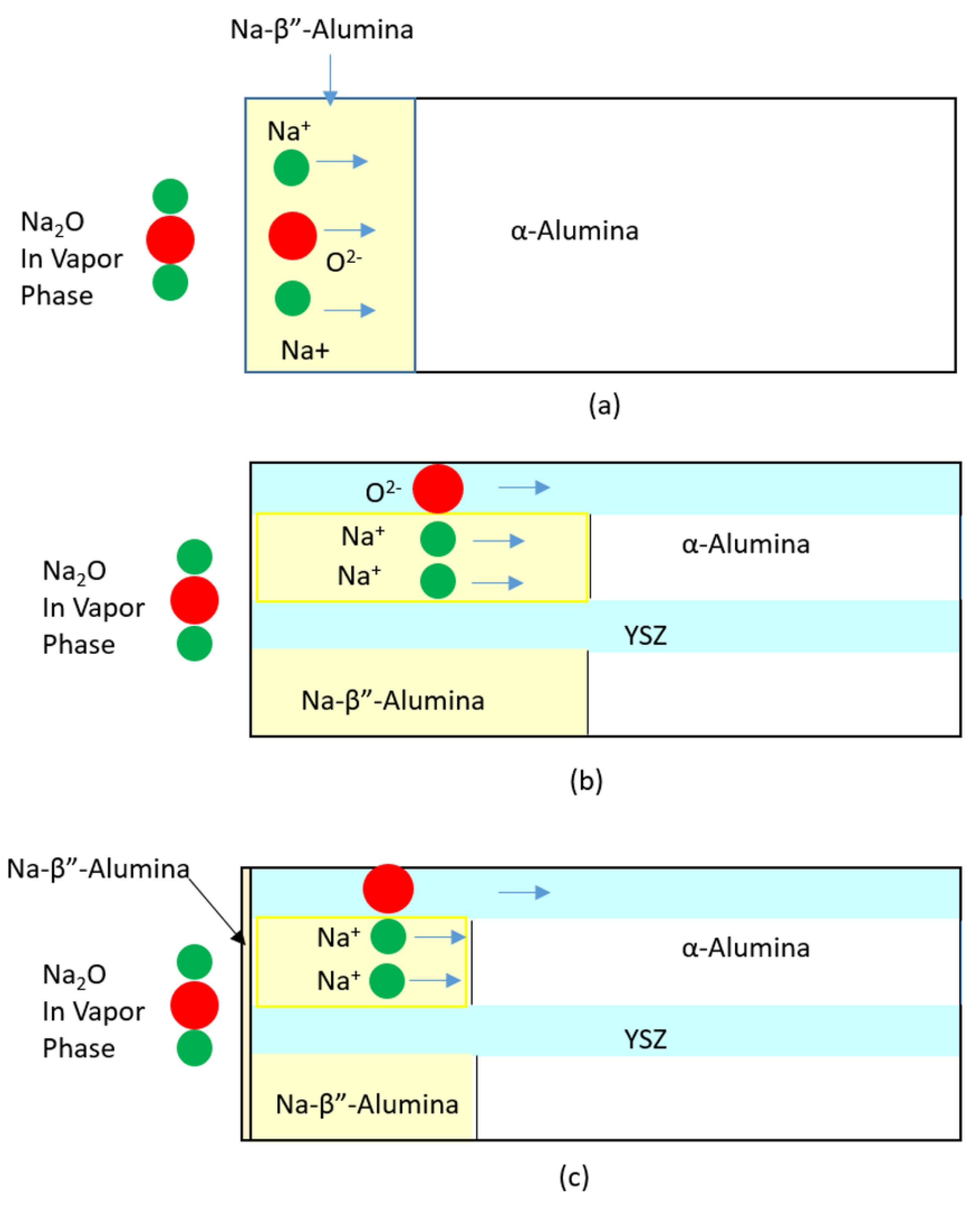
Appendix B. Study of Kinetics of Vapor Phase Conversion by Weight Measurement
References
- Weber, N.; Kummer, J.T. Sodium-sulfur Secondary Battery. Annu. Power Sources Conf. 1967, 21, 3–39. [Google Scholar]
- Sudworth, J.L. Zebra batteries. J. Power Sources 1994, 51, 105–114. [Google Scholar] [CrossRef]
- Hunt, T.K.; Weber, N.; Cole, T. High efficiency thermoelectric conversion with beta″-alumina electrolytes, the sodium heat engine. Solid State Ion. 1981, 5, 263–265. [Google Scholar] [CrossRef]
- Fertig, M.P.; Skadell, K.; Schulz, M.; Dirksen, C.; Adelhelm, P.; Stelter, M. From High- to Low-Temperature: The Revival of Sodium-Beta Alumina for Sodium Solid-State Batteries. Batter. Supercaps 2022, 5, e202100131. [Google Scholar] [CrossRef]
- Ligon, S.C.; Bay, M.C.; Heinz, M.V.; Battaglia, C.; Graule, T.; Blugan, G. Large Planar Na-β″-Al2O3 Solid Electrolytes for Next Generation Na-Batteries. Materials 2020, 13, 433. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Wang, X.; Dong, C.; Chen, J.; Wang, D.; Mao, Z. Constructing effective interface for room-temperature Beta-Al2O3 based sodium metal batteries. J. Power Sources 2022, 523, 231034. [Google Scholar] [CrossRef]
- Ligon, S.C.; Blugan, G.; Bay, M.C.; Battaglia, C.; Heinz, M.V.; Graule, T. Performance analysis of Na-β″-Al2O3/YSZ solid electrolytes produced by conventional sintering and by vapor conversion of α-Al2O3/YSZ. Solid State Ion. 2020, 345, 115169. [Google Scholar] [CrossRef]
- Bay, M.C.; Wang, M.; Grissa, R.; Heinz, M.V.; Sakamoto, J.; Battaglia, C. Sodium Plating from Na-β″-Alumina Ceramics at Room Temperature, Paving the Way for Fast-Charging All-Solid-State Batteries. Adv. Energy Mater. 2020, 10, 1902899. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.G.; Ahn, B.M.; Ahn, C.W.; Choi, J.H.; Lee, D.H.; Lim, S.K. Fabrication of a Full-Scale Pilot Model of a Cost-Effective Sodium Nickel-Iron Chloride Battery Over 40 Ah. J. Electrochem. Sci. Technol. 2021, 12, 398–405. [Google Scholar] [CrossRef]
- Sudworth, J.; Tiley, A.R. Sodium Sulfur Battery, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Zhu, L.; Virkar, A. Sodium, Silver and Lithium-Ion Conducting β″-Alumina + YSZ Composites, Ionic Conductivity and Stability. Crystals 2021, 11, 293. [Google Scholar] [CrossRef]
- Youngblood, G.E.; Virkar, A.V.; Cannon, W.R. Sintering Processes and Heat Treatment Schedules for Conductive, Lithia-stabilized beta″-Al2O3. Am. Ceram. Soc. Bull. 1977, 56, 206–210, 212. [Google Scholar]
- Virkar, A.V.; Armstrong, T.J.; Weber, N.; Fung, K.-Z.; Jue, J.-F. Role of coupled transport in the fabrication of sodium beta-alumina containing ceramics by a vapor phase process. Electrochem. Soc. Proc. 2002, 2002-5, 200–211. [Google Scholar]
- Virkar, A.V.; Jue, J.F.; Fung, K.Z. Alkali-Metal-β- and β″-Alumina and Gallate Polycrystalline Ceramics and Fabrication by a Vapor Phase Method. Google Patent US-6632763-B2, 14 October 2003. [Google Scholar]
- Li, G.; Lu, X.; Kim, J.Y.; Meinhardt, K.D.; Chang, H.J.; Canfield, N.L.; Sprenkle, V.L. Advanced intermediate temperature sodium–nickel chloride batteries with ultra-high energy density. Nat. Commun. 2016, 7, 10683. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Lu, X.; Kim, J.Y.; Lemmon, J.P.; Sprenkle, V.L. Cell degradation of a Na-NiCl2 (ZEBRA) battery. J. Mater. Chem. A 2013, 1, 14935–14942. [Google Scholar] [CrossRef]
- Wang, L.; Lu, Y.; Liu, J.; Xu, M.; Cheng, J.; Zhang, D.; Goodenough, J.B. A superior low-cost cathode for a Na-Ion battery. Angew. Chem. Int. Ed. 2013, 52, 1964–1967. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Li, G.; Kim, J.Y.; Meinhardt, K.D.; Sprenkle, V.L. Enhanced sintering of β″-Al2O3/YSZ with the sintering aids of TiO2 and MnO2. J. Power Sources 2015, 295, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Kirby, B.W.; Xu, W.; Li, G.; Kim, J.Y.; Lemmon, J.P.; Sprenkle, V.L.; Yang, Z. Advanced intermediate-temperature Na–S battery. Energy Environ. Sci. 2012, 6, 299–306. [Google Scholar] [CrossRef]
- Lin, G.-Y.; Virkar, A.V. Development of Surface Compressive Stresses in Zirconia-Alumina Composites by an Ion-Exchange Process. J. Am. Ceram. Soc. 2004, 84, 1321–1326. [Google Scholar] [CrossRef]
- Canfield, N.L.; Kim, J.Y.; Bonnett, J.F.; Pearson, R.; Sprenkle, V.L.; Jung, K. Effects of fabrication conditions on mechanical properties and microstructure of duplex β″-Al2O3 solid electrolyte. Mater. Sci. Eng. B 2015, 197, 43–50. [Google Scholar] [CrossRef]
- Parthasarathy, P.; Virkar, A.V. Vapor Phase Conversion of α-Alumina + Zirconia Composites into Sodium Ion Conducting Na-β″-Alumina + Zirconia Solid Electrolytes. J. Electrochem. Soc. 2013, 160, A2268–A2280. [Google Scholar] [CrossRef]
- Vignarooban, K.; Kushagra, R.; Elango, A.; Badami, P.; Mellander, B.-E.; Xu, X.; Tucker, T.; Nam, C.; Kannan, A. Current trends and future challenges of electrolytes for sodium-ion batteries. Int. J. Hydrogen Energy 2016, 41, 2829–2846. [Google Scholar] [CrossRef]
- Fergus, J.W. Ceramic and polymeric solid electrolytes for lithium-ion batteries. J. Power Sources 2010, 195, 4554–4569. [Google Scholar] [CrossRef]
- Koh, J.-H.; Weber, N.; Virkar, A.V. Synthesis of lithium-beta-alumina by various ion-exchange and conversion processes. Solid State Ion. 2012, 220, 32–38. [Google Scholar] [CrossRef]
- Dahbi, M.; Ghamouss, F.; Tran-Van, F.; Lemordant, D.; Anouti, M. Comparative study of EC/DMC LiTFSI and LiPF6 electrolytes for electrochemical storage. J. Power Sources 2011, 196, 9743–9750. [Google Scholar] [CrossRef]
- Jimenez, R.; Rivera, A.; Varez, A.; Sanz, J. Li mobility in Li0.5−xNaxLa0.5TiO3 perovskites (0 ≤ x ≤ 0.5) Influence of structural and compositional parameters. Solid State Ion. 2009, 180, 1362–1371. [Google Scholar]
- Knauth, P. Inorganic solid Li ion conductors: An overview. Solid State Ion. 2009, 180, 911–916. [Google Scholar] [CrossRef]
- Kosova, N.V.; Devyatkina, E.T.; Stepanov, A.P.; Buzlukov, A.L. Lithium conductivity and lithium diffusion in NASICON-type Li1+xTi2−xAlx(PO4)3 (x = 0; 0.3) prepared by mechanical activation. Ionics 2008, 14, 303–311. [Google Scholar] [CrossRef]
- Kim, J.; Jo, S.H.; Bhavaraju, S.; Eccleston, A.; Kang, S.O. Low temperature performance of sodium–nickel chloride batteries with NaSICON solid electrolyte. J. Electroanal. Chem. 2015, 759 Pt 2, 201–206. [Google Scholar] [CrossRef]
- Fine, M.E. Introduction to Phase Transformations in Condensed Systems; Macmillan: New York, NY, USA, 1964. [Google Scholar]



| Samples | ||
|---|---|---|
| Non-coated α-alumina/YSZ composite | 2.33 × 10−6 | 1.74 × 10−7 |
| ~2.5 µm Na-β”-alumina-coated α-alumina + YSZ composite | 6.45 × 10−7 | 1.74 × 10−7 |
| ~15 µm Na-β”-alumina-coated α-alumina + YSZ composite | 2.26 × 10−7 | 1.74 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Virkar, A.V. Conversion Kinetics and Ionic Conductivity in Na-β”-Alumina + YSZ (Naβ”AY) Sodium Solid Electrolyte via Vapor Phase Conversion Process. Membranes 2022, 12, 567. https://doi.org/10.3390/membranes12060567
Zhu L, Virkar AV. Conversion Kinetics and Ionic Conductivity in Na-β”-Alumina + YSZ (Naβ”AY) Sodium Solid Electrolyte via Vapor Phase Conversion Process. Membranes. 2022; 12(6):567. https://doi.org/10.3390/membranes12060567
Chicago/Turabian StyleZhu, Liangzhu, and Anil V. Virkar. 2022. "Conversion Kinetics and Ionic Conductivity in Na-β”-Alumina + YSZ (Naβ”AY) Sodium Solid Electrolyte via Vapor Phase Conversion Process" Membranes 12, no. 6: 567. https://doi.org/10.3390/membranes12060567
APA StyleZhu, L., & Virkar, A. V. (2022). Conversion Kinetics and Ionic Conductivity in Na-β”-Alumina + YSZ (Naβ”AY) Sodium Solid Electrolyte via Vapor Phase Conversion Process. Membranes, 12(6), 567. https://doi.org/10.3390/membranes12060567






