Experimental Investigations on the Conductance of Lipid Membranes under Differential Hydrostatic Pressure
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
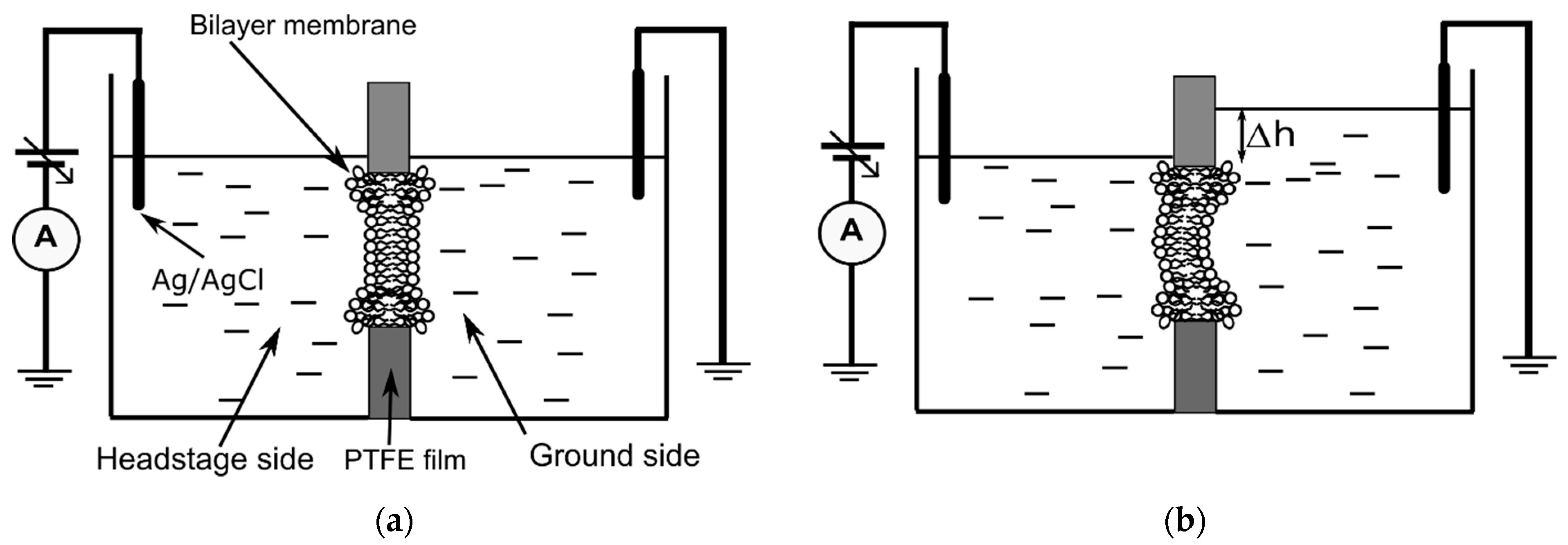
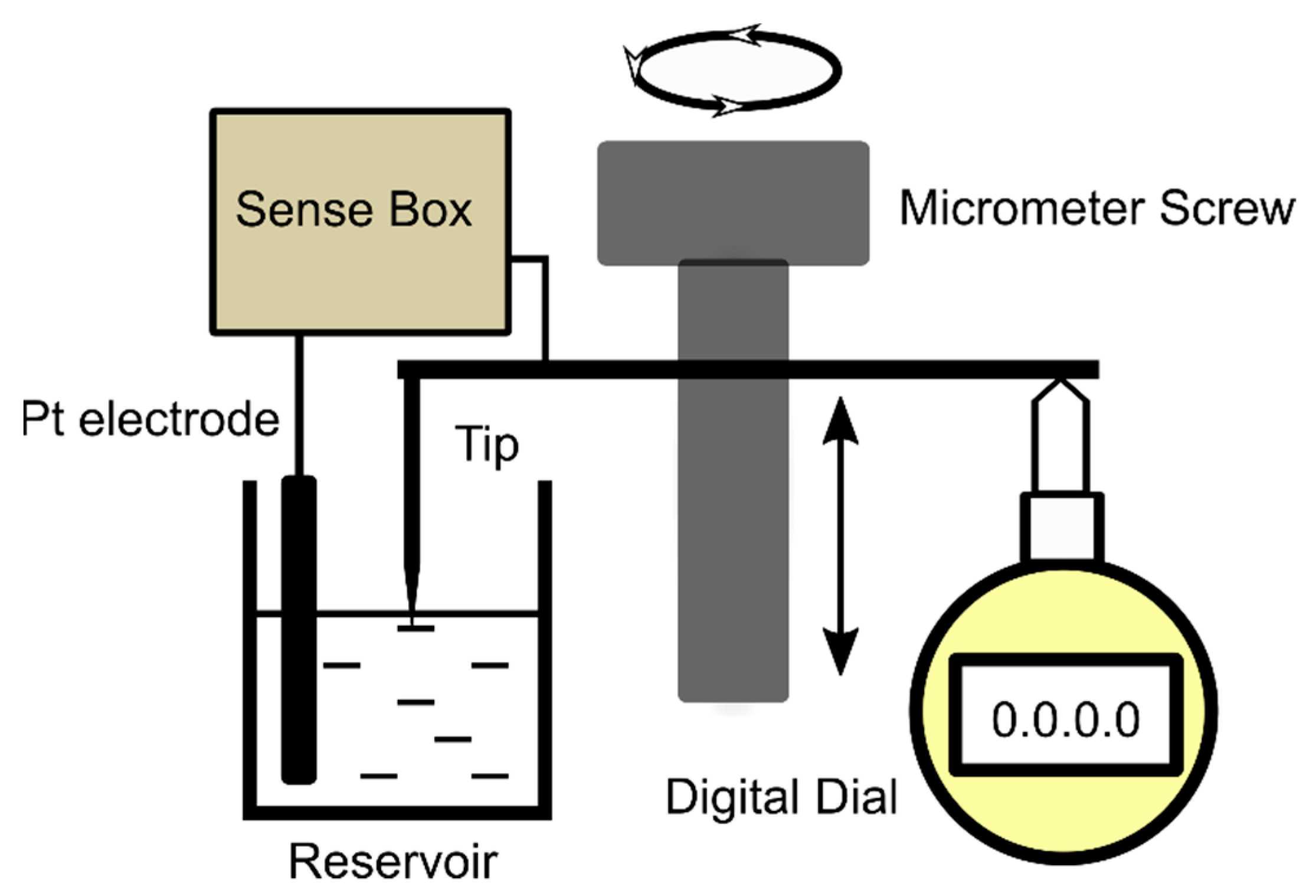
2.2. Production and Characterization of Planar and Curved Bilayer Lipid Membranes (BLM)
3. Results and Discussion
3.1. Height Calibration of the BLM Reservoir
3.2. Preliminary Investigations on the Influence of Differential Pressure on Membranes’ Conductance
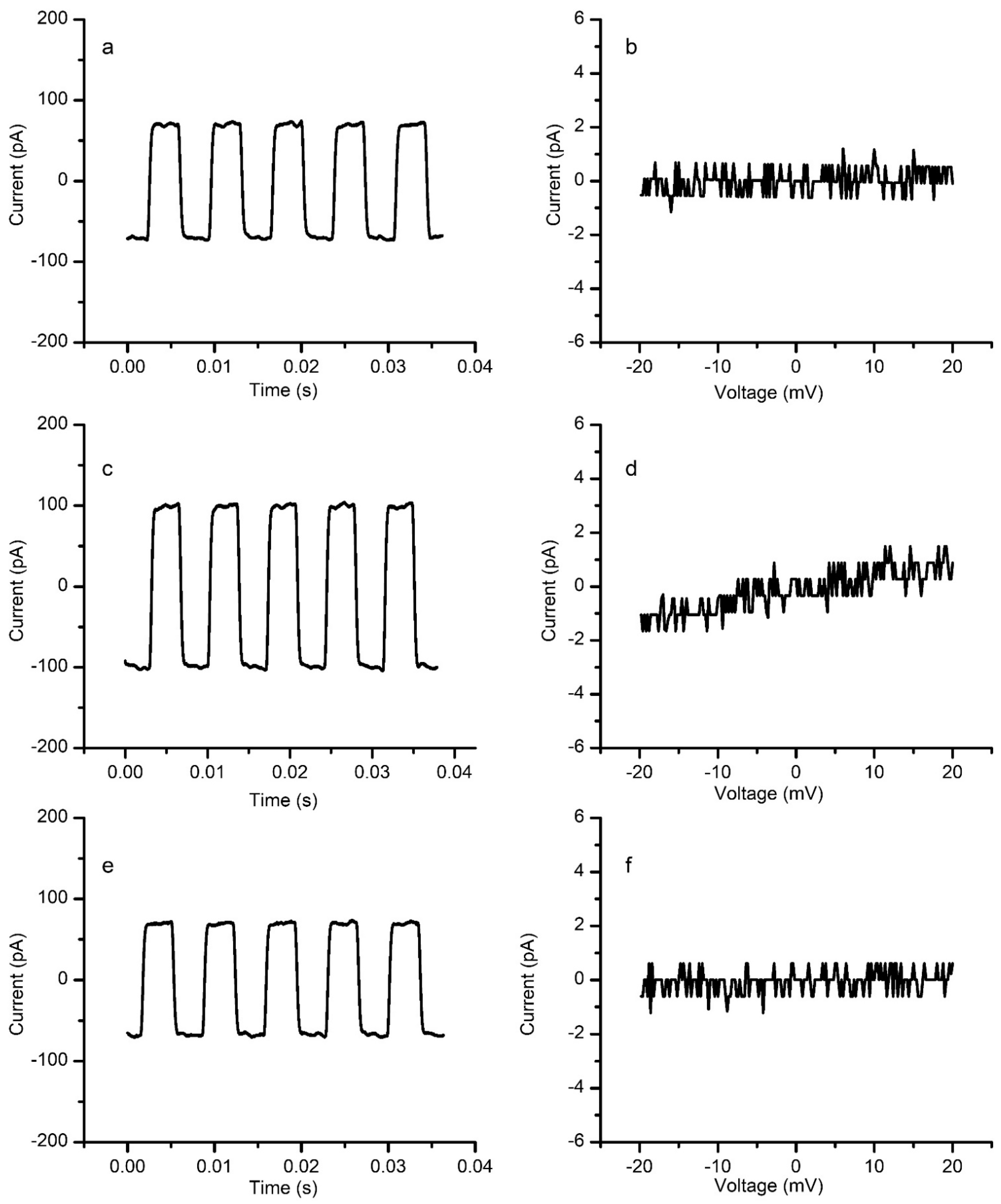
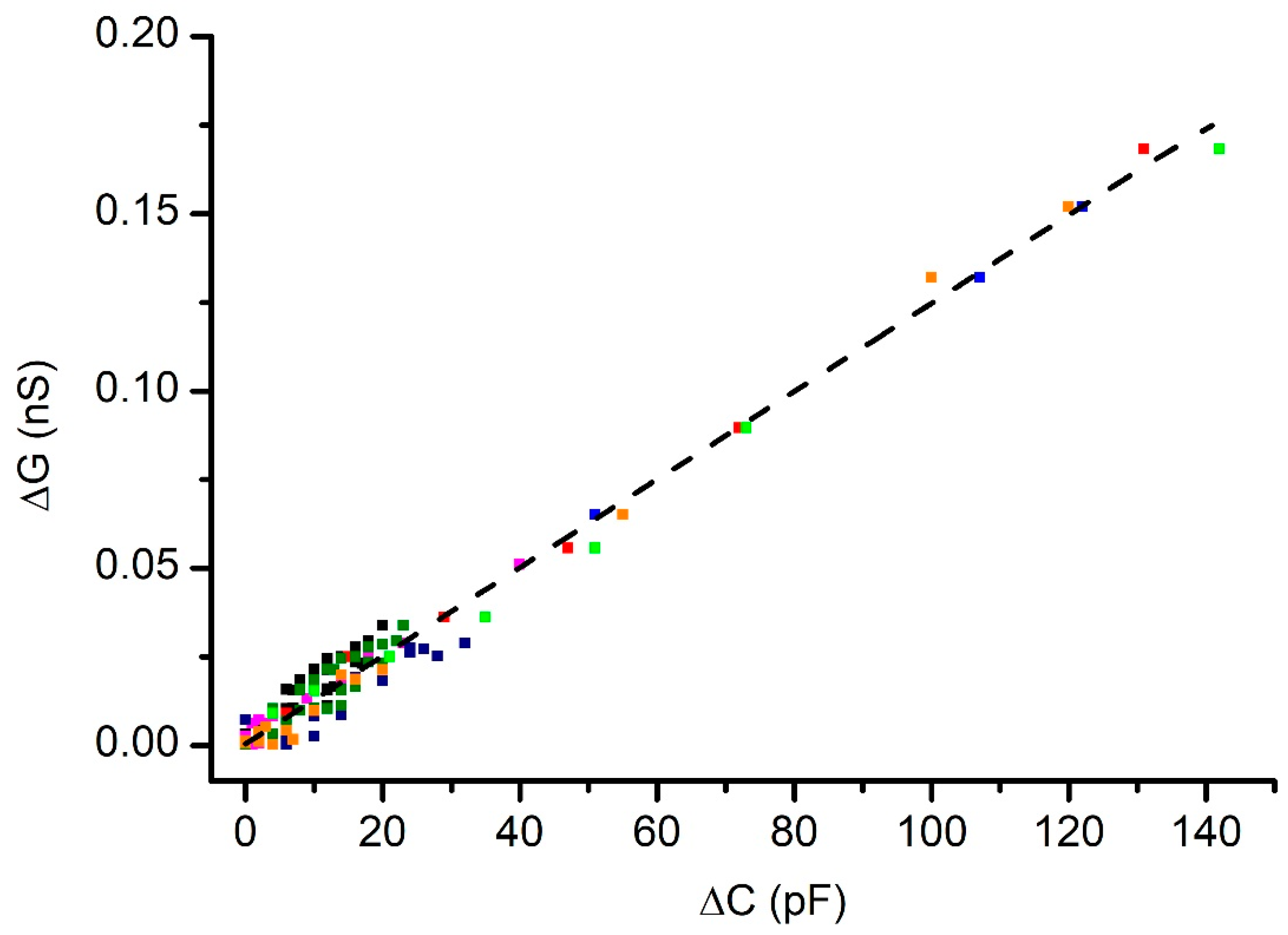
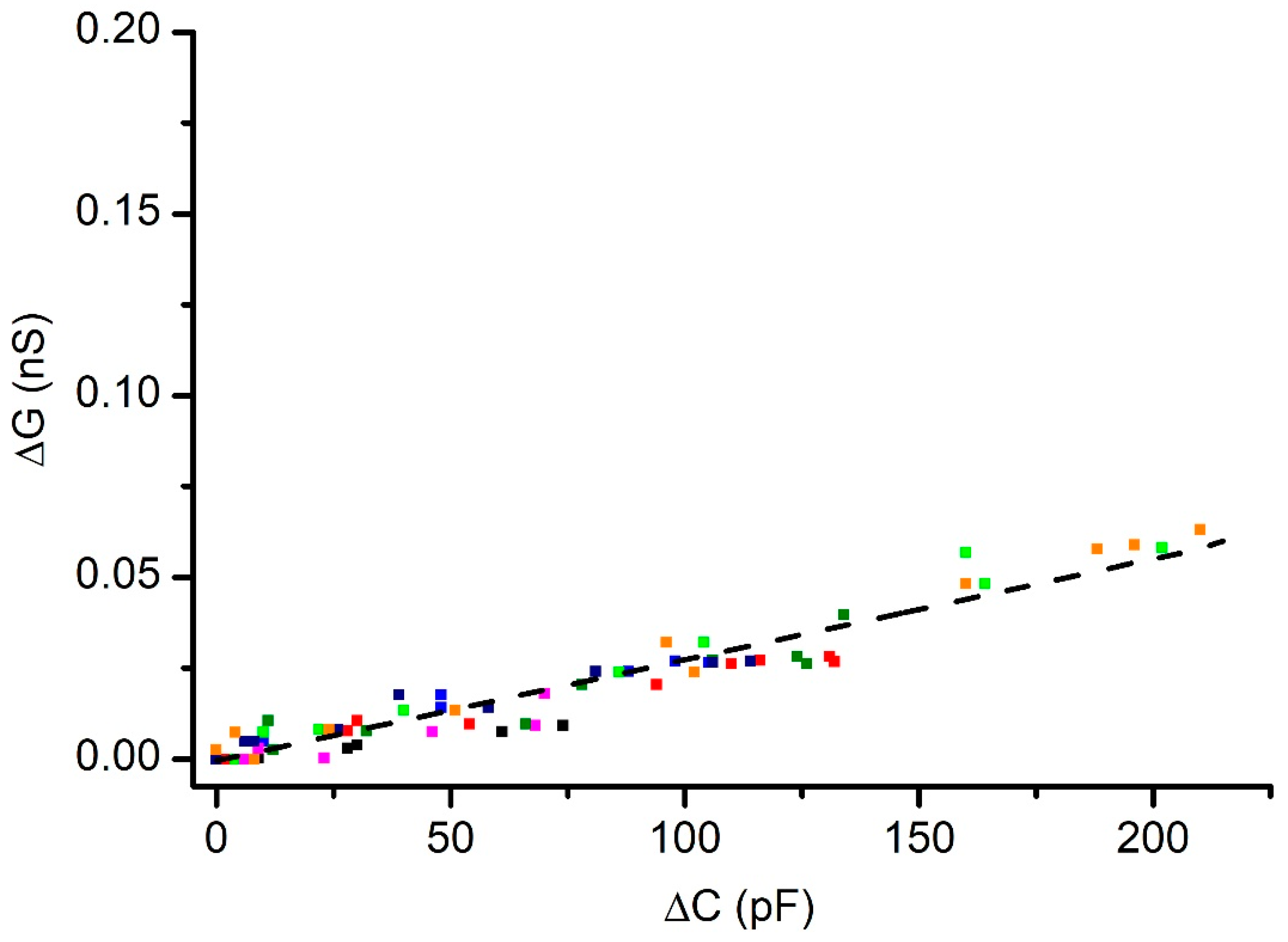
3.3. Pressure Influences the Ionic Conductance of Cholesterol-Free Membranes
3.4. Effects of Pressure on the Conductance of Membranes with Cholesterol
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martinac, B. Mechanosensitive ion channels: Molecules of mechanotransduction. J. Cell Sci. 2004, 117, 2449–2460. [Google Scholar] [CrossRef] [PubMed]
- Ridone, P.; Vassalli, M.; Martinac, B. Piezo1 mechanosensitive channels: What are they and why are they important. Biophys. Rev. 2019, 11, 795–805. [Google Scholar] [CrossRef] [PubMed]
- Flegler Vanessa, J.; Rasmussen, A.; Borbil, K.; Boten, L.; Chen, H.-A.; Deinlein, H.; Halang, J.; Hellmanzik, K.; Löffler, J.; Schmidt, V.; et al. Mechanosensitive channel gating by delipidation. Proc. Natl. Acad. Sci. USA 2021, 118, e2107095118. [Google Scholar] [CrossRef] [PubMed]
- Corey, D. Sensory transduction in the ear. J. Cell Sci. 2003, 116, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Corey, D.P. New TRP Channels in Hearing and Mechanosensation. Neuron 2003, 39, 585–588. [Google Scholar] [CrossRef]
- Gillespie, P.G.; Walker, R.G. Molecular basis of mechanosensory transduction. Nature 2001, 413, 194–202. [Google Scholar] [CrossRef] [PubMed]
- Le Roux, A.-L.; Quiroga, X.; Walani, N.; Arroyo, M.; Roca-Cusachs, P. The plasma membrane as a mechanochemical transducer. Philos. Trans. R. Soc. B Biol. Sci. 2019, 374, 20180221. [Google Scholar] [CrossRef]
- Blount, P.; Iscla, I. Life with Bacterial Mechanosensitive Channels, from Discovery to Physiology to Pharmacological Target. Microbiol. Mol. Biol. Rev. 2020, 84, e00055-19. [Google Scholar] [CrossRef]
- Chen, Y.; Ju, L.; Rushdi, M.; Ge, C.; Zhu, C. Receptor-mediated cell mechanosensing. Mol. Biol. Cell 2017, 28, 3134–3155. [Google Scholar] [CrossRef]
- Haswell, E.S.; Phillips, R.; Rees, D.C. Mechanosensitive Channels: What Can They Do and How Do They Do It? Structure 2011, 19, 1356–1369. [Google Scholar] [CrossRef]
- Janmey, P.A.; McCulloch, C.A. Cell Mechanics: Integrating Cell Responses to Mechanical Stimuli. Annu. Rev. Biomed. Eng. 2007, 9, 1–34. [Google Scholar] [CrossRef]
- Andersen, O.S.; Fuchs, M. Potential energy barriers to ion transport within lipid bilayers. Studies with tetraphenylborate. Biophys. J. 1975, 15, 795–830. [Google Scholar] [CrossRef]
- Deamer, D. The Role of Lipid Membranes in Life’s Origin. Life 2017, 7, 5. [Google Scholar] [CrossRef] [PubMed]
- Parsegian, A. Energy of an Ion crossing a Low Dielectric Membrane: Solutions to Four Relevant Electrostatic Problems. Nature 1969, 221, 844–846. [Google Scholar] [CrossRef]
- Khavrutskii, I.V.; Gorfe, A.A.; Lu, B.; McCammon, J.A. Free Energy for the Permeation of Na+ and Cl- Ions and Their Ion-Pair through a Zwitterionic Dimyristoyl Phosphatidylcholine Lipid Bilayer by Umbrella Integration with Harmonic Fourier Beads. J. Am. Chem. Soc. 2009, 131, 1706–1716. [Google Scholar] [CrossRef][Green Version]
- Vorobyov, I.; Bekker, B.; Allen, T.W. Electrostatics of Deformable Lipid Membranes. Biophys. J. 2010, 98, 2904–2913. [Google Scholar] [CrossRef]
- Vorobyov, I.; Olson, T.E.; Kim, J.H.; Koeppe, R.E., II; Andersen, O.S.; Allen, T.W. Ion-induced defect permeation of lipid membranes. Biophys. J. 2014, 106, 586–597. [Google Scholar] [CrossRef]
- Yesylevskyy, S.; Rivel, T.; Ramseyer, C. Curvature increases permeability of the plasma membrane for ions, water and the anti-cancer drugs cisplatin and gemcitabine. Sci. Rep. 2019, 9, 17214. [Google Scholar] [CrossRef]
- Yesylevskyy, S.A.-O.; Rivel, T.; Ramseyer, C. The influence of curvature on the properties of the plasma membrane. Insights from atomistic molecular dynamics simulations. Sci. Rep. 2017, 7, 16078. [Google Scholar] [CrossRef]
- Khmelinskii, I.; Makarov, V. On the Effects of Mechanical Stress of Biological Membranes in Modeling of Swelling Dynamics of Biological Systems. Sci. Rep. 2020, 10, 8395. [Google Scholar] [CrossRef]
- Kuchel, P.W.; Cox, C.D.; Daners, D.; Shishmarev, D.; Galvosas, P. Surface model of the human red blood cell simulating changes in membrane curvature under strain. Sci. Rep. 2021, 11, 13712. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, K.; Morishita, T.; Aburai, K.; Ito, D.; Imura, T.; Sakai, K.; Abe, M.; Nakase, I.; Futaki, S.; Sakai, H. Direct entry of cell-penetrating peptide can be controlled by maneuvering the membrane curvature. Sci. Rep. 2021, 11, 31. [Google Scholar] [CrossRef] [PubMed]
- Montal, M.; Mueller, P. Formation of Bimolecular Membranes from Lipid Monolayers and a Study of Their Electrical Properties. Proc. Natl. Acad. Sci. USA 1972, 69, 3561–3566. [Google Scholar] [CrossRef] [PubMed]
- Nikoleli, G.-P.; Siontorou, C.; Nikolelis, M.-T.; Bratakou, S.; Bendos, D. Recent Lipid Membrane-Based Biosensing Platforms. Appl. Sci. 2019, 9, 1745. [Google Scholar] [CrossRef]
- Calleja, M.; Tello, M.; García, R. Size determination of field-induced water menisci in noncontact atomic force microscopy. J. Appl. Phys. 2002, 92, 5539–5542. [Google Scholar] [CrossRef]
- Naumowicz, M.; Figaszewski, Z.A. Pore Formation in Lipid Bilayer Membranes made of Phosphatidylcholine and Cholesterol Followed by Means of Constant Current. Cell Biochem. Biophys. 2013, 66, 109–119. [Google Scholar] [CrossRef][Green Version]
- Ries, R.S.; Choi, H.; Blunck, R.; Bezanilla, F.; Heath, J.R. Black Lipid Membranes: Visualizing the Structure, Dynamics, and Substrate Dependence of Membranes. J. Phys. Chem. B 2004, 108, 16040–16049. [Google Scholar] [CrossRef]
- Needham, D.; Haydon, D.A. Tensions and free energies of formation of "solventless" lipid bilayers. Measurement of high contact angles. Biophys. J. 1983, 41, 251–257. [Google Scholar] [CrossRef]
- White, S.H.; Petersen, D.C.; Simon, S.; Yafuso, M. Formation of planar bilayer membranes from lipid monolayers. A critique. Biophys. J. 1976, 16, 481–489. [Google Scholar] [CrossRef]
- Tsemperouli, M.; Amstad, E.; Sakai, N.; Matile, S.; Sugihara, K. Black Lipid Membranes: Challenges in Simultaneous Quantitative Characterization by Electrophysiology and Fluorescence Microscopy. Langmuir 2019, 35, 8748–8757. [Google Scholar] [CrossRef]
- Saeedimasine, M.; Montanino, A.; Kleiven, S.; Villa, A. Role of lipid composition on the structural and mechanical features of axonal membranes: A molecular simulation study. Sci. Rep. 2019, 9, 8000. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Barraza Kevin, M.; Beauchamp, J.L. Cholesterol provides nonsacrificial protection of membrane lipids from chemical damage at air-water interface. Proc. Natl. Acad. Sci. USA 2018, 115, 3255–3260. [Google Scholar] [CrossRef] [PubMed]
- Al-Rekabi, Z.; Contera, S. Multifrequency AFM reveals lipid membrane mechanical properties and the effect of cholesterol in modulating viscoelasticity. Proc. Natl. Acad. Sci. USA 2018, 115, 2658–2663. [Google Scholar] [CrossRef] [PubMed]
- Banuelos-Frias, A.; Castaneda-Montiel, V.M.; Alvizo-Paez, E.R.; Vazquez-Martinez, E.A.; Gomez, E.; Ruiz-Garcia, J. Thermodynamic and Mechanical Properties of DMPC/Cholesterol Mixed Monolayers at Physiological Conditions. Front. Phys. 2021, 9, 91. [Google Scholar] [CrossRef]
- Gumi-Audenis, B.; Costa, L.; Carla, F.; Comin, F.; Sanz, F.; Giannotti, M.I. Structure and Nanomechanics of Model Membranes by Atomic Force Microscopy and Spectroscopy: Insights into the Role of Cholesterol and Sphingolipids. Membranes 2016, 6, 58. [Google Scholar] [CrossRef]
- Henriksen, J.; Rowat, A.C.; Brief, E.; Hsueh, Y.W.; Thewalt, J.L.; Zuckermann, M.J.; Ipsen, J.H. Universal Behavior of Membranes with Sterols. Biophys. J. 2006, 90, 1639–1649. [Google Scholar] [CrossRef]
- Hissa, B.; Pontes, B.; Roma, P.M.S.; Alves, A.P.; Rocha, C.D.; Valverde, T.M.; Aguiar, P.H.N.; Almeida, F.P.; Guimaraes, A.J.; Guatimosim, C.; et al. Membrane Cholesterol Removal Changes Mechanical Properties of Cells and Induces Secretion of a Specific Pool of Lysosomes. PLoS ONE 2013, 8, e82988. [Google Scholar] [CrossRef]
- Hung, W.-C.; Lee, M.-T.; Chen, F.-Y.; Huang, H.W. The Condensing Effect of Cholesterol in Lipid Bilayers. Biophys. J. 2007, 92, 3960–3967. [Google Scholar] [CrossRef]
- Bieberich, E. Sphingolipids and lipid rafts: Novel concepts and methods of analysis. Chem. Phys. Lipids 2018, 216, 114–131. [Google Scholar] [CrossRef]
- Munro, S. Lipid Rafts: Elusive or Illusive? Cell 2003, 115, 377–388. [Google Scholar] [CrossRef]
- Campelo, F.; Arnarez, C.; Marrink, S.J.; Kozlov, M.M. Helfrich model of membrane bending: From Gibbs theory of liquid interfaces to membranes as thick anisotropic elastic layers. Adv. Colloid Interface Sci. 2014, 208, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Deserno, M. Fluid lipid membranes: From differential geometry to curvature stresses. Chem. Phys. Lipids 2015, 185, 11–45. [Google Scholar] [CrossRef] [PubMed]
- Guckenberger, A.; Gekle, S. Theory and algorithms to compute Helfrich bending forces: A review. J. Phys. Condens. Matter 2017, 29, 203001. [Google Scholar] [CrossRef] [PubMed]
- Colom, A.; Derivery, E.; Soleimanpour, S.; Tomba, C.; Molin, M.D.; Sakai, N.; Gonzalez-Gaitan, M.; Matile, S.; Roux, A. A fluorescent membrane tension probe. Nat. Chem. 2018, 10, 1118–1125. [Google Scholar] [CrossRef]
- García-Calvo, J.; Maillard, J.; Fureraj, I.; Strakova, K.; Colom, A.; Mercier, V.; Roux, A.; Vauthey, E.; Sakai, N.; Fürstenberg, A.; et al. Fluorescent Membrane Tension Probes for Super-Resolution Microscopy: Combining Mechanosensitive Cascade Switching with Dynamic-Covalent Ketone Chemistry. J. Am. Chem. Soc. 2020, 142, 12034–12038. [Google Scholar] [CrossRef]
- Goujon, A.; Colom, A.; Straková, K.; Mercier, V.; Mahecic, D.; Manley, S.; Sakai, N.; Roux, A.; Matile, S. Mechanosensitive Fluorescent Probes to Image Membrane Tension in Mitochondria, Endoplasmic Reticulum, and Lysosomes. J. Am. Chem. Soc. 2019, 141, 3380–3384. [Google Scholar] [CrossRef]
- Kamat, N.P.; Liao, Z.; Moses, L.E.; Rawson, J.; Therien, M.J.; Dmochowski, I.J.; Hammer, D.A. Sensing membrane stress with near IR-emissive porphyrins. Proc. Natl. Acad. Sci. USA 2011, 108, 13984–13989. [Google Scholar] [CrossRef]
- Lopez-Andarias, J.; Eblighatian, K.; Pasquer, Q.T.L.; Assies, L.; Sakai, N.; Hoogendoorn, S.; Matile, S. Photocleavable Fluorescent Membrane Tension Probes: Fast Release with Spatiotemporal Control in Inner Leaflets of Plasma Membrane, Nuclear Envelope, and Secretory Pathway. Angew. Chem. Int. Ed. 2022, 61, e202113163. [Google Scholar] [CrossRef]
- Tretiakova, D.S.; Alekseeva, A.S.; Galimzyanov, T.R.; Boldyrev, A.M.; Chernyadyev, A.Y.; Ermakov, Y.A.; Batishchev, O.V.; Vodovozova, E.L.; Boldyrev, I.A. Lateral stress profile and fluorescent lipid probes. FRET pair of probes that introduces minimal distortions into lipid packing. Biochim. Biophys. Acta Biomembr. 2018, 1860, 2337–2347. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Whiting, R.; Finn, P.W.; Bogard, A.; McKinney, F.; Pankratz, D.; Smith, A.R.; Gardner, E.A.; Fologea, D. Experimental Investigations on the Conductance of Lipid Membranes under Differential Hydrostatic Pressure. Membranes 2022, 12, 479. https://doi.org/10.3390/membranes12050479
Whiting R, Finn PW, Bogard A, McKinney F, Pankratz D, Smith AR, Gardner EA, Fologea D. Experimental Investigations on the Conductance of Lipid Membranes under Differential Hydrostatic Pressure. Membranes. 2022; 12(5):479. https://doi.org/10.3390/membranes12050479
Chicago/Turabian StyleWhiting, Rose, Pangaea W. Finn, Andrew Bogard, Fulton McKinney, Dallin Pankratz, Aviana R. Smith, Elen A. Gardner, and Daniel Fologea. 2022. "Experimental Investigations on the Conductance of Lipid Membranes under Differential Hydrostatic Pressure" Membranes 12, no. 5: 479. https://doi.org/10.3390/membranes12050479
APA StyleWhiting, R., Finn, P. W., Bogard, A., McKinney, F., Pankratz, D., Smith, A. R., Gardner, E. A., & Fologea, D. (2022). Experimental Investigations on the Conductance of Lipid Membranes under Differential Hydrostatic Pressure. Membranes, 12(5), 479. https://doi.org/10.3390/membranes12050479






