Porous Cellulose Substrate Study to Improve the Performance of Diffusion-Based Ionic Strength Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Sensor Principal of Operation
2.2. Sensor Materials
2.2.1. Porous Membrane Substrate
2.2.2. Reagents
2.3. Numerical Simulation
2.3.1. Fluid Flow and Diffusion Phenomena
2.3.2. Model Boundary Conditions
2.4. Experimental Setup
Errors and Data Curing
3. Results and Discussion
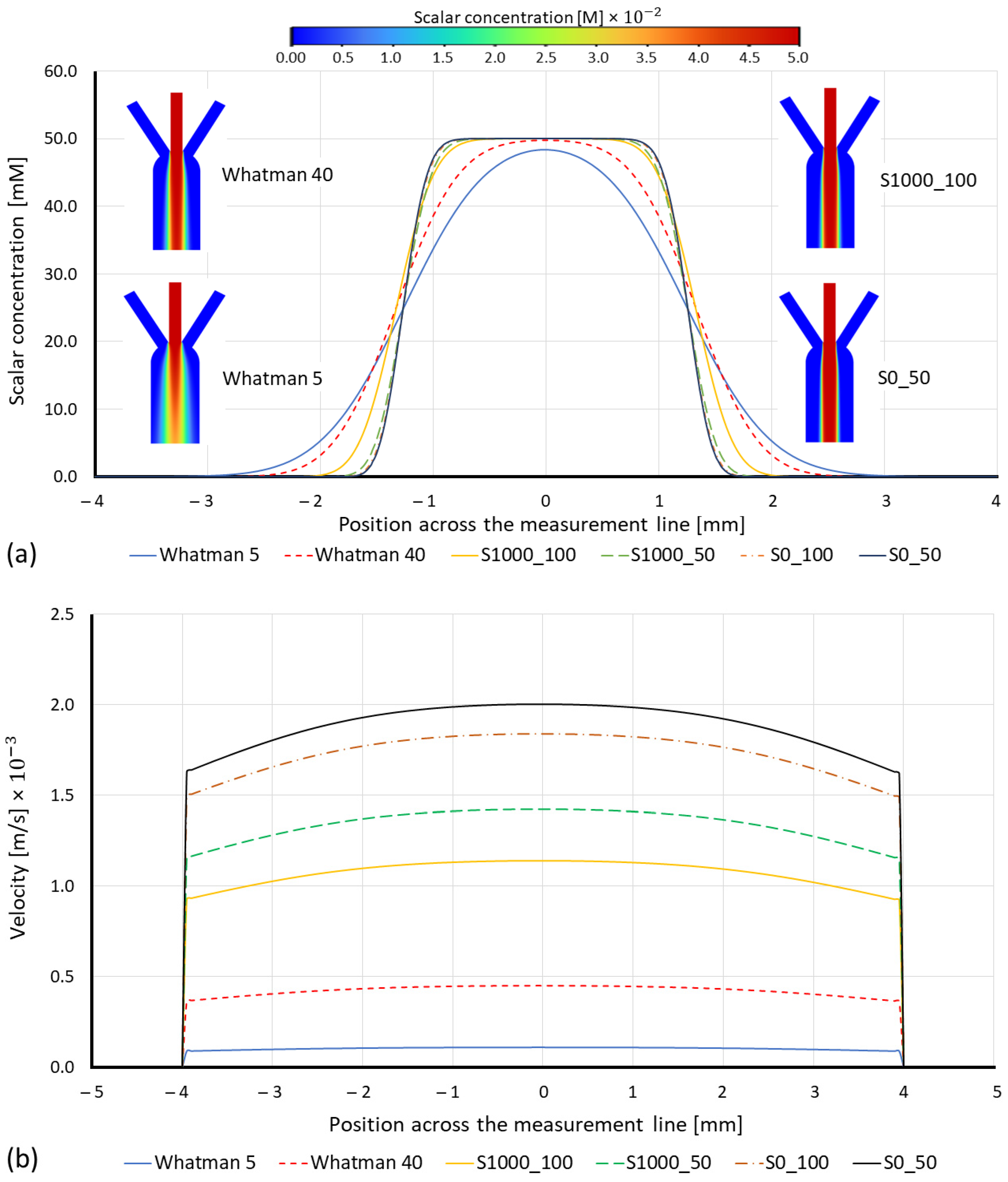
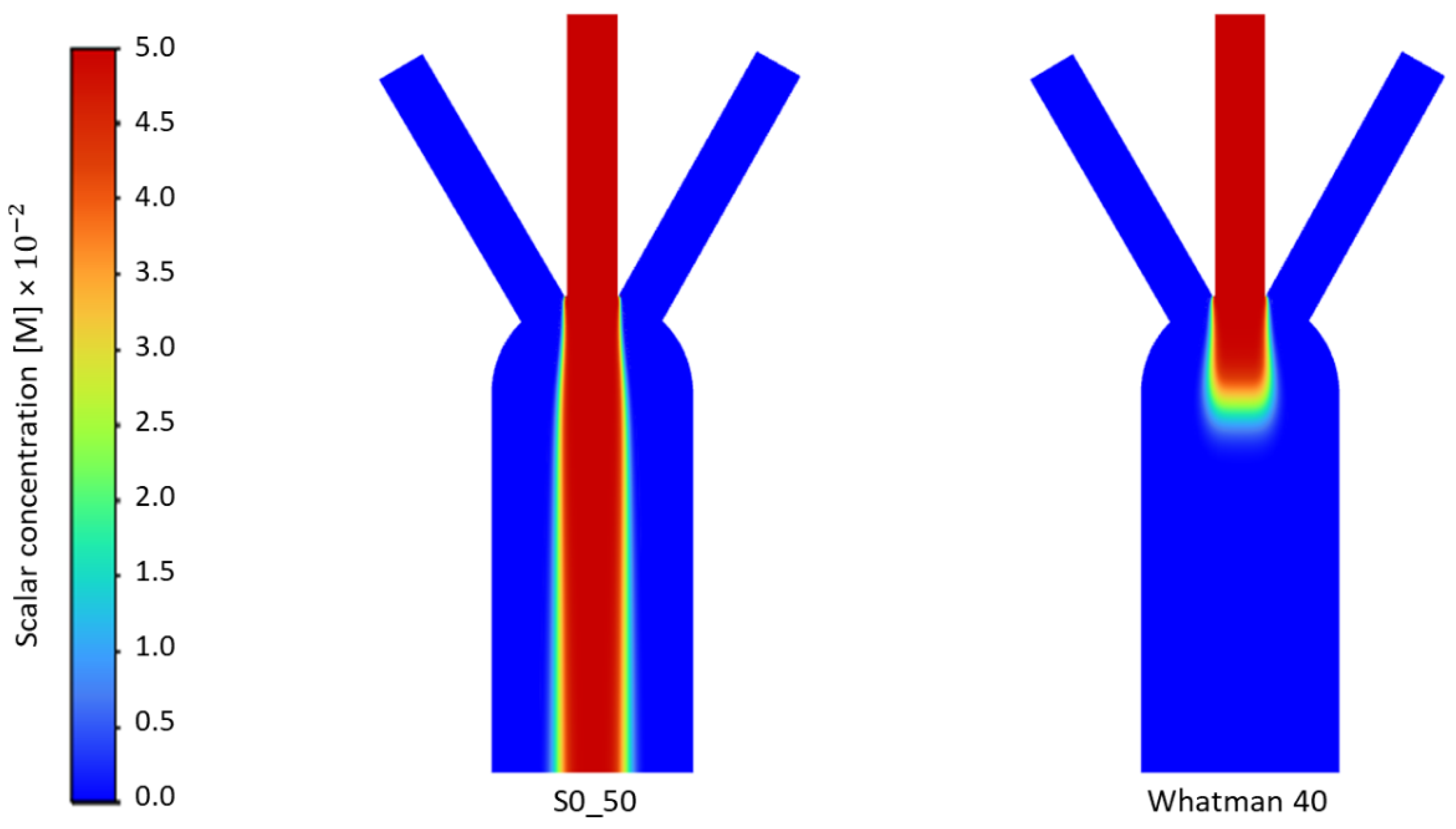
3.1. Numerical Results
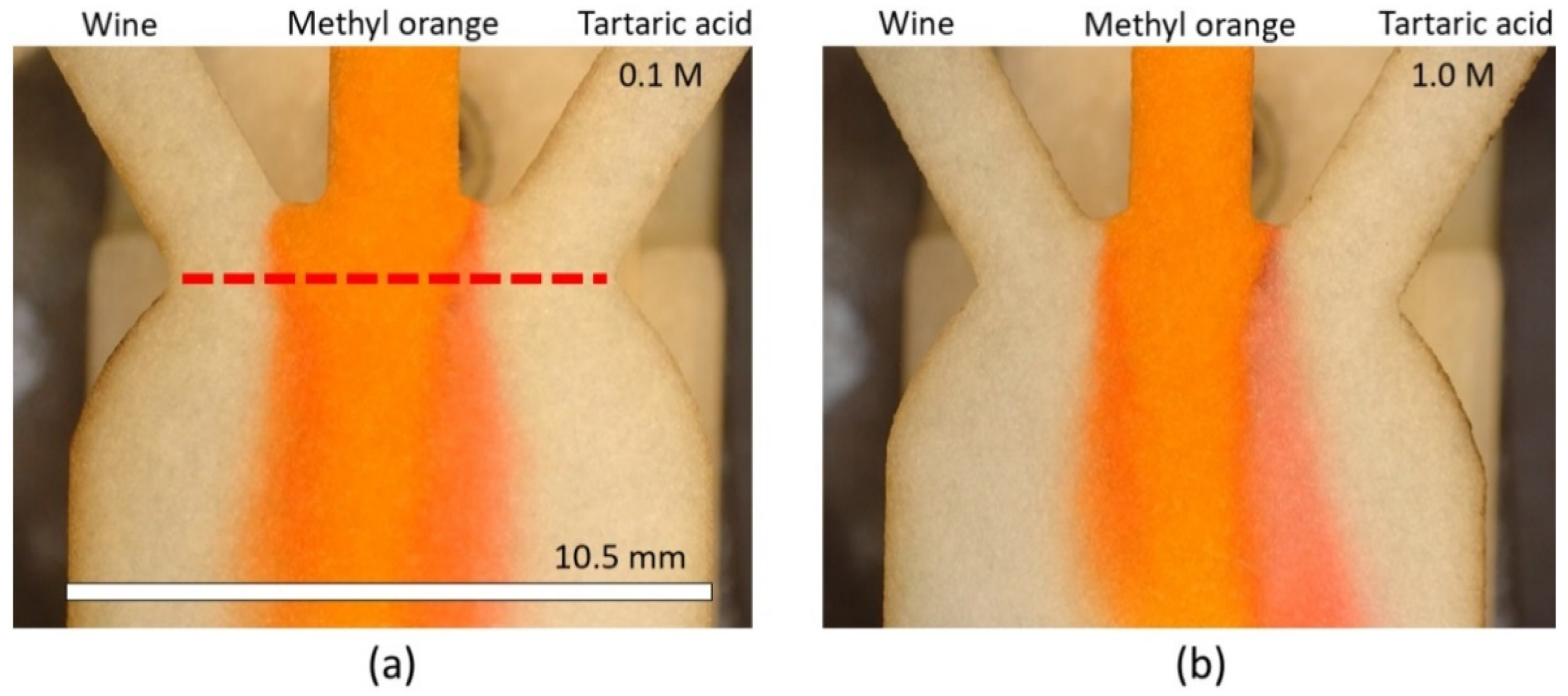
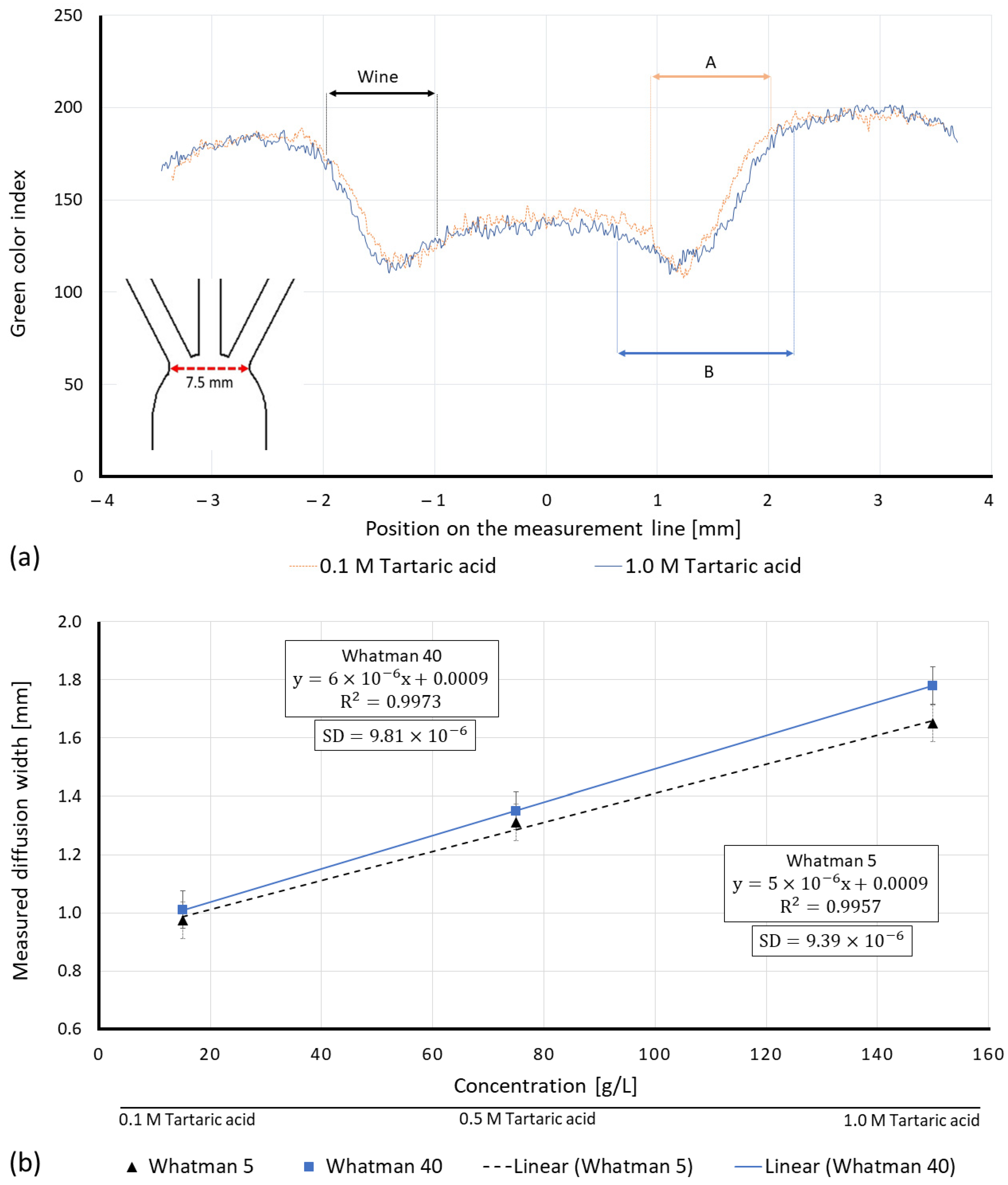
3.2. Experimental Results
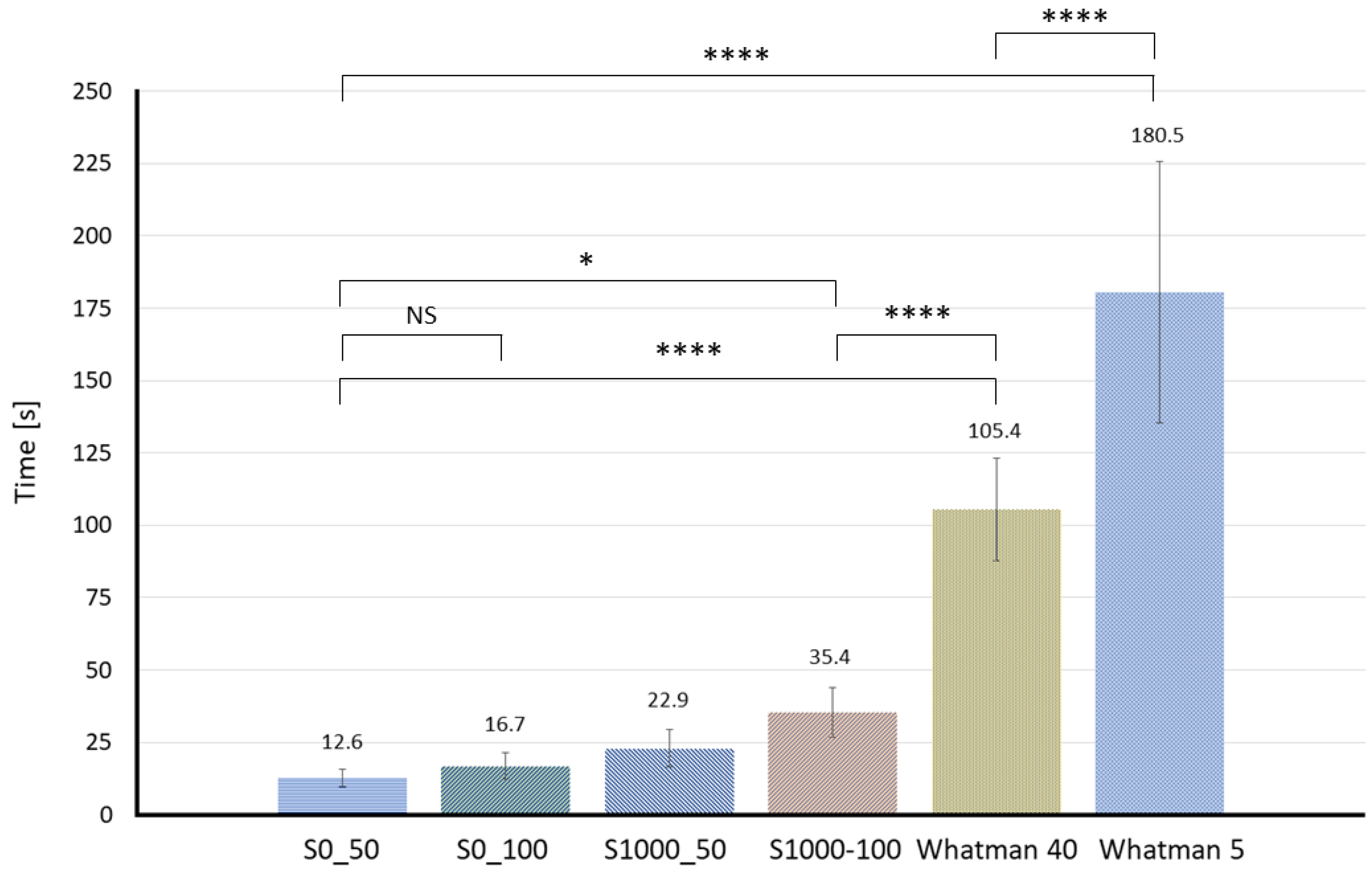
3.2.1. Time to Achieve One Millimeter Diffusion Width
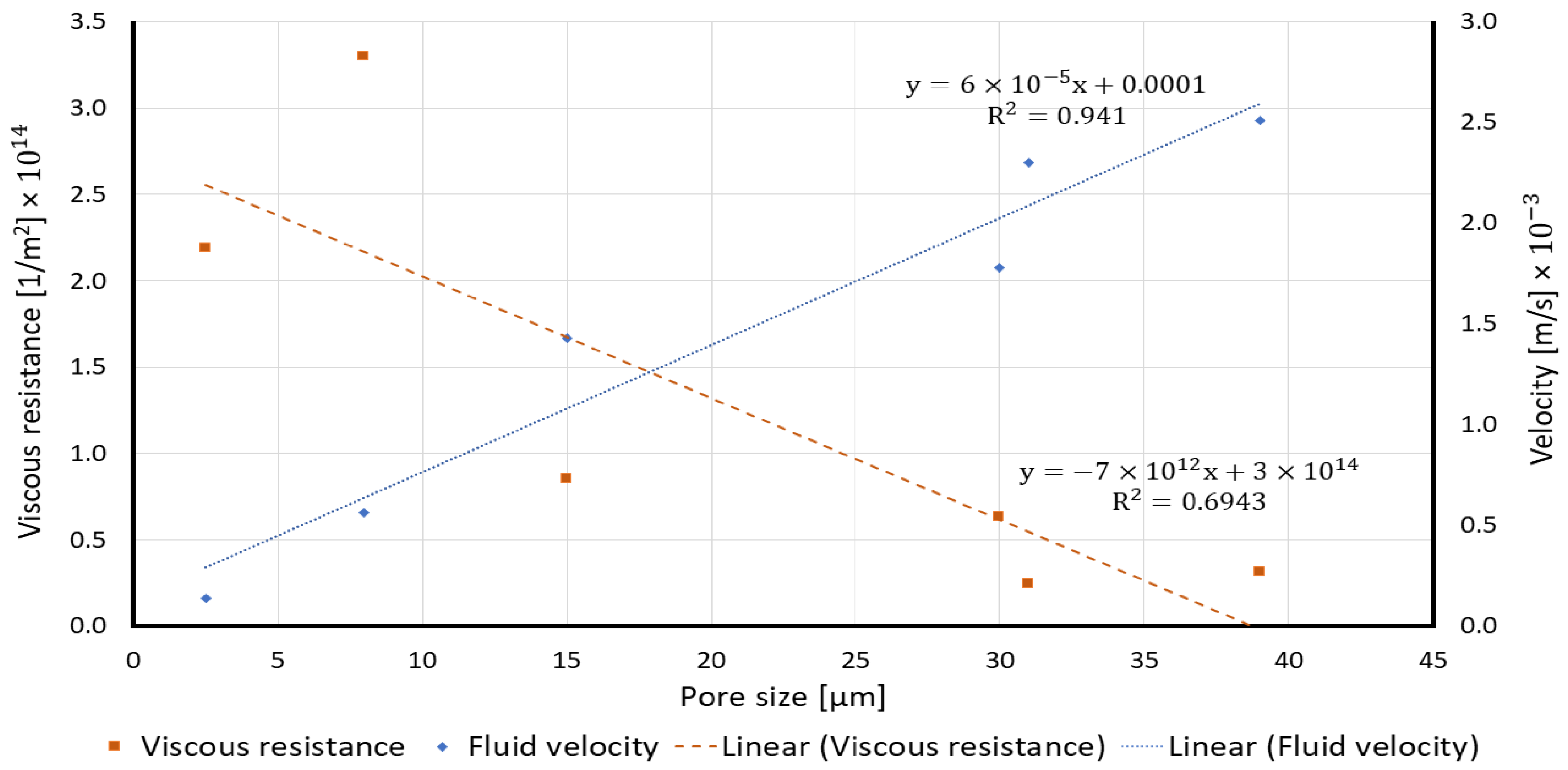
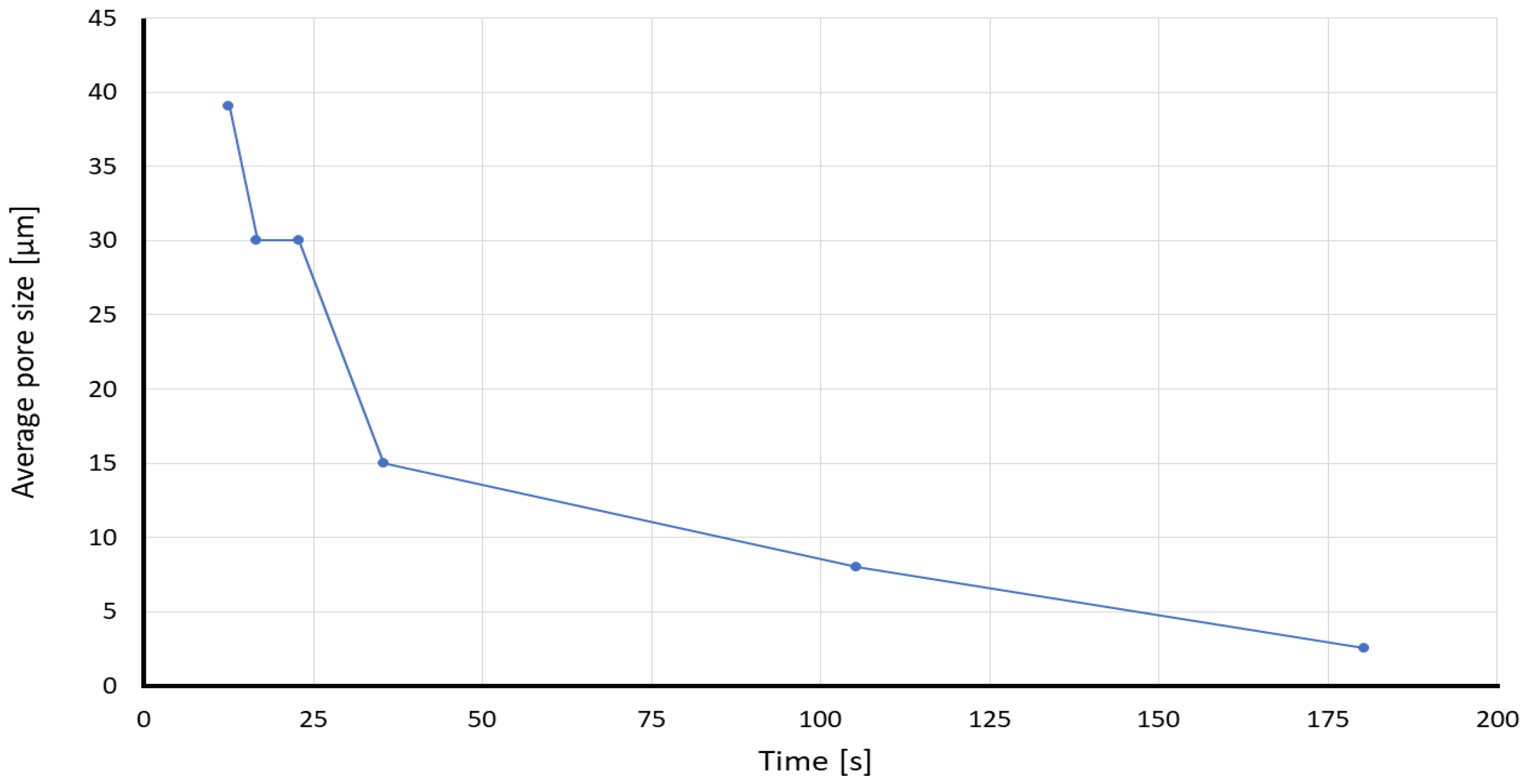
3.2.2. Influence of Pore Size and Viscous Resistance on the Sensor’s Sensitivity
3.2.3. Influence of Papers’ Viscous Resistance on the Turnaround Time of Sensor Results
3.2.4. Influence of Basis Weight and Pore Size on the Limit of Detection
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chinnadayyala, S.R.; Park, J.; Le, H.T.N.; Santhosh, M.; Kadam, A.N.; Cho, S. Recent Advances in Microfluidic Paper-Based Electrochemiluminescence Analytical Devices for Point-of-Care Testing Applications. Biosens. Bioelectron. 2019, 126, 68–81. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Fohlerová, Z.; Pekárek, J.; Basova, E.; Neužil, P. Recent Advances in Lab-on-a-Chip Technologies for Viral Diagnosis. Biosens. Bioelectron. 2020, 153, 112041. [Google Scholar] [CrossRef] [PubMed]
- Akyazi, T.; Basabe-Desmonts, L.; Benito-Lopez, F. Review on Microfluidic Paper-Based Analytical Devices towards Commercialisation. Anal. Chim. Acta 2018, 1001, 1–17. [Google Scholar] [CrossRef]
- Nikshad, A.; Aghlmandi, A.; Safaralizadeh, R.; Aghebati-Maleki, L.; Warkiani, M.E.; Khiavi, F.M.; Yousefi, M. Advances of Microfluidic Technology in Reproductive Biology. Life Sci. 2021, 265, 118767. [Google Scholar] [CrossRef] [PubMed]
- Amor-Gutiérrez, O.; Costa-Rama, E.; Fernández-Abedul, M.T. Sampling and Multiplexing in Lab-on-Paper Bioelectroanalytical Devices for Glucose Determination. Biosens. Bioelectron. 2019, 135, 64–70. [Google Scholar] [CrossRef]
- Karimi, S.; Mehrdel, P.; Casals-Terré, J.; Farré-Llados, J. Cost-Effective Microfabrication of Sub-Micron-Depth Channels by Femto-Laser Anti-Stiction Texturing. Biofabrication 2020, 12, 25021. [Google Scholar] [CrossRef]
- Karimi, S.; Mehrdel, P.; Farré-Lladós, J.; Casals-Terré, J. A Passive Portable Microfluidic Blood–Plasma Separator for Simultaneous Determination of Direct and Indirect ABO/Rh Blood Typing. Lab Chip 2019, 19, 3249–3260. [Google Scholar] [CrossRef]
- Ai, Y.; Zhang, F.; Wang, C.; Xie, R.; Liang, Q. Recent Progress in Lab-on-a-Chip for Pharmaceutical Analysis and Pharmacological/Toxicological Test. TrAC Trends Anal. Chem. 2019, 117, 215–230. [Google Scholar] [CrossRef]
- Dabbagh, S.R.; Becher, E.; Ghaderinezhad, F.; Havlucu, H.; Ozcan, O.; Ozkan, M.; Yetisen, A.K.; Tasoglu, S. Increasing the Packing Density of Assays in Paper-Based Microfluidic Devices. Biomicrofluidics 2021, 15, 11502. [Google Scholar] [CrossRef]
- Whitesides, G.M. The Origins and the Future of Microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
- Yetisen, A.K.; Akram, M.S.; Lowe, C.R. Based Microfluidic Point-of-Care Diagnostic Devices. Lab Chip 2013, 13, 2210–2251. [Google Scholar] [CrossRef] [PubMed]
- Lisowski, P.; Zarzycki, P.K. Microfluidic Paper-Based Analytical Devices (µPADs) and Micro Total Analysis Systems (µTAS): Development, Applications and Future Trends. Chromatographia 2013, 76, 1201–1214. [Google Scholar] [CrossRef] [PubMed]
- Sriram, G.; Bhat, M.P.; Patil, P.; Uthappa, U.T.; Jung, H.-Y.; Altalhi, T.; Kumeria, T.; Aminabhavi, T.M.; Pai, R.K.; Kurkuri, M.D. Based Microfluidic Analytical Devices for Colorimetric Detection of Toxic Ions: A Review. TrAC Trends Anal. Chem. 2017, 93, 212–227. [Google Scholar] [CrossRef]
- Gong, F.; Wei, H.; Qi, J.; Ma, H.; Liu, L.; Weng, J.; Zheng, X.; Li, Q.; Zhao, D.; Fang, H. Pulling-Force Spinning Top for Serum Separation Combined with Paper-Based Microfluidic Devices in COVID-19 ELISA Diagnosis. ACS Sens. 2021, 6, 2709–2719. [Google Scholar] [CrossRef]
- Islam, M.; Ahmed, I.; Anik, M.I.; Ferdous, M.; Khan, M.S. Developing Paper Based Diagnostic Technique to Detect Uric Acid in Urine. Front. Chem. 2018, 6, 496. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Li, B.; Qi, J.; Ji, X.; Yang, S.; Wang, W.; Chen, L. Low Cost Fabrication of Microfluidic Paper-Based Analytical Devices with Water-Based Polyurethane Acrylate and Their Application for Bacterial Detection. Sens. Actuators Chem. 2020, 303, 127213. [Google Scholar] [CrossRef]
- Ghosh, R.; Gopalakrishnan, S.; Savitha, R.; Renganathan, T.; Pushpavanam, S. Fabrication of Laser Printed Microfluidic Paper-Based Analytical Devices (LP-µPADs) for Point-of-Care Applications. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Chowdury, M.A.; Khalid, F. Application of Microfluidic Paper-based Analytical Device (µPAD) to Detect COVID-19 in Energy Deprived Countries. Int. J. Energy Res. 2021, 45, 18275–18280. [Google Scholar] [CrossRef]
- Gerold, C.T.; Bakker, E.; Henry, C.S. Selective Distance-Based K+ Quantification on Paper-Based Microfluidics. Anal. Chem. 2018, 90, 4894–4900. [Google Scholar] [CrossRef]
- Kim, W.; Lee, S.; Jeon, S. Enhanced Sensitivity of Lateral Flow Immunoassays by Using Water-Soluble Nanofibers and Silver-Enhancement Reactions. Sens. Actuators Chem. 2018, 273, 1323–1327. [Google Scholar] [CrossRef]
- Choi, Y.-S.; Im, M.K.; Lee, M.R.; Kim, C.S.; Lee, K.-H. Highly Sensitive Enclosed Multilayer Paper-Based Microfluidic Sensor for Quantifying Proline in Plants. Anal. Chim. Acta 2020, 1105, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Zargaryan, A.; Farhoudi, N.; Haworth, G.; Ashby, J.F.; Au, S.H. Hybrid 3D Printed-Paper Microfluidics. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Strong, E.B.; Schultz, S.A.; Martinez, A.W.; Martinez, N.W. Fabrication of Miniaturized Paper-Based Microfluidic Devices (MicroPADs). Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Charbaji, A.; Heidari-Bafroui, H.; Anagnostopoulos, C.; Faghri, M. A New Paper-Based Microfluidic Device for Improved Detection of Nitrate in Water. Sensors 2021, 21, 102. [Google Scholar] [CrossRef]
- Akbulut, Y.; Zengin, A. A Molecularly Imprinted Whatman Paper for Clinical Detection of Propranolol. Sens. Actuators Chem. 2020, 304, 127276. [Google Scholar] [CrossRef]
- Martinez, A.W.; Phillips, S.T.; Wiley, B.J.; Gupta, M.; Whitesides, G.M. FLASH: A Rapid Method for Prototyping Paper-Based Microfluidic Devices. Lab Chip 2008, 8, 2146–2150. [Google Scholar] [CrossRef]
- Schaumburg, F.; Berli, C.L.A. Assessing the Rapid Flow in Multilayer Paper-Based Microfluidic Devices. Microfluid. Nanofluidics 2019, 23, 1–10. [Google Scholar] [CrossRef]
- Ostrov, N.; Jimenez, M.; Billerbeck, S.; Brisbois, J.; Matragrano, J.; Ager, A.; Cornish, V.W. A Modular Yeast Biosensor for Low-Cost Point-of-Care Pathogen Detection. Sci. Adv. 2017, 3, e1603221. [Google Scholar] [CrossRef]
- Arrastia, M.; Avoundjian, A.; Ehrlich, P.S.; Eropkin, M.; Levine, L.; Gomez, F.A. Development of a Microfluidic-based Assay on a Novel Nitrocellulose Platform. Electrophoresis 2015, 36, 884–888. [Google Scholar] [CrossRef]
- Lashgari, M.; Yamini, Y. An Overview of the Most Common Lab-Made Coating Materials in Solid Phase Microextraction. Talanta 2019, 191, 283–306. [Google Scholar] [CrossRef]
- Gutorova, S.V.; Apyari, V.V.; Kalinin, V.I.; Furletov, A.A.; Tolmacheva, V.V.; Gorbunova, M.V.; Dmitrienko, S.G. Composable Paper-Based Analytical Devices for Determination of Flavonoids. Sens. Actuators Chem. 2021, 331, 129398. [Google Scholar] [CrossRef]
- Selvakumar, B.; Kathiravan, A. Sensory Materials for Microfluidic Paper Based Analytical Devices-A Review. Talanta 2021, 235, 122733. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.-T.; Song, S.; Park, S.; Joo, C. Recent Advances in High-Sensitivity Detection Methods for Paper-Based Lateral-Flow Assay. Biosens. Bioelectron. 2020, 152, 112015. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Liu, J.; Guo, L.; Wang, J.; Zhang, K.; He, J.; Cui, H. High-Resolution Temporally Resolved Chemiluminescence Based on Double-Layered 3D Microfluidic Paper-Based Device for Multiplexed Analysis. Biosens. Bioelectron. 2019, 141, 111472. [Google Scholar] [CrossRef]
- Tortorich, R.P.; Shamkhalichenar, H.; Choi, J.-W. Inkjet-Printed and Paper-Based Electrochemical Sensors. Appl. Sci. 2018, 8, 288. [Google Scholar] [CrossRef]
- Hertaeg, M.J.; Tabor, R.F.; McLiesh, H.; Garnier, G. A Rapid Paper-Based Blood Typing Method from Droplet Wicking. Analyst 2021, 146, 1048–1056. [Google Scholar] [CrossRef]
- Casals-Terré, J.; Farré-Lladós, J.; Zuñiga, A.; Roncero, M.B.; Vidal, T. Novel Applications of Nonwood Cellulose for Blood Typing Assays. J. Biomed. Mater. Res. Part Appl. Biomater. 2019, 107, 1533–1541. [Google Scholar] [CrossRef]
- Casals-Terré, J.; Farré-Lladós, J.; López, J.A.; Vidal, T.; Roncero, M.B. Enhanced Fully Cellulose Based Forward and Reverse Blood Typing Assay. J. Biomed. Mater. Res. Part Appl. Biomater. 2020, 108, 439–450. [Google Scholar] [CrossRef]
- Lim, H.; Jafry, A.T.; Lee, J. Fabrication, Flow Control, and Applications of Microfluidic Paper-Based Analytical Devices. Molecules 2019, 24, 2869. [Google Scholar] [CrossRef]
- Jeong, S.-G.; Kim, J.; Jin, S.H.; Park, K.-S.; Lee, C.-S. Flow Control in Paper-Based Microfluidic Device for Automatic Multistep Assays: A Focused Minireview. Korean J. Chem. Eng. 2016, 33, 2761–2770. [Google Scholar] [CrossRef]
- Lutz, B.; Liang, T.; Fu, E.; Ramachandran, S.; Kauffman, P.; Yager, P. Dissolvable Fluidic Time Delays for Programming Multi-Step Assays in Instrument-Free Paper Diagnostics. Lab Chip 2013, 13, 2840–2847. [Google Scholar] [CrossRef] [PubMed]
- Apilux, A.; Ukita, Y.; Chikae, M.; Chailapakul, O.; Takamura, Y. Development of Automated Paper-Based Devices for Sequential Multistep Sandwich Enzyme-Linked Immunosorbent Assays Using Inkjet Printing. Lab Chip 2013, 13, 126–135. [Google Scholar] [CrossRef] [PubMed]
- Fu, E.; Liang, T.; Spicar-Mihalic, P.; Houghtaling, J.; Ramachandran, S.; Yager, P. Two-Dimensional Paper Network Format That Enables Simple Multistep Assays for Use in Low-Resource Settings in the Context of Malaria Antigen Detection. Anal. Chem. 2012, 84, 4574–4579. [Google Scholar] [CrossRef] [PubMed]
- Toley, B.J.; McKenzie, B.; Liang, T.; Buser, J.R.; Yager, P.; Fu, E. Tunable-Delay Shunts for Paper Microfluidic Devices. Anal. Chem. 2013, 85, 11545–11552. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Al-Tamimi, M.; Garnier, G. Engineering Paper as a Substrate for Blood Typing Bio-Diagnostics. Cellulose 2012, 19, 1749–1758. [Google Scholar] [CrossRef]
- Li, L.; Huang, X.; Liu, W.; Shen, W. Control Performance of Paper-Based Blood Analysis Devices through Paper Structure Design. ACS Appl. Mater. Interfaces 2014, 6, 21624–21631. [Google Scholar] [CrossRef]
- Mehrdel, P.; Khosravi, H.; Karimi, S.; López Martínez, J.A.; Casals-terré, J. Flow Control in Porous Media: From Numerical Analysis to Quantitative Μpad for Ionic Strength Measurements. Sensors 2021, 21, 3328. [Google Scholar] [CrossRef]
- Bolton, P.D.; Ellis, J.; Fleming, K.A.; Lantzke, I.R. Protonation o f Azobenzene Derivatives. I. Methyl orange and ortho-methyl orange. Aust. J. Chem. 1973, 26, 1005–1014. [Google Scholar] [CrossRef]
- Danner, L.; Niimi, J.; Wang, Y.; Kustos, M.; Muhlack, R.A.; Bastian, S.E.P. Dynamic Viscosity Levels of Dry Red and White Wines and Determination of Perceived Viscosity Difference Thresholds. Am. J. Enol. Vitic. 2019, 70, 205–211. [Google Scholar] [CrossRef]
- Agmon, N. The Grotthuss Mechanism. Chem. Phys. Lett. 1995, 244, 456–462. [Google Scholar] [CrossRef]
- Du Plessis, E.; Woudberg, S. Modelling of Diffusion in Porous Structures. WIT Trans. Eng. Sci. 2009, 63, 399–408. [Google Scholar] [CrossRef]
- Yazdchi, K.; Srivastava, S.; Luding, S. On the Validity of the Carman-Kozeny Equation in Random Fibrous Media. In Proceedings of the International Conference on Particle-Based Methods (PARTICLES)-II International Conference on Particle-Based Methods: Fundamentals and Applications (PARTICLES 2011), Barcelona, Spain, 26–28 October 2011; pp. 264–273. [Google Scholar]
- Prenesti, E.; Berto, S.; Toso, S.; Daniele, P.G. Acid-Base Chemistry of White Wine: Analytical Characterisation and Chemical Modelling. Sci. World J. 2012, 2012, 249041. [Google Scholar] [CrossRef] [PubMed][Green Version]
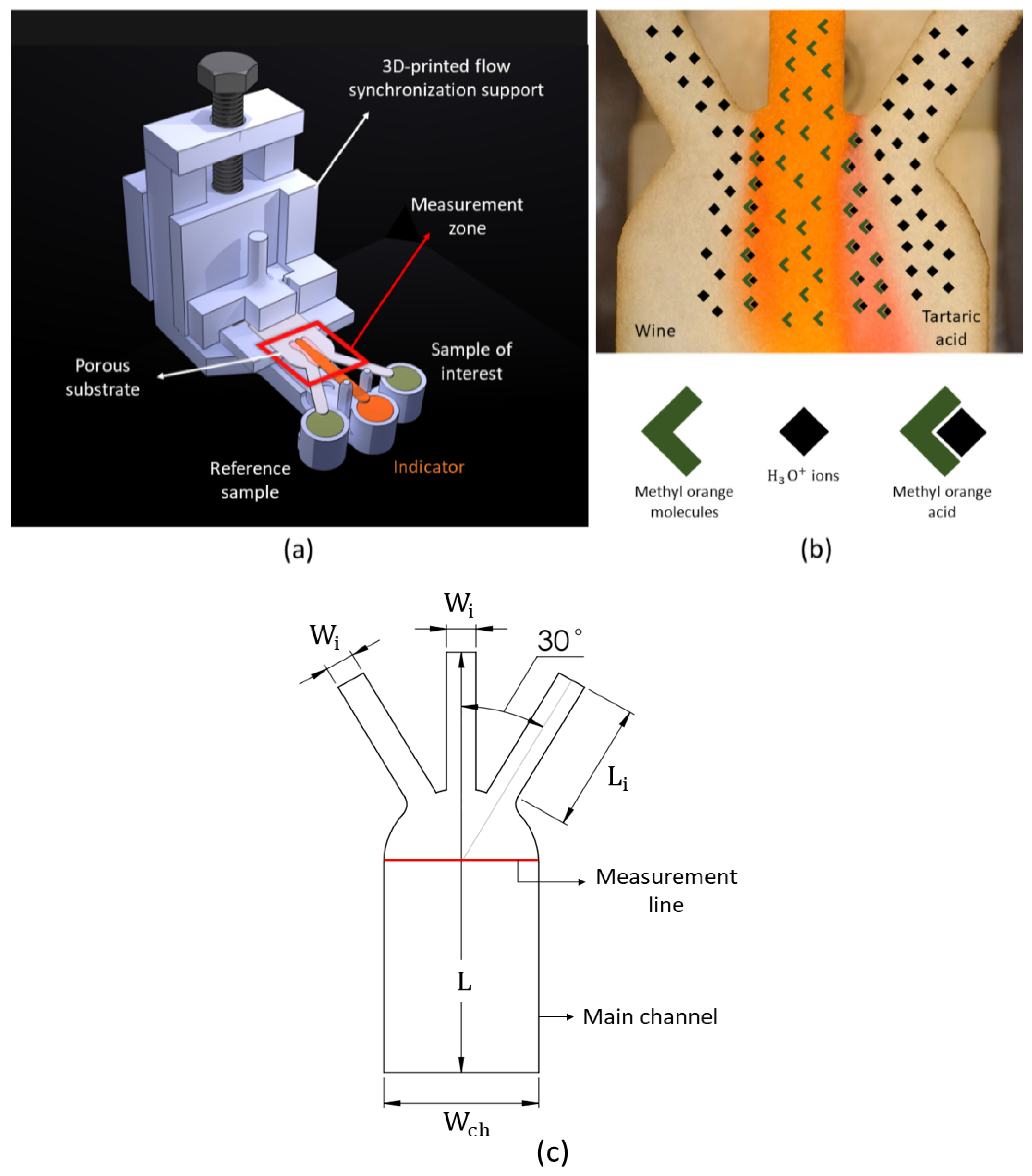

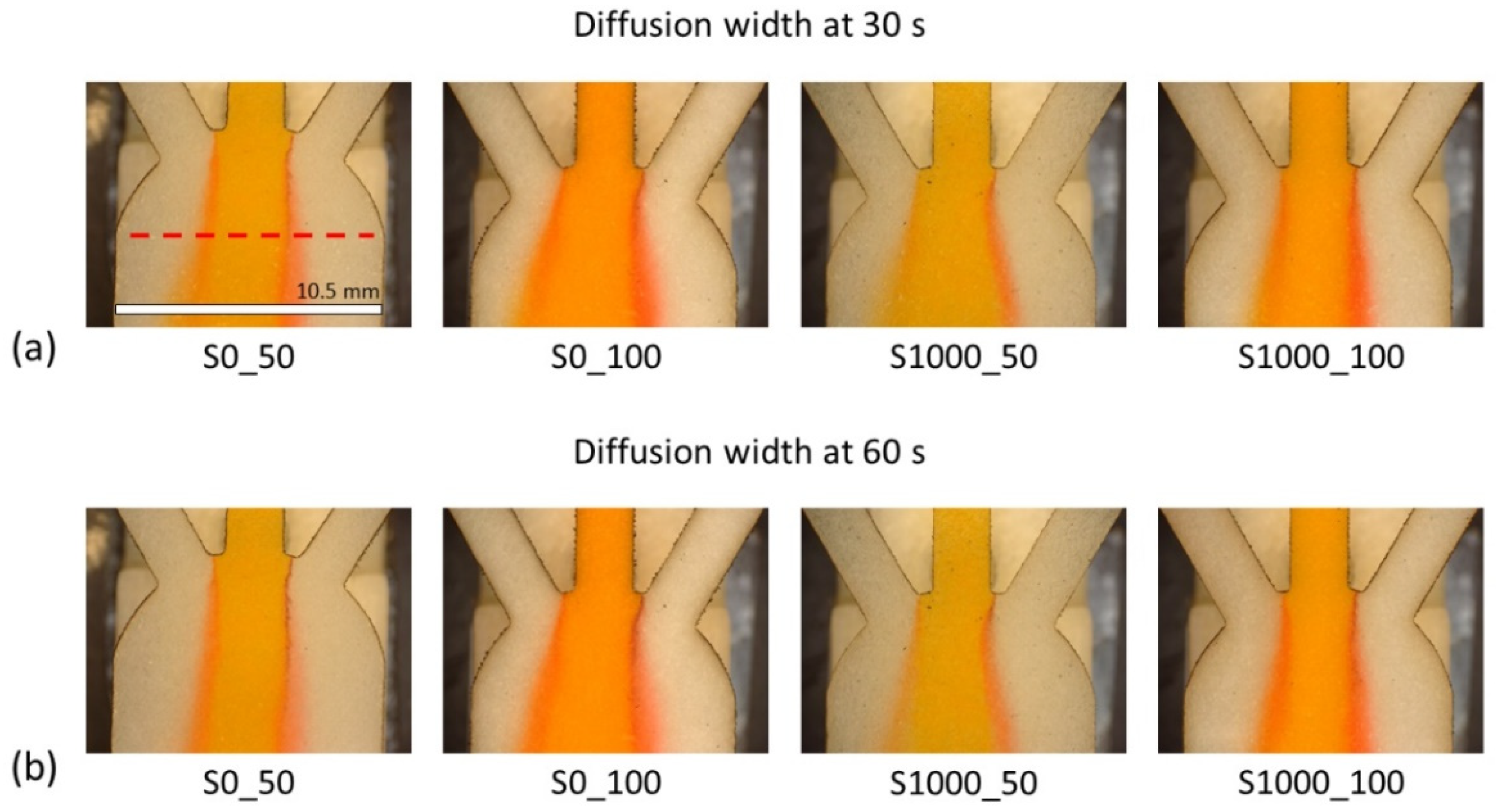

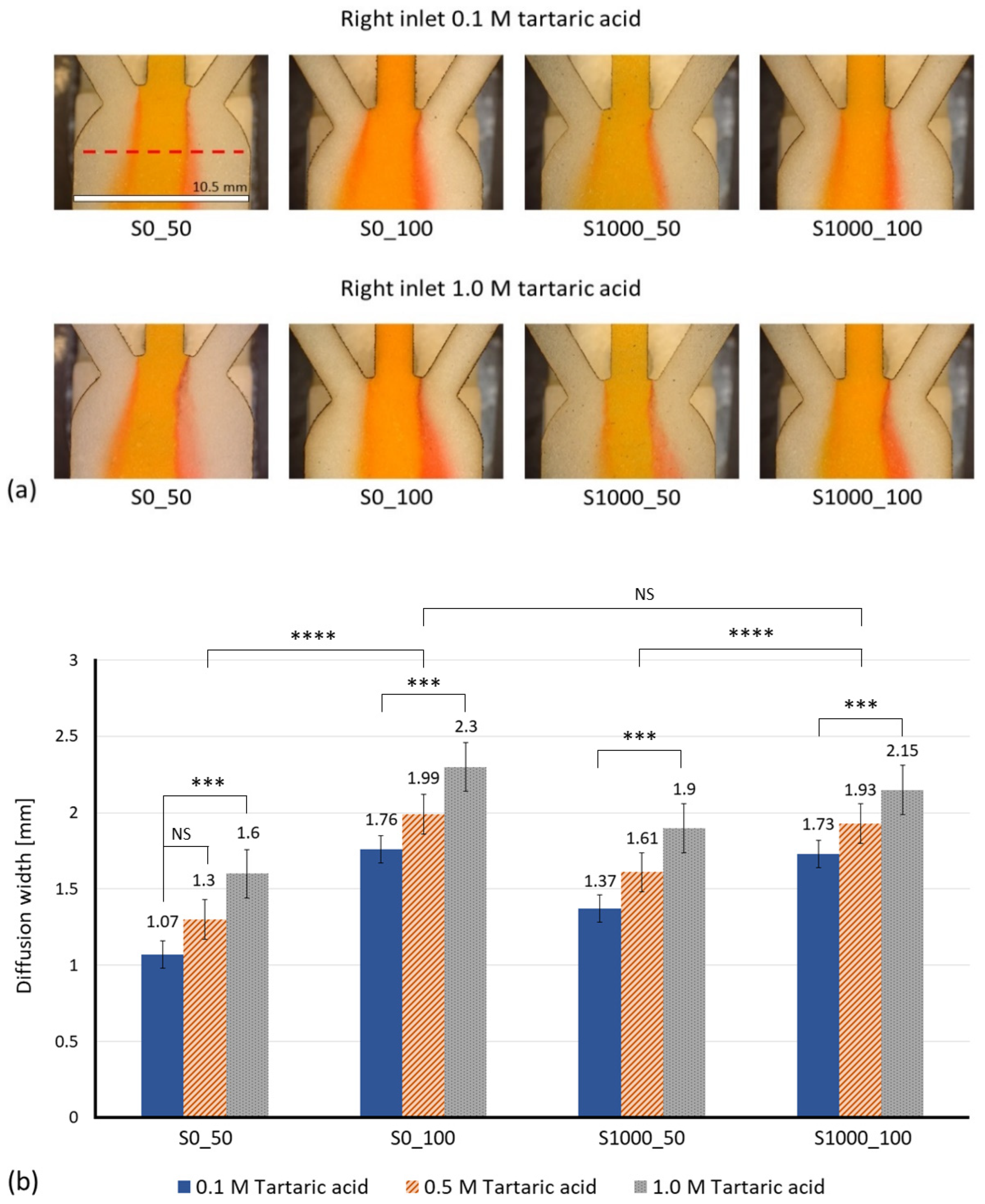
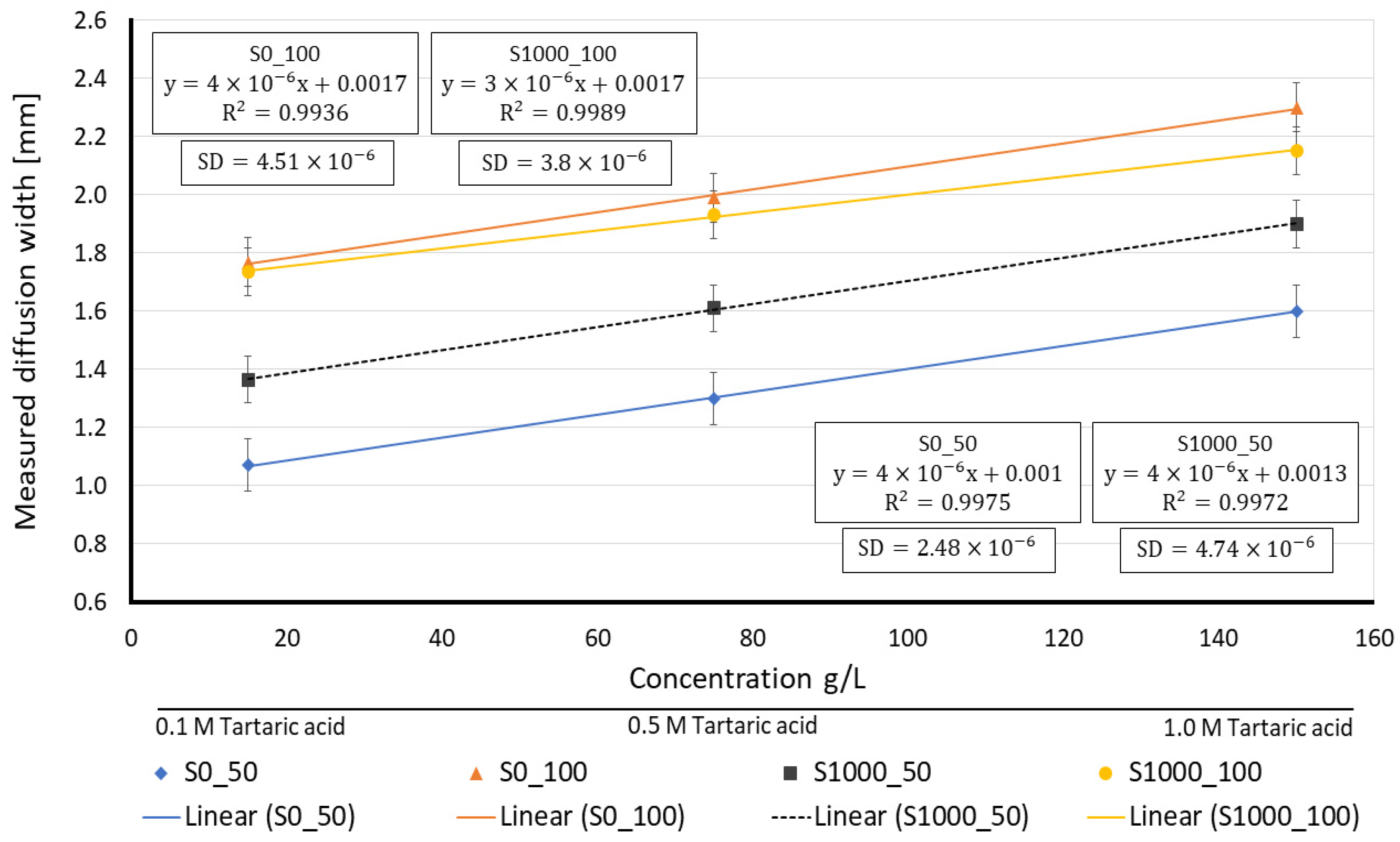
| Property | Value |
|---|---|
| Total length (L) | 30 mm |
| Main channel width () | 10.5 mm |
| Measurement line | 10.5 mm |
| Inlet length () | 9.75 mm |
| Inlet width () | 2 mm |
| Property | Whatman 5 | Whatman 40 | S0_50 | S0_100 | S1000_50 | S1000_100 |
|---|---|---|---|---|---|---|
| Basis weight (g/m2) | 98.4 ± 0.59 [37] | 88.18 ± 0.58 [37] | 50.9 ± 1 [38] | 104 ± 2 [38] | 47.2 ± 0.9 [38] | 96.2 ± 2.2 [38] |
| Density of cellulose (g/m3) | 1.5 [37] | 1.5 [37] | 1.45 [37] | 1.45 [37] | 1.45 [37] | 1.45 [37] |
| Density of the paper (g/m3) | 0.53 [37] | 0.45 [37] | 0.36 [38] | 0.33 [38] | 0.43 [38] | 0.47 [38] |
| Diameter of the cellulose fiber (µm) | 19.6 [37] | 19.6 [37] | 16.03 [37] | 16.03 [37] | 16.03 [37] | 16.03 [37] |
| Average length of the cellulose fiber (µm) | 830 [37] | 510 [37] | 1500 [38] | 1500 [38] | 1400 [38] | 1400 [38] |
| Thickness (µm) | 186 ± 1 [37] | 192 ± 2 [37] | 143 ± 11 [38] | 301 ± 50 [38] | 109 ± 5 [38] | 203 ± 5 [38] |
| Average pore size (µm) | 2.5 * | 8 * | 39 ± 3 [38] | 30 ± 7 [38] | 31 ± 5 [38] | 15 ± 0.7 [38] |
| Refining(rev) | - | - | 0 | 0 | 1000 | 1000 |
| Property | Value |
|---|---|
| White wine density | 1080 kg/m3 |
| White wine viscosity | 0.00148 kg/m.s [49] |
| Tartaric acid molar mass | 150.078 g/mol |
| Tartaric acid viscosity | 0.00121 kg/m.s (Merck’s catalogue) |
| Paper Type | Porosity | Permeability | (kg/m.s) |
|---|---|---|---|
| Whatman 5 | 0.6467 | ||
| Whatman 40 | 0.7 | ||
| S0_50 | 0.7517 | ||
| S0_100 | 0.7724 | ||
| S1000_50 | 0.7034 | ||
| S1000_100 | 0.6758 |
| Paper Type | Viscous Resistance (1/m2) | Fluid Velocity (m/s) |
|---|---|---|
| Whatman 5 | ||
| Whatman 40 | ||
| S0_50 | ||
| S0_100 | ||
| S1000_50 | ||
| S1000_100 |
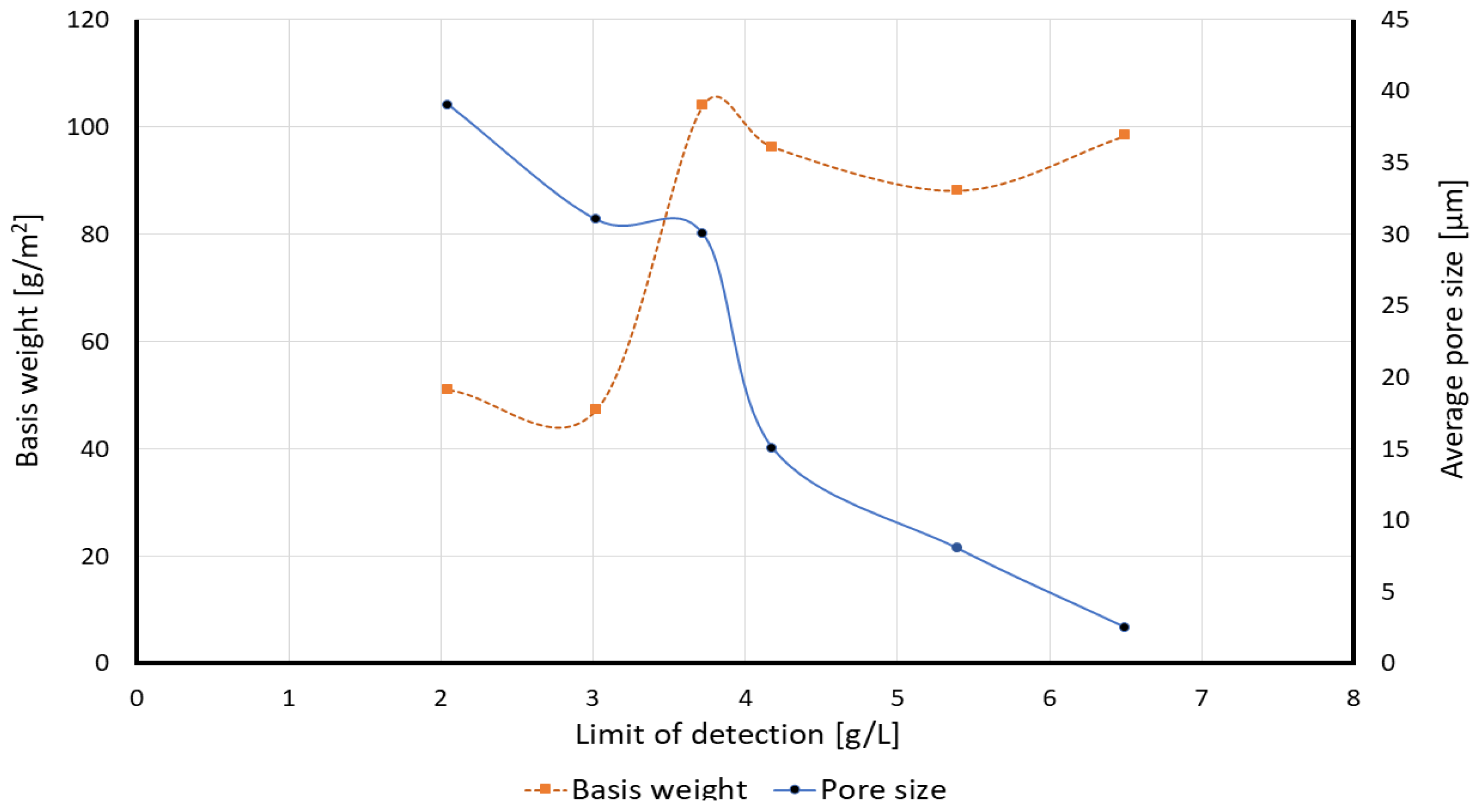
| Paper Type | Average Pore Size [µm] | Basis Weight [g/m2] | LOD at 30 s [g/L] | LOD at 120 s [g/L] |
|---|---|---|---|---|
| S0_50 | 39 ± 3 | 50.9 ± 1 | 2.05 | - |
| S1000_50 | 31 ± 5 | 47.2 ± 0.9 | 3.02 | - |
| S0_100 | 30 ± 7 | 104 ± 2 | 3.72 | - |
| S1000_100 | 15 ± 0.7 | 96.2 ± 2.2 | 4.18 | - |
| Whatman 40 | 8 | 88.18 ± 0.58 | - | 5.4 |
| Whatman 5 | 2.5 | 98.4 ± 0.58 | - | 6.2 [47] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khosravi, H.; Mehrdel, P.; Martínez, J.A.L.; Casals-Terré, J. Porous Cellulose Substrate Study to Improve the Performance of Diffusion-Based Ionic Strength Sensors. Membranes 2022, 12, 1074. https://doi.org/10.3390/membranes12111074
Khosravi H, Mehrdel P, Martínez JAL, Casals-Terré J. Porous Cellulose Substrate Study to Improve the Performance of Diffusion-Based Ionic Strength Sensors. Membranes. 2022; 12(11):1074. https://doi.org/10.3390/membranes12111074
Chicago/Turabian StyleKhosravi, Hamid, Pouya Mehrdel, Joan Antoni López Martínez, and Jasmina Casals-Terré. 2022. "Porous Cellulose Substrate Study to Improve the Performance of Diffusion-Based Ionic Strength Sensors" Membranes 12, no. 11: 1074. https://doi.org/10.3390/membranes12111074
APA StyleKhosravi, H., Mehrdel, P., Martínez, J. A. L., & Casals-Terré, J. (2022). Porous Cellulose Substrate Study to Improve the Performance of Diffusion-Based Ionic Strength Sensors. Membranes, 12(11), 1074. https://doi.org/10.3390/membranes12111074








