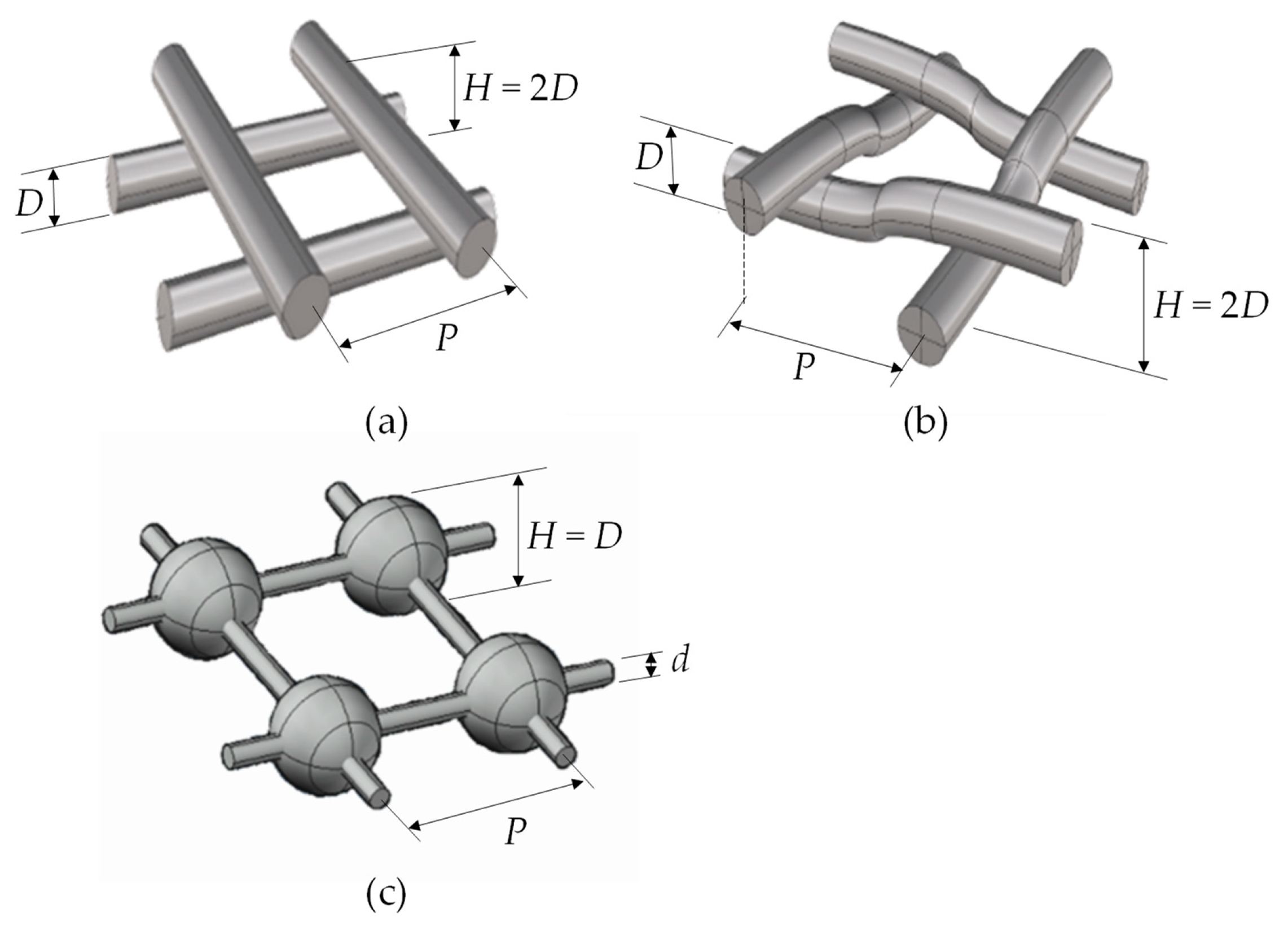
3.1. Friction Coefficient
The Darcy friction coefficient
f is defined as:
in which
L is the distance between the two pressure tappings (~0.5 m in the present tests) and Δ
p is the measured pressure drop between them.
Figure 5 reports the measured Darcy friction coefficient
f as a function of the Reynolds number Re for all six combinations of spacer geometry (woven, overlapped and spheres) and orientation (0–90° or 45°).
The results show that the flow attack angle affected f significantly only in the case of the woven spacers, where the 0–90° orientation yielded values of f that are up to 60% higher than they are in the 45° orientation. For the other two geometries (overlapped and spheres spacers), the difference is much lower (~10% or less).
By far the highest values of f are associated with the woven spacer, while the lowest values are provided by the spheres spacer. The advantage of this latter result with respect to conventional spacers increases with Re; at the highest Re that was tested (2500), the f (spheres) is about one half of f (overlapped) and about one tenth of f (woven).
For comparison purposes,
Figure 5 reports also the Hagen-Poiseuille behavior of
f for the laminar flow in an indefinite plane channel (96/Re); it can be observed that the friction increase caused by the spacers ranges that are between ~1.5 orders of magnitude (spheres) and ~2 orders of magnitude (woven).
3.2. Influence of Buoyancy
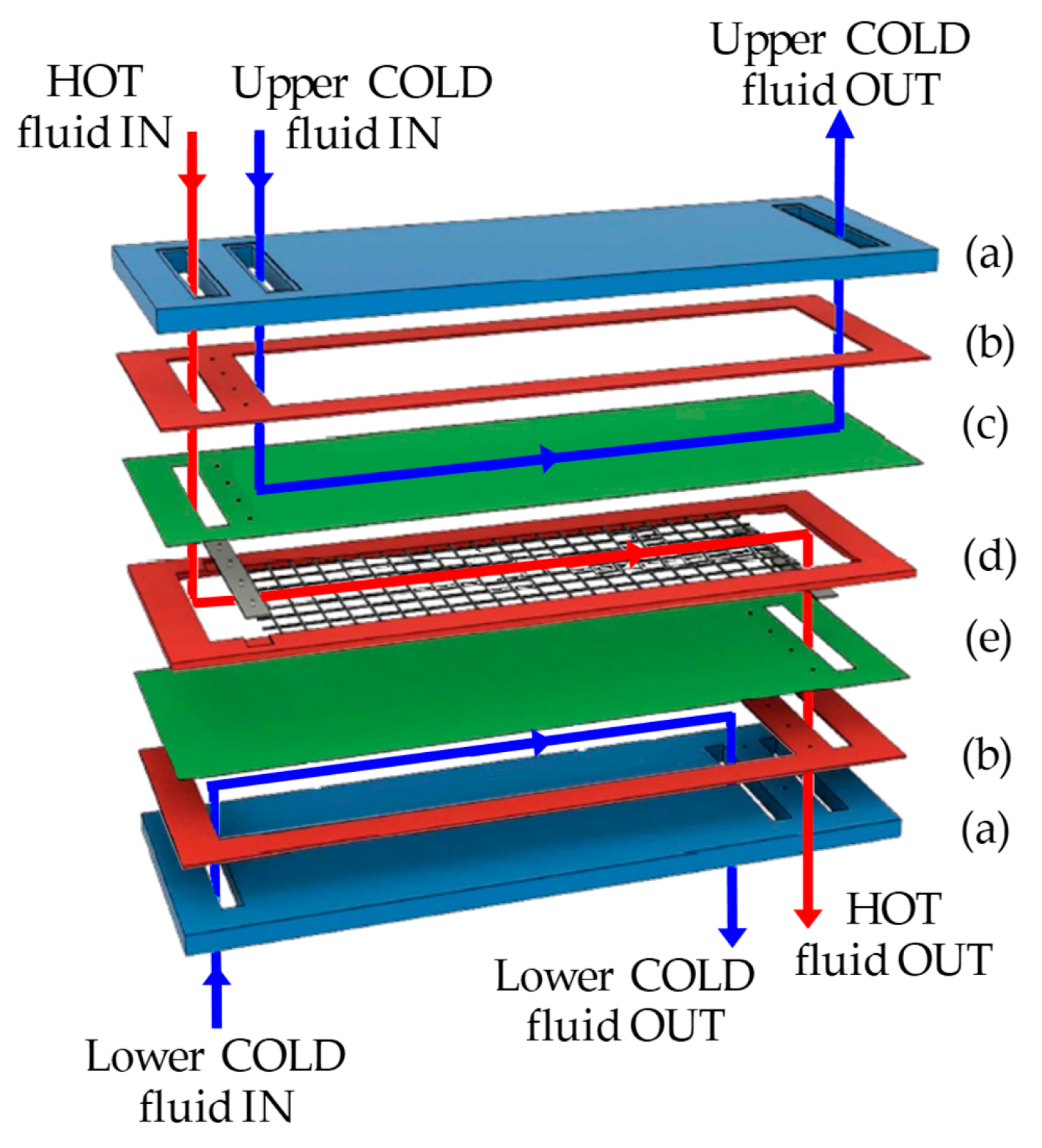
Preliminarily, in order to assess the possible effects of thermal buoyancy, the measurements of the heat transfer coefficient were performed with no spacer in the hot channel using the same TLC-based technique as that which was used for the spacer-filled channels (see
Section 2.3). Note that for laminar parallel flow in a plane channel with the two-side cooling, the Nusselt number varies depending on the exact thermal boundary conditions, between ~7.54 (uniform
Thw) and ~8.24 (uniform
q″) [
20].
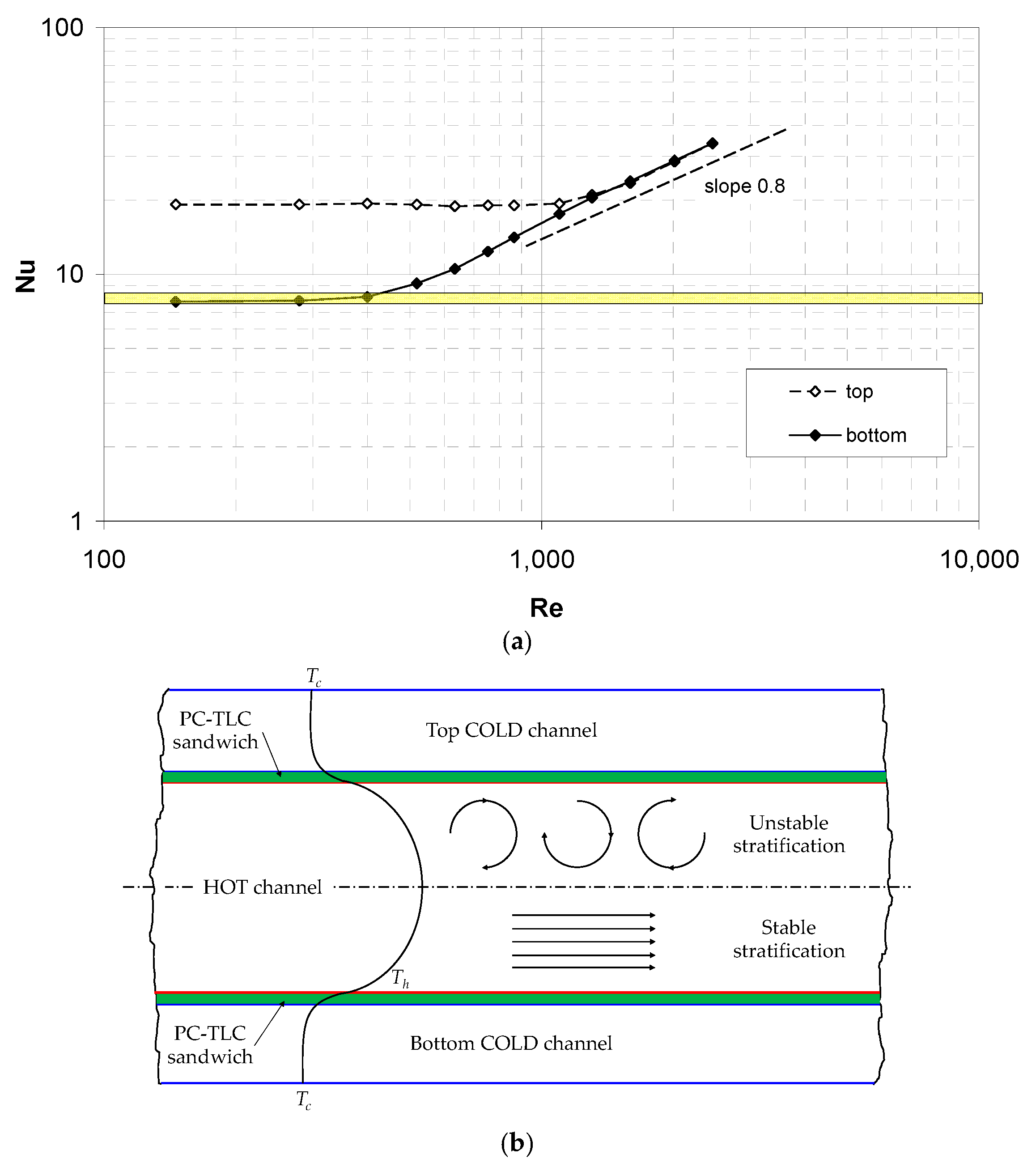
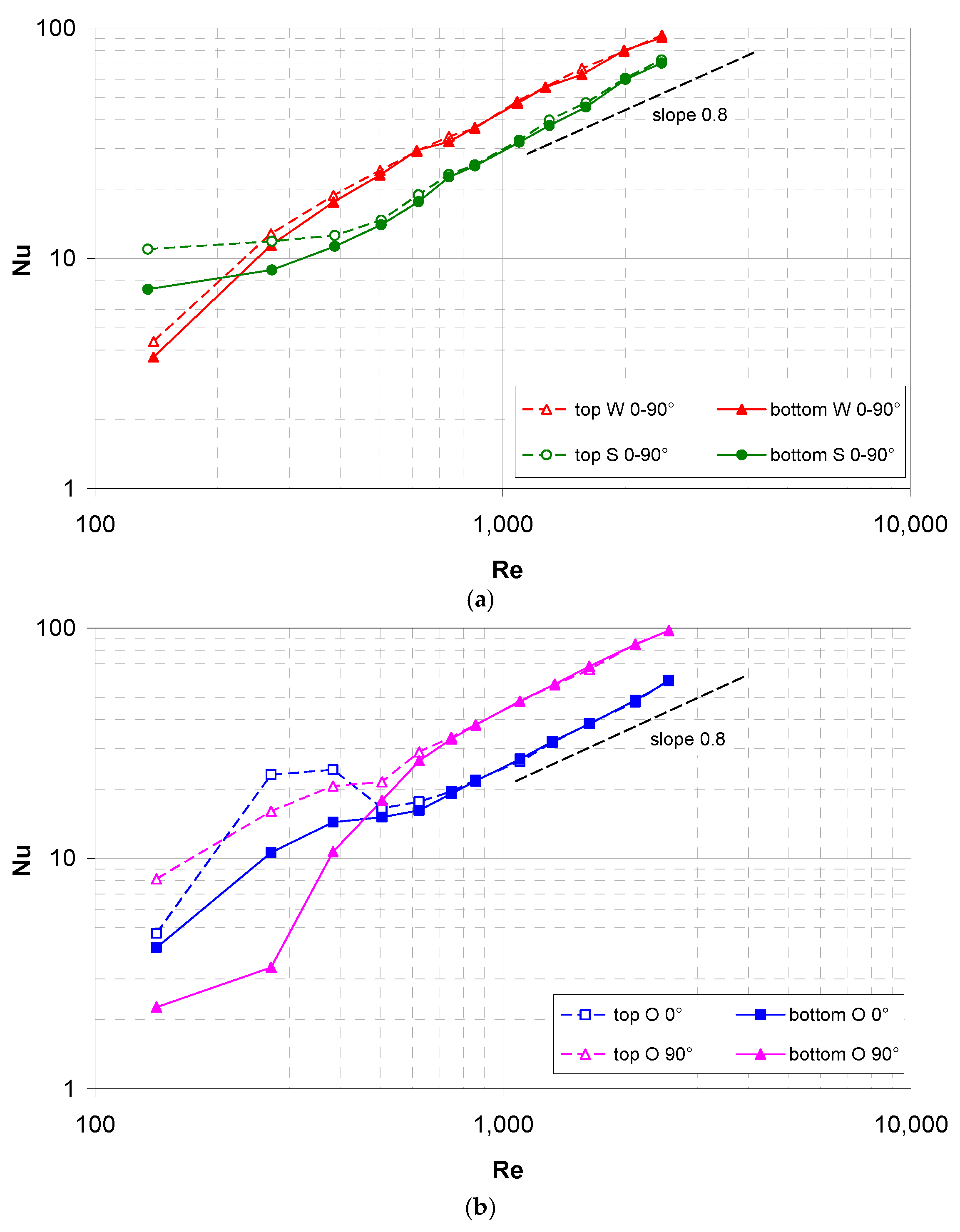
Figure 6a reports the mean Nusselt number, Equation (5), on the top and bottom walls. The experimental data exhibit a behaviour that is completely different from the above theoretical predictions. The Nusselt number on the bottom wall remains constant at a value of ~7.8, which is intermediate between the two above theoretical limits, only up to Re ≈ 300–400 and then increases strongly. On the other hand, the Nusselt number on the top wall remains approximately constant at a much larger value (~19) up to Re ≈ 1200. For larger values of Re, the two Nusselt numbers merge and increase with the Re following a ~0.8-power law, which is characteristic of the turbulent flow in the simple channels.
This strongly asymmetric behaviour can only be explained by the influence of thermal buoyancy on the basis of the schematic representation of the temperature distribution in the hot channel in
Figure 6b. In the upper half of the channel, an unstable thermal stratification exists, which causes convective motions and a strong heat transfer enhancement even at very low Re. On the other hand, in the lower half of the channel, the thermal stratification is stable, causing the flow to remain laminar and parallel and the Nusselt number to settle to a value that is compatible with the theoretical parallel-flow predictions.
The above qualitative remarks can be made quantitative on the basis of the definitions of the Rayleigh (Ra) and Richardson (Ri) numbers:
in which
g is the acceleration due to gravity,
β,
ν and
α are the thermal expansion coefficient, the kinematic viscosity and the thermal diffusivity of the fluid, respectively, while the channel height
Hh, the hot wall temperature
Thw and the hot fluid bulk temperature
Th have been defined earlier. The Rayleigh number was computed on the basis of the channel half-height,
Hh/2.
Under typical test conditions, one has Th ≈ 38 °C and Thw ≈ 35.5 °C, while Hh = 1.1·10−2 m, g = 9.81 m/s2 and, for water at ~38 °C, β = 3.21·10−3 K−1, ν = 6.65·10−7 m2/s and α = 1.56·10−7 m2/s, thereby yielding Ra = 1.26·105. Therefore, the Richardson number, which measures the importance of the natural convection with respect to the forced convection, is (for example) ~3.16 for Re = 200, ~0.35 for Re = 600 and ~0.039 for Re = 1800. These figures explain why the influence of natural convection (thermal buoyancy) is negligible at the high Reynolds numbers, important at the intermediate Re (e.g., 600) and dominating at a very low Re.
3.3. Mean Nusselt Number in Spacer-Filled Channels
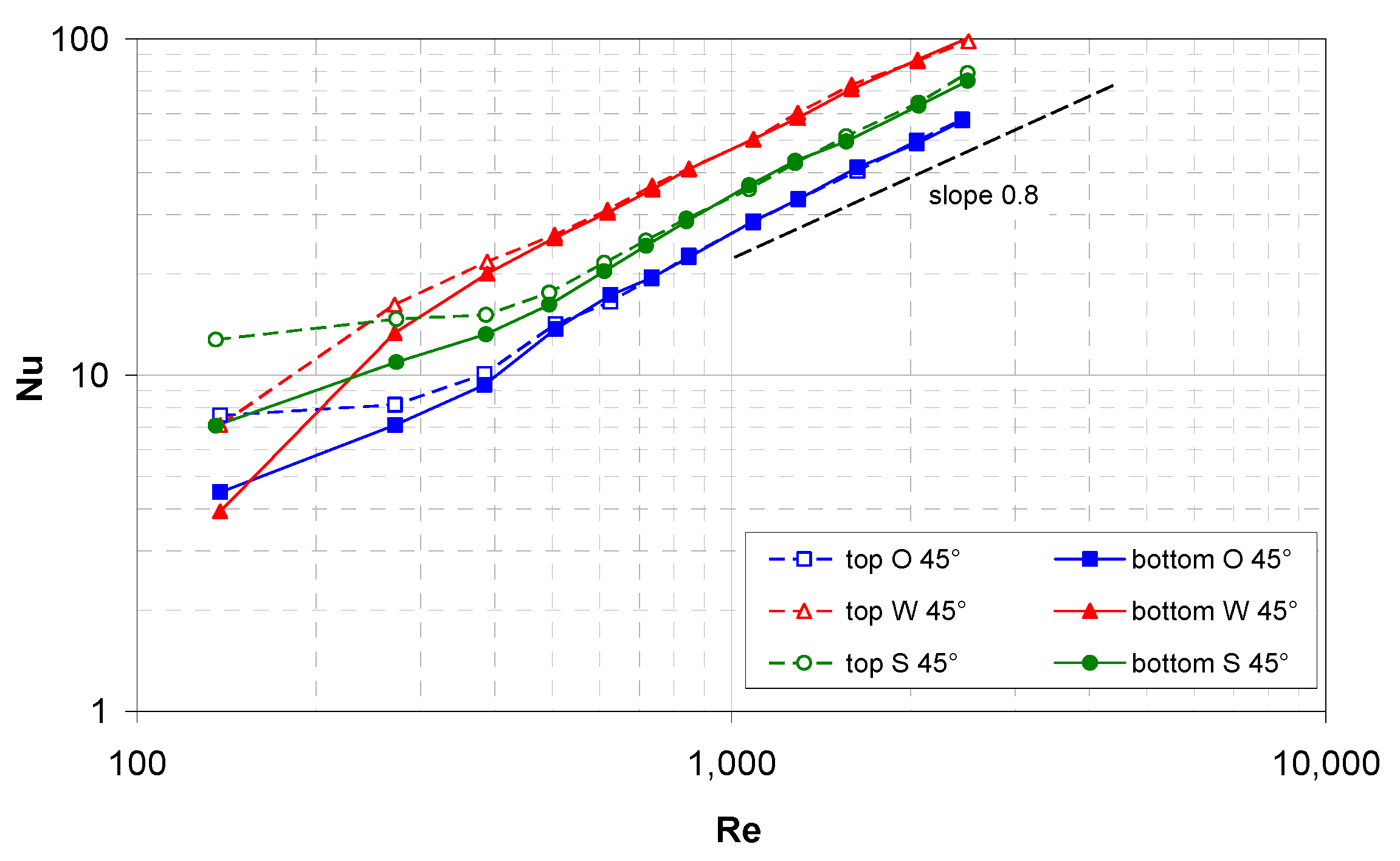
Figure 7 reports the mean Nusselt number on the top and bottom walls of the hot channel for the three spacers (O = overlapped, W = woven and S = spheres), whereby all of them are arranged at
ϕ = 45° with respect to the flow direction. In these configurations, for symmetry reasons, any difference between the Nusselt numbers on the two walls is only due to buoyancy effects (apart from experimental uncertainties).
In the presence of the spacers, the effects of buoyancy (promoting heat transfer in the top half of the channel) extended only up to Re ≈ 500 (Richardson number Ri ≈ 0.5), and these effects are much smaller than they are in the spacer-less channel. A possible reason is that the spacer hinders the formation of the buoyancy-induced secondary motions that are responsible for heat transfer enhancement, while they cause the buoyancy-independent mixing. For Re>~500, the Nu curves pertaining to the two walls merge and increase in all of the cases following a ~0.8-power law as is typical of turbulent flow in simple channels. The highest values of Nu are provided by the W spacer, the lowest ones are provided by the O spacer and intermediate values are provided by the novel S spacer.
Figure 8 reports similar results for
ϕ = 0–90° (spacer filaments parallel and orthogonal to the flow direction). For clarity purposes, the results for the W and S spacers on one hand, and for the O spacer on the other hand are shown in separate graphs.
In particular, graph (a) pertains to the woven (W) and spheres (S) spacers that are arranged at 0–90°. For symmetry reasons, also in this orientation the W and S spacers are expected to exhibit the same mean Nusselt numbers on the two walls apart from the effects of buoyancy. The results are much similar to those that are reported in
Figure 7 for the 45° orientation: the influence of buoyancy extends only up to Re ≈ 500 (Ri ≈ 0.5) and it is small, especially for the W spacer. As in the 45° orientation, the woven spacer yields values of Nu that are higher than they are for the spheres spacer.
Graph (b) pertains to the overlapped (O) spacers that were arranged at 0–90°. In this case, even in the absence of buoyancy, different mean Nusselt numbers were expected on the two opposite walls, according to whether the wall-adjacent spacer filaments were arranged at 0° or 90° with respect to the flow direction. The presence of buoyancy further changes the results according to whether a given wall is placed on the top or on the bottom of the channel, and so four different curves are to be considered.
Unlike the previous results for the W and S spacers, the present ones exhibit a large and complex influence of buoyancy, suggesting that the overlapped spacers interfere less with the buoyancy-induced motions. A maximum in Nu at Re ≈ 300–400 can even be observed on the 0° side when this is placed at the top. However, also in the present case, the effects of buoyancy become insignificant in the range Re > ~500, wherein the top and bottom curves for each orientation merge and follow the ~0.8-power law. In this range, the mean Nusselt number is almost double on the 90° wall (where the wall-adjacent spacer filaments are orthogonal to the flow) that on the 0° wall (where the wall-adjacent spacer filaments are parallel to the flow). In comparison with the woven and spheres geometries, Nu is slightly larger than with the W spacers on the 90° wall, and it is smaller than the S spacers on the 0° wall.
The strong asymmetry between the 0°-wall and the 90°-wall in terms of heat transfer makes the O 0–90° configuration unsuitable for MD applications, where, for thermodynamic reasons, it is desirable to achieve the same overall heat (and thus, water vapor) transfer from the two sides of the hot (feed) channel.
3.4. Performance Comparison
In the context of membrane distillation, the main performance parameters of a spacer are the mean Nusselt number Nu and the friction coefficient f. However, they have a rather different impact on the design and cost of a MD unit: for any given product (freshwater) outflow, a high mean Nusselt number allows a reduction in the membrane surface and/or of the driving temperature difference, with direct benefits on the plant’s cost and/or on the cost of the required thermal energy, which are the most relevant cost items. On the other hand, the benefits of a low friction coefficient are usually small in terms of the pumping power savings, but they may become crucial in terms of the design if LEP issues are involved.
Therefore, comparisons being made between the alternative spacers based on a single figure of merit (e.g., Nu/
f) are inappropriate. A better comparison method is based on introducing two dimensionless numbers N
Δp =
f·Re
2 (pressure number, which is proportional to the inlet-to-outlet pressure drop) and N
W=
f·Re
3 (power number, which is proportional to the required pumping power) and reporting the mean Nusselt number as a function of either parameter [
21]. If the Nu(N
Δp) curve for spacer A lies above that for spacer B, then spacer A will provide a better performance for any pressure drop, while, if the Nu(N
W) curve for spacer A lies above that for spacer B, then spacer A will provide a better performance for any pumping power consumption.
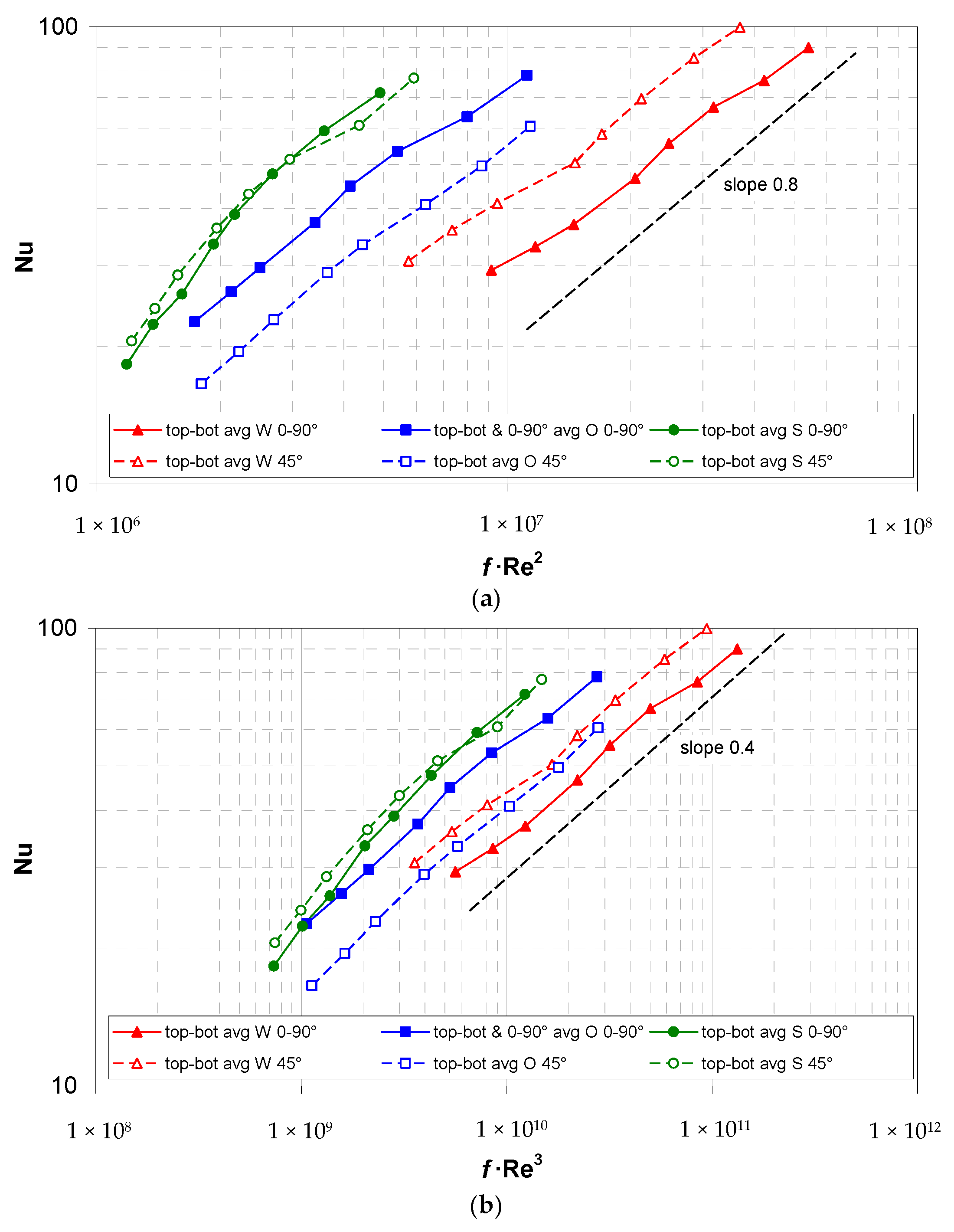
For all of the spacer configurations that were investigated, both of the above types of curves are shown in
Figure 9a,b. For the sake of clarity, in all of the cases, the reported mean Nusselt number is an average between the top and bottom values, and only cases with Re > 500, wherein it was negligibly affected by the buoyancy effects, are included. Moreover, in order to allow for an easy comparison with the W and S geometries, for the overlapped (O) spacer that was oriented at 0–90° with respect to the flow direction also the relevant 0° and 90° values have been averaged.
The graphs show that, among the geometries that were tested, in the range Re > 500 and regardless of the spacer orientation, the best performance was provided by the novel spheres geometry both for any given pressure drop and for any given pumping power, whereas the worst performance was provided by the woven geometry at 0–90°, despite its high Nu values. Note that, at the present pitch-to-channel height ratio
P/
H = 4, the ranking of the overlapped and woven spacers is different from that which was observed in the comparative study [
12], which was for
P/
H = 2. Note also that thanks to the favourable friction coefficient of the spheres spacer, the relative ranking of the spheres and the woven spacers in both of the graphs of
Figure 9 is reversed with respect to those which is reported in
Figure 7 and
Figure 8a which have Re as the abscissa.
These results suggest that the woven spacers should be used only if an increase in the mean heat transfer coefficient, and thus a reduction in the membrane surface area, is the only or the main goal, e.g., if the membrane cost is the dominant cost item. In all of the other circumstances, the spheres spacers should be preferred both to reduce the maximum trans-membrane pressure, thereby avoiding LEP issues, and to reduce the pumping power consumption.
3.5. Local Heat Transfer Coefficient Distributions
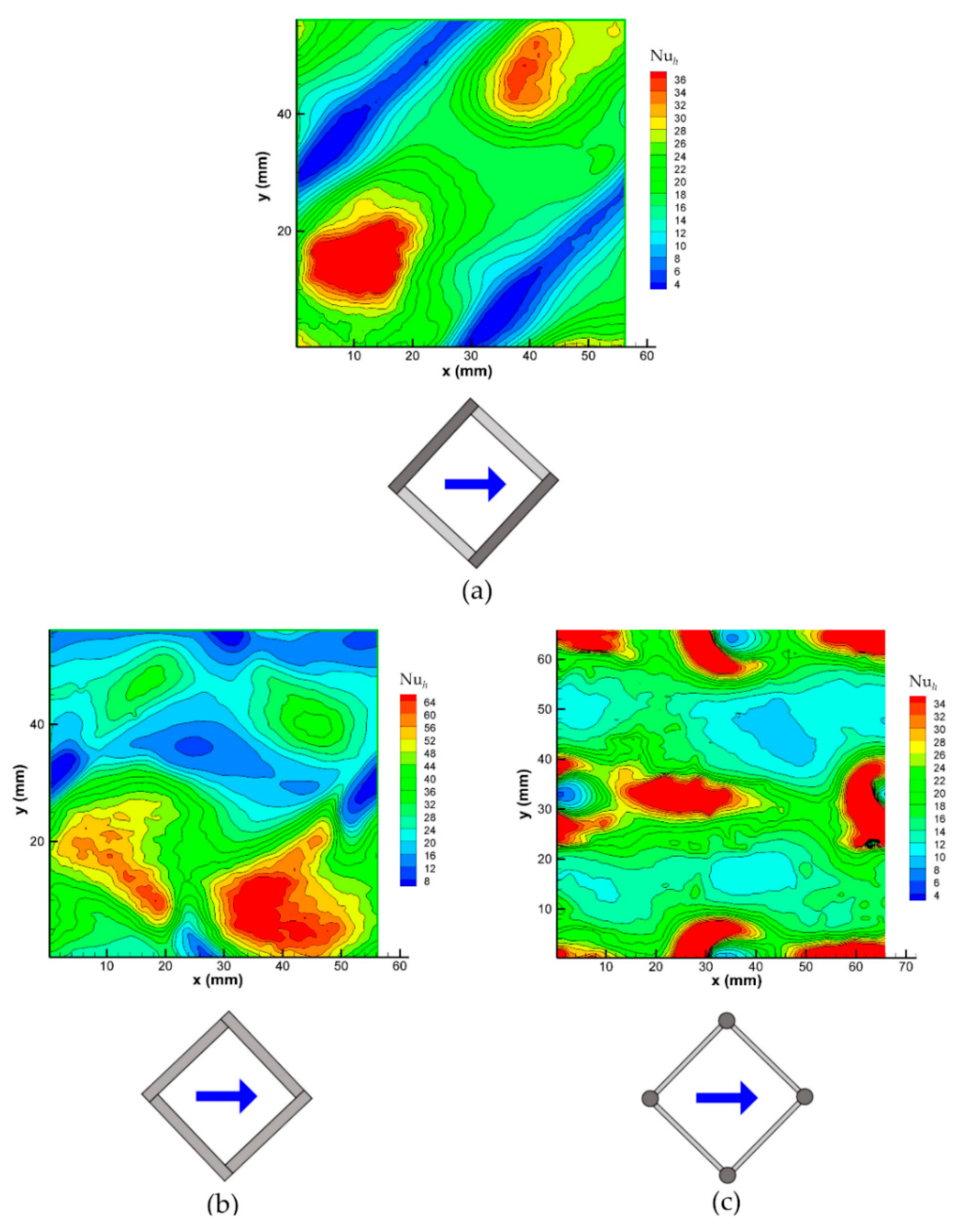
The following figures report examples of the local Nusselt number distributions on the channel walls in a unit cell of the spacer lattice, which were obtained with different spacers. In all of the cases, the Reynolds number was ~500 so that buoyancy effects were negligible, and the distinction between top and bottom sides of the channel is irrelevant. All of the maps are represented from the same viewpoint; the insets below each map show the arrangement of the spacer with respect to the flow direction. In the case of the overlapped spacers, the filaments touching the wall that is under consideration are represented in a darker shade of grey.
Graph (a) pertains to the 0° wall of a channel that is filled with an overlapped spacer that is oriented at 0–90° (O 0–90°). It shows the minima of Nu
h around the wall-filament contact lines, while the maxima of Nu
h are attained in the central region of the sides, lying above the opposite filaments (adjacent to the 90° wall), where the flow passage area is restricted and the local velocity is at its highest. The mean Nusselt number, which was computed from Equation (5), is ~16, (see
Figure 8b).
Graph (b) pertains to the 90° wall in the presence of the same spacer (O 0–90°). It shows the minima of Nu
h around the wall-filament contact lines, which of course are now orthogonal to those that are represented for the opposite wall in graph (a). The maxima of Nu
h are attained at about 1/3
rd of the pitch
P downstream of each wall-adjacent filament in correspondence with the reattachment of the flow separating it from the upstream wall-adjacent filament. The mean Nusselt number Nu, which was computed from Equation (5), is ~19, which is only slightly larger than that on the 0° wall, as shown also in
Figure 8b, while the absolute maximum of the local Nusselt number Nu
h is much larger than it is on the 0° wall.
Graph (c) pertains to one wall of a channel that is filled with a woven spacer (W 0–90°). The four small contact areas at the corners of the unit cell surrounding the point-like contacts between the spacer and the wall are characterized by very low values of Nu
h. As indicated by the preliminary CFD simulations, the absolute and relative maxima of Nu
h correspond to the regions in which the complex flow that is induced by the spacer impacts against the wall that is under consideration. The mean Nusselt number Nu, which was computed from Equation (5), is ~23, as shown also in
Figure 8a, while the absolute maximum of the local Nusselt number Nu
h is ~60; both of these values are the highest among all of the configurations in this figure.
Finally, graph (d) reports the distribution of Nu
h on one wall of a channel that is filled with the spheres spacer (S 0–90°). Note that the pitch
P is now 44 mm, which is slightly larger than it is for the previous geometry. In this case, the Nu
h minima at the four corners of the unit cell, which are associated with the point-like contacts between the spacer spheres and the wall, are surrounded by horseshoe structures that are characterized by high Nu
h values upstream of each sphere, which are associated with the impact of the flow against this latter. Other eye-catching structures are the low Nu
h wakes that result from the downstream side of each sphere. Apart from the mentioned features, the Nu
h distribution over the remaining part of the wall appears to be less structured and exhibits intermediate values. The mean Nusselt number Nu, which was computed from Equation (5), is ~15, see
Figure 8a, while the absolute maximum of the local Nusselt number Nu
h is ~25; therefore, the spheres geometry is that which exhibits the flattest distribution of the local heat transfer coefficient.
Figure 11 shows the 45° orientation. Note that in this case, the unit cells are larger by a factor
(i.e., the area is double the size) with respect to those in
Figure 10.
Graph (a) pertains to one wall of a channel that is filled with an overlapped spacer (O 45°). For this orientation, due to symmetry reasons, the distributions of Nu
h on the opposite walls of the hot channel are essentially identical, when we are disregarding the reflections, so it is sufficient to show a single wall. The map shows the minima of Nu
h around the diagonal wall-filament contact lines, while the Nu
h maxima are attained in two separate regions that are located between the filaments and presumably corresponding to the flow reattachment regions as in the O 90° case in
Figure 10b. The mean Nusselt number Nu, which was computed from Equation (5), is ~14, see
Figure 7, while the Nu
h maxima are much higher (>36).
Graph (b) pertains to one wall of a channel that is filled with a woven spacer (W 45°). The four areas surrounding the point-like contacts between the spacer and the wall, and those that are characterized by very low values of Nu
h, are now located at the centers of the four sides of the unit cell. As in the 0–90° case (
Figure 10c), an isolated and intense Nu
h maximum can be observed, thus corresponding as indicated by preliminary CFD simulations, to a region in which the spacer-induced flow impinges against the wall that is under consideration. The mean Nusselt number Nu, which was obtained by calculating Equation (5), is ~26, see
Figure 7, while the absolute maximum of Nu
h is >64; both of these values are the highest among all of the configurations in this figure.
Finally, graph (c) reports the distribution of Nu
h on one wall of a channel that is filled with the spheres spacer (S 45°). As in the 0–90° orientation (
Figure 10d), the Nu
h minima at the four point-like sphere-wall contacts are surrounded by horseshoe structures that are characterized by high Nu
h values that are upstream of each sphere. However, unlike in the 0–90° case, the wake region of each sphere exhibits a complex structure with a minimum value immediately downstream that is followed by a maximum of the same amplitude as that in the horseshoe region, which is presumably caused by the confluence of the vortex streets issuing from the 45° filaments that connect the spheres. The mean Nusselt number Nu, which was calculated using Equation (5), is ~17, see
Figure 7, while the absolute maximum of Nu
h is >34.