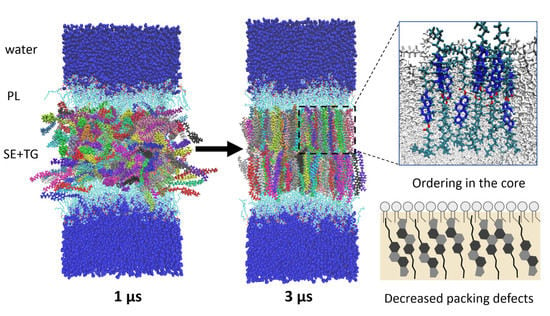
Capturing the Liquid-Crystalline Phase Transformation: Implications for Protein Targeting to Sterol Ester-Rich Lipid Droplets
Abstract
1. Introduction
2. Materials and Methods
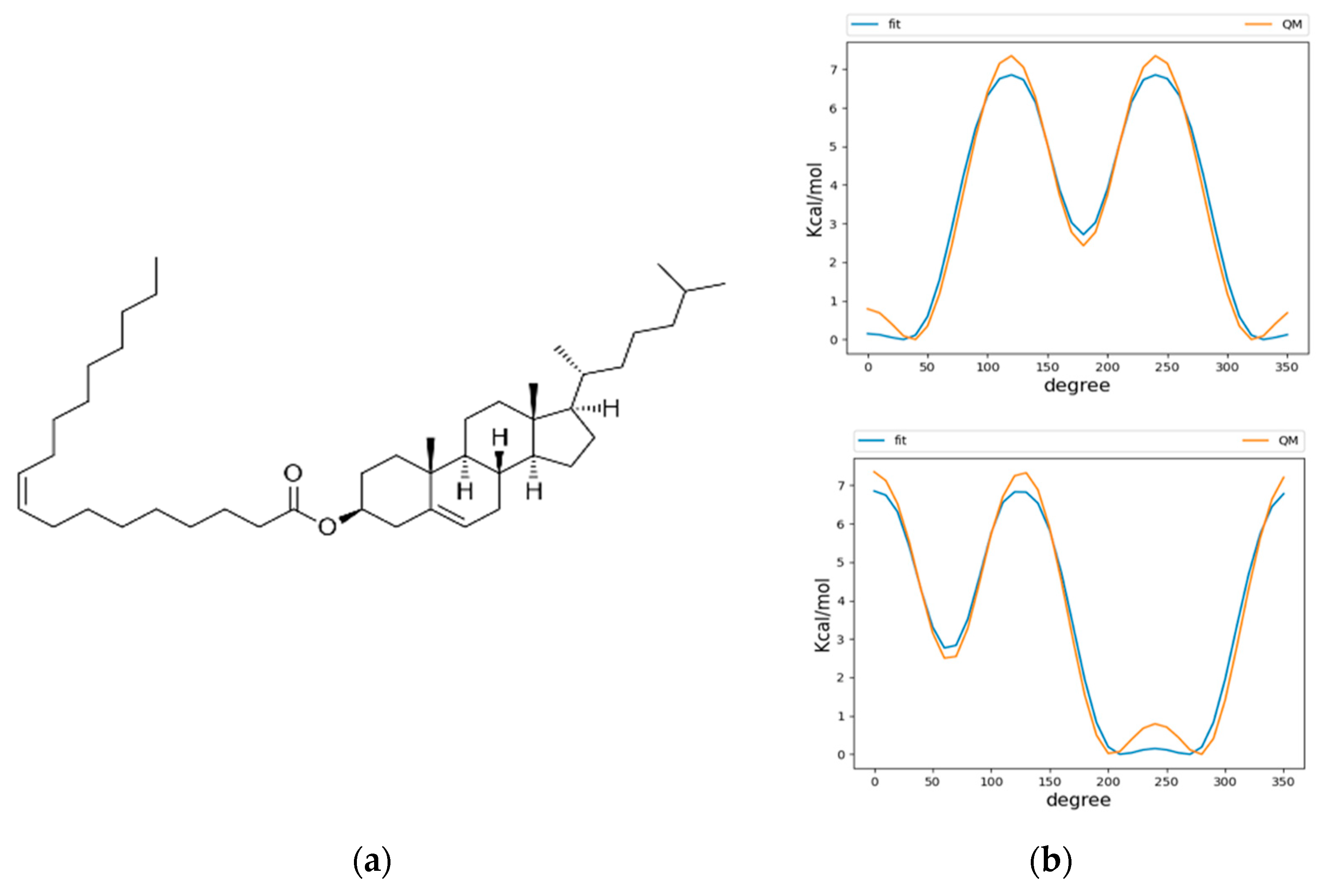
2.1. Parameterization of CHYO
2.2. System Setup
2.3. Order Parameters
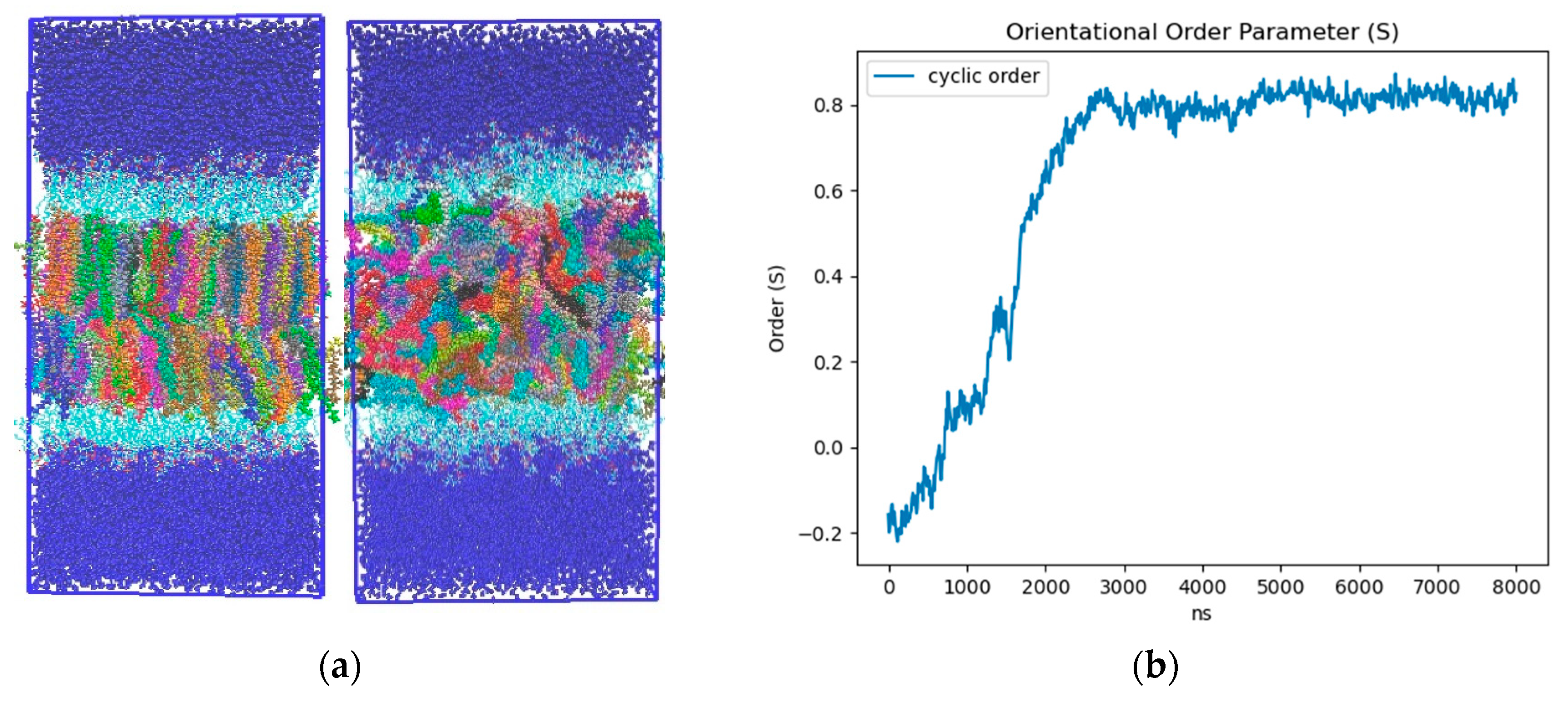
2.3.1. Liquid Crystal Ordering
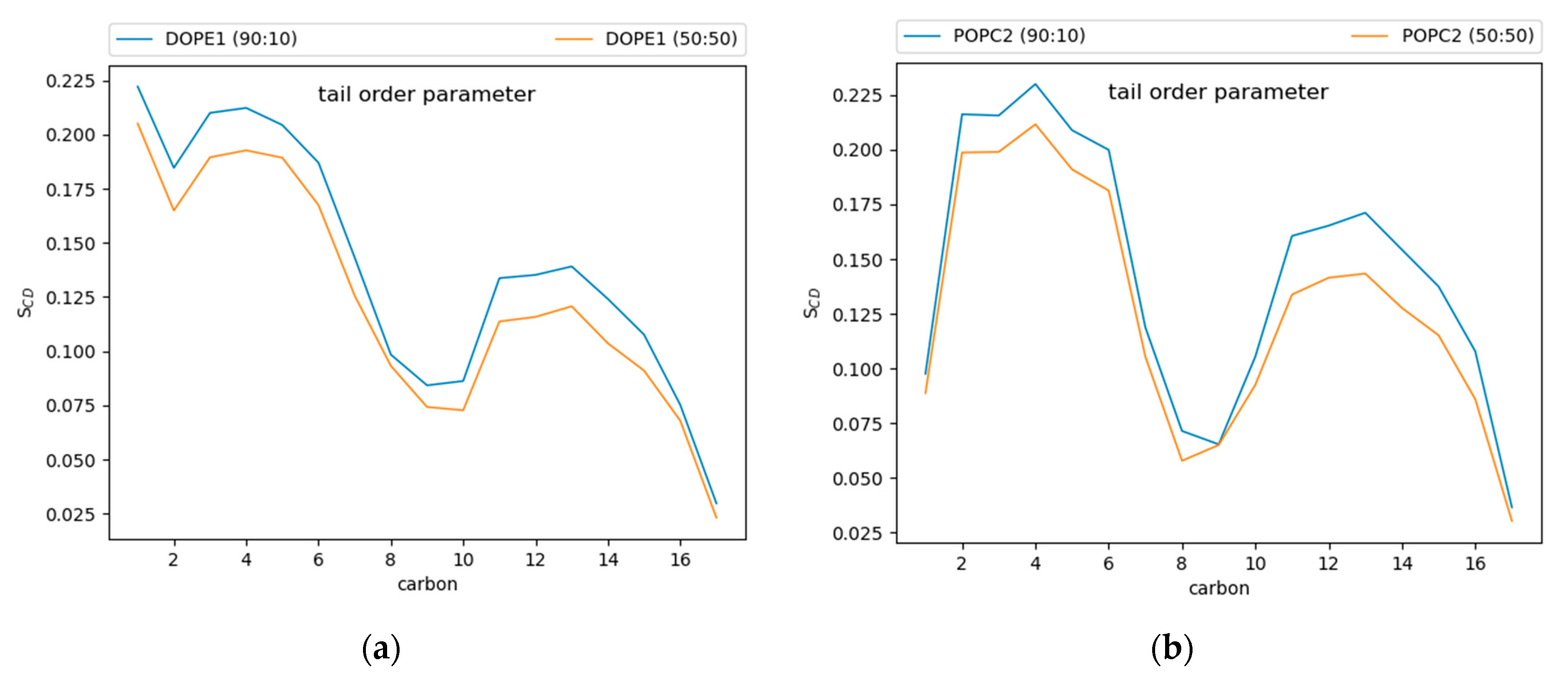
2.3.2. Phospholipid Tail Order Parameters
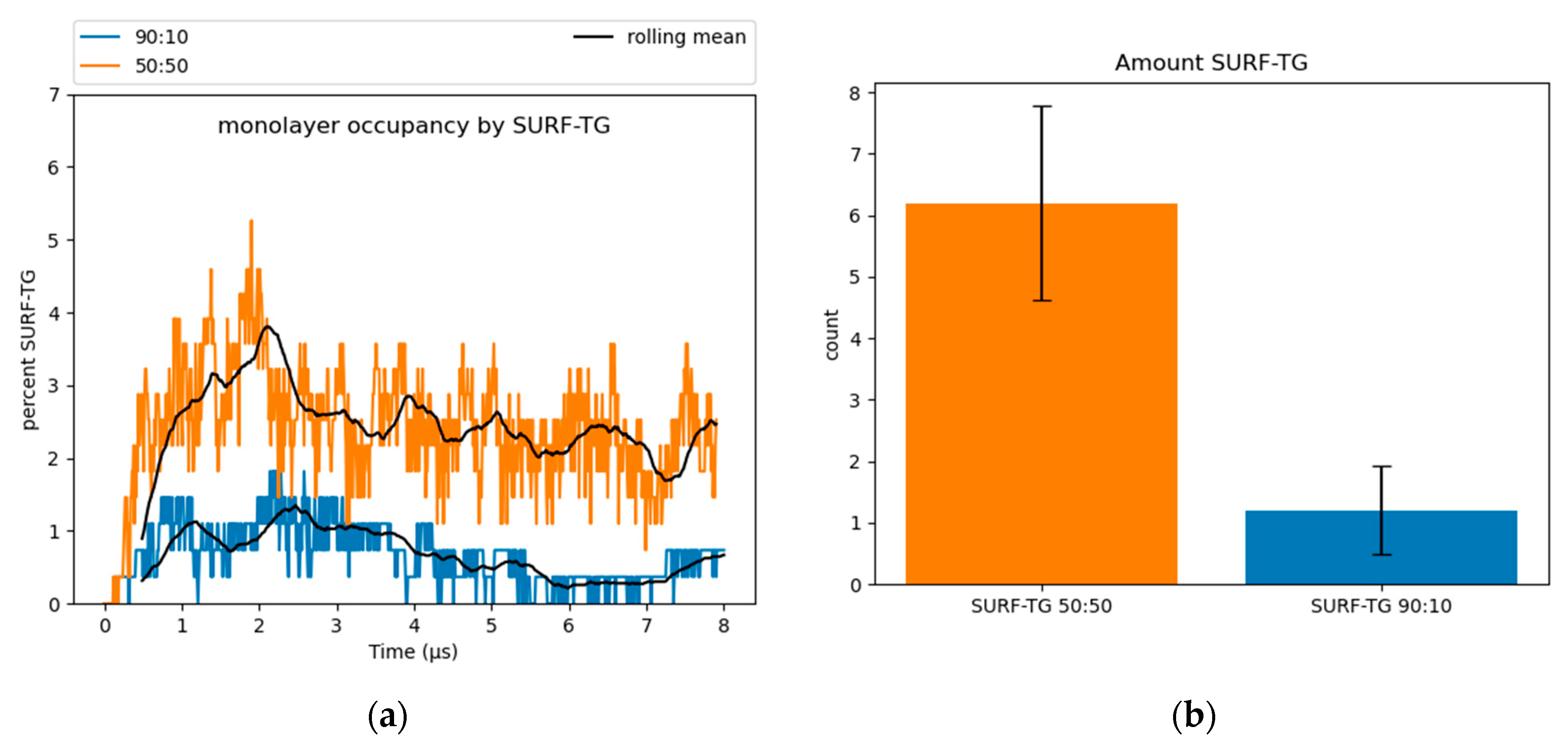
2.4. Classifying Surface Molecules
2.5. Interdigitation
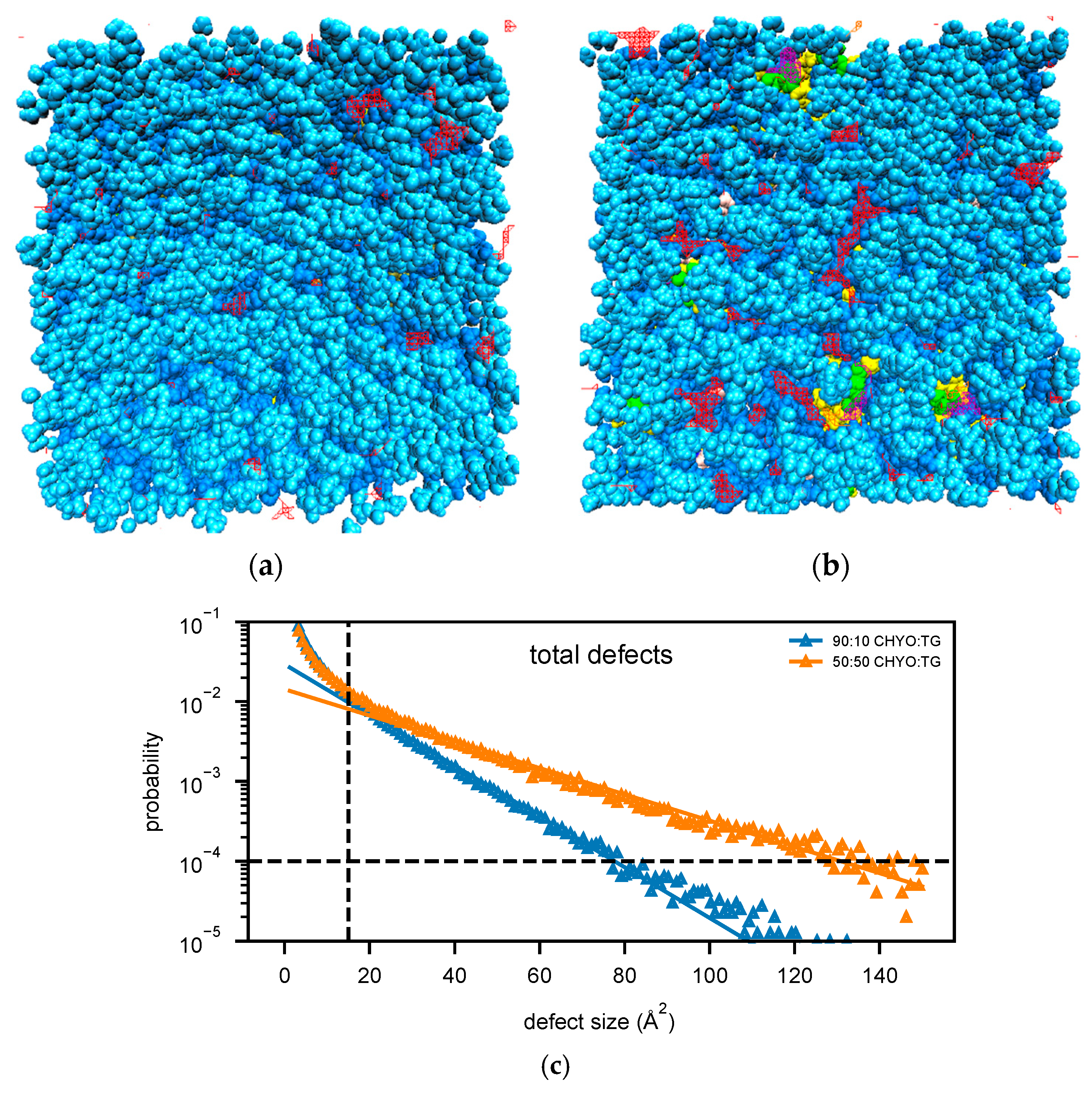
2.6. Packing Defect Analysis
3. Results
3.1. Liquid Crystalline Smectic Phase Transformation
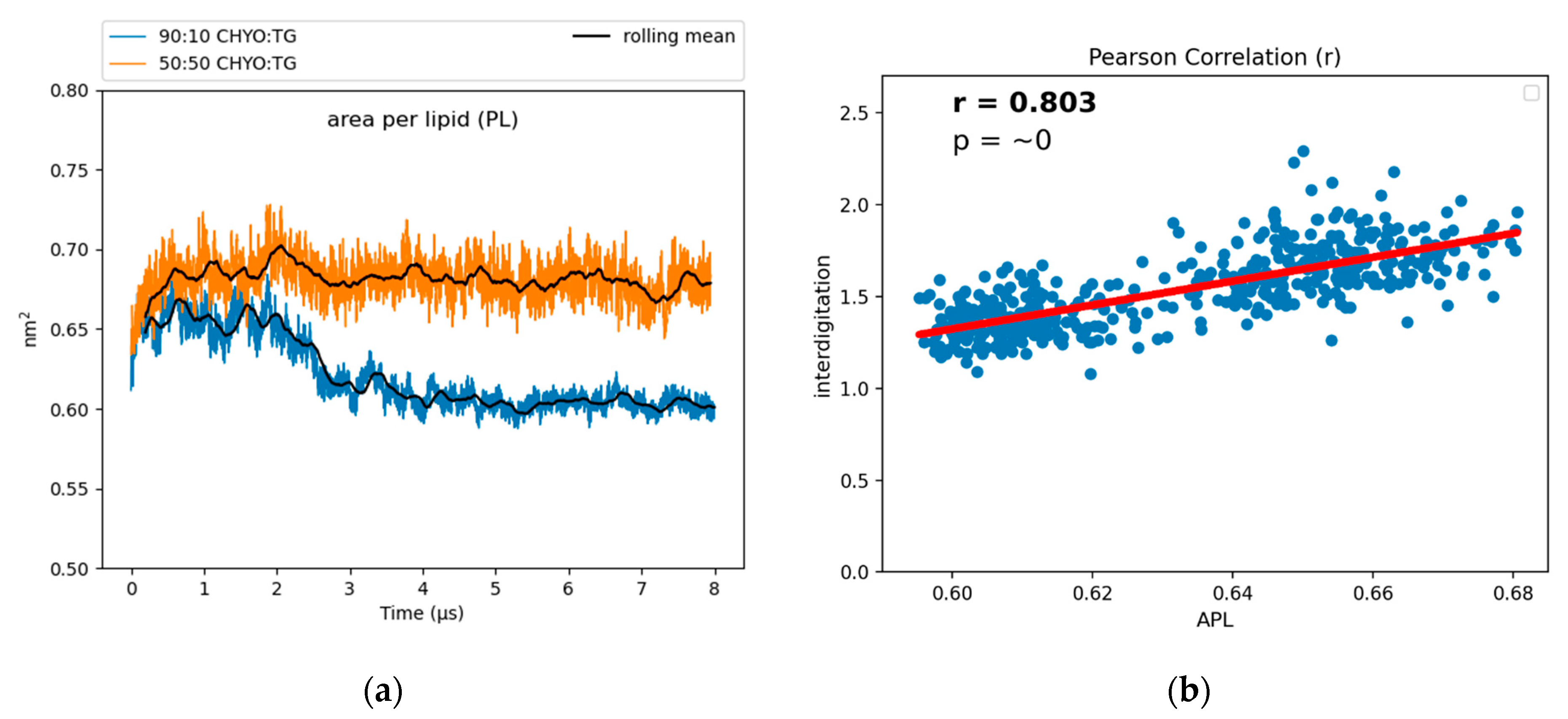
3.2. Physical Properties of SE-Rich LDs
3.3. Interdigitation
3.4. Phospholipid Properties
3.5. Packing Defects
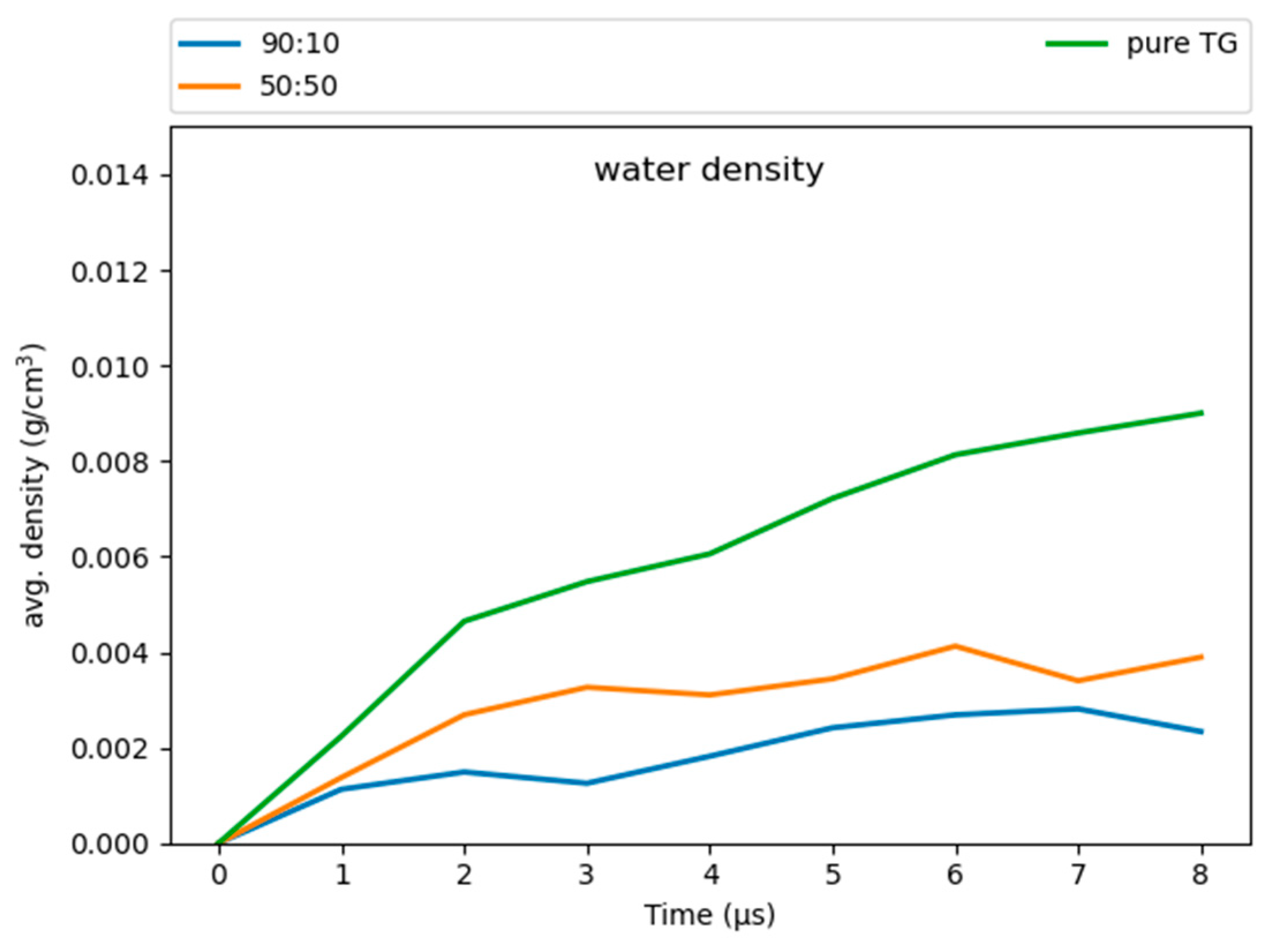
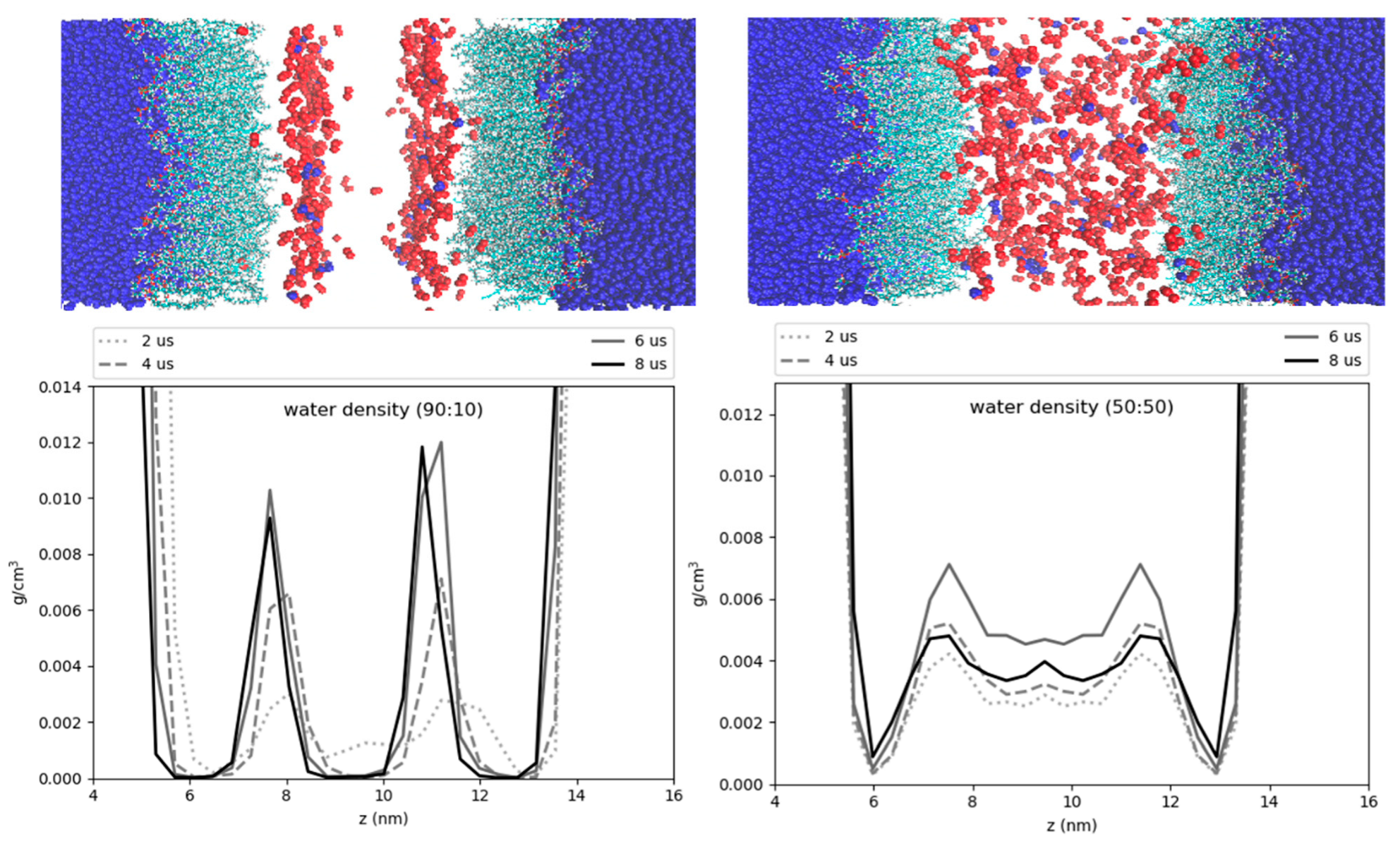
3.6. Hydration of the LD Core
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C.; Liu, P. The New Face of the Lipid Droplet: Lipid Droplet Proteins. Proteomics 2019, 19, 1700223. [Google Scholar] [CrossRef] [PubMed]
- Olarte, M.J.; Swanson, J.M.J.; Walther, T.C.; Farese, R.V. The CYTOLD and ERTOLD pathways for lipid droplet–protein targeting. Trends Biochem. Sci. 2021, 47, 39–51. [Google Scholar] [CrossRef] [PubMed]
- Walther, T.C.; Chung, J.; Farese, R.V. Lipid Droplet Biogenesis. Annu. Rev. Cell Dev. Biol. 2017, 33, 491–510. [Google Scholar] [CrossRef]
- Mejhert, N.; Kuruvilla, L.; Gabriel, K.R.; Elliott, S.D.; Guie, M.-A.; Wang, H.; Lai, Z.W.; Lane, E.A.; Christiano, R.; Danial, N.N.; et al. Partitioning of MLX-Family Transcription Factors to Lipid Droplets Regulates Metabolic Gene Expression. Mol. Cell 2020, 77, 1251–1264.e9. [Google Scholar] [CrossRef]
- Bosch, M.; Sánchez-Álvarez, M.; Fajardo, A.; Kapetanovic, R.; Steiner, B.; Dutra, F.; Moreira, L.; López, J.A.; Campo, R.; Marí, M.; et al. Mammalian lipid droplets are innate immune hubs integrating cell metabolism and host defense. Science 2020, 370, eaay8085. [Google Scholar] [CrossRef] [PubMed]
- Onal, G.; Kutlu, O.; Gozuacik, D.; Emre, S.D. Lipid Droplets in Health and Disease. Lipids Health Dis. 2017, 16, 128. [Google Scholar] [CrossRef]
- Bartz, R.; Li, W.-H.; Venables, B.; Zehmer, J.K.; Roth, M.R.; Welti, R.; Anderson, R.G.W.; Liu, P.; Chapman, K.D. Lipidomics reveals that adiposomes store ether lipids and mediate phospholipid traffic. J. Lipid Res. 2007, 48, 837–847. [Google Scholar] [CrossRef]
- Meyers, A.; Weiskittel, T.M.; Dalhaimer, P. Lipid Droplets: Formation to Breakdown. Lipids 2017, 52, 465–475. [Google Scholar] [CrossRef]
- McGilvray, P.T.; Anghel, S.A.; Sundaram, A.; Zhong, F.; Trnka, M.J.; Fuller, J.R.; Hu, H.; Burlingame, A.L.; Keenan, R.J. An ER translocon for multi-pass membrane protein biogenesis. Elife 2020, 9, e56889. [Google Scholar] [CrossRef]
- Kim, P.K.; Hettema, E.H. Multiple pathways for protein transport to peroxisomes. J. Mol. Biol. 2015, 427, 1176–1190. [Google Scholar] [CrossRef]
- Kim, S.; Oh, M.I.; Swanson, J.M.J. Stressed Lipid Droplets: How Neutral Lipids Relieve Surface Tension and Membrane Expansion Drives Protein Association. J. Phys. Chem. B 2021, 125, 5572–5586. [Google Scholar] [CrossRef] [PubMed]
- Chorlay, A.; Thiam, A.R. Neutral lipids regulate amphipathic helix affinity for model lipid droplets. J. Cell Biol. 2020, 219, e201907099. [Google Scholar] [CrossRef]
- Olarte, M.J.; Kim, S.; Sharp, M.E.; Swanson, J.M.J.; Farese, R.V.; Walther, T.C. Determinants of Endoplasmic Reticulum-to-Lipid Droplet Protein Targeting. Dev. Cell 2020, 54, 471–487.e7. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Swanson, J.M.J. The Surface and Hydration Properties of Lipid Droplets. Biophys. J. 2020, 119, 1958–1969. [Google Scholar] [CrossRef]
- Prévost, C.; Sharp, M.E.; Kory, N.; Lin, Q.; Voth, G.A.; Farese, R.V.; Walther, T.C. Mechanism and Determinants of Amphipathic Helix-Containing Protein Targeting to Lipid Droplets. Dev. Cell 2018, 44, 73–86.e4. [Google Scholar] [CrossRef] [PubMed]
- Bacle, A.; Gautier, R.; Jackson, C.L.; Fuchs, P.F.J.; Vanni, S. Interdigitation between Triglycerides and Lipids Modulates Surface Properties of Lipid Droplets. Biophys. J. 2017, 112, 1417–1430. [Google Scholar] [CrossRef]
- Mahamid, J.; Tegunov, D.; Maiser, A.; Arnold, J.; Leonhardt, H.; Plitzko, J.M.; Baumeister, W. Liquid-crystalline phase transitions in lipid droplets are related to cellular states and specific organelle association. Proc. Natl. Acad. Sci. USA 2019, 116, 16866–16871. [Google Scholar] [CrossRef]
- Czabany, T.; Wagner, A.; Zweytick, D.; Lohner, K.; Leitner, E.; Ingolic, E.; Daum, G. Structural and biochemical properties of lipid particles from the yeast Saccharomyces cerevisiae. J. Biol. Chem. 2008, 283, 17065–17074. [Google Scholar] [CrossRef]
- Rogers, S.; Gui, L.; Kovalenko, A.; Reetz, E.; Nicastro, D.; Henne, W.M. Liquid-crystalline lipid phase transitions in lipid droplets selectively remodel the LD proteome. BioRxiv 2021. [Google Scholar] [CrossRef]
- Watt, M.J.; Spriet, L.L.; Watt, M.J. Triacylglycerol lipases and metabolic control: Implications for health and disease. Am. J. Physiol.-Endocrinol. Metab. 2010, 299, 162–168. [Google Scholar] [CrossRef]
- Ayyappan, J.P.; Paul, A.; Goo, Y.H. Lipid droplet-associated proteins in atherosclerosis (Review). Mol. Med. Rep. 2016, 13, 4527–4534. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Zhang, L.; Li, Y.; Zhu, X.; Xu, S.; Zhou, X.-M.; Wang, H.; Zhang, H.; Liang, B.; Liu, P. The Adrenal Lipid Droplet is a New Site for Steroid Hormone Metabolism. Proteomics 2018, 18, e1800136. [Google Scholar] [CrossRef] [PubMed]
- Saupel, A. Recent Results in the Field of Liquid Crystals. Angew. Chem. Int. Ed. Engl. 1968, 7, 97–112. [Google Scholar] [CrossRef]
- Khor, V.K.; Ahrends, R.; Lin, Y.; Shen, W.-J.; Adams, C.M.; Roseman, A.N.; Cortez, Y.; Teruel, M.N.; Azhar, S.; Kraemer, F.B. The proteome of cholesteryl-ester-enriched versus triacylglycerol-enriched lipid droplets. PLoS ONE 2014, 9, e105047. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.L.; Dunbrack, R.L., Jr.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Head-Gordon, M.; Pople, J.A.; Frisch, M.J. MP2 energy evaluation by direct methods. Chem. Phys. Lett. 1988, 153, 503–506. [Google Scholar] [CrossRef]
- Moller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Venable, R.M.; Sodt, A.J.; Rogaski, B.; Rui, H.; Hatcher, E.; MacKerell, A.D.; Pastor, R.W.; Klauda, J.B. CHARMM all-atom additive force field for sphingomyelin: Elucidation of hydrogen bonding and of positive curvature. Biophys. J. 2014, 107, 134–145. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Guvench, O.; MacKerell, A.D. Automated conformational energy fitting for force-field development. J. Mol. Model. 2008, 14, 667–679. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell, A.D. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.W.; Small, D.M. Triolein-cholesteryl oleate-cholesterol-lecithin emulsions: Structural models of triglyceride-rich lipoproteins. Biochemistry 1983, 22, 443–451. [Google Scholar] [CrossRef]
- Small, D.M. Handbook of Lipid Research; Plenum Press: New York, NY, USA, 1986; Volume 4, pp. 149–180. [Google Scholar]
- Fujimoto, T.; Parton, R.G. Not just fat: The structure and function of the lipid droplet. Cold Spring Harb. Perspect. Biol. 2011, 3, a004838. [Google Scholar] [CrossRef]
- Croll, D.H.; Small, D.M.; Hamilton, J.A. Molecular motions and thermotropic phase behavior of cholesteryl esters with triolein. Biochemistry 1985, 24, 7971–7980. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Yang, Y.; Lee, M.; Fairn, G.D. Phospholipid subcellular localization and dynamics. J. Biol. Chem. 2018, 293, 6230–6240. [Google Scholar] [CrossRef]
- Martinez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Hess, B. P-LINCS: A parallel linear constraint solver for molecular simulation. J. Chem. Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef] [PubMed]
- Gowers, R.J.; Linke, M.; Barnoud, J.; Reddy, T.J.E.; Melo, M.N.; Seyler, S.L.; Domanski, J.; Dotson, D.L.; Buchoux, S.; Kenney, I.M.; et al. MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations. In Proceedings of the Python in Science Conference, Austin, TX, USA, 11–17 July 2016; pp. 102–109. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Mcmillan, W.L. Simple Molecular Model for the SmecticAPhase of Liquid Crystals. Phys. Rev. A 1971, 4, 1238–1246. [Google Scholar] [CrossRef]
- Singh, G.; Agra-Kooijman, D.M.; Fisch, M.R.; Vengatesan, M.R.; Song, J.-K.; Kumar, S. Orientational Order in the Nematic and Heliconical Nematic Liquid Crystals. arXiv 2015, arXiv:1510.08362. [Google Scholar]
- Schindler, H.; Seelig, J. Order parameters in relation to thermodynamic properties of a phospholipid bilayer. Statistical mechanical interpretation. Biochemistry 1975, 14, 2283–2287. [Google Scholar] [CrossRef]
- Das, C.; Noro, M.G.; Olmsted, P.D. Simulation studies of stratum corneum lipid mixtures. Biophys. J. 2009, 97, 1941–1951. [Google Scholar] [CrossRef]
- Gautier, R.; Bacle, A.; Tiberti, M.L.; Fuchs, P.F.; Vanni, S.; Antonny, B. PackMem: A Versatile Tool to Compute and Visualize Interfacial Packing Defects in Lipid Bilayers. Biophys. J. 2018, 115, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.; Lyman, E.; Voth, G.A. Mechanism of membrane curvature sensing by amphipathic helix containing proteins. Biophys. J. 2011, 100, 1271–1279. [Google Scholar] [CrossRef]
- Vanni, S.; Vamparys, L.; Gautier, R.; Drin, G.; Etchebest, C.; Fuchs, P.F.; Antonny, B. Amphipathic lipid packing sensor motifs: Probing bilayer defects with hydrophobic residues. Biophys. J. 2013, 104, 575–584. [Google Scholar] [CrossRef] [PubMed]
- Degirolamo, C.; Shelness, G.S.; Rudel, L.L. LDL cholesteryl oleate as a predictor for atherosclerosis: Evidence from human and animal studies on dietary fat. J. Lipid Res. 2009, 50, S434–S439. [Google Scholar] [CrossRef] [PubMed]
- Poll, K.; Sims, M.T. An insight into de Vries behaviour of smectic liquid crystals from atomistic molecular dynamics simulations. J. Mater. Chem. C 2020, 8, 13040–13052. [Google Scholar] [CrossRef]
- Das, P.; Basu, S.; Sinha, R.K.; Das, U. Dipole-induced chiral smectic-C phase in a eutectic mixture of cholesterol esters. Chem. Phys. Lett. 2005, 410, 417–422. [Google Scholar] [CrossRef]
- Haege, C.; Jagiella, S.; Giesselmann, F. Molecular Electron Density Distribution and X-Ray Diffraction Patterns of Smectic A Liquid Crystals—A Simulation Study. ChemPhysChem 2019, 20, 2466–2472. [Google Scholar] [CrossRef]
- Burks, C.; Engelman, D.M. Cholesteryl myristate conformation in liquid crystalline mesophases determined by neutron scattering. Proc. Natl. Acad. Sci. USA 1981, 78, 6863–6867. [Google Scholar] [CrossRef]
- Venable, R.M.; Brown, F.L.H.; Pastor, R.W. Mechanical properties of lipid bilayers from molecular dynamics simulation. Chem. Phys. Lipids 2015, 192, 60–74. [Google Scholar] [CrossRef]
- Nuscher, B.; Kamp, F.; Mehnert, T.; Odoy, S.; Haass, C.; Kahle, P.J.; Beyer, K. α-synuclein has a high affinity for packing defects in a bilayer membrane: A thermodynamics study. J. Biol. Chem. 2004, 279, 21966–21975. [Google Scholar] [CrossRef]
- Kim, S.; Voth, G.A. Physical Characterization of Triolein and Implications for Its Role in Lipid Droplet Biogenesis. J. Phys. Chem. B 2021, 125, 6874–6888. [Google Scholar] [CrossRef] [PubMed]
- Campomanes, P.; Prabhu, J.; Zoni, V.; Vanni, S. Recharging your fats: CHARMM36 parameters for neutral lipids triacylglycerol and diacylglycerol. Biophys. Rep. 2021, 1, 100034. [Google Scholar] [CrossRef] [PubMed]
- Platford, R.F. The octanol-water partitioning of some hydrophobic and hydrophilic compounds. Chemosphere 1983, 12, 1107–1111. [Google Scholar] [CrossRef]
- Miller, K.W.; Small, D.M. Surface-to-Core and Interparticle Equilibrium Distributions of Triglyceride-rich Lipoprotein Lipids. J. Biol. Chem. 1983, 258, 13772–13784. [Google Scholar] [CrossRef]
- Chorlay, A.; Forêt, L.; Thiam, A.R. Origin of gradients in lipid density and surface tension between connected lipid droplet and bilayer. Biophys. J. 2021, 120, 5491–5503. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Swanson, J.M.J.; Voth, G.A. Computational Studies of Lipid Droplets. J. Phys. Chem. B 2022, 126, 2145–2154. [Google Scholar] [CrossRef]
- Hsieh, K.; Lee, Y.K.; Londos, C.; Raaka, B.M.; Dalen, K.T.; Kimmel, A.R. Perilipin family members preferentially sequester to either triacylglycerol-specific or cholesteryl-esterspecific intracellular lipid storage droplets. J. Cell Sci. 2012, 125, 4067–4076. [Google Scholar] [CrossRef]
- Leadbetter, A.J.; Norris, E.K. Distribution functions in three liquid crystals from X-ray diffraction measurements. Mol. Phys. 1979, 38, 669–686. [Google Scholar] [CrossRef]
- Engelman, D.M.; Humlan, G.M. Molecular Organization of the Cholesteryl Ester Droplets in the Fatty Streaks of Human Aorta. J. Clin. Investig. 1976, 58, 997–1007. [Google Scholar] [CrossRef]
- Hamilton, J.A.; Miller, K.W.; Small, D.M. Solubilization of triolein and cholesteryl oleate in egg phosphatidylcholine vesicles. J. Biol. Chem. 1983, 258, 12821–12826. [Google Scholar] [CrossRef]
- Spooner, P.J.R.; Small, D.M. Effect of Free Cholesterol on Incorporation of Triolein in Phospholipid Bilayers. Biochemistry 1986, 26, 5820–5825. [Google Scholar] [CrossRef] [PubMed]
- Chaban, V.V.; Khandelia, H. Distribution of neutral lipids in the lipid droplet core. J. Phys. Chem. B 2014, 118, 11145–11151. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braun, R.J.; Swanson, J.M.J. Capturing the Liquid-Crystalline Phase Transformation: Implications for Protein Targeting to Sterol Ester-Rich Lipid Droplets. Membranes 2022, 12, 949. https://doi.org/10.3390/membranes12100949
Braun RJ, Swanson JMJ. Capturing the Liquid-Crystalline Phase Transformation: Implications for Protein Targeting to Sterol Ester-Rich Lipid Droplets. Membranes. 2022; 12(10):949. https://doi.org/10.3390/membranes12100949
Chicago/Turabian StyleBraun, R. Jay, and Jessica M. J. Swanson. 2022. "Capturing the Liquid-Crystalline Phase Transformation: Implications for Protein Targeting to Sterol Ester-Rich Lipid Droplets" Membranes 12, no. 10: 949. https://doi.org/10.3390/membranes12100949
APA StyleBraun, R. J., & Swanson, J. M. J. (2022). Capturing the Liquid-Crystalline Phase Transformation: Implications for Protein Targeting to Sterol Ester-Rich Lipid Droplets. Membranes, 12(10), 949. https://doi.org/10.3390/membranes12100949