Abstract
By using the recently generalized version of Newton’s shell theorem, analytical equations are derived to calculate the electric interaction energy between two separated, charged spheres surrounded outside and inside by electrolyte. This electric interaction energy is calculated as a function of the electrolyte’s ion concentration, temperature, distance between the spheres and size of the spheres. At the same distance between the spheres, the absolute value of the interaction energy decreases with increasing electrolyte ion concentration and increases with increasing temperature. At zero electrolyte ion concentration, the derived analytical equation transforms into the Coulomb Equation Finally, the analytical equation is generalized to calculate the electric interaction energy of N separated, charged spheres surrounded by electrolyte.
1. Introduction
Recently, an analytical equation was derived that is a generalization of Newton’s shell theorem [1,2]. By using this equation (see Equation (1)), one can calculate the electric potential, , around a surface-charged sphere surrounded inside and outside by electrolyte at a distance Z from the center of the sphere (see also Equation (9) in e.g., [1]):
where ke = (4πε0)−1 is the Coulomb’s constant, is the vacuum permittivity, λD is the Debye length, Q is the total charge of the homogeneously charged surface of the sphere of radius R and εr is the relative static permittivity of the electrolyte. Note that recently, by using Equation (1), the electric energies have been calculated [3], such as the potential electric energy needed to build up a surface-charged sphere, and the field and polarization energy of the electrolyte inside and around the surface-charged sphere. In this paper, Equation (1) is used to derive an analytical equation to calculate the interaction energy between two separated surface-charged spheres surrounded inside and outside by electrolyte. This equation is a generalization of Coulomb’s law [4] that gives the interaction energy between two charges embedded in a vacuum. By means of the equation derived in this paper, one may get closer to study the long-range charge–charge interaction between vesicles or cells. The head groups of membrane lipids have either a single charge (e.g., tetraether lipids [5,6]) or an electric dipole (e.g., phospholipids [7,8]). Theoretical models of lipid membranes usually focus on short-range (Van der Waals) lateral interactions between the nearest neighbor lipids and ignore the long-range charge–charge interactions [8]. This is because in the case of long-range interactions one has to consider the entire system rather than the lateral interactions between the nearest neighbor lipids only. It is much more difficult to model a lipid membrane containing single-charged head groups [9]. Between lipids with single-charged head groups there is long-range interaction, i.e., where the two-body potential decays algebraically at large distances with a power smaller than the spatial dimension [10], and, thus, when modeling this system one has to consider the entire system rather than the interactions between the nearest-neighbor lipids.
Deriving Equation (1), the general solution of the screened Poisson equation was utilized (see Equation (4) in [1] or (A5) in Appendix A), an equation that is valid if the electrolyte is electrically neutral [11]. It is important to note that the screened Poisson equation (Equation (A4)) is different from the Poisson—Boltzmann equation (see Equations (A1) and (A3)). The Poisson—Boltzmann equation can be used to calculate the potential energy of an arbitrary, electroneutral ion solution (i.e., electrolyte). However, for the solution (see Equation (A2)) one has to know the charge density of the ions in the electrolyte (i.e., the Boltzmann distribution; see Equation (A3)), which depends on the potential, V, itself. Thus, only an approximative solution is available (the Debye–Hückel approximation [12]), which is valid when |ziqV/(kBT)| ≪ 1 (where q: charge of a monovalent ion (either positive or negative), zi: charge number (or valence) of the i-th type of ion, kB: Boltzmann constant, T: absolute temperature). Using the screened Poisson equation (Equation (A4)), one can calculate the potential energy of an electrolyte that also contains external charges. The external charges are embedded into the electrolyte (like the charges of the surface-charged sphere) but are not part of the electrolyte itself. For the solution, one has to know the charge density of the external charges, (see Equation (4) in [1] or Equation (A5) in Appendix A), i.e., distribution of the charges on the surface-charged sphere and not the distribution of the ions in the electrolyte. In our case, it is assumed that the charges on the surface of the sphere are homogeneously distributed and, in this case, Equation (1) is the exact solution of the screened Poisson Equation
Finally, we notice that by means of the analytical equation derived in this paper one can calculate the dependence of the electric interaction energy from the distance, charge and size of the spheres and from the electrolyte’s ion concentration and the temperature. In the case of our calculations, the surface-charge density of the charged spheres at every radius is ρs = −0.266 × C/m2. This is the charge density of PLFE (bipolar tetraether lipid with the polar lipid fraction E) vesicles if the cross-sectional area of a PLFE is 0.6 nm2 and the charge of a PLFE molecule is −1.6 × 10−19 C [5,6].
2. Model
Figure 1 shows two charged spheres. The distance between the centers of the two spheres is Z. The potential created by the left charged sphere is calculated at point P2.
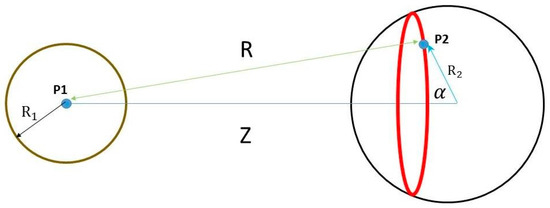
Figure 1.
Two charged spheres: left circle represents a charged sphere of radius R1 and its total surface charge is Q1. Right circle represents a charged sphere of radius R2 and its total surface charge is Q2. The distance between the centers of the two spheres is Z. The potential created by the left charged sphere is calculated at point P2.
The red ring represents charges on the right charged sphere. Their distance from point P1 is R. α is the angle between vector Z and a vector pointing from the center of the right sphere to any of the points (P2) of the red ring.
Based on the generalized shell theorem [1], the electric potential created by the left charged sphere at point P2 is Equation (2):
The distance between point P1 and any of the point charges located on the red ring is Equation (3):
The interaction energy between the left charged sphere and the charges of the red ring is Equation (4):
where 2R2sin (α)πR2 × dα is the surface area of the red ring.
Finally, the interaction energy between the left and right sphere is Equation (5):
where
Let us do the following substitution in the integral: u = cos (α).
Thus, in Equation (5) sin(α) dα can be substituted by −du and we get Equation (6):
Finally, let us do this substitution in Equation (6): and thus
and we get Equation (7):
where
while in the case of Z > R2:
Thus, from Equations (7)–(9) we get Equation (10):
where .
3. Results
In Figure 2 and Figure 3, based on Equation (10), the interaction energy between two charged spheres (surrounded inside and outside by electrolyte) are calculated as a function of the distance between the centers of the spheres.

Figure 2.
Interaction energy of two charged spheres surrounded by electrolyte (dependence from electrolyte’s ion concentration and temperature): the smaller sphere with radius R1 = 5 × 10−7 m is located to the left of the larger sphere with radius R2 = 10−6 m (Figure 1). The interaction energy between the two spheres, 𝐸, is calculated by Equation (10) and plotted against the distance between the centers of the two spheres, (≥R1 + R2 = 1.5 × 10−6 m). (A) The ion concentration, C, of the electrolyte (and the respective Debye length from Equation (A2)) is: red curve: 0.007 mol/m3 (λD = 1.15 × 10−7 m); blue curve: 0.01 mol/m3 (λD = 9.62 × 10−8 m); and black curve: 0.013 mol/m3 (λD = 8.44 × 10−8 m), and the temperature in the case of each curve is T = 300 K. (B) The ion concentration of the electrolyte is: green dotted curve: 0 mol/m3 (λD = ∞ m); blue curve: 0.000001 mol/m3 (λD = 9.62 × 10−6 m); red curve: 0.00001 mol/m3 (λD = 3.04 × 10−6 m); and black curve: 0.0001 mol/m3 (λD = 9.62 × 10−7 m), and the temperature in the case of each curve is T = 300 K. (C) The system’s temperature (and the respective Debye length) is: blue curve: 340 K (λD = 1.02 × 10−7 m); red dotted curve: 310 K (λD = 9.78 × 10−8 m); and black curve: 280 K (λD = 9.30 × 10−8 m), and the electrolyte’s ion concentration in the case of each curve is 0.01 mol/m3. In the case of our calculations, the surface-charge density of each charged sphere is ρs = −0.266 × C/m2.
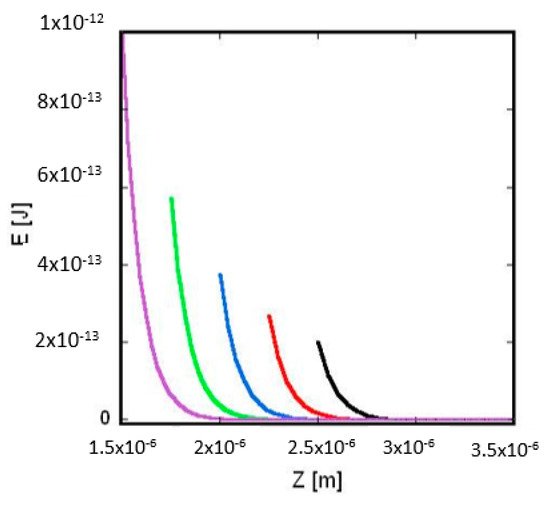
Figure 3.
Interaction energy of two charged spheres surrounded by electrolyte (dependence from radius): the interaction energy between the two spheres, 𝐸, is plotted against the distance between the centers of the two spheres, Z. The total charge of the left and right sphere is Q1 = −8.3566 × 10−13 C and Q2 = −3.34265 × 10−12 C, respectively. The radius of the right sphere (see Figure 1) is R2 = 10−6 m, the electrolyte’s ion concentration is C = 0.01 mol/m3, the temperature is T = 300 K and the respective Debye length (calculated by Equation (A2)) is λD = 9.62 × 10−8 m. Purple curve: R1 = 5 × 10−7 m; green curve: R1 = 7.5 × 10−7 m; blue curve: R1 = 1 × 10−6 m; red curve: R1 = 1.25 × 10−6 m; black curve: R1 = 1.5 × 10−6 m.
4. Discussion
Here, by using the recently generalized shell theorem [1], Equation (10) is derived to calculate the electric interaction energy between two charged spheres surrounded by electrolyte. Because of the increased screening effect of the electrolyte’s ions (i.e., with decreasing Debye length), at any given Z distance between the spheres, the interaction energy decreases with increasing electrolyte ion concentration (Figure 2A,B). The primary reason of this decrease is that the last factor of Equation (10) , at a given Z decreases fast when the Debye length, λD, decreases because of the increasing electrolyte ion concentration (see Figure 2A,B). On the other hand, λD increases with increasing temperature (see interaction energy between two charged spheres (see Figure 2C)).
By increasing the radius R1, the 𝐸 vs. Z curves are shifting to the right (see Figure 3) because the lowest value of Z𝑚i𝑛 (= R1 + R2) increases. In addition, at Z𝑚i𝑛 the electric interaction energy E(Z𝑚i𝑛) is getting smaller. This is the case because with increasing R1 the distance between the charges of the spheres is increasing and, thus, the screening effect of the electrolyte’s ions increases too.
By using Equation (10), one can calculate the electric interaction energy between two charged spheres surrounded inside and outside by electrolyte. This equation is a generalization of the Coulomb equation (for charge–charge interaction in a vacuum [4]). One can get from Equation (10) an equation by taking the infinite long Debye length (that is the case at zero electrolyte ion concentration, i.e., when (see Equation (A7))):
Equation (11) is similar to the Coulomb equation except that is not the relative permittivity of vacuum but the relative permittivity of the pure water. Calculating the curves in Figure 2 and Figure 3, constant electrolyte permittivity (= 78) was taken that is characteristic to pure water at a temperature of . Note that the relative permittivity of electrolytes depends on the temperature, ion concentration and type of the ions (see Appendix A). With increasing temperature and ion concentration, the relative permittivity of the electrolyte slightly and close to linearly decreases and affects the calculated value of the interaction energy too (see Appendix A).
By using Equation (10), one can also calculate the total electric interaction energy of several separated, charged spheres surrounded inside and outside by electrolyte Equation (12):
where N is the number of spheres, Qi and Ri are the total charge and radius of the i-th sphere, respectively, and Zij (where Zij > Ri + Rj) is the distance between the centers of the i-th and j-th sphere.
5. Conclusions
By using the recently generalized version of Newton’s shell theorem [1], analytical equations are derived to calculate the electric interaction energy between two separated, charged spheres surrounded outside and inside by electrolyte. This electric interaction energy is calculated as a function of the electrolyte’s ion concentration, temperature, distance between the spheres and the size of the spheres. At the same distance, the absolute value of the interaction energy decreases with increasing electrolyte ion concentration and increases with increasing temperature. At zero electrolyte ion concentration, the derived analytical equation transforms into the Coulomb Equation Finally, the analytical equation is generalized to calculate the electric interaction energy of N separated, charged spheres surrounded by electrolyte.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author is very thankful to Chinmoy Kumar Ghose.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The Poisson equation is [11]:
where ρ(r) is the charge density, ε0 is the vacuum permittivity and εr is the relative static permittivity.
The solution of the above Poisson equation is [11]:
In the case of the Poisson–Boltzmann equation [11,12]:
where q is the elementary charge (positive or negative depending on the charge of the i-th type of ion), zi is the charge number of the i-th type of ion, kB is the Boltzmann constant, T is the absolute temperature, (r) is the charge density of the ions in the electrolyte and εr is the relative static permittivity of the electrolyte.
The screened Poisson equation is [9]:
where ρex(r) is the density of the external charge at position r, ε0 is the electric constant and εr is the relative static permittivity of the electrolyte and λD is the Debye length. Note that Equation (A4) is valid if the electrolyte itself is electrically neutral. The solution of this equation is [11], i.e., the potential is the superposition of the so-called screened Coulomb potential of the external charges:
The Debye length in an electrolyte is calculated by [13]:
where ε0 = 8.85 × 10−12 C2J−1m−1 is the vacuum permittivity, is the relative static permittivity of the electrolyte, kB = 1.38 × 10−23 JK−1 is the Boltzmann constant, T is the absolute temperature, e = 1.6 × 10−19 C is the charge of a positive monovalent ion, N𝑎 = 6 × 1023 mol−1 is the Avogadro’s number, Cj0 mol/m3 is the mean concentration of the j-th species of ions in the electrolyte and qj is the number of elementary charges in an ion of the j-th species (e.g., in the case of bivalent ions qj = 2). In this paper, we consider overall neutral electrolytes containing only monovalent positive and negative ions of the same concentration, C. In this case, Equation (A6) is simplified to:
The relative static permittivity of the neutral electrolyte depends on (a) the type of ions solved in the water, (b) the temperature and (c) the concentration of the ions . The temperature dependence of for pure water (from to ) is [14]:
where is the temperature in Celsius and is the ion concentration in the pure water. The dependence of the static permittivity from the NaCl concentration of the electrolyte (at temperature ) is [15]:
where and . Calculating the curves in Figure 2 and Figure 3, a constant relative permittivity of the electrolyte () was considered. This is the relative permittivity of pure water at 300 K. By means of Equations (A8) and (A9), one may take into consideration the temperature and ion-concentration dependence of the relative permittivity of the electrolyte when calculating the interaction energy between two charged spheres by Equation (10). Since the relative permittivity slightly and close to linearly decreases, with increasing temperature and ion concentration one can estimate how the interaction energy is changing. Based on Equation (A8), if the temperature of pure water is higher than 300 K the relative permittivity is lower than 78 and the interaction energy, calculated by Equation (10) becomes higher than the interaction energy calculated with constant relative permittivity (). If, beside the higher temperature, the ion concentration of the electrolyte is the relative permittivity is even lower than 78 and, thus, the interaction energy calculated by Equation (10) becomes even higher than the interaction energy calculated with constant relative permittivity ().
References
- Sugár, I.P. A generalization of the Shell Theorem. Electric potential of charged spheres and vesicles surrounded by electrolyte. AIMS Biophys. 2020, 7, 76–89. [Google Scholar] [CrossRef]
- Newton, I. Philosophiae Naturalis Mathematica; London, UK. 1687. pp. Theorem XXXI. Available online: https://books.google.com.sg/books/about/Philosophiae_naturalis_principia_mathema.html?id=-dVKAQAAIAAJ&redir_esc=y (accessed on 1 August 2022).
- Sugár, I.P. Electric energies of a charged sphere surrounded by electrolyte. AIMS Biophys. 2021, 8, 157–164. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 3rd ed.; Pearson: London, UK; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Gabriel, J.L.; Chong, P.L.G. Molecular modeling of archaebacterial bipolar tetraether lipid membranes. Chem. Phys. Lipids 2000, 105, 193–200. [Google Scholar] [CrossRef]
- Chong, P. Archaebacterial bipolar tetraether lipids: Physico-chemical and membrane properties. Chem. Phys. Lipids 2010, 163, 253–265. [Google Scholar] [CrossRef] [PubMed]
- Almeida, P.F.F. Thermodynamics of lipid interactions in complex bilayers. Biochim. Biophys. Acta 2009, 1788, 72–85. [Google Scholar] [CrossRef] [PubMed]
- Sugár, I.P.; Thompson, T.E.; Biltonen, R.L. Monte Carlo simulation of two-component bilayers: DMPC/DSPC mixtures. Biophys. J. 1999, 76, 2099–2110. [Google Scholar] [CrossRef]
- Bohinc, K.; Špadina, M.; Reščič, J.; Shimokawa, N.; Spada, S. Influence of Charged Lipid Head Group Structures on Electric Double Layer Properties. J. Chem. Theory Comput. 2022, 18, 448–460. [Google Scholar] [CrossRef] [PubMed]
- Ewald, P.P. Die Berechnung Optischer und Elektrostatischer Gitterpotentiale. Ann. Phys. 1921, 369, 253–287. [Google Scholar] [CrossRef]
- Fetter, A.L.; Walecka, J.D. Theoretical Mechanics of Particles and Continua; Dover Publications: Mineola, NY, USA, 2003; pp. 307–310. [Google Scholar]
- The Collected Papers of Peter J. W. Debye; Interscience Publishers, Inc.: New York, NY, USA, 1954; p. 233.
- Shohet, J.L. Encyclopedia of Physical Science and Technology, 3rd ed.; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Malmberg, C.G.; Mariott, A.A. Dielectric constant of water from 0 °C to 100 °C. J. Res. Natl. Bur. Stand. 1956, 56, 1–8. [Google Scholar] [CrossRef]
- Bramley, A. Dielectric constants of aqueous solutions of sodium chloride. J. Frankl. Inst. 1928, 205, 649–657. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).