Ultra-Low Thermal Conductivity of Moiré Diamanes
Abstract
1. Introduction
2. Computational Methodology
2.1. Geometry Relaxation with Dft
2.2. Training of Ml Potentials via Aimd Simulations
2.3. Lattice Thermal Conductivity
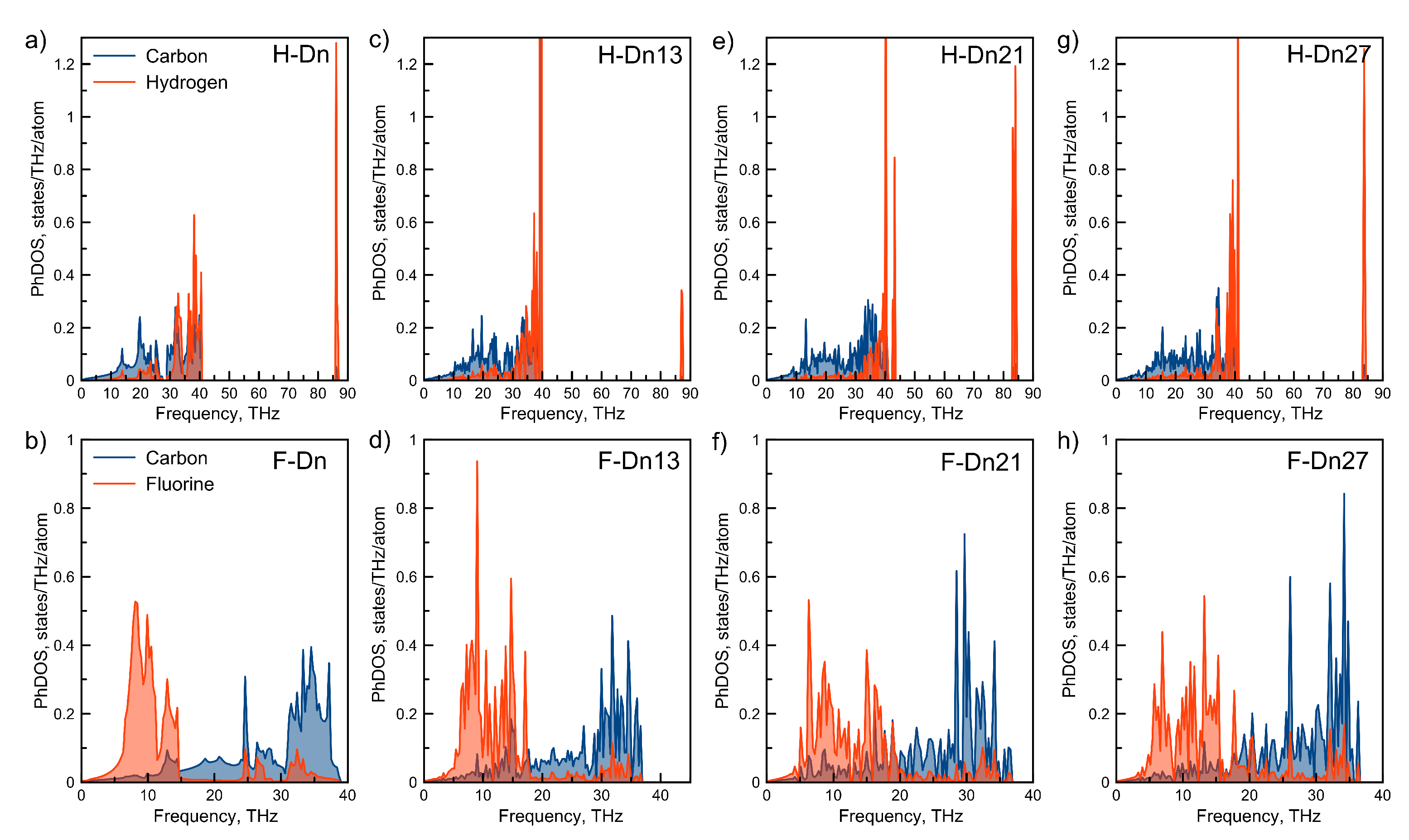
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pandey, R.; Thapa, P.; Kumar, V.; Zhu, Y.; Wang, N.; Bystrzejewski, M.; Tiwari, S.K. Updates in phase change materials for thermoelectric devices: Status and challenges. Materialia 2022, 21, 101357. [Google Scholar] [CrossRef]
- Lavini, F.R.M.; Riedo, E. Two-dimensional diamonds from sp2-to-sp3 phase transitions. Nat. Rev. Mater. 2022, 1–19. [Google Scholar] [CrossRef]
- Chernozatonskii, L.A.; Sorokin, P.B.; Kvashnin, A.G.; Kvashnin, D.G. Diamond-like C 2 H nanolayer, diamane: Simulation of the structure and properties. JETP Lett. 2009, 90, 134–138. [Google Scholar] [CrossRef]
- Chernozatonskii, L.A.; Demin, V.A.; Kvashnin, D.G. Fully Hydrogenated and Fluorinated Bigraphenes–Diamanes: Theoretical and Experimental Studies. J. Carbon Res. 2021, 7, 17. [Google Scholar] [CrossRef]
- Kvashnin, A.G.; Sorokin, P.B. Lonsdaleite Films with Nanometer Thickness. J. Phys. Chem. Lett. 2014, 5, 541–548. [Google Scholar] [CrossRef]
- Chernozatonskii, L.A.; Sorokin, P.B.; Kuzubov, A.A.; Sorokin, B.P.; Kvashnin, A.G.; Kvashnin, D.G.; Avramov, P.V.; Yakobson, B.I. Influence of Size Effect on the Electronic and Elastic Properties of Diamond Films with Nanometer Thickness. J. Phys. Chem. C 2010, 115, 132–136. [Google Scholar] [CrossRef]
- Sorokin, P.B.; Yakobson, B.I. Two-Dimensional Diamond—Diamane: Current State and Further Prospects. Nano Lett. 2021, 21, 5475–5484. [Google Scholar] [CrossRef]
- Ge, L.; Liu, H.; Wang, J.; Huang, H.; Cui, Z.; Huang, Q.; Fu, Z.; Lu, Y. Properties of diamane anchored with different groups. Phys. Chem. Chem. Phys. 2021, 23, 14195–14204. [Google Scholar] [CrossRef]
- Zhu, L.; Li, W.; Ding, F. Giant thermal conductivity in diamane and the influence of horizontal reflection symmetry on phonon scattering. Nanoscale 2019, 11, 4248. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, T. Suppressed thermal conductivity in fluorinated diamane: Optical phonon dominant thermal transport. Appl. Phys. Lett. 2019, 115, 151904. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, L. Sensitively tuning the thermal conductivity of diamane via engineering the mass of functional groups. Nanotechnology 2020, 31, 435409. [Google Scholar] [CrossRef] [PubMed]
- Raeisi, M.; Mortazavi, B.; Podryabinkin, E.V.; Shojaei, F.; Zhuang, X.; Shapeev, A.V. High Thermal Conductivity in Semiconducting Janus and Non-Janus Diamanes. Carbon 2020, 167, 51–61. [Google Scholar] [CrossRef]
- Hu, Y.; Li, D.; Yin, Y.; Li, S.; Ding, G.; Zhou, H.; Zhang, G. The important role of strain on phonon hydrodynamics in diamond-like bi-layer graphene. Nanotechnology 2020, 31, 335711. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Li, D.; Feng, C.; Li, S.; Chen, D.; Li, D.; Zhang, G. Nanostructure engineering of two-dimensional diamonds toward high thermal conductivity and approaching zero Poisson’s ratio. Phys. Chem. Chem. Phys. 2022, 24, 15340–15348. [Google Scholar] [CrossRef]
- Barboza, A.P.M.; Guimaraes, M.H.D.; Massote, D.V.P.; Campos, L.C.; Neto, N.M.B.; Cancado, L.G.; Lacerda, R.G.; Chacham, H.; Mazzoni, M.S.C.; Neves, B.R.A. Room-Temperature Compression-Induced Diamondization of Few-Layer Graphene. Adv. Mater. 2011, 23, 3014–3017. [Google Scholar] [CrossRef]
- Bakharev, P.V.; Huang, M.; Saxena, M.; Lee, S.W.; Joo, S.H.; Park, S.O.; Dong, J.; Camacho-Mojica, D.C.; Jin, S.; Kwon, Y.; et al. Chemically induced transformation of chemical vapour deposition grown bi-layer graphene into fluorinated single-layer diamond. Nat. Nanotechnol. 2019, 15, 59–66. [Google Scholar] [CrossRef]
- Piazza, F.; Cruz, K.; Monthioux, M.; Puech, P.; Gerber, I. Raman evidence for the successful synthesis of diamane. Carbon 2020, 169, 129–133. [Google Scholar] [CrossRef]
- Chernozatonskii, L.A.; Demin, V.A.; Kvashnin, D.G. Ultrawide-bandgap Moiré diamanes based on bigraphenes with the twist angles Θ~30°. Appl. Phys. Lett. 2020, 117, 253104. [Google Scholar] [CrossRef]
- Chernozatonskii, L.A.; Katin, K.P.; Demin, V.A.; Maslov, M.M. Moiré diamanes based on the hydrogenated or fluorinated twisted bigraphene: The features of atomic and electronic structures, Raman and infrared spectra. Appl. Surf. Sci. 2021, 537, 148011. [Google Scholar] [CrossRef]
- Nam, N.N.T.; Koshino, M. Lattice relaxation and energy band modulation in twisted bi-layer graphene. Phys. Rev. B 2017, 96, 075311. [Google Scholar] [CrossRef]
- Zou, L.; Po, H.C.; Vishwanath, A.; Senthil, T. Band structure of twisted bi-layer graphene: Emergent symmetries, commensurate approximants, and Wannier obstructions. Phys. Rev. B 2018, 98, 085435. [Google Scholar] [CrossRef]
- Liu, J.B.; Li, P.J.; Chen, Y.F.; Wang, Z.G.; Qi, F.; He, J.R.; Zheng, B.J.; Zhou, J.H.; Zhang, W.L.; Gu, L.; et al. Observation of tunable electrical bandgap in large-area twisted bi-layer graphene synthesized by chemical vapor deposition. Sci. Rep. 2015, 5, 15285. [Google Scholar] [CrossRef] [PubMed]
- Brihuega, I.; Mallet, P.; González-Herrero, H.; Laissardière, G.T.D.; Ugeda, M.M.; Magaud, L.; Gómez-Rodríguez, J.M.; Ynduráin, F.; Veuillen, J.Y. Unraveling the intrinsic and robust nature of van hove singularities in twisted bi-layer graphene by scanning tunneling microscopy and theoretical analysis. Phys. Rev. Lett. 2012, 109, 196802. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Shapeev, A.V. Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials. Multiscale Model. Simulations 2016, 14, 1153–1173. [Google Scholar] [CrossRef]
- Schütt, K.T.; Kindermans, P.; Sauceda, H.E.; Chmiela, S.; Tkatchenko, A.; Müller, K.R. SchNet: A Continuous-filter Convolutional Neural Network for Modeling Quantum Interactions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 992–1002. [Google Scholar]
- Botu, V.; Batra, R.; Chapman, J.; Ramprasad, R. Machine Learning Force Fields: Construction, Validation, and Outlook. J. Phys. Chem. C 2017, 121, 511–522. [Google Scholar] [CrossRef]
- Zuo, Y.; Chen, C.; Li, X.; Deng, Z.; Chen, Y.; Behler, J.; Csányi, G.; Shapeev, A.V.; Thompson, A.P.; Wood, M.A. Performance and Cost Assessment of Machine Learning Interatomic Potentials. J. Phys. Chem. A 2020, 124, 731–745. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B.; Podryabinkin, E.V.; Novikov, I.S.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. Accelerating First-principles Estimation of Thermal Conductivity by Machine-learning Interatomic Potentials: A MTP/ShengBTE Solution. Comput. Phys. Commun. 2021, 258, 107583. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Mortazavi, B.; Novikov, I.S.; Podryabinkin, E.V.; Roche, S.; Rabczuk, T.; Shapeev, A.V.; Zhuang, X. Exploring Phononic Properties of Two-dimensional Materials using Machine Learning Interatomic Potentials. Appl. Mater. Today 2020, 20, 100685. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Novikov, I.S.; Gubaev, K.; Podryabinkin, E.V.; Shapeev, A.V. The MLIP package: Moment tensor potentials with MPI and active learning. Mach. Learn. Sci. Technol. 2021, 2, 025002. [Google Scholar] [CrossRef]
- Podryabinkin, E.V.; Tikhonov, E.V.; Shapeev, A.V.; Oganov, A.R. Accelerating Crystal Structure Prediction by Machine-learning Interatomic Potentials with Active Learning. Phys. Rev. B 2019, 99, 064114. [Google Scholar] [CrossRef]
- Korotaev, P.; Novoselov, I.; Yanilkin, A.; Shapeev, A. Accessing Thermal Conductivity of Complex Compounds by Machine Learning Interatomic Potentials. Phys. Rev. B 2019, 100, 144308. [Google Scholar] [CrossRef]
- Ghosal, S.; Chowdhury, S.; Jana, D. Electronic and Thermal Transport in Novel Carbon-based bi-layer with Tetragonal Rings: A Combined Study using First-principles and Machine Learning Approach. Phys. Chem. Chem. Phys. 2021, 23, 14608–14616. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B. Ultrahigh thermal conductivity and strength in direct-gap semiconducting graphene-like BC6N: A first-principles and classical investigation. Carbon 2021, 182, 373–383. [Google Scholar] [CrossRef]
- Ziman, J.M. Electrons and Phonons: The Theory of Transport Phenomena in Solids; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Lindroth, D.O.; Brorsson, J.; Fransson, E.; Eriksson, F.; Palmqvist, A.; Erhart, P. Thermal conductivity in intermetallic clathrates: A first-principles perspective. Phys. Rev. B 2019, 100, 045206. [Google Scholar] [CrossRef]
- Wu, X.; Varshney, V.; Lee, J.; Pang, Y.; Roy, A.K.; Luo, T. How to Characterize Thermal Transport Capability of 2D Materials Fairly?–Sheet Thermal Conductance and the Choice of Thickness. Chem. Phys. Lett. 2017, 669, 233–237. [Google Scholar] [CrossRef]
- Campanera, J.M.; Savini, G.; Suarez-Martinez, I.; Heggie, M.I. Density Functional Calculations on the Intricacies of Moiré Patterns on Graphite. Phys. Rev. B 2007, 75, 235449. [Google Scholar] [CrossRef]
- Muniz, A.R.; Maroudas, D. Opening and tuning of band gap by the formation of diamond superlattices in twisted bi-layer graphene. Phys. Rev. B 2012, 86, 075404. [Google Scholar] [CrossRef]
- Koren, E.; Duerig, U. Superlubricity in quasicrystalline twisted bi-layer graphene. Phys. Rev. B 2016, 93, 201404. [Google Scholar] [CrossRef]
- Chernozatonskii, L.A.; Demin, V.A.; Kvashnin, A.G.; Kvashnin, D.G. Diamane quasicrystals. Appl. Surf. Sci. 2022, 572, 151362. [Google Scholar] [CrossRef]
- Wilson, J.; Fu, Y.; Sarma, S.; Pixley, J. Disorder in twisted bi-layer graphene. Phys. Rev. Res. 2020, 2, 023325. [Google Scholar] [CrossRef]
- Veeravenkata, H.P.; Jain, A. Density functional theory driven phononic thermal conductivity prediction of biphenylene: A comparison with graphene. Carbon 2021, 183, 893–898. [Google Scholar] [CrossRef]
- Raeisi, M.; Ahmadi, S.; Rajabpour, A. Modulated thermal conductivity of 2D hexagonal boron arsenide: A strain engineering study. Nanoscale 2019, 11, 21799. [Google Scholar] [CrossRef]
- Keshtkar, M.; Mehdipour, N.; Eslami, H. Thermal Conductivity of Polyamide-6,6/Carbon Nanotube Composites: Effects of Tube Diameter and Polymer Linkage between Tubes. Polymers 2019, 11, 1465. [Google Scholar] [CrossRef]
- Eslami, H.; Mohammadzadeh, L.; Mehdipour, N. Reverse nonequilibrium molecular dynamics simulation of thermal conductivity in nanoconfined polyamide-6,6. J. Chem. Phys. 2011, 135, 064703. [Google Scholar] [CrossRef]
- Ghosal, S.; Chowdhury, S.; Jana, D. Impressive Thermoelectric Figure of Merit in Two-Dimensional Tetragonal Pnictogens: A Combined First-Principles and Machine-Learning Approach. ACS Appl. Mater. Interfaces 2021, 13, 59092–59103. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, S.K.; Pandey, R.; Wang, N.; Kumar, V.; Sunday, O.J.; Bystrzejewski, M.; Zhu, Y.; Mishra, Y.K. Progress in Diamanes and Diamanoids Nanosystems for Emerging Technologies. Adv. Sci. 2022, 9, 2105770. [Google Scholar] [CrossRef]
- Takenaka, K. Negative thermal expansion materials: Technological key for control of thermal expansion. Sci. Technol. Adv. Mater. 2012, 13, 013001. [Google Scholar]
- Sanson, A.; Chen, J. Towards the control of thermal expansion: From 1996 to today. Front. Chem. 2019, 7, 284. [Google Scholar]

| Angle | 0 | 13.2 | 21.8 | 27.8 |
| H- | −1.98 | −2.29 | −1.27 | −1.36 |
| F- | −1.07 | −1.55 | −1.48 | −1.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, S.; Demin, V.A.; Chernozatonskii, L.A.; Kvashnin, A.G. Ultra-Low Thermal Conductivity of Moiré Diamanes. Membranes 2022, 12, 925. https://doi.org/10.3390/membranes12100925
Chowdhury S, Demin VA, Chernozatonskii LA, Kvashnin AG. Ultra-Low Thermal Conductivity of Moiré Diamanes. Membranes. 2022; 12(10):925. https://doi.org/10.3390/membranes12100925
Chicago/Turabian StyleChowdhury, Suman, Victor A. Demin, Leonid A. Chernozatonskii, and Alexander G. Kvashnin. 2022. "Ultra-Low Thermal Conductivity of Moiré Diamanes" Membranes 12, no. 10: 925. https://doi.org/10.3390/membranes12100925
APA StyleChowdhury, S., Demin, V. A., Chernozatonskii, L. A., & Kvashnin, A. G. (2022). Ultra-Low Thermal Conductivity of Moiré Diamanes. Membranes, 12(10), 925. https://doi.org/10.3390/membranes12100925







