Short-Circuit Current in Polymeric Membrane-Based Thermocells: An Experimental Study
Abstract
:1. Introduction
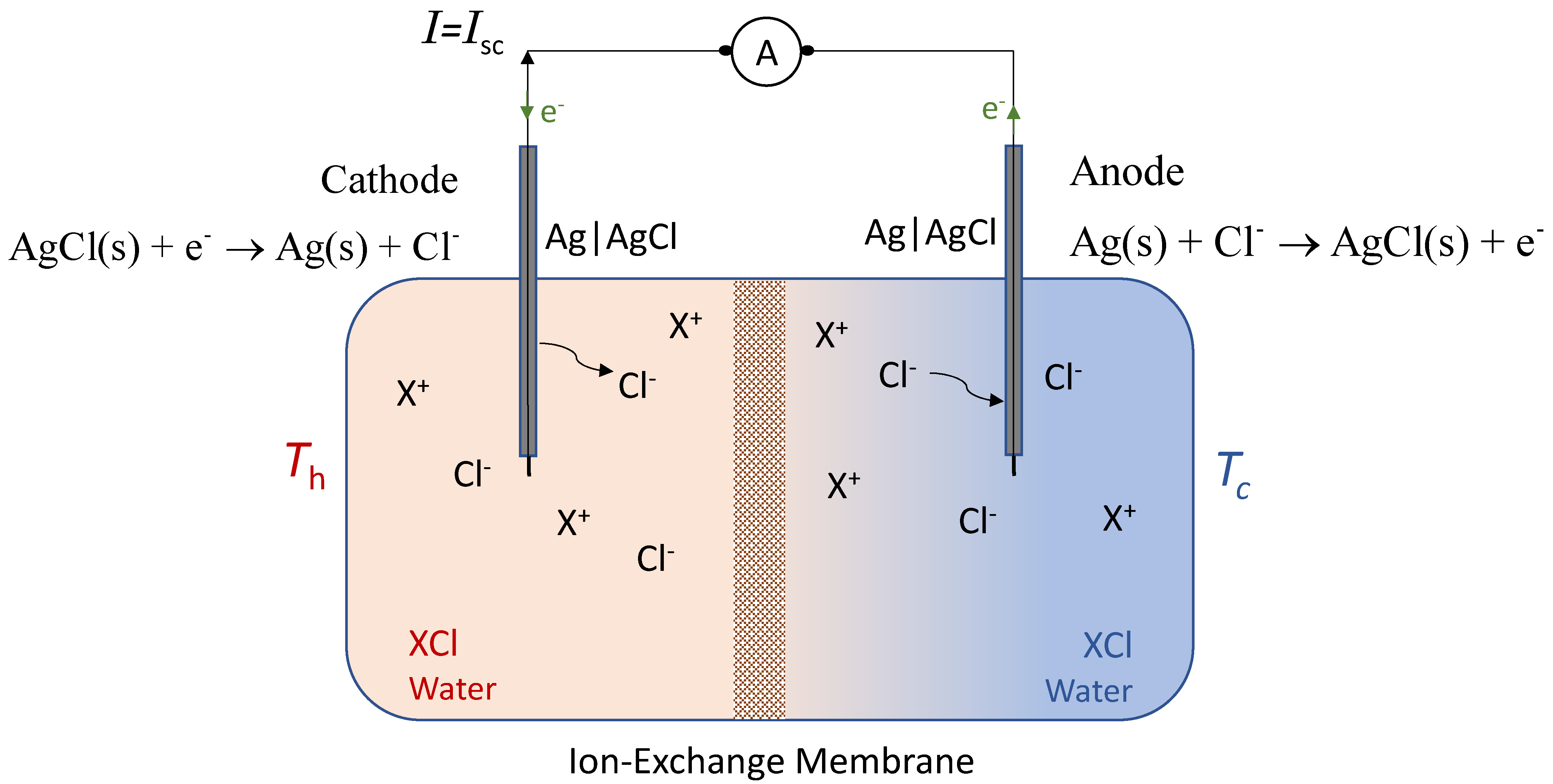
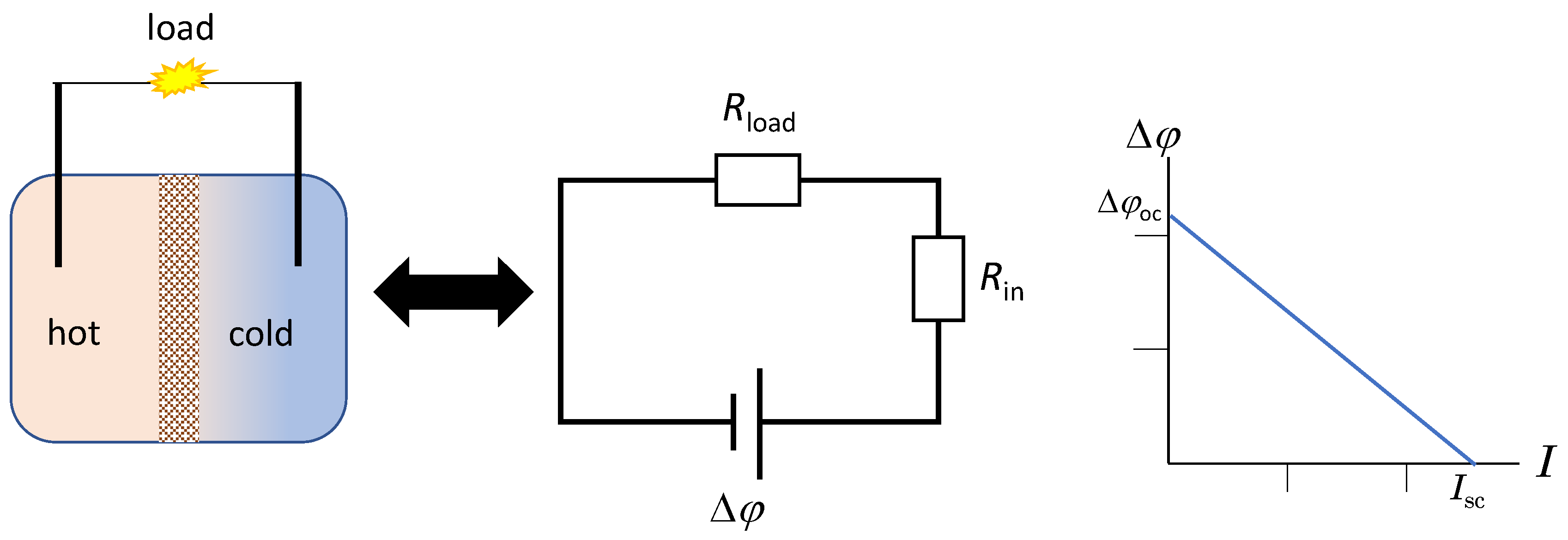
2. The Membrane-Based Thermocell
3. Experimental
3.1. Materials
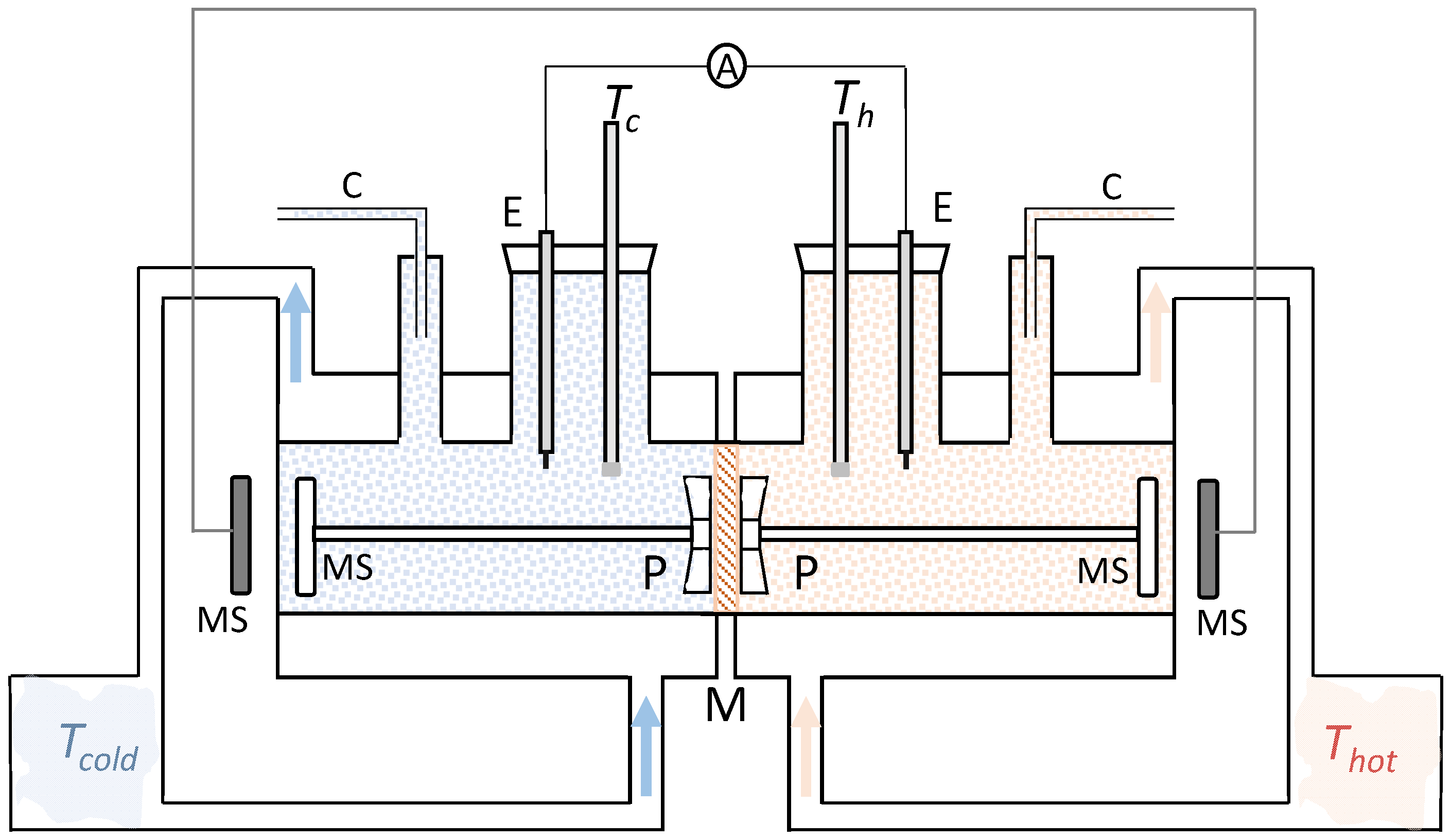
3.2. Method
4. Results and Discussion
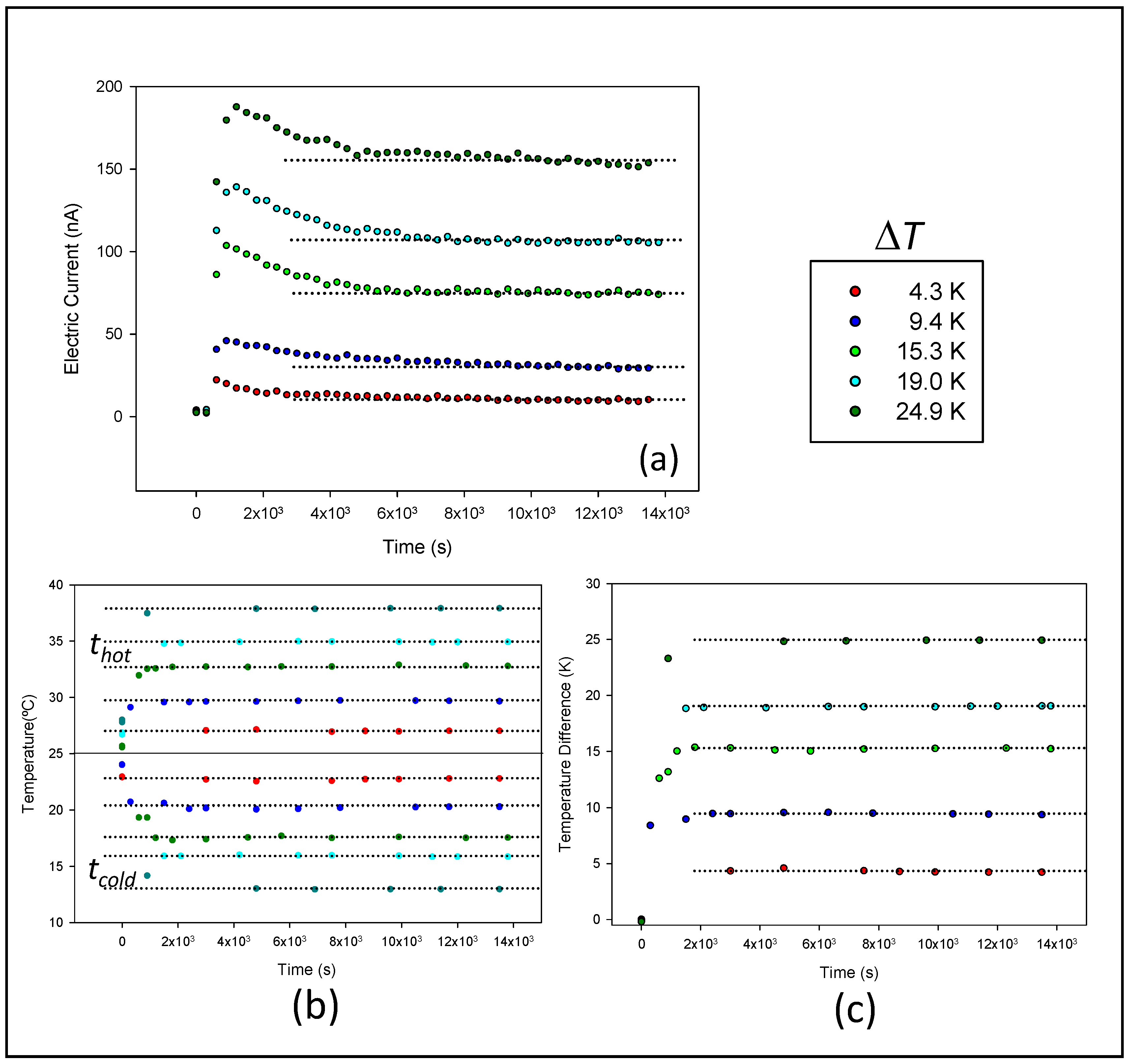
4.1. Curves (Isc-t)
4.2. Short-Circuit Current Density vs. Temperature Difference
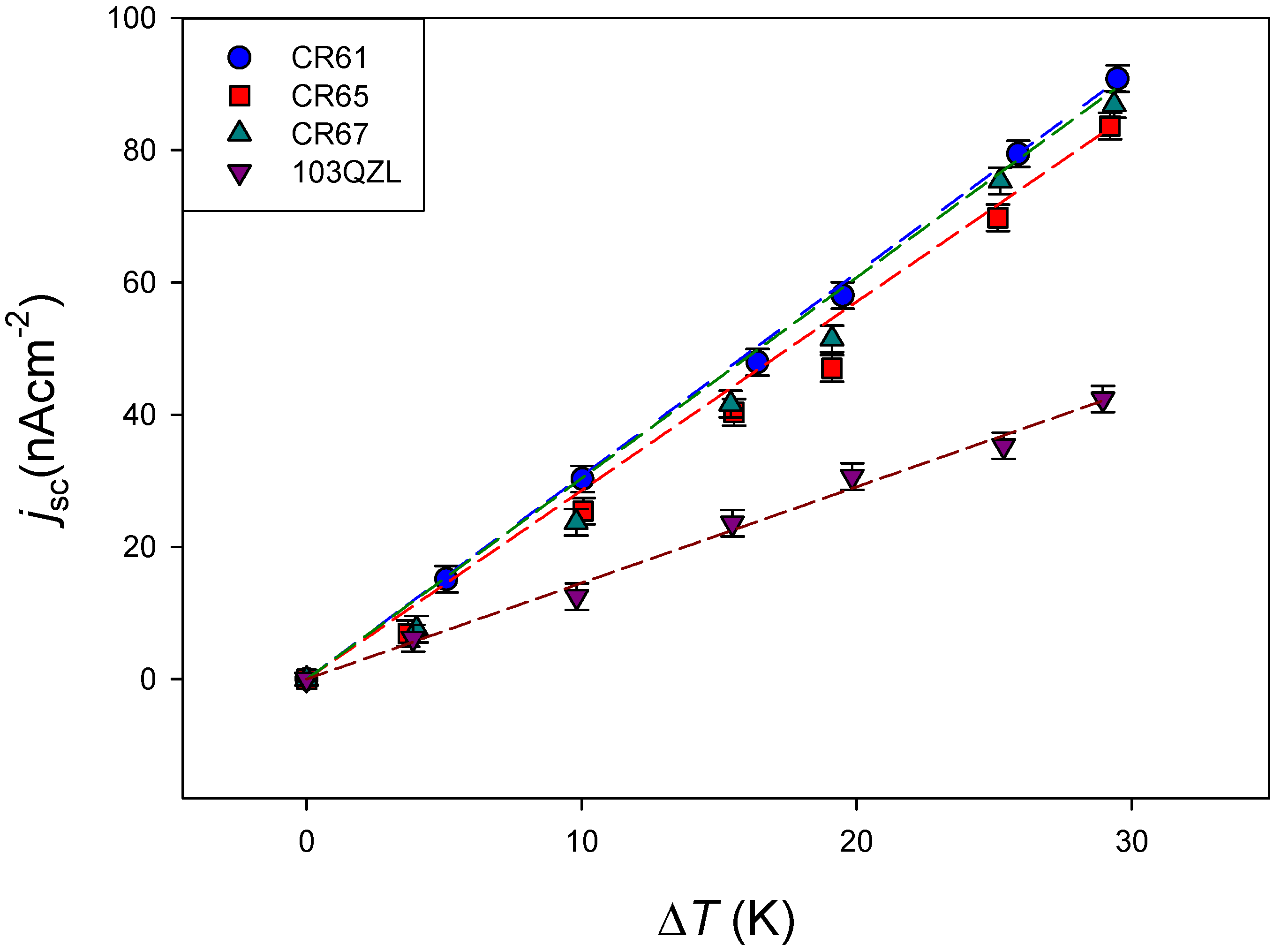
4.2.1. Effect of the Membrane
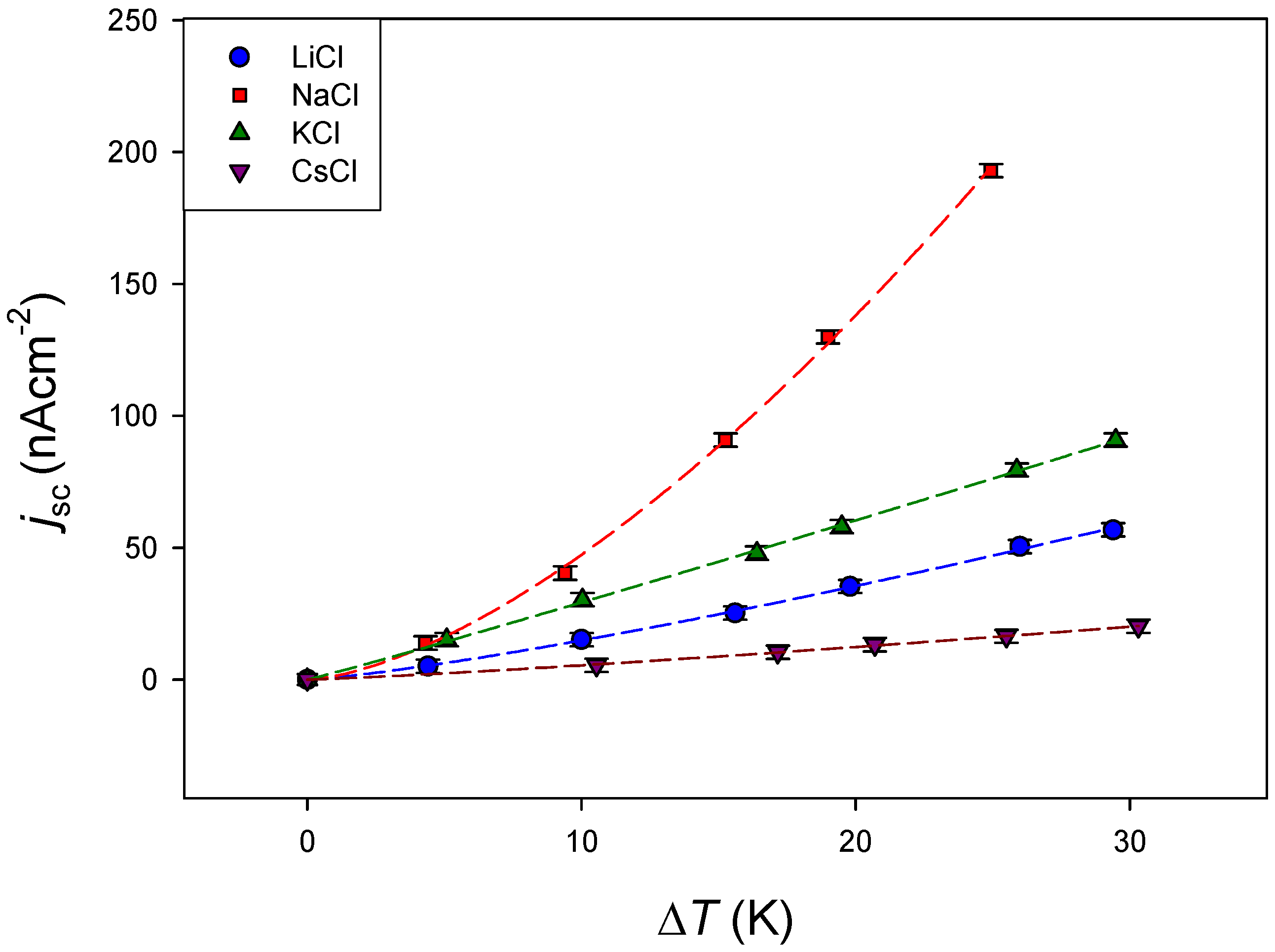
4.2.2. Effect of the Electrolyte
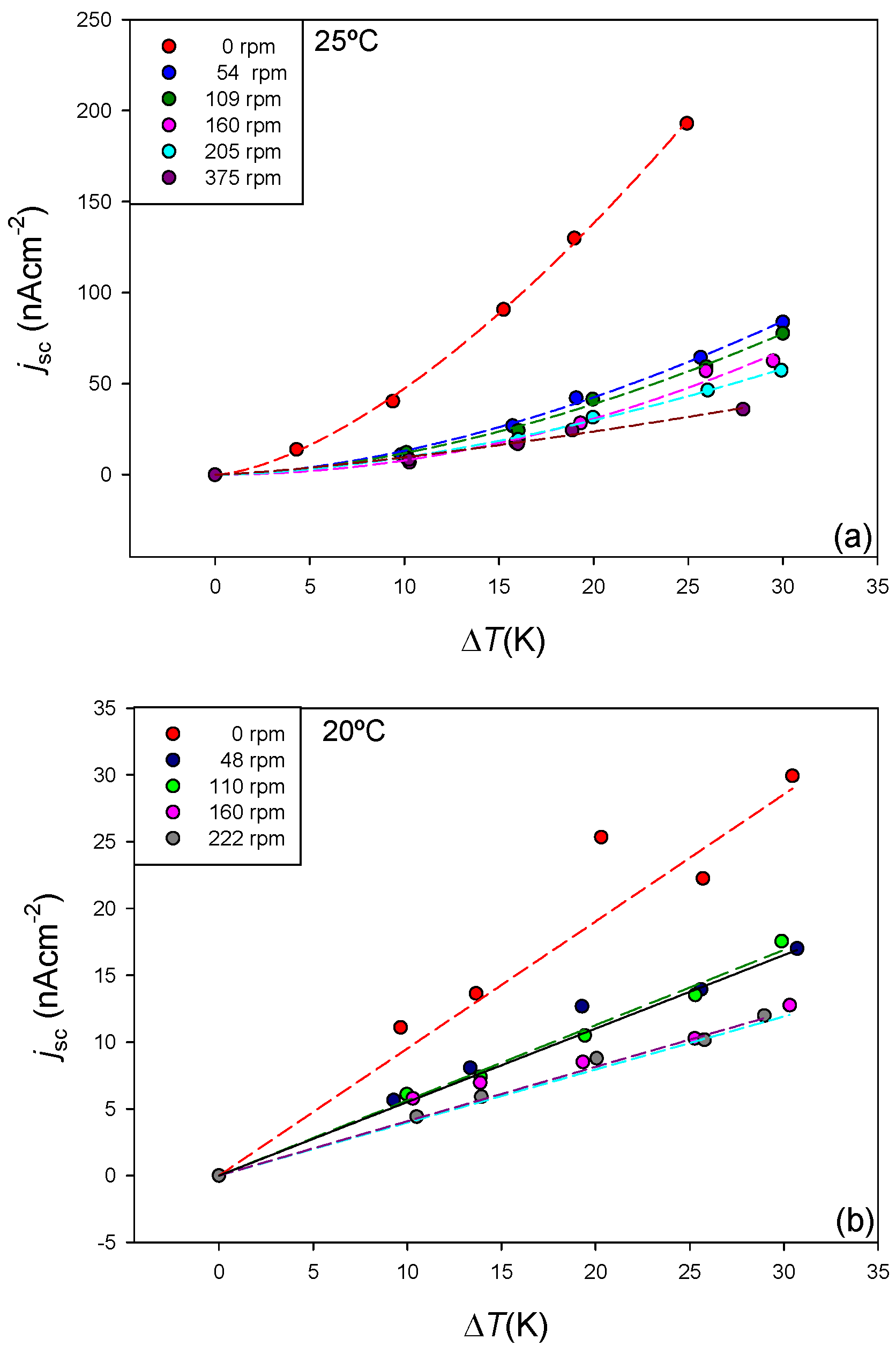
4.2.3. Effect of the Solution Stirring Rate
4.3. Molar Flux Density of Ionic Species
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Maciá-Barber, E. Thermoelectric Materials, Advances and Applications; Pan Stanford Publishing: Singapore, 2015. [Google Scholar]
- Laksminarayanaiah, N. Transport Phenomena in Membranes; Academic Press: London, UK, 1969. [Google Scholar]
- Leblanc, S.; Yee, S.K.; Scullin, M.L.; Dames, C.; Goodson, K.E. Material and manufacturing cost considerations for thermoelec-trics. Renew. Sustain. Energy Rev. 2014, 32, 313–327. [Google Scholar] [CrossRef]
- Dupont, M.F.; MacFarlane, D.R.; Pringle, H.M. Thermo-electrochemical cells for waste heat harvesting- progress and per-spectives. Chem. Comm. 2017, 53, 6288–6302. [Google Scholar] [CrossRef] [PubMed]
- Duan, J.; Feng, G.; Yu, B.; Li, J.; Chen, M.; Yang, P.; Feng, J.; Liu, K.; Zhou, J. Aqueous thermogalvanic cells with a high Seebeck coefficient for low-grade heat harvest. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, D.; Würger, A.; Crispin, X. Ionic thermoelectric materials and devices. J. Energy Chem. 2021, 61, 88–103. [Google Scholar] [CrossRef]
- Barragán, V.M.; Kristiansen, K.R.; Kjelstrup, S. Perspectives on Thermoelectric Energy Conversion in Ion-Exchange Membranes. Entropy 2018, 20, 905. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Sun, H.; Wang, S.; Jiang, L.; Sun, G. A solid state thermogalvanic cell harvesting low-grade thermal energy. Int. J. Hydrogen Energy 2017, 42, 25877–25881. [Google Scholar] [CrossRef]
- Kim, S.L.; Hsu, J.-H.; Yu, C. Thermoelectric effects in solid-state polyelectrolytes. Org. Electron. 2018, 54, 231–236. [Google Scholar] [CrossRef]
- Tasaka, M.; Hanaoka, K.; Kurosawa, Y.; Wada, C. Thermal membrane potential through charged membranes in electrolyte solutions. Biophys. Chem. 1975, 3, 331–337. [Google Scholar] [CrossRef]
- Tasaka, M. Thermal membrane potential and thermoosmosis across charged membranes. Pure Appl. Chem. 1986, 58, 1637–1646. [Google Scholar] [CrossRef] [Green Version]
- Rahimi, M.; Straub, A.P.; Zhang, F.; Zhu, X.; Elimelech, M.; Gorski, C.A.; Logan, B.E. Emerging electrochemical and membrane-based systems to convert low-grade heat to electricity. Energy Environ. Sci. 2018, 11, 276–285. [Google Scholar] [CrossRef]
- Li, T.; Zhang, X.; Lacey, S.D.; Mi, R.; Zhao, X.; Jiang, F.; Song, J.; Liu, Z.; Chen, G.; Dai, J.; et al. Cellulose ionic conductors with high differential thermal voltage for low-grade heat harvesting. Nat. Mater. 2019, 18, 608–613. [Google Scholar] [CrossRef] [PubMed]
- Kristiansen, K.R.; Barragán, V.M.; Kjelstrup, S. Thermoelectric Power of Ion Exchange Membrane Cells Relevant to Reverse Electrodialysis Plants. Phys. Rev. Appl. 2019, 11, 044037. [Google Scholar] [CrossRef] [Green Version]
- Jokinen, M.; Manzanares, J.A.; Kontturi, K.; Murtomäki, L. Thermal potential of ion-exchange membranes and its application to thermoelectric power generation. J. Membr. Sci. 2016, 499, 234–244. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, T.; Valadez Huerta, G.; Kabelac, S. Modelling a thermocell with proton exchange membrane and hydrogen electrodes. Int. J. Hydrogen Energy 2018, 43, 19841–19850. [Google Scholar] [CrossRef]
- Rojas, J.P.; Singh, D.; Inayat, S.B.; Sevilla, G.A.T.; Fahad, H.M.; Hussain, M.M. Review—Micro and Nano-Engineering Enabled New Generation of Thermoelectric Generator Devices and Applications. ECS J. Solid State Sci. Technol. 2017, 6, N3036–N3044. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, C.A.B.; Olivares-Robles, M.A.; Chanona-Perez, J.J. Design of Nano-Structured Micro-Thermoelectric Generator: Load Resistance and Inflections in the Efficiency. Entropy 2019, 21, 224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buckingham, M.A.; Aldous, L. Thermogalvanic cells: A side-by-side comparison of measurement methods. J. Electroanal. Chem. 2020, 872, 114280. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Bedeaux, D. Thermodynamics of Electrochemical Systems. In Springer Handbook of Electrochemical Energy; Breitkopf, C., Swider-Lyons, K., Eds.; Springer Handbooks: Berlin, Germany, 2017; pp. 69–93. [Google Scholar]
- Førland, K.S.; Førland, T.; Ratkje, S.K. Irreversible Thermodynamics: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
- Haase, R. Thermodynamics of Irreversible Processes; Dover Publications Inc.: New York, NY, USA, 1990. [Google Scholar]
- Barragán, V.; Ruiz-Bauzá, C. Effect of unstirred solution layers on the thermal membrane potential through cation-exchange membranes. J. Membr. Sci. 1997, 125, 219–229. [Google Scholar] [CrossRef]
- Barragán, V.; Ruiz-Bauzá, C. On the dependence of the thermal membrane potential across cation-exchange membranes on the mean temperature. J. Membr. Sci. 1997, 134, 75–84. [Google Scholar] [CrossRef]
- Ganz, G.J. Silver-Silver Halide Electrodes. In Reference Electrodes; Ives, D.J.G., Ganz, G.J., Eds.; Academic Press: London, UK, 1961; pp. 179–230. [Google Scholar]
- Wu, J.; Black, J.J.; Aldous, L. Thermoelectrochemistry using conventional and novel gelled electrolytes in heat-to-current thermocells. Electrochim. Acta 2017, 225, 482–492. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, T. Transported Entropies and Conventional Eastman Entropies of the Transfer of Some Univalent Ions in Aqueous Solutions at 25 °C. Bull. Chem. Soc. Jpn. 1964, 37, 1485–1489. [Google Scholar] [CrossRef]
- Salazar, P.F.; Kumar, S.; Cola, B.A. Design and optimization of thermo-electrochemical cells. J. Appl. Electrochem. 2013, 44, 325–336. [Google Scholar] [CrossRef]
- Kiyono, R.; Tanaka, Y.; Sekiguchi, O.; Tasaka, M. Thermal membrane potential across cation-exchange membranes for various halide solutions. Colloid Polym. Sci. 1993, 271, 1183–1190. [Google Scholar] [CrossRef]
- Buckingham, M.A.; Hammoud, S.; Li, H.; Beale, C.J.; Sengel, J.T.; Aldous, L. A fundamental study of the thermoelectrochemistry of ferricyanide/ ferrocyanide: Cation, concentration, ratio, and heterogeneous and homogeneous electrocatalysis effects in thermogalvanic cells. Sustain. Energ. Fuels 2020, 4, 3388–3399. [Google Scholar] [CrossRef]
- Tanaka, Y. Concentration polarization in ion-exchange membrane electrodialysisThe events arising in an unforced flowing solution in a desalting cell. J. Membr. Sci. 2004, 244, 1–16. [Google Scholar] [CrossRef]
- Barragán, V.; Ruiz-Bauzá, C.; Mengual, J. Effect of Unstirred Solution Layers on Electro-Osmotic Permeability of Cation-Exchange Membranes. J. Colloid Interface Sci. 1994, 168, 458–464. [Google Scholar] [CrossRef]
| Membrane | Ion-Exchange Capacity (meq/dry Gram Resin) | Area Specific Resistance * (Ω cm2) | Dry Thickness (10−3 m) | Water Content (%) |
|---|---|---|---|---|
| CR61 | 2.7 | 13 | 0.60 | 43 |
| CR65 | 2.3 | 8.1 | 0.61 | 56 |
| CR67 | 2.1 | 10.1 | 0.57 | 70 |
| 103QZL | 2.1 | 15 | 0.63 | 46 |
| Membrane | r | |
|---|---|---|
| CR61 | 30.7 ± 0.3 | 0.999 |
| CR65 | 28.5 ± 1.0 | 0.991 |
| CR67 | 30.4 ± 0.11 | 0.990 |
| 103QZL | 14.5 ± 0.5 | 0.996 |
| Electrolyte | r | |
|---|---|---|
| LiCl | 19.9 ± 0.9 | 0.984 |
| NaCl | 43 ± 4 | 0.987 |
| KCl | 30.7 ± 0.03 | 0.999 |
| CsCl | 6.7 ± 0.2 | 0.990 |
| Electrolyte | α | β | r |
|---|---|---|---|
| LiCl | 0.83 ± 0.08 | 1.26 ± 0.03 | 0.9995 |
| NaCl | 1.35 ± 0.13 | 1.54 ± 0.03 | 0.9997 |
| KCl | 2.65 ± 0.15 | 1.04 ± 0.02 | 0.9995 |
| CsCl | 0.35 ± 0.04 | 1.19 ± 0.03 | 0.9995 |
| rpm | α | β′ | r |
|---|---|---|---|
| 0 | 1.38 ± 0.13 | 0.54 ± 0.04 | 0.998 |
| 54 | 0.21 ± 0.05 | 0.76 ± 0.07 | 0.995 |
| 109 | 0.22 ± 0.05 | 0.72 ± 0.07 | 0.995 |
| 160 | 0.06 ± 0.04 | 1.09 ± 0.15 | 0.99 |
| 205 | 0.19 ± 0.03 | 0.70 ± 0.06 | 0.997 |
| 375 | 0.32 ± 0.13 | 0.43 ± 0.13 | 0.99 |
| rpm | r | |
|---|---|---|
| 0 | 0.95 ± 0.07 | 0.96 |
| 48 | 0.55 ± 0.03 | 0.99 |
| 110 | 0.56 ± 0.04 | 0.996 |
| 160 | 0.40 ± 0.03 | 0.97 |
| 222 | 0.41 ± 0.01 | 0.998 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barragán, V.M. Short-Circuit Current in Polymeric Membrane-Based Thermocells: An Experimental Study. Membranes 2021, 11, 480. https://doi.org/10.3390/membranes11070480
Barragán VM. Short-Circuit Current in Polymeric Membrane-Based Thermocells: An Experimental Study. Membranes. 2021; 11(7):480. https://doi.org/10.3390/membranes11070480
Chicago/Turabian StyleBarragán, V. María. 2021. "Short-Circuit Current in Polymeric Membrane-Based Thermocells: An Experimental Study" Membranes 11, no. 7: 480. https://doi.org/10.3390/membranes11070480
APA StyleBarragán, V. M. (2021). Short-Circuit Current in Polymeric Membrane-Based Thermocells: An Experimental Study. Membranes, 11(7), 480. https://doi.org/10.3390/membranes11070480






