An Enhanced Sherwood Number to Model the Hydrogen Transport in Membrane Steam Reformers
Abstract
:1. Introduction
2. Statement of the Problem
- An isothermal 2D model, in which mass and momentum transport in both the axial and radial directions were considered, described in detail in [16], was used as benchmark;
- A simplified 2D model, derived in [17], was employed to derive an expression for the enhanced Sherwood number, valid when the performance of the system is not limited by hydrogen permeation across the membrane;
- The range of operating conditions in which the expression of the Sherwood number is meaningful was identified;
- A 1D model making use of the Sherwood number was employed to assess the performance of membrane reactors.
- Negligible axial dispersion;
- Negligible radial convection;
- Gas density independent of composition;
- Excess steam in feed;
- Local equilibrium conditions;
- Infinite membrane permeability.
3. Modelling Approach
3.1. Sherwood Number
3.2. 1D Model
4. Discussion of Simplifying Assumptions
4.1. Infinite Membrane Permeability
4.2. Effect of Radial Convection
5. Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| membrane area per unit length of reactor (m) | |
| diffusion coefficient (m/s) | |
| effective dispersion tensor (m/s) | |
| f | average molar weight (kg/mol) |
| inlet flow rate of hydrogen (kg/s) | |
| hydrogen mass flux (kgm s)) | |
| k | rate constant of the methane reforming reaction (mol/(msPa)) |
| equilibrium constant of the methane reforming reaction (Pa) | |
| L | reactor length (m) |
| unit vector normal to the membrane surface | |
| total molar flux of the i-the component (mol/ms) | |
| P | pressure (Pa) |
| partial pressure of the i-th component (Pa) | |
| outlet pressure (Pa) | |
| membrane permeability (kg(ms· Pa)) | |
| r | radial coordinate (m) |
| volume-specific mass rate of production of the i-th component (kg/(m s · Pa)) | |
| gas constant (J/(mol · K)) | |
| hdyrogen recovery | |
| inner reactor radius (m) | |
| outer reactor radius (m) | |
| volume-specific molar rate of methane consumption (mol/(ms· Pa)) | |
| S | reactor cross-section (m |
| Sherwood number | |
| T | temperature (K) |
| U | inlet gas velocity (m/s) |
| mass average velocity (m/s) | |
| molar weight of the i-th component (kg/mol) | |
| x | re-scaled radial coordinate |
| y | molar fraction |
| Y | linear combination of hydrogen and methane molar fractions |
| z | axial coordinate |
| Greek Symbols | |
| ratio between characteristic and inlet velocities | |
| proximity to reaction equilibrium | |
| packed bed permeability (m | |
| gas viscosity (Pa · s) | |
| gas density (kg/m) | |
| density of the i-th component (kg/m) | |
| geometric ratio, | |
| stoichiometric coefficient of the i-th component | |
| mass fraction of the i-th component | |
| linear combination of hydrogen and methane mass fractions | |
| Dimensionless Parameters | |
| Damkholer number | |
| dimensionless radial dispersion | |
| dimensionless dispersion | |
| Peclet number | |
| dimensionless outlet pressure | |
| dimensionless permeability parameter | |
| Subscripts and Superscripts | |
| c | carbon dioxide |
| h | hydrogen |
| m | methane |
| w | water |
| M | membrane |
References
- Palo, E.; Salladini, A.; Morico, B.; Palma, V.; Ricca, A.; Iaquaniello, G. Application of Pd-based membrane reactors: An industrial perspective. Membranes 2018, 8, 101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mosca, L.; Jimenez, J.A.M.; Wassie, S.A.; Gallucci, F.; Palo, E.; Colozzi, M.; Taraschi, S.; Galdieri, G. Process design for green hydrogen production. Int. J. Hydrog. Energy 2020, 45, 7266–7277. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Sosio, F.; Manzolini, G.; Campanari, S. Fixed bed membrane reactor for hydrogen production from steam methane reforming: Experimental and modeling approach. Int. J. Hydrog. Energy 2015, 40, 7559–7567. [Google Scholar] [CrossRef]
- Ma, R.; Castro-Dominguez, B.; Mardilovich, I.; Dixon, A.; Ma, Y. Experimental and simulation studies of the production of renewable hydrogen through ethanol steam reforming in a large-scale catalytic membrane reactor. Chem. Eng. J. 2016, 303, 302–313. [Google Scholar] [CrossRef] [Green Version]
- Marin, P.; Patino, Y.; Diez, F.; Ordonez, S. Modelling of hydrogen perm-selective membren reactors for catalytic methane steam reforming. Int. J. Hydrog. Energy 2012, 37, 18433–18445. [Google Scholar] [CrossRef]
- Patrascu, M.; Sheintuch, M. On-site pure hydrogen production by methane steam reforming in high flux membrane reactors: Experimental validation, model predictions and membrane inhibition. Chem. Eng. J. 2015, 262, 862–874. [Google Scholar] [CrossRef]
- Bi, Y.; Xu, H.; Li, W.; Goldbach, A. Water-gas shift reaction in a Pd membrane reactor over Pt/Ce0.6Zr0.4O2 catalyst. Int. J. Hydrog. Energy 2009, 34, 2965–2971. [Google Scholar] [CrossRef]
- Mori, N.; Nakamura, T.; Noda, K.I.; Sakai, O.; Takahashi, A.; Ogawa, N.; Sakai, H.; Iwamoto, Y.; Hattori, T. Reactor configuration and concentration-polarization in methane steam reforming membrane reactor with a highly hydrogen permeable membrane. Ndustrial Eng. Chem. Res. 2007, 46, 1952–1958. [Google Scholar] [CrossRef]
- Bian, Z.; Xia, H.; Wang, Z.; Jiang, B.; Yu, Y.; Yu, K.; Zhong, W.; Kawi, S. CFD simualtion of a hydrogen-permeable membrane reactor for CO2 reforming of CH4: The interplay of the reaction and hydrogen permeation. Energy Fuels 2020, 34, 12366–12378. [Google Scholar] [CrossRef]
- Saidi, M.; Moradi, P. Conversion of biodeies synthesis waste to hydrogen in membrane reactor: Theoretical study of glycerol steam reforming. Int. J. Hydrog. Energy 2020, 45, 8715–8726. [Google Scholar] [CrossRef]
- Lee, H.; Kim, A.; Lee, B.; Lim, H. Comparative numerical analysis for an efficient hydrogen production via a steam methane reforming with a packed-bed reactor, a membrane reactor, and a sorption-enhanced menbrane reactor. Energy Convers. Manag. 2020, 213, 112839. [Google Scholar] [CrossRef]
- Atak, Y.N.; Colpan, C.O.; Iulianelli, A. A review on mathematical modeling of packed bed membrane reactors for hydrogen production from methane. Int. J. Energy Res. 2021, 1–33. [Google Scholar] [CrossRef]
- Catalano, J.; Giacinti Baschetti, M.; Sarti, G.C. Influence of the gas phase resistance on hydrogen flux through palladium-silver membranes. J. Membr. Sci. 2009, 339, 57–67. [Google Scholar] [CrossRef]
- Nekhamkina, O.; Sheintuch, M. Effective approximations for concentration-polarization in Pd-membrane separators. Chem. Eng. J. 2015, 260, 835–845. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C.; Sheintuch, M. Derivation of an enhanced Sherwood number accounting for reaction rate in membrane reactors. Steam reforming of metahne as case study. Catal. Today 2021, 364, 285–293. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. Transport-reaction-permeation regimes in catalytic membrane reactors for hydrogen production. The steam reforming of methane as a case study. Chem. Eng. Sci. 2017, 162, 88–103. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. An equilibrium theory for catalytic steam reforming in membrane reactors. Chem. Eng. Sci. 2017, 160, 291–303. [Google Scholar] [CrossRef]
- Habib, M.A.; Harale, A.; Paglieri, S.; Alrashed, F.S.; Al-Sayoud, A.; Rao, M.V.; Nemitallah, M.A.; Hossain, S.; Hussien, M.; Ali, A.; et al. Palladium-alloy membrane reactors of fuel reforming and hydrogen production: A review. Energy Fuels 2021, 35, 5558–5593. [Google Scholar] [CrossRef]
- Wei, J.; Iglesia, E. Isotopic and kinetic assessment of the mechanism of reaction of CH4 with CO2 or H2O to form synthesis gas and carbon on nickel catalysts. J. Catal. 2004, 224, 370–383. [Google Scholar] [CrossRef]
- Delgado, J.M.P.Q. A critical review of dispersion in packed beds. Heat Mass Transf. 2006, 42, 279–310. [Google Scholar] [CrossRef]
- van Meurs, M. Implementing Concentration Polarization in a 1-D PBMR Model. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2015. [Google Scholar]

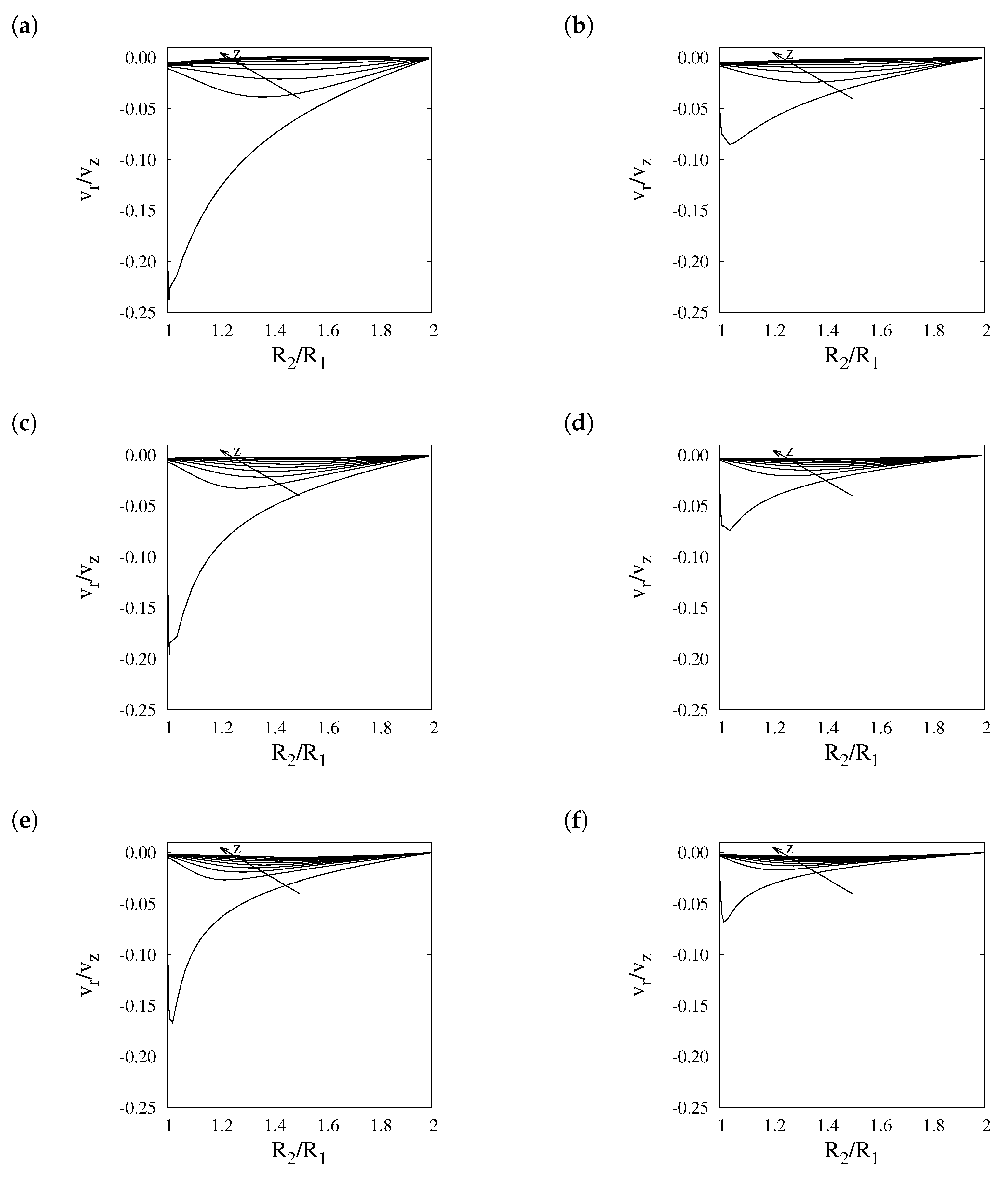


| Dimensional Formulation | ||
|---|---|---|
| Continuity, Momentum, and Mass | ||
| Boundary conditions | ||
| Dimensionless Formulation | ||
| Continuity, Momentum, and Mass | ||
| Boundary Conditions | ||
| P (atm) | |
|---|---|
| 6 | <1.2 |
| 13 | <3.5 |
| 26 | <10 |
| 50 | <11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murmura, M.A.; Rocchetti, C.; Annesini, M.C. An Enhanced Sherwood Number to Model the Hydrogen Transport in Membrane Steam Reformers. Membranes 2021, 11, 805. https://doi.org/10.3390/membranes11110805
Murmura MA, Rocchetti C, Annesini MC. An Enhanced Sherwood Number to Model the Hydrogen Transport in Membrane Steam Reformers. Membranes. 2021; 11(11):805. https://doi.org/10.3390/membranes11110805
Chicago/Turabian StyleMurmura, Maria Anna, Chiara Rocchetti, and Maria Cristina Annesini. 2021. "An Enhanced Sherwood Number to Model the Hydrogen Transport in Membrane Steam Reformers" Membranes 11, no. 11: 805. https://doi.org/10.3390/membranes11110805
APA StyleMurmura, M. A., Rocchetti, C., & Annesini, M. C. (2021). An Enhanced Sherwood Number to Model the Hydrogen Transport in Membrane Steam Reformers. Membranes, 11(11), 805. https://doi.org/10.3390/membranes11110805







