Assessment of Sieverts Law Assumptions and ‘n’ Values in Palladium Membranes: Experimental and Theoretical Analyses
Abstract
:1. Introduction
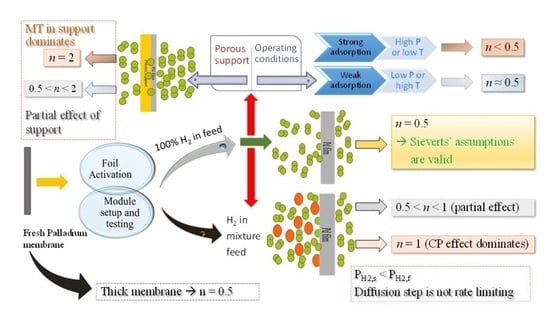
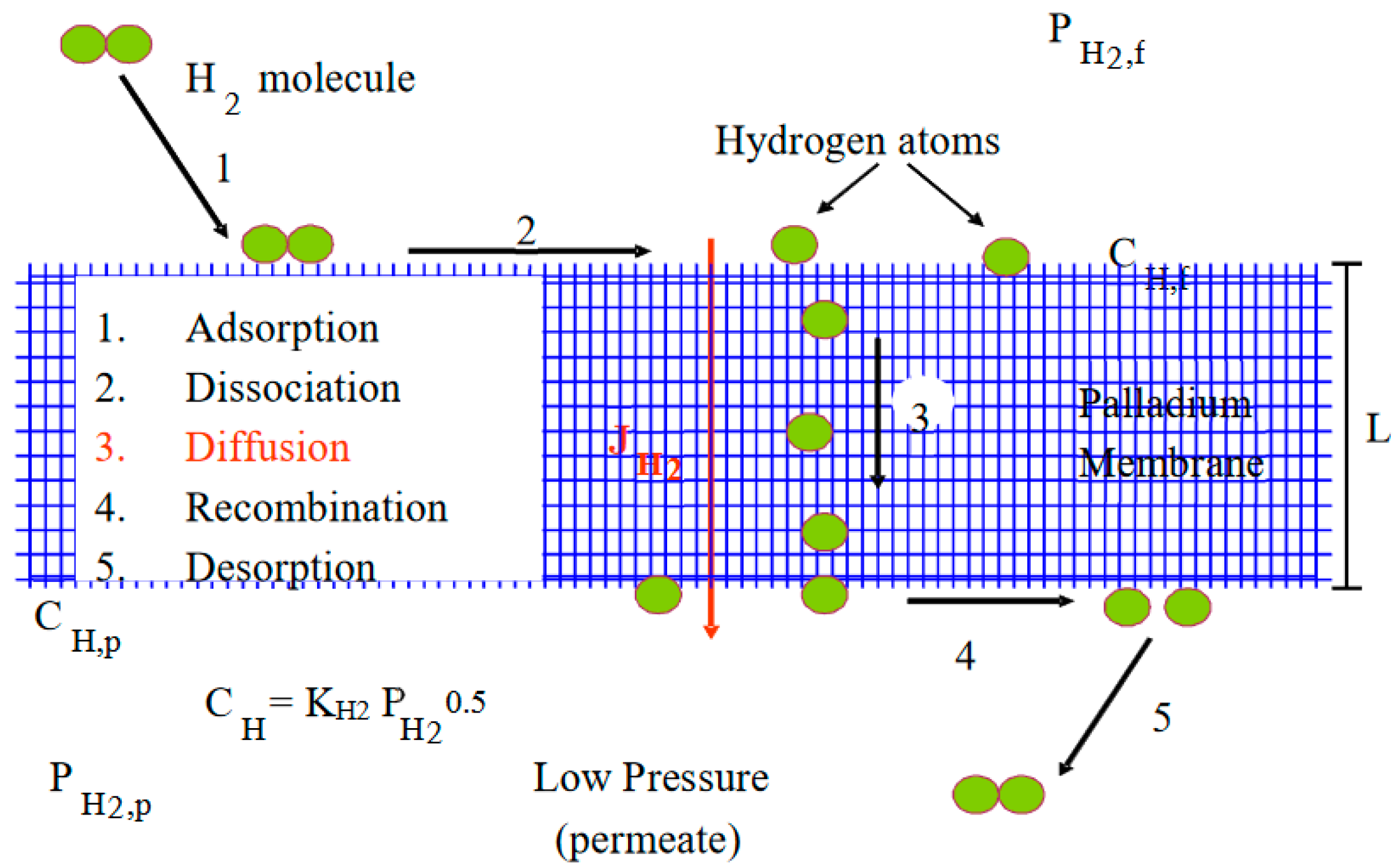
2. Theory
- Diffusion of H through Pd metal is rate limiting (for membrane thickness ≥10 µm);
- Surface coverage of H at both the feed and permeate sides of the membrane is in equilibrium with the respective fluid phases;
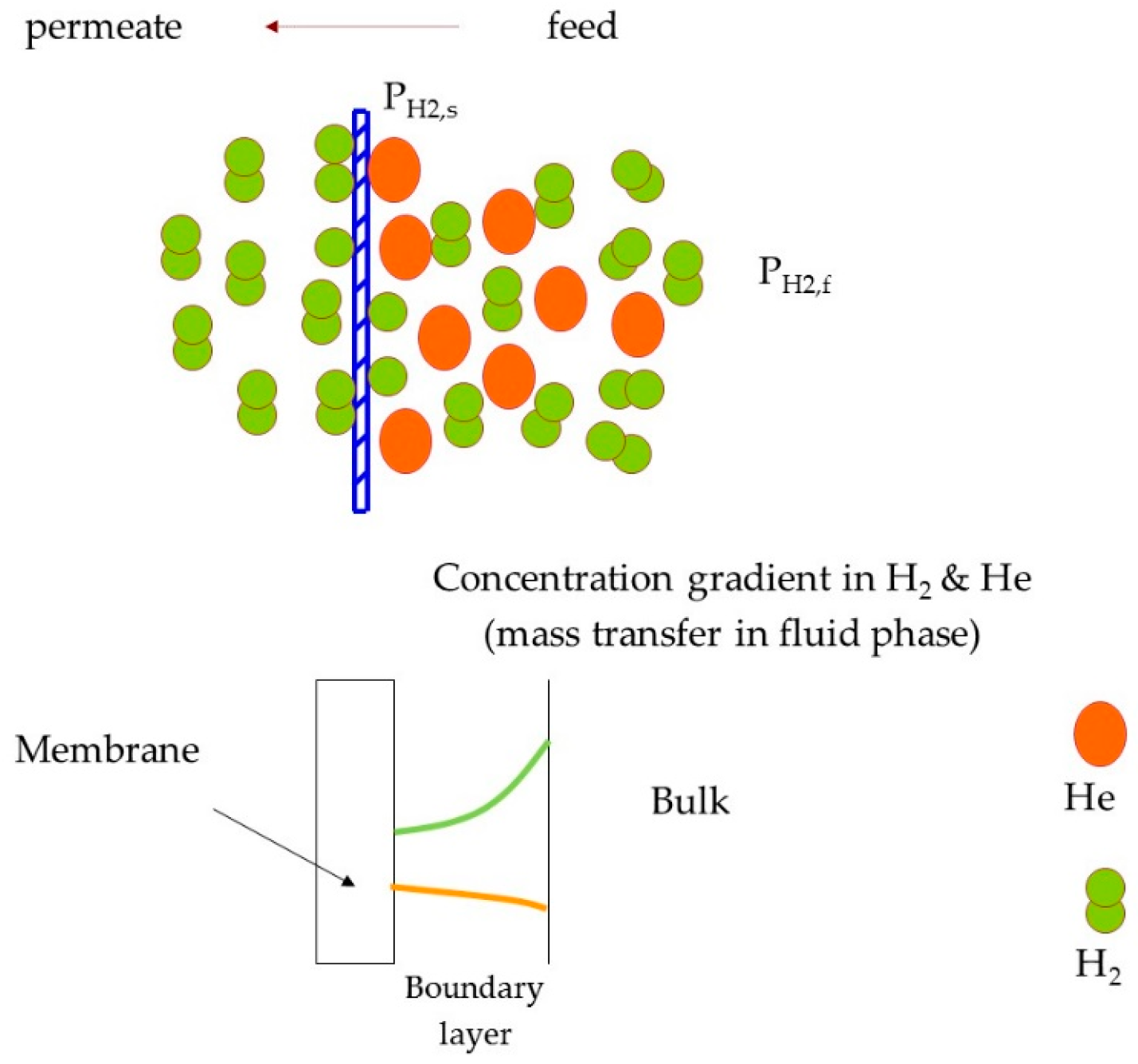
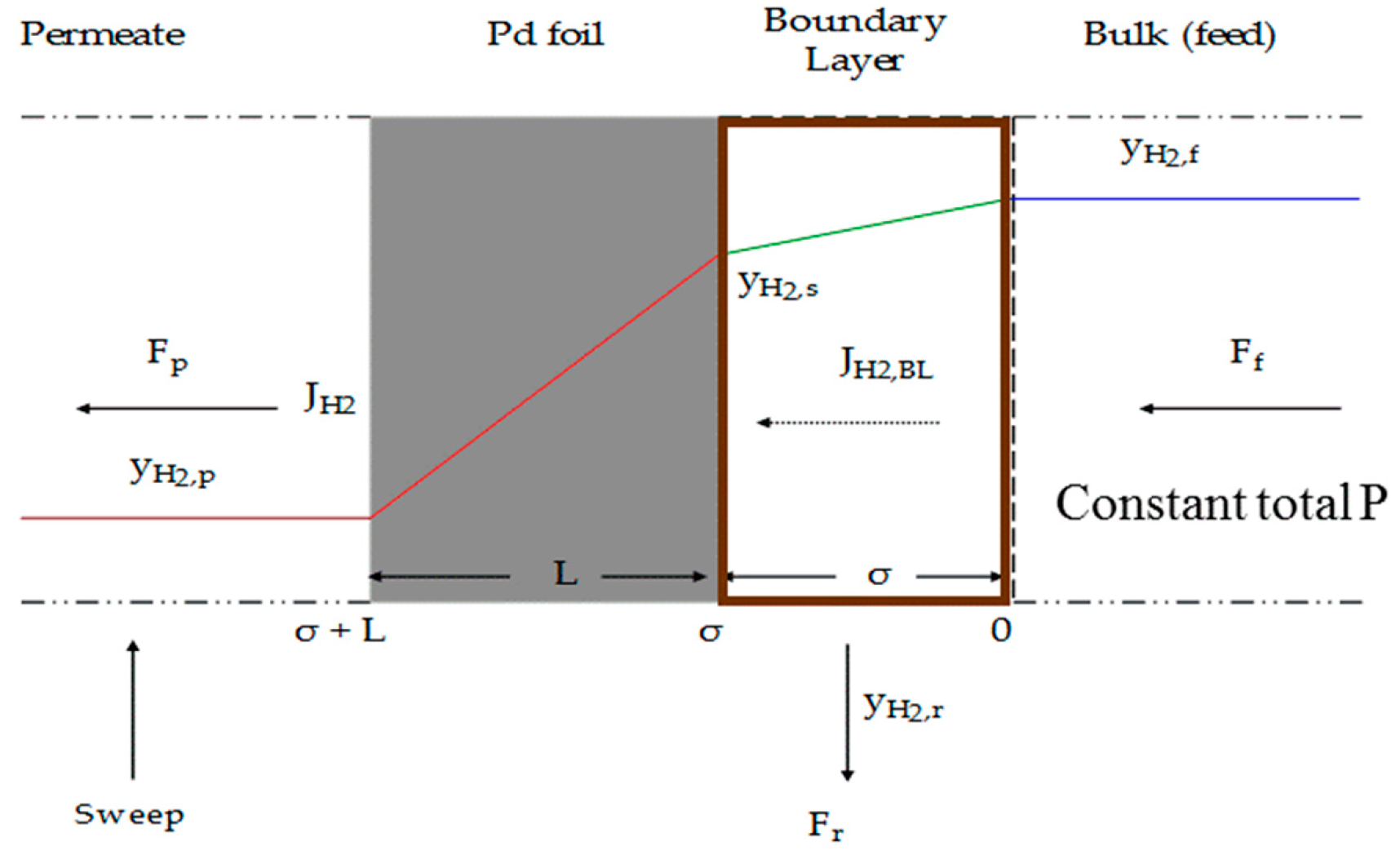
- There is no concentration gradient at feed side (i.e., from bulk feed to membrane surface);
- Constant diffusion coefficient in Pd, i.e., D ≠ f (PH2);
- Linear H in metal phase concentration profile, i.e., Fick’s Law can be applied;
- No species other than H on surface—either adsorbed molecules or contaminants, i.e., palladium sites are not blocked and hence the effective area for permeation is the same throughout the process.
3. Materials and Methods
3.1. Materials
3.2. Methods
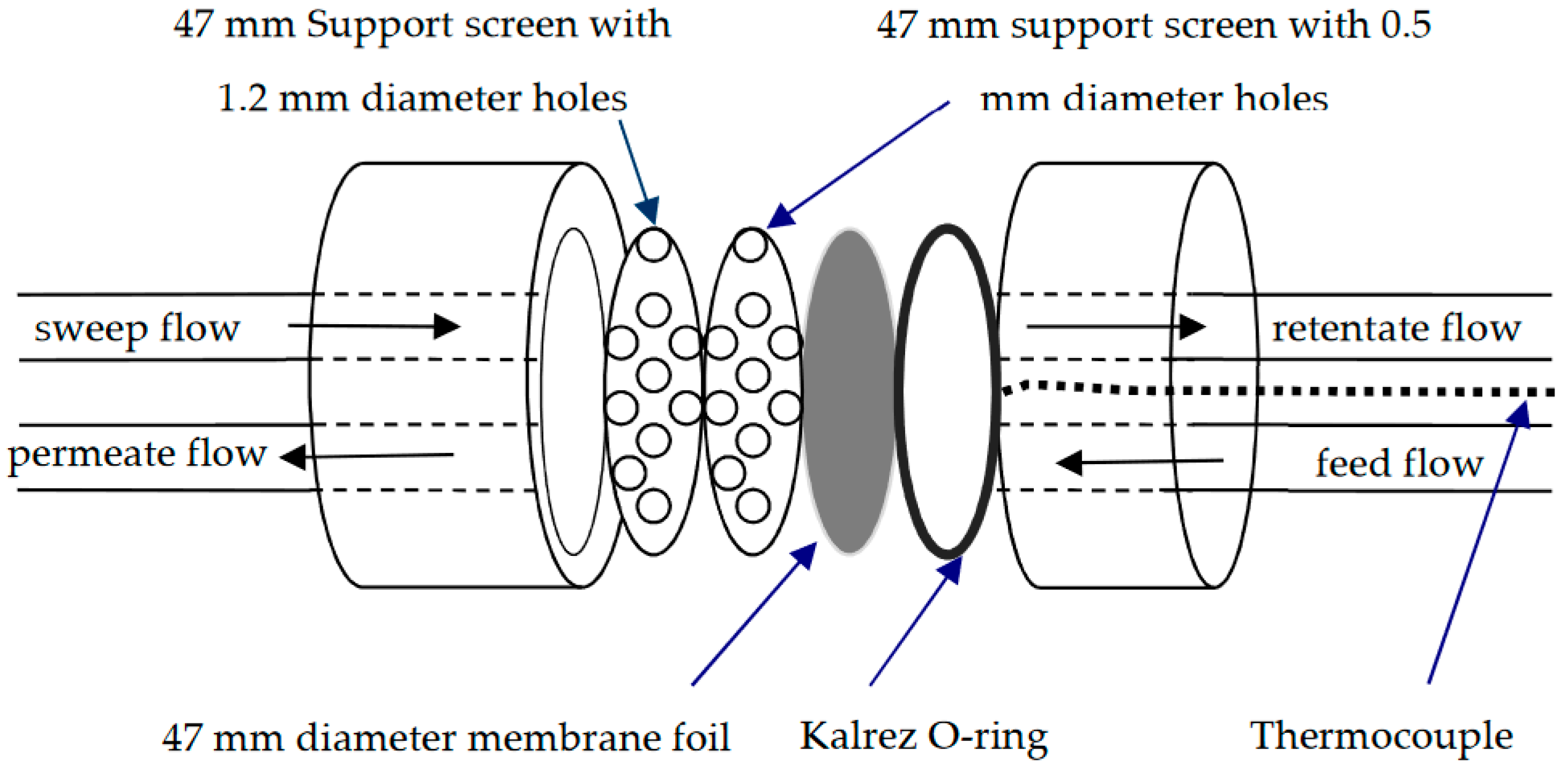
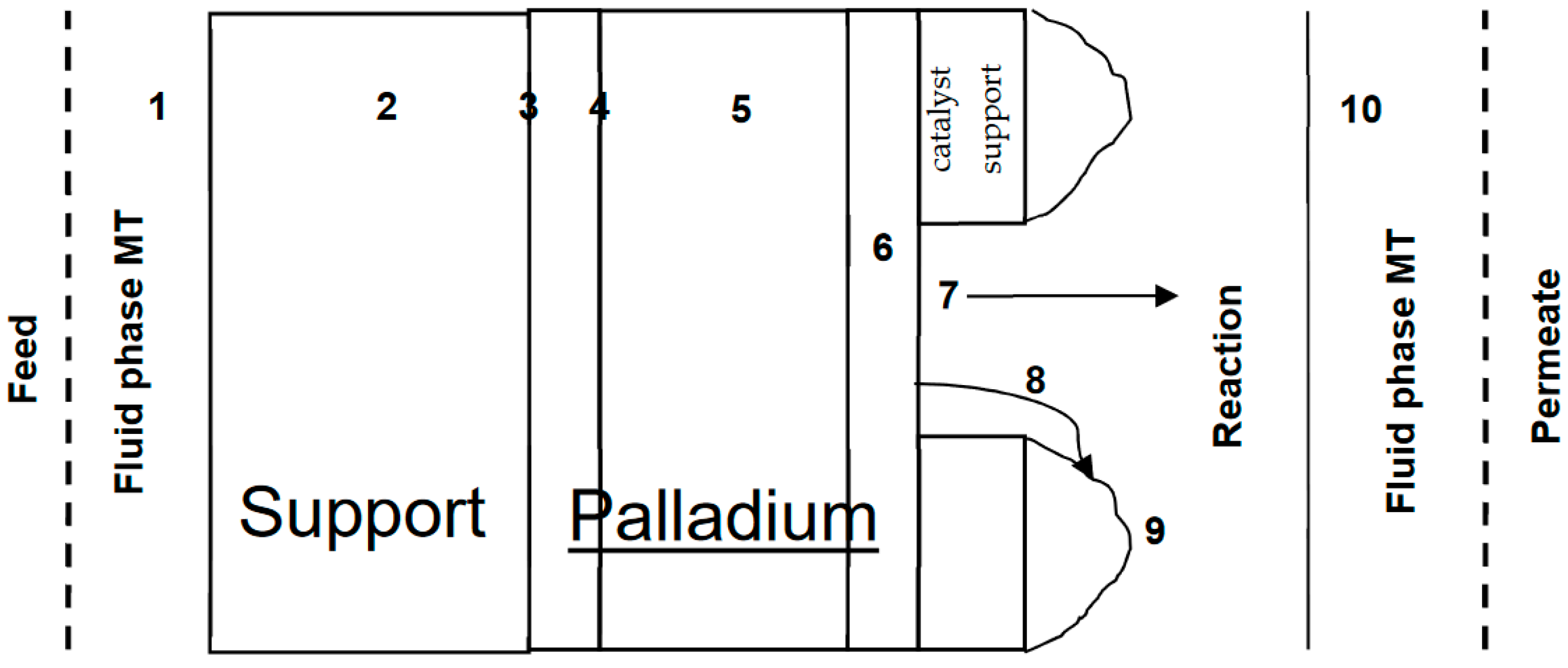
3.2.1. Membrane Module Design
3.2.2. Membrane Foil Pretreatment
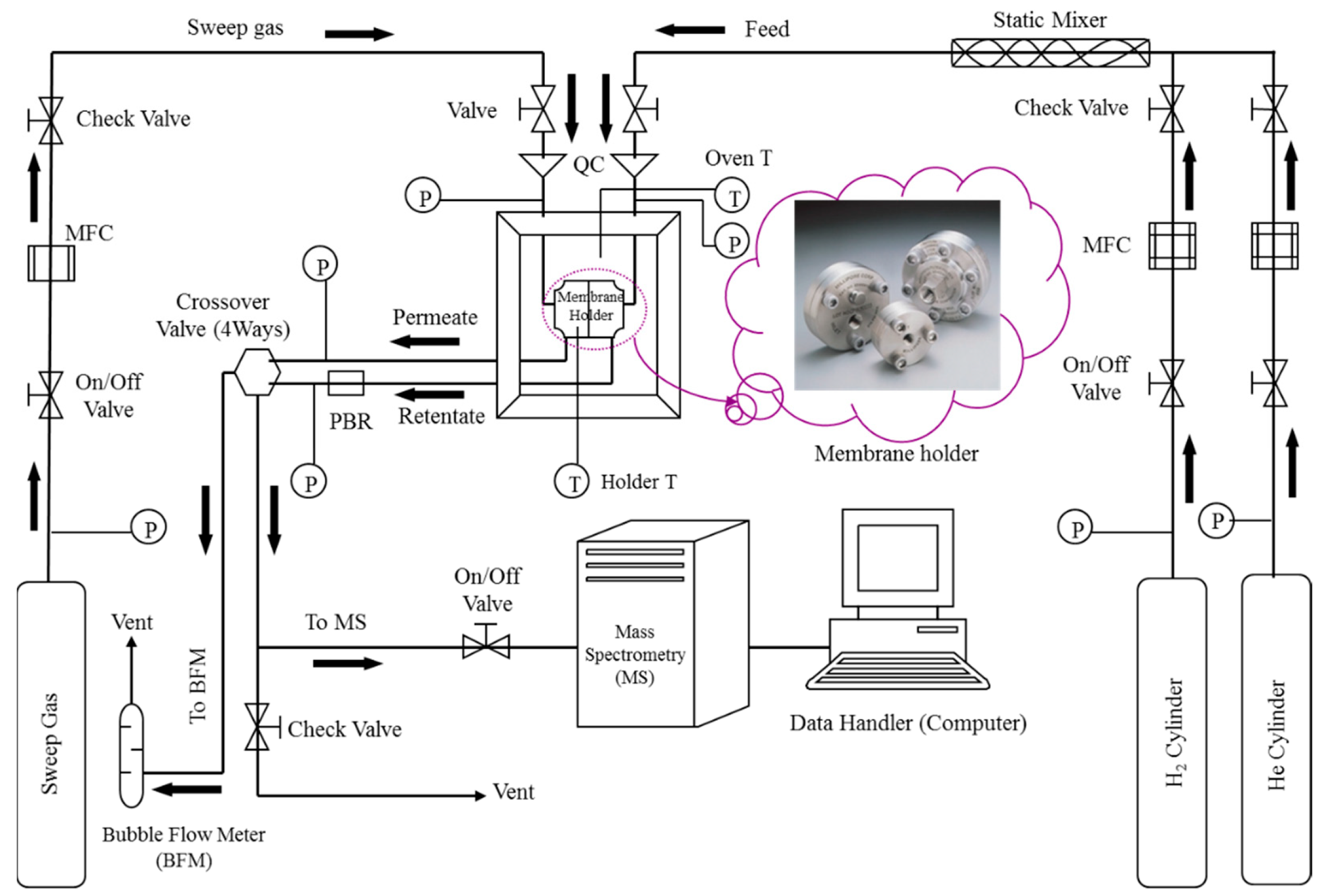
3.2.3. Experimental Setup
3.2.4. Theoretical Calculations
4. Results and Discussion
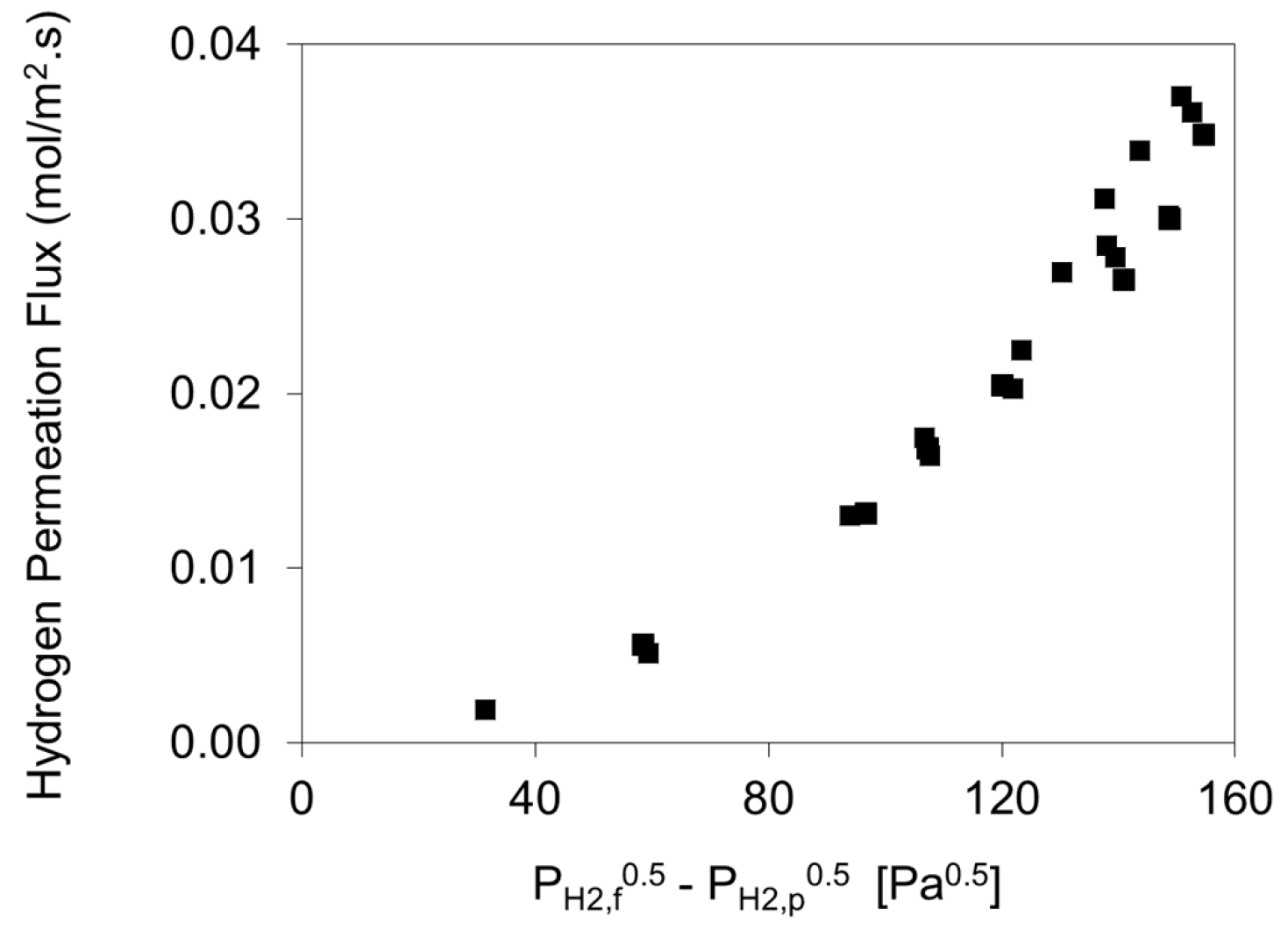
4.1. Permeability of H2 through Pure Palladium Foils
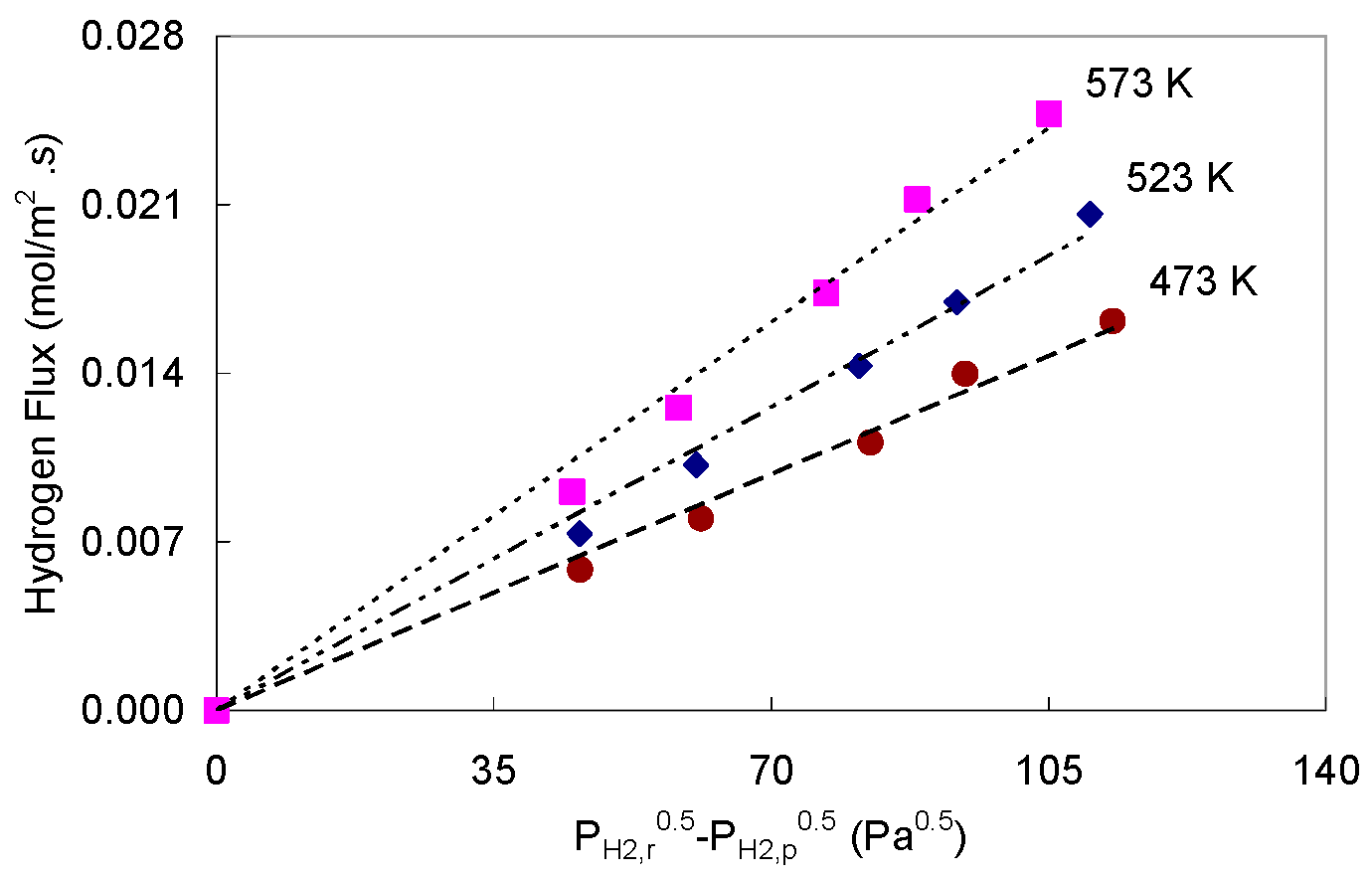
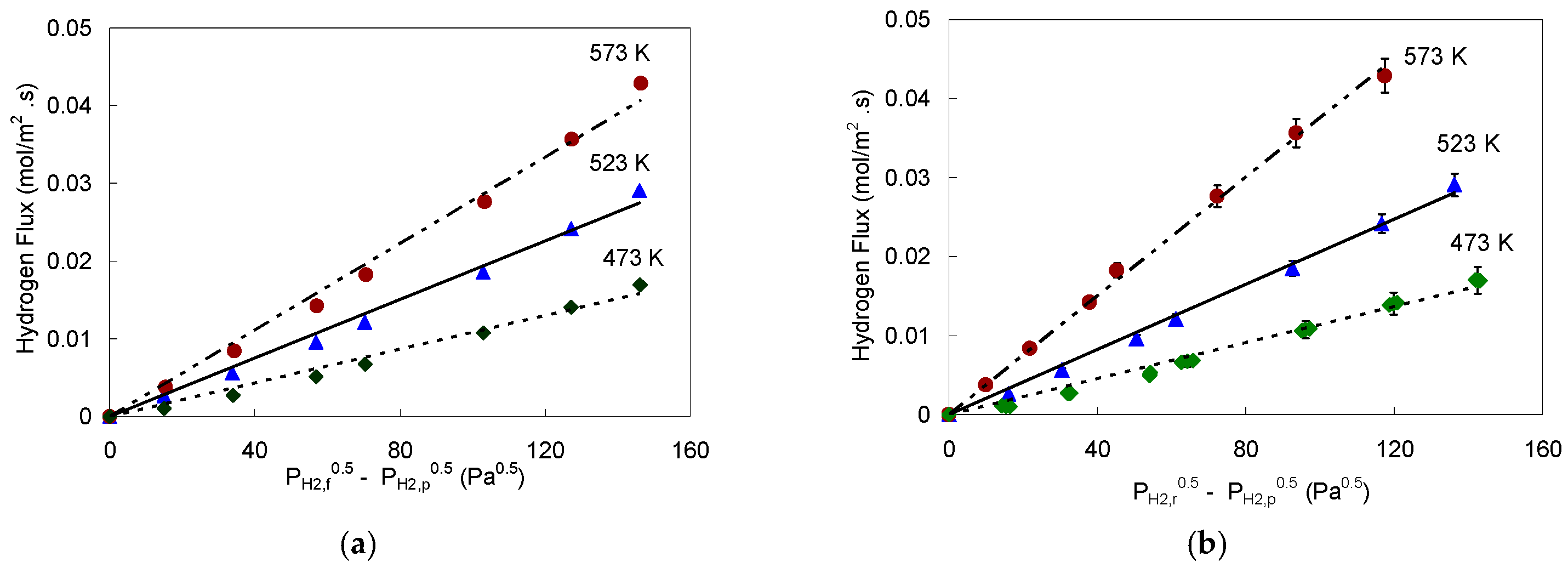
4.1.1. Palladium Foil Pd-1
4.1.2. Palladium Foil Pd-2
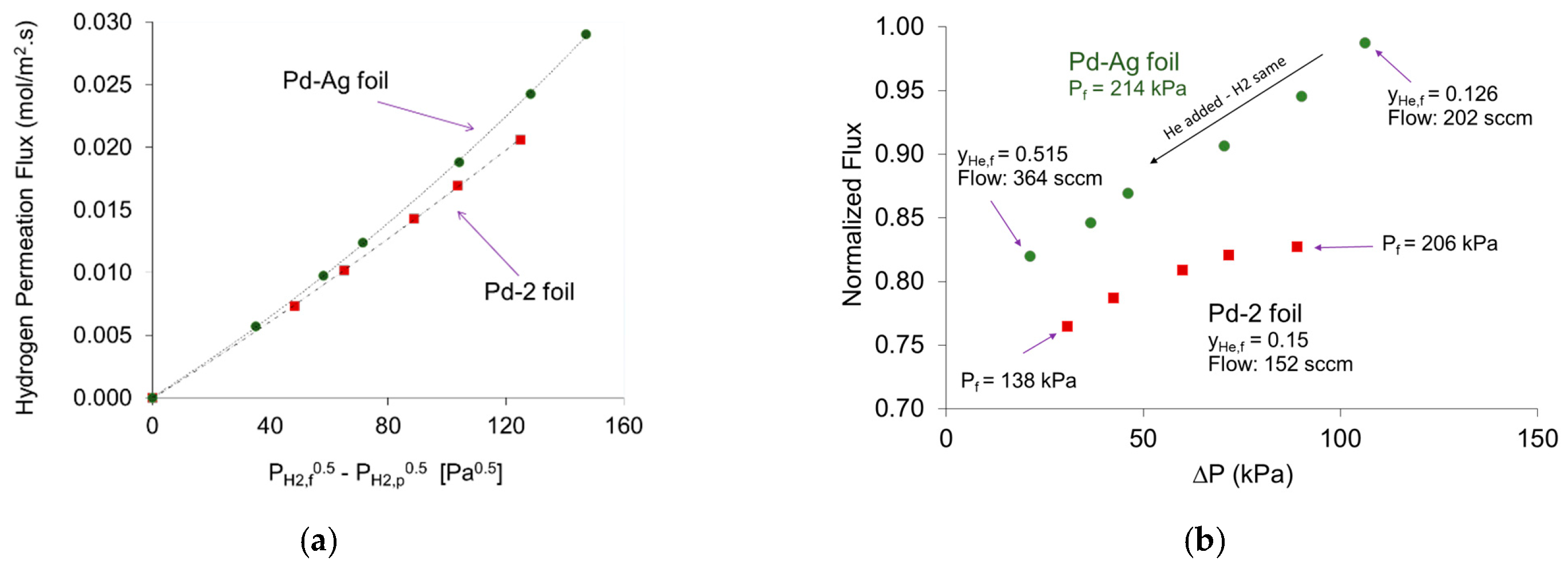
4.2. Permeability of H2 through Palladium–Silver Foils
4.3. Analyzing Sieverts’ Law Assumptions for the Mixed Feeds Permeation in Pd and Pd-Ag Foils
5. Mathematical Modeling
5.1. Effect of High Pressure Limits (Strong Adsorption)
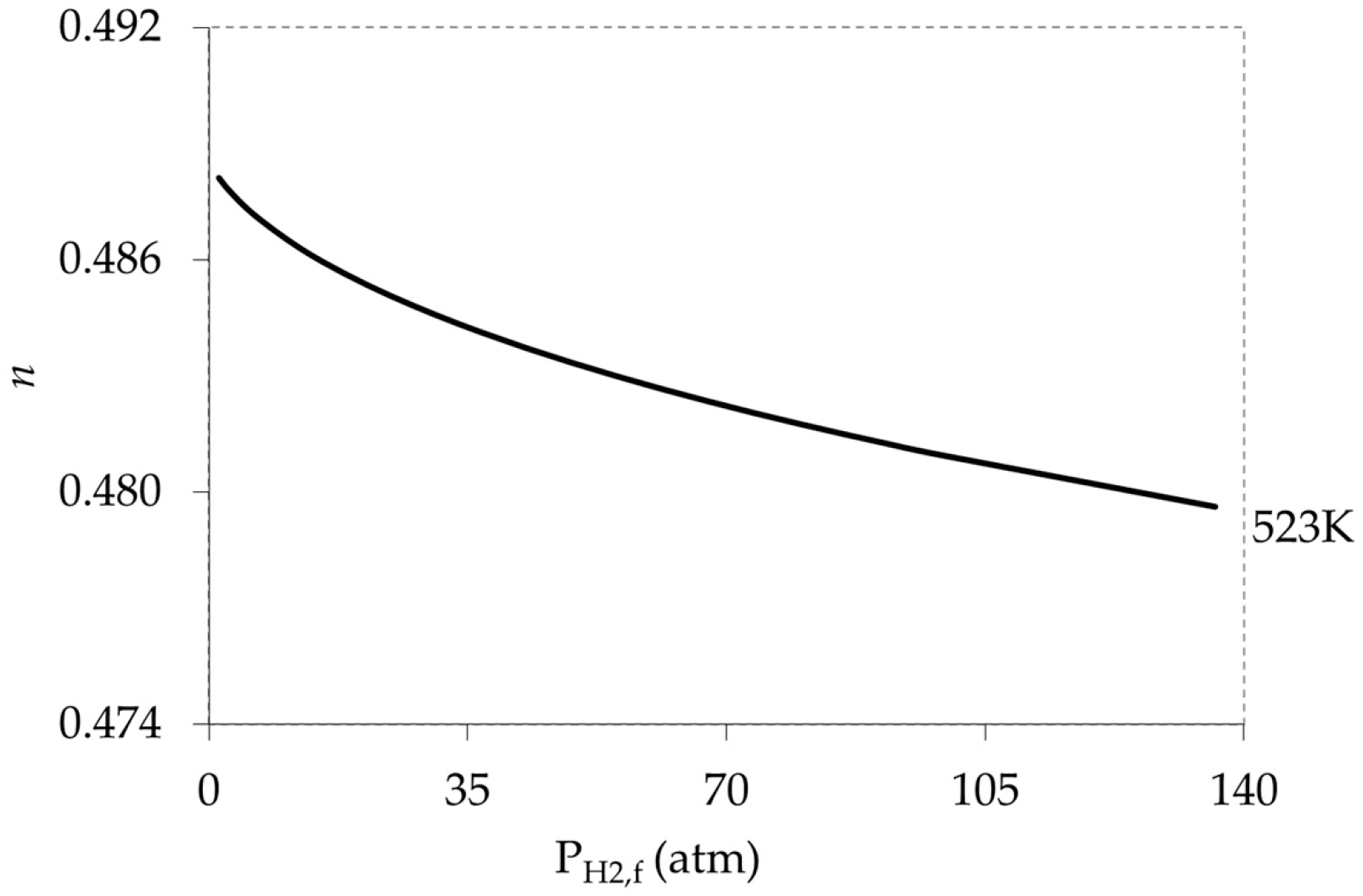
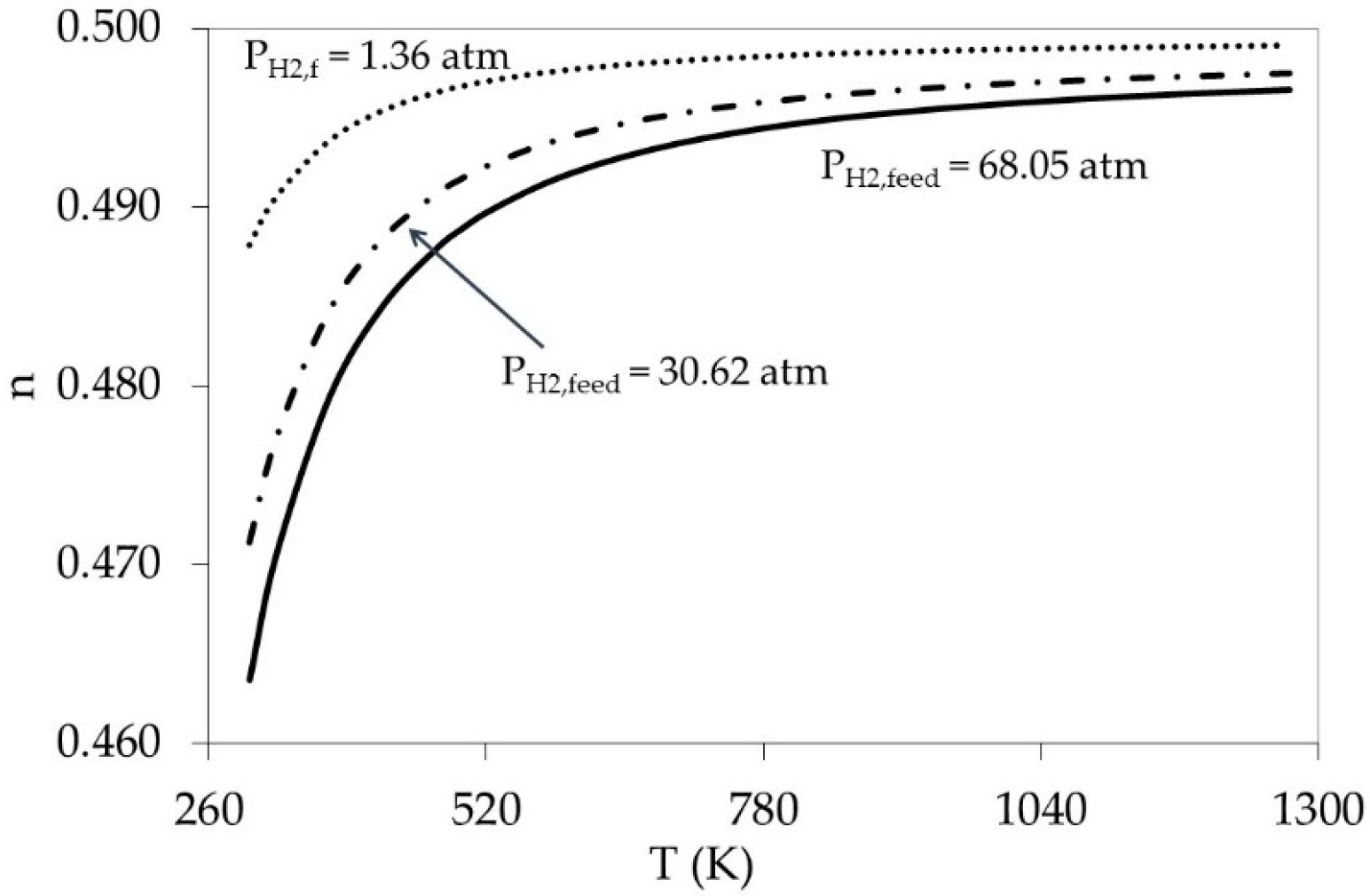
5.2. Effect of Weak Adsorption (High Temperature Limits) on Pressure Exponent (n)
5.3. Combining the Effect of Pressure and Temperature in the Model
6. Explaining the Literature (n) Values and the Future Work Direction
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, L.; Liao, Z.; Wang, J.; Jiang, B.; Yang, Y. Hydrogen sulfide removal process embedded optimization of hydrogen network. Int. J. Hydrogen Energy 2012, 37, 18163–18174. [Google Scholar] [CrossRef]
- Chinchen, G.; Denny, P.; Jennings, J.; Spencer, M.; Waugh, K. Synthesis of Methanol. Appl. Catal. 1988, 36, 1–65. [Google Scholar] [CrossRef]
- Khila, Z.; Hajjaji, N.; Pons, M.-N.; Renaudin, V.; Houas, A. A comparative study on energetic and exergetic assessment of hydrogen production from bioethanol via steam reforming, partial oxidation and auto-thermal reforming processes. Fuel Process. Technol. 2013, 112, 19–27. [Google Scholar] [CrossRef]
- Wiheeb, A.; Martunus; Helwani, Z.; Shamsudin, I.; Kim, J.; Othman, M. Pore morphological identification of hydrotalcite from nitrogen adsorption. Chaos, Solitons Fractals 2013, 49, 7–15. [Google Scholar] [CrossRef]
- Chaubey, R.; Sahu, S.; James, O.; Maity, S. A review on development of industrial processes and emerging techniques for production of hydrogen from renewable and sustainable sources. Renew. Sustain. Energy Rev. 2013, 23, 443–462. [Google Scholar] [CrossRef]
- Osman, A.I.; Deka, T.J.; Baruah, D.C.; Rooney, D.W. Critical challenges in biohydrogen production processes from the organic feedstocks. Biomass-Convers. Biorefinery 2020, 1–19. [Google Scholar] [CrossRef]
- Tian, H.; Li, J.; Yan, M.; Tong, Y.W.; Wang, C.-H.; Wang, X. Organic waste to biohydrogen: A critical review from technological development and environmental impact analysis perspective. Appl. Energy 2019, 256, 113961. [Google Scholar] [CrossRef]
- Chandrasekhar, K.; Lee, Y.-J.; Lee, D.-W. Biohydrogen Production: Strategies to Improve Process Efficiency through Microbial Routes. Int. J. Mol. Sci. 2015, 16, 8266–8293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kapoor, D.; Oberoi, A.S.; Nijhawan, P. Hydrogen Production and Subsequent Adsorption/Desorption Process within a Modified Unitized Regenerative Fuel Cell. Process 2019, 7, 238. [Google Scholar] [CrossRef] [Green Version]
- Assabumrungrat, S.; Wongsakulphasatch, S.; Kim, P.L.; Rodrigues, A.E. Special Issue on “Hydrogen Production Technologies”. Process 2020, 8, 1268. [Google Scholar] [CrossRef]
- Tashie-Lewis, B.C.; Nnabuife, S.G. Hydrogen Production, Distribution, Storage and Power Conversion in a Hydrogen Economy - A Technology Review. Chem. Eng. J. Adv. 2021, 8, 100172. [Google Scholar] [CrossRef]
- Lan, R.; Irvine, J.; Tao, S. Ammonia and related chemicals as potential indirect hydrogen storage materials. Int. J. Hydrogen Energy 2012, 37, 1482–1494. [Google Scholar] [CrossRef]
- Dunbar, Z.W. Hydrogen purification of synthetic water gas shift gases using microstructured palladium membranes. J. Power Sources 2015, 297, 525–533. [Google Scholar] [CrossRef]
- Ahluwalia, R.; Hua, T.; Peng, J. On-board and Off-board performance of hydrogen storage options for light-duty vehicles. Int. J. Hydrogen Energy 2012, 37, 2891–2910. [Google Scholar] [CrossRef]
- Lu, G.; da Costa, J.C.D.; Duke, M.; Giessler, S.; Socolow, R.; Williams, R.; Kreutz, T. Inorganic membranes for hydrogen production and purification: A critical review and perspective. J. Colloid Interface Sci. 2007, 314, 589–603. [Google Scholar] [CrossRef]
- Sánchez, J.; Barreiro, M.; Maroño, M. Bench-scale study of separation of hydrogen from gasification gases using a palladium-based membrane reactor. Fuel 2014, 116, 894–903. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, D.; He, M.; Xu, H.; Li, W. Experimental and simulation studies on concentration polarization in H2 enrichment by highly permeable and selective Pd membranes. J. Membr. Sci. 2006, 274, 83–91. [Google Scholar] [CrossRef]
- Rahimpour, M.R.; Samimi, F.; Babapoor, A.; Tohidian, T.; Mohebi, S. Palladium membranes applications in reaction systems for hydrogen separation and purification: A review. Chem. Eng. Process. Process. Intensif. 2017, 121, 24–49. [Google Scholar] [CrossRef]
- Brunetti, A.; Zito, P.F.; Giorno, L.; Drioli, E.; Barbieri, G. Membrane reactors for low temperature applications: An overview. Chem. Eng. Process. Process. Intensif. 2018, 124, 282–307. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Binotti, M.; Manzolini, G.; Viviente, J.L.; Arratibel, A.; Roses, L.; Gallucci, F. Achievements of European projects on membrane reactor for hydrogen production. J. Clean. Prod. 2017, 161, 1442–1450. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Wang, Z.; Qiao, Z.; Liu, Y.; Cao, X.; Li, W.; Wang, J.; Wang, S. Recent developments in membranes for efficient hydrogen purification. J. Membr. Sci. 2015, 495, 130–168. [Google Scholar] [CrossRef]
- Ward, T.L.; Dao, T. Model of hydrogen permeation behavior in palladium membranes. J. Membr. Sci. 1999, 153, 211–231. [Google Scholar] [CrossRef]
- Caravella, A.; Hara, S.; Drioli, E.; Barbieri, G. Sieverts law pressure exponent for hydrogen permeation through Pd-based membranes: Coupled influence of non-ideal diffusion and multicomponent external mass transfer. Int. J. Hydrogen Energy 2013, 38, 16229–16244. [Google Scholar] [CrossRef]
- Morreale, B.D.; Ciocco, M.V.; Enick, R.M.; Morsi, B.I.; Howard, B.H.; Cugini, A.V.; Rothenberger, K.S. The permeability of hydrogen in bulk palladium at elevated temperatures and pressures. J. Membr. Sci. 2003, 212, 87–97. [Google Scholar] [CrossRef]
- Gielens, F.; Tong, H.; Vorstman, M.; Keurentjes, J. Measurement and modeling of hydrogen transport through high-flux Pd membranes. J. Membr. Sci. 2007, 289, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Dunbar, Z.W.; Lee, I.C. Effects of elevated temperatures and contaminated hydrogen gas mixtures on novel ultrathin palladium composite membranes. Int. J. Hydrogen Energy 2017, 42, 29310–29319. [Google Scholar] [CrossRef]
- Hara, S.; Caravella, A.; Ishitsuka, M.; Suda, H.; Mukaida, M.; Haraya, K.; Shimano, E.; Tsuji, T. Hydrogen diffusion coefficient and mobility in palladium as a function of equilibrium pressure evaluated by permeation measurement. J. Membr. Sci. 2012, 421–422, 355–360. [Google Scholar] [CrossRef]
- Pati, S.; Jat, R.A.; Anand, N.; Derose, D.J.; Karn, K.; Mukerjee, S.; Parida, S. Pd-Ag-Cu dense metallic membrane for hydrogen isotope purification and recovery at low pressures. J. Membr. Sci. 2017, 522, 151–158. [Google Scholar] [CrossRef]
- Jia, H.; Wu, P.; Zeng, G.; Colera, E.S.; Serrano, A.; Castro, G.R.; Xu, H.; Sun, C.; Goldbach, A. High-temperature stability of Pd alloy membranes containing Cu and Au. J. Membr. Sci. 2017, 544, 151–160. [Google Scholar] [CrossRef]
- Deveau, N.; Ma, Y.H.; Datta, R. Beyond Sieverts’ law: A comprehensive microkinetic model of hydrogen permeation in dense metal membranes. J. Membr. Sci. 2013, 437, 298–311. [Google Scholar] [CrossRef]
- Caravella, A.; Hara, S.; Sun, Y.; Drioli, E.; Barbieri, G. Coupled influence of non-ideal diffusion and multilayer asymmetric porous supports on Sieverts law pressure exponent for hydrogen permeation in composite Pd-based membranes. Int. J. Hydrogen Energy 2014, 39, 2201–2214. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Flanagan, D. Fundamental of Diffusion and Dissolution. Developing Solid Oral Dosage Forms 2017, 253–270. [Google Scholar] [CrossRef]
- Flanagan, T.B.; Wang, D.; Luo, S. Thermodynamics of hydrogen absorption (desorption) in unoxidized and internally oxidized Pd–Ti alloys. J. Alloy. Compd. 2017, 701, 981–992. [Google Scholar] [CrossRef] [Green Version]
- Flanagan, T.B.; Wang, D. Exponents for the Pressure Dependence of Hydrogen Permeation through Pd and Pd−Ag Alloy Membranes. J. Phys. Chem. C 2010, 114, 14482–14488. [Google Scholar] [CrossRef]
- Hara, S.; Ishitsuka, M.; Suda, H.; Mukaida, M.; Haraya, K. Pressure-Dependent Hydrogen Permeability Extended for Metal Membranes Not Obeying the Square-Root Law. J. Phys. Chem. B 2009, 113, 9795–9801. [Google Scholar] [CrossRef] [PubMed]
- Peters, T.; Stange, M.; Klette, H.; Bredesen, R. High pressure performance of thin Pd–23%Ag/stainless steel composite membranes in water gas shift gas mixtures; influence of dilution, mass transfer and surface effects on the hydrogen flux. J. Membr. Sci. 2008, 316, 119–127. [Google Scholar] [CrossRef]
- Bhattacharya, S. Concentration polarization, separation factor, and Peclet number in membrane processes. J. Membr. Sci. 1997, 132, 73–90. [Google Scholar] [CrossRef]
- Gao, H.; Lin, Y.S.; Li, A.Y.; Zhang, B. Chemical Stability and Its Improvement of Palladium-Based Metallic Membranes. Ind. Eng. Chem. Res. 2004, 43, 6920–6930. [Google Scholar] [CrossRef]
- Chen, W.-H.; Syu, W.-Z.; Hung, C.-I. Numerical characterization on concentration polarization of hydrogen permeation in a Pd-based membrane tube. Int. J. Hydrogen Energy 2011, 36, 14734–14744. [Google Scholar] [CrossRef]
- Lüdtke, O.; Behling, R.-D.; Ohlrogge, K. Concentration polarization in gas permeation. J. Membr. Sci. 1998, 146, 145–157. [Google Scholar] [CrossRef]
- Mardilovich, P.P.; She, Y.; Ma, Y.H.; Rei, M.-H. Defect-free palladium membranes on porous stainless-steel support. AIChE J. 1998, 44, 310–322. [Google Scholar] [CrossRef]
- Tong, J.; Su, L.; Haraya, K.; Suda, H. Thin Pd membrane on α-Al2O3 hollow fiber substrate without any interlayer by electroless plating combined with embedding Pd catalyst in polymer template. J. Membr. Sci. 2008, 310, 93–101. [Google Scholar] [CrossRef]
- Chen, W.-H.; Chiu, I.-H. Transient dynamic of hydrogen permeation through a palladium membrane. Int. J. Hydrogen Energy 2009, 34, 2440–2448. [Google Scholar] [CrossRef]
- Algieri, C.; Coppola, G.; Mukherjee, D.; Shammas, M.; Calabro, V.; Curcio, S.; Chakraborty, S. Catalytic Membrane Reactors: The Industrial Applications Perspective. Catalysts 2021, 11, 691. [Google Scholar] [CrossRef]
- Al-Shammary, A.F.Y.; Caga, I.T.; Winterbottom, J.M.; Tata, A.Y.; Harris, I.R. Palladium-based diffusion membranes as catalysts in ethylene hydrogenation. J. Chem. Technol. Biotechnol. 1991, 52, 571–585. [Google Scholar] [CrossRef]
- Unlu, D.; Hilmioglu, N.D. Pervaporation catalytic membrane reactor application over functional chitosan membrane. J. Membr. Sci. 2018, 559, 138–147. [Google Scholar] [CrossRef]
- Chen, Y.-R.; Tsuru, T.; Kang, D.-Y. Simulation and design of catalytic membrane reactor for hydrogen production via methylcyclohexane dehydrogenation. Int. J. Hydrogen Energy 2017, 42, 26296–26307. [Google Scholar] [CrossRef]
- Baráth, E. Hydrogen Transfer Reactions of Carbonyls, Alkynes, and Alkenes with Noble Metals in the Presence of Alcohols/Ethers and Amines as Hydrogen Donors. Catalysts 2018, 8, 671. [Google Scholar] [CrossRef] [Green Version]
- Fellechner, O.; Blatkiewicz, M.; Smirnova, I. Reactive Separations for In Situ Product Removal of Enzymatic Reactions: A Review. Chem. Ing. Tech. 2019, 91, 1522–1543. [Google Scholar] [CrossRef]
- Manthiram, A.; Zhao, X.; Li, W. Developments in membranes, catalysts and membrane electrode assemblies for direct methanol fuel cells (DMFCs). Funct. Mater. Sustain. Energy Appl. 2012, 312–369. [Google Scholar] [CrossRef]
- Su, Y.; Lv, H.; Zhou, W.; Zhang, C. Review of the Hydrogen Permeability of the Liner Material of Type IV On-Board Hydrogen Storage Tank. World Electr. Veh. J. 2021, 12, 130. [Google Scholar] [CrossRef]
- Kian, K.; Woodall, C.M.; Wilcox, J.; Liguori, S. Performance of Pd-Based Membranes and Effects of Various Gas Mixtures on H2 Permeation. Environments 2018, 5, 128. [Google Scholar] [CrossRef] [Green Version]
- Paglieri, S.N.; Way, J.D. Innovations in palladium membrane research. Sep. Purif. Methods 2002, 31, 1–169. [Google Scholar] [CrossRef]
- Pinacci, P.; Basile, A. Palladium-Based Composite Membranes for Hydrogen Separation in Membrane Reactors; Elsevier: Amsterdam, The Netherlands, 2013; pp. 149–182. [Google Scholar]
- Allevi, C.; Collodi, G. Hydrogen production in IGCC systems. In Integrated Gasification Combined Cycle (IGCC) Technologies; Elsevier: Amsterdam, The Netherlands, 2017; pp. 419–443. [Google Scholar]
- Elkina, I.B.; Meldon, J.H. Hydrogen transport in palladium membranes. Desalination 2002, 147, 445–448. [Google Scholar] [CrossRef]
- Yun, S.; Oyama, S.T. Correlations in palladium membranes for hydrogen separation: A review. J. Membr. Sci. 2011, 375, 28–45. [Google Scholar] [CrossRef]
- Shu, J.; Grandjean, B.P.A.; Van Neste, A.; Kaliaguine, S. Catalytic palladium-based membrane reactors: A review. Can. J. Chem. Eng. 1991, 69, 1036–1060. [Google Scholar] [CrossRef]
- Turnbull, A. Hydrogen diffusion and trapping in metals. Gaseous Hydrog. Embrittlement Mater. Energy Technol. 2012, 89–128. [Google Scholar] [CrossRef]
- Flynn, G.; Yalkowsky, S.; Roseman, T. Mass transport Phenomena and Models: Theoretical Concepts. J. Pharm. Sci. 1974, 63, 479–510. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.-H.; Hsia, M.-H.; Chi, Y.-H.; Lin, Y.-L.; Yang, C.-C. Polarization phenomena of hydrogen-rich gas in high-permeance Pd and Pd–Cu membrane tubes. Appl. Energy 2014, 113, 41–50. [Google Scholar] [CrossRef]
- Abdollahi, M.; Yu, J.; Liu, P.K.; Ciora, R.; Sahimi, M.; Tsotsis, T.T. Ultra-pure hydrogen production from reformate mixtures using a palladium membrane reactor system. J. Membr. Sci. 2012, 390-391, 32–42. [Google Scholar] [CrossRef]
- McLeod, L.; Degertekin, F.; Fedorov, A. Determination of the rate-limiting mechanism for permeation of hydrogen through microfabricated palladium–silver alloy membranes. J. Membr. Sci. 2009, 341, 225–232. [Google Scholar] [CrossRef]
- Holleck, G.L. Diffusion and solubility of hydrogen in palladium and palladium--silver alloys. J. Phys. Chem. 1970, 74, 503–511. [Google Scholar] [CrossRef]
- Smirnov, L.I.; Gol’Tsov, V.A. Nonlinear and crossover effects in the diffusion penetration of hydrogen through a metallic membrane. J. Eng. Phys. Thermophys. 1988, 55, 981–985. [Google Scholar] [CrossRef]
- Hurlbert, R.C.; Konecny, J.O. Diffusion of Hydrogen through Palladium. J. Chem. Phys. 1961, 34, 655–658. [Google Scholar] [CrossRef]
- Katsuta, H.; Farraro, R.J.; McLellan, R.B. The diffusivity of Hydrogen in palladium. Acta Metall. 1979, 27, 1111–1114, ISSN 0001-6160. [Google Scholar] [CrossRef]
- Caravella, A.; Barbieri, G.; Drioli, E. Concentration polarization analysis in self-supported Pd-based membranes. Sep. Purif. Technol. 2009, 66, 613–624. [Google Scholar] [CrossRef]
- Roa, F.; Block, M.J.; Way, J. The influence of alloy composition on the H2 flux of composite Pd-Cu membranes. Desalination 2002, 147, 411–416. [Google Scholar] [CrossRef]
- Fuerst, T.F.; Humrickhouse, P.W.; Taylor, C.N.; Shimada, M. Surface effects on deuterium permeation through vanadium membranes. J. Membr. Sci. 2021, 620, 118949. [Google Scholar] [CrossRef]
- Ali, J.K.; Newson, E.; Rippin, D. Deactivation and regeneration of Pd-Ag membranes for dehydrogenation reactions. J. Membr. Sci. 1994, 89, 171–184. [Google Scholar] [CrossRef]
- Yamakawa, K.; Ege, M.; Ludescher, B.; Hirscher, M. Surface adsorbed atoms suppressing hydrogen permeation of Pd membranes. J. Alloy. Compd. 2003, 352, 57–59. [Google Scholar] [CrossRef]
- Suzuki, A.; Yukawa, H. A Review for Consistent Analysis of Hydrogen Permeability through Dense Metallic Membranes. Membranes 2020, 10, 120. [Google Scholar] [CrossRef] [PubMed]
- Caravella, A.; Barbieri, G.; Drioli, E. Modelling and simulation of hydrogen permeation through supported Pd-alloy membranes with a multicomponent approach. Chem. Eng. Sci. 2008, 63, 2149–2160. [Google Scholar] [CrossRef]
 ), 62 kPa (
), 62 kPa (  ), and 117 kPa (
), and 117 kPa (  ); (b) for a 30% He feed stream (
); (b) for a 30% He feed stream (  ) compared to 5% He feed stream (
) compared to 5% He feed stream (  ) with ∆PH2 = 58 kPa and PH2,f = 152 kPa.
) with ∆PH2 = 58 kPa and PH2,f = 152 kPa.
 ), 62 kPa (
), 62 kPa (  ), and 117 kPa (
), and 117 kPa (  ); (b) for a 30% He feed stream (
); (b) for a 30% He feed stream (  ) compared to 5% He feed stream (
) compared to 5% He feed stream (  ) with ∆PH2 = 58 kPa and PH2,f = 152 kPa.
) with ∆PH2 = 58 kPa and PH2,f = 152 kPa.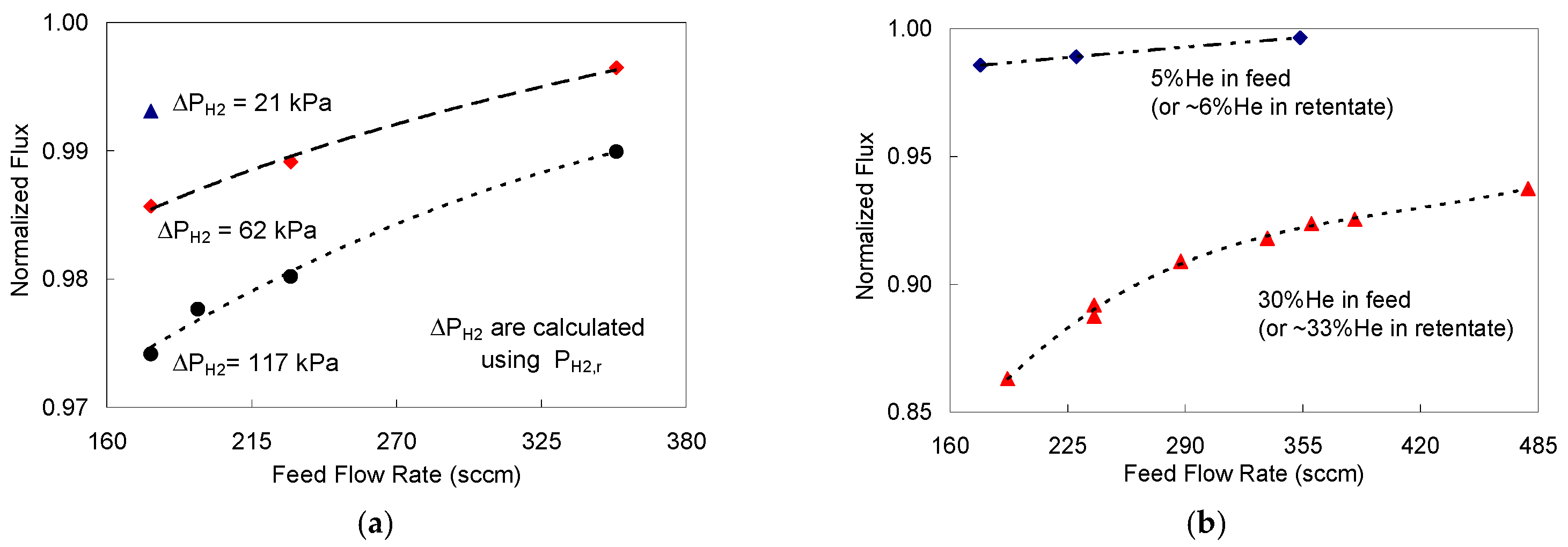
| Temperature (K) | Partial Pressure Drop (kPa) | Feed Mixture % He in H2 | Feed Flow Rate (sccm) |
|---|---|---|---|
| 473, 523, 573 | ~29, 40, 55, 64, 79 | ~13.5% | 114 |
| Temperature (K) | Feed Mixture % He in H2 | Feed Flow Rate (sccm) | Feed Pressure (kPa) | H2 Feed Flow Rate (sccm) | Permeate Pressure (kPa) |
|---|---|---|---|---|---|
| 473, 523, 573 | 10–57% | 15–172 | 214 | 129 | 93 |
| Parameter | Value | Units | References |
|---|---|---|---|
| Qo | 9.29 × 10−8 | mol/m s Pa0.5 | (Current study) |
| Ep | 11.7 | kJ/mol | (Current study) |
| Do | 4.5 × 10−7 | m2/s | Birnbaum and Wert(1972) [59] |
| ED | 24.1 | kJ/mol | Birnbaum and Wert (1972) [59] |
| −8.4 | kJ/mol | Holleck (1991) [64] | |
| −48.7 | J/mol K | Holleck (1991) [64] | |
| Nb | 1.13 × 105 | mol Pd/ m3 | Ward and Dao (1999) [22] |
| Xm | 0.65 | mol H/mol Pd | Smirnov and Gol’tsov(1988) [65] |
| R | 8.314 | J/mol K | (Gas constant) |
| References | Hurlbert and Konecny [66] | Katsuta et al. [67] | Morreale et al. [24] | Gielens et al. [25] | Gielens et al. [25] | Chen et al. [61] | Chen et al. [61] |
|---|---|---|---|---|---|---|---|
| Parameters | |||||||
| L (µm) | 10–150 | 940 | 1000 | 0.9 | 0.5 | 6.93 | 6.63 |
| no support | no support | no support | no support | with support | Tubular | Tubular | |
 |  |  |  |  |  |  | |
| T (K) | 623–773 | 769–1219 | 623–1173 | 623–873 | 623–873 | 623 | 623 |
| Feed gas | H2 | H2 | 90% H2–10% He | 20% H2–80% He | 20% H2–80% He | H2 | 75% H2–25% N2 |
| Ptotal,f (kPa) | 101–710 | 101 | 101–2760 | 101–505 | 101–505 | 101–202 | 303–506 |
| PH2,f (kPa) | 101–710 | 101 | 91–2480 | 20–101 | 20–101 | 101–202 | 303–506 |
| P total,p (kPa) | Vacuum | Vacuum | 118 | 101 | 101 | 101 | 101 |
| Permeate condition | Vacuum | Vacuum | Ar sweep | N2 sweep | N2 sweep | N2 sweep | N2 sweep |
| n | 0.68 | 0.5 | 0.62 | 0.5–1.04 ** | 0.58–1.41 ** | 0.5 | 1.0 |
| Possible justification of (n) | L-Thick Pd *** Pure H2 (n ≈ 0.5), high P (n < 0.5), High T (n ~ 0.5), high ΔPH2 desorption rate limiting (n ≈ 1) → Avg. (n) = 0.7 | H-Thick Pd Pure H2 (n = 0.5), (low P and high T) (n = 0.5), low ΔPH2 → Sieverts’ Law (n = 0.5) | Thick Pd (n = 0.5), with lower CP * effect at feed (n ~ 0.8), Very high P (n < 0.5), high T (n ~ 0.5), → Avg. (n) = 0.63 | Thin Pd Strong mixed effect (CP *) and sweep (n = 1), High T (n ~ 0.5), moderate P (n ~ 0.5), → Very thin membrane with strong CP (n = 1) | Thin Pd Strong mixed feed or CP * (n = 1), high T (n ~ 0.5), Viscous flow in support flux α PH22 (n = 2), moderate P (n ~ 0.5) → Avg. (n) = 1.38 | Thin Pd Pure H2 low P (n = 0.5), High T (n = 0.5), → Avg. (n ~ 0.5) | Thin Pd Strong mixed feed or CP * (n = 1), low P (n = 0.5), High T (n = 0.5), → mass transfer in fluid phase is the limiting step (n ~1.0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alraeesi, A.; Gardner, T. Assessment of Sieverts Law Assumptions and ‘n’ Values in Palladium Membranes: Experimental and Theoretical Analyses. Membranes 2021, 11, 778. https://doi.org/10.3390/membranes11100778
Alraeesi A, Gardner T. Assessment of Sieverts Law Assumptions and ‘n’ Values in Palladium Membranes: Experimental and Theoretical Analyses. Membranes. 2021; 11(10):778. https://doi.org/10.3390/membranes11100778
Chicago/Turabian StyleAlraeesi, Abdulrahman, and Tracy Gardner. 2021. "Assessment of Sieverts Law Assumptions and ‘n’ Values in Palladium Membranes: Experimental and Theoretical Analyses" Membranes 11, no. 10: 778. https://doi.org/10.3390/membranes11100778
APA StyleAlraeesi, A., & Gardner, T. (2021). Assessment of Sieverts Law Assumptions and ‘n’ Values in Palladium Membranes: Experimental and Theoretical Analyses. Membranes, 11(10), 778. https://doi.org/10.3390/membranes11100778