The Acid–Base Flow Battery: Sustainable Energy Storage via Reversible Water Dissociation with Bipolar Membranes
Abstract
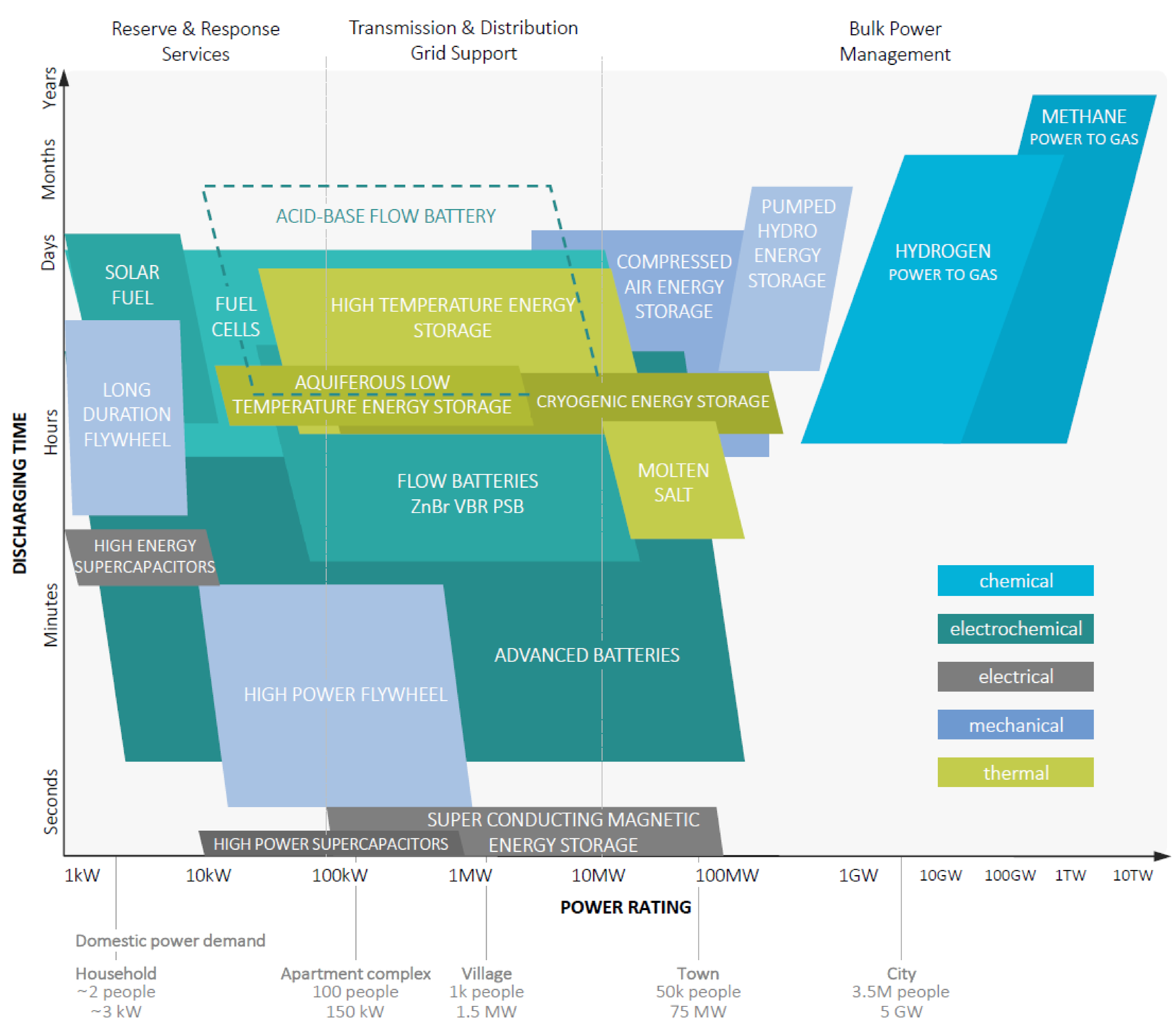
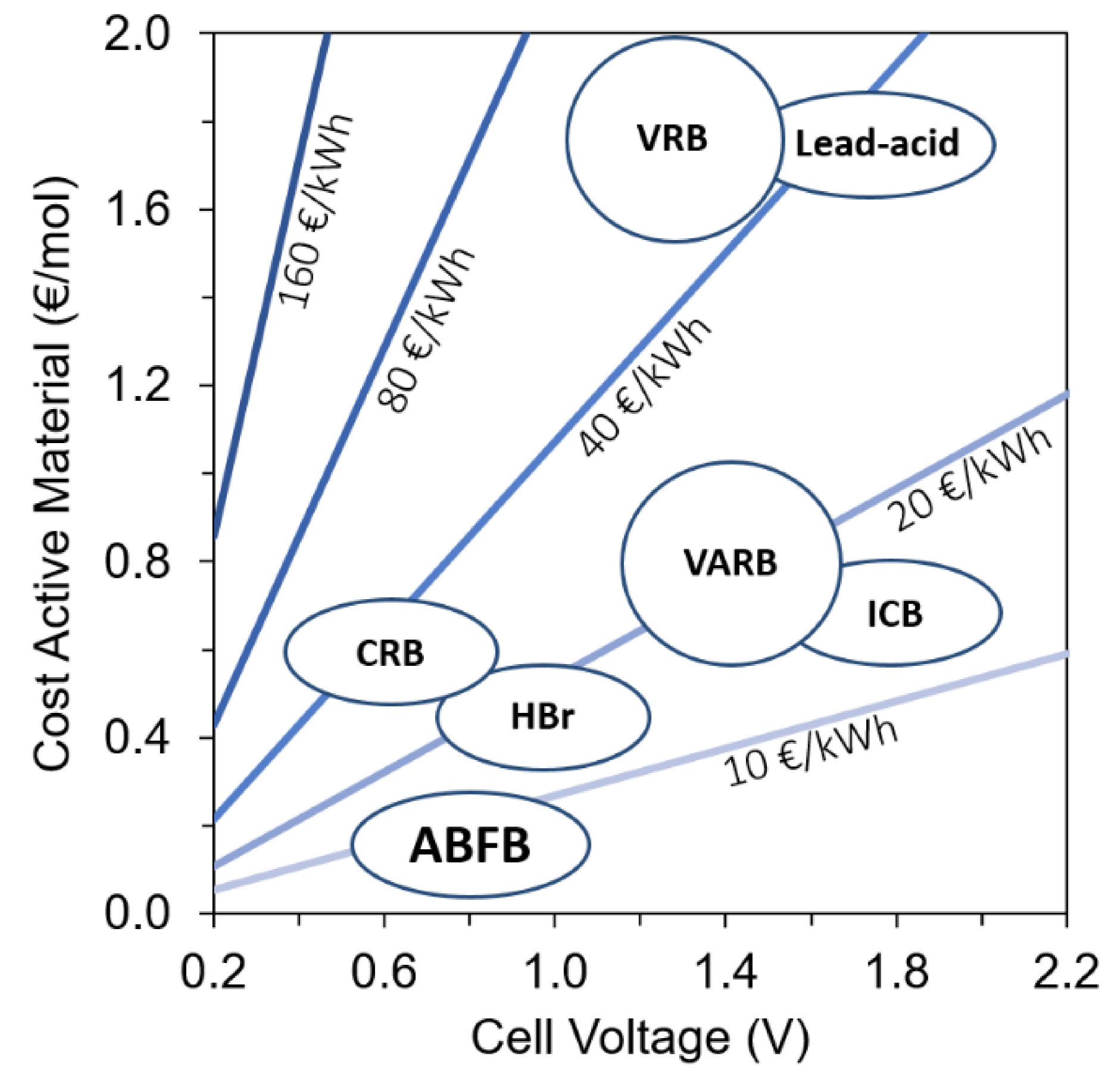
1. Introduction
Development, Principles, and State-of-the-Art of the Acid–Base Flow Battery
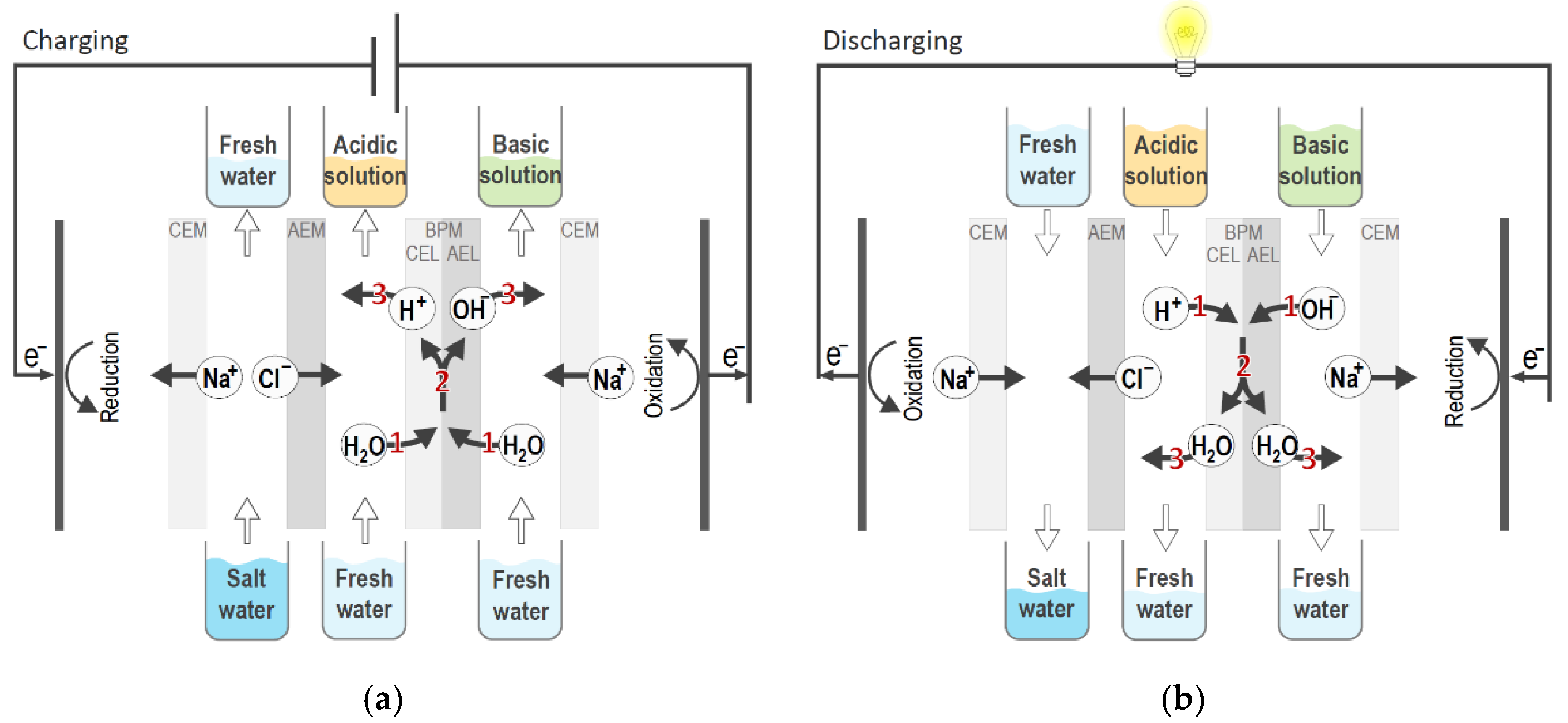
2. Battery Components and Design
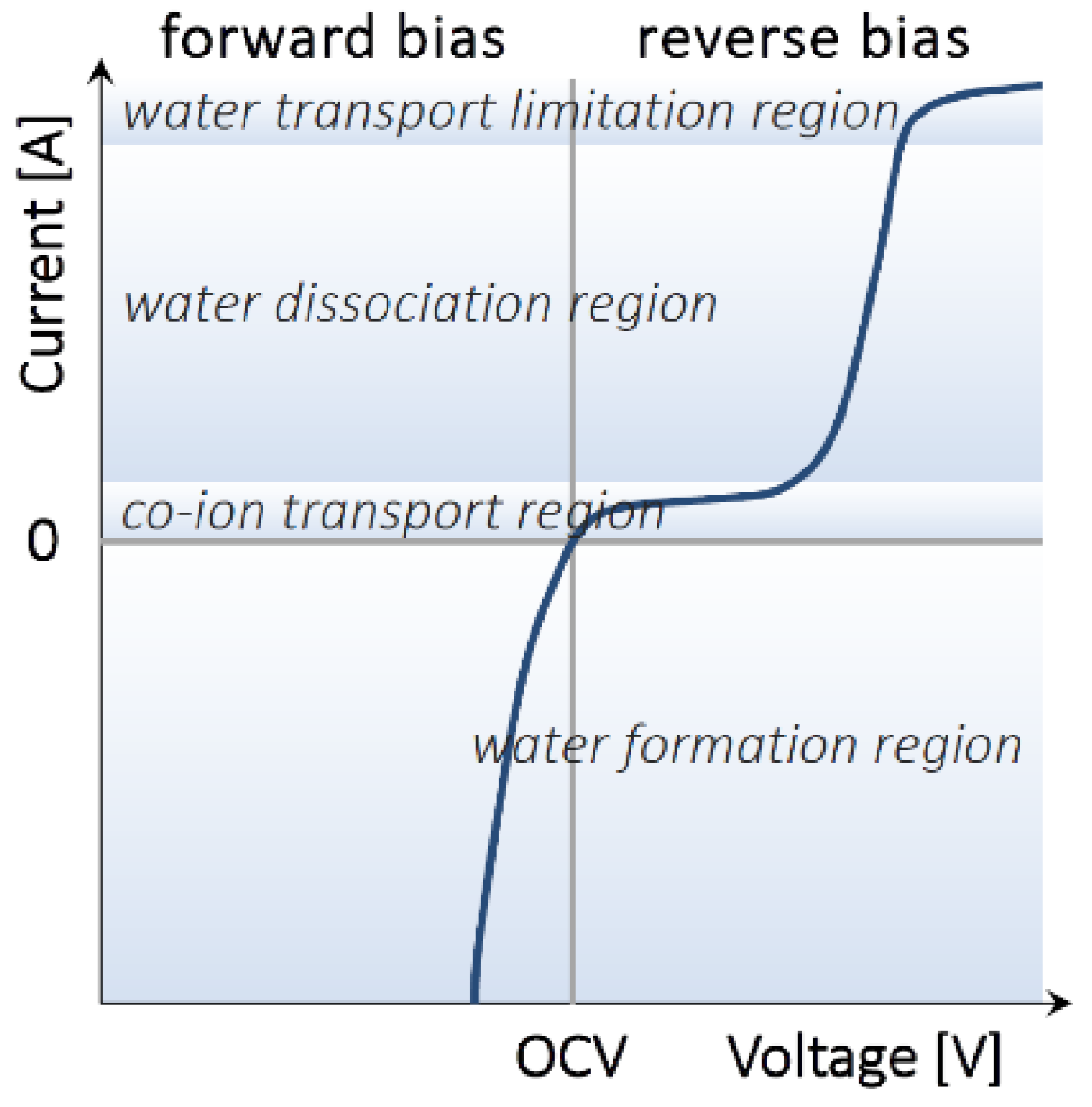
2.1. Bipolar and Monopolar Membranes
2.2. Battery Chemistry: Optimizing Electrolytes for Acid–Base Flow Batteries
2.3. Stack Design
3. Simulation of Upscaled Scenarios for Technology Demonstration at kW–MW Scale
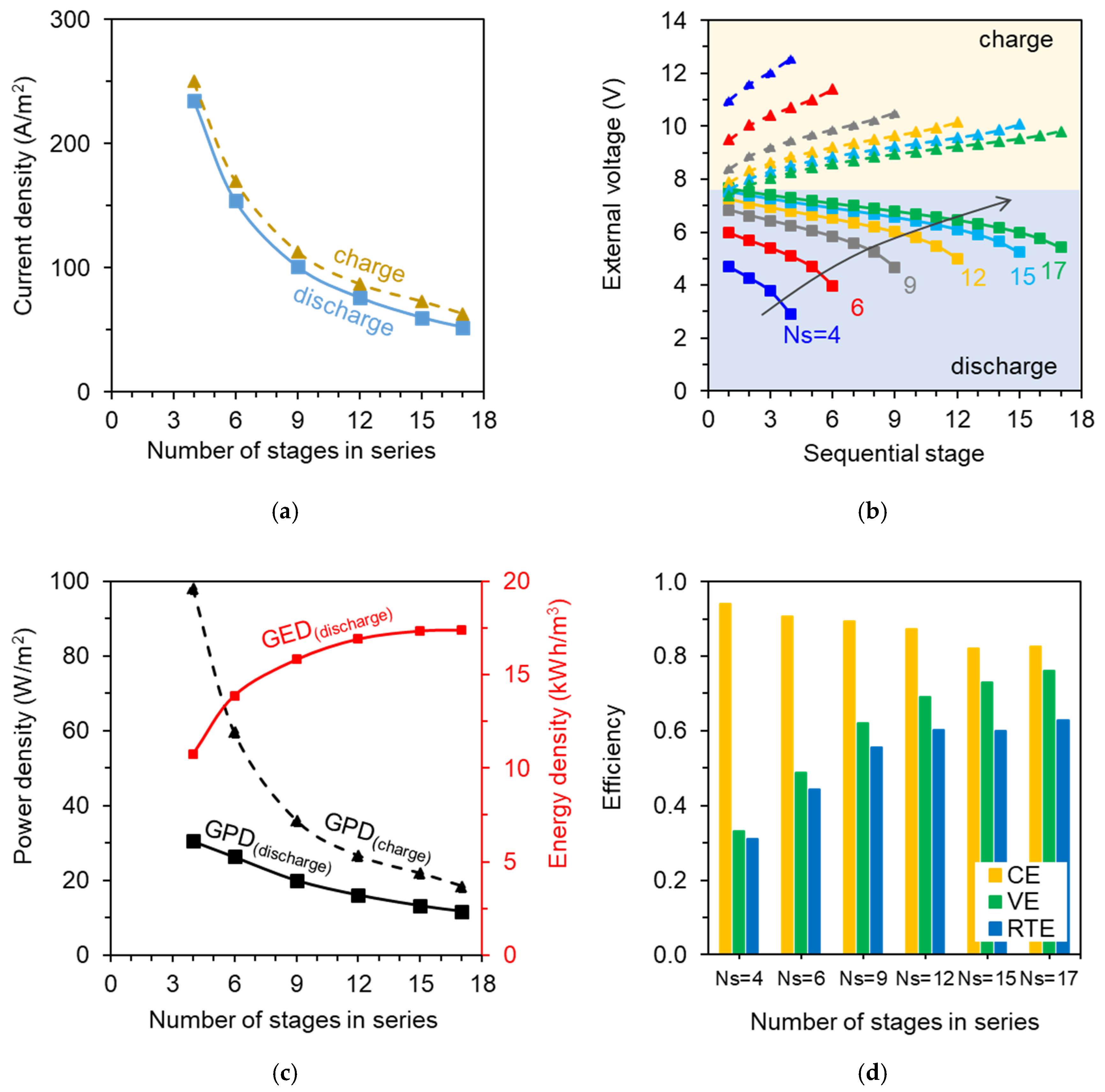
3.1. Performance of Upscaled Multi-Stage ABFB System as Function of the Number of Stages
4. Techno-Economic Assessment of First Pilot Plant and Technology Scale-Up
5. Outlook and Perspectives
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- International Energy Agency. Global Energy Review 2019: The Latest trends in Energy and Emissions in 2019. 2020. Available online: https://www.iea.org/reports/global-energy-review-2019 (accessed on 9 December 2020).
- International Hydropower Association. Pumped Storage Tracking Tool. 2019. Available online: https://www.hydropower.org/hydropower-pumped-storage-tool (accessed on 30 August 2020).
- International Renewable Energy Agency (IRENA). Renewable Energy Statistics 2020. 2020. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2020/Jul/IRENA_Renewable_Energy_Statistics_2020.pdf (accessed on 9 December 2020).
- International Renewable Energy Agency (IRENA). Renewable Energy Capacity Statistics 2020. 2020. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2020/Mar/IRENA_RE_Capacity_Statistics_2020.pdf (accessed on 9 December 2020).
- Hunt, J.D.; Byers, E.; Wada, Y.; Parkinson, S.; Gernaat, D.E.H.J.; Langan, S.; van Vuuren, D.P.; Riahi, K. Global resource potential of seasonal pumped hydropower storage for energy and water storage. Nat. Commun. 2020, 11, 947. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Q.; Wang, D.; Li, H.; Huang, Z.; Li, X.; Zhao, Y.; Dong, B.; Zhi, C. A rechargeable Al–N 2 battery for energy storage and highly efficient N 2 fixation. Energy Environ. Sci. 2020, 13, 2888–2895. [Google Scholar] [CrossRef]
- Comello, S.; Reichelstein, S. The emergence of cost effective battery storage. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef]
- Boruah, B.D.; Mathieson, A.; Wen, B.; Feldmann, S.; Dose, W.M.; De Volder, M. Photo-rechargeable zinc-ion batteries. Energy Environ. Sci. 2020, 13, 2414–2421. [Google Scholar] [CrossRef]
- International Renewable Energy Agency (IRENA). Electricity Storage and Renewables: Costs and Markets to 2030. 2017. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2017/Oct/IRENA_Electricity_Storage_Costs_2017.pdf (accessed on 9 December 2020).
- Waldman, J.; Sharma, S.; Afshari, S.; Fekete, B. Solar-power replacement as a solution for hydropower foregone in US dam removals. Nat. Sustain. 2019, 2, 872–878. [Google Scholar] [CrossRef]
- Albertus, P.; Manser, J.S.; Litzelman, S. Long-Duration Electricity Storage Applications, Economics, and Technologies. Joule 2020, 4, 21–32. [Google Scholar] [CrossRef]
- Van Egmond, W.J.; Saakes, M.; Porada, S.; Meuwissen, T.; Buisman, C.J.N.; Hamelers, H.V.M. The concentration gradient flow battery as electricity storage system: Technology potential and energy dissipation. J. Power Source 2016, 325, 129–139. [Google Scholar] [CrossRef]
- Bazinet, L.; Geoffroy, T.R. Electrodialytic Processes: Market Overview, Membrane Phenomena, Recent Developments and Sustainable Strategies. Membranes (Basel) 2020, 10, 221. [Google Scholar] [CrossRef]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G. Electrodialysis Applications in Wastewater Treatment for Environmental Protection and Resources Recovery: A Systematic Review on Progress and Perspectives. Membranes (Basel) 2020, 10, 146. [Google Scholar] [CrossRef]
- Jang, J.; Kang, Y.; Han, J.-H.; Jang, K.; Kim, C.-M.; Kim, I.S. Developments and future prospects of reverse electrodialysis for salinity gradient power generation: Influence of ion exchange membranes and electrodes. Desalination 2020, 491, 114540. [Google Scholar] [CrossRef]
- Pawlowski, S.; Huertas, R.M.; Galinha, C.F.; Crespo, J.G.; Velizarov, S. On operation of reverse electrodialysis (RED) and membrane capacitive deionisation (MCDI) with natural saline streams: A critical review. Desalination 2020, 476, 114183. [Google Scholar] [CrossRef]
- Pattle, R.E. Production of Electric Power by mixing Fresh and Salt Water in the Hydroelectric Pile. Nature 1954, 174, 660. [Google Scholar] [CrossRef]
- Kingsbury, R.S.; Chu, K.; Coronell, O. Energy storage by reversible electrodialysis: The concentration battery. J. Memb. Sci. 2015, 495, 502–516. [Google Scholar] [CrossRef]
- Aquabattery, B.V. Blue Battery Pilot Projects, Pilot I TheGreenVillage. 2018. Available online: http://aquabattery.nl/bluebatterypilotprojects/ (accessed on 29 October 2020).
- Walther, J.F. Process for Production of Electrical Energy from the Neutralization of Acid and Base in a Bipolar Membrane Cell, US4311771A. 1980. Available online: https://patents.google.com/patent/US4311771A/en (accessed on 9 December 2020).
- Frilette, V.J. Preparation and Characterization of Bipolar Ion Exchange Membranes. J. Phys. Chem. 1956, 60, 435–439. [Google Scholar] [CrossRef]
- Pärnamäe, R.; Mareev, S.; Nikonenko, V.; Melnikov, S.; Sheldeshov, N.; Zabolotskii, V.; Hamelers, H.V.M.; Tedesco, M. Bipolar membranes: A review on principles, latest developments, and applications. J. Memb. Sci. 2020, 617, 118538. [Google Scholar] [CrossRef]
- Sáez, A.; Montiel, V.; Aldaz, A. An Acid-Base Electrochemical Flow Battery as energy storage system. Int. J. Hydrogen Energy 2016, 41, 17801–17806. [Google Scholar] [CrossRef]
- van Egmond, W.J.; Saakes, M.; Noor, I.; Porada, S.; Buisman, C.J.N.; Hamelers, H.V.M. Performance of an environmentally benign acid base flow battery at high energy density. Int. J. Energy Res. 2018, 42, 1524–1535. [Google Scholar] [CrossRef]
- Emrén, A.T.; Holmström, V.J.M. Energy storage in a fuel cell with bipolar membranes burning acid and hydroxide. Energy 1983, 8, 277–282. [Google Scholar] [CrossRef]
- Pretz, J.; Staude, E. Reverse electrodialysis (RED) with bipolar membranes, an energy storage system. Ber. Bunsenges. Phys. Chem. 1998, 102, 676–685. [Google Scholar] [CrossRef]
- Zholkovskij, E.K.; Müller, M.C.; Staude, E. The storage battery with bipolar membranes. J. Memb. Sci. 1998, 141, 231–243. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, J.H.; Maurya, S.; Shin, S.H.; Lee, J.Y.; Chang, I.S.; Moon, S.H. Proof-of-concept experiments of an acid-base junction flow battery by reverse bipolar electrodialysis for an energy conversion system. Electrochem. Commun. 2016, 72, 157–161. [Google Scholar] [CrossRef]
- Xia, J.; Eigenberger, G.; Strathmann, H.; Nieken, U. Flow battery based on reverse electrodialysis with bipolar membranes: Single cell experiments. J. Memb. Sci. 2018, 565, 157–168. [Google Scholar] [CrossRef]
- Xia, J.; Eigenberger, G.; Strathmann, H.; Nieken, U. Acid-Base Flow Battery, Based on Reverse Electrodialysis with Bi-Polar Membranes: Stack Experiments. Processes 2020, 8, 99. [Google Scholar] [CrossRef]
- Veerman, J.; Post, J.W.; Saakes, M.; Metz, S.J.; Harmsen, G.J. Reducing power losses caused by ionic shortcut currents in reverse electrodialysis stacks by a validated model. J. Memb. Sci. 2008, 310, 418–430. [Google Scholar] [CrossRef]
- Tang, A.; McCann, J.; Bao, J.; Skyllas-Kazacos, M. Investigation of the effect of shunt current on battery efficiency and stack temperature in vanadium redox flow battery. J. Power Source 2013, 242, 349–356. [Google Scholar] [CrossRef]
- Culcasi, A.; Gurreri, L.; Zaffora, A.; Cosenza, A.; Tamburini, A.; Cipollina, A.; Micale, G. Ionic shortcut currents via manifolds in reverse electrodialysis stacks. Desalination 2020, 485, 114450. [Google Scholar] [CrossRef]
- Culcasi, A.; Gurreri, L.; Zaffora, A.; Cosenza, A.; Tamburini, A.; Micale, G. On the modelling of an Acid/Base Flow Battery: An innovative electrical energy storage device based on pH and salinity gradients. Appl. Energy 2020, 277, 115576. [Google Scholar] [CrossRef]
- Zaffora, A.; Culcasi, A.; Gurreri, L.; Cosenza, A.; Tamburini, A.; Santamaria, M.; Micale, G. Energy Harvesting by Waste Acid/Base Neutralization via Bipolar Membrane Reverse Electrodialysis. Energies 2020, 13, 5510. [Google Scholar] [CrossRef]
- Kishino, M.; Yuzuki, K.; Fukuta, K. Bipolar Membrane, EP3444295A1. 2017. Available online: https://patents.google.com/patent/EP3444295A1/en (accessed on 9 December 2020).
- Zabolotsky, V.; Utin, S.; Bespalov, A.; Strelkov, V. Modification of asymmetric bipolar membranes by functionalized hyperbranched polymers and their investigation during pH correction of diluted electrolytes solutions by electrodialysis. J. Memb. Sci. 2015, 494, 188–195. [Google Scholar] [CrossRef]
- Simons, R. Preparation of a high performance bipolar membrane. J. Memb. Sci. 1993, 78, 13–23. [Google Scholar] [CrossRef]
- McDonald, M.B.; Freund, M.S.; Hammond, P.T. Catalytic, Conductive Bipolar Membrane Interfaces through Layer-by-Layer Deposition for the Design of Membrane-Integrated Artificial Photosynthesis Systems. ChemSusChem 2017, 10, 4599–4609. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.S.; Choi, Y.J.; Lee, H.J.; Moon, S.H. Effects of inorganic substances on water splitting in ion-exchange membranes: I. Electrochemical characteristics of ion-exchange membranes coated with iron hydroxide/oxide and silica sol. J. Colloid Interface Sci. 2004, 273, 523–532. [Google Scholar] [CrossRef] [PubMed]
- Strathmann, H.; Krol, J.J.; Rapp, H.J.; Eigenberger, G. Limiting current density and water dissociation in bipolar membranes. J. Memb. Sci. 1997, 125, 123–142. [Google Scholar] [CrossRef]
- Blommaert, M.A.; Verdonk, J.A.H.; Blommaert, H.C.B.; Smith, W.A.; Vermaas, D.A. Reduced Ion Crossover in Bipolar Membrane Electrolysis via Increased Current Density, Molecular Size, and Valence. ACS Appl. Energy Mater. 2020, 3, 6. [Google Scholar] [CrossRef]
- Mikhaylin, S.; Bazinet, L. Fouling on ion-exchange membranes: Classi fi cation, characterization and strategies of prevention and control. Adv. Colloid Interface Sci. 2016, 229, 34–56. [Google Scholar] [CrossRef]
- Haddad, M.; Mikhaylin, S.; Bazinet, L.; Savadogo, O.; Paris, J. Electrochemical acidification of Kraft black liquor by electrodialysis with bipolar membrane: Ion exchange membrane fouling identification and mechanisms. J. Colloid Interface Sci. 2017, 488, 39–47. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Xu, T. Which is more competitive for production of organic acids, ion-exchange or electrodialysis with bipolar membranes? J. Memb. Sci. 2011, 374, 150–156. [Google Scholar] [CrossRef]
- Kim, S. Vanadium Redox Flow Batteries: Electrochemical Engineering. In Energy Storage Devices; Demirkan, M.T., Attia, A., Eds.; IntechOpen Limited: London, UK, 2019. [Google Scholar]
- Rubinstein, I.; Pretz, J.; Staude, E. Open circuit voltage in a reverse electrodialysis cell. Phys. Chem. Chem. Phys. 2001, 3, 1666–1667. [Google Scholar] [CrossRef]
- Trahey, L.; Brushett, F.R.; Balsara, N.P.; Ceder, G.; Cheng, L.; Chiang, Y.-M.; Hahn, N.T.; Ingram, B.J.; Minteer, S.D.; Moore, J.S.; et al. Energy storage emerging: A perspective from the Joint Center for Energy Storage Research. Proc. Natl. Acad. Sci. USA 2020, 117, 12550–12557. [Google Scholar] [CrossRef]
- Tanaka, Y. Chapter 7 Donnan Dialysis. In Ion Exchange Membranes: Fundamentals and Applications; Elsevier: Amsterdam, The Netherlands, 2007; pp. 495–503. [Google Scholar]
- Minke, C.; Kunz, U.; Turek, T. Techno-economic assessment of novel vanadium redox flow batteries with large-area cells. J. Power Source 2017, 361, 105–114. [Google Scholar] [CrossRef]
- Viswanathan, V.; Crawford, A.; Stephenson, D.; Kim, S.; Wang, W.; Li, B.; Coffey, G.; Thomsen, E.; Graff, G.; Balducci, P.; et al. Cost and performance model for redox flow batteries. J. Power Source 2014, 247, 1040–1051. [Google Scholar] [CrossRef]
- Noack, J.; Wietschel, L.; Roznyatovskaya, N.; Pinkwart, K.; Tübke, J. Techno-economic modeling and analysis of redox flow battery systems. Energies 2016, 9, 627. [Google Scholar] [CrossRef]
- Shen, C.; Wycisk, R.; Pintauro, P.N. High performance electrospun bipolar membrane with a 3D junction. Energy Environ. Sci. 2017, 10, 1435–1442. [Google Scholar] [CrossRef]
- Xergy Inc. XION™ Composite Bipolar Membranes. 2020. Available online: https://www.xergyincstore.com/product-category/xion-composite-bipolar-membranes/ (accessed on 19 October 2020).
- Weifang Senya Chemical, Ltd. The Bipolar (Anion/Cation) Exchange Membrane, (n.d.). Available online: http://ion-exchangemembrane.com/BipolarMembrane.html (accessed on 19 October 2020).
- Liu, B.; Zheng, M.; Sun, J.; Yu, Z. No-mixing design of vanadium redox flow battery for enhanced effective energy capacity. J. Energy Storage 2019, 23, 278–291. [Google Scholar] [CrossRef]

| Authors, Year (Source) | Battery Composition | Membranes | Charge/Discharge Conditions | Performance * |
|---|---|---|---|---|
| Emrén and Holmström, 1983 [26] | 7-triplet stack, copper electrodes. 0.85 M NaCl (all compartments) | Self-made BPM (modified polysulphones), CEM/AEM: not specified. Membrane active area: 7 cm2 | Charge: 1.4–56 A/m2 (for 2 h) Discharge: constant load | Voltage 1.8 V at 1.4 A/m2; EE 0.1% |
| Pretz and Staude, 1998 [27] | 20-triplet stack, platinized Ti electrodes. Electrolyte composition: 0.1, 0.5, or 1.0 M NaCl-HCl-NaOH | BPM: Stantech, or self-made by casting or gluing. CEM/AEM: self-made from polysulphones, Thomapor MC3470/MA3475, Tokuyama CMS/ACS | Only discharge: 0–50 A/m2 | Power density: 3.63 W/m2 (10.9 W/m2 triplet) with 0.5 M HCl-NaOH; EE 22% |
| Zholkovskij et al., 1998 [28] | 1-triplet stack + extra salt comp., platinized Ti electrodes. Batchwise operation (no flow). 0.03 M HCl-NaOH (acid/base comp.) | BPM: Stantech; CEM/AEM: Selemion CMV/AMV. Membrane active area: 28 cm2 | Charge: 3.57 A/m2 for 50 min, 35.7 A/m2 for 5 min, or 357 A/m2 for 0.5 min. Discharge: 0.4 mA/m2 for 30 h (slow discharge), 1.7 A/m2 for 10 min (fast discharge) | At slow discharge (30 h): specific capacity: 0.3 Ah/kg; energy density: 0.1 Wh/kg; max power density: 0.005 W/kg product. At fast discharge (10 min): specific capacity: 0.15 Ah/kg; energy density: 3 × 10−2 Wh/kg; max power density: 0.5 W/kg product. Efficiency: 45–61% |
| Kim et al., 2016 [29] | 1-triplet stack, carbon-felt electrodes. Electrolyte composition: 0.1 M NaCl, 0.1, 0.2, …, 0.6, or 0.7 M HCl-NaOH. Electrode rinse solution: 0.01 M FeSO4/Fe2(SO4)3, 0.01 M Na2SO4. | BPM: Tokuyama BP-1; CEM/AEM: Tokuyama CMS, CMX/AM-1 | 13 cycles with 0.5 M HCl-NaOH system at 2.9 A/m2. Cycle voltage range: 1.25–0.40 V. | Max power density 2.9 W/m2 (11.6 W/m2 per single-cell stack) with 0.6 M HCl-NaOH. Cyclability tests with 0.5 M HCl-NaOH: CE 98.3%, VE 76.0%, EE 77.3% from 2nd to 9th cycle on average. Average charge capacity 1.12 Ah/L, average discharge capacity 1.11 Ah/L. Rapid decline in charge/discharge capacities after 9th cycle. |
| Van Egmond et al., 2018 [25] | 1-triplet stack, Ir/Ru-coated Ti electrodes. Electrolyte composition: 0.214 M NaCl (salt comp.), 1 M HCl + 0.5 M NaCl (acid comp.), 1 M NaOH + 0.5 M NaCl (base comp.). Electrode rinse solution: 0.5 M Na2SO4. | BPM: Fumasep FBM. CEM: Nafion N117. AEM: Fumasep FAB-PK-30 (proton blocking). Membrane active area: 100 cm2. | 9 charge/discharge cycles. Voltage range: 0–0.83 V. Charge: 50–150 A/m2; discharge: 5–15 A/m2. Discharge time: 7 h at 5 A/m2, and 5 h at 15 A/m2 | Power density up to 3.7 W/m2. Energy density 2.9 Wh/L |
| Xia et al., 2018 [30] | 1-triplet stack + extra salt comp., platinized Ti mesh electrodes. Electrolyte composition: 0.5 M NaCl (salt comp), 0.25, 0.5, 0.75, or 1.0 M HCl-NaOH (acid/base comp.). Electrode rinse solution: 0.25 M Na2SO4. | BPM: Fumasep FBM; CEM/AEM: Fumasep FKB/FAB. Membrane active area: 25 cm2. | 20 cycles with 0.75 M HCl-NaOH system at 400 A/m2 charge/discharge; 20 min charge, 20 min discharge per cycle | OCV 0.775 V; mean voltage over the BPM: 0.87 V at charge, 0.63 V at discharge (BPM VE 72%) |
| Xia et al., 2020 [31] | 20-triplet stack. Electrolyte composition: 0.5 M NaCl (salt comp), 0.5 or 1.0 M HCl-NaOH (acid/base comp). Electrode rinse solution: 0.25 M Na2SO4 | BPM: Fumasep FBM; CEM/AEM: Fumasep FKB/FAB. Membrane active area: 100 cm2. | 90 A/m2 charge and discharge, both 5 min. | ~15 W/m2 excluding electrode losses, for 20- triplet stack with 1 M HCl-NaOH at 100 A/m2. |
| Zaffora et al., 2020 [36] | 5–38-triplet stack. Ti/mixed-metal oxide electrodes. Electrolyte composition: 0.25 M NaCl (salt comp.), 0.2, 0.6 or 1.0 M HCl-NaOH (acid/base comp). Electrode rinse solution: 0.25 M Na2SO4 or 0.5 M FaCl2/FeCl3. | BPM: Fumasep FBM; CEM/AEM: Fumasep FKB/FAB. Membrane active area: 100 cm2. | Only discharge with single pass, up to 100 A/m2. | ~17 W/m2 for 10-triplet stack with 1 M HCl-NaOH at 100 A/m2. Estimated energy density of 10.3 kWh/m3 acid for complete discharge. |
| Geometrical Parameters of the Stack | ||||
|---|---|---|---|---|
| Units | Value | |||
| Spacer length, L | cm | 50 | ||
| Spacer width, b | cm | 50 | ||
| Spacer thickness | μm | 475 | ||
| Membrane Properties | ||||
| Units | AEM | CEM | BPM | |
| Thickness | µm | 130 | 130 | 190 |
| Areal resistance | Ω cm2 | 4.0 | 3.5 | 5.0 |
| H+ diffusivity a | m2/s | 2.0 × 10−11 | 0.7 × 10−11 | - |
| Na+ diffusivity | m2/s | 1.6 × 10−11 | 0.5 × 10−11 | - |
| Cl− diffusivity | m2/s | 1.7 × 10−11 | 0.6 × 10−11 | - |
| OH− diffusivity | m2/s | 1.9 × 10−11 | 0.6 × 10−11 | - |
| Fixed charge density | mol/m3 | 5000 | 5000 | - |
| Feed Conditions in the First Stage | ||||
| Feed Composition | Units | Charge phase (0% SOC) | Discharge (100% SOC) | |
| HCl in acid compartment | mol/m3 | 50 | 1000 | |
| NaCl in acid compartment | mol/m3 | 250 | ||
| HCl in salt solution compartment | mol/m3 | 10 | ||
| NaCl in salt solution compartment | mol/m3 | 1000 | ||
| NaOH in base compartment | mol/m3 | 50 | ||
| NaCl in base compartment | mol/m3 | 250 | ||
| Fluid flow velocity | cm/s | 1.0 | 1.0 | |
| Electrode Compartments and Triplets | ||||
| Units | Value | |||
| Blank resistance b | Ω cm2 | 12 | ||
| Number of triplets (repeating units) per stack, N | - | 10 | ||
| Quantity | Units | Value |
|---|---|---|
| Average external voltage in charge 1 | V | 6.7 |
| Average external voltage in discharge 1 | V | 4.3 |
| Average Gross Power Density in charge | W/m2 | 32.0 |
| Average Gross Power Density in discharge | W/m2 | 20.6 |
| Gross Energy Density in discharge | kWh/m3acid | 18.0 |
| Current Efficiency | - | 86.8% |
| Voltage Efficiency | - | 64.4% |
| Round Trip Efficiency | - | 55.9% |
| CAPEX (Materials) | Demonstration Pilot (2020) 1 kW/7 kWh | FOAK Commercial Unit (2025) 100 kW/700 kWh | ||
|---|---|---|---|---|
| Power subsystem (membrane, spacers, electrodes) | €85,000 | €85,000/kW | €152,000 | €1520/kW |
| Energy subsystem (storage tanks, electrolyte) | €13,000 | €1900/kWh | €35,000 | €50/kWh |
| Periphery (battery management systems, sensors) | €39,000 | €39,000/unit | €22,000 | €22,000/unit |
| System (total) | €137,000 | €19,600/kWh | €328,000 | €470/kWh |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pärnamäe, R.; Gurreri, L.; Post, J.; van Egmond, W.J.; Culcasi, A.; Saakes, M.; Cen, J.; Goosen, E.; Tamburini, A.; Vermaas, D.A.; et al. The Acid–Base Flow Battery: Sustainable Energy Storage via Reversible Water Dissociation with Bipolar Membranes. Membranes 2020, 10, 409. https://doi.org/10.3390/membranes10120409
Pärnamäe R, Gurreri L, Post J, van Egmond WJ, Culcasi A, Saakes M, Cen J, Goosen E, Tamburini A, Vermaas DA, et al. The Acid–Base Flow Battery: Sustainable Energy Storage via Reversible Water Dissociation with Bipolar Membranes. Membranes. 2020; 10(12):409. https://doi.org/10.3390/membranes10120409
Chicago/Turabian StylePärnamäe, Ragne, Luigi Gurreri, Jan Post, Willem Johannes van Egmond, Andrea Culcasi, Michel Saakes, Jiajun Cen, Emil Goosen, Alessandro Tamburini, David A. Vermaas, and et al. 2020. "The Acid–Base Flow Battery: Sustainable Energy Storage via Reversible Water Dissociation with Bipolar Membranes" Membranes 10, no. 12: 409. https://doi.org/10.3390/membranes10120409
APA StylePärnamäe, R., Gurreri, L., Post, J., van Egmond, W. J., Culcasi, A., Saakes, M., Cen, J., Goosen, E., Tamburini, A., Vermaas, D. A., & Tedesco, M. (2020). The Acid–Base Flow Battery: Sustainable Energy Storage via Reversible Water Dissociation with Bipolar Membranes. Membranes, 10(12), 409. https://doi.org/10.3390/membranes10120409







