A DFT Study on the Kinetics of HOO•, CH3OO•, and O2•− Scavenging by Quercetin and Flavonoid Catecholic Metabolites
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
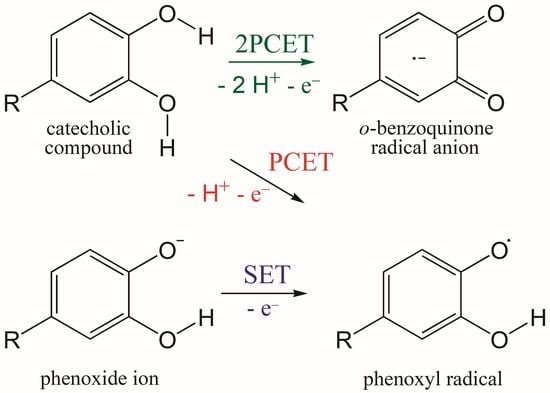
3.1. PCET from OH Groups and SET from Phenoxide Anions of Q to HOO• and CH3OO• Radicals
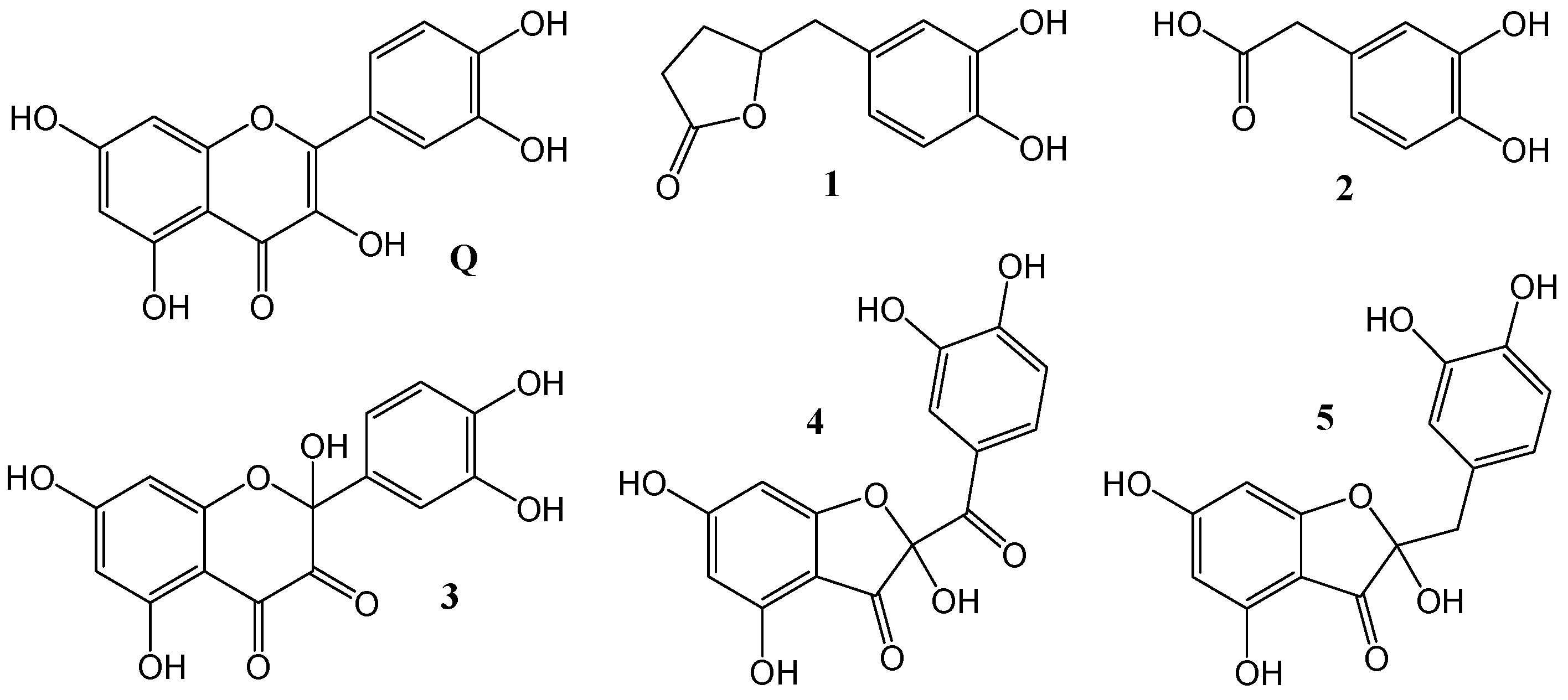
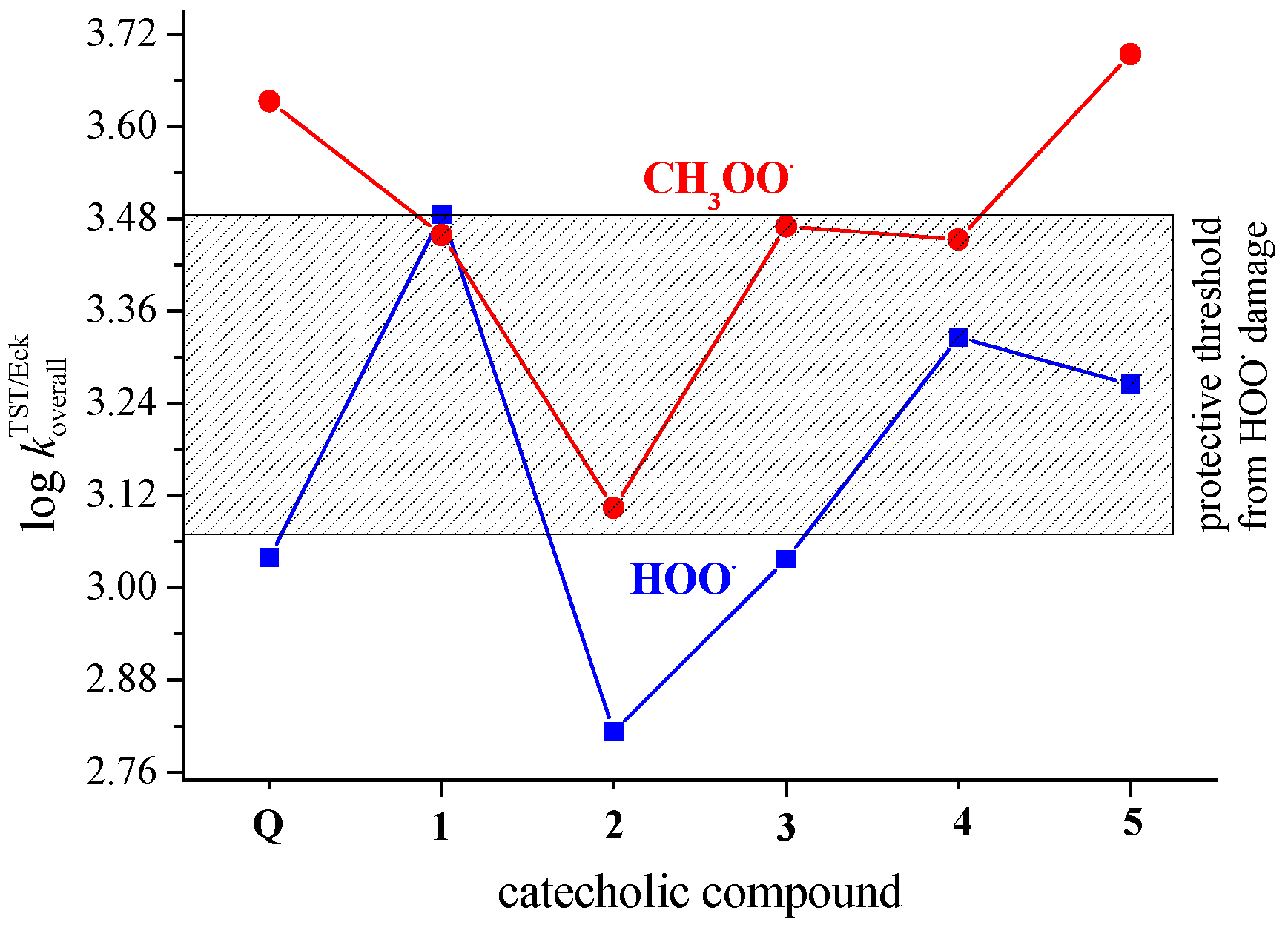
3.2. PCET from OH Groups of Q and 1–5 to HOO• and CH3OO• Radicals in Non-Polar Media
3.3. SET from Phenoxide Anions of Q and 1–5 to HOO• and CH3OO• Radicals in Polar Media
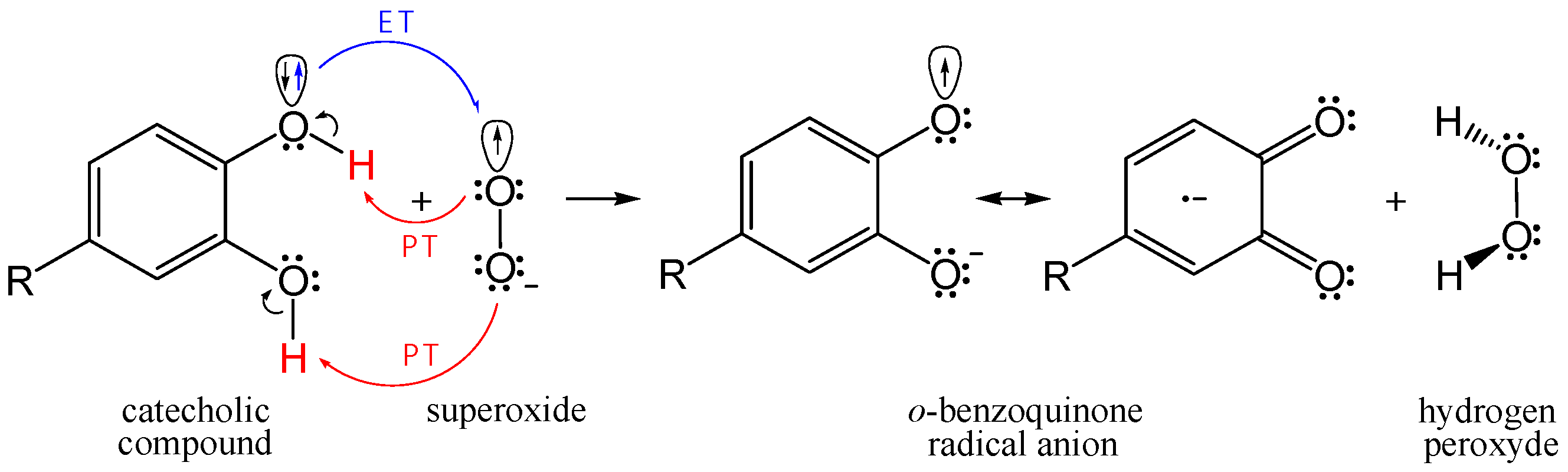
3.4. Concerted Two-Proton–Coupled Electron Transfer from Catechol Moiety of Q and 1–5 to O2•−
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carregosa, D.; Carecho, R.; Figueira, I.; Santos, C.N. Low-molecular weight metabolites from polyphenols as effectors for attenuating neuroinflammation. J. Agric. Food. Chem. 2020, 68, 1790–1807. [Google Scholar] [CrossRef] [PubMed]
- Finkel, T.; Holbrook, N.J. Oxidants, oxidative stress and the biology of ageing. Nature 2000, 408, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Galleano, M.; Verstraeten, S.V.; Oteiza, P.I.; Fraga, C.G. Antioxidant actions of flavonoids: Thermodynamic and kinetic analysis. Arch. Biochem. Biophys. 2010, 501, 23–30. [Google Scholar] [CrossRef] [PubMed]
- González-Sarrías, A.; Espin, J.C.; Tomás-Barberán, F.A. Non-extractable polyphenols produce gut microbiota metabolites that persist in circulation and show anti-inflammatory and free radical-scavenging effects. Trends Food Sci. Technol. 2017, 69, 281–288. [Google Scholar] [CrossRef]
- Dangles, O.; Dufour, C.; Tonnele, C.; Trouillas, P. The physical chemistry of polyphenols: Insights into the activity of polyphenols in humans at the molecular level. In Recent Advances in Polyphenol Research; Yoshida, K., Cheynier, V., Quiedau, S., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 1–35. [Google Scholar]
- Forman, H.J.; Davies, K.J.A.; Ursini, F. How do nutritional antioxidants really work: Nucleophilic tone and para-hormesis versus free radical scavenging in vivo. Free Radic. Biol. Med. 2014, 66, 24–35. [Google Scholar] [CrossRef]
- Hollman, P.C.H. Unravelling of the health effects of polyphenols is a complex puzzle complicated by metabolism. Arch. Biochem. Biophys. 2014, 559, 100–105. [Google Scholar] [CrossRef]
- Halliwell, B.; Gutteridge, J.M.C. Free Radicals in Biology and Medicine, 5th ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Bors, W.; Heller, W.; Michel, C.; Saran, M. Flavonoids as antioxidants: Determination of radical-scavenging efficiencies. In Methods in Enzymology; Packer, L., Glazer, A.N., Eds.; Academic Press: San Diego, CA, USA, 1990; pp. 343–355. [Google Scholar]
- Rice-Evans, C.A.; Miller, N.J.; Paganga, G. Structure–antioxidant activity relationships of flavonoids and phenolic acids. Free Radic. Biol. Med. 1996, 20, 933–956. [Google Scholar] [CrossRef]
- Amić, A.; Lučić, B.; Stepanić, V.; Marković, Z.; Marković, S.; Dimitrić Marković, J.M.; Amić, D. Free radical scavenging potency of quercetin catecholic colonic metabolites: Thermodynamics of 2H+/2e− processes. Food Chem. 2017, 218, 144–151. [Google Scholar] [CrossRef]
- Lambert, J.D.; Sang, S.; Yang, C.S. Biotransformation of green tea polyphenols and the biological activities of those metabolites. Mol. Pharm. 2007, 4, 819–825. [Google Scholar] [CrossRef]
- Yang, C.S.; Chen, L.; Lee, M.-J.; Balentine, D.; Kuo, M.C.; Schantz, S.P. Blood and urine levels of tea catechins after ingestion of different amounts of green tea by human volunteers. Cancer Epidemiol. Biomarkers Prev. 1998, 7, 351–354. [Google Scholar]
- Pietta, P.G.; Simonetti, P.; Gardana, C.; Brusamolino, A.; Morazzoni, P.; Bombardelli, E. Catechin metabolites after intake of green tea infusions. BioFactors 1998, 8, 111–118. [Google Scholar] [CrossRef]
- Liu, C.; Vervoort, J.; Beekmann, K.; Baccaro, M.; Kamelia, L.; Wesseling, S.; Rietjens, I.M.C.M. Interindividual differences in human intestinal microbial conversion of (−)-epicatechin to bioactive phenolic compounds. J. Agric. Food Chem. 2020, 68, 14168–14181. [Google Scholar] [CrossRef]
- Appeldoorn, M.M.; Vincken, J.-P.; Aura, A.-M.; Hollman, P.C.H.; Gruppen, H. Procyanidin dimers are metabolized by human microbiota with 2-(3,4-dihydroxyphenyl)acetic acid and 5-(3,4-dihydroxyphenyl)-γ-valerolactone as the major metabolites. J. Agric. Food Chem. 2009, 57, 1084–1092. [Google Scholar] [CrossRef]
- Rodriguez-Mateos, A.; Vauzour, D.; Krueger, C.G.; Shanmuganayagam, D.; Reed, J.; Calani, L.; Mena, P.; Del Rio, D.; Crozier, A. Bioavailability, bioactivity and impact on health of dietary flavonoids and related compounds: An update. Arch. Toxicol. 2014, 88, 1803–1853. [Google Scholar] [CrossRef]
- Halliwell, B.; Rafter, J.; Jenner, A. Health promotion by flavonoids, tocopherols, tocotrienols, and other phenols: Direct or indirect effects? Antioxidant or not? Am. J. Clin. Nutr. 2005, 81, 268S–276S. [Google Scholar] [CrossRef]
- Fraga, C.G.; Galleano, M.; Verstraeten, S.V.; Oteiza, P.I. Basic biochemical mechanisms behind the health benefits of polyphenols. Mol. Aspects Med. 2010, 31, 435–445. [Google Scholar] [CrossRef]
- Mena, P.; Del Rio, D. Gold standards for realistic (poly)phenol research. J. Agric. Food Chem. 2018, 66, 8221–8223. [Google Scholar] [CrossRef]
- Amorati, R.; Baschieri, A.; Cowden, A.; Valgimigli, L. The antioxidant activity of quercetin in water solution. Biomimetics 2017, 2, 9. [Google Scholar] [CrossRef]
- Guo, Y.; Bruno, R.S. Endogenous and exogenous mediators of quercetin bioavailability. J. Nutr. Biochem. 2015, 26, 201–210. [Google Scholar] [CrossRef]
- Tang, S.-M.; Deng, X.-T.; Zhou, J.; Li, Q.-P.; Ge, X.X.; Miao, L. Pharmacological basis and new insights of quercetin action in respect to its anti-cancer effects. Biomed. Pharmacother. 2020, 121, 109604. [Google Scholar] [CrossRef]
- Ulusoy, H.G.; Sanlier, N. A minireview of quercetin: From its metabolism to possible mechanisms of its biological activities. Crit. Rev. Food Sci. Nutr. 2020, 60, 3290–3303. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, L.V.; Cornett, C.; Justesen, U.; Skibsted, L.H.; Dragsted, L.O. Two-electron electrochemical oxidation of quercetin and kaempferol changes only the flavonoid C-ring. Free Rad. Res. 1998, 29, 339–350. [Google Scholar] [CrossRef] [PubMed]
- Krishnamachari, V.; Levine, L.H.; Pare, P.W. Flavonoid oxidation by the radical generator AIBN: A unified mechanism for quercetin radical scavenging. J. Agric. Food Chem. 2002, 50, 4357–4363. [Google Scholar] [CrossRef] [PubMed]
- Ly, T.N.; Hazama, C.; Shimoyamada, M.; Ando, H.; Kato, K.; Yamauchi, R. Antioxidative compounds from the outer scales of onion. J. Agric. Food Chem. 2005, 53, 8183–8189. [Google Scholar] [CrossRef] [PubMed]
- Braune, A.; Gütschow, M.; Engst, W.; Blaut, M. Degradation of quercetin and luteolin by Eubacterium ramulus. Appl. Environ. Microbiol. 2001, 67, 5558–5567. [Google Scholar] [CrossRef] [PubMed]
- Gülşen, A.; Turan, B.; Makris, D.P.; Kefalas, P. Copper(II)-mediated biomimetic oxidation of quercetin: Generation of a naturally occurring oxidation product and evaluation of its in vitro antioxidant properties. Eur. Food Res. Technol. 2007, 225, 435–441. [Google Scholar] [CrossRef]
- Fuentes, J.; Atala, E.; Pastene, E.; Carrasco-Pozo, C.; Speisky, H. Quercetin oxidation paradoxically enhances its antioxidant and cytoprotective properties. J. Agric. Food Chem. 2017, 65, 11002–11010. [Google Scholar] [CrossRef]
- Kim, T.H.; Lee, J.; Kim, H.-J.; Jo, C. Plasma-induced degradation of quercetin associated with the enhancement of biological activities. J. Agric. Food Chem. 2017, 65, 6929–6935. [Google Scholar] [CrossRef]
- Vasquez-Espinal, A.; Yanez, O.; Osorio, E.; Areche, C.; Garcia-Beltran, O.; Ruiz, L.M.; Cassels, B.K.; Tiznado, W. Theoretical study of the antioxidant activity of quercetin oxidation products. Front. Chem. 2019, 7, 818. [Google Scholar] [CrossRef]
- Fuentes, J.; Arias-Sante, M.F.; Atala, E.; Pastene, E.; Kogan, M.J.; Speisky, H. Low nanomolar concentrations of a quercetin oxidation product, which naturally occurs in onion peel, protect cells against oxidative damage. Food Chem. 2020, 314, 126166. [Google Scholar] [CrossRef]
- Milanović, Ž.B.; Antonijević, M.R.; Amić, A.D.; Avdović, E.H.; Dimić, D.S.; Milenković, D.A.; Marković, Z.S. Inhibitory activity of quercetin, its metabolite, and standard antiviral drugs towards enzymes essential for SARS-CoV-2: The role of acid–base equilibria. RSC Adv. 2021, 11, 2838–2847. [Google Scholar] [CrossRef]
- Hayyan, M.; Hashim, M.A.; AlNashef, I.M. Superoxide ion: Generation and chemical implications. Chem. Rev. 2016, 116, 3029–3085. [Google Scholar] [CrossRef]
- Bielski, B.H.J.; Arudi, R.L.; Sutherland, M.W. A study of the reactivity of HO2/O2− with unsaturated fatty acids. J. Biol. Chem. 1983, 258, 4759–4761. [Google Scholar] [CrossRef]
- Prasad, A.K.; Mishra, P.C. Mechanism of action of sulforaphane as a superoxide radical anion and hydrogen peroxide scavenger by double hydrogen transfer: A model for iron superoxide dismutase. J. Phys. Chem. B 2015, 19, 7825–7836. [Google Scholar] [CrossRef]
- Hool, L.C. Reactive oxygen species in cardiac signalling: From mitochondria to plasma membrane ion channels. Clin. Exp. Pharmacol. Physiol. 2006, 33, 146–151. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Galano, A.; Alvarez-Idaboy, J.R. A computational methodology for accurate predictions of rate constants in solution: Application to the assessment of primary antioxidant activity. J. Comput. Chem. 2013, 34, 2430–2445. [Google Scholar] [CrossRef]
- Chiodo, S.G.; Leopoldini, M.; Russo, N.; Toscano, M. The inactivation of lipid peroxide radical by quercetin. A theoretical insight. Phys. Chem. Chem. Phys. 2010, 12, 7662–7670. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Galano, A.; Mazzone, G.; Alvarez-Diduk, R.; Marino, T.; Alvarez-Idaboy, J.R.; Russo, N. Food antioxidants: Chemical insights at the molecular level. Annu. Rev. Food Sci. Technol. 2016, 7, 335–352. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Hase, W.L.; Hynes, J.T. Current status of transition-state theory. J. Phys. Chem. 1983, 87, 2664–2682. [Google Scholar] [CrossRef]
- Dzib, E.; Cabellos, J.L.; Ortiz-Chi, F.; Pan, S.; Galano, A.; Merino, G. Eyringpy: A program for computing rate constants in the gas phase and in solution. Int. J. Quantum Chem. 2019, 119, e25686. [Google Scholar] [CrossRef]
- Eckart, C. The penetration of a potential barrier by electrons. Phys. Rev. 1930, 35, 1303–1309. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron transfer reactions in chemistry. Theory and experiment. Pure Appl. Chem. 1997, 69, 13–29. [Google Scholar] [CrossRef]
- Martinez, A.; Hernandez-Marin, E.; Galano, A. Xanthones as antioxidants: A theoretical study on the thermodynamics and kinetics of the single electron transfer mechanism. Food Funct. 2012, 3, 442–450. [Google Scholar] [CrossRef]
- Collins, F.C.; Kimball, G.E. Diffusion-controlled reaction rates. J. Colloid Sci. 1949, 4, 425–437. [Google Scholar] [CrossRef]
- Smoluchowski, M. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. Phys. Chem. 1917, 92, 129–168. [Google Scholar] [CrossRef]
- Amić, A.; Mastiľák Cagardová, D. DFT Study of the direct radical scavenging potency of two natural catecholic compounds. Int. J. Mol. Sci. 2022, 23, 14497. [Google Scholar] [CrossRef]
- Jovanovic, S.V.; Steenken, S.; Hara, Y.; Simic, M.G. Reduction potentials of flavonoid and model phenoxyl radicals. Which ring in flavonoids is responsible for antioxidant activity? J. Chem. Soc. Perkin Trans. 1996, 2, 2497–2504. [Google Scholar] [CrossRef]
- Li, Z.; Moalin, M.; Zhang, M.; Vervoort, L.; Mommers, A.; Haenen, G.R.M.M. Delocalization of the unpaired electron in the quercetin radical: Comparison of experimental ESR data with DFT calculations. Int. J. Mol. Sci. 2020, 21, 2033. [Google Scholar] [CrossRef]
- Ingold, K.U.; Pratt, D.A. Advances in radical-trapping antioxidant chemistry in the 21st century: A kinetics and mechanisms perspective. Chem. Rev. 2014, 114, 9022–9046. [Google Scholar] [CrossRef]
- Alvarez-Idaboy, J.R.; Mora-Diez, N.; Boyd, R.J.; Vivier-Bunge, A. On the importance of prereactive complexes in molecule–radical reactions: Hydrogen abstraction from aldehydes by OH. J. Am. Chem. Soc. 2001, 123, 2018–2024. [Google Scholar] [CrossRef]
- Litwinienko, G.; Ingold, K.U. Abnormal solvent effects on hydrogen atom abstractions. 1. The reactions of phenols with 2,2-diphenyl-1-picrylhydrazyl (dpph•) in alcohols. J. Org. Chem. 2003, 68, 3433–3438. [Google Scholar] [CrossRef]
- Foti, M.C.; Daquino, C.; Geraci, C. Electron-transfer reaction of cinnamic acids and their methyl esters with the DPPH• radical in alcoholic solutions. J. Org. Chem. 2004, 69, 2309–2314. [Google Scholar] [CrossRef]
- Kim, D.-O.; Lee, C.Y. Comprehensive study on vitamin C equivalent antioxidant capacity (VCEAC) of various polyphenolics in scavenging a free radical and its structural relationship. Crit. Rev. Food Sci. Nutr. 2004, 44, 253–273. [Google Scholar] [CrossRef]
- Cai, Y.-Z.; Sun, M.; Xing, J.; Luo, Q.; Corke, H. Structure–radical scavenging activity relationships of phenolic compounds from traditional Chinese medicinal plants. Life Sci. 2006, 78, 2872–2888. [Google Scholar] [CrossRef]
- Galano, A. Free radicals induced oxidative stress at a molecular level: The current status, challenges and perspectives of computational chemistry based protocols. J. Mex. Chem. Soc. 2015, 59, 231–262. [Google Scholar] [CrossRef]
- Villuendas-Rey, Y.; Alvarez-Idaboy, J.R.; Galano, A. Assessing the protective activity of a recently discovered phenolic compound against oxidative stress using computational chemistry. J. Chem. Inf. Model. 2015, 55, 2552–2561. [Google Scholar] [CrossRef]
- Galano, A.; Alvarez-Idaboy, J.R. Computational strategies for predicting free radical scavengers’ protection against oxidative stress: Where are we and what might follow? Int. J. Quantum Chem. 2019, 119, e25665. [Google Scholar] [CrossRef]
- Pérez-González, A.; Alvarez-Idaboy, J.R.; Galano, A. Dual antioxidant/pro-oxidant behavior of the tryptophan metabolite 3-hydroxyanthranilic acid: A theoretical investigation of reaction mechanisms and kinetics. New J. Chem. 2017, 41, 3829–3845. [Google Scholar] [CrossRef]
- Alvarez-Diduk, R.; Ramirez-Silva, M.T.; Galano, A.; Merkoci, A. Deprotonation mechanism and acidity constants in aqueous solution of flavonols: A combined experimental and theoretical study. J. Phys. Chem. B 2013, 117, 12347–12359. [Google Scholar] [CrossRef] [PubMed]
- Borges, F.; Guimaraes, C.; Lima, J.L.F.C.; Pinto, I.; Reis, S. Potentiometric studies on the complexation of copper(II) by phenolic acids as discrete ligand models of humic substances. Talanta 2005, 66, 670–673. [Google Scholar] [CrossRef] [PubMed]
- ACD/Percepta. ACD/Labs Release 2020.2.0. Available online: https://www.acdlabs.com/products/percepta/predictors/pka/ (accessed on 4 September 2022).
- Unno, T.; Tamemoto, K.; Yayabe, F.; Kakuda, T. Urinary excretion of 5-(3′,4′-dihydroxyphenyl)-γ-valerolactone, a ring-fission metabolite of (-)-epicatechin, in rats and its in vitro antioxidant activity. J. Agric. Food Chem. 2003, 51, 6893–6898. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Sharma, S.; Khanna, M.; Raj, H.G. Effect of Quercetin on lipid peroxidation and changes in lung morphology in experimental influenza virus infection. Int. J. Exp. Path. 2003, 84, 127–133. [Google Scholar] [CrossRef]
- Sroka, Z.; Cisowski, W. Hydrogen peroxide scavenging, antioxidant and anti-radical activity of some phenolic acids. Food Chem. Toxicol. 2003, 41, 753–758. [Google Scholar] [CrossRef]
- Raneva, V.; Shimasaki, H.; Ishida, Y.; Ueta, N.; Niki, E. Antioxidative activity of 3,4-dihydroxyphenylacetic acid and caffeic acid in rat plasma. Lipids 2001, 36, 1111–1116. [Google Scholar] [CrossRef]
- Carrasco-Pozo, C.; Gotteland, M.; Castillo, R.L.; Chen, C. 3,4-dihydroxyphenylacetic acid, a microbiota-derived metabolite of quercetin, protects against pancreatic β-cells dysfunction induced by high cholesterol. Exp. Cell Res. 2015, 334, 270–282. [Google Scholar] [CrossRef]
- Taubert, D.; Breitenbach, T.; Lazar, A.; Censarek, P.; Harlfinger, S.; Berkels, R.; Klaus, W.; Roesen, R. Reaction rate constants of superoxide scavenging by plant antioxidants. Free Radic. Biol. Med. 2003, 35, 1599–1607. [Google Scholar] [CrossRef]
- Nakayama, T.; Uno, B. Importance of proton-coupled electron transfer from natural phenolic compounds in superoxide scavenging. Chem. Pharm. Bull. 2015, 63, 967–973. [Google Scholar] [CrossRef]
- Nakayama, T.; Uno, B. Concerted two-proton–coupled electron transfer from catechols to superoxide via hydrogen bonds. Electrochim. Acta 2016, 208, 304–309. [Google Scholar] [CrossRef]
- Nakayama, T.; Uno, B. Structural properties of 4-substituted phenols capable of proton-coupled electron transfer to superoxide. Int. J. Adv. Res. Chem. Sci. 2016, 3, 11–19. [Google Scholar]
- Nakayama, T.; Uno, B. Reactivities of hydroxycinnamic acid derivatives involving caffeic acid toward electrogenerated superoxide in N,N-dimethylformamide. Electrochem 2022, 3, 347–360. [Google Scholar] [CrossRef]
- Alvarez-Idaboy, J.R.; Mora-Diez, N.; Vivier-Bunge, A. A quantum chemical and classical transition state theory explanation of negative activation energies in OH addition to substituted ethenes. J. Am. Chem. Soc. 2000, 122, 3715–3720. [Google Scholar] [CrossRef]
- Mozurkewich, M.; Benson, S.W. Negative activation energies and curved Arrhenius plots. 1. Theory of reactions over potential wells. J. Phys. Chem. 1984, 88, 6429–6435. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Atkins’ Physical Chemistry, 8th ed.; Oxford University Press: Oxford, UK, 2006; pp. 822–823. [Google Scholar]
- Bors, W.; Saran, M.; Michel, C. Pulse-radiolytic investigations of catechols and catecholamines. 3. Adrenalone. J. Phys. Chem. 1979, 83, 2447–2452. [Google Scholar] [CrossRef]
- Jovanovic, S.V.; Steenken, S.; Tosic, M.; Marjanovic, B.; Simic, M.G. Flavonoids as antioxidants. J. Am. Chem. Soc. 1994, 116, 4846–4851. [Google Scholar] [CrossRef]
- Jovanovic, S.V.; Simic, M.G. Antioxidants in nutrition. Ann. N. Y. Acad. Sci. 2000, 899, 326–334. [Google Scholar] [CrossRef]
- Paganga, G.; Rice-Evans, C.A. The identification of flavonoids as glycosides in human plasma. FEBS Lett. 1997, 401, 78–82. [Google Scholar] [CrossRef]
- Košinova, P.; Berka, K.; Wykes, M.; Otyepka, M.; Trouillas, P. Positioning of antioxidant quercetin and its metabolites in lipid bilayer membranes: Implication for their lipid-peroxidation inhibition. J. Phys. Chem. B 2012, 116, 1309–1318. [Google Scholar] [CrossRef]

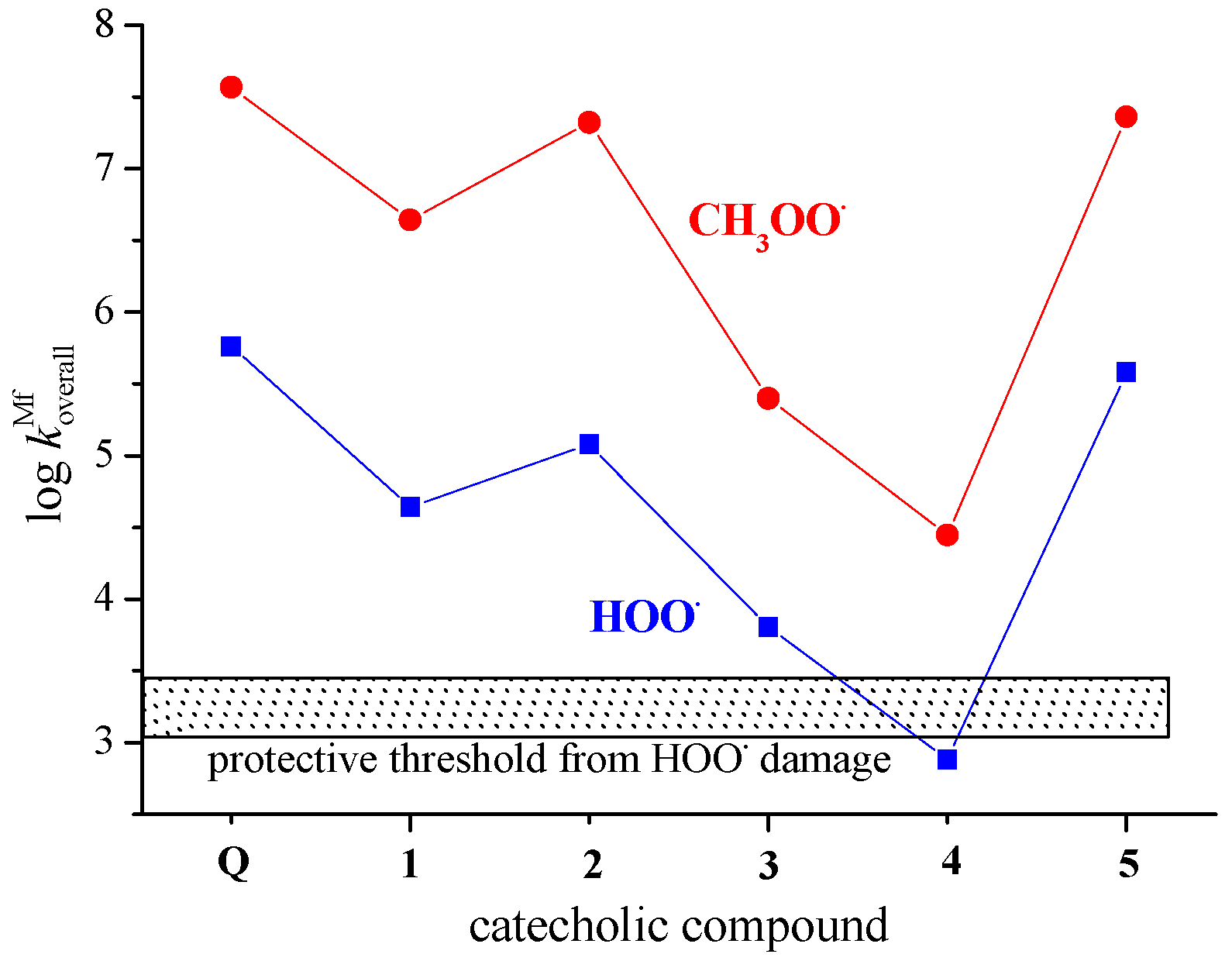

| Compound | Path | ΔrG | ν | ΔG≠ | kTST | κEck | kTST/Eck | |
|---|---|---|---|---|---|---|---|---|
| Q | C-3 | −1.3 | −4273.77 | 18.3 | 2.3 × 10−1 | 7,090,769.7 | 1.6 × 106 | 1.1 × 103 |
| C-5 | 12.7 | −3894.44 | 27.2 | 7.8 × 10−8 | 318,443.4 | 2.5 × 10−2 | ||
| C-7 | 8.1 | −2521.38 | 23.3 | 5.2 × 10−5 | 1448.4 | 7.5 × 10−2 | ||
| C-3’ | −3.4 | −1883.66 | 16.3 | 7.6 × 100 | 84.8 | 6.4 × 102 | ||
| C-4’ | −5.8 | −1843.08 | 16.4 | 6.1 × 100 | 64.8 | 4.0 × 102 | ||
| 1 | C-3 | −5.5 | −1652.96 | 16.3 | 6.5 × 100 | 25.1 | 1.6 × 102 | 3.06 × 103 |
| C-4 | −6.6 | −1644.00 | 14.7 | 1.0 × 102 | 27.8 | 2.9 × 103 | ||
| 2 | C-3 | −5.3 | −1674.57 | 16.1 | 1.0 × 101 | 35.8 | 3.6 × 102 | 6.5 × 102 |
| C-4 | −5.6 | −1739.57 | 16.2 | 8.0 × 100 | 36.1 | 2.9 × 102 | ||
| 3 | C-5 | 13.3 | −3018.24 | 29.0 | 3.4 × 10−9 | 22,708.0 | 7.7 × 10−5 | 1.09 × 103 |
| C-7 | 24.2 | −2496.43 | 25.4 | 1.4 × 10−6 | 1091.0 | 1.6 × 10−3 | ||
| C-3’ | −3.3 | −1945.28 | 16.6 | 3.9 × 100 | 194.1 | 7.5 × 102 | ||
| C-4’ | −2.8 | −1983.78 | 17.0 | 2.3 × 100 | 150.5 | 3.4 × 102 | ||
| 4 | C-5 | 27.3 | −3936.12 | 25.8 | 7.4 × 10−7 | 433,548.2 | 3.2 × 10−1 | 2.12 × 103 |
| C-7 | 24.7 | −2362.23 | 24.7 | 5.0 × 10−6 | 829.8 | 4.2 × 10−3 | ||
| C-3’ | −2.5 | −2108.97 | 16.5 | 5.2 × 100 | 385.6 | 2.0 × 103 | ||
| C-4’ | −2.2 | −2142.87 | 18.2 | 2.6 × 10−1 | 454.2 | 1.2 × 102 | ||
| 5 | C-5 | 27.3 | −4228.32 | 24.8 | 4.4 × 10−6 | 1,026,701.2 | 4.5 × 100 | 1.84 × 103 |
| C-7 | 24.3 | −2398.24 | 24.3 | 1.0 × 10−5 | 1040.3 | 1.1 × 10−2 | ||
| C-3’ | −4.2 | −2289.25 | 15.6 | 2.2 × 101 | 60.4 | 1.3 × 103 | ||
| C-4’ | −5.1 | −1813.86 | 16.3 | 7.1 × 100 | 76.4 | 5.4 × 102 |
| Compound | Path | ΔrG | ν | ΔG≠ | kTST | κEck | kTST/Eck | |
|---|---|---|---|---|---|---|---|---|
| Q | C-3 | 0.9 | −3359.24 | 22.7 | 1.4 × 10−4 | 198,437.3 | 2.8 × 101 | 4.3 × 103 |
| C-5 | 14.9 | −2631.22 | 30.6 | 2.5 × 10−10 | 2359.1 | 5.8 × 10−7 | ||
| C-7 | 10.4 | −2455.59 | 23.3 | 4.9 × 10−5 | 281.5 | 1.4 × 10−2 | ||
| C-3’ | −1.1 | −2226.66 | 16.3 | 7.2 × 100 | 333.0 | 2.4 × 103 | ||
| C-4’ | −3.5 | −2259.20 | 16.5 | 4.7 × 100 | 411.2 | 1.9 × 103 | ||
| 1 | C-3 | −3.2 | −1919.02 | 16.7 | 3.4 × 100 | 81.6 | 2.8 × 102 | 2.88 × 103 |
| C-4 | −4.3 | −2067.59 | 15.7 | 1.9 × 101 | 137.2 | 2.6 × 103 | ||
| 2 | C-3 | −3.0 | −1965.19 | 16.8 | 3.2 × 100 | 105.2 | 3.4 × 102 | 1.27 × 103 |
| C-4 | −3.4 | −2124.71 | 16.5 | 5.3 × 100 | 175.6 | 9.3 × 102 | ||
| 3 | C-5 | 15.6 | −2536.63 | 30.9 | 1.3 × 10−10 | 866.4 | 1.2 × 10−7 | 2.95 × 103 |
| C-7 | 26.5 | −2250.15 | 25.1 | 2.5 × 10−6 | 175.7 | 4.5 × 10−4 | ||
| C-3’ | −1.0 | −2201.80 | 16.3 | 7.2 × 100 | 363.0 | 2.6 × 103 | ||
| C-4’ | −0.5 | −2331.38 | 17.9 | 4.9 × 10−1 | 706.9 | 3.5 × 102 | ||
| 4 | C-5 | 29.6 | −2473.36 | 26.4 | 2.8 × 10−7 | 540.9 | 1.5 × 10−4 | 2.84 × 103 |
| C-7 | 26.9 | −2231.42 | 24.8 | 4.2 × 10−6 | 186.5 | 7.9 × 10−4 | ||
| C-3’ | −0.2 | −2345.66 | 16.7 | 3.7 × 100 | 711.6 | 2.6 × 103 | ||
| C-4’ | 0.1 | −2364.37 | 18.3 | 2.3 × 10−1 | 1010.0 | 2.4 × 102 | ||
| 5 | C-5 | 26.6 | −2472.03 | 25.6 | 1.0 × 10−6 | 737.6 | 7.7 × 10−4 | 4.94 × 103 |
| C-7 | 26.6 | −2286.09 | 24.8 | 4.1 × 10−6 | 240.5 | 9.9 × 10−4 | ||
| C-3’ | −2.0 | −2133.49 | 16.7 | 3.3 × 100 | 284.1 | 9.4 × 102 | ||
| C-4’ | −2.8 | −2254.05 | 16.0 | 1.1 × 101 | 349.2 | 4.0 × 103 |
| Compound | Path | ΔrG | ΔG≠ | λ | kD | kapp | kMf | Γ | |
|---|---|---|---|---|---|---|---|---|---|
| Q | 3-O− | 3.0 | 5.9 | 16.9 | 8.2 × 109 | 3.1 × 108 | 5.2 × 105 | 90.3 | 5.8 × 105 |
| 5-O− | 13.4 | 13.5 | 15.1 | 8.3 × 109 | 8.0 × 102 | 1.3 × 100 | 0 | ||
| 7-O− | 18.5 | 18.8 | 14.3 | 8.2 × 109 | 1.0 × 10−1 | 1.7 × 10−4 | 0 | ||
| 3′-O− | 5.8 | 7.5 | 16.2 | 8.2 × 109 | 2.0 × 107 | 3.4 × 104 | 5.7 | ||
| 4′-O− | 6.3 | 7.7 | 15.6 | 8.2 × 109 | 1.4 × 107 | 2.4 × 104 | 4.0 | ||
| 1 | 3′-O− | 1.4 | 5.0 | 17.1 | 8.0 × 109 | 1.1 × 109 | 1.4 × 104 | 31.5 | 4.4 × 104 |
| 4′-O− | 0.6 | 4.4 | 16.6 | 7.9 × 109 | 2.4 × 109 | 3.00 × 104 | 68.5 | ||
| 2 | 3′-O− | 0.2 | 4.3 | 16.9 | 7.9 × 109 | 2.7 × 109 | 4.3 × 104 | 34.3 | 1.2 × 105 |
| 4′-O− | −1.5 | 3.6 | 17.2 | 7.8 × 109 | 5.1 × 109 | 8.0 × 104 | 65.7 | ||
| 3 | 5-O− | 32.9 | 102.5 | 3.2 | 8.1 × 109 | 4.6 × 10−63 | 5.1 × 10−66 | 0 | 6.4× 103 |
| 7-O− | 33.6 | 36.7 | 18.4 | 8.1 × 109 | 8.1 × 10−15 | 9.0 × 10−18 | 0 | ||
| 3′-O− | 7.0 | 8.4 | 16.3 | 8.3 × 109 | 4.7 × 106 | 5.2 × 103 | 81.0 | ||
| 4′-O− | 8.2 | 9.2 | 16.3 | 8.2 × 109 | 1.1 × 106 | 1.2 × 103 | 19.0 | ||
| 4 | 7-O− | 37.2 | 42.2 | 18.1 | 8.1 × 109 | 7.2 × 10−19 | 9.1 × 10−22 | 0 | 7.6 × 102 |
| 3′-O− | 8.5 | 9.6 | 17.1 | 8.2 × 109 | 6.0 × 105 | 7.6 × 102 | 100 | ||
| 4′-O− | 14.0 | 14.1 | 16.6 | 8.1 × 109 | 2.7 × 102 | 3.4 × 10−1 | 0 | ||
| 5 | 5-O− | 30.7 | 31.9 | 20.8 | 8.2 × 109 | 2.8 × 10−11 | 3.1 × 10−14 | 0.0 | 3.8 × 105 |
| 7-O− | 29.7 | 31.4 | 18.5 | 8.2 × 109 | 6.5 × 10−11 | 7.2 × 10−14 | 0.0 | ||
| 3′-O− | 3.8 | 6.4 | 17.1 | 8.2 × 109 | 1.3 × 108 | 1.4 × 105 | 36.8 | ||
| 4′-O− | 3.4 | 6.1 | 16.7 | 8.2 × 109 | 2.2 × 108 | 2.4 × 105 | 63.2 |
| Compound | Path | ΔrG | ΔG≠ | λ | kD | kapp | kMf | Γ | |
|---|---|---|---|---|---|---|---|---|---|
| Q | 3-O− | 4.9 | 6.9 | 16.5 | 7.7 × 109 | 5.1 × 107 | 3.4 × 107 | 99.8 | 3.7 × 107 |
| 5-O− | 15.4 | 15.4 | 14.7 | 7.8 × 109 | 3.4 × 101 | 2.3 × 101 | 0 | ||
| 7-O− | 20.4 | 21.2 | 13.9 | 7.8 × 109 | 1.9 × 10−3 | 1.3 × 10−3 | 0 | ||
| 3′-O− | 7.8 | 8.8 | 15.8 | 7.7 × 109 | 2.3 × 106 | 1.5 × 106 | 0.1 | ||
| 4′-O− | 8.3 | 9.0 | 15.2 | 7.7 × 109 | 1.5 × 106 | 1.0 × 106 | 0.1 | ||
| 1 | 3′-O− | 3.3 | 6.0 | 16.7 | 7.6 × 109 | 2.4 × 108 | 1.2 × 106 | 27.0 | 4.4 × 106 |
| 4′-O− | 2.5 | 5.4 | 16.1 | 7.5 × 109 | 6.5 × 108 | 3.2 × 106 | 73.0 | ||
| 2 | 3′-O− | 2.1 | 5.3 | 16.5 | 7.5 × 109 | 7.9 × 108 | 5.0 × 106 | 24.0 | 2.1 × 107 |
| 4′-O− | 0.4 | 4.4 | 16.7 | 7.5 × 109 | 2.5 × 109 | 1.6 × 107 | 76.0 | ||
| 3 | 5-O− | 34.8 | 128.3 | 2.7 | 7.7 × 109 | 5.3 × 10−82 | 2.3 × 10−82 | 0 | 2.5 × 105 |
| 7-O− | 35.5 | 39.7 | 18.0 | 7.7 × 109 | 4.8 × 10−17 | 2.1 × 10−17 | 0 | ||
| 3′-O− | 8.9 | 9.7 | 15.9 | 7.8 × 109 | 4.8 × 105 | 2.1 × 105 | 82.8 | ||
| 4′-O− | 10.1 | 10.6 | 15.9 | 7.8 × 109 | 1.0 × 105 | 4.4 × 104 | 17.2 | ||
| 4 | 7-O− | 39.1 | 45.6 | 17.7 | 7.7 × 109 | 2.5 × 10−21 | 1.3 × 10−21 | 0 | 2.8 × 104 |
| 3′-O− | 10.4 | 11.0 | 16.7 | 8.2 × 109 | 5.5 × 104 | 2.8 × 104 | 100 | ||
| 4′-O− | 15.9 | 15.9 | 16.2 | 8.1 × 109 | 1.3 × 101 | 6.5 × 100 | 0 | ||
| 5 | 5-O− | 32.6 | 34.4 | 20.3 | 7.7 × 109 | 3.6 × 10−13 | 1.6 × 10−13 | 0 | 2.3 × 107 |
| 7-O− | 31.6 | 34.1 | 18.1 | 7.7 × 109 | 6.4 × 10−13 | 2.8 × 10−13 | 0 | ||
| 3′-O− | 5.7 | 7.5 | 16.6 | 7.7 × 109 | 1.9 × 107 | 8.4 × 106 | 35.9 | ||
| 4′-O− | 5.4 | 7.2 | 16.2 | 7.7 × 109 | 3.4 × 107 | 1.5 × 107 | 64.1 |
| Compound | ΔrG | ν | ΔG≠ | kTST | kD | kapp |
|---|---|---|---|---|---|---|
| Q | −14.9 | −4882.49 | −2.8 | 3.6 × 1014 | 8.2 × 109 | 8.2 × 109 |
| 1 | −10.6 | −5177.82 | 0.2 | 4.8 × 1012 | 8.2 × 109 | 8.2 × 109 |
| 2 | −11.0 | −4923.04 | 0.4 | 1.5 × 1012 | 8.0 × 109 | 8.0 × 109 |
| 3 | −14.3 | −5112.75 | −3.1 | 1.1 × 1015 | 8.5 × 109 | 8.5 × 109 |
| 4 | −18.7 | −4798.18 | −6.8 | 2.9 × 1017 | 8.5 × 109 | 8.5 × 109 |
| 5 | −12.4 | −5039.88 | −2.0 | 1.9 × 1014 | 8.2 × 109 | 8.2 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amić, A.; Mastiľák Cagardová, D. A DFT Study on the Kinetics of HOO•, CH3OO•, and O2•− Scavenging by Quercetin and Flavonoid Catecholic Metabolites. Antioxidants 2023, 12, 1154. https://doi.org/10.3390/antiox12061154
Amić A, Mastiľák Cagardová D. A DFT Study on the Kinetics of HOO•, CH3OO•, and O2•− Scavenging by Quercetin and Flavonoid Catecholic Metabolites. Antioxidants. 2023; 12(6):1154. https://doi.org/10.3390/antiox12061154
Chicago/Turabian StyleAmić, Ana, and Denisa Mastiľák Cagardová. 2023. "A DFT Study on the Kinetics of HOO•, CH3OO•, and O2•− Scavenging by Quercetin and Flavonoid Catecholic Metabolites" Antioxidants 12, no. 6: 1154. https://doi.org/10.3390/antiox12061154
APA StyleAmić, A., & Mastiľák Cagardová, D. (2023). A DFT Study on the Kinetics of HOO•, CH3OO•, and O2•− Scavenging by Quercetin and Flavonoid Catecholic Metabolites. Antioxidants, 12(6), 1154. https://doi.org/10.3390/antiox12061154