Sketching the Power of Machine Learning to Decrypt a Neural Systems Model of Behavior
Abstract
1. Introduction
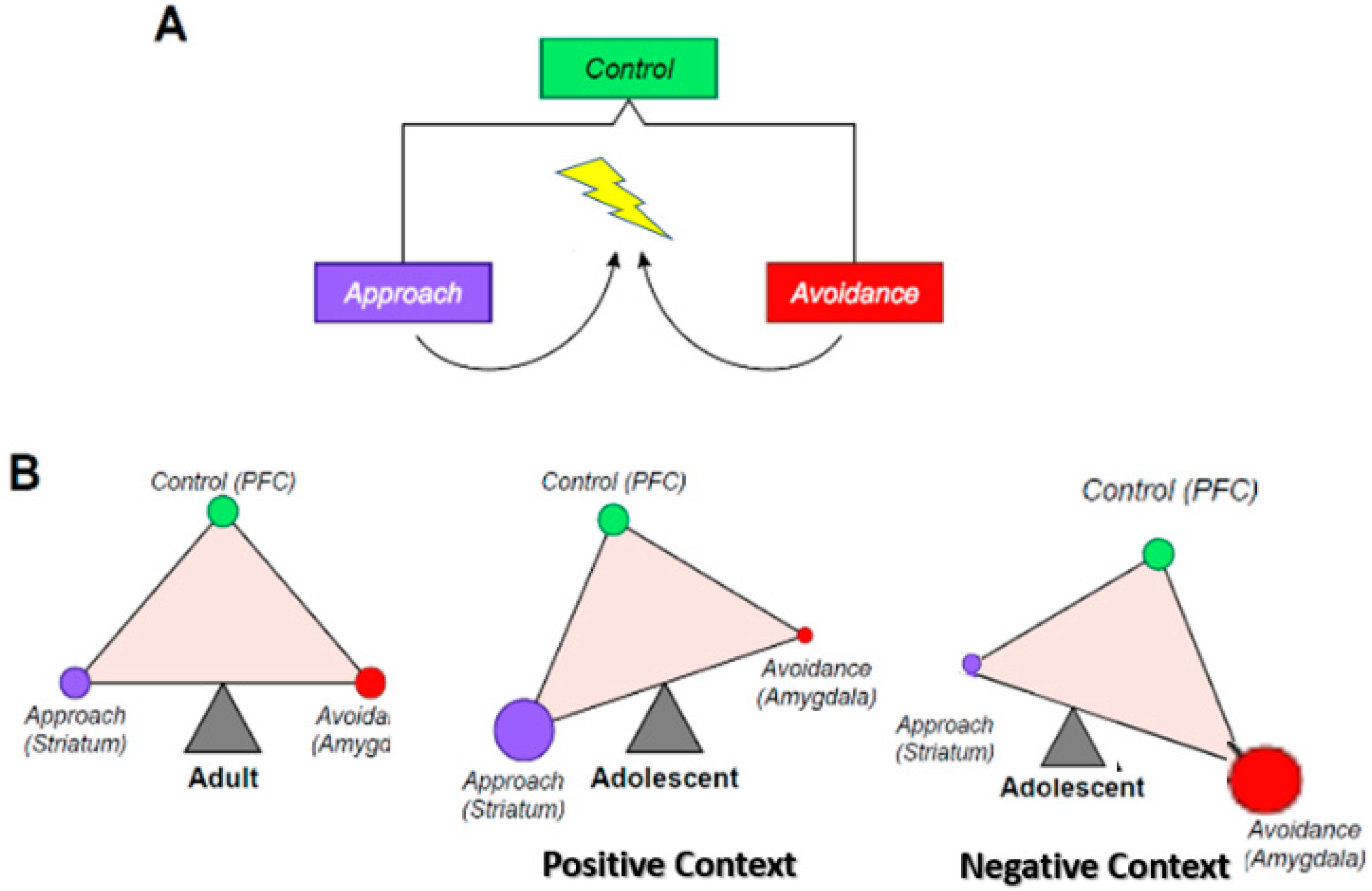
2. The Triadic Neural Systems Model
2.1. Conceptual Definition
2.2. Neural Substrates
2.2.1. Approach System
2.2.2. Avoidance System
2.2.3. Control System
2.3. Triadic Model in Adolescence
3. Testing the Triadic Neural Systems Model
3.1. Introduction to Machine Learning Tools
3.2. Overall Strategy for Testing the Triadic Neural Systems Model
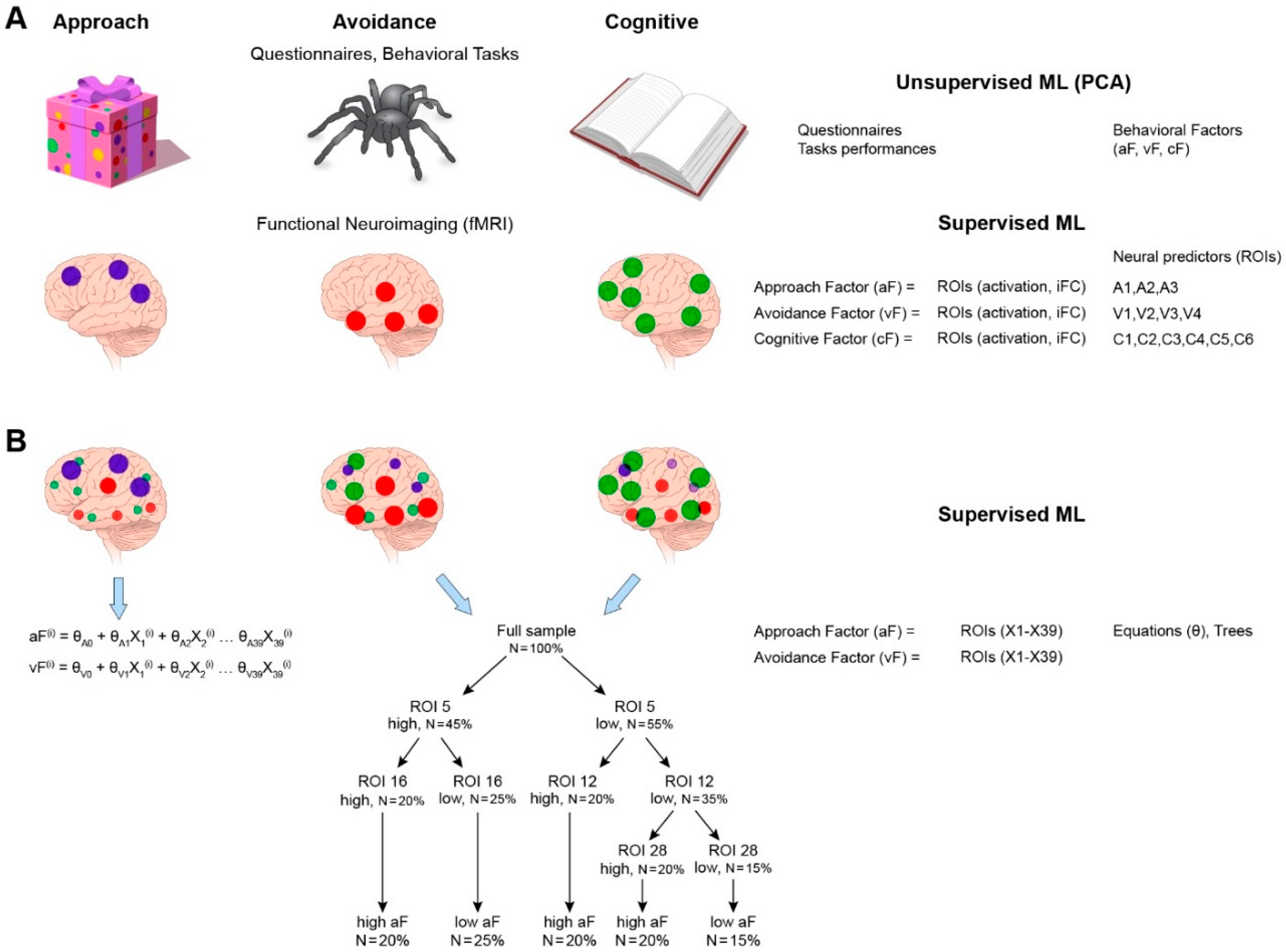
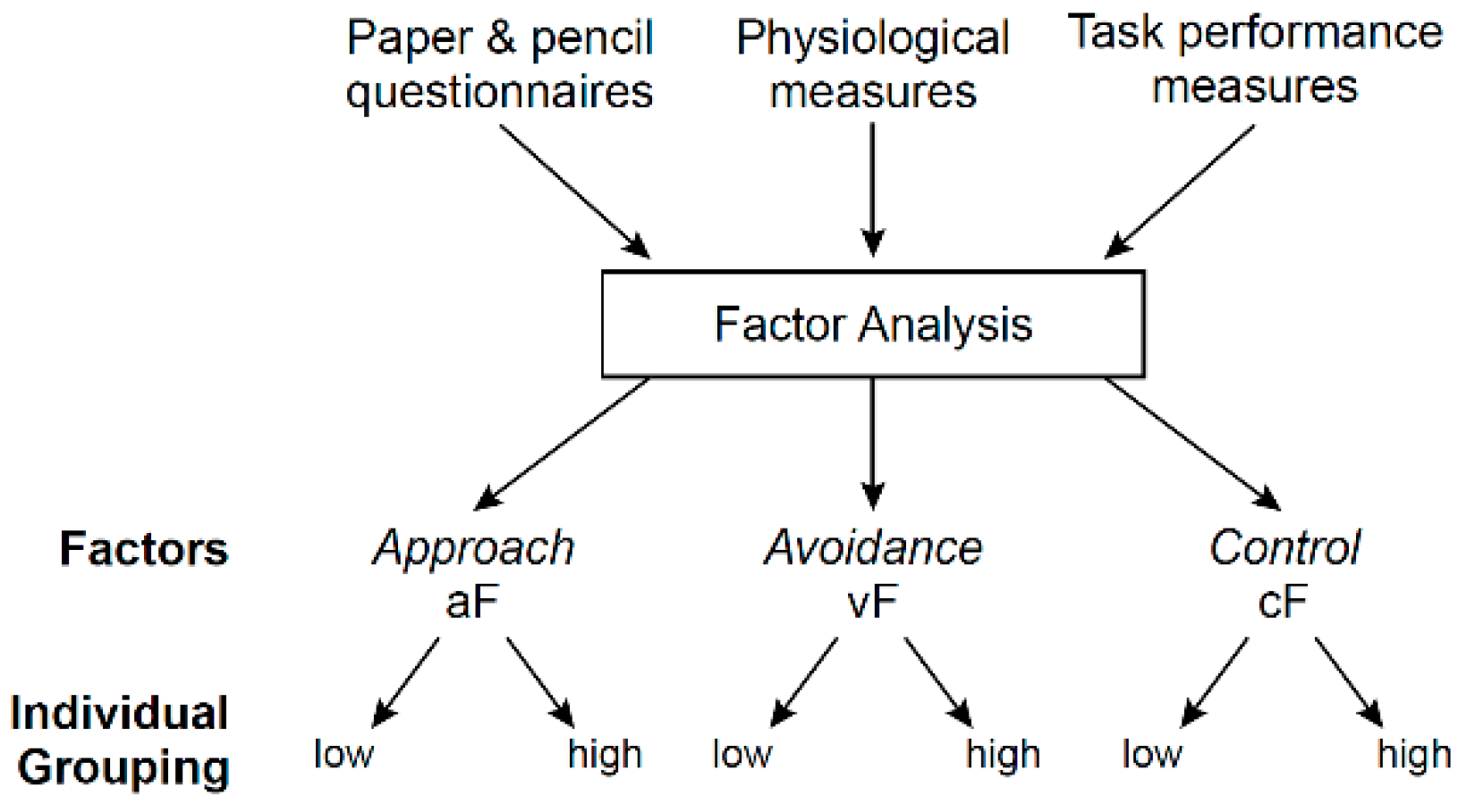
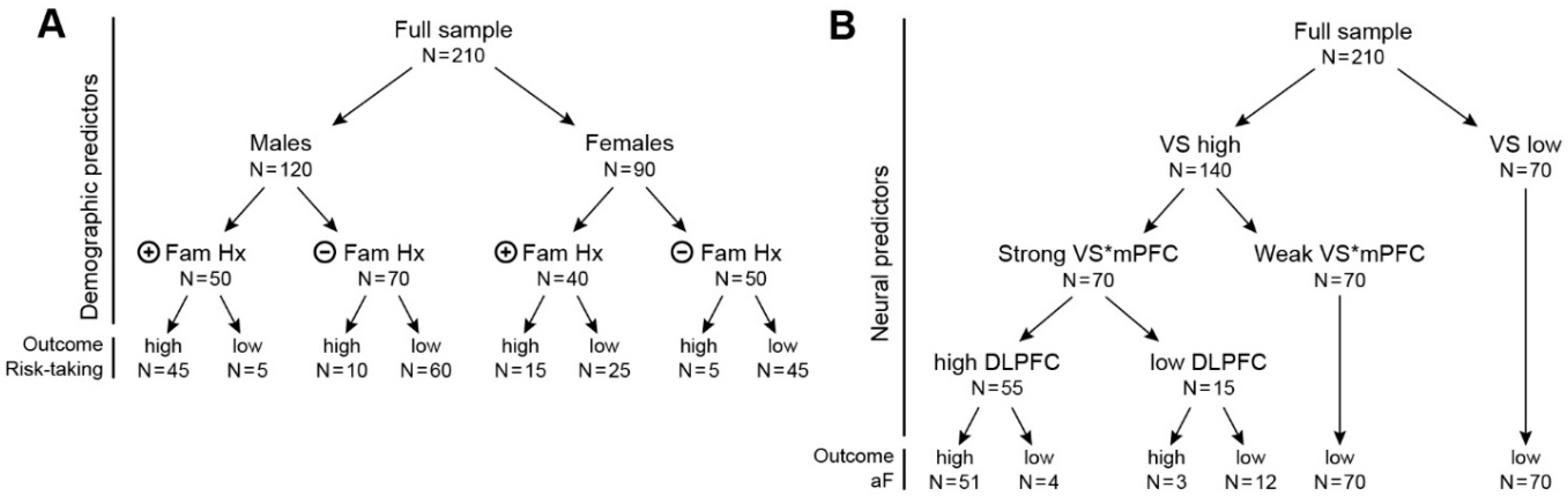
3.3. Question 1: Functional Architecture of Each System
3.3.1. Data Organization/Reduction
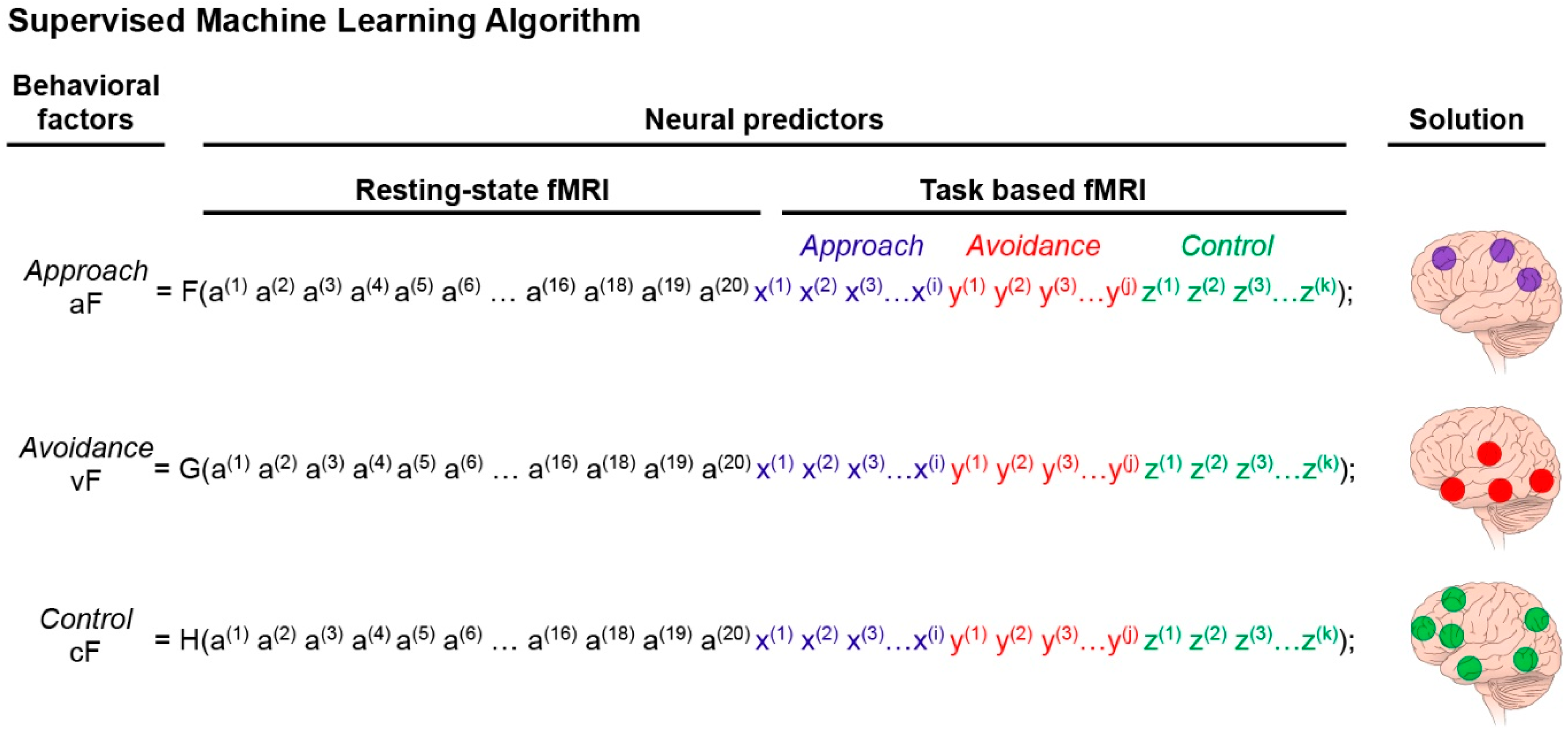
3.3.2. The Predictive Model
3.3.3. Output of the Predictive Model of the Characterization of the Three Neural Systems
3.4. Question 2: Dynamic Interactions among the Three Systems
3.4.1. Question 2, Step 1
3.4.2. Question 2, Step 2
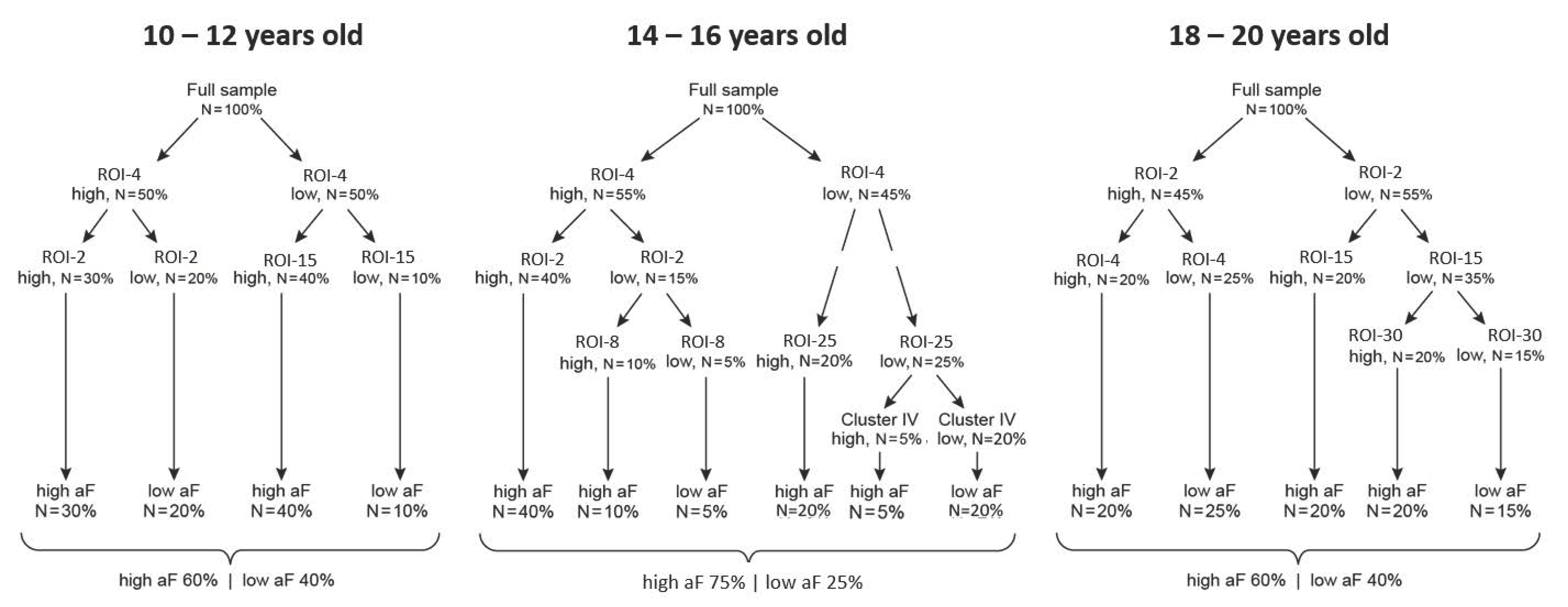
3.5. Question 3: Maturation of the Triadic Neural System Dynamics
- (a)
- Step 1: Behavioral characterization. The predicted behavior outcome measures are computed as in Question 1 by conducting a factor analysis of all available behavioral data, at each follow-up.
- (b)
- Step 2: Brain-behavior classification: This step gives rise to two types of results: trees that depict the hierarchical organization of predictors at each follow-up point and equations that quantify the contribution of each cluster to a given behavioral domain, respectively.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Casey, B.J.; Jones, R.M.; Hare, T.A. The adolescent brain. Annu. N. Y. Acad. Sci. 2008, 1124, 111–126. [Google Scholar] [CrossRef] [PubMed]
- Ernst, M.; Pine, D.S.; Hardin, M. Triadic model of the neurobiology of motivated behavior in adolescence. Psychol. Med. 2006, 36, 299–312. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, L. A social neuroscience perspective on adolescent risk-taking. Dev. Rev. 2008, 28, 78–106. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, L. A dual systems model of adolescent risk-taking. Dev. Psychobiol. 2010, 53, 216–224. [Google Scholar] [CrossRef] [PubMed]
- Vink, M.; Derks, J.M.; Hoogendam, J.M.; Hillegers, M.; Kahn, R.S. Functional differences in emotion processing during adolescence and early adulthood. NeuroImage 2014, 91, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Galvan, A. Adolescent development of the reward system. Front. Hum. Neurosci. 2010, 4, 6. [Google Scholar] [CrossRef]
- Ernst, M. The triadic model perspective for the study of adolescent motivated behavior. Brain Cogn. 2014, 89, 104–111. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Elliot, A.J.; Covington, M.V. Approach and avoidance motivation. Educ. Psychol. Rev. 2001, 13, 73–92. [Google Scholar] [CrossRef]
- Lammel, S.; Lim, B.K.; Malenka, R.C. Reward and aversion in a heterogeneous midbrain dopamine system. Neuropharmacology 2014, 76, 351–359. [Google Scholar] [CrossRef]
- Mathews, A.; Mackintosh, B. A cognitive model of selective processing in anxiety. Cogn. Ther. Res. 1998, 22, 539–560. [Google Scholar] [CrossRef]
- Brody, C.D.; Hanks, T.D. Neural underpinnings of the evidence accumulator. Curr. Opin. Neurobiol. 2016, 37, 149–157. [Google Scholar] [CrossRef]
- Cisek, P.; Kalaska, J.F. Neural correlates of reaching decisions in dorsal premotor cortex: Specification of multiple direction choices and final selection of action. Neuron 2005, 45, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Rushworth, M.F.S.; Kolling, N.; Sallet, J.; Mars, R.B. Valuation and decision-making in frontal cortex: One or many serial or parallel systems? Curr. Opin. Neurobiol. 2012, 22, 946–955. [Google Scholar] [CrossRef] [PubMed]
- Song, J.-H.; Nakayama, K. Hidden cognitive states revealed in choice reaching tasks. Trends Cogn. Sci. 2009, 13, 360–366. [Google Scholar] [CrossRef] [PubMed]
- Burle, B.; Vidal, F.; Tandonnet, C.; Hasbroucq, T. Physiological evidence for response inhibition in choice reaction time tasks. Brain Cogn. 2004, 56, 153–164. [Google Scholar] [CrossRef] [PubMed]
- Hunt, L.T.; Kolling, N.; Soltani, A.; Woolrich, M.W.; Rushworth, M.F.; Behrens, T.E. Mechanisms underlying cortical activity during value-guided choice. Nat. Neurosci. 2012, 15, 470–479. [Google Scholar] [CrossRef] [PubMed]
- Strait, C.E.; Blanchard, T.C.; Hayden, B.Y. Reward value comparison via mutual inhibition in ventromedial prefrontal cortex. Neuron 2014, 82, 1357–1366. [Google Scholar] [CrossRef]
- Usher, M.; McClelland, J.L. The time course of perceptual choice: The leaky, competing accumulator model. Psychol. Rev. 2001, 108, 550–592. [Google Scholar] [CrossRef]
- Balleine, B.W.; O’Doherty, J.P. Human and rodent homologies in action control: Corticostriatal determinants of goal-directed and habitual action. Neuropsychopharmacology 2010, 35, 48–69. [Google Scholar] [CrossRef]
- Berridge, K.C.; Kringelbach, M.L. Neuroscience of affect: Brain mechanisms of pleasure and displeasure. Curr. Opin. Neurobiol. 2013, 23, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Berridge, K.C.; Kringelbach, M.L. Pleasure systems in the brain. Neuron 2015, 86, 646–664. [Google Scholar] [CrossRef] [PubMed]
- Berridge, K.C.; Robinson, T.E. Parsing reward. Trends Neurosci. 2003, 26, 507–513. [Google Scholar] [CrossRef]
- Delgado, M.R.; Gillis, M.M.; Phelps, E.A. Regulating the expectation of reward via cognitive strategies. Nat. Neurosci. 2008, 11, 880–881. [Google Scholar] [CrossRef]
- Delgado, M.R.; Jou, R.L.; Phelps, E.A. Neural systems underlying aversive conditioning in humans with primary and secondary reinforcers. Front. Neurosci. 2011, 5, 71. [Google Scholar] [CrossRef] [PubMed]
- Saga, Y.; Tremblay, L. Ventral striatopallidal pathways involved in appetitive and aversive motivational processes. Decis. Neurosci. 2017, 47–58. [Google Scholar] [CrossRef]
- McCutcheon, J.E.; Ebner, S.R.; Loriaux, A.L.; Roitman, M.F. Encoding of aversion by dopamine and the nucleus accumbens. Front. Neurosci.-Switz. 2012, 6, 137. [Google Scholar] [CrossRef]
- Anderson, A.K.; Phelps, E.A. Expression without recognition: Contributions of the human amygdala to emotional communication. Psychol. Sci. 2000, 11, 106–111. [Google Scholar] [CrossRef] [PubMed]
- Mirenowicz, J.; Schultz, W. Preferential activation of midbrain dopamine neurons by appetitive rather than aversive stimuli. Nature 1996, 379, 449–451. [Google Scholar] [CrossRef] [PubMed]
- Schultz, W. Behavioral dopamine signals. Trends Neurosci. 2007, 30, 203–210. [Google Scholar] [CrossRef]
- Bromberg-Martin, E.S.; Matsumoto, M.; Hikosaka, O. Dopamine in motivational control: Rewarding, aversive, and alerting. Neuron 2010, 68, 815–834. [Google Scholar] [CrossRef] [PubMed]
- Goode, T.D.; Maren, S. Role of the bed nucleus of the stria terminalis in aversive learning and memory. Learn. Mem. 2017, 24, 480–491. [Google Scholar] [CrossRef] [PubMed]
- Maren, S. Parsing reward and aversion in the amygdala. Neuron 2016, 90, 209–211. [Google Scholar] [CrossRef] [PubMed]
- Sanford, C.A.; Soden, M.E.; Baird, M.A.; Miller, S.M.; Schulkin, J.; Palmiter, R.D.; Clark, M.; Zweifel, L.S. A central amygdala CRF circuit facilitates learning about weak threats. Neuron 2017, 93, 164–178. [Google Scholar] [CrossRef] [PubMed]
- Balleine, B.W.; Killcross, S. Parallel incentive processing: An integrated view of amygdala function. Trends Neurosci. 2006, 29, 272–279. [Google Scholar] [CrossRef] [PubMed]
- Gottfried, J.A.; O’Doherty, J.; Dolan, R.J. Encoding predictive reward value in human amygdala and orbitofrontal cortex. Science 2003, 301, 1104–1107. [Google Scholar] [CrossRef]
- Murray, E.A. The amygdala, reward and emotion. Trends Cogn. Sci. 2007, 11, 489–497. [Google Scholar] [CrossRef]
- Tye, K.M.; Cone, J.J.; Schairer, W.W.; Janak, P.H. Amygdala neural encoding of the absence of reward during extinction. J. Neurosci. 2010, 30, 116–125. [Google Scholar] [CrossRef]
- Wassum, K.M.; Izquierdo, A. The basolateral amygdala in reward learning and addiction. Neurosci. Biobehav. Rev. 2015, 57, 271–283. [Google Scholar] [CrossRef]
- Kragel, P.A.; LaBar, K.S. Decoding the nature of emotion in the brain. Trends Cogn. Sci. 2016, 20, 444–455. [Google Scholar] [CrossRef]
- Murphy, F.C.; Nimmo-Smith, I.; Lawrence, A.D. Functional neuroanatomy of emotions: A meta-analysis. Cogn. Affect. Behav. Neurosci. 2003, 3, 207–233. [Google Scholar] [CrossRef]
- Banich, M.T. Executive function. Curr. Dir. Psychol. Sci. 2009, 18, 89–94. [Google Scholar] [CrossRef]
- Petrides, M. Lateral prefrontal cortex: Architectonic and functional organization. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2005, 360, 781–795. [Google Scholar] [CrossRef] [PubMed]
- Christoff, K.; Gabrieli, J.D.E. The frontopolar cortex and human cognition: Evidence for a rostrocaudal hierarchical organization within the human prefrontal cortex. Psychobiology 2000, 28, 168–186. [Google Scholar] [CrossRef]
- Stuss, D.T.; Alexander, M.P. Is there a dysexecutive syndrome? Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2007, 362, 901–915. [Google Scholar] [CrossRef]
- Kouneiher, F.; Charron, S.; Koechlin, E. Motivation and cognitive control in the human prefrontal cortex. Nat. Neurosci. 2009, 12, 939–945. [Google Scholar] [CrossRef] [PubMed]
- LeDoux, J.; Daw, N.D. Surviving threats: Neural circuit and computational implications of a new taxonomy of defensive behaviour. Nat. Rev. Neurosci. 2018, 19, 269–282. [Google Scholar] [CrossRef] [PubMed]
- Ernst, M.; Nelson, E.E.; Jazbec, S.; McClure, E.B.; Monk, C.S.; Leibenluft, E.; Blair, J.; Pine, D.S. Amygdala and nucleus accumbens in responses to receipt and omission of gains in adults and adolescents. NeuroImage 2005, 25, 1279–1291. [Google Scholar] [CrossRef]
- Smith, A.R.; Chein, J.; Steinberg, L. Impact of socio-emotional context, brain development, and pubertal maturation on adolescent risk-taking. Horm. Behav. 2013, 64, 323–332. [Google Scholar] [CrossRef]
- Sturman, D.A.; Moghaddam, B. The neurobiology of adolescence: Changes in brain architecture, functional dynamics, and behavioral tendencies. Neurosci. Biobehav. Rev. 2011, 35, 1704–1712. [Google Scholar] [CrossRef]
- Ernst, M.; Daniele, T.; Frantz, K. New perspectives on adolescent motivated behavior: Attention and conditioning. Dev. Cogn. Neurosci. 2011, 1, 377–389. [Google Scholar] [CrossRef] [PubMed]
- Silvers, J.A.; McRae, K.; Gabrieli, J.D.; Gross, J.J.; Remy, K.A.; Ochsner, K.N. Age-related differences in emotional reactivity, regulation, and rejection sensitivity in adolescence. Emotion 2012, 12, 1235–1247. [Google Scholar] [CrossRef]
- Hare, T.A.; Tottenham, N.; Galvan, A.; Voss, H.U.; Glover, G.H.; Casey, B.J. Biological substrates of emotional reactivity and regulation in adolescence during an emotional go-nogo task. Biol. Psychiatry 2008, 63, 927–934. [Google Scholar] [CrossRef] [PubMed]
- Quevedo, K.M.; Benning, S.D.; Gunnar, M.R.; Dahl, R.E. The onset of puberty: Effects on the psychophysiology of defensive and appetitive motivation. Dev. Psychopathol. 2009, 21, 27–45. [Google Scholar] [CrossRef] [PubMed]
- Dwyer, D.B.; Falkai, P.; Koutsouleris, N. Machine learning approaches for clinical psychology and psychiatry. Annu. Rev. Clin. Psychol. 2018, 14, 91–118. [Google Scholar] [CrossRef]
- Foster, K.R.; Koprowski, R.; Skufca, J.D. Machine learning, medical diagnosis, and biomedical engineering research–commentary. Biomed. Eng. Online 2014, 13, 94–103. [Google Scholar] [CrossRef]
- Bzdok, D.; Meyer-Lindenberg, A. Machine learning for precision psychiatry: Opportunities and challenges. Biol. Psychiatry: Cogn. Neurosci. Neuroimaging 2018, 3, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Iniesta, R.; Stahl, D.; McGuffin, P. Machine learning, statistical learning and the future of biological research in psychiatry. Psychol. Med. 2016, 46, 2455–2465. [Google Scholar] [CrossRef] [PubMed]
- IMAGEN. Welcome to the IMAGEN Study. Available online: https://imagen-europe.com/ (accessed on 25 January 2019).
- CONNECTOME. Connectome Coordination Facility. Available online: https://www.humanconnectome.org (accessed on 25 January 2019).
- NCANDA. National Consortium on Alcohol and Neurodevelopment in Adolescence. Available online: http://ncanda.org (accessed on 25 January 2019).
- ABCD. Adolescent Brain Cognitive Development Study. Available online: https://abcdstudy.org (accessed on 25 January 2019).
- Marcus, D.S.; Harms, M.P.; Snyder, A.Z.; Jenkinson, M.; Wilson, J.A.; Glasser, M.F.; Barch, D.M.; Archie, K.A.; Burgess, G.C.; Ramaratnam, M.; et al. Human Connectome Project informatics: Quality control, database services, and data visualization. NeuroImage 2013, 80, 202–219. [Google Scholar] [CrossRef] [PubMed]
- Jernigan, T.L.; Brown, S.A. Introduction. Dev. Cogn. Neurosci. 2018, 32, 1–3. [Google Scholar] [CrossRef]
- Deng, L.; Yu, D. Deep Learning: Methods and Applications. Found. Trends Signal 2014, 7, 197–387. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Marblestone, A.H.; Wayne, G.; Kording, K.P. Toward an integration of deep learning and neuroscience. Front. Comput. Neurosci. 2016, 10, 1–41. [Google Scholar] [CrossRef] [PubMed]
- Tarca, A.L.; Carey, V.J.; Chen, X.W.; Romero, R.; Draghici, S. Machine learning and its applications to biology. PLoS Comput. Biol. 2007, 3, e116. [Google Scholar] [CrossRef] [PubMed]
- Varoquaux, G.; Craddock, R.C. Learning and comparing functional connectomes across subjects. NeuroImage 2013, 80, 405–415. [Google Scholar] [CrossRef] [PubMed]
- Varoquaux, G.; Raamana, P.R.; Engemann, D.A.; Hoyos-Idrobo, A.; Schwartz, Y.; Thirion, B. Assessing and tuning brain decoders: Cross-validation, caveats, and guidelines. NeuroImage 2017, 145, 166–179. [Google Scholar] [CrossRef] [PubMed]
- Gleason, P.M.; Boushey, C.J.; Harris, J.E.; Zoellner, J. Publishing nutrition research: A review of multivariate techniques—Part 3: Data reduction methods. J. Acad. Nutr. Diet. 2015, 115, 1072–1082. [Google Scholar] [CrossRef]
- Ernst, M.; Spear, L.P. Reward systems. In Handbook of Developmental Social Neuroscience; de Haan, M., Gunnar, M.R., Eds.; Guilford Press: New York, NY, USA, 2009; pp. 324–341. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ernst, M.; Gowin, J.L.; Gaillard, C.; Philips, R.T.; Grillon, C. Sketching the Power of Machine Learning to Decrypt a Neural Systems Model of Behavior. Brain Sci. 2019, 9, 67. https://doi.org/10.3390/brainsci9030067
Ernst M, Gowin JL, Gaillard C, Philips RT, Grillon C. Sketching the Power of Machine Learning to Decrypt a Neural Systems Model of Behavior. Brain Sciences. 2019; 9(3):67. https://doi.org/10.3390/brainsci9030067
Chicago/Turabian StyleErnst, Monique, Joshua L. Gowin, Claudie Gaillard, Ryan T. Philips, and Christian Grillon. 2019. "Sketching the Power of Machine Learning to Decrypt a Neural Systems Model of Behavior" Brain Sciences 9, no. 3: 67. https://doi.org/10.3390/brainsci9030067
APA StyleErnst, M., Gowin, J. L., Gaillard, C., Philips, R. T., & Grillon, C. (2019). Sketching the Power of Machine Learning to Decrypt a Neural Systems Model of Behavior. Brain Sciences, 9(3), 67. https://doi.org/10.3390/brainsci9030067




