Obtaining Human Experience for Intelligent Dredger Control: A Reinforcement Learning Approach

Featured Application

This work has its application in the development of an unmanned intelligent system of a cutter suction dredger. The proposed approach can learn the manipulation skills based on the historical dredging data of a human operator, but can outperform human manipulation in respect of production.

Abstract

This work presents a reinforcement learning approach for intelligent decision-making of a Cutter Suction Dredger (CSD), which is a special type of vessel for deepening harbors, constructing ports or navigational channels, and reclaiming landfills. Currently, CSDs are usually controlled by human operators, and the production rate is mainly determined by the so-called cutting process (i.e., cutting the underwater soil into fragments). Long-term manual operation is likely to cause driving fatigue, resulting in operational accidents and inefficiencies. To reduce the labor intensity of the operator, we seek an intelligent controller the can manipulate the cutting process to replace human operators. To this end, our proposed reinforcement learning approach consists of two parts. In the first part, we employ a neural network model to construct a virtual environment based on the historical dredging data. In the second part, we develop a reinforcement learning model that can lean the optimal control policy by interacting with the virtual environment to obtain human experience. The results show that the proposed learning approach can successfully imitate the dredging behavior of an experienced human operator. Moreover, the learning approach can outperform the operator in a way that can make quick responses to the change in uncertain environments.

1. Introduction

The Cutter Suction Dredger (CSD) is a special vessel designed for the maintenance of rivers, lakes, or ports. The CSD can dredge nearly all kinds of soils (sand, clay, rock) into fragments with a cutter head, and then the dredged materials will be pumped into a pipeline and transported to the discharge zone. Currently, the CSD is usually controlled by human operators, and it is a daunting challenge for them to maintain a good production rate during the so-called cutting process. This is because the geological conditions of the working site are uncertain and dynamic for the operators. In other words, the operators cannot have prior knowledge about the types of soils to be dredged, so they must concentrate on observing instrument changes in real time during the cutting process. Operating the CSD requires that the slurry density in the pipeline cannot be too low. However, it is also dangerous to maintain a high slurry density because the pipeline can be blockage [1,2,3]. As a result, long-term manual operation often causes driving fatigue, resulting in operational accidents and inefficiencies. To reduce the labor intensity of the operator, in this work we aim at developing an intelligent cutter controller that can replace the human operators to manipulate the cutting process of the CSD.

The operation of the CSD need to continuously manipulate several motion controls, such as the cutter or swing control, the spud carrier control, the anchor control, and the pump control. Those motion controls need to be geared to one another during a full dredging cycle. In this work, we are in particular interested in the cutter or swing control ( named as the cutting process throughout this work) because it directly determines the production rate of a CSD. Moreover, the cutter control is the most boring but daunting mission for human operators, compared to other motion controls. Thus, an intelligent cutter controller is the decisive processor to release the operators from heavy workload.

To design an intelligent controller for the cutting process is not a trivial task. The major challenge is that the geological conditions of the working site are uncertain and dynamic. Thus, it is intractable to build up a precise model that can be applied to handle a diversity of geological conditions. Learning is an effective means of making real-time responses to the environment through trial-and-error interactions. Among the learning methodologies, Reinforcement Learning (RL) can obtain the optimal control policy for sequential decision-making with little prior knowledge [4,5]. It has been shown that the agents in many RL tasks can successfully achieve a goal or win a game, e.g., Atari games [6], robots [7], the game of Go [8], and fighting game Street Fighter [9].

For a learning agent to imitate human behavior in controlling the cutting process, it must understand the intentions or objectives of the operators. However, in real-world industrial problems, we cannot easily find a win or lose mechanism as in games to repeat the learning episodes. Moreover, since the terminal state is not obvious, we must figure out the task objective of the cutting process based on the historical dredging data produced by experienced human operators. Thus, we need to analyze the cutting process to understand what to achieve regarding a RL task.

Unlike many robot leaning tasks [10,11,12] and strategy learning tasks [13,14], we cannot allow the learning agent to directly make trial-and-error interactions with real dredging environments so as to lean the optimal behavior. This is because it is dangerous for an inexperienced controller to explore the action space in practical dredging projects, and controlling a real CSD to make trial-and-error interactions is unnecessarily expensive. In this work, our learning approach will construct a virtual environment based on historical dredging data. Those data are collected during experienced human operators carry out actual dredging projects. Thus, the learning agent can interact with the virtual environment to gain the operator’s experience in an efficient and economical manner.

The main contribution of our work is the proposed learning approach that combines a neural network model for obtaining the dynamics of the dredging environments with a RL model for learning the optimal control policy. The neural network model is responsible for constructing a concise virtual environment so that the learning agent can interact with it. The virtual environment can ensure that the learning agent can explore the entire state space and the action space as in playing games in [15,16]. Afterwards, we present the RL model to learn the optimal control policy by interacting with the virtual environment, and a reward scheme is also designed to guarantee that the state transitions are safe for the dredging operation.

This paper is organized as follows. We first analyze the cutting process of a CSD and formulate the problem in Section 2. Then, we investigate the state space and the action space for the cutting process, and the virtual environment is built up by means of a neural network structure in Section 3. In Section 4, an on-policy temporal difference learning method is presented to learn the optimal control policy. To evaluate the proposed learning approach, we compare the performance of an experienced human operator with the proposed approach in Section 5. Finally, we conclude this work and discuss the future research directions in Section 6.

2. Cutting Process Analysis

To identify potential problems, we will begin by analyzing the cutting process of a CSD in this section. Then we will investigate what to control to maintain appropriate slurry density in the pipeline. At the end of this section, we will formalize the decision-making problem of the cutting process.

2.1. General Layout of a CSD

Figure 1 shows the main components of a CSD and depicts the cutting process that will be studied in this work. The cutter head is mounted at the forefront of the cutter ladder, connecting to the dredge pump(s) through a suction pipe. The cutter head can cut hard soil or rock into fragments by rotating along the axis of the suction pipe, and it is an efficient tool for excavating nearly all kinds of soils. When the soil is cut or loosened, it is then sucked up by centrifugal dredge pumps. A suction inlet located beneath the cutter head is connected by the suction pipe directly to one or more centrifugal dredge pumps. The vacuum force at the suction inlet sucks up the loosened soil. Afterwards, the pumped slurry will be transported to a discharge zone through a pipeline.

As shown in Figure 1, the CSD is not driven by a propeller to carry out the cutting process. Instead, the dredging operations take place in a stationary position, even a self-propelled CSD will be moored with spuds and anchors while at work. The CSD usually has two spud poles. The working spud pole, mounted on a movable spud carriage, can be moved lengthwise along the vessel, while the auxiliary spud pole is set out of the centerline, usually on the starboard side of the stern of the pontoon. The auxiliary spud pole is used to keep the CSD in position when the working spud pole is raised, and the spud carrier is move back to its initial position. When cutting the soil, the CSD rotates around the working spud pole, producing an arc trajectory. The control action of such a swing movement is the swing speed. When a swing movement is completed, the CSD will be pushed forward a small step to start a new swing.

2.2. Problem Statement

To manipulate the cutting process by an intelligent learning system, we first need to figure out what needs to be controlled automatically, and what parameters are associated with the cutting process. In brief, the intelligent controller should ensure that the solids level in the pipeline is not too low or too high. If the slurry density is too low, the cutting process cannot lead to high production. If the slurry density is too high, the pipeline can be blocked occasionally, which will result in serious accidents of pipeline transportation.

Intuitively, the rotation of the cutter head and the swing speed dominate the among of sediment particles in the pipeline. The speed of the cutter head can affect the amount of spillage, i.e., the soil that is cut but not sucked up into the suction pipe. Thus, spillage will reduce the productivity of a CSD and needs to be minimized. Usually, the speed of the cutter head must match the pump capacity to optimize the particle size of dredged materials, and, eventually, reduce spillage. In practice, the speed of the cutter head does not need to change frequently in a dredging site because the soil types do not change much but the terrain is uneven. Therefore, the swing speed becomes the leading parameter that mainly determines the extent to which the soil is removed from the water bed.

In this work, we are in particular interested in finding the optimal policy for the swing speed control in dynamic and uncertain environments. The implicit objective of the controller is to maintain a high production rate (i.e., slurry density), taking account of safety constraints, e.g., the permitted torque on the cutter head and swing winches, the permitted slurry density in the pipeline, etc.

2.3. Problem Formulation

We will formulate the cutting process problem as a sequential decision-making task that can be modelled by Markov Decision Process (MDP). For the sake of consistency, in this work some notations follow [4,17]. An MDP task is defined as a tuple $\langle S,A,P_{s{s}^{\prime }}^a,R_{s{s}^{\prime }}^a,\gamma \rangle$, where

• S denotes the finite set of state spaces,
• A denotes the finite set of action space,
• $P_{s{s}^{\prime }}^a$ represents the conditional transition probability that defines the probability of arriving at the next state $s^{\prime }$ after performing action $a\in A$ in state $s\in S$,
• $R_{s{s}^{\prime }}^a$ specifies the expected immediate reward after executing action $a\in A$ in state $s\in S$ at the next state $s^{\prime }\in S$, and
• $\gamma \in [0,1)$ is the discount factor that determines the importance of future rewards.

The goal of the sequential decision-making task is to find the optimal control policy for the cutting process. To this end, a learning agent must be deployed into the environment to explore the entire state space and action space, as shown in Figure 2.

In this work, we assume discrete time steps, so at each time-step t the agent has to choose an action $a_t\in A$ to perform, based on the perception of the current state state $s_t\in S$. Performing the action will result in a state transition to the next state $s_{t+1}$. At the next state, the agent will receive the environmental feedback, called reward $r_{t+1}\in R$, to examine the effect of the action. We use policy $\pi :S\mapsto A$ to describe the action selection strategies in each state, i.e., what action should be selected in each state.

However, as mentioned above, in our work we cannot allow the learning agent to make trial-and-error interactions with a physical environment, due to the safety and cost concerns. Instead, the learning agent must interact with a virtual environment that can reflect the characteristics of a physical dredging environment. Thus, the proposed learning approach consists of two parts. The first part is responsible for constructing a concise virtual environment based on the historical dredging data collected during experienced human operators manipulating the CSD. The second part takes charge of learning the optimal control policy by exacting the experience of human operators.

3. Neural Network Model to Construct Virtual Environment

In this section, we will discuss how to build up a concise virtual environment so that the learning agent can interact with it to learn the optimal control policy. Thus, the virtual environment must be able to reflect the dynamics of the practical dredging process. In this work, the virtual environment will be constructed based on historical dredging data by means of a neural network, in which the inputs are the current states $s_t$ and action $a_t$ at time-step t, while the outputs are the next states $s_{t+1}$. To do so, we need to specify the state space and the action space for the cutting process problem.

3.1. Representation of State Space

As we intent to develop a learning system that can imitate the dredging manipulation of an experienced human operator, the variables involved in the state space are consistent with the data that the operator can observe. The states are also related to the production of a CSD, since the main objective of the dredging operation is to maintain an appropriate production rate. In this work, the data are collected from a real CSD, and we selected the following variables that are observable for human operators to form the state space

$$s:=[C_v,V_s,I_c,I_p,D_v,V_f]\in {\mathbb{R}}^6$$

(1)

where $C_v\in \mathbb{R}$ is the direct factor that indicates the solids level in the pipeline, and it is measured by a nuclear-based gamma densitometer installed at the stern of a CSD. Other five factors are indirect indicators that are related to the slurry density, but also can reflect the internal information about the dredger and external information about the environment.

• Swing speed, denoted by $V_s\in \mathbb{R}$, can indicate the among of the soils that are dredged in a swing movement along an arc trajectory. In such a swing, the CSD rotates around the working pole by slacking (or pulling) the cable of the starboard anchor (or the port side anchor). Those anchor cables are connected to the deck winches via the sheaves on both side of the cuter head. Thus, when the deck winches pull or slack the cables for the swing movement, it also produces a reaction force on the cutter head.
• Motor current of the cutter head, denoted by $I_c\in \mathbb{R}$, indicates the reaction forces on the cutter head. The reaction forces are mainly affected by the soil type, as well as the rotation and swing movements of the cutter head. Even if the swing speed remains the same, the reaction forces of the clockwise rotation and the counterclockwise rotation must be different. As mentioned above, the swing movement also produces a reaction force on the cutter head via the anchor cables.
• Motor current of the underwater pump, denoted by $I_p\in \mathbb{R}$, can indicate the extent to which the dredged soil is sucked up by the underwater pump. If the slurry density between the cutter head and the underwater pump remains at a high level, more torque is needed to drive the impeller of the pump for rotating, which results in the increase of the motor current of the underwater pump.
• Degree of suction vacuum, denoted by $D_v\in \mathbb{R}$, can also indicate the extent to which the dredged soil is sucked up by the underwater pump, but this parameter is different from the motor of the underwater pump. Here the reason is that the slurry with high density requires more power to be sucked up, and the degree of the suction vacuum must be maintained at a high level to pump the dredged soil from the inlet of the cutter head.
• Flow velocity, denoted by $V_f\in \mathbb{R}$, can reflect the among of sediment particles in the pipeline. Usually, the rotating speed of the pump(s) is not adjusted frequently, so the changes of the flow velocity are directly related to the slurry density in the pipeline. If the slurry density drops, it will be easier to transport the sediment particles in the pipeline, which will result in the increase of the flow velocity.

3.2. Representation of Action Space

In the cutting process, at any time-step t the learning agent has to select an action $a_t$ to change the swing speed. Of course, the swing speed must be constrained by the permitted torque on the swing winches. In our work, we use a discretized set $C=\{0,1,2,3,\dots ,16\}$ to represent the permitted state space of the swing speed, thus we have $V_s\in C$. Assuming that the agent is at state s at time-step t, in order to mitigate adverse effects of sharp changes on the swing speed, the action at state $s_t$ will be defined as

$$a_t\in A\left(s_t\right),\mathrm{where}A\left(s_t\right):=\{V_s\left(t\right),V_s\left(t\right)\pm 1,V_s\left(t\right)\pm 2,V_s\left(t\right)\pm 3\}\cap C.$$

(2)

Here we use $V_s\left(t\right)$ to denote the swing speed at time-step t. Thus, $A\left(s_t\right)$ is the action space that is available at state $s_t$ for the learning agent to choose an appropriate action, and it will be updated based on the current swing speed. When the CSD is working in a dredging site, once an action is selected to be executed, the change of the swing speed will cause the change of the states.

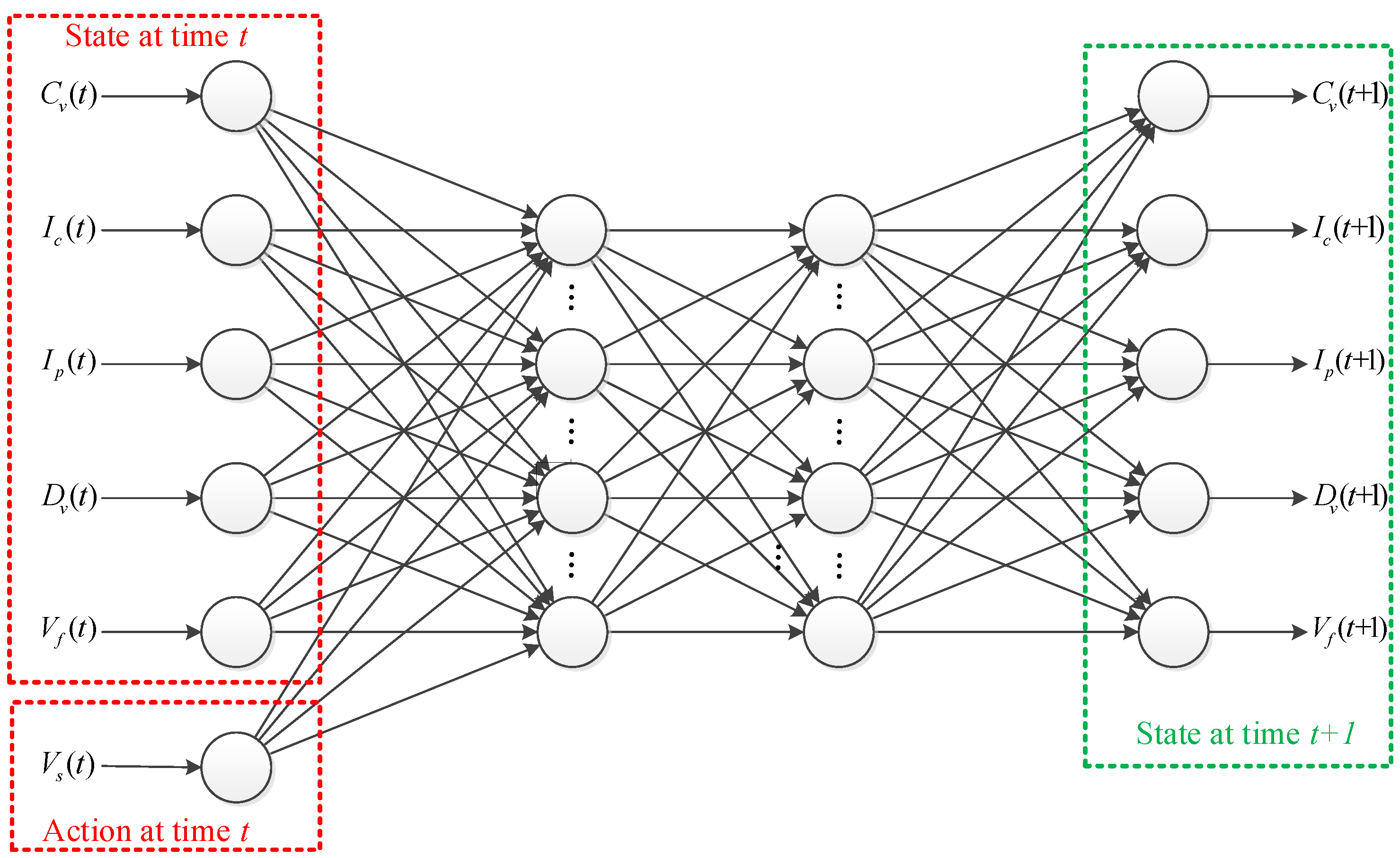
3.3. State Transitions in Neural Networks

As we cannot use a real CSD to obtain the state transitions and rewards, we must construct a virtual environment or a predictor that can precisely provide the feedbacks to the learning agent about the next state after executing an action. To predict the coming state, we use a nonlinear dynamic function $s_{t+1}=f(s_t,a_t)$ (e.g., in Reference [18]) to represent that if the agent performs action $a_t$ at state $s_t$, the environment will be transitioned to state $s_{t+1}$. Here f denotes the approximate function parameterized by the current state and action. As can be seen in Figure 3, we apply an artificial neural network (ANN) to predict the state transitions based on the historical dredging data.

The structure of the ANN is organized in successive layers. The input layer is the states and the action at time t, and the output layer is the coming states at time $t+1$. Tow intermediate layers are designed as the hidden layers. The detailed information of neural networks will not be discussed here but can be found in [19,20]. In this work, we summarize the parameters of the ANN architecture for predicting state transitions in

Table 1. Summary of the parameters of the ANN architecture.

Parameters	Value
neurons of the input layer	6
neurons of two hidden layers	50, 50
activation function of two hidden layers	ReLU, ReLU
neurons of the output layer	5
activation function of the output layer	Linear
learning rate	0.1
training episodes	500

.

We use the above multilayer neural network model to construct a concise virtual environment that can predict state transitions and inform that agent about the coming state. Afterwards, the learning agent can lean the optimal control policy through trial-and-error iterations with the virtual environment.

4. Reinforcement Learning to Find Optimal Control Policy

When a virtual environmental is available, the learning agent can explore the environment to maximize the long-term sum of discounted return,

$$R_t=\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k+1}.$$

(3)

In a RL task, the optimal policy ${\pi }^{*}$ is defined as a policy $\pi$ that has the highest $R_t$ than the other policies. We can use the so-called value function $V^{\pi }\left(s\right)$ to represent the discounted future reward $R_t$ by following the policy $\pi$ from state s,

$$V^{\pi }\left(s\right)={\mathbb{E}}_{\pi }\left\{\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k+1}|s_t=s\right\}.$$

(4)

The above value function describes the expected return with respect to a specific state. We can also use the action-value function $Q^{\pi }(s,a)$ to specify the expected return of selecting action a in state s. Then the above value function can be formalized as

$$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }\left\{\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k+1}|s_t=s,a_t=a\right\}.$$

(5)

The optimal control policy ${\pi }^{*}\left(s\right)$ can be defined as a function of optimal action-value $Q^{*}(s,a)$

$${\pi }^{*}\left(s\right)=arg\underset{a\in A\left(s\right)}{max}\sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a\left[R_{s{s}^{\prime }}^a+\gamma \underset{a^{\prime }\in A\left(s\right)}{max}{Q}^{*}(s^{\prime },a^{\prime })\right].$$

(6)

4.1. Reward Scheme

In the learning task of the cutting process, the objective of the controller is to maintain a high production rate (i.e., slurry density), and at the same time ensure that the CSD should be operated safely without pipeline blockage and overloaded motors. Thus, the reward is defined by a performance function p,

$$p\left(s\right)=\left\{\begin{array}{ccc}\hfill -100& \mathrm{if}\hfill & \hfill I_c\notin (930,950)\vee I_p\notin (110,180)\\ & & \hfill \vee D_v\notin (-70,-10)\vee V_f\notin (5,7)\\ \hfill C_v& \mathrm{if}\hfill & \hfill I_c\in (930,950)\wedge I_p\in (110,180)\\ & & \hfill \wedge D_v\in (-70,-10)\wedge V_f\in (5,7)\wedge C_v\le 45\\ \hfill 10\times C_v& \mathrm{if}\hfill & \hfill I_c\in (930,950)\wedge I_p\in (110,180)\\ & & \hfill \wedge D_v\in (-70,-10)\wedge V_f\in (5,7)\wedge C_v>45\\ \hfill -10& & \hfill \mathrm{otherwise}.\end{array}\right.$$

(7)

According to the above cost function, the learning agent will receive a big negative reward −100, if the resulting state exceeds the limit of the motor current of the cutter head, the motor current of the underwater pump, the degree of suction vacuum, or the flow velocity. If the resulting state does not go beyond the permitted limits and at the same time the slurry density is less than 45%, the learning agent will receive a positive reward, i.e., the actual value of $C_v$. If the resulting state locates in the safety range and the slurry density is greater than 45%, the learning agent can receive a big positive reward, i.e., $10\times C_v$. In other cases, the learning agent will receive a small negative feedback −10.

4.2. Model-Free Learning Algorithm

In a RL task, if the learning agent has prior knowledge about the state transitions and the coming rewards, it only needs to search the optimal control policy based on the model of the environment. To this end, we can apply model-based algorithms, such as dynamic programming [21], to calculate the expected return by traversing all possible actions and states. However, in this work the state transitions and the reward functions are not initially available for the agent to perform model-based calculation. Thus, it must interact with the virtual environment constructed in the above section to establish the model of the environment.

As a typical model-free learning paradigm, Temporal difference (TD) learning can update estimates based on previous learned estimates, without calculating the true expected return. According to Equation (6), the optimal control policy can be obtained if the optimal action-value function is found. In this work, we employ the on-policy SARSA-Learning algorithm [22] that updates the policy $\pi$ as it follows. Specifically, the learning agent will not choose the best future $Q(s,a)$, but select the action $a^{\prime }$ to execute and at time same time to update $Q(s,a)$. The SARSA learning rule is defined as:

$$Q(s,a)\leftarrow Q(z,a)+\alpha [p\left(s\right)+\gamma Q(z^{\prime },a^{\prime })-Q(z,a)],$$

(8)

where $\alpha$ is the learning rate, $\gamma$ is the discount factor, and $s^{\prime }$ and $a^{\prime }$ represents the next state and action, respectively. The above SARSA learning rule is also named as one-step SARSA learning, because the reward will only be propagated one step backwards. A disadvantages of one-step learning is that the learning agent often needs to take many non-exploitive actions until the optimal control policy is obtained. Comparatively, the Monte Carlo learning can speed up the learning process because it can update the entire trajectory from the beginning state to the final state. Thus, the combination of one-step learning and Monte Carlo learning can be a choice. The eligibility trace $Tr(s,a)\in {\mathbb{R}}^{+}$ can be defined to indicate to what extent the current reward will influence $Q(s,a)$ at time-step t. Naturally, the current reward should exert more influence on the recently visited states. To do so, the state-action pair indicating the eligibility trace should be decayed by a parameter in each time-step. Here we use $\gamma \lambda$ to decay the eligibility trace, and then Equation (8) can be formalized as

$$\begin{array}{c}Q(s,a)\leftarrow Q(s,a)+\alpha \delta Tr(s,a)\hfill \\ \delta =p\left(s\right)+\gamma Q(s^{\prime },a^{\prime })-Q(s,a)\hfill \end{array}$$

(9)

where

$$Tr(s,a)=\left\{\begin{array}{ccc}\hfill \gamma \lambda Tr(s,a)+1& \mathrm{if}\hfill & \hfill (s,a)=(s_t,a_t)\\ \hfill \gamma \lambda Tr(s,a)& \mathrm{if}\hfill & \hfill (s,a)\ne (s_t,a_t).\end{array}\right.$$

(10)

We use $\delta$ to represent the TD. According to the above equation, the eligibility trace of state-action pairs are required to be updated in each episode. In episode tasks, the state-action pairs that will not be visited during an episode will be zero. However, for non-episode tasks, it will be a challenge to store all the previously visited state-action pairs since the entire list can be very large. Thus, in the cutting process problem, we need to consider how to configure the episodes for updating the state-action pairs.

In this work, we will evaluate three intelligent control models, i.e., Q-learning, SARSA, and SARSA($\lambda$). The state space is discretized as: $C_v=\{0,5,10,\dots ,70\}$, $V_s=\{0,1,2,\dots ,16\}$, $I_c=\{900,905,915,\dots ,970\}$, $I_p=\{80,85,90,\dots ,200\}$, $D_v=\{0,-5,-10,\dots ,-80\}$, and $V_f=\{4.0,4.2,4.4,\dots ,8.0\}$. It should be noted that although we have developed tabular-based learning methods, we do not create a fixed list to store the Q-values and the eligibility trace for all the states when implementing them. Instead, the lists of storing Q-values and the eligibility trace will be appended incrementally when the learning agent visits a new state.

5. Evaluation and Results

To evaluate the proposed learning system in this work, we first require an experienced human operator to manipulate a real CSD for 6 hours, and the operation data are collected and sent to the learning system. We use the collected data to train the neural network model, and then the RL model employs the collected data to obtain the optimal control policy. As the operator’s working time for a shift is 6-8 hours, the subsequent dredging data are compared with the intelligent control methods. To examine the prediction accuracy of the neural network model, the human’s action and the current states are inputs of the network, while its predicted outputs will be compared with the real collected data. To evaluate the control policy, the human and the learning system will start from the same initial state and then control the cutting process, respectively.

5.1. Prediction of the Dynamics of the Environment

Figure 4 shows the prediction results of the trained neural network model, in which the output neurons include the slurry density, the motor current of the cutter head, the motor current of the pump, the suction vacuum and the flow velocity.

To demonstrate the performance and the effectiveness of the trained neural network model, we compare the prediction results with the actual data. In general, we can see that the neural network model can predict the state transitions of the environment, as the prediction curves fit very well with the actual curves (see Figure 4). Moreover, in order to further illustrate the accuracy of the predictions, we use Figure 5 to depict the relative percentage error of the predictions compared to the actual data. The relative percentage errors of the slurry density, the motor current of the cutter head, the motor current of the pump, the suction vacuum, and the flow velocity are $0.76\%$, $0.19\%$, $1.40\%$, $3.42\%$, and $2.60\%$, respectively. We can see that the prediction of the suction vacuum has the worst accuracy, but its relative error is only $3.42\%$. Thus, we can conclude that the neural network model can predict the state transitions of the environment.

Using the neural network model, we can build up the virtual environment. Then, the RL agent can be deployed to interact with the virtual environment to learn the optimal control policy. In the next subsection, we will discuss the evaluation of the reinforcement learning model.

5.2. Intelligent Control of the Cutting Process

In the experiment of controlling the cutting process, we set the performance of an experienced human operator as the baseline. We evaluate three intelligent control models, i.e., the proposed SARSA($\lambda$) learning with the typical Q-learning and SARSA algorithms. In this work, it is expected that the intelligent control models can manipulate the swing speed control by imitating the dredging behavior of the experienced human operator. Moreover, the intelligent control models should be able to outperform the human operator in a way that can produce quick responses to the changes of uncertain terrains.

As mentioned above, since the cutting process is a non-episode task, in order to facilitate the learning period, each learning episode of the Q-learning, SARSA, and SARSA($\lambda$) can run a maximum of 1000 time steps. We confine the maximum time steps because the cutting process does not have an explicit goal state to terminate a learning episode. Thus, a new learning episode can simply start if the learning time steps reach the maximum. In the experiments, the learning agent is required to complete 2000 episodes to find the optimal control policy. In each episode, the initial state will be set randomly, so the learning agent is expected to explore the state space thoroughly for gathering enough information about the dynamics of the cutting process. In the simulation, we set the parameters of Q-learning, SARSA, and SARSA($\lambda$) as follows: $\alpha =0.01$, $\gamma =0.9$, $\lambda =0.9$. When the learning period is over, we compare the performance of three intelligent control models with the experienced human operator in 500 time steps.

5.2.1. Results and Analysis

In Figure 6, we have compared the performance of the experienced human operator with Q-learning, SARSA, and SARSA($\lambda$) with respect to the slurry density, the motor current of the cutter head, the motor current of the pump, the suction vacuum, the flow velocity and the swing speed.

In the cutting process, the swing speed is the control variable, so its behavior will affect the changes of other variables. For example, if the swing speed is increased, the amount of the soil to be cut (i.e., the slurry density) will grow accordingly. As the swing operation causes the CSD to move around the working spud pole by pulling and slacking on the fore sideline wires of two side anchors, it also produces a reaction force on the cutter head. Thus, the increase of the swing speed will also lead to the rise of the cutting torque, which will be reflected in the motor current of the cutter head. For the same reason, if the amount of the dredged soil is increased, it will be harder for the underwater pump to suck up the slurry. Hence, the motor current of the underwater pump and the suction vacuum will also be increased as well. The flow velocity, however, will be deceased since it becomes harder for the pump to transport the slurry with higher density.

Slurry Density.

As the objective of the cutting process control is to maintain a high production rate (i.e., slurry density) in the pipeline, the intelligent control models should try to maximize this value. However, according to the reward scheme defined in Equation (7), the action selection should consider the restriction of the other states. In general, Figure 6 demonstrates that the slurry density of the Q-learning, SARSA, and SARSA($\lambda$) change more gently and keep at higher levels of slurry density than the human. Among the intelligent control models, the SARSA($\lambda$) can lead to the highest level of the slurry density. Thus, we can say that the intelligent control models enable the slurry density to be maintained at a consistently high level.

The main reason can be explained by the reward scheme, in which we allow the learning agent to receive a big positive reward, i.e., $10\times C_v$ if the slurry density is greater than $45\%$, so the agent will always try to maximize the slurry density. It should be noted that the reason the slurry density cannot always maintain a high level is because of the environmental uncertainties, e.g., the terrains of the water bed. Nevertheless, we can conclude that the intelligent control models can outperform the experienced human operator with respect to the slurry density, as the intelligent control models have the inherent advantage of maximizing its rewards by selecting the optimal actions in dynamic situations.

Swing Speed.

In Figure 6, we have observed that the slurry density of three intelligent control models changes more gently than human operation. The deeper reason is that the intelligent control models can make quicker responses to the changes of uncertain terrains than the human. The phenomena can also be observed in Figure 6, where the learning agent can flexibly adjust its swing speed to cope with environmental uncertainties. In other words, the learning agent can select the action that can maximize the expected return based on the evaluation of the current states.

Time delay is the underlying reason it is difficult for the human operator to make real-time response to the dynamic environment. For example, the operator has begun to reduce the swing speed at time-step 400, but the measured slurry density still maintained at a high level, as shown in Figure 6. This is because the slurry density measured by a nuclear-based gamma densitometer is installed at the stern of the CSD, so there is a time lag between the swing operation and the measured data. Thus, the operator cannot accurately predict the trend of the slurry density, and, as a result, he continues to decrease the swing speed at around time-step 405, which results in a sharp decline in the subsequent slurry density at around time-step 425. We can conclude that the intelligent control models can outperform the human in a way that can take future rewards into consideration. Comparatively, the decision-making of the human operator mainly depends on the currently collected data, and it will be hard to solve long time lag problems, i.e., the measured slurry density cannot reflect the change of the swing speed in time.

In this work, when the learning agent explores the environment, we do not explicitly provide the information about the time lag problem, and the virtual environment is built up based on historical dredging data. All the data are collected when experienced human operators manipulates the CSD, so the data also contains many samples of unreasonable manipulations. However, from the results we can conclude that the intelligent control methods can learn from the experience of the human operator, and, in addition, improve the performance to avoid unreasonable manipulations.

Motor Current.

When we look at the motor current of the cutter head and the motor current of the pump, we can also find that the curves of the Q-learning, SARSA, and SARSA($\lambda$) change more gently then the curve of the human operation. The motor current of the cutter head reflects the cutting forces and the type of soil to be dredged, while the motor current of the pump indicates the slurry density between the cutter head and the underwater pump. In practice, it is hoped that the change of the motor current does not fluctuate too much and can be stabilized within the rated voltage range. However, it is a challenge task even for the experienced operator to achieve such a goal, as can be seen in Figure 6. Comparatively, all the intelligent control models can ensure that the change of the motor current will be stable and gentle, which is conducive to the safe operation of the motor and improve the service life of the motor. The reason the intelligent control models can keep the motor current stable in uncertain environments is also because of the ability of quick responses. Thus, we can conclude that the reward scheme designed in Equation (7) is effective to ensure the safe operation of the motors of the cutter head and the pump.

Suction Vacuum.

The degree of suction vacuum can indicate the pipeline concentration between the cutter head and the underwater pump, and if the value is too low, it is hard for the underwater pump to suck up the dredged slurry. In this case, the human operator or the intelligent control models should decrease the swing speed. Otherwise, the low vacuum can result in cavitation in the pipeline, which will affect the normal operation of the underwater pump. Thus, in Figure 6 we can see that all the intelligent control models are able to guarantee that the degree of suction vacuum will be kept with the range of −68 to −38 bar. Comparatively, the curve of the suction vacuum produced by the human violently oscillates between −81 to −28 bar. Thus, we can conclude that the adjustment of the swing speed of the intelligent control models takes account of the degree of suction vacuum and ensures that the value will be kept within a suitable range.

Flow Velocity.

As mentioned before, the flow velocity in the pipeline can also indicate the slurry density, and it is considered to be the key indicator for the prevention of blockage. In other words, if the flow velocity is too low, the solids level in the pipeline must be high, and the pipeline will be in danger of being blocked. Thus, the flow velocity must be maintained within a reasonable range. In Figure 6, we can see that all the intelligent control models can maintain the flow velocity at a relatively stable range, while the flow velocity of the human operation varies widely. Hence, we can say that the reward scheme designed in Equation (7) is effective to stabilize the flow velocity. Such a stabilization is achieved by adjusting the swing speed in quick responses, so the flow velocity can be kept with a safety range to avoid the risk of blockage.

5.2.2. Comparison of Production

In Figure 6, we have obtained a general impression that all of the three intelligent control models can outperform the experienced human operator, but we cannot clearly distinguish the performance of the Q-learning, SARSA, and SARSA($\lambda$). Thus, in order to quantitatively distinguish them, Figure 7 depicts the production curves. The production W at time t can be calculated

$$W\left(t\right)=\pi {(D/2)}^2{V}_f\left(t\right)C_v\left(t\right)$$

(11)

where $D=800$ mm is the diameter of the pipeline, $V_f$ is the flow velocity and $C_v$ is the slurry density.

In accordance with Figure 6, we calculate the accumulative production in 500 s in Figure 7. We can see that when the human controls the swing process, its accumulative production is the lowest, i.e., 550 m³. When Q-learning and SARSA take charge of the swing process, their respective production is not much different, and the Q-learning is slightly better than SARSA. Compared with others, the proposed SARSA($\lambda$) can produce the highest production, i.e., 645 m³, and its production has increased by nearly 17.27% in comparison with the human control.

Therefore, we can conclude that the proposed SARSA($\lambda$) is the most effective method to control the swing process for a CSD. It can outperform the human operator in two aspects. First, the intelligent control method can ensure that all the key variables, such as the motor current, suction vacuum, and the flow velocity, will be kept within a reasonable and safety range. Second, the intelligent control method can always try to maximize the slurry density while ensuring safe operation of equipment. As a result, its production also exceeds the human operation.

6. Conclusions

The operation of CSDs is affected by various uncertainties such as the type of soil, the terrain of the water bed, as well as the measurement errors of instruments. Even for an experienced human operator, it is hard to manipulate the cutting process in a stable and efficient manner. In this work, we focus on a learning approach to the sequential decision-making problem of the cutting process. Since the dredging environments contain various uncertainties, it is intractable to design a static model to describe the dynamics of the cutting process. Thus, the proposed learning approach combines a neural network model with a RL model. The neural network model is supposed to construct a concise a virtual environment based on the data collected during the time when an experienced human operator manipulates the CSD. Afterwards, the RL model can learn the optimal control policy by interacting with the virtual environment, without worrying about accidents or mistakes in the trial-and-error learning period. The results show that the proposed learning approach can gain the experience of human operators from historical data, and, in addition, can outperform the experienced human operator with respect to the production, taking account of various operational constraints. It should be noted that after several hours of learning from the data of a single operator, the RL agent cannot build up a perfect mode to cope with all future uncertainties. However, when the RL agent can imitate the behavior of an experienced human operator within a virtual environment, we can allow it to directly interact with a real-world scenario to further improve the model. In this work, we cannot allow the RL agent to learn from scratch in a real CSD because of the safety reasons. Once the learning agent is affordable to control a real CSD, we can allow it to improve itself through trial-and-error interactions in the real-world scenario, which will be investigated in our future work.

Future work will also investigate the RL approach in continuous state space and action space, as well as function approximation methods to store the state transitions, etc.. Moreover, we will look at the model-based RL approach to this problem, in which the environmental model can be built up from samples, and then planning (instead of model-free learning) methods can be used to find the optimal action for each state based on the learned environment model. Lastly, we would like to evaluate the proposed approaches in a real CSD, and it is also our ultimate goal to release human operators from the boring but daunting mission of manipulating the cutting process of a CSD.