Deterministic and Probabilistic Wind Power Forecasting Based on Bi-Level Convolutional Neural Network and Particle Swarm Optimization

Abstract

The intermittency and uncertainty of wind power result in challenges for large-scale wind power integration. Accurate wind power prediction is becoming increasingly important for power system planning and operation. In this paper, a probabilistic interval prediction method for wind power based on deep learning and particle swarm optimization (PSO) is proposed. Variational mode decomposition (VMD) and phase space reconstruction are used to pre-process the original wind power data to obtain additional details and uncover hidden information in the data. Subsequently, a bi-level convolutional neural network is used to learn nonlinear features in the pre-processed wind power data for wind power forecasting. PSO is used to determine the uncertainty of the point-based wind power prediction and to obtain the probabilistic prediction interval of the wind power. Wind power data from a Chinese wind farm and modeled wind power data provided by the United States Renewable Energy Laboratory are used to conduct extensive tests of the proposed method. The results show that the proposed method has competitive advantages for the point-based and probabilistic interval prediction of wind power.

1. Introduction

Due to limitations associated with conventional energy use and increasing environmental issues, wind energy is widely implemented because it represents a source of green renewable energy [1,2]. The main use of wind energy is power generation, converting wind energy into electricity. However, due to the complex nature of the Earth’s atmosphere, the instability of wind energy results in volatility and intermittency of the output power; this creates challenges for large-scale wind power projects and the planning and construction of power grids. Accurate wind power forecasting is one of the most effective measures to meet these challenges [3].

In recent years, many scholars have conducted research on wind power forecasting methods focused on three categories [4]—physical methods, statistical methods, and hybrid methods. Physical methods rely on numerical weather forecasting information and physical information, such as landforms near the wind turbines, to establish a mathematical forecasting model. The calculation process is cumbersome and, therefore, not convenient for real-time forecasting in wind farms [5,6]. Statistical methods are usually based on historical data of wind speed and power, and establish a forecasting model to fit a nonlinear relationship. Statistical methods can be further subdivided into time series methods and machine learning methods [7]. In [8], a linear and nonlinear autoregressive moving average model (ARMA) was established to forecast wind speed; the model provided good forecasting performance in terms of mean absolute error, root mean square error, and mean absolute percentage error. A hybrid model based on the autoregressive integral moving average (ARIMA) was proposed in [9] to achieve ultra-short-term, short-term, medium-term, and long-term forecasting of wind speed. In [10], an autoregressive moving average (ARMAX) model was established to forecast wind power, wind speed, and wind direction, using exogenous variables and a threshold autoregressive method to deal with the intermittency of wind power. As a result of the rapid development of artificial intelligence, some scholars have used artificial neural networks, extreme learning machines, support vector machines, and fuzzy logic systems for wind power forecasting. In [11], a nonlinear autoregressive neural network model was established to forecast multi-step wind speed using direct and recursive strategies. A cross-optimization algorithm was used in [12] to train an extreme learning machine after the second decomposition of a wind power time series for wind power forecasting. Compared to similar models, the proposed method had several advantages. Data mining was used in [13] to correct the original data; a kernel function was optimized and a penalty factor was used in the support vector machine using a cuckoo algorithm to improve the forecasting accuracy of the wind power. In [14], a fuzzy neural network wind power forecasting model based on particle swarm optimization (PSO) was proposed, and fuzzy expert knowledge and neural network learning methods were combined. The hybrid method combines two or more forecasting methods to minimize forecasting errors and improve the reliability of wind power forecasting. In [15], a support vector machine, extreme learning machine, a bat back-propagation neural network (BPNN), and an Elman neural network are combined with dynamic weights to minimize the disadvantages and retain the advantages of the individual networks to improve forecasting accuracy. In [16], a combined forecasting model based on data preprocessing, a nondominated sorting genetic algorithm (NSGA-III) with three objective functions, and four models were proposed and successfully applied to forecasting wind speed.

Although the aforementioned forecasting methods have improved the accuracy of wind power forecasting to varying degrees, they are all shallow learning models, regardless of whether they are time series methods, machine learning methods, or hybrid methods. The learning occurs at a shallow level and not at a deep level. Considering the strong instability of wind power data, shallow learning models are not suitable for modeling the deep nonlinearity of wind power data. In recent years, deep learning models, which are widely used in computer vision and natural language processing, have demonstrated better feature extraction ability than shallow learning models. Therefore, some scholars have used deep learning models for wind power forecasting.

To date, deep learning methods applied in the field of wind power forecasting have included stack automatic encoders, deep belief networks, and convolutional neural networks (CNNs). In [17], deep learning was first used for wind speed forecasting; a stack denoising auto-encoder was used for the unsupervised and supervised classification of wind speed data for forecasting. In [18], the wind speed was forecast using a wavelet transform, a deep-belief network, and quantile regression; the experimental results demonstrated the effectiveness and high accuracy of the proposed method. The abovementioned deep learning models provide more accurate forecasting results than the shallow models, but these results are often based on massive amounts of data, and the calculations and training processes are computationally expensive. Therefore, it is very important to design a forecasting model with less computational complexity. Due to the weight sharing used in CNNs, the number of parameters that have to be optimized are greatly reduced, making the training process simpler and easier to implement. For this reason, a CNN was first used for wind power forecasting in [19]. The probability forecasting of wind power was achieved by combining a wavelet transform with an ensemble approach. The experimental results for different seasons, different temporal resolutions, and different degrees of forecasting confidence showed that this method had great advantages. First, the conversion of wind power values from a one-dimensional time series to matrices that could be used by the CNN was achieved by a simple rearrangement. Considering that a CNN is well suited for extracting local features from input matrices, further research on suitable input matrices is required. Second, the aforementioned method used an ensemble approach to optimize the forecasting results of the CNN and the performance was good, but the advantages of the CNN in extracting depth features can be reused, and the use of multilevel CNNs may extract deeper features. In [20], a phase space reconstruction (PSR) was used to expand the wind power value of a one-dimensional time series into a high-dimensional phase space, permitting the hidden features from the one-dimensional phase space to be revealed in the high-dimensional phase space; subsequently, accurate forecasting of wind power was achieved using a resource allocation network. Based on the success of this research, a bi-level CNN wind power forecasting model that combines variational mode decomposition (VMD) and PSR is proposed in this study. This model takes advantage of the deep-feature extraction of the CNN to improve the accuracy of wind power forecasting. In addition, we determined the uncertainty of wind power forecasting and used a PSO algorithm to optimize the power segment, allowing us to obtain the wind power forecasting interval. The main contributions of this paper are as follows:

(1)

The wind power data is preprocessed using VMD and PSR to obtain data that are better suited for CNNs.

(2)

A forecasting model based on a bi-level CNN and PSO is developed; the model makes full use of the characteristics of CNNs to extract deep features and obtain the probabilistic forecasting interval via PSO.

(3)

The superiority of the proposed method is verified using the wind power data of a Chinese wind farm and the modeled wind power data of the United States Renewable Energy Laboratory.

2. Data Preprocessing

2.1. Variational Mode Decomposition

Due to the instability of wind power, the forecasting error is relatively large when the original wind power sequence is used. Therefore, some scholars have used a decomposition of the original wind power sequence to reduce the complexity of the data, thereby improving forecasting accuracy. At present, commonly used decomposition methods include wavelet transform [21], collective empirical mode decomposition (EEMD) [22], and local mean decomposition (LMD) [23]. The VMD has better anti-noise ability than these decomposition methods, with fewer components; in addition, VMD is capable of separating two pure harmonic signals with similar frequencies [24,25]. Because of to these advantages, VMD is used to decompose the original wind power sequence in this study.

The VMD is a signal decomposition and estimation method for solving variational problems. The objective is to divide the frequency band according to the frequency domain characteristics of the original signal and decompose it into a fixed number of modes. Each mode is a band-pass signal, and its center frequency is automatically updated during the decomposition process. The bandwidth determination is performed as follows: first, the parsed signal of all modes are obtained by using the Hilbert transform; second, the parsed signal spectrum is moved to the baseband; finally, the bandwidth of each mode is estimated using the Gaussian smoothing index H1 of the frequency-shifted signal.

Assuming that the wind power sequence f is decomposed into K modes, the constraint variation problem shown in the following equation can be constructed:

$$\{\begin{array}{c}\underset{\left\{u_k\right\},\left\{{\omega }_k\right\}}{\min }\left\{{\displaystyle \sum _{k=1}^K{\Vert {\partial }_t\left[\left(\sigma (t)+\frac{j}{\pi t}\right)u_k(t)\right]e^{-j{w}_{k}t}\Vert }_2^2}\right\}\\ s.t\begin{array}{cc}& {\displaystyle \sum _{k=1}^K{u}_k(t)=f(t)}\end{array}\end{array}$$

(1)

where $\left\{u_k\right\}=\left\{u_1,\cdot \cdot \cdot ,u_K\right\}$ represents the set of all modes, and $\left\{{\omega }_k\right\}=\left\{{\omega }_1,\cdot \cdot \cdot ,{\omega }_K\right\}$ indicates the center frequency of each mode.

In order to solve the constrained variational model, we need to use a quadratic penalty function term and a Lagrange multiplier to transform Equation (1) into the unconstrained model as shown in Equation (2).

$$L\left(\left\{u_k\right\},\left\{{\omega }_k\right\},\lambda \right)=\alpha {\displaystyle \sum _{k=1}^K{\Vert {\partial }_t\left[\left(\sigma (t)+\frac{j}{\pi t}\right)u_k(t)\right]e^{-j{\omega }_{k}t}\Vert }_2^2}+{\Vert f(t)-{\displaystyle \sum _{k=1}^K{u}_k(t)}\Vert }_2^2+\langle \lambda (t),f(t)-{\displaystyle \sum _{k=1}^K{u}_k(t)}\rangle$$

(2)

In Equation (2), α is the penalty factor, and λ is the Lagrange multiplier. By using the alternating direction multiplier algorithm to obtain the saddle point of the unconstrained model, the final solution to Equation (1) is obtained; this results in the adaptive decomposition of the wind power sequence so that the modes can be obtained.

2.2. Phase Space Reconstruction

The mode obtained by VMD of the original wind power sequence is still a relatively complex signal sequence, which can be regarded as a chaotic time series. The chaotic time series is reconstructed into a high-dimensional phase space using PSR. The obtained high-dimensional phase space matrix not only retains the main features of the mode sequence, but also provides the implicit information of the mode. In this study, the PSR based on the coordinate delay method is used to reconstruct the phase space of the modes.

For a mode sequence $x_1,x_2,\cdot \cdot \cdot ,x_N$, delay time τ and embedding dimension m are used in the coordinate delay reconstruction method to form an m-dimensional phase space:

$$X_i=\left[x_i,x_{i+\tau },\cdot \cdot \cdot ,x_{i+(m-1)\tau }\right]$$

(3)

where $i=1,2,\cdot \cdot \cdot ,L$, $L=N-(m-1)\tau$.

The phase space trajectory matrix X of the reconstructed mode is shown in Equation (4):

$$X=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_L\end{array}\right]=\left[\begin{array}{cccc}{x}_1& x_{1+\tau }& \cdots & x_{1+(m-1)\tau }\\ x_2& x_{2+\tau }& \cdots & x_{2+(m-1)\tau }\\ ⋮& ⋮& & ⋮\\ x_L& x_{L+\tau }& \cdots & x_{L+(m-1)\tau }\end{array}\right]$$

(4)

where the row vector X_i constitutes the phase point of the multi-dimensional phase space L phase points that jointly constitute the phase space trajectory reconstructed by the modes.

During the PSR of the modes, delay time τ and embedding dimension m have to be chosen carefully. If the delay time is too small, the coordinate correlation is too strong to ensure that each phase point in the phase space can provide new information; however, if it is too large, it is difficult to ensure the continuity of the trajectory. Similarly, although a higher-dimensional phase space provides more information, it can also increase the computational time and obscure the structural relationship. Therefore, we use the recently developed C-C method to calculate the delay time τ and the embedding dimension m for the PSR of the modes. For details on the C-C method, please refer to [26].

3. Convolutional Neural Network

A CNN is a deep learning method and has been widely used in the field of computer vision. The weight-sharing mechanism of a CNN is similar to that of biological neural networks in that the complexity of the network model and the number of weights are low. In addition, unlike shallow neural networks, CNNs have a number of hidden layers that perform nonlinear transformations, which is suitable for complex problems and environments. Since conventional neural networks are not well suited for long time-series and are prone to gradient disappearance and overfitting, a CNN is used in this study to predict wind power using the advantage of deep-feature extraction. The core structure of the CNN consists of a convolutional layer and a pooling layer. The network is trained using a Back-Propagation algorithm. The structure of a CNN model is shown in Figure 1.

3.1. Convolutional Layer

The use of the convolutional layer was inspired by the local receptive field of visual cells in living organisms. In a convolutional layer, the upper layer’s map is convolved with a convolution weight, and the output features map is obtained via the activation function. In order to extract the local features of an input map, the convolutional layer usually contains multiple convolution weights to obtain a multiple-output feature map. The size of each output feature map is (N – m + 1) × (N – m + 1), where N is the size of the input feature map, and m is the size of the convolution weight. The details of the convolutional layer are defined in Equation (5):

$$x_j^l=f(b_j^l+{\displaystyle \sum _{i\in M_j}{w}_{ij}^l\ast x_i^{l-1}})$$

(5)

where $x_j^l$ denotes the jth output feature map of the lth layer, the activation function is represented by $f(\cdot )$, $M_j$ is a set of input feature maps, $w_{ij}^l$ is the convolution weight, and $b_j^l$ is the bias.

3.2. Pooling Layer

The pooling operation of the CNN is a downsampling process that further reduces the dimension of the map without affecting the intrinsic data link. By using the principle of local correlation of the matrix data in the downsampling, the matrix data is sub-sampled to reduce the data volume while retaining valuable information. We use a mean pooling algorithm to perform the downsampling, as defined in Equation (6):

$$x_j^l=\frac{1}{N}\ast \left({\displaystyle \sum _{i\in P_j}{x}_i^{l-1}}\right)$$

(6)

where N is the total number of input feature map elements, and $P_j$ is a collection of input feature maps.

3.3. Back-Propagation Training of the CNN

The training of the CNN is based on a classic BP algorithm; each layer of the convolution weight $w_{ij}^l$ and bias $b_j^l$ is adjusted with the objective of minimizing the cumulative error square function $E_m$ of the training output data $t_i$ and the CNN output $p_i$. $E_m$ is specified as follows:

$$E_k=\frac{1}{k}{\displaystyle \sum _{i=1}^k{(t_i-p_i)}^2}$$

(7)

where k is the minimum batch size required for training.

Subsequently, the convolution weights $w_{ij}^l$ and bias are iteratively updated using the stochastic gradient descent method:

$$w_{ij}^l=w_{ij}^l-\eta \cdot \partial E_m/\partial w_{ij}^l$$

(8)

$$b_j^l=b_j^l-\eta \cdot \partial E_m/\partial b_j^l$$

(9)

4. Proposed Approach for Forecasting the Wind Power Intervals

The structure of the proposed model for predicting wind power intervals is shown in Figure 2.

4.1. Wind Power Forecasting Model Based on CNN

In this study, historical wind power data are used as input data for the wind power forecasting. Due to the nonlinearity, non-stationarity, and randomness of the historical wind power data, a bi-level CNN point-based wind power forecasting model based on VMD and PSR is proposed. First, the historical wind power data are smoothed using VMD and decomposed into modes at different scales; each mode is transformed from a one-dimensional sequence into a high-dimensional matrix using the PSR method. Subsequently, each high-dimensional matrix is fed into the first-layer CNN sub-model, and training with a BP algorithm is performed to obtain the forecasted value of each mode. Finally, the forecasted values of the modes and the real values of the modes corresponding to the previous moments are used to create a high-dimensional matrix, which is fed into the second-layer CNN. The final forecasted wind power values are also obtained by training with a BP algorithm. The flowchart of the point-based wind power forecasting model is shown in Figure 3.

4.1.1. Wind Power Data Preprocessing by VMD and PSR

The matrix data in a CNN are similar to the data in image pixels. For one-dimensional wind power data, the convolution and pooling operations require preprocessing (as described in Section 2.1 and Section 2.2) to reduce the complexity of the original wind power data, uncover additional information in the data, and extract high-dimensional matrix information from one-dimensional wind power data. This meets the requirements of the first-layer CNN sub-model for input data, and provides more-accurate modes of forecasting values.

4.1.2. The Second-Layer CNN

Due to the randomness of the wind power data, the modes that are forecast by the first-layer CNN inevitably contain errors. Additional processing is required to minimize the errors and obtain the final point-based wind power data. The second-layer CNN is used for this purpose. The input matrix D of the second layer of the CNN consists of the mode forecasted value $u_{pred}^{i,t}$ of all first-layer CNN sub-models and the previous n mode true values $\left[u_{\mathrm{meas}}^{i,t-1},u_{\mathrm{meas}}^{i,t-2},\cdots ,u_{\mathrm{meas}}^{i,t-n}\right]$. The details are as follows:

$$D=\left[\begin{array}{cccc}{u}_{\mathrm{meas}}^{1,t-n}& \cdots & u_{\mathrm{meas}}^{1,t-1}& u_{\mathrm{pred}}^{1,t}\\ u_{\mathrm{meas}}^{2,t-n}& \cdots & u_{\mathrm{meas}}^{2,t-1}& u_{\mathrm{pred}}^{2,t}\\ ⋮& & ⋮& ⋮\\ u_{\mathrm{meas}}^{p,t-n}& \cdots & u_{\mathrm{meas}}^{p,t-1}& u_{\mathrm{pred}}^{p,t}\end{array}\right]$$

(10)

4.2. Wind Power Probability Interval Prediction

Because wind power data are time series data, there is considerable uncertainty of its prediction results, which has an adverse effect on the safe and stable operation of the power system. Currently, quantitative analysis methods for determining uncertainties in wind power prediction are usually based on the probability distribution of the estimated prediction errors, such as Gaussian distribution and non-parametric kernel density. The former method requires a prior assumption of the prediction error distribution, whereas, in the latter method, it is difficult to determine suitable bandwidth parameters for the estimation. An alternate method for wind power uncertainty analysis is the use of an optimization algorithm to predict the wind power interval; this method does not require statistical inference and hypothesis testing. Therefore, we use PSO to optimize the predicted value of wind power in different power segments, and to then obtain the predicted wind power interval. A detailed schematic diagram of the process is shown in Figure 4.

4.2.1. Optimizing the Objective Function

The selection of the objective function in PSO is very important because it affects the optimization results. Reliability and accuracy are two indices for evaluating the prediction interval. Reliability is defined as the probability that the actual observation falls within the prediction interval. The value should be as large as possible to make the prediction more reliable. Accuracy is used to predict the width of the interval, which should be as small as possible so that the prediction width is as narrow as possible. However, the two indices are contradictory; therefore, we construct a comprehensive optimization objective function F that takes both accuracy and reliability into account.

$$\underset{\beta }{\min }F={\displaystyle \sum _{i=1}^n}\left[{\gamma }_i\left|PIC{E}_t^{\left(\alpha \right)}\right|+{\phi }_i\left|PINA{W}_t^{\alpha }\right|\right]$$

(11)

where ${\gamma }_i$ and ${\phi }_i$ are the weights of prediction interval coverage error (PICE) and prediction interval normalized average width (PINAW), and $|\cdot |$ are the absolute values of PICE and PINAW. PICE = |PINC − PICP| (prediction interval nominal confidence (PINC) is the confidence level). The prediction interval coverage probability (PICP) reflects the probability that the actual observation value $t_i$ falls within the upper and lower bounds of the prediction interval:

$$\mathrm{PICP}=\frac{1}{N_t}{\displaystyle \sum _{i=1}^{N_t}}{\kappa }^{\left(\alpha \right)}$$

(12)

where $N_t$ is the number of predicted samples, and $k$ is the Boolean quantity. If the predicted target value $t_i$ is included in the upper and lower bounds of the prediction interval, then $k=1$; otherwise $k=0$. PICP should be close to PINC.

PINAW is the average bandwidth index of the prediction interval and reflects sharpness. If the PINAW is too wide, it cannot effectively predict information of uncertainty.

$$\mathrm{PINAW}=\frac{1}{N_t}{\displaystyle \sum _{i=1}^{N_t}}\left[U_t^{\alpha }\left(x_i\right)-L_t^{\alpha }\left(x_i\right)\right]$$

(13)

Adjusting the weight factor controls the degree of influence of different criteria on the optimization results.

4.2.2. PSO of the Prediction Interval in Different Power Segments

The characteristics of wind power differ in different wind power segments. To eliminate these differences, the prediction interval in different power segments is optimized using PSO. First, the wind power sequence is equally divided into power segments and PSO is used to optimize the different power segments. The specific process for each power segment is as follows.

The optimal prediction interval is divided into a training stage and a prediction stage. The wind power prediction data are divided into a training dataset $p_1$ and a testing dataset $p_2$. In the training stage, the training dataset $p_1$ represents the input. The observation values of the prediction data are multiplied by the initial upper-limit coefficient ${\beta }_{up}^0$ and the initial lower-limit coefficient ${\beta }_{low}^0$ to represent the initial upper limit $U_0$ and the initial lower limit $L_0$ of the prediction interval, respectively. Next, the initial upper-limit coefficient ${\beta }_{up}^0$ and the initial lower-limit coefficient ${\beta }_{low}^0$ are optimized using PSO to minimize the objective function $F$. The optimal upper-limit coefficient ${\beta }_{up}^{best}$ and the optimal lower-limit coefficient ${\beta }_{low}^{best}$ are obtained. In the prediction stage, the testing dataset $p_2$ is multiplied by ${\beta }_{up}^{best}$ and ${\beta }_{low}^{best}$ to obtain the final wind power prediction interval $\left[U_t,L_t\right]$.

5. Case Analysis

In Section 5.1, the proposed method for wind power prediction based on VMD, PSR, bi-level CNN, and PSO is extensively evaluated and benchmarked using real data from a wind farm in Gansu province, China. In order to further illustrate the universality of the proposed method, the modeled wind power data provided by the United States Renewable Energy Laboratory are used to conduct tests of the proposed method in Section 5.2.

5.1. Investigations of a Wind Farm in Gansu Province

5.1.1. Experimental Settings

Wind power data from a 2-MW standard wind turbine located at a wind farm in Gansu province from 1 July 2014 to 31 August 31 2014 were used as the experimental data. The data was sampled at 10-minute intervals and normalized. The first 7000 points of data were used as the training set, and the next 1500 points were used as the test set. The input parameters of the point-based wind power prediction model were the previous nine wind power values, with the number of required data points determined by repeated trials. The input wind power sequence was decomposed into five modes using VMD, and five modes were reconstructed using PSR to obtain five matrices of 3 × 5. The matrices were fed into the first-layer CNN sub-models to obtain the predicted values of the modes. The predicted values of the five modes and the four previous actual values formed a 5 × 5 matrix, which was fed into the second-layer CNN to obtain the predicted values of the wind power. Finally, the wind power interval was obtained using PSO.

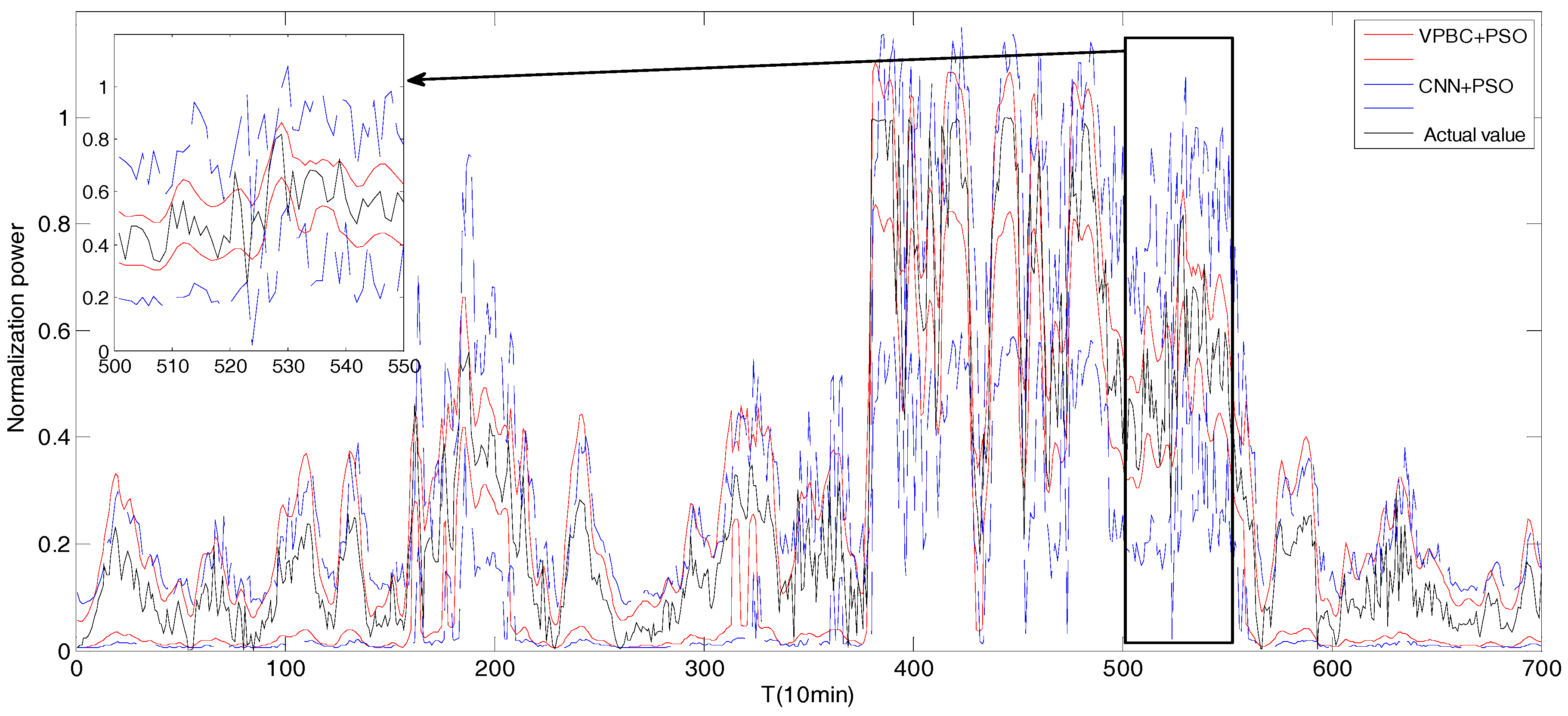
5.1.2. Experimental Results

CNN has more advantages than a BP neural network and support vector machine (SVM) in the field of wind power prediction, which was proven in [18]. Therefore, in order to verify the advantages of the VPBC (VMD + PSR + bi-level CNN) + PSO proposed in this paper, the performance of point prediction and interval prediction were compared and verified, respectively. Comparing the point-based forecasting results with the persistence method, CNN, and VPCB (VMD + PSR + CNN-BPNN), the interval prediction results were compared with CNN + PSO, VPCB + PSO. The above prediction algorithms were implemented in MATLAB (2014a, The MathWorks, Natick, MA, USA).

1. Point-Based Forecasting Performance

The normalized mean absolute error (NMAE), normalized root mean square error (NRMSE) and mean absolute percentage error (MAPE) were used to evaluate the accuracy of the forecasting results. The definitions of the NMAE and NRMSE are provided in [3], and the definition of the MAPE is provided in [18]. The one-step forecasting results of the modes obtained by the five sub-models of the first-layer CNN are shown in Figure 5.

It is observed in Figure 5 that the forecasting results of the first-layer CNN using VPBC + PSO were in good agreement with the actual modes, especially for the high-frequency modes, which is attributed to the strong periodicity of the high-frequency modes.

The partial forecasting results of the VPBC method are shown in Figure 6. The NMAE, NRSME, and MAPE values of the different methods are listed in

Table 1. Forecasting error indices of the different methods. NMAE: normalized mean absolute error; NRSME: normalized root mean square error; MAPE: mean absolute percentage error; VPCB: VMD + PSR + CNN-BPNN.

Method	NMAE	NRSME	MAPE
VPBC	3.69%	0.3339	6.46%
CNN	6.52%	0.3811	11.41%
VPCB	4.64%	0.3663	8.11%
Persistence	5.01%	0.3375	8.56%

.

Figure 6 indicates that the prediction results of the VPBC method were in good agreement with the actual wind power data, demonstrating a good performance for short-term wind power forecasting. The peak values at 180–280 points in Figure 6 show that the forecasted wind power was lower than the actual wind power. The input data for the models were the historical wind power data, and the forecasted values at a given time depended on the actual values of the previous time, so the models had certain predictive inertia. However, the VPBC method provided more accurate predictions than the other models.

As shown in Table 1, the VPBC method had the smallest NMAE, NRMSE, and MAPE, and therefore had the highest forecasting accuracy. The VPBC method had a significantly better forecasting performance than the VPCB and persistence methods, and the historical real value of the mode in the second-layer CNN was used to modify the forecasted value.

2. Interval forecasting performance

The PICP and PINAW indices for the different methods and different confidence levels are listed in

Table 2. Performance indicators for the interval forecasting of the different methods. PINC: prediction interval nominal confidence; PICP: prediction interval coverage probability; PINAW: prediction interval normalized average width.

Method	PINC 80%		PINC 85%		PINC 90%
	PICP	PINAW	PICP	PINAW	PICP	PINAW
VPBC + PSO	85.14%	0.1371	87.86%	0.1587	91.86%	0.1876
VPCB + PSO	81.29%	0.1521	85.43%	0.1725	89.57%	0.2041
CNN + PSO	83.71%	0.2182	86.00%	0.2477	90.14%	0.2885

. Figure 7, Figure 8 and Figure 9 show the interval forecasting results of the VPBC + PSO method and CNN + PSO method for different confidence levels, and Figure 10, Figure 11 and Figure 12 show the interval forecasting results of the VPBC + PSO method and VPCB + PSO method for different confidence levels.

The results in Table 2 show that the PICP indices of the VPBC + PSO method at the 80%–90% PINC met the confidence level requirements; the method exhibited the highest reliability in terms of wind power interval forecasting, while the PINAW index was lowest for this method at the 80%–90% confidence level. This indicates that this forecasting accuracy was the highest. The VPBC + PSO method had better predictive ability than the other two methods.

Figure 7, Figure 8 and Figure 9 show that the forecasting intervals for different PICP levels obtained from the VPBC + PSO and CNN + PSO methods were similar to the actual values of the wind power; however, the inserts in Figure 7, Figure 8 and Figure 9 show that the forecasting intervals were smaller for the VPBC + PSO method than the CNN + PSO method in each time period, demonstrating the advantages of the VPBC + PSO method. This is in agreement with the PINAW index data shown in Table 2.

Figure 10, Figure 11 and Figure 12 indicate that the bandwidth of the forecasting intervals for the different PICP levels was narrow in the VPBC + PSO and VPCB + PSO methods; however, the inserts in Figure 10, Figure 11 and Figure 12 show that the forecasting intervals obtained from the VPBC + PSO method were more similar to the true values of the wind power than those obtained from the CNN + PSO method for each time period. These results demonstrate the advantages of the VPBC + PSO method, which is in agreement with the PICP index results shown in Table 2.

3. PSO performance

In order to verify the performance of the PSO in the VPBC + PSO method, we used a genetic algorithm (GA) optimization for comparison.

The results of the forecasting intervals obtained by the two optimization algorithms are listed in

Table 3. Comparison of the performance indicators for wind power interval forecasting using PSO and GA optimization. GA: genetic algorithm.

Method	PINC 80%		PINC 85%		PINC 90%
	PICP	PINAW	PICP	PINAW	PICP	PINAW
VPBC + PSO	85.14%	0.1371	87.86%	0.1587	91.86%	0.1876
VPBC + GA	83.86%	0.1381	86.29%	0.1624	91.14%	0.1880

and Figure 13 and Figure 14.

Table 3 shows that the PICP and PINAW indices were slightly higher for the PSO than the GA optimization for the 80%–90% PINC. However, it is observed in Figure 13 and Figure 14 that for the PSO, the objective function decreased faster and the number of iterations required to obtain the optimal solution was less than half that of the GA. These results clearly show that the PSO optimization was more efficient than the GA optimization.

5.2. Investigations on the Danforth Wind Farm

5.2.1. Experimental Settings

The Danforth wind farm has a total capacity of 25.5 MW and 17 wind turbines, each of which produces 1.5 MW. Wind power data with a length of 8500 sampling points from 1 January 1 2012 was obtained using a five-minute sampling interval. The data were normalized. The first 7000 points of the dataset were used as the training set, and the next 1500 points were used as the test set. The other parameters were the same as described in Section 5.1.

5.2.2. Experimental Results

Table 4. Comparison of the forecasting error indices of the different methods.

Method	NMAE	NRSME	MAPE
VPBC	1.39%	0.2548	2.65%
CNN	3.14%	0.3295	5.97%
VPCB	2.10%	0.2686	3.99%
Persistence	1.42%	0.2313	2.69%

lists the point-based forecasting error indicators for each forecasting method, and Figure 14 and Figure 15 show the performance indicators for the interval forecasting of each method.

Table 4 shows that the VPBC method had the smallest NMAE and MAPE, and the NRMSE was close to the smallest value of persistence method, indicating that the point-based prediction accuracy was superior for this method. However, the accuracy of the VPBC method was not significantly higher than that of the other three methods. The reason for this is that the Danforth wind power data provided by the United States Renewable Energy Laboratory were modeling data, and contained less noise. Therefore, the prediction error for the three methods was significantly lower than the errors shown in Table 1.

Figure 15 shows that for different PINC levels, the PICP index was highest for the VPBC method, indicating that this method has higher reliability for predicting wind power intervals. Figure 16 shows that the interval widths forecast by the VPBC method were smaller than those of the other two methods for the different PINC levels, demonstrating a higher forecasting accuracy for this method.

6. Conclusions

The intermittency and volatility of wind power generation pose challenges to the safety and stable operation of power grids. Accurate and reliable probabilistic prediction of wind power is of great significance to solving this problem. In this paper, a new wind power probability interval prediction method based on VMD, PSR, CNN, and PSO was proposed. In case studies of the analysis of wind power data from the Gansu wind farm in China and the Danforth wind farm data provided by the Renewable Energy Laboratory, the VPBC + PSO method provided better predictive performance than comparable methods, and this performance advantage was especially apparent for the Gansu wind farm data. Due to the strong anti-interference ability of VMD, the ability of PSR to extract hidden information from the sequence, and the ability of CNNs to learn deep-feature information, the proposed method exhibits good performance for the prediction of wind power intervals in practical applications. Although the advantages of CNNs for deep-feature extraction and for forecasting wind power were demonstrated, there is room for improvement when using these methods in the field of wind power generation, and we will focus on this in future studies.