Experimental Study on Mechanical Properties and Fractal Dimension of Pore Structure of Basalt–Polypropylene Fiber-Reinforced Concrete
Abstract
:1. Introduction
2. Materials and Test Methods
2.1. Materials
2.2. Mix Proportions
2.3. Test Method
2.3.1. Mechanical Properties
2.3.2. Pore Structure
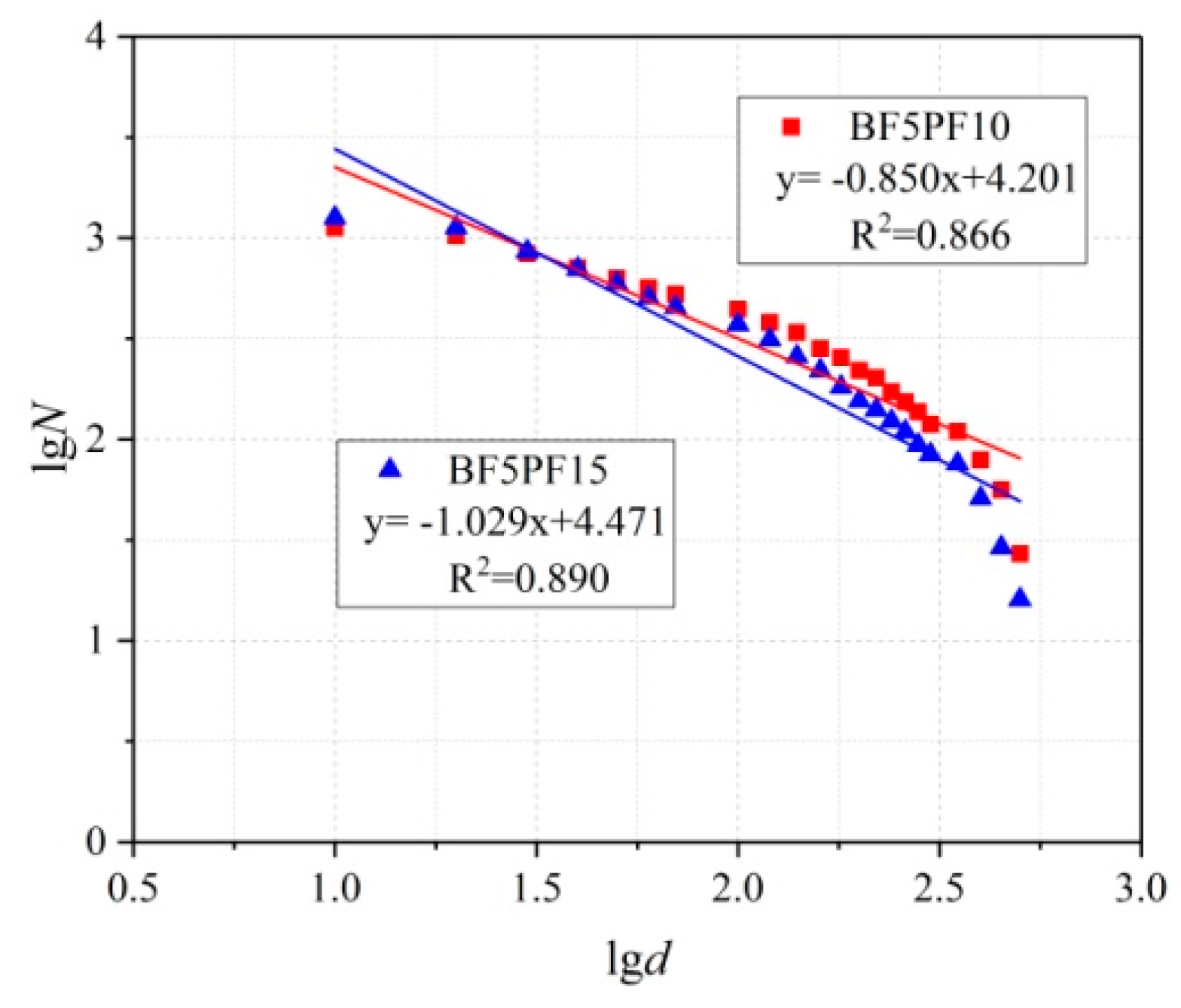
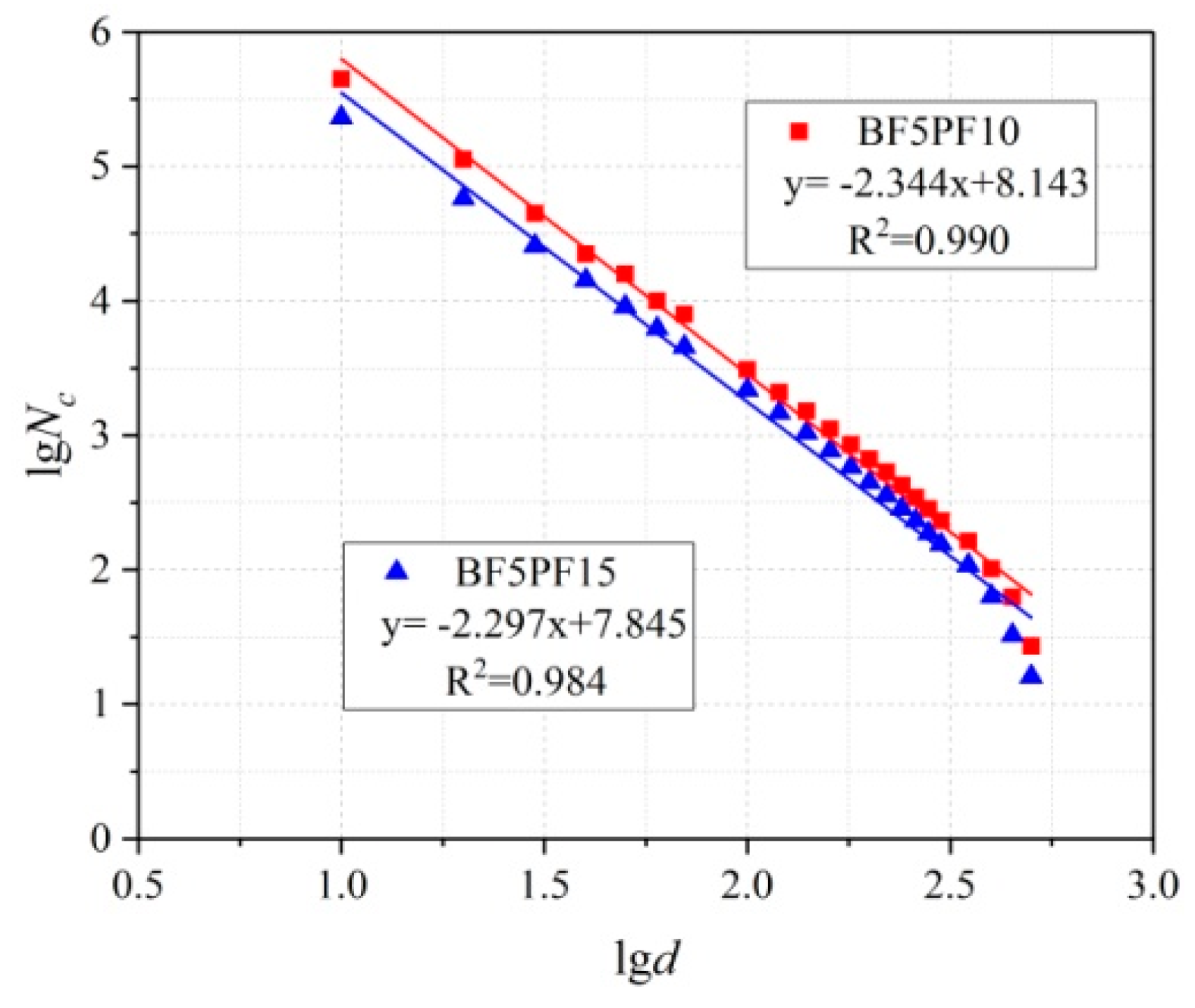
3. Fractal Model Based on Optical Method
4. Experimental Results and Discussion
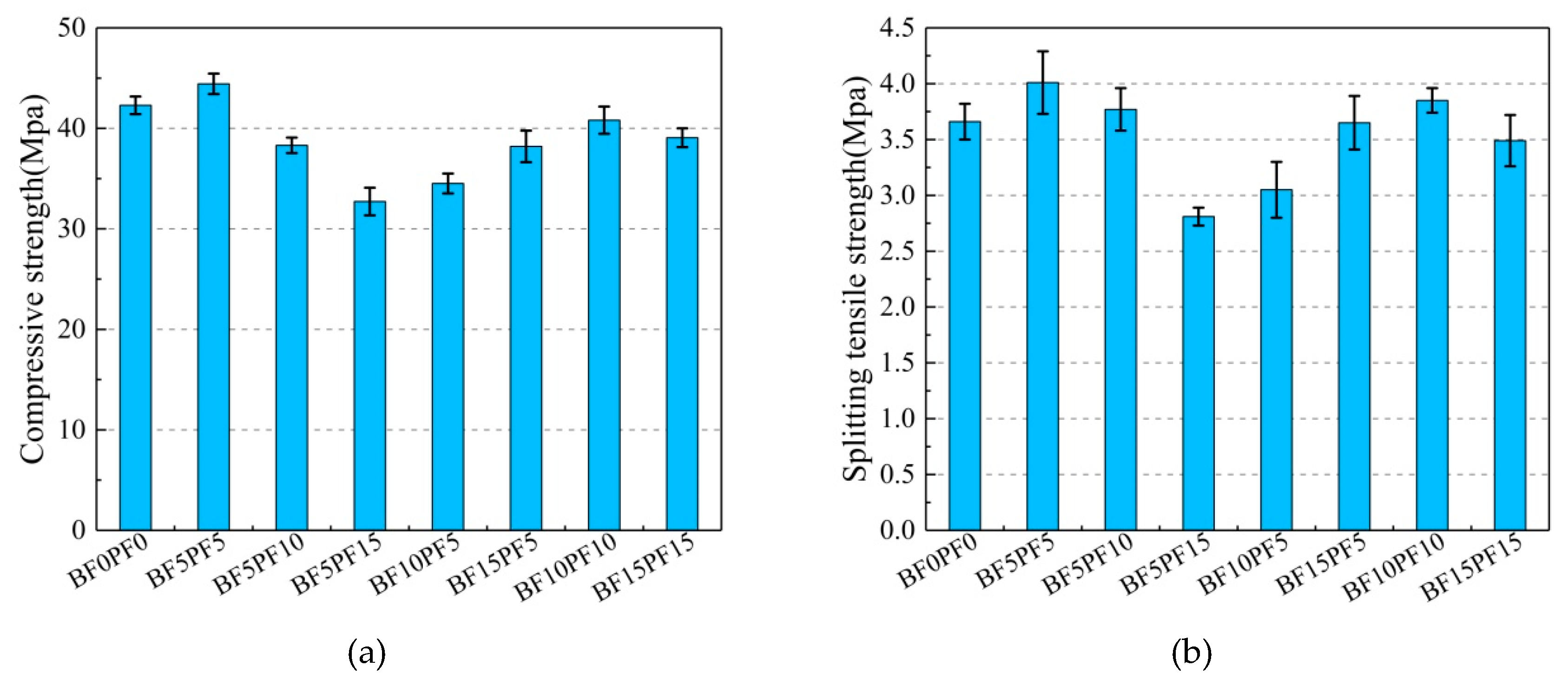
4.1. Mechanical Properties
4.2. Fractal Dimension of Hardened Concrete
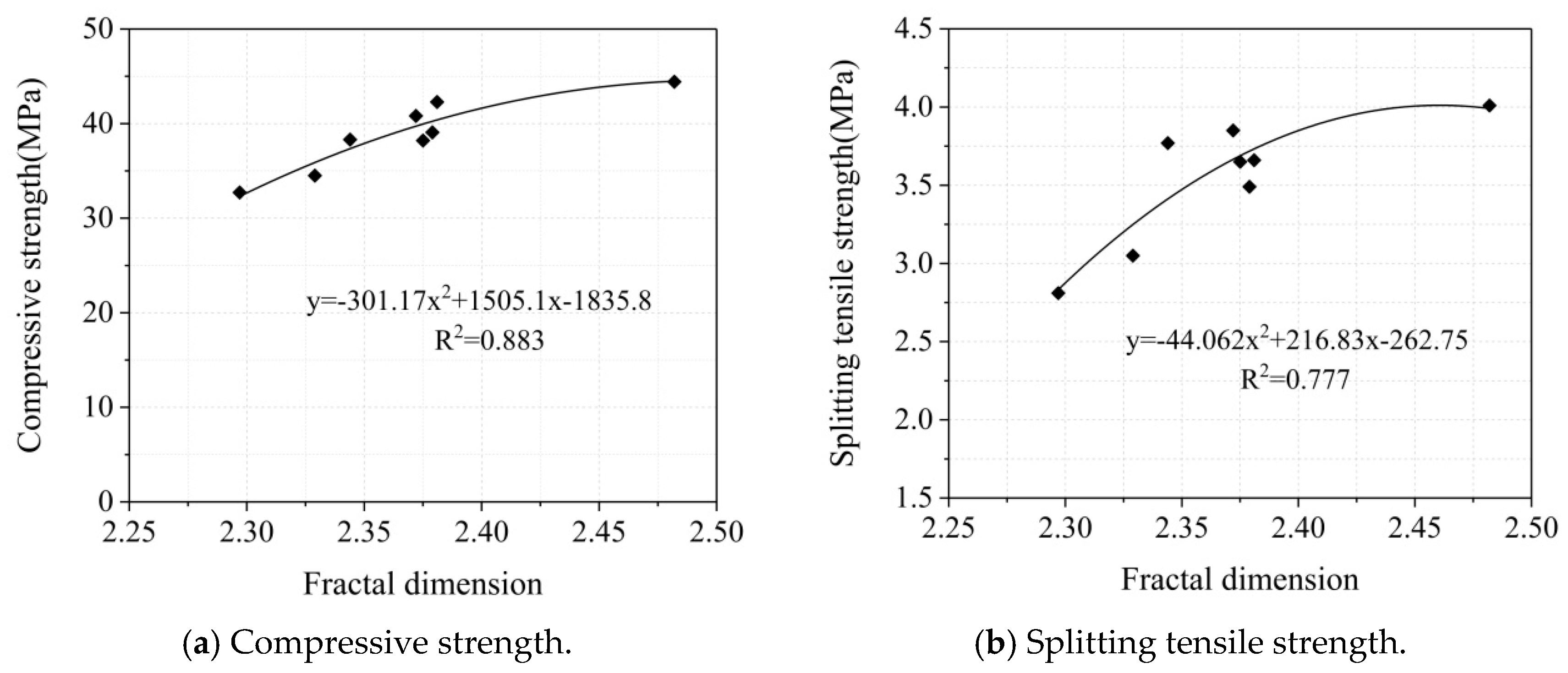
4.3. Relationship Between Fractal Dimension and Mechanical Properties
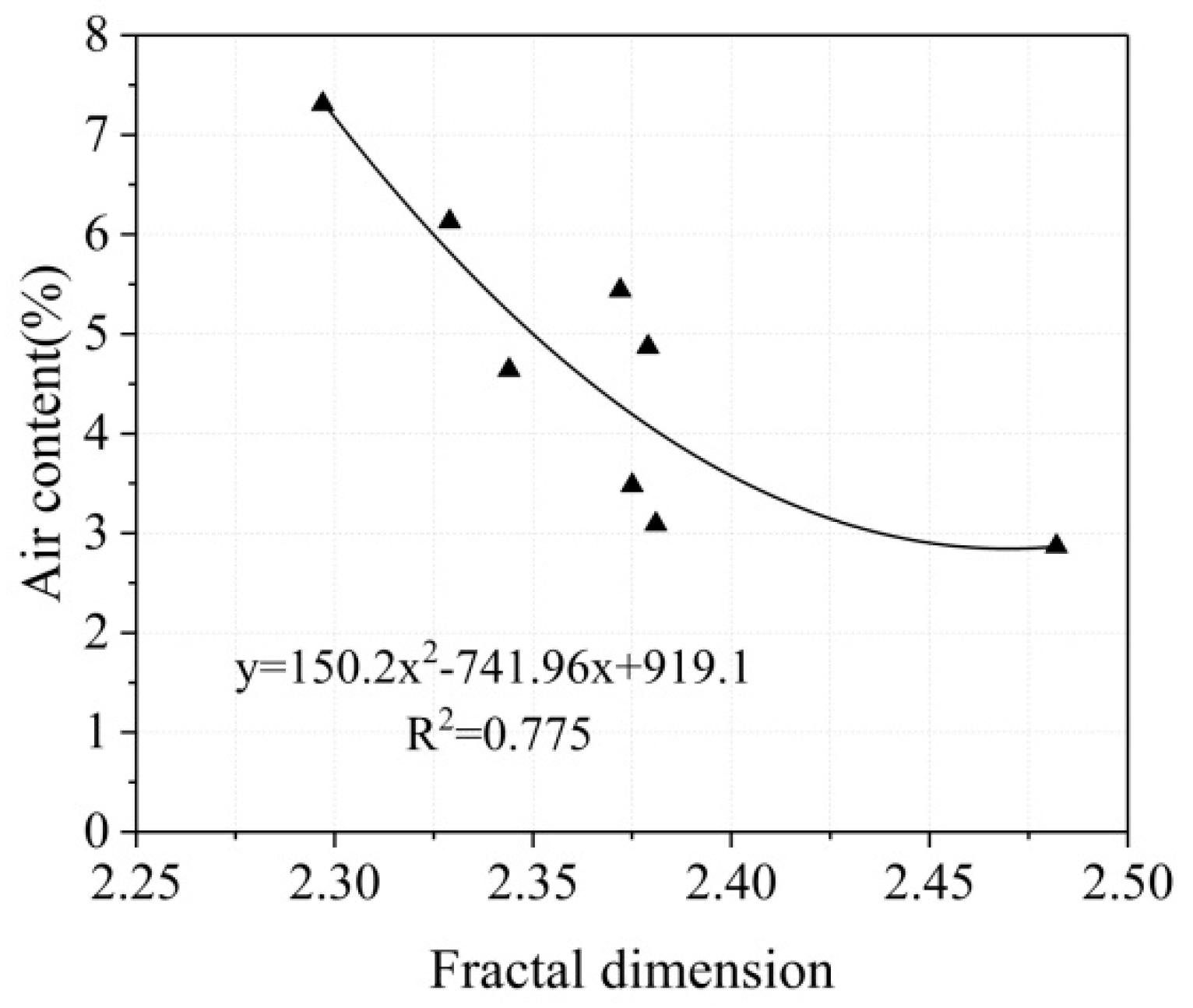
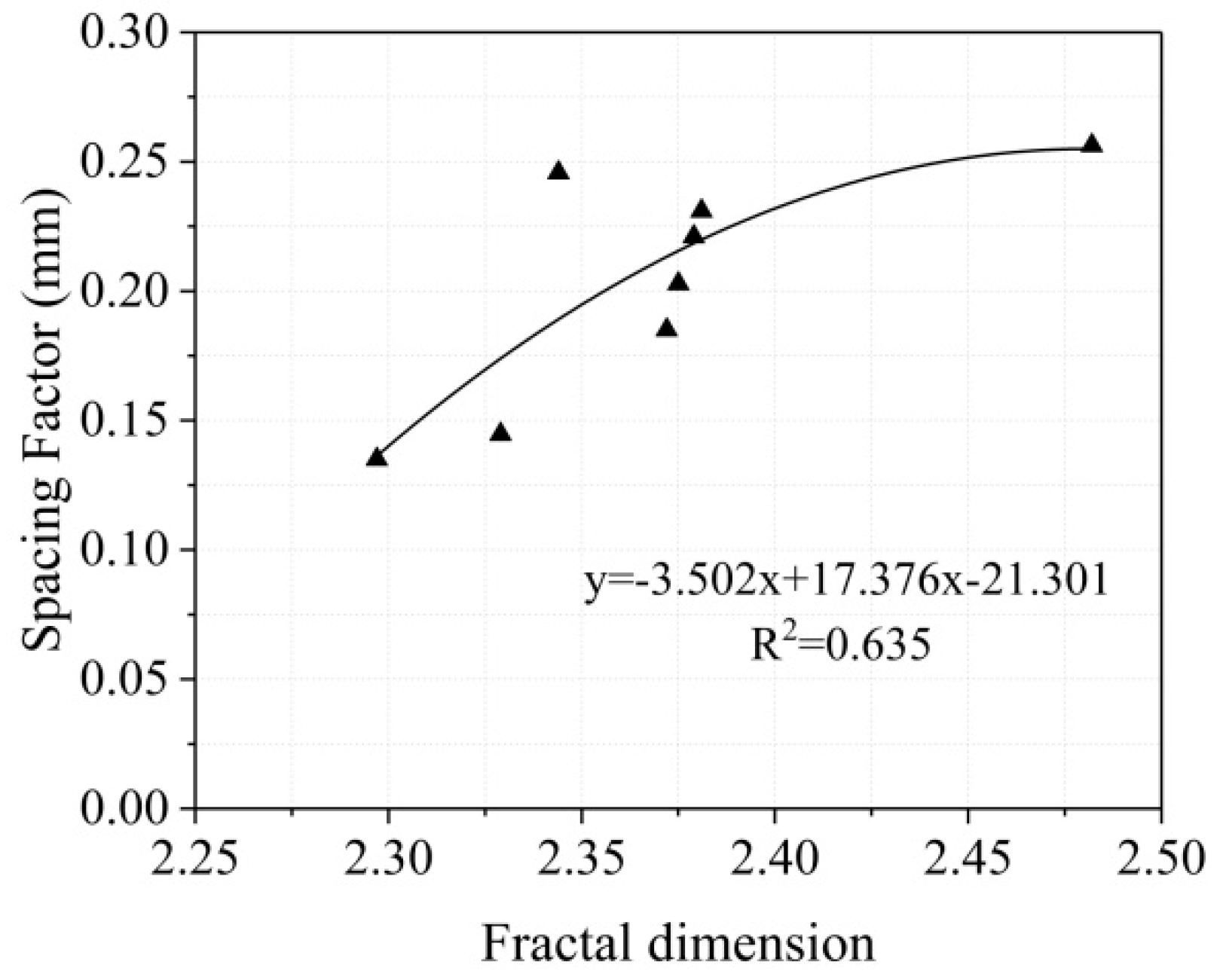
4.4. Relationship Between Fractal Dimension and Pore Structure Parameters
5. Conclusions
- Incorporation of a hybrid mixture of BF and PF into concrete has both positive and adverse effects on the mechanical properties of concrete. The synergistic effect of the hybrid fibers is greatest when the BF and PF contents are 0.05% each; the corresponding increments in the compressive strength and splitting tensile strength 5.06% and 9.56%, respectively. The effect of the hybrid fibers on the splitting tensile strength is greater than that on compressive strength. However, when the fiber content is too high, the hybrid fibers have adverse effects on the mechanical properties. Therefore, accurate control of the fiber content of concrete is necessary.
- The pore structure of BPFRC exhibits fractal characteristics. The fractal dimension of the pore structure calculated using a fractal model based on an optical method is in the range of 2.297–2.482, with a high correlation coefficient (R2 > 0.977); this indicates that the fractal dimension calculated using this model can well-characterize the pore size distribution characteristics of concrete.
- The fractal dimension of BPFRC is closely related to the air content and spacing factor. As the fractal dimension increases, the air content decreases and the spacing factor increases. Therefore, the pore structure characteristics of BPFRC can be evaluated comprehensively using the fractal dimension. In addition, the fractal dimension has a strong positive correlation with the compressive strength and splitting tensile strength of concrete. That is, the larger the fractal dimension, the higher the compressive strength and splitting tensile strength. This indicates that the complexity of the pore structure is an important factor affecting the macroscopic mechanical properties of concrete.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jin, W.L.; Zhao, Y.X. Durability of Concrete Structures, 2nd ed.; Science Press: Beijing, China, 2014; pp. 13–17. [Google Scholar]
- Li, Y.; Zhao, W. Resistance Crack Toughening and Durability of Hybrid Fiber Concrete, 1st ed.; Science Press: Beijing, China, 2012; pp. 1–6. [Google Scholar]
- Xue, M.K. Research of Mechanical Properties for Basalt and Polypropylene Mixed Fiber Concrete. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2018. [Google Scholar]
- Ghazy, A.; Bassuoni, M.T.; Maguire, E.; Oloan, M. Properties of Fiber-Reinforced Mortars Incorporating Nano-Silica. Fibers 2016, 4, 6. [Google Scholar] [CrossRef]
- Afroughsabet, V.; Biolzi, L.; Ozbakkaloglu, T. High-Performance Fiber-Reinforced Concrete: A Review. J. Mater. Sci. 2016, 51, 6517–6551. [Google Scholar] [CrossRef]
- Tadepalli, P.R.; Mo, Y.L.; Hsu, T.T.C. Mechanical Properties of Steel Fibre Concrete. Mag. Concr. Res. 2013, 65, 462–474. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Xu, Q.W. Microscopic, Physical and Mechanical Analysis of Polypropylene Fiber Reinforced Concrete. Mater. Sci. Eng. A 2009, 527, 198–204. [Google Scholar] [CrossRef]
- Badogiannis, E.G.; Christidis, K.I.; Tzanetatos, G.E. Evaluation of the Mechanical Behavior of Pumice Lightweight Concrete Reinforced with Steel and Polypropylene Fibers. Constr. Build. Mater. 2019, 196, 443–456. [Google Scholar] [CrossRef]
- Pajak, M. Investigation on Flexural Properties of Hybrid Fibre Reinforced Self-Compacting Concrete. Procedia Eng. 2016, 161, 121–126. [Google Scholar] [CrossRef]
- Aslani, F.; Nejadi, S. Self-Compacting Concrete Incorporating Steel and Polypropylene Fibers: Compressive and Tensile Strengths, Moduli of Elasticity and Rupture, Compressive Stress-Strain Curve, and Energy Dissipated Under Compression. Compos. Part B Eng. 2013, 53, 121–133. [Google Scholar] [CrossRef]
- Li, C.R.; Wang, X.Z.; Liu, H.X.; Hu, K.X.; Li, G. Research Progress of Hybrid Fiber Reinforced Concrete. J. Mater. Sci Eng. 2018, 36, 504–510. [Google Scholar]
- Jiang, C.H.; Fan, K.; Wu, F.; Chen, D. Experimental Study on the Mechanical Properties and Microstructure of Chopped Basalt Fibre Reinforced Concrete. Mater. Des. 2014, 58, 187–193. [Google Scholar]
- Fiore, V.; Scalici, T.; Bella, G.D.; Valenza, A. A Review on Basalt Fibre and its Composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Wang, D.H.; Ju, Y.Z.; Shen, H.; Xu, L.B. Mechanical Properties of High Performance Concrete Reinforced with Basalt Fiber and Polypropylene Fiber. Constr. Build. Mater. 2019, 197, 464–473. [Google Scholar] [CrossRef]
- Kong, X.Q.; Yuan, S.L.; Dong, J.K.; Gang, J.M.; Zhang, W.J. Experimental Study on Performance of Polypropylene-Basalt Hybrid Fiber Reinforced Recycled Aggregate Concrete after Exposure to Elevated Temperatures. Sci. Technol. Eng. 2018, 18, 101–106. [Google Scholar]
- Zhao, B.B.; He, J.J.; Wang, X.Z.; Zheng, S.W. Experimental Study on Mechanical Properties of Concrete with Basalt-Polypropylene Hybrid Fiber. China Concr. Cem. Prod. 2014, 8, 51–55. [Google Scholar]
- He, J.J.; Shi, J.P.; Wang, X.Z.; Han, T.L. Effect of Hybrid Effect on the Mechanical Properties of Hybrid Fiber Reinforced Concrete. Fiber Reinf Plast Compos. 2016, 9, 26–31. [Google Scholar]
- Wu, P.; Wang, J.; Wang, X.Y. A Critical Review of the Use of 3-D Printing in the Construction Industry. Autom. Constr. 2016, 68, 21–31. [Google Scholar] [CrossRef]
- Christ, S.; Schnabel, M.; Vorndran, E.; Groll, J.; Gbureck, U. Fiber Reinforcement during 3D Printing. Mater. Lett. 2015, 139, 165–168. [Google Scholar] [CrossRef]
- Hambach, M.; Volkmer, D. Properties of 3D-Printed Fiber-Reinforced Portland Cement Paste. Cem. Concr. Compos. 2017, 79, 62–70. [Google Scholar] [CrossRef]
- Panda, B.; Paul, S.C.; Tan, M.J. Anisotropic Mechanical Performance of 3D Printed Fiber Reinforced Sustainable Construction Material. Mater. Lett. 2018, 184, 1005–1010. [Google Scholar] [CrossRef]
- Ma, G.W.; Li, Z.J.; Wang, L.; Wang, F.; Sanjayan, J. Mechanical Anisotropy of Aligned Fiber Reinforced Composite for Extrusion-Based 3D Printing. Constr. Build. Mater. 2019, 202, 770–783. [Google Scholar] [CrossRef]
- Yousfi, A.; Fréour, S.; Jacquemin, F. Eshelby-Kröner Viscoelastic Self-Consistent Model: Multi-Scale Behavior of Polymer Composites Under Creep Loading. Adv. Mater. Res. 2013, 682, 105–112. [Google Scholar] [CrossRef]
- Xiao, J.H.; Xu, Y.L.; Zhang, F.C. A Generalized Self-Consistent Method for Nano Composites Accounting for Fiber Section Shape under Antiplane Shear. Mech. Mater. 2015, 81, 94–100. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Lukkassen, D.; Persson, L.-E.; Wall, P. Some Engineering and Mathematical Aspects on the Homogenization Method. Compos. Eng. 1995, 5, 519–531. [Google Scholar] [CrossRef]
- Cai, Y.W. Asymptotic Homogenization of Periodic Plate and Micro-Structural Optimization. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2014. [Google Scholar]
- Lian, C.; Zhuge, Y.; Beecham, S. The Relationship between Porosity and Strength for Porous Concrete. Constr. Build. Mater. 2011, 25, 4294–4298. [Google Scholar] [CrossRef]
- Arandigoyen, M.; Alvarze, J.I. Pore structure and Mechanical Properties of Cement–Lime Mortars. Cem. Concr. Res. 2007, 37, 767–775. [Google Scholar] [CrossRef]
- Jin, S.S.; Zhang, J.X.; Han, S. Fractal Analysis of Relation between Strength and Pore Structure of Hardened Mortal. Constr. Build. Mater. 2017, 135, 1–7. [Google Scholar] [CrossRef]
- Cui, S.A.; Liu, P.; Cui, E.Q.; Su, J.; Huang, B. Experimental Study on Mechanical Property and Pore Structure of Concrete for Shotcrete use in a Hot-Dry Environment of High Geothermal Tunnels. Constr. Build. Mater. 2018, 173, 124–135. [Google Scholar] [CrossRef]
- Zhao, Y.R.; Guo, Z.L.; Fan, X.Q.; Shi, J.N.; Wang, L. Basalt Fiber Reinforced Concrete Stress-Strain Relationship and Pore Structure Analysis. Bull. Chin. Ceram. Soc. 2017, 36, 4142–4150. [Google Scholar]
- Yu, L.H.; Ou, H.; Duan, Q.P. Research on Pore Volume Fractal Dimension and its Relation to Pore Structure and Strength in Cement Paste with Perlite Admixture. J. Mater. Sci. Eng. 2007, 25, 201–204. [Google Scholar]
- Ji, X.; Chan, S.Y.N.; Feng, N. Fractal Model for Simulating the Space-Filling Process of Cement Hydrates and Fractal Dimensions of Pore Structure of Cement-Based Materials. Cem. Concr. Res. 1997, 27, 1691–1699. [Google Scholar] [CrossRef]
- Chinese National Standards. GB/T 50081-2002, Standard for Method of Mechanical Properties on Ordinary Concrete, 1st ed.; China Architecture and Building Press: Beijing, China, 2003; pp. 12–24. [Google Scholar]
- Chu, W.Y. Fractals in Materials Science, 1st ed.; Chemical Industry Press: Beijing, China, 2004; pp. 3–32. [Google Scholar]
- Hu, W. Modeling the Influence of Composition and Pore Structure on Mechanical Properties of Autoclaved Cellular Concrete. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 1997. [Google Scholar]
- Tang, M. Study on Fractal Characteristics and Application of Concrete Materials. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2003. [Google Scholar]
- Zhang, J.X.; Jin, S.S. Micropore Structure of Cement Concrete and Its Function, 1st ed.; Science Press: Beijing, China, 2014; pp. 34–44. [Google Scholar]
- Sadrinejad, I.; Madandoust, R.; Ranjbar, M.M. The Mechanical and Durability Properties of Concrete Containing Hybrid Synthetic Fibers. Constr. Build. Mater. 2018, 178, 72–82. [Google Scholar] [CrossRef]
- Liu, D.C. Study on the Properties of Basalt and Polypropylene Mixed Fiber Concrete. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2018. [Google Scholar]
- Mydin, M.A.O.; Soleimanzadeh, S. Effect of Polypropylene Fiber Content on Flexural Strength of Lightweight Foamed Concrete at Ambient and Elevated Temperatures. Adv. Appl. Sci. Res. 2012, 3, 2837–2846. [Google Scholar]
- Yap, S.P.; Alengaram, U.J.; Jumaat, M.Z. Enhancement of Mechanical Properties in Polypropylene-and Nylon-Fibre Reinforced Oil Palm Shell Concrete. Mater. Des. 2013, 49, 1034–1041. [Google Scholar] [CrossRef]
- Li, Y.X.; Chen, Y.M.; He, X.Y. Pore Volume Fractal Dimension of Fly Ash-Cement Paste and its Relationship between the Pore Structure and Strength. J. Chin. Ceram. Soc. 2003, 31, 774–779. [Google Scholar]
- Liu, H.Y.; Li, H.Y.; Zou, C.X. Effect of Fiber Elastic Modulus on Concrete Bubble Fractal Dimension and Frost Durability of Light-Weight Aggregate Concrete. Bull. Chin. Ceram. Soc. 2015, 34, 3039–3044. [Google Scholar]
- Shi, Y.; Yang, H.Q.; Chen, X.; Li, X.; Zhou, S.H. Influence of Aggregate Variety on Pore Structure and Microscopic Interface of Concrete. J. Build. Mater. 2015, 18, 133–138. [Google Scholar]
- Powers, T.C. Void Spacing as a Basis for Producing Air-Entrained Concrete. J. Am. Concr. Inst. 1954, 50, 741–759. [Google Scholar]



| Item | OPC | BFS | SF | FA |
|---|---|---|---|---|
| SiO2 (%) | 21.18 | 34.65 | 85.04 | 35.71 |
| Al2O3 (%) | 5.02 | 14.21 | 0.97 | 16.57 |
| Fe2O3 (%) | 3.14 | 0.49 | 1.04 | 8.92 |
| CaO (%) | 63.42 | 34.11 | 1.63 | 21.14 |
| MgO (%) | 3.12 | 11.15 | 0.32 | 1.41 |
| SO3 (%) | 2.30 | 1.00 | - | 1.94 |
| Other | 1.82 | 3.74 | 10 | 12.49 |
| Loss of ignition (%) | 2.79 | 0.3 | 5.48 | 2.85 |
| Density (g/cm3) | 3.10 | 2.86 | 2.1 | 2.35 |
| Item | Length (mm) | Diameter (μm) | Density (g/cm3) | Elastic Modulus (GPa) | Tensile Strength (GPa) | Elongation (%) |
|---|---|---|---|---|---|---|
| BF | 18 | 15 | 2.56 | 75 | 4.5 | 3.15 |
| PF | 19 | 30 | 0.91 | 3 | 0.27 | 40 |
| Specimen | OPC | SF | FA | BFS | PBS | Water | Sand | CA | BF | PF |
|---|---|---|---|---|---|---|---|---|---|---|
| Volume Fraction (%) | ||||||||||
| BF0PF0 | 241.6 | 15.8 | 79.2 | 59.4 | 3.96 | 150.5 | 683.4 | 1163.6 | 0.0 | 0.0 |
| BF5PF5 | 241.6 | 15.8 | 79.2 | 59.4 | 3.96 | 150.5 | 683.4 | 1163.6 | 0.05 | 0.05 |
| BF5PF10 | 241.6 | 15.8 | 79.2 | 59.4 | 3.96 | 150.5 | 683.4 | 1163.6 | 0.05 | 0.10 |
| BF5PF15 | 241.6 | 15.8 | 79.2 | 59.4 | 3.96 | 150.5 | 683.4 | 1163.6 | 0.05 | 0.15 |
| BF10PF5 | 241.6 | 15.8 | 79.2 | 59.4 | 3.96 | 150.5 | 683.4 | 1163.6 | 0.10 | 0.05 |
| BF15PF5 | 241.6 | 15.8 | 79.2 | 59.4 | 3.96 | 150.5 | 683.4 | 1163.6 | 0.15 | 0.05 |
| BF10PF10 | 241.6 | 15.8 | 79.2 | 59.4 | 3.96 | 150.5 | 683.4 | 1163.6 | 0.10 | 0.10 |
| BF15PF15 | 241.6 | 15.8 | 79.2 | 59.4 | 3.96 | 150.5 | 683.4 | 1163.6 | 0.15 | 0.15 |
| Specimen | Compressive Strength (MPa) | Splitting Tensile Strength (MPa) | ||||
|---|---|---|---|---|---|---|
| Mean | SD. | Sig. | Mean | SD. | Sig. | |
| BF0PF0 | 42.29 | 0.88 | - | 3.66 | 0.16 | - |
| BF5PF5 | 44.43 | 1.02 | 0.066 | 4.01 | 0.28 | 0.199 |
| BF5PF10 | 38.31 | 0.77 | 0.022 | 3.77 | 0.19 | 0.561 |
| BF5PF15 | 32.72 | 1.37 | 0.003 | 2.81 | 0.08 | 0.002 |
| BF10PF5 | 34.51 | 0.99 | 0.009 | 3.05 | 0.25 | 0.045 |
| BF15PF5 | 38.21 | 1.57 | 0.021 | 3.65 | 0.24 | 1.000 |
| BF10PF10 | 40.81 | 1.35 | 0.447 | 3.85 | 0.11 | 0.237 |
| BF15PF15 | 39.07 | 0.93 | 0.113 | 3.49 | 0.23 | 0.441 |
| Specimen | Fractal Dimension | R2 |
|---|---|---|
| BF0PF0 | 2.381 | 0.979 |
| BF5PF5 | 2.482 | 0.977 |
| BF5PF10 | 2.344 | 0.990 |
| BF5PF15 | 2.297 | 0.984 |
| BF10PF5 | 2.329 | 0.986 |
| BF15PF5 | 2.375 | 0.980 |
| BF10PF10 | 2.372 | 0.982 |
| BF15PF15 | 2.379 | 0.977 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, D.; Huang, D.; Zheng, H.; Su, L.; Fu, Q.; Luo, D. Experimental Study on Mechanical Properties and Fractal Dimension of Pore Structure of Basalt–Polypropylene Fiber-Reinforced Concrete. Appl. Sci. 2019, 9, 1602. https://doi.org/10.3390/app9081602
Niu D, Huang D, Zheng H, Su L, Fu Q, Luo D. Experimental Study on Mechanical Properties and Fractal Dimension of Pore Structure of Basalt–Polypropylene Fiber-Reinforced Concrete. Applied Sciences. 2019; 9(8):1602. https://doi.org/10.3390/app9081602
Chicago/Turabian StyleNiu, Ditao, Daguan Huang, Hao Zheng, Li Su, Qiang Fu, and Daming Luo. 2019. "Experimental Study on Mechanical Properties and Fractal Dimension of Pore Structure of Basalt–Polypropylene Fiber-Reinforced Concrete" Applied Sciences 9, no. 8: 1602. https://doi.org/10.3390/app9081602
APA StyleNiu, D., Huang, D., Zheng, H., Su, L., Fu, Q., & Luo, D. (2019). Experimental Study on Mechanical Properties and Fractal Dimension of Pore Structure of Basalt–Polypropylene Fiber-Reinforced Concrete. Applied Sciences, 9(8), 1602. https://doi.org/10.3390/app9081602





