Computational Study of Wet Steam Flow to Optimize Steam Ejector Efficiency for Potential Fire Suppression Application
Abstract
:1. Introduction
- The simulation will take advantage of a wet steam model to investigate the condensation effect on the flow behavior and steam ejector performance.
- The numerical model will be validated against experimental data and the results will also be compared with the ideal gas model.
- Different wall functions and turbulences models will be tested to determine the most optimized model in terms of prediction accuracy.
- A series of simulations with different wetness operating conditions will be performed to investigate the relationship between the wetness of working flows and pump efficiency.
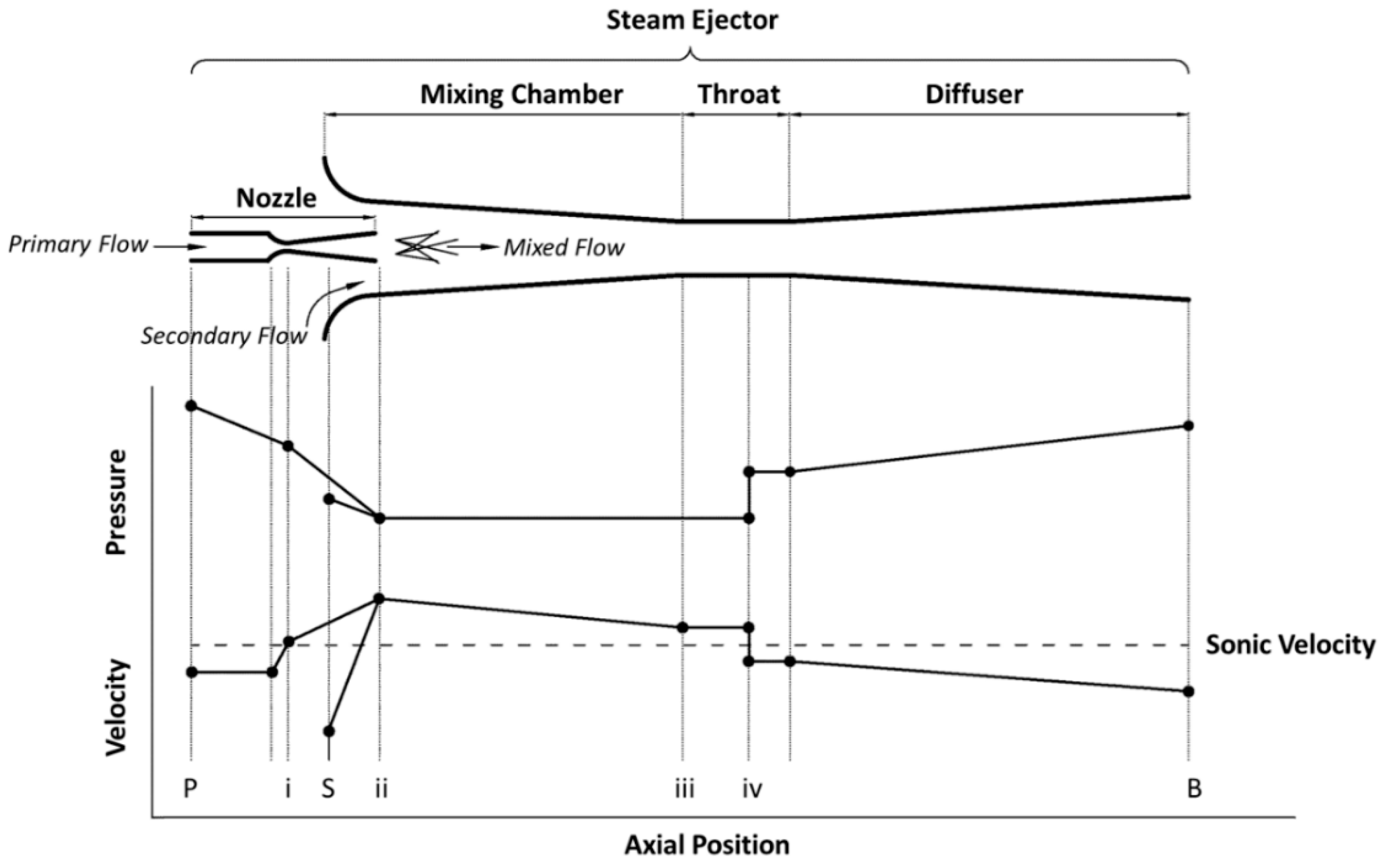
2. Mathematical Model
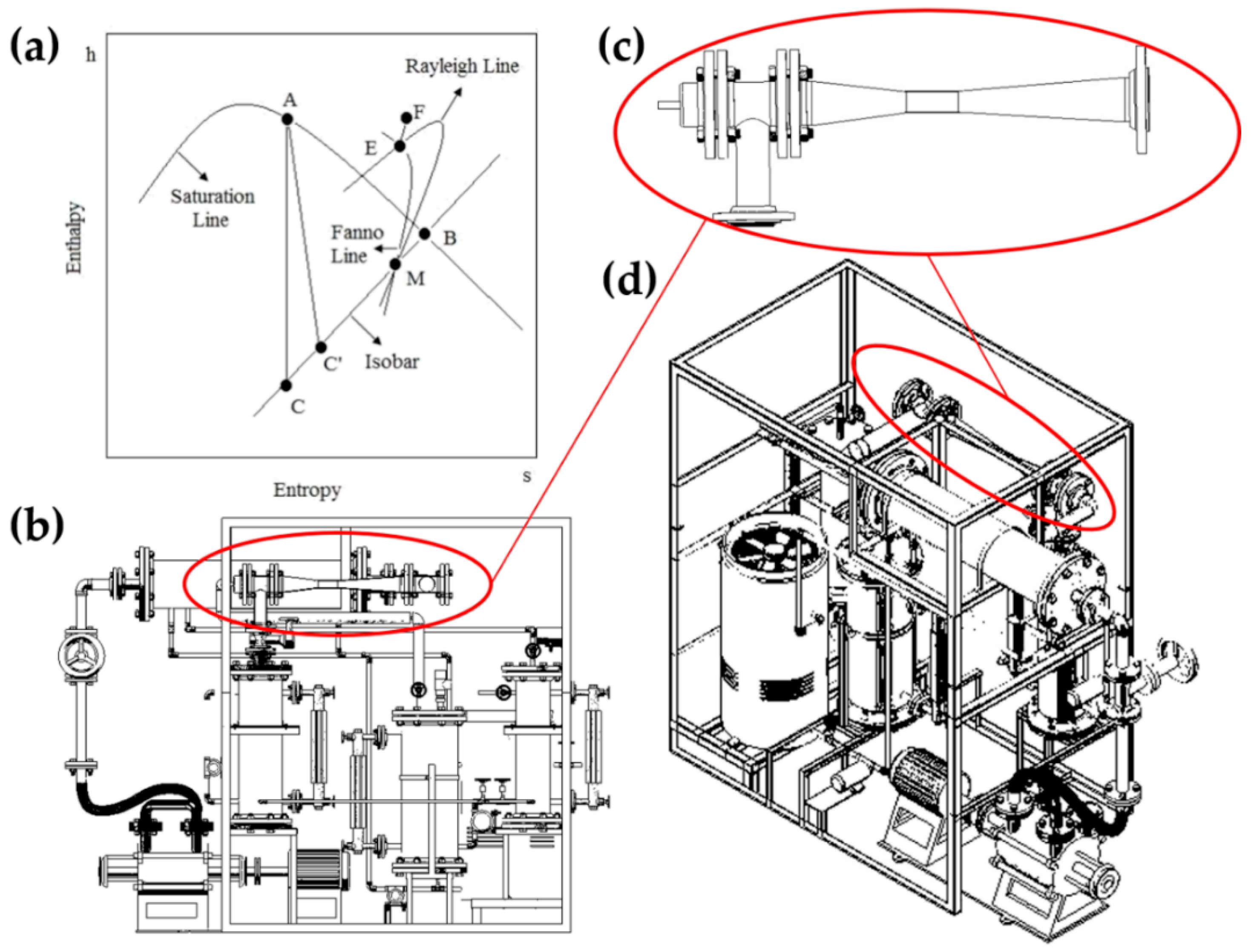
2.1. Wet Steam Modeling
2.2. Wet Steam Equation of State
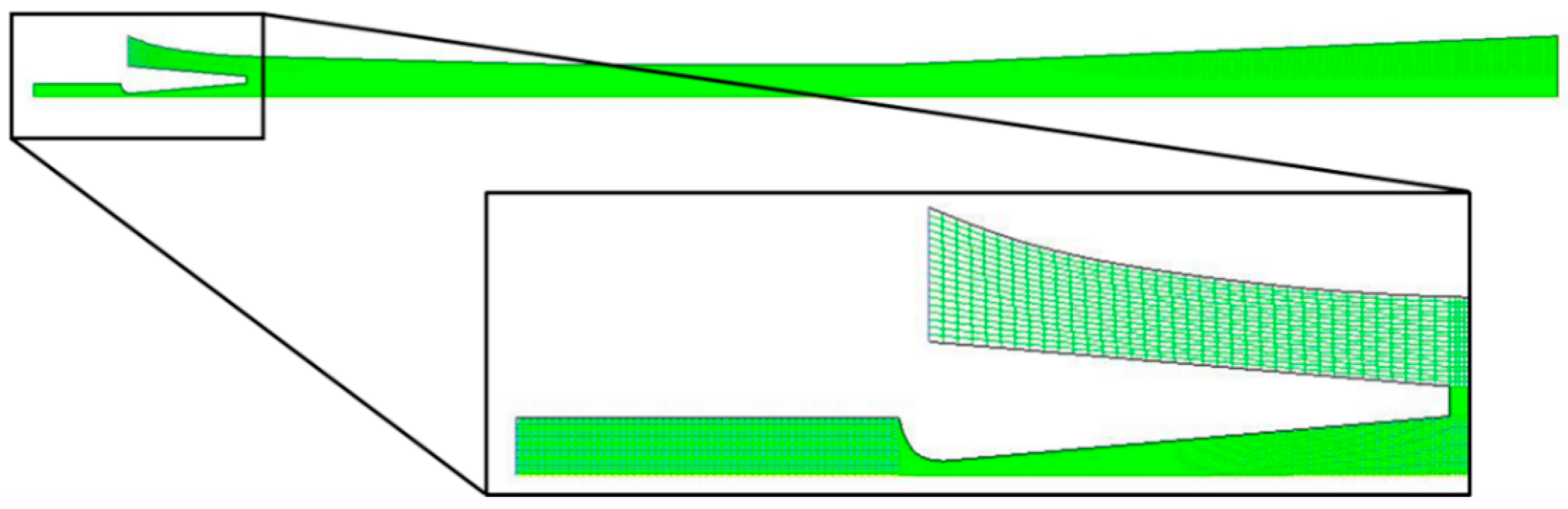
3. Modeling Setup and Boundary Conditions
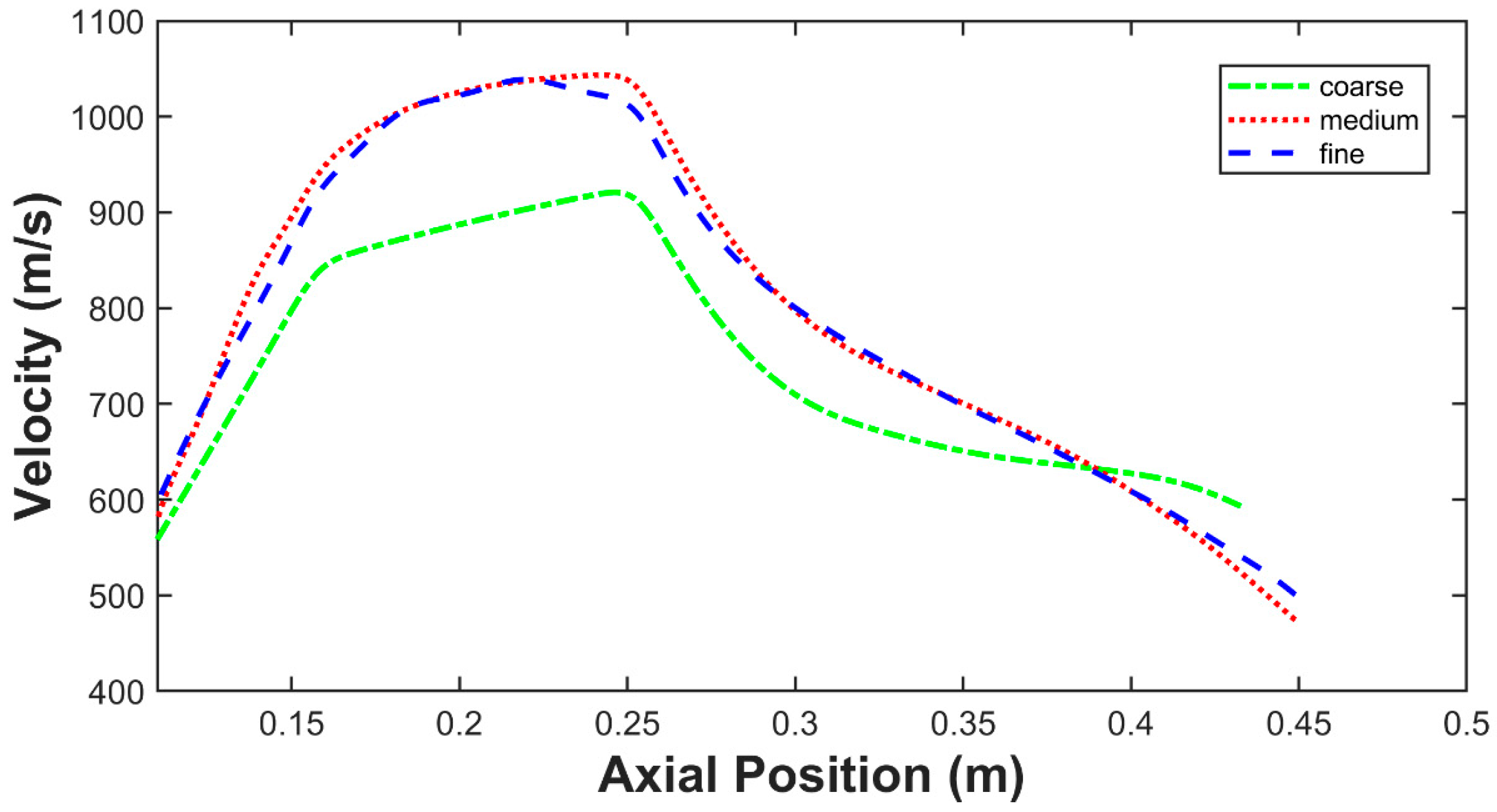
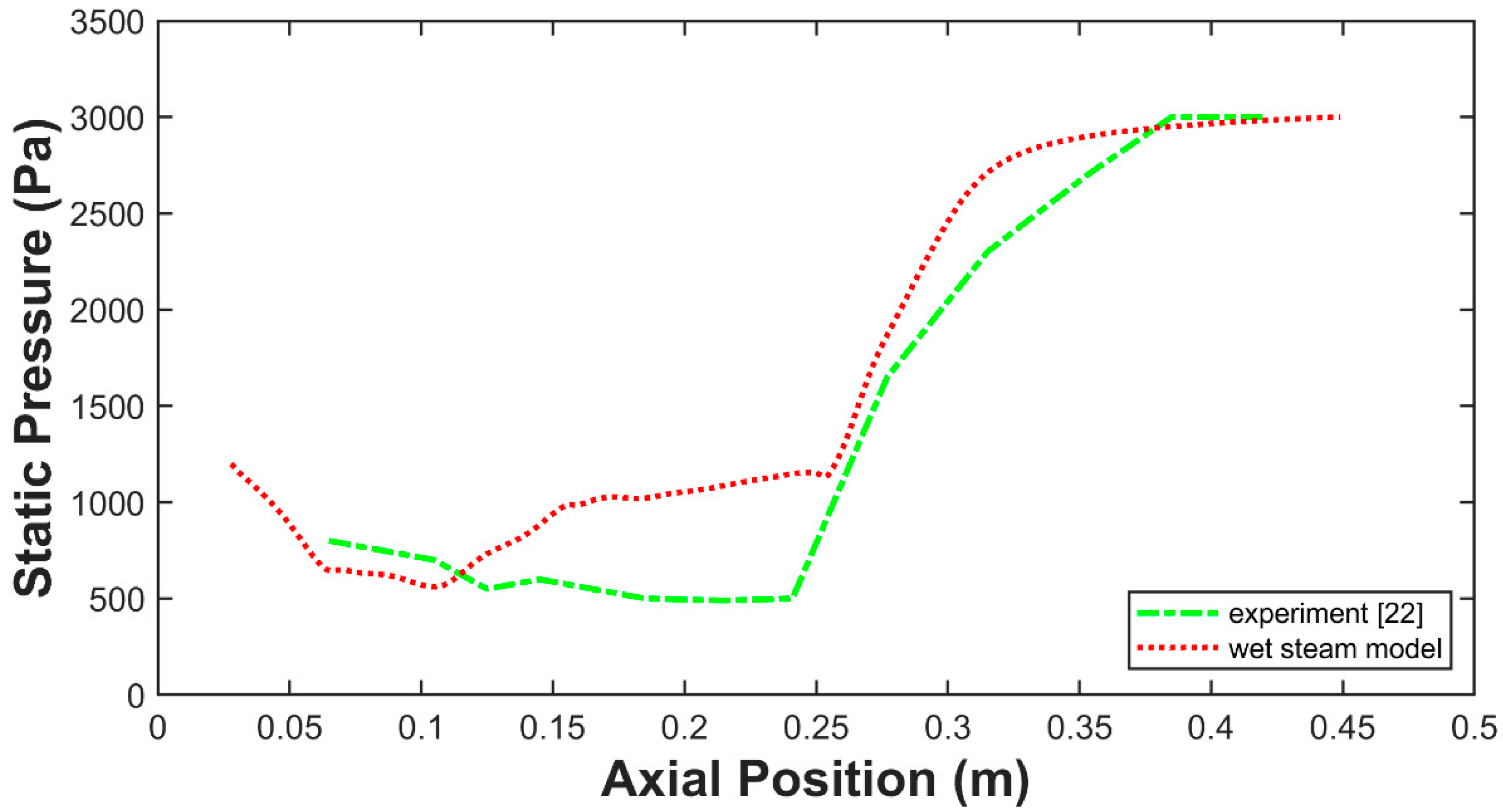
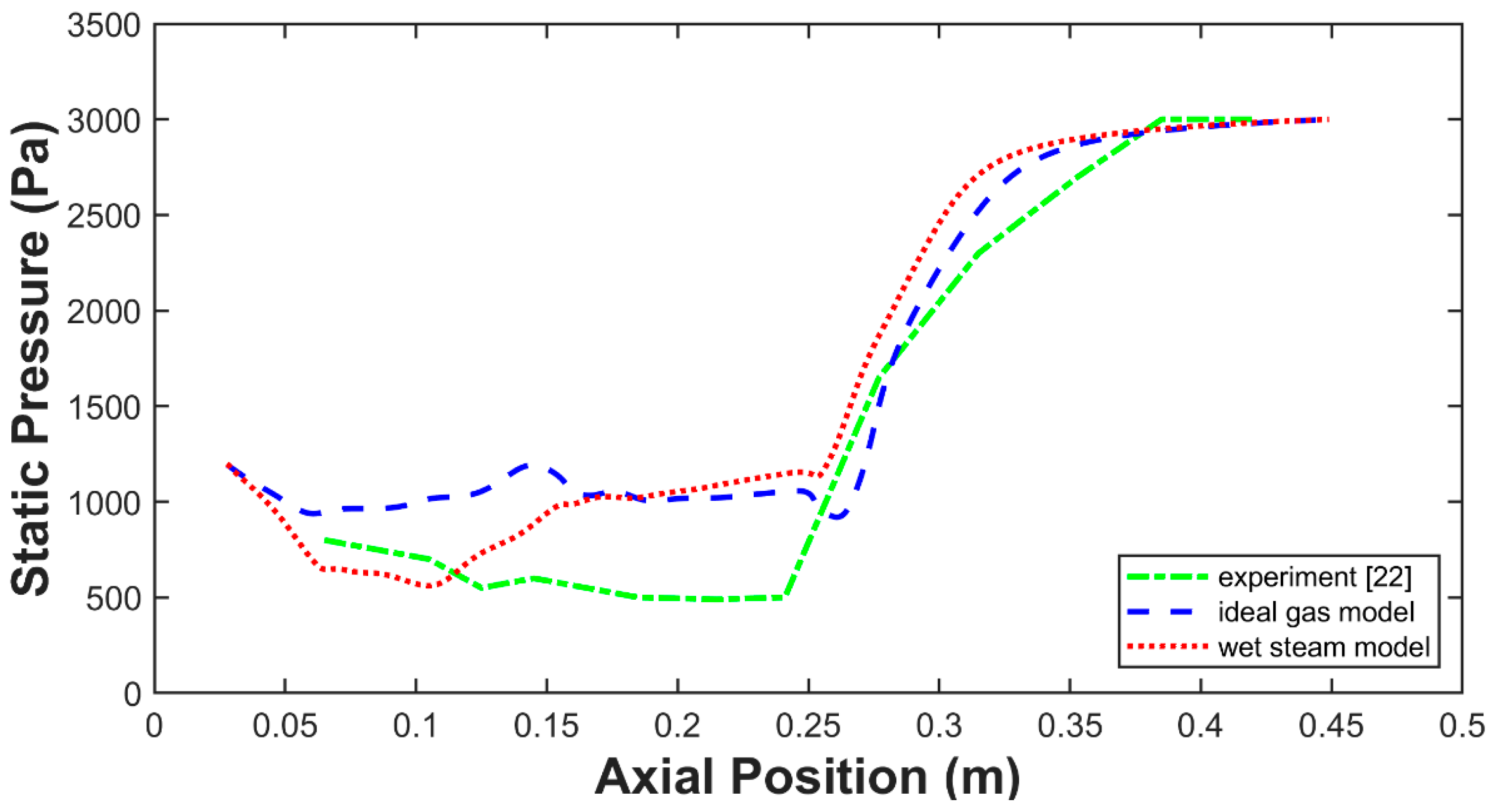
4. Validation of the Numerical Model
5. Results and Discussion
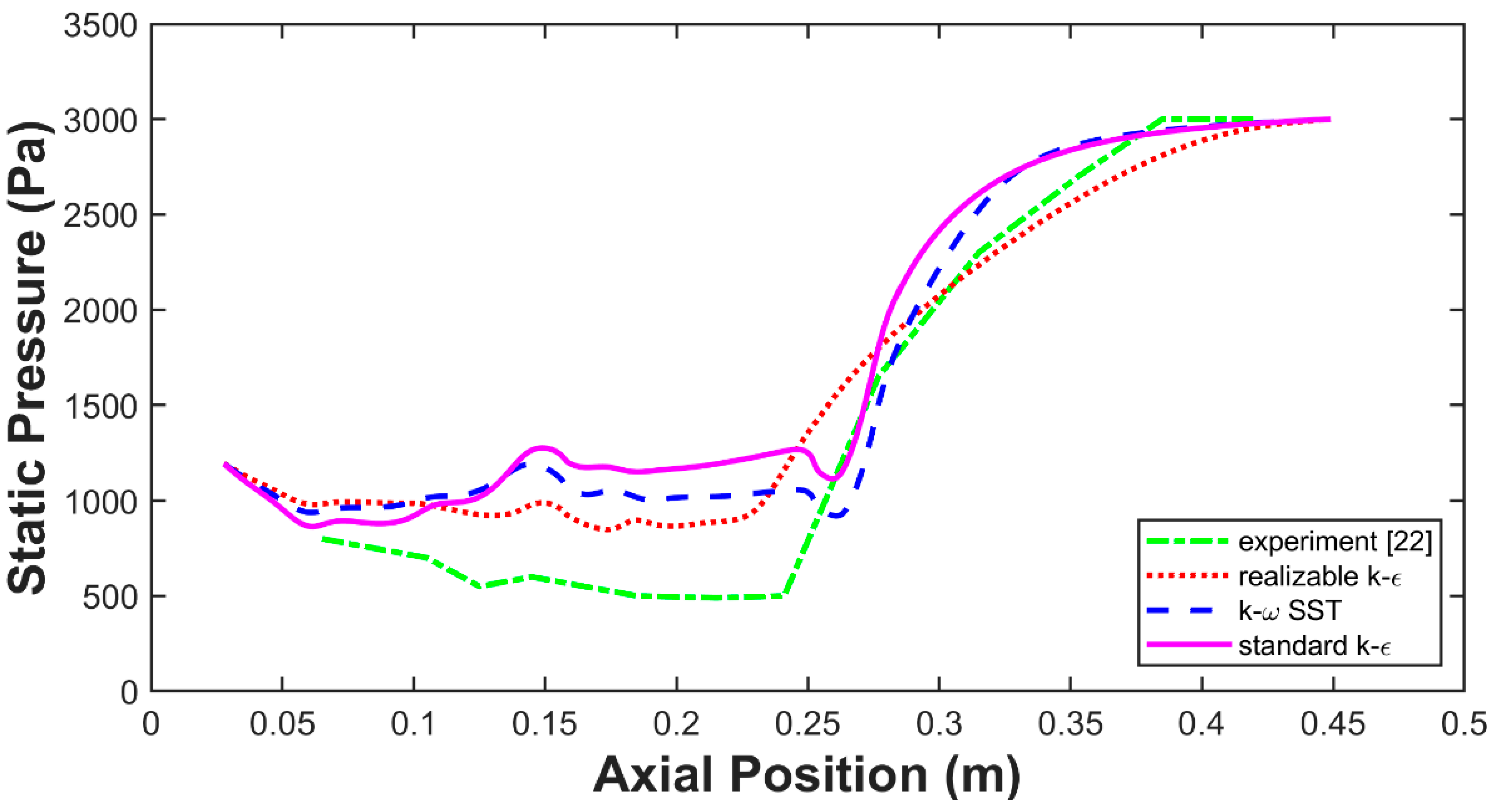
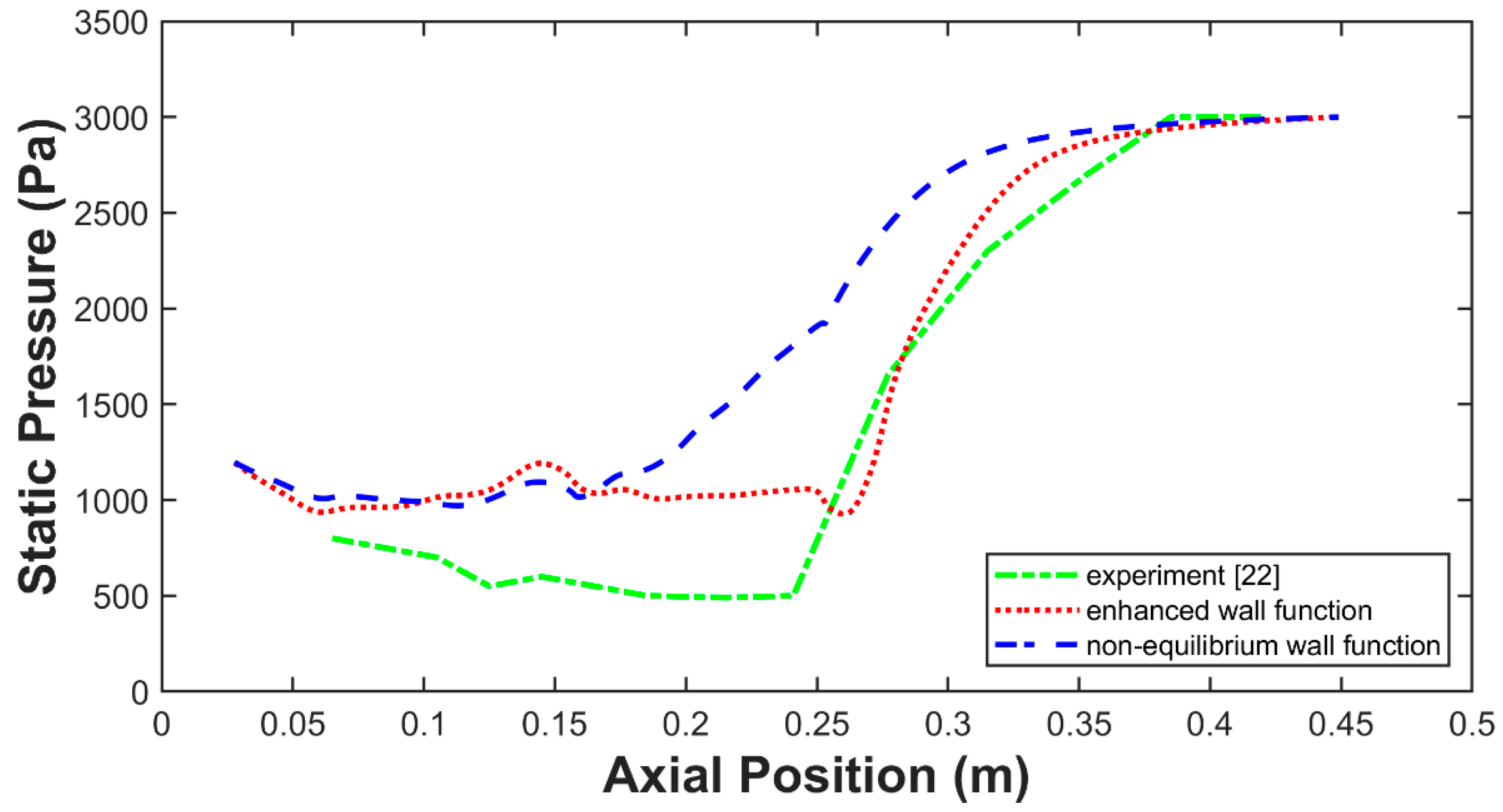
5.1. Turbulence Model and Wall Functions for Steam Ejector Modeling
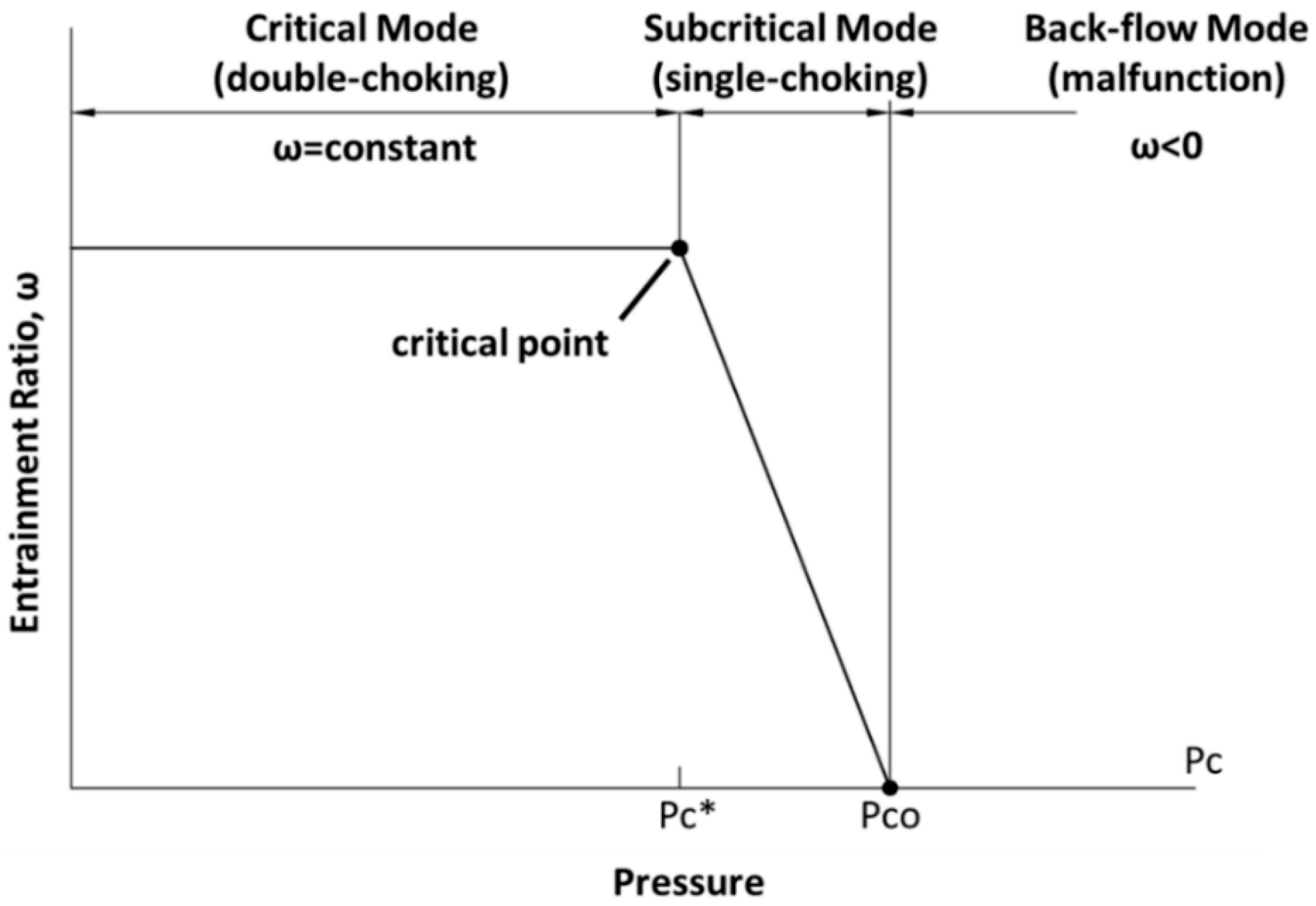
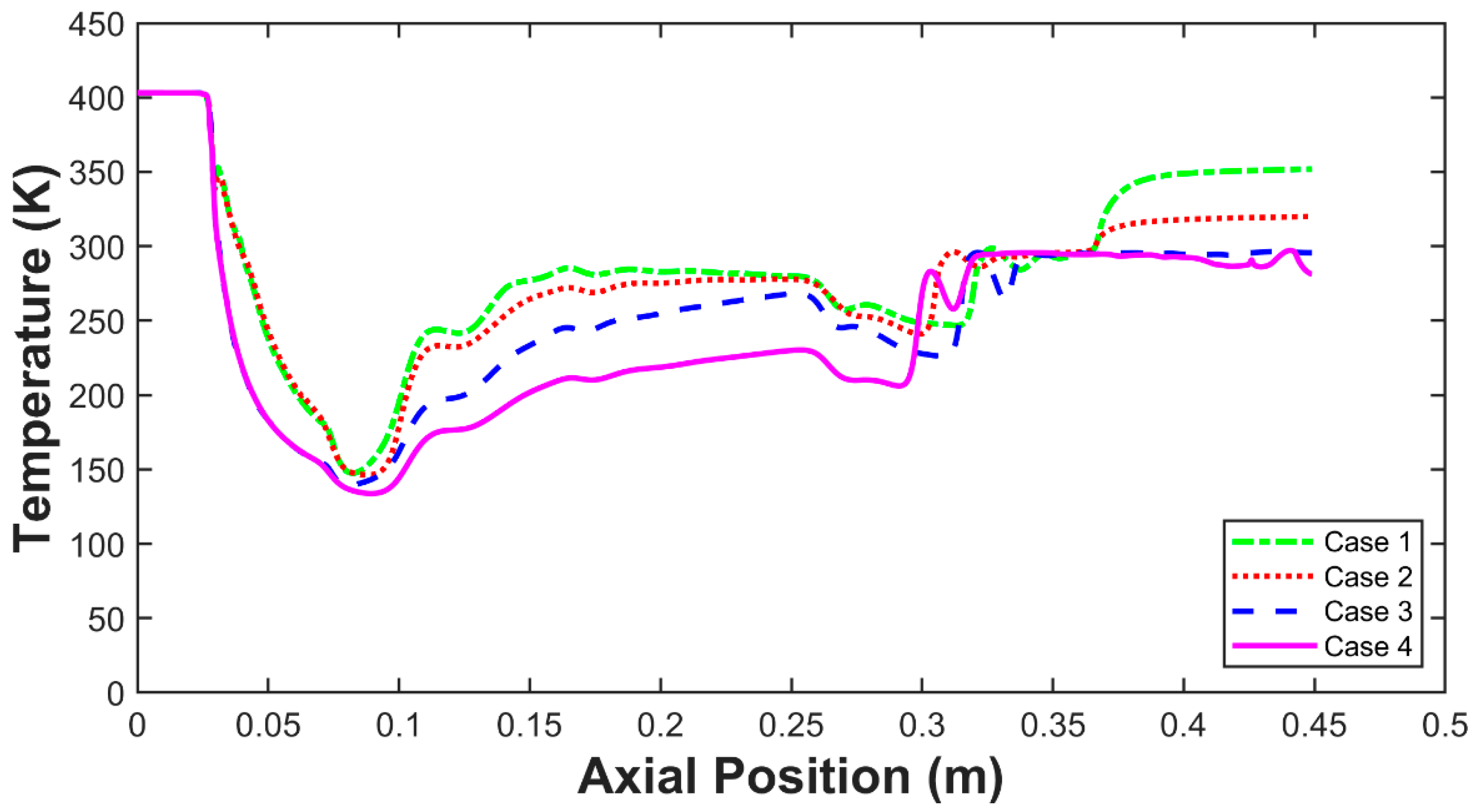
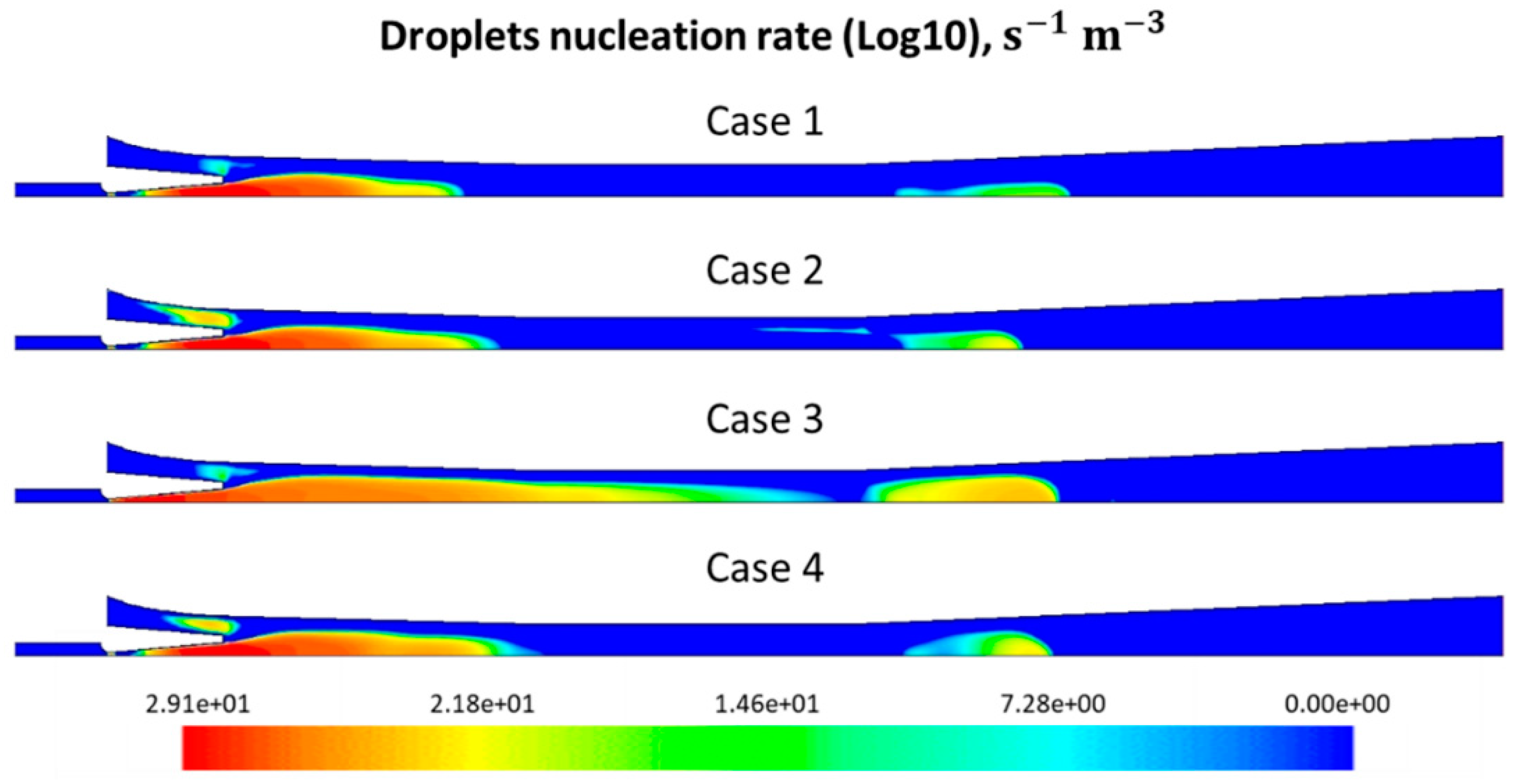
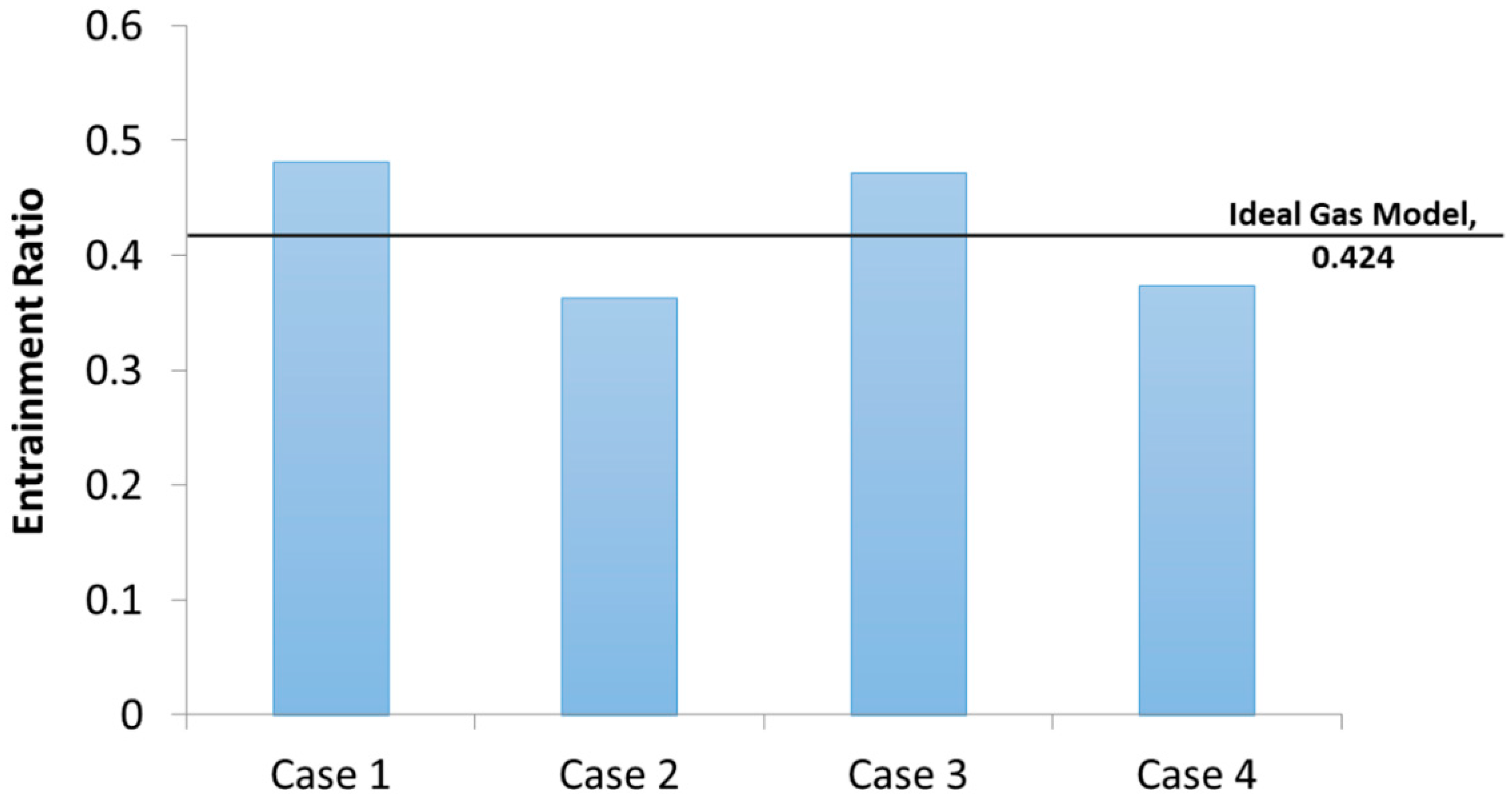
5.2. Wetness Influences of Inlets on Entrainment Ratio
6. Conclusions
- Based on the ideal gas model, the realizable k−ε turbulence model with enhanced wall functions showed a better performance of simulating the working process of the steam ejector.
- Compared with the ideal gas model, the wet steam model showed a better agreement against the experimental data, especially in the mixing chamber section with approximately 23% improvement.
- The spontaneous condensation happened in the nozzle and during the mixing chamber, the condensation effect had an influence on the entrainment ratio.
- By reducing the wetness of the secondary fluid or improving the wetness of the primary fluid, the condensation effect lasted longer and improved the entrainment ratio, which means the performance of the steam ejector is enhanced.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| B, C | virial coefficients (m3/kg, m6/kg2) |
| Cp, Cp0 | isobaric heat capacity, standard state heat capacity (J/kg·K) |
| Em | entrainment ratio |
| h, h0, hl, hv, hlv | specific enthalpy, standard state enthalpy, liquid specific enthalpy, vapor specific enthalpy, specific enthalpy between phases (J/kg) |
| I | nucleation rate (1/s) |
| Kb | Boltzmann constant (J/mol·K) |
| k | turbulent kinetic energy (m2/s2) |
| M | molecular mass (kg) |
| pressure (Pa) | |
| back pressure (Pa) | |
| critical back pressure (Pa) | |
| reversing back pressure (Pa) | |
| saturation pressure | |
| qc | evaporation coefficient |
| R | gas-law constant (J/mol·k) |
| droplet average radius (m) | |
| critical droplet radius (m) | |
| S | super saturation ratio |
| s, s0, sv | specific entropy, standard state entropy, vapor specific entropy (J/kg·mol·K) |
| T | thermal temperature (K) |
| T0 | droplet temperature (K) |
| t | time (s) |
| u | velocity (m/s) |
| Vd | average droplet volume (m3) |
| αv | volume fraction |
| β | mass fraction |
| γ | specific heat capacities ratio |
| Γ | mass generation rate (kg/s) |
| ε | turbulent energy dissipation rate (m2/s3) |
| η | droplet number density (1/m3) |
| θ | non-isothermal correction factor |
| μ, μt | dynamic viscosity, turbulent viscosity (Pa·s) |
| ν | kinetic viscosity (m2/s), |
| ρ, ρl, ρv | mixture density, liquid density, vapor density (kg/m3) |
| σ | droplet surface tension (N/m) |
| E | internal energy |
References
- Riffat, S.; Jiang, L.; Gan, G. Recent development in ejector technology—A review. Int. J. Ambient Energy 2005, 26, 13–26. [Google Scholar] [CrossRef]
- Lucas, C.; Koehler, J. Experimental investigation of the COP improvement of a refrigeration cycle by use of an ejector. Int. J. Refrig. 2012, 35, 1595–1603. [Google Scholar] [CrossRef]
- Dopazo, J.A.; Fernandez-Seara, J. Experimental evaluation of an ejector as liquid re-circulator in an overfeed NH3 system with a plate evaporator. Int. J. Refrig. 2011, 34, 1676–1683. [Google Scholar] [CrossRef]
- Han, B.; Liu, Z.L.; Wu, H.Q.; Li, Y.X. Experimental study on a new method for improving the performance of thermal vapor compressors for multi-effect distillation desalination systems. Desalination 2014, 344, 391–395. [Google Scholar] [CrossRef]
- Wang, X.; Dong, J.; Lei, H.; Li, A.; Wang, R.; Chen, W.; Tu, J. Modeling and simulation of steam-jet vacuum pump. Zhenkong Kexue yu Jishu Xuebao/J. Vac. Sci. Technol. 2013, 33, 1069–1073. [Google Scholar]
- Yinshui, L.; Zhuo, J.; Dan, W.; Xiaohui, L. Experimental research on the water mist fire suppression performance in an enclosed space by changing the characteristics of nozzles. Exp. Thermal Fluid Sci. 2014, 52, 174–181. [Google Scholar] [CrossRef]
- Yang, P.Z.; Liu, T.; Qin, X.A. Experimental and numerical study on water mist suppression system on room fire. Build Environ. 2010, 45, 2309–2316. [Google Scholar] [CrossRef]
- Beji, T.; Zadeh, S.E.; Maragkos, G.; Merci, B. Influence of the particle injection rate, droplet size distribution and volume flux angular distribution on the results and computational time of water spray CFD simulations. Fire Saf. J. 2017, 91, 586–595. [Google Scholar] [CrossRef]
- Chunnanond, K.; Aphornratana, S. An experimental investigation of a steam ejector refrigerator: The analysis of the pressure profile along the ejector. Appl. Therm. Eng. 2004, 24, 311–322. [Google Scholar] [CrossRef]
- Huang, B.J.; Jiang, C.B.; Hu, F.L. Ejector Performance-Characteristics and Design Analysis of Jet Refrigeration System. J. Eng. Gas Turbines Power 1985, 107, 792–802. [Google Scholar] [CrossRef]
- Huang, B.J.; Chang, J.M.; Wang, C.P.; Petrenko, V.A. A 1-D analysis of ejector performance. Int. J. Refrig. 1999, 22, 354–364. [Google Scholar] [CrossRef]
- Sankarlal, T.; Mani, A. Experimental investigations on ejector refrigeration system with ammonia. Renew. Energy 2007, 32, 1403–1413. [Google Scholar] [CrossRef]
- Aidoun, Z.; Ouzzane, A. The effect of operating conditions on the performance of a supersonic ejector for refrigeration. Int. J. Refrig. 2004, 27, 974–984. [Google Scholar] [CrossRef]
- Wang, X.D.; Dong, J.L. Numerical study on the performances of steam-jet vacuum pump at different operating conditions. Vacuum 2010, 84, 1341–1346. [Google Scholar] [CrossRef]
- Varga, S.; Oliveira, A.C.; Diaconu, B. Influence of geometrical factors on steam ejector performance—A numerical assessment. Int. J. Refrig. 2009, 32, 1694–1701. [Google Scholar] [CrossRef]
- Varga, S.; Oliveira, A.C.; Diaconu, B. Numerical assessment of steam ejector efficiencies using CFD. Int. J. Refrig. 2009, 32, 1203–1211. [Google Scholar] [CrossRef]
- Varga, S.; Oliveira, A.C.; Ma, X.L.; Omer, S.A.; Zhang, W.; Riffat, S.B. Experimental and numerical analysis of a variable area ratio steam ejector. Int. J. Refrig. 2011, 34, 1668–1675. [Google Scholar] [CrossRef]
- Ma, X.L.; Zhang, W.; Omer, S.A.; Riffat, S.B. Experimental investigation of a novel steam ejector refrigerator suitable for solar energy applications. Appl. Therm. Eng. 2010, 30, 1320–1325. [Google Scholar] [CrossRef]
- Yadav, R.L.; Patwardhan, A.W. Design aspects of ejectors: Effects of suction chamber geometry. Chem. Eng. Sci. 2008, 63, 3886–3897. [Google Scholar] [CrossRef]
- Riffat, S.B.; Omer, S.A. CFD modelling and experimental investigation of an ejector refrigeration system using methanol as the working fluid. Int. J. Energy Res. 2001, 25, 115–128. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Aidoun, Z.; Desevaux, P.; Mercadier, Y. Numerical and experimental investigations on supersonic ejectors. Int. J. Heat Fluid Flow 2005, 26, 56–70. [Google Scholar] [CrossRef]
- Sun, D.W. Variable geometry ejectors and their applications in ejector refrigeration systems. Energy 1996, 21, 919–929. [Google Scholar] [CrossRef]
- Cizungu, K.; Groll, M.; Ling, Z.G. Modelling and optimization of two-phase ejectors for cooling systems. Appl. Therm. Eng. 2005, 25, 1979–1994. [Google Scholar] [CrossRef]
- Chaiwongsa, P.; Wongwises, S. Experimental study on R-134a refrigeration system using a two-phase ejector as an expansion device. Appl. Therm. Eng. 2008, 28, 467–477. [Google Scholar] [CrossRef]
- Ruangtrakoon, N.; Aphornratana, S.; Sriveerakul, T. Experimental studies of a steam jet refrigeration cycle: Effect of the primary nozzle geometries to system performance. Exp. Thermal Fluid Sci. 2011, 35, 676–683. [Google Scholar] [CrossRef]
- Ruangtrakoon, N.; Thongtip, T.; Aphornratana, S.; Sriveerakul, T. CFD simulation on the effect of primary nozzle geometries for a steam ejector in refrigeration cycle. Int. J. Therm. Sci. 2013, 63, 133–145. [Google Scholar] [CrossRef]
- Gerber, A.; Kermani, M. A pressure based Eulerian–Eulerian multi-phase model for non-equilibrium condensation in transonic steam flow. Int. J. Heat Mass Transf. 2004, 47, 2217–2231. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Yeoh, G.H.; Timchenko, V.; Chen, T.B.Y.; Chan, Q.N.; Wang, C.; Li, D.D. Comparison of detailed soot formation models for sooty and non-sooty flames in an under-ventilated ISO room. Int. J. Heat Mass Transf. 2017, 115, 717–729. [Google Scholar] [CrossRef]
- Wang, X.D.; Dong, J.L.; Wang, T.; Tu, J.Y. Numerical analysis of spontaneously condensing phenomena in nozzle of steam-jet vacuum pump. Vacuum 2012, 86, 861–866. [Google Scholar] [CrossRef]
- Munday, J.T.; Bagster, D.F. A new ejector theory applied to steam jet refrigeration. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 442–449. [Google Scholar] [CrossRef]
- Yang, Y.; Walther, J.H.; Yan, Y.Y.; Wen, C. CFD modeling of condensation process of water vapor in supersonic flows. Appl. Therm. Eng. 2017, 115, 1357–1362. [Google Scholar] [CrossRef]
- Mazzelli, F.; Giacomelli, F.; Milazzo, A. CFD modeling of condensing steam ejectors: Comparison with an experimental test-case. Int. J. Therm. Sci. 2018, 127, 7–18. [Google Scholar] [CrossRef]
- Wang, X.D.; Lei, H.J.; Dong, J.L.; Tu, J.Y. The spontaneously condensing phenomena in a steam-jet pump and its influence on the numerical simulation accuracy. Int. J. Heat Mass Transf. 2012, 55, 4682–4687. [Google Scholar] [CrossRef]
- Sharifi, N.; Boroomand, M.; Sharifi, M. Numerical assessment of steam nucleation on thermodynamic performance of steam ejectors. Appl. Therm. Eng. 2013, 52, 449–459. [Google Scholar] [CrossRef]
- Wang, X.D.; Dong, J.L.; Li, A.; Lei, H.J.; Tu, J.Y. Numerical study of primary steam superheating effects on steam ejector flow and its pumping performance. Energy 2014, 78, 205–211. [Google Scholar] [CrossRef]
- Wang, X.D.; Dong, J.L.; Zhang, G.L.; Fu, Q.; Li, H.; Han, Y.; Tu, J.Y. The primary pseudo-shock pattern of steam ejector and its influence on pumping efficiency based on CFD approach. Energy 2019, 167, 224–234. [Google Scholar] [CrossRef]
- Bakhtar, F.; Tochai, M.M. An investigation of two-dimensional flows of nucleating and wet steam by the time-marching method. Int. J. Heat Fluid Flow 1980, 2, 5–18. [Google Scholar] [CrossRef]
- Ishizaka, K. A high-resolution numerical method for transonic non-equilibrium condensation flow through a steam turbine cascade. Proc. of the 6th ISCFD 1995, 1, 479–484. [Google Scholar]
- Yuen, A.C.Y.; Yeoh, G.H.; Timchenko, V.; Cheung, S.C.P.; Barber, T.J. Importance of detailed chemical kinetics on combustion and soot modelling of ventilated and under-ventilated fires in compartment. Int. J. Heat Mass Transf. 2016, 96, 171–188. [Google Scholar] [CrossRef]
- Chen, T.B.Y.; Yuen, A.C.Y.; Yeoh, G.H.; Timchenko, V.; Cheung, S.C.P.; Chan, Q.N.; Yang, W.; Lu, H. Numerical study of fire spread using the level-set method with large eddy simulation incorporating detailed chemical kinetics gas-phase combustion model. J. Comput. Sci. 2018, 24, 8–23. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, X.; Yan, Y.; Ding, H.; Wen, C. Performance of supersonic steam ejectors considering the nonequilibrium condensation phenomenon for efficient energy utilisation. Appl. Energy 2019, 242, 157–167. [Google Scholar] [CrossRef]
- Wen, C.; Karvounis, N.; Walther, J.H.; Yan, Y.; Feng, Y.; Yang, Y. An efficient approach to separate CO2 using supersonic flows for carbon capture and storage. Appl. Energy 2019, 238, 311–319. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, S.Q. Numerical simulation on non-equilibrium spontaneous condensation in supersonic steam flow. Int. Commun. Heat Mass Transf. 2009, 36, 902–907. [Google Scholar] [CrossRef]
- Young, J. Two-dimensional, nonequilibrium, wet-steam calculations for nozzles and turbine cascades. J. Turbomach. 1992, 114, 569–579. [Google Scholar] [CrossRef]
- Young, J.B. An Equation of State for Steam for Turbomachinery and Other Flow Calculations. J. Eng. Gas Turbines Power 1988, 110, 1–7. [Google Scholar] [CrossRef]
- Young, J. Spontaneous condensation of steam in supersonic nozzles. Physicochem. Hydrodyn. 1982, 3, 57–82. [Google Scholar]
- Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 1. Validation of the CFD results. Int. J. Therm. Sci. 2007, 46, 812–822. [Google Scholar] [CrossRef]
- Pianthong, K.; SeehanaM, W.; Behnia, M.; SriveerakUl, T.; Aphornratana, S. Investigation and improvement of ejector refrigeration system using computational fluid dynamics technique. Energy Convers. Manag. 2007, 48, 2556–2564. [Google Scholar] [CrossRef]
| Geometry | Value |
|---|---|
| Diameter of Nozzle inlet | 7.75 mm |
| Diameter of Nozzle outlet | 8 mm |
| Diameter of Mixing chamber inlet | 24 mm |
| Diameter of Mixing throat | 19 mm |
| Length of Nozzle | 60 mm |
| Length of Mixing chamber | 130 mm |
| Length of Throat | 95 mm |
| Length of Diffuse | 180 mm |
| Expanded angle of nozzle | 10° |
| Nozzle exit position | 0 mm |
| Inlet Fluid | Temperature (K) | Pressure (Pa) |
|---|---|---|
| Primary fluid | 393.15 | 200,000 |
| Secondary fluid | 283.15 | 1200 |
| Case Number | Wetness of Primary Flow (Inlet 1) | Wetness of Secondary Flow (Inlet 2) |
|---|---|---|
| Case 1 | 0 | 0 |
| Case 2 | 0 | 0.1 |
| Case 3 | 0.1 | 0 |
| Case 4 | 0.1 | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, A.; Yuen, A.C.Y.; Chen, T.B.Y.; Wang, C.; Liu, H.; Cao, R.; Yang, W.; Yeoh, G.H.; Timchenko, V. Computational Study of Wet Steam Flow to Optimize Steam Ejector Efficiency for Potential Fire Suppression Application. Appl. Sci. 2019, 9, 1486. https://doi.org/10.3390/app9071486
Li A, Yuen ACY, Chen TBY, Wang C, Liu H, Cao R, Yang W, Yeoh GH, Timchenko V. Computational Study of Wet Steam Flow to Optimize Steam Ejector Efficiency for Potential Fire Suppression Application. Applied Sciences. 2019; 9(7):1486. https://doi.org/10.3390/app9071486
Chicago/Turabian StyleLi, Ao, Anthony Chun Yin Yuen, Timothy Bo Yuan Chen, Cheng Wang, Hengrui Liu, Ruifeng Cao, Wei Yang, Guan Heng Yeoh, and Victoria Timchenko. 2019. "Computational Study of Wet Steam Flow to Optimize Steam Ejector Efficiency for Potential Fire Suppression Application" Applied Sciences 9, no. 7: 1486. https://doi.org/10.3390/app9071486
APA StyleLi, A., Yuen, A. C. Y., Chen, T. B. Y., Wang, C., Liu, H., Cao, R., Yang, W., Yeoh, G. H., & Timchenko, V. (2019). Computational Study of Wet Steam Flow to Optimize Steam Ejector Efficiency for Potential Fire Suppression Application. Applied Sciences, 9(7), 1486. https://doi.org/10.3390/app9071486













