Resonant Terahertz Light Absorption by Virtue of Tunable Hybrid Interface Phonon–Plasmon Modes in Semiconductor Nanoshells
Abstract
1. Introduction
2. Phonons and Plasmons in Nanoshells
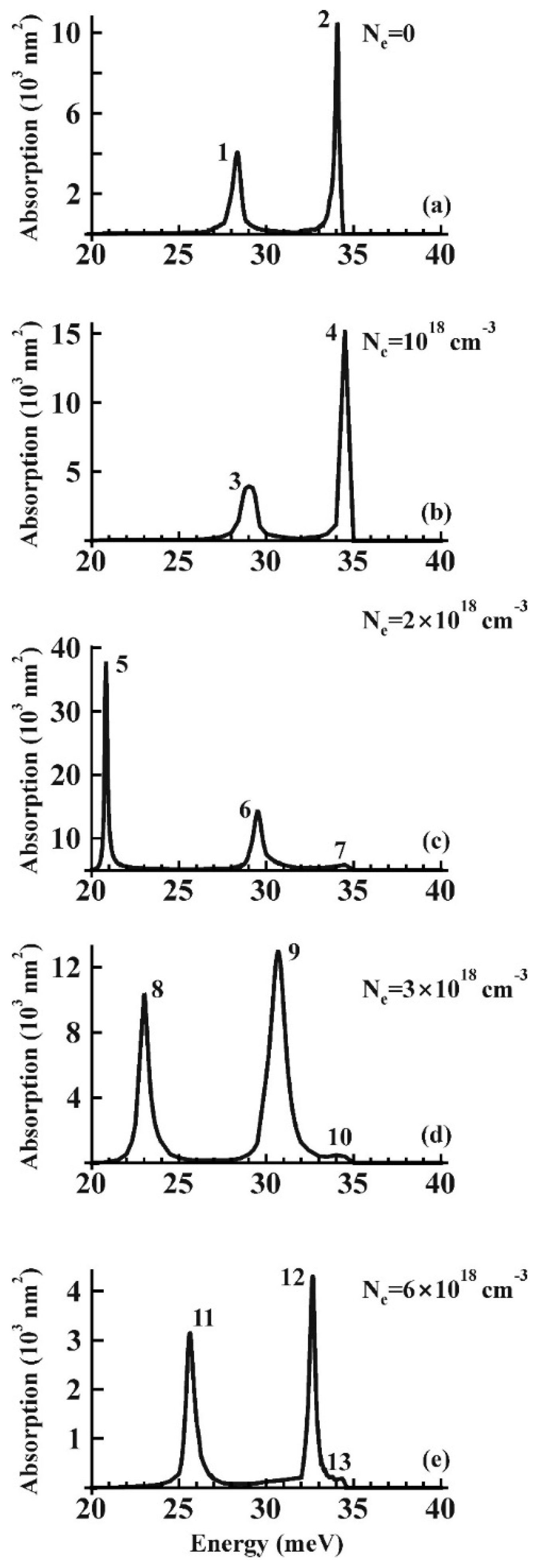
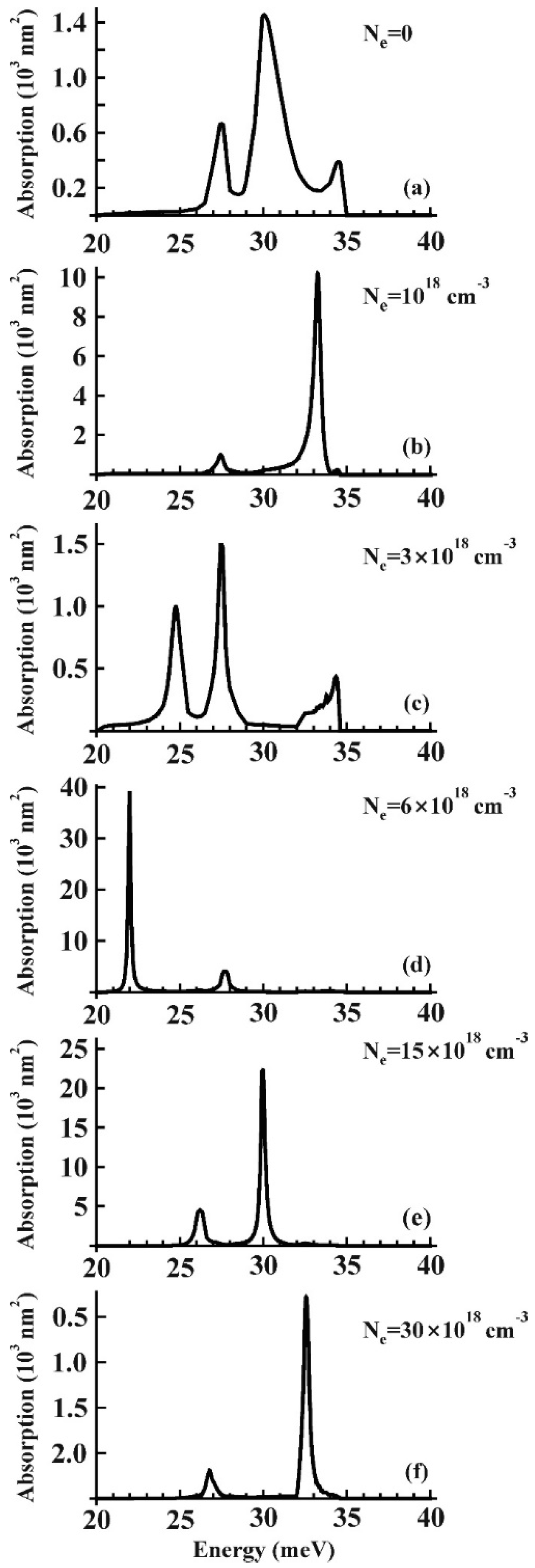
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sothmann, B.R.; Sánchez, R.; Jordan, A.N.; Büttiker, M. Powerful energy harvester based on resonant-tunneling quantum wells. New J. Phys. 2013, 15, 095021. [Google Scholar] [CrossRef]
- Xia, Y.; Yang, P.; Sun, Y.; Wu, Y.; Mayers, B.; Gates, B.; Yin, Y.; Kim, F.; Yan, H. One-Dimensional Nanostructures: Synthesis, Characterization, and Applications. Adv. Matter. 2003, 15, 353–389. [Google Scholar] [CrossRef]
- Corfdir, P.; Marquardt, O.; Lewis, R.B.; Sinito, C.; Ramsteiner, M.; Trampert, A.; Jahn, U.; Geelhaar, L.; Brandt, O.; Fomin, V.M. Excitonic Aharonov–Bohm Oscillations in Core–Shell Nanowires. Adv. Mater. 2019, 31, 1805645. [Google Scholar] [CrossRef] [PubMed]
- Nika, D.L.; Balandin, A.A. Phonons and thermal transport in graphene and graphene-based materials. Rep. Prog. Phys. 2017, 80, 036502. [Google Scholar] [PubMed]
- Renteria, J.D.; Nika, D.L.; Balandin, A.A. Graphene thermal properties: Applications in thermal management and energy storage. Appl. Sci. 2014, 4, 525–547. [Google Scholar] [CrossRef]
- Cocemasov, A.I.; Isacova, C.I.; Nika, D.L. Thermal transport in semiconductor nanostructures, graphene, and related two-dimensional materials. Chin. Phys. B 2018, 27, 056301. [Google Scholar] [CrossRef]
- Deneke, C.; Songmuang, R.; Jin-Phillipp, N.Y.; Schmidt, O.G. The structure of hybrid radial superlattices. J. Phys. D Appl. Phys. 2009, 42, 103001. [Google Scholar] [CrossRef]
- Fomin, V.M.; Balandin, A.A. Phonon Spectrum Engineering in Rolled-up Micro- and Nano-Architectures. Appl. Sci. 2015, 5, 728–746. [Google Scholar]
- Li, G.; Yarali, M.; Cocemasov, A.; Baunack, S.; Nika, D.L.; Fomin, V.M.; Singh, S.; Gemming, T.; Zhu, F.; Mavrokefalos, A.; et al. In-plane thermal conductivity of radial and planar Si/SiOx hybrid nanomembrane superlattices. ACS Nano 2017, 11, 8215–8222. [Google Scholar] [CrossRef] [PubMed]
- Fomin, V.M. (Ed.) Physics of Quantum Rings, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2018; 596p. [Google Scholar]
- Bimberg, D. (Ed.) Semiconductor Nanostructures; Springer: Berlin/Heidelberg, Germany, 2008; 357p. [Google Scholar]
- Chen, Y.; Zopf, M.; Keil, R.; Ding, F.; Schmidt, O.G. Highly-efficient extraction of entangled photons from quantum dots using a broadband optical antenna. Nat. Commun. 2018, 9, 2994. [Google Scholar] [CrossRef] [PubMed]
- Daniel, M.-C.; Astruc, D. Gold Nanoparticles: Assembly, Supramolecular Chemistry, Quantum-Size-Related Properties, and Applications toward Biology, Catalysis, and Nanotechnology. Chem. Rev. 2004, 104, 293–346. [Google Scholar] [CrossRef] [PubMed]
- Myroshnychenko, V.; Rodríguez-Fernández, J.; Pastoriza-Santos, I.; Funston, A.M.; Novo, C.; Mulvaney, P.; Liz-Marzán, L.M.; García de Abajo, F.J. Modeling the optical response of gold nanoparticles. Chem. Soc. Rev. 2008, 37, 1792–1805. [Google Scholar] [CrossRef] [PubMed]
- Bardhant, R.; Grady, N.K.; Ali, T.; Halas, N.J. Metallic nanoshells with semiconductor cores: Optical characteristics modified by core medium properties. ACS Nano 2010, 4, 6169–6179. [Google Scholar] [CrossRef]
- Chen, X.; Fang, J.; Zhang, X.D.; Zhao, Y.; Gu, M. Optical/electrical integrated design of core–shell aluminum-based plasmonic nanostructures for record-breaking efficiency enhancements in photovoltaic devices. ACS Photonics 2017, 4, 2102–2110. [Google Scholar] [CrossRef]
- Choi, C.K.K.; Zhuo, X.L.; Chiu, Y.T.E.; Yang, H.R.; Wang, J.F.; Choi, C.H.J. Polydopamine-based concentric nanoshells with programmable architectures and plasmonic properties. Nanoscale 2017, 9, 16968–16980. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Guo, K.; Liu, G.; Yang, Y.; Li, K.; Zhai, W. Enhancement of surface plasmon resonances on nonlinear optical properties in spherical dome semiconductor nanoshells. Superlattice Microstruct. 2018, 122, 394–403. [Google Scholar] [CrossRef]
- Ktatami, M.; Alijani, H.Q.; Nejad, M.S.; Varma, R.S. Core@shell Nanoparticles: Greener Synthesis Using Natural Plant Products. Appl. Sci. 2018, 8, 411. [Google Scholar] [CrossRef]
- Averitt, R.D.; Sarkar, D.; Halas, N.J. Plasmon resonance shifts of au-coated Au2S nanoshells: Insight into multicomponent nanoparticle growth. Phys. Rev. Lett. 1997, 78, 4217. [Google Scholar] [CrossRef]
- Oldenburg, S.J.; Averitt, R.D.; Westcott, S.L.; Halas, N.J. Nanoengineering of optical resonances. Chem. Phys. Lett. 1998, 288, 243–247. [Google Scholar] [CrossRef]
- Prodan, E.; Nordlander, P. Exchange and correlations effects in small metallic nanoshells. Chem. Phys. Lett. 2001, 349, 153–160. [Google Scholar] [CrossRef]
- Prodan, E.; Nordlander, P. Electronic structure and polarizability of metallic nanoshells. Chem. Phys. Lett. 2002, 352, 140–146. [Google Scholar] [CrossRef]
- Prodan, E.; Lee, A.; Nordlander, P. The effect of a dielectric core and embedding medium on the polarizability of metallic nanoshells. Chem. Phys. Lett. 2002, 360, 325–332. [Google Scholar] [CrossRef]
- Amendola, V.; Pilot, R.; Frasconi, M.; Marago, O.M.; Iati, M.A. Surface plasmon resonance in gold nanoparticles:a review. J. Phys. Cond. Matt. 2017, 29, 203002. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Physik 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Karker, N.A.; Carpenter, M.A. High figure of merit hydrogen sensor using multipolar plasmon resonance modes. Sens. Actuators B 2017, 252, 385–390. [Google Scholar] [CrossRef]
- Esmaeilzadeh, H.; Rivard, M.; Arzi, E.; Légaré, F.; Hassani, A. Smart textile plasmonic fiber dew sensors. Opt. Express 2015, 23, 14981–14992. [Google Scholar] [CrossRef]
- Li, J.F.; Zhang, Y.J.; Ding, S.Y.; Panneerselvam, R.; Tian, Z.Q. Core–Shell Nanoparticle-Enhanced Raman Spectroscopy. Chem. Rev. 2017, 117, 5002–5069. [Google Scholar] [CrossRef]
- Agrawat, A.; Cho, S.H.; Zandi, O.; Ghosh, S.; Johns, R.W.; Milliron, D.J. Localized Surface Plasmon Resonance in Semiconductor Nanocrystals. Chem. Rev. 2018, 118, 3121–3207. [Google Scholar] [CrossRef]
- Lee, J.D. Optical absorption of semiconducting and metallic nanospheres with the confined electron-phonon coupling. J. Chem Phys. 2006, 124, 194706. [Google Scholar] [CrossRef]
- Santavicca, D.F.; Reulet, B.; Karasik, B.S.; Pereverzev, S.V.; Olaya, D.; Gershenson, M.E.; Frunzio, L.; Prober, D.E. Energy resolution of terahertz single-photon-sensitive bolometric detectors. Appl. Phys. Lett. 2010, 96, 083505. [Google Scholar] [CrossRef]
- Ryzhii, V.; Ryzhii, M.; Mitin, V.; Otsuji, T. Terahertz and infrared photodetection using p-i-n multiple-graphene-layer structures. J. Appl. Phys. 2010, 107, 054512. [Google Scholar] [CrossRef]
- Marinchio, H.; Chusseau, L.; Torres, J.; Nouvel, P.; Varani, L.; Sabatini, G.; Palermo, C.; Shiktorov, P.; Starikov, E.; Gružinskis, V. Room-temperature terahertz mixer based on the simultaneous electronic and optical excitations of plasma waves in a field effect transistor. Appl. Phys. Lett. 2010, 96, 013502. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917. [Google Scholar] [CrossRef]
- Foteinopoulou, S.; Kafesaki, M.; Economou, E.N.; Soukoulis, C.M. Two-dimensional polaritonic photonic crystals as terahertz uniaxial metamaterials. Phys. Rev. B 2012, 84, 035128. [Google Scholar] [CrossRef]
- Sugunan, A.; Zhao, Y.; Mitra, S.; Dong, L.; Li, S.; Popov, S.; Marcinkevicius, S.; Toprak, M.S.; Muhammed, M. Synthesis of tetrahedral quasi-type-II CdSe–CdS core–shell quantum dots. Nanotechnology 2011, 22, 425202. [Google Scholar] [CrossRef]
- Clark, S.W.; Harbold, J.M.; Wise, F.W. Resonant energy transfer in PbS quantum dots. J. Phys. Chem. 2007, 111, 7302–7305. [Google Scholar] [CrossRef]
- Yang, H.-J.; Tuan, H.-Y. Efficient and scalable synthesis of quantum dots using hexane as the solvent in a non-microfluidic flow reactor system. RSC Adv. 2014, 4, 51926–51934. [Google Scholar] [CrossRef]
- Material parameters of InAs and GaAs. Available online: http://www.ioffe.ru/SVA/NSM/Semicond/ (accessed on 2 April 2019).
- Vurgaftman, I.; Meyer, J.R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Schooss, D.; Mews, A.; Eychmuller, A.; Weller, H. Quantum-dot quantum well CdS/HgS/CdS: Theory and experiment. Phys. Rev. B 1994, 49, 17072. [Google Scholar] [CrossRef]
- Adachi, S. Optical Constants of Crystalline and Amorphous Semiconductor: Numerical Data and Graphical Information; Kluwer Academic Publishers: Boston, MA, USA, 2004; 714p. [Google Scholar]
- Schaller, R.D.; Pietryga, J.M.; Klimov, V.I. Carrier Multiplication in InAs Nanocrystal Quantum Dots with an Onset Defined by the Energy Conservation Limit. Nano Lett. 2007, 7, 3469. [Google Scholar] [CrossRef]
- Lim, H.; Zhang, W.; Tsao, S.; Sills, T.; Szafraniec, J.; Mi, K.; Movaghar, B.; Razeghi, M. Quantum dot infrared photodetectors: Comparison of experiment and theory. Phys. Rev. B 2005, 72, 085332. [Google Scholar] [CrossRef]
- Makeev, M.A. Self-Organized Quantum Dot Superstructures for Nanoelectronic and Optoelectronic Applications. J. Nanoelectron. Optoelectron. 2006, 1, 176. [Google Scholar] [CrossRef]
- Sargent, E.H. Colloidal quantum dot solar cells. Nat. Photonics 2012, 6, 133. [Google Scholar] [CrossRef]
- Fomin, V.M.; Pokatilov, E.P. Optical Properties of Multi-Layer Structures. IV. Non-Linear Absorption of light in Multi-Layer Structures. Phys. Stat. Sol. B 1993, 176, 355. [Google Scholar] [CrossRef]
- Ridley, B.K. Electrons and Phonons in Semiconductor Multilayers; Cambridge University Press: Cambridge, UK, 1997; 330p. [Google Scholar]
- Stroscio, M.A.; Dutta, M. Phonons in Nanostructures; Cambridge University Press: Cambridge, UK, 2001; 274p. [Google Scholar]
- Klimin, S.N.; Pokatilov, E.P.; Fomin, V.M. Bulk and interface polarons in quantum wires and dots. Phys. Stat. Sol. B 1994, 184, 373. [Google Scholar] [CrossRef]
- Zhu, H.; Song, N.; Lian, T. Wave function engineering for ultrafast charge separation and slow charge recombination in type II core/shell quantum dots. J. Am. Chem. Soc. 2011, 133, 8762. [Google Scholar] [CrossRef]
- Predeep, T. Nano: The Essentials. Understanding of Nanoscience and Nanotechnology; McGraw-Hill: New Delhi, NY, USA, 2007; 267p. [Google Scholar]
- Vukmirović, N.; Gačević, Ž; Ikonić, Z.; Indjin, D.; Harrison, P.; Milanović, V. Intraband absorption in InAs/GaAs quantum dot infrared photodetectors—Effective mass versus k × p modelling. Semicond. Sci. Technol. 2006, 21, 1098–1104. [Google Scholar]
- Aden, A.L.; Kerker, M. Scattering of electromagnetic waves from two concentric spheres. J. Appl. Phys. 1951, 22, 1242–1246. [Google Scholar] [CrossRef]
- Tzarouchis, D.; Sihvola, A. Light scattering by a dielectric sphere: Perspectives on the Mie resonances. Appl. Sci. 2018, 8, 184. [Google Scholar] [CrossRef]
- Reithmaier, J.P.; Benyoucef, M. III-V on Silicon nanocomposites. In Semiconductors and Semimetals; Lourdudoss, S., Chen, R., Jagadish, C., Eds.; Academic Press: Cambridge, MA, USA, 2018; Volume 2, pp. 27–42. [Google Scholar]
- Jing, P.; Zheng, J.; Zeng, Q.; Zhang, Y.; Liu, X.; Liu, X.; Kong, X.; Zhao, J.J. Shell-dependent electroluminescence from colloidal CdSe quantum dots in multilayer light-emitting diodes. Appl. Phys. 2009, 105, 044313. [Google Scholar] [CrossRef]
- Lalayan, A.; Avetisyan, A.; Djotyan, A. The luminescence properties of the colloidal GaAs and CdS semiconductor quantum dots. Laser Phys. Lett. 2005, 2, 12–15. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, C.; Li, Q.; Chen, Z.; Gong, Q. Preparation, characterization and nonlinear optical properties of colloidal gallium arsenide nanocrystals. Rare Metals 2006, 25, 118–123. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nika, D.L.; Pokatilov, E.P.; Fomin, V.M.; Devreese, J.T.; Tempere, J. Resonant Terahertz Light Absorption by Virtue of Tunable Hybrid Interface Phonon–Plasmon Modes in Semiconductor Nanoshells. Appl. Sci. 2019, 9, 1442. https://doi.org/10.3390/app9071442
Nika DL, Pokatilov EP, Fomin VM, Devreese JT, Tempere J. Resonant Terahertz Light Absorption by Virtue of Tunable Hybrid Interface Phonon–Plasmon Modes in Semiconductor Nanoshells. Applied Sciences. 2019; 9(7):1442. https://doi.org/10.3390/app9071442
Chicago/Turabian StyleNika, Denis L., Evghenii P. Pokatilov, Vladimir M. Fomin, Josef T. Devreese, and Jacques Tempere. 2019. "Resonant Terahertz Light Absorption by Virtue of Tunable Hybrid Interface Phonon–Plasmon Modes in Semiconductor Nanoshells" Applied Sciences 9, no. 7: 1442. https://doi.org/10.3390/app9071442
APA StyleNika, D. L., Pokatilov, E. P., Fomin, V. M., Devreese, J. T., & Tempere, J. (2019). Resonant Terahertz Light Absorption by Virtue of Tunable Hybrid Interface Phonon–Plasmon Modes in Semiconductor Nanoshells. Applied Sciences, 9(7), 1442. https://doi.org/10.3390/app9071442





