Centrosymmetric Optical Vortex
Abstract
:1. Introduction
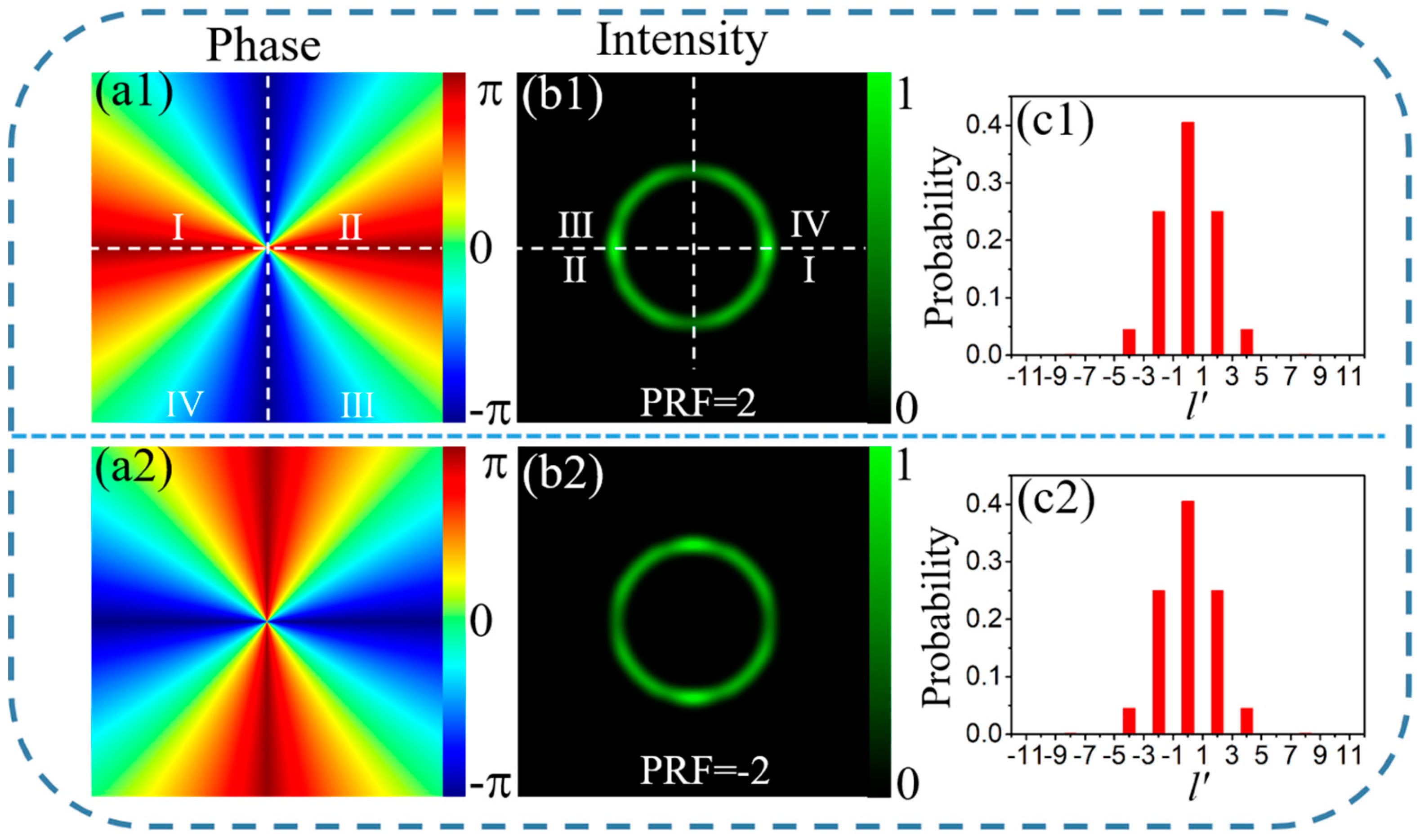
2. Basic Theory
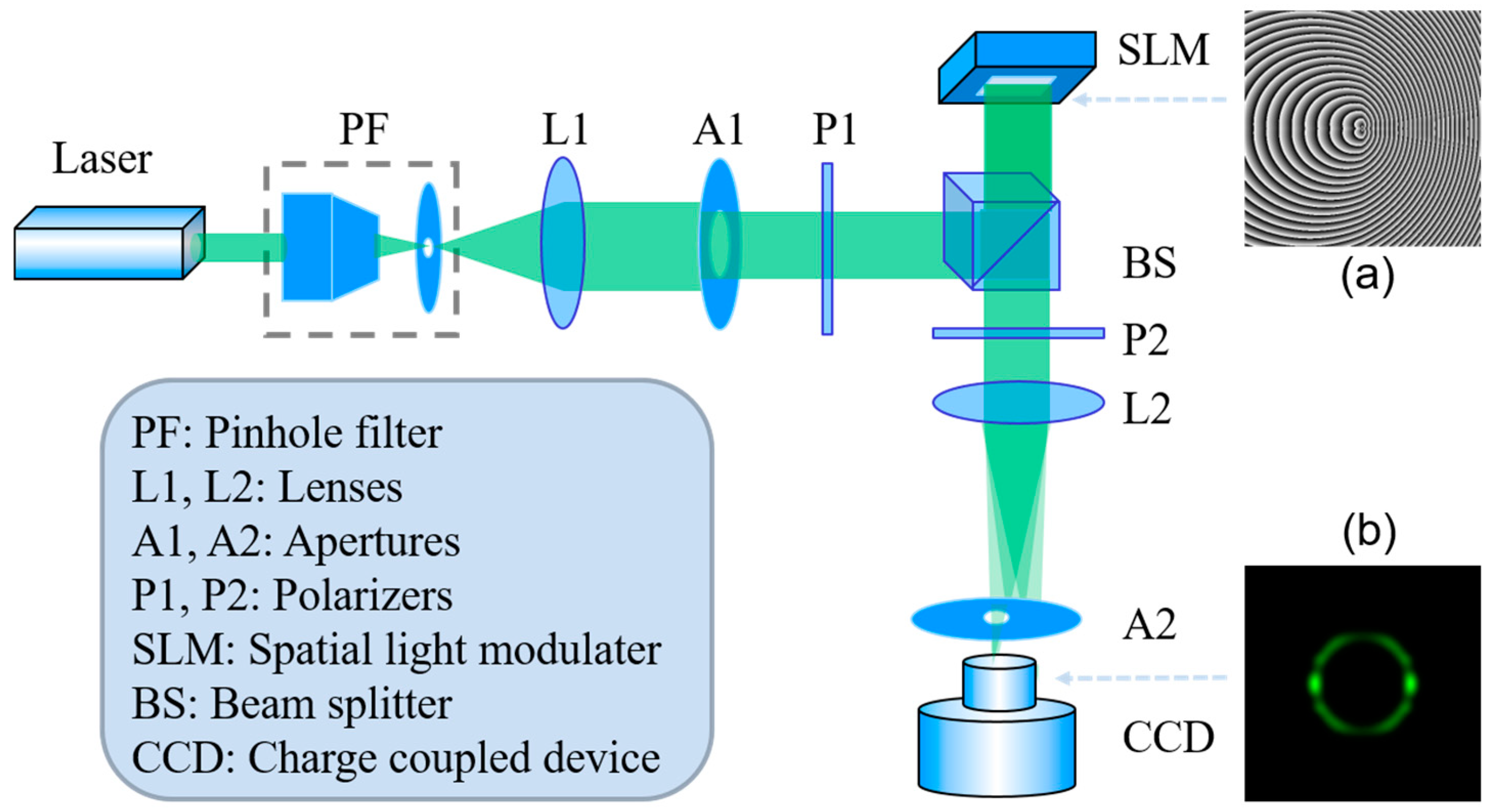
3. Experimental Setup
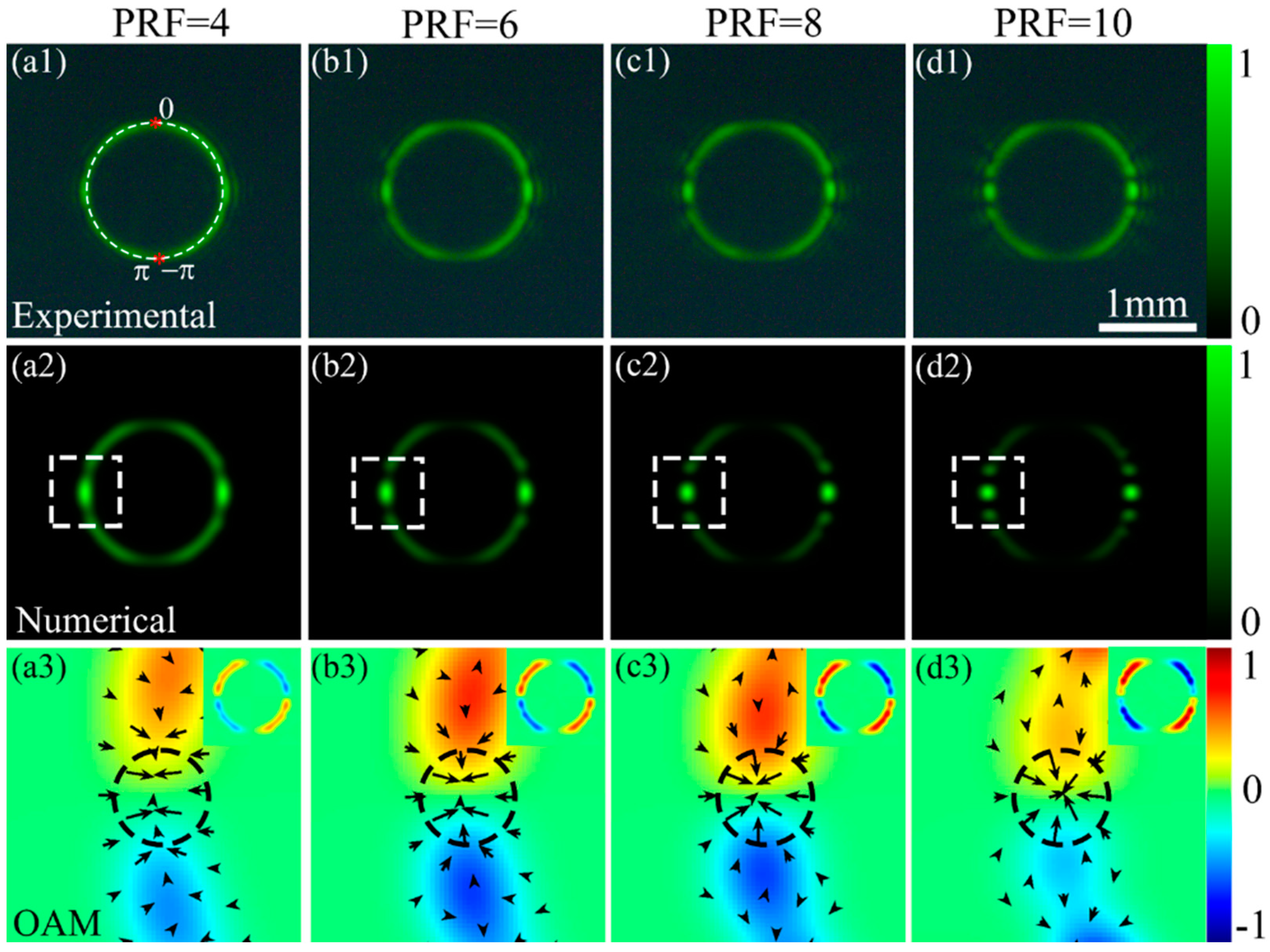
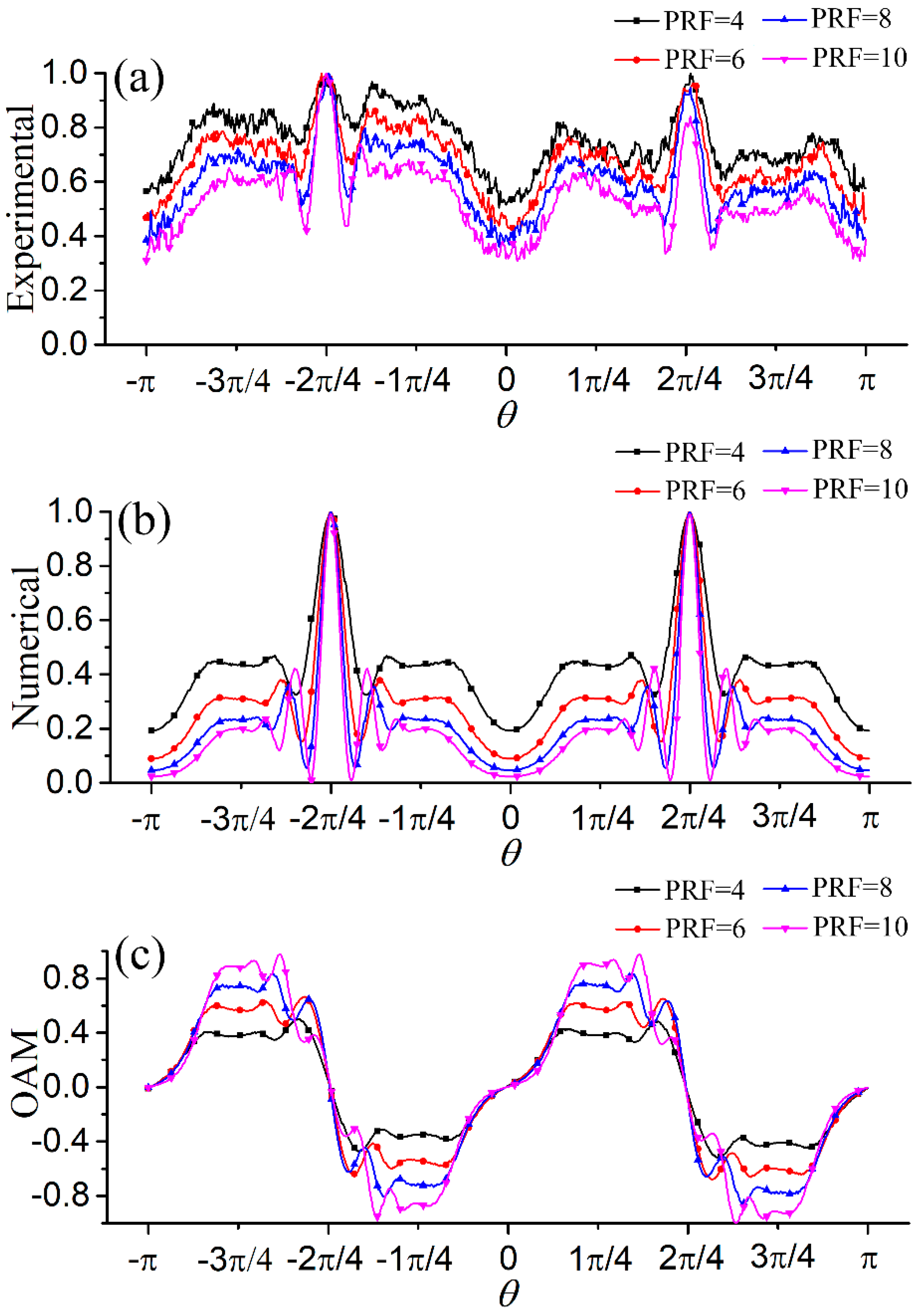
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810. [Google Scholar] [CrossRef] [PubMed]
- Dholakia, K.; Čižmár, T. Shaping the future of manipulation. Nat. Photonics 2011, 5, 335. [Google Scholar] [CrossRef]
- Chen, M.; Mazilu, M.; Arita, Y.; Wright, E.M.; Dholakia, K. Dynamics of microparticles trapped in a perfect vortex beam. Opt. Lett. 2013, 38, 4919–4922. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, J.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, K.; Wang, F.; Zhao, C.; Cai, Y. Coupling efficiency of a partially coherent radially polarized vortex beam into a single-mode fiber. Appl. Sci. 2018, 8, 1313. [Google Scholar] [CrossRef]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Li, X.; Tai, Y.; Li, H.; Wang, J.; Tang, M.; Wang, Y.; Tang, J.; Nie, Z. In situ measurement of the topological charge of a perfect vortex using the phase shift method. Opt. Lett. 2017, 42, 135–138. [Google Scholar] [CrossRef]
- Aleksanyan, A.; Kravets, N.; Brasselet, E. Multiple-star system adaptive vortex coronagraphy using a liquid crystal light valve. Phys. Rev. Lett. 2017, 118, 203902. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A.; Soifer, V.A. Asymmetric Bessel modes. Opt. Lett. 2014, 39, 2395–2398. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. Optical trapping and moving of microparticles by using asymmetrical Laguerre-Gaussian beams. Opt. Lett. 2016, 41, 2426–2429. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Asymmetric Gaussian optical vortex. Opt. Lett. 2017, 42, 139–142. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. A highly efficient element for generating elliptic perfect optical vortices. Appl. Phys. Lett. 2017, 110, 5. [Google Scholar] [CrossRef]
- Li, X.; Ma, H.; Yin, C.; Tang, J.; Li, H.; Tang, M.; Wang, J.; Tai, Y.; Li, X.; Wang, Y. Controllable mode transformation in perfect optical vortices. Opt. Express 2018, 26, 651–662. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Liu, S.; Peng, T.; Xie, G.; Gan, X.; Zhao, J. Spiral autofocusing Airy beams carrying power-exponent-phase vortices. Opt. Express 2014, 22, 7598–7606. [Google Scholar] [CrossRef]
- Ma, H.; Li, X.; Zhang, H.; Tang, J.; Li, H.; Tang, M.; Wang, J.; Cai, Y. Optical vortex shaping via a phase jump factor. Opt. Lett. 2019, 44, 1379–1382. [Google Scholar] [CrossRef]
- Abramochkin, E.G.; Volostnikov, V.G. Spiral light beams. Phys. Usp. 2004, 47, 1177–1203. [Google Scholar] [CrossRef]
- Rodrigo, J.A.; Alieva, T.; Abramochkin, E.; Castro, I. Shaping of light beams along curves in three dimensions. Opt. Express 2013, 21, 20544–20555. [Google Scholar] [CrossRef]
- Rodrigo, J.A.; Alieva, T. Freestyle 3D laser traps: Tools for studying light-driven particle dynamics and beyond. Optica 2015, 2, 812–815. [Google Scholar] [CrossRef]
- Bezryadina, A.S.; Preece, D.C.; Chen, J.; Chen, Z. Optical disassembly of cellular clusters by tunable ‘tug-of-war’ tweezers. Light-Sci. Appl. 2016, 5, e16158. [Google Scholar] [CrossRef]
- Frankearnold, S. Quantum formulation of fractional orbital angular momentum. J. Mod. Opt. 2007, 54, 1723–1738. [Google Scholar]
- Tkachenko, G.; Chen, M.; Dholakia, K.; Mazilu, M. Is it possible to create a perfect fractional vortex beam? Optica 2017, 4, 330–333. [Google Scholar] [CrossRef]
- Arlt, J. Handedness and azimuthal energy flow of optical vortex beams. J. Mod. Opt. 2003, 50, 1573–1580. [Google Scholar] [CrossRef]
- Li, X.; Ma, H.; Zhang, H.; Tang, M.; Li, H.; Tang, J.; Wang, Y. Is it possible to enlarge the trapping range of optical tweezers via a single beam? Appl. Phys. Lett. 2019, 114, 081903. [Google Scholar] [CrossRef]
- Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R. Soc. Lond. A-Math. Phys. Eng. Sci. 1974, 336, 165–190. [Google Scholar] [CrossRef]
- Gbur, G. Fractional vortex Hilbert’s Hotel. Optica 2016, 3, 222–225. [Google Scholar] [CrossRef]
- Vaity, P.; Rusch, L. Perfect vortex beam: Fourier transformation of a Bessel beam. Opt. Lett. 2015, 40, 597–600. [Google Scholar] [CrossRef]
- Ohtake, Y.; Ando, T.; Fukuchi, N.; Matsumoto, N.; Ito, H.; Hara, T. Universal generation of higher-order multiringed Laguerre-Gaussian beams by using a spatial light modulator. Opt. Lett. 2007, 32, 1411–1413. [Google Scholar] [CrossRef]
- O’Neil, A.T.; MacVicar, I.; Allen, L.; Padgett, M.J. Intrinsic and extrinsic nature of the orbital angular momentum of a light beam. Phys. Rev. Lett. 2002, 88, 053601. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, Y.; Zhu, Z.; Rui, G.; Cui, Y.; Gu, B. Theoretical investigation on asymmetrical spinning and orbiting motions of particles in a tightly focused power-exponent azimuthal-variant vector field. Opt. Express 2018, 26, 4318–4329. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, X.; Ma, H.; Tang, M.; Li, H.; Cai, Y. Centrosymmetric Optical Vortex. Appl. Sci. 2019, 9, 1429. https://doi.org/10.3390/app9071429
Zhang H, Li X, Ma H, Tang M, Li H, Cai Y. Centrosymmetric Optical Vortex. Applied Sciences. 2019; 9(7):1429. https://doi.org/10.3390/app9071429
Chicago/Turabian StyleZhang, Hao, Xinzhong Li, Haixiang Ma, Miaomiao Tang, Hehe Li, and Yangjian Cai. 2019. "Centrosymmetric Optical Vortex" Applied Sciences 9, no. 7: 1429. https://doi.org/10.3390/app9071429
APA StyleZhang, H., Li, X., Ma, H., Tang, M., Li, H., & Cai, Y. (2019). Centrosymmetric Optical Vortex. Applied Sciences, 9(7), 1429. https://doi.org/10.3390/app9071429





