Effect of Vinyl Flooring on the Modal Properties of a Steel Footbridge
Abstract
1. Introduction
2. Unexpected High Experimental Damping Ratios of the Jorge Manrique Footbridge
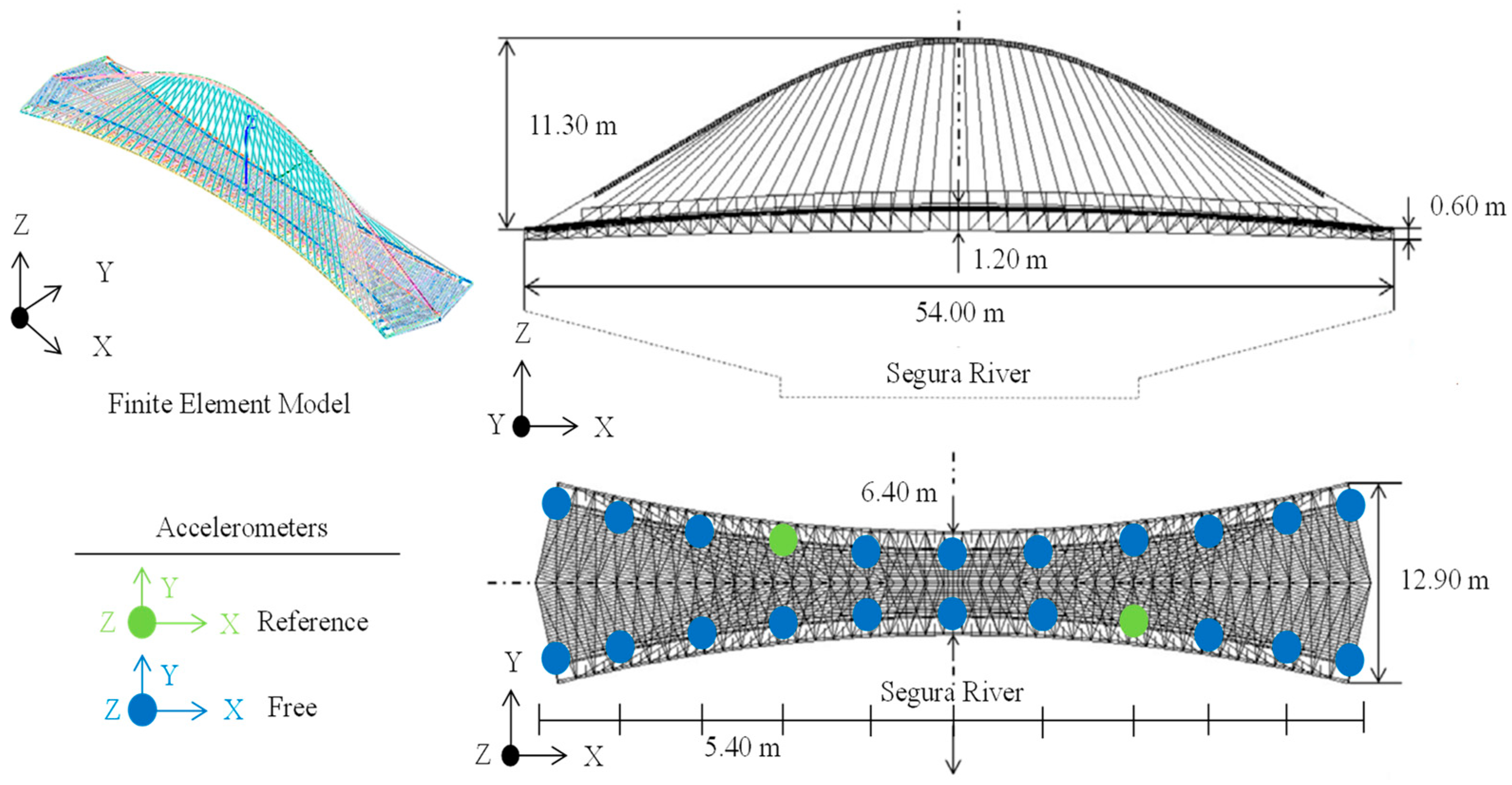
2.1. Description of the Structure, Numerical Finite Element (FE) Model and Numerical Modal Analysis
2.2. Experimental Identification of the Modal Parameters of the Jorge Manrique Footbridge
3. Viscous Damping Mechanisms for Vibrating Footbridges
- ζs,j
- is the structural damping ratio (associated with the structural elements) [%].
- ζns,j
- is the non-structural damping ratio (associated with the non-structural elements) [%].
- ζa,j
- is the aerodynamic damping ratio (associated with the air-structure interaction) [%].
- ζd,j
- is the special devices damping ratio (associated with installed external damping devices as tuned mass dampers, sloshing tanks, etc.) [%].
4. Assessment of the Dynamic Behavior of a Laboratory Footbridge without and with the Vinyl Flooring
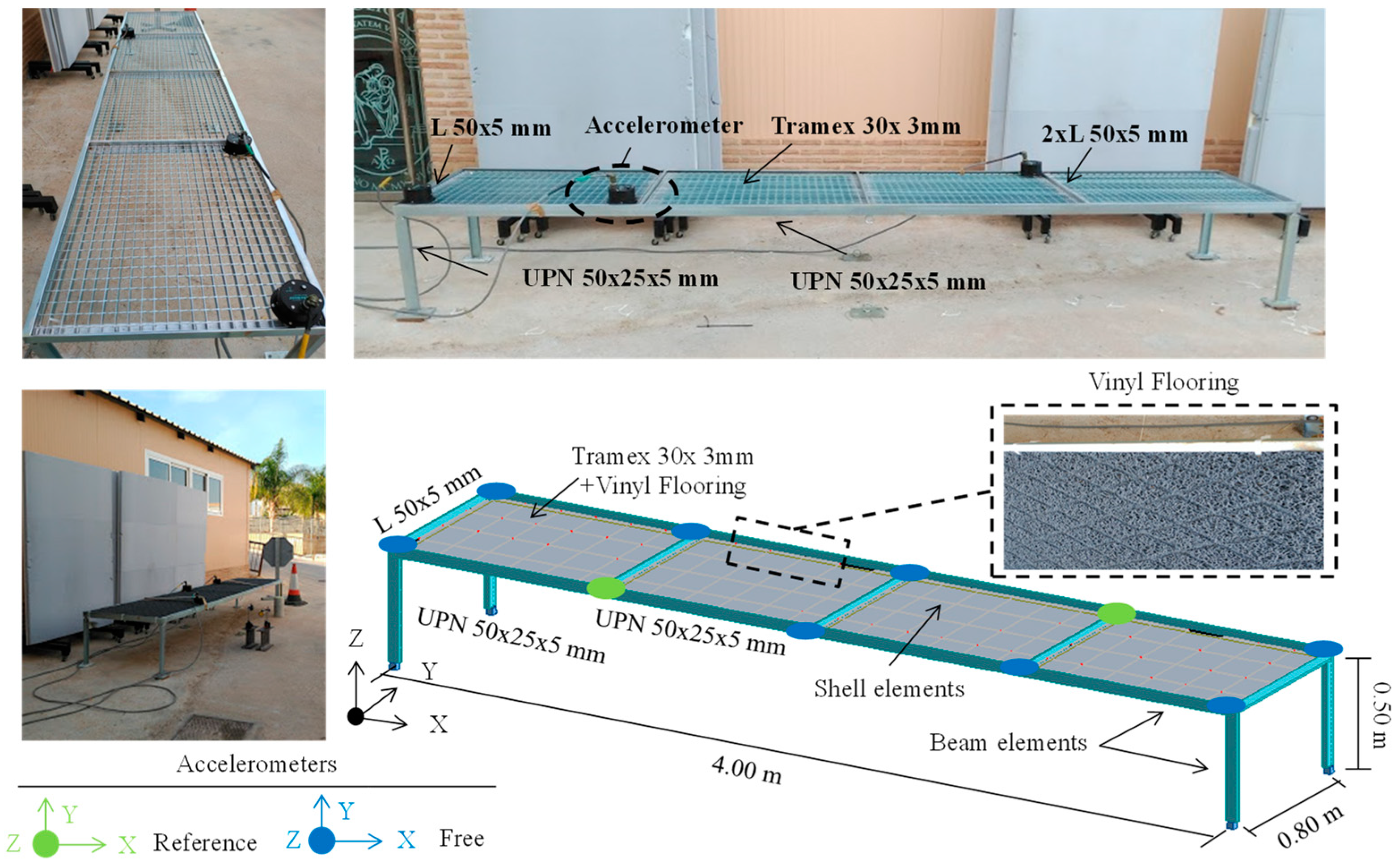
4.1. Description of the Structure, Numerical FE Model and Numerical Modal Analysis
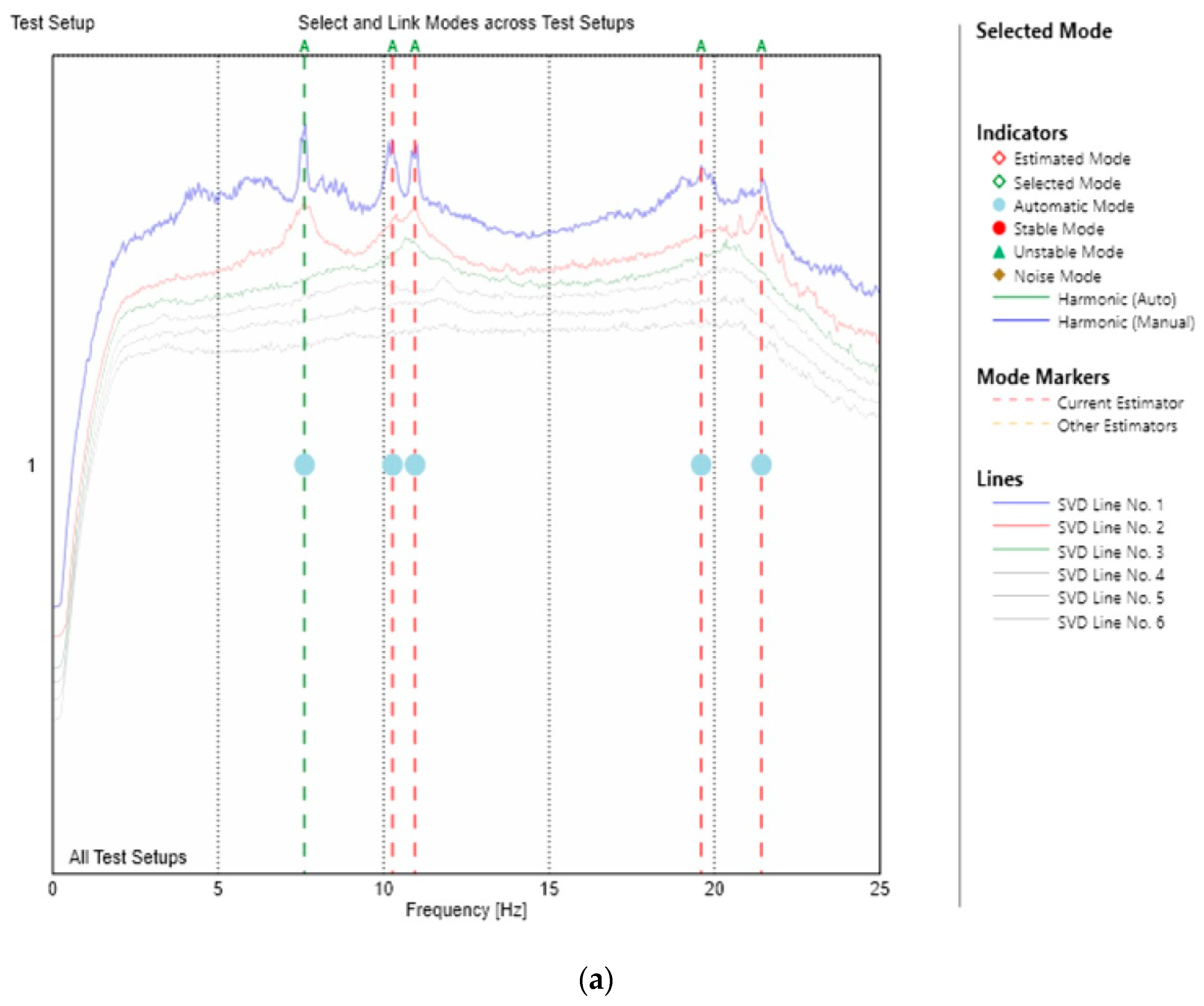
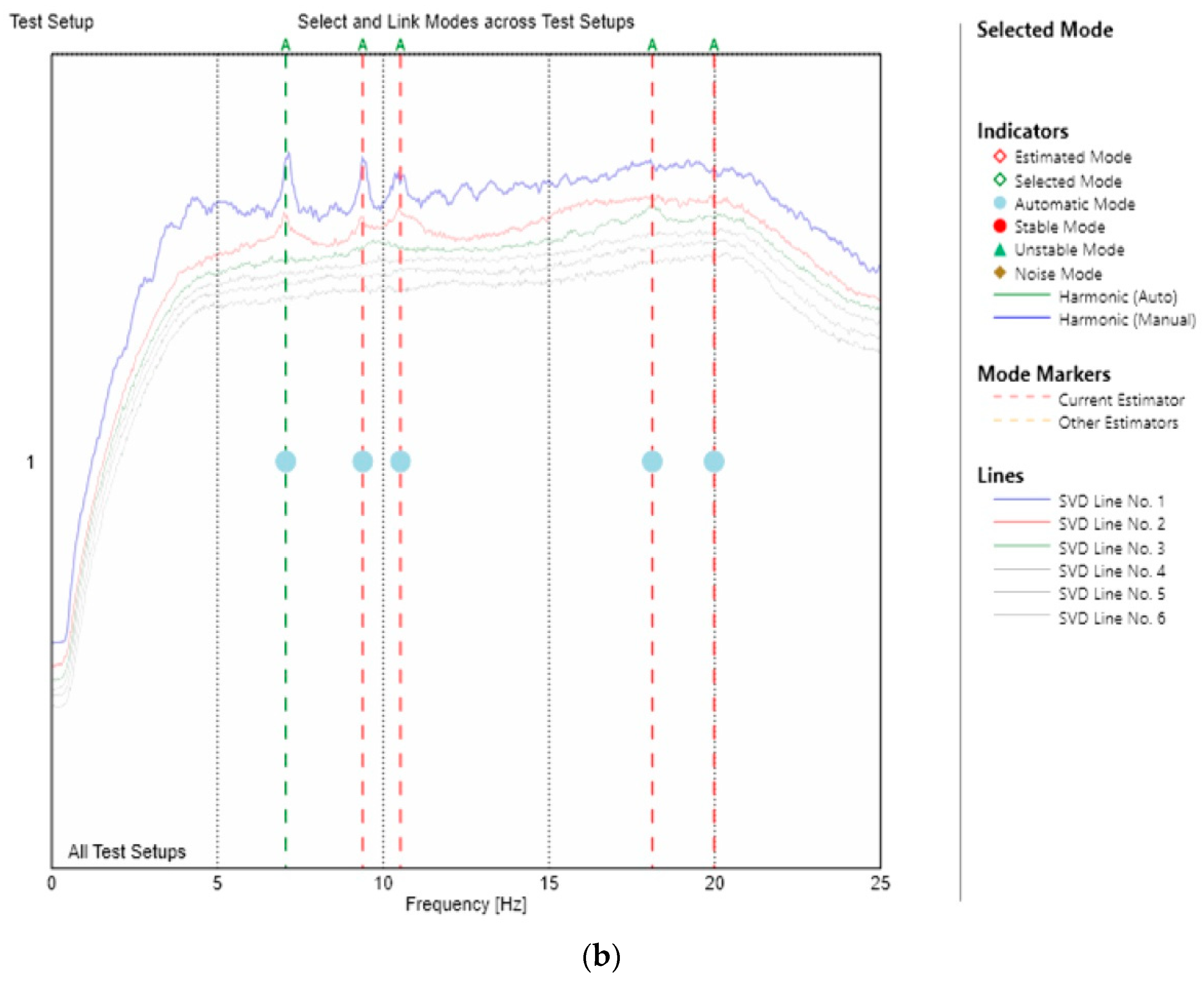
4.2. Experimental Identification of the Modal Parameters of the Laboratory Footbridge
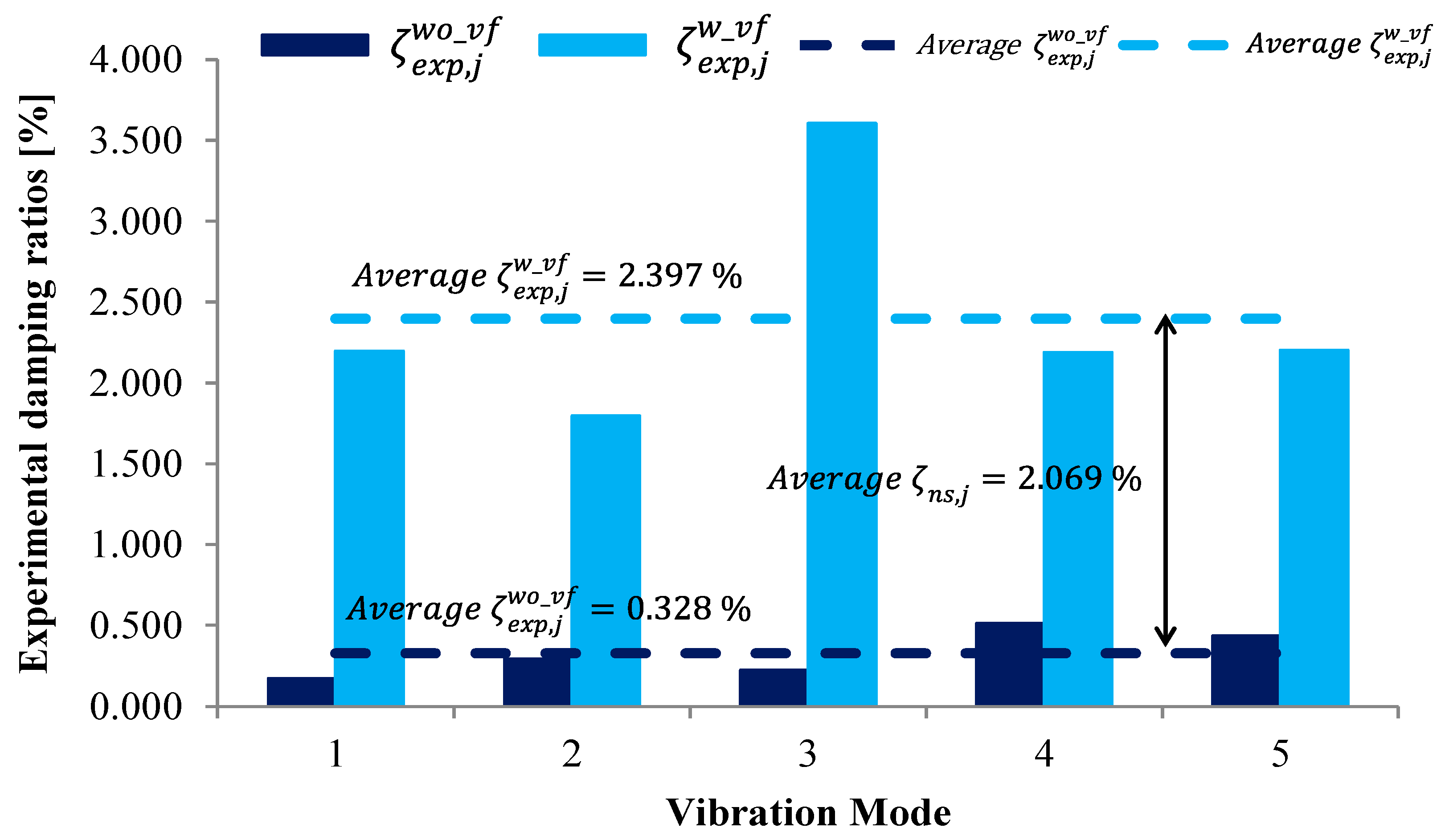
4.3. Discussion of the Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zivanovic, S.; Pavic, A.; Reynolds, P. Vibration serviceability of footbridges under human-induced excitation: A literature review. J. Sound. Vib. 2005, 279, 1–74. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Wasoodev, H.; Raoul, J. Footbridge Vibration Design, 1st ed.; CRC Press Balkema: Leiden, The Netherlands, 2009. [Google Scholar]
- Dallard, P.; Fitzpatrick, A.J.; Le Bourva, S.; Low, A.; Smith, R.; Willford, M.; Flint, A. The London Millenium Footbridge. Struct. Eng. 2001, 79, 17–33. [Google Scholar]
- Dziuba, P.; Grillaud, G.; Flamand, O.; Sanquier, S.; Tétard, Y. La passerelle Solférino comportement dynamique. Bull. Ouvrages Métalliques 2001, 1, 34–57. (In French) [Google Scholar]
- Jiménez-Alonso, J.F.; Sáez, A. Motion-based optimum design of a slender steel footbridge and assessment of its dynamic behaviour. Int. J. Steel Struct. 2017, 17, 1459–1470. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Sáez, A. Controlling the Human-Induced Longitudinal Vibrations of a Nielsen-Truss Footbridge Via the Modification of its Natural Frequencies. Int. J. Struct. Stab. Dyn. 2017, 17, 1750061. [Google Scholar] [CrossRef]
- Oliveira, C.S. Fundamental Frequencies of Vibration of Footbridges in Portugal: From in Situ Measurements to Numerical Modelling. Shock Vib. 2014, 2014, 925437. [Google Scholar]
- Naranjo-Pérez, J.; Jiménez-Manfredi, J.; Jiménez-Alonso, J.F.; Sáez, A. Motion-Based Design of Passive Damping Devices to Mitigate Wind-Induced Vibrations in Stay Cables. Vibration 2018, 1, 269–289. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Zhang, Q. Application of an Artificial Fish Swarm Algorithm in an Optimum Tuned Mass Damper Design for a Pedestrian Bridge. Appl. Sci. 2018, 8, 175. [Google Scholar] [CrossRef]
- Soong, T.T.; Costantinou, M.C. Passive and Active Control Structural Vibration Control in Civil Engineering; State University of New York at Buffalo: Buffalo, NY, USA, 1994. [Google Scholar]
- Rodriguez, V. La ciudad estrena la pasarela del ingeniero Calatrava. La verdad 1999, 20. (In Spanish) [Google Scholar]
- Montesinos, M.J. Adiós a los resbalones. La verdad. 2012. Available online: https://www.laverdad.es/murcia/v/20120809/murcia/adios-resbalones-20120809.html (accessed on 26 March 2018).
- Setra/AFGC. Guide Méthodologique Passerelles Piétonnes; Technical Guide Footbridges: Assessment of Vibration Behavior of Footbridge under Pedestrian Loading; Setra/AFGC: Paris, France, 2006. [Google Scholar]
- Butz, C.H.; Heinemeyer, C.H.; Goldack, A.; Keil, A.; Lukic, M.; Caetano, E.; Cunha, A. Advanced Load Models for Synchronous Pedestrian Excitation and Optimised Design Guidelines for Steel Footbridges (SYNPEX); Research Fund for Coal and Steel: Brussels, Belgium, 2007. [Google Scholar]
- Qin, C.L.; Zhao, D.Y.; Bai, X.D.; Zhang, X.G.; Zhang, B.; Jin, Z.; Niu, H.J. Vibration damping properties of gradient polyurethane/vinyl ester resin interpenetrating polymer network. Mater. Chem. Phys. 2006, 97, 517–524. [Google Scholar] [CrossRef]
- ABC. Atlas, Bilbao cubre con una alfombra antideslizanete el Puente de Calatrava. 2010. Available online: https://www.abc.es/20101221/espana/alfombra-puente-calatrava-201012211207.html html (accessed on 26 March 2018).
- Devin, A.; Fanning, P.J.; Pavic, A. Modelling effect of non-structural partitions on floor modal properties. Eng. Struct. 2015, 91, 58–69. [Google Scholar] [CrossRef]
- ASTM F1303-04(2014). Standard Specification for Sheet Vinyl Floor Covering with Backing; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Forbo Flooring Systems 2018. Available online: http://www.forbo.com/ (accessed on 26 March 2018).
- Magalhães, F.; Cunha, A. Explaining Operational Modal Analysis with data from an arch bridge. Mech. Syst. Signal Process. 2011, 25, 1431–1450. [Google Scholar] [CrossRef]
- Midas FEA 2016. Available online: http://en.midasuser.com/ (accessed on 7 May 2018).
- Eurocode 3. EN 1993-1-1: Design of Steel Structures: Part 1-1: General Rules and Rules for Buildings; European Committee for Standardisation: Brussels, Belgium, 2005. [Google Scholar]
- Clough, R.; Penzien, J. Dynamic of Structures; McGraw-Hill, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Sun, H.; Büyüköztürk, O. Optimal sensor placement in structural health monitoring using discrete optimization. Smart Mater. Struct. 2015, 24, 1–16. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, A.; Caetano, E.; Brincker, R. Damping estimation using free decays and ambient vibration tests. Mech. Syst. Signal Process. 2010, 24, 1274–1290. [Google Scholar]
- ARTeMIS Modal Pro. 2016. Available online: http://www.svibs.com/ (accessed on 7 May 2018).
- Zivanovic, S.; Pavic, A.; Reynolds, P. Finite element modelling and updating of a lively footbridge: The complete process. Eng. Struct. 2007, 301, 126–145. [Google Scholar]
- Van Nimmen, K.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. Vibration serviceability of footbridges: Evaluation of the current codes of practice. Eng. Struct. 2014, 59, 448–461. [Google Scholar] [CrossRef]
- Connor, J. Introduction to Structural Motion Control; Prentice Hall. Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Akay, A.; Carcaterra, A. Damping Mechanisms. In Book Active and Passive Vibration Control of Structures, 1st ed.; Hagedorn, P., Spelsberg-Korspeter, G., Eds.; CISM International Centre for Mechanical Sciences: Vienna, Austria, 2014; Volume 558, pp. 259–299. [Google Scholar]
- Adhikari, S. Damping Models for Structural Vibration. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2000. [Google Scholar]
- Eurocode 1. EN 1991-1-4: Actions on Structures-General Actions—Part. 1-4: Wind Actions; European Committee for Standardisation: Brussels, Belgium, 2004. [Google Scholar]

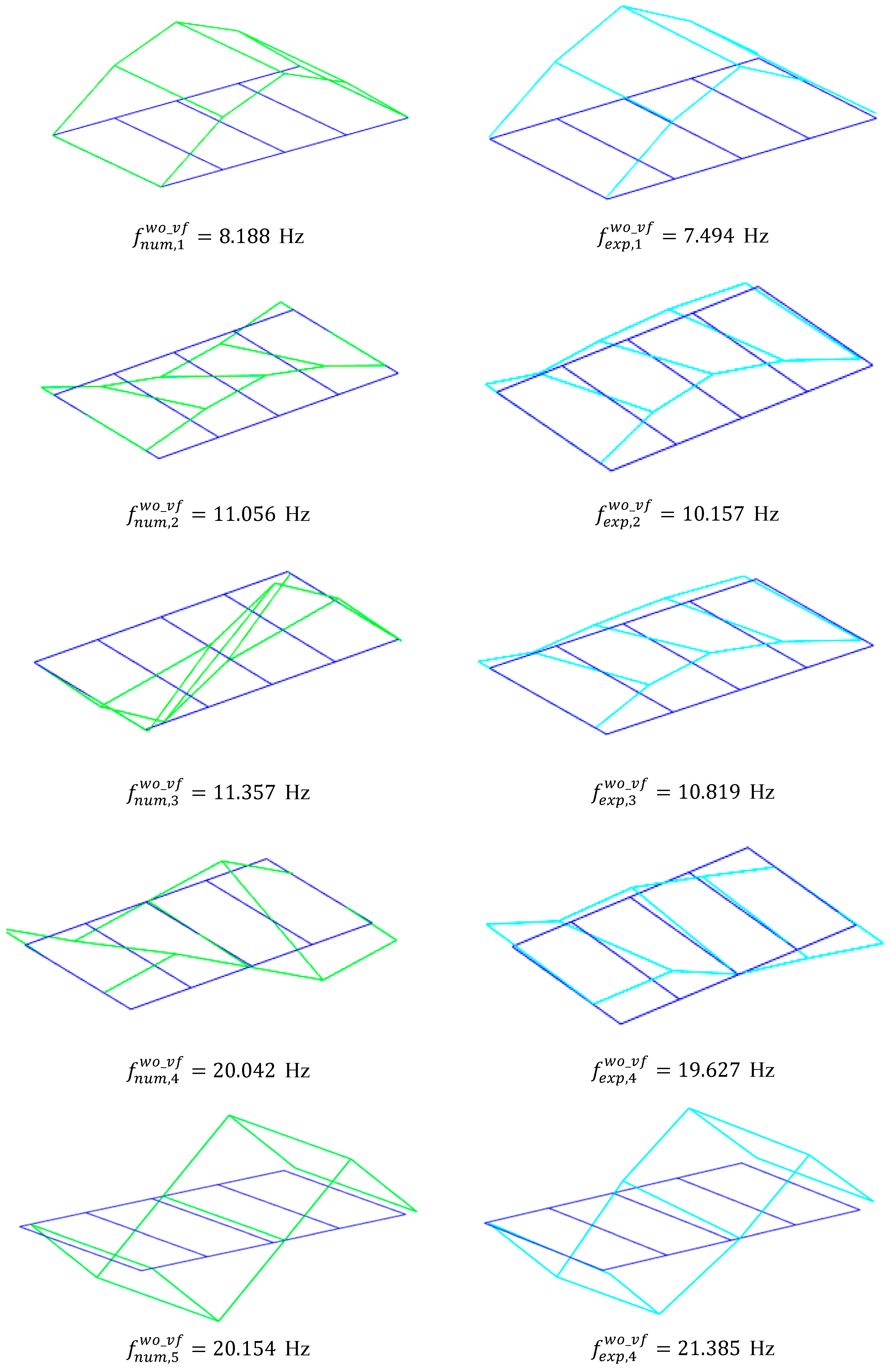
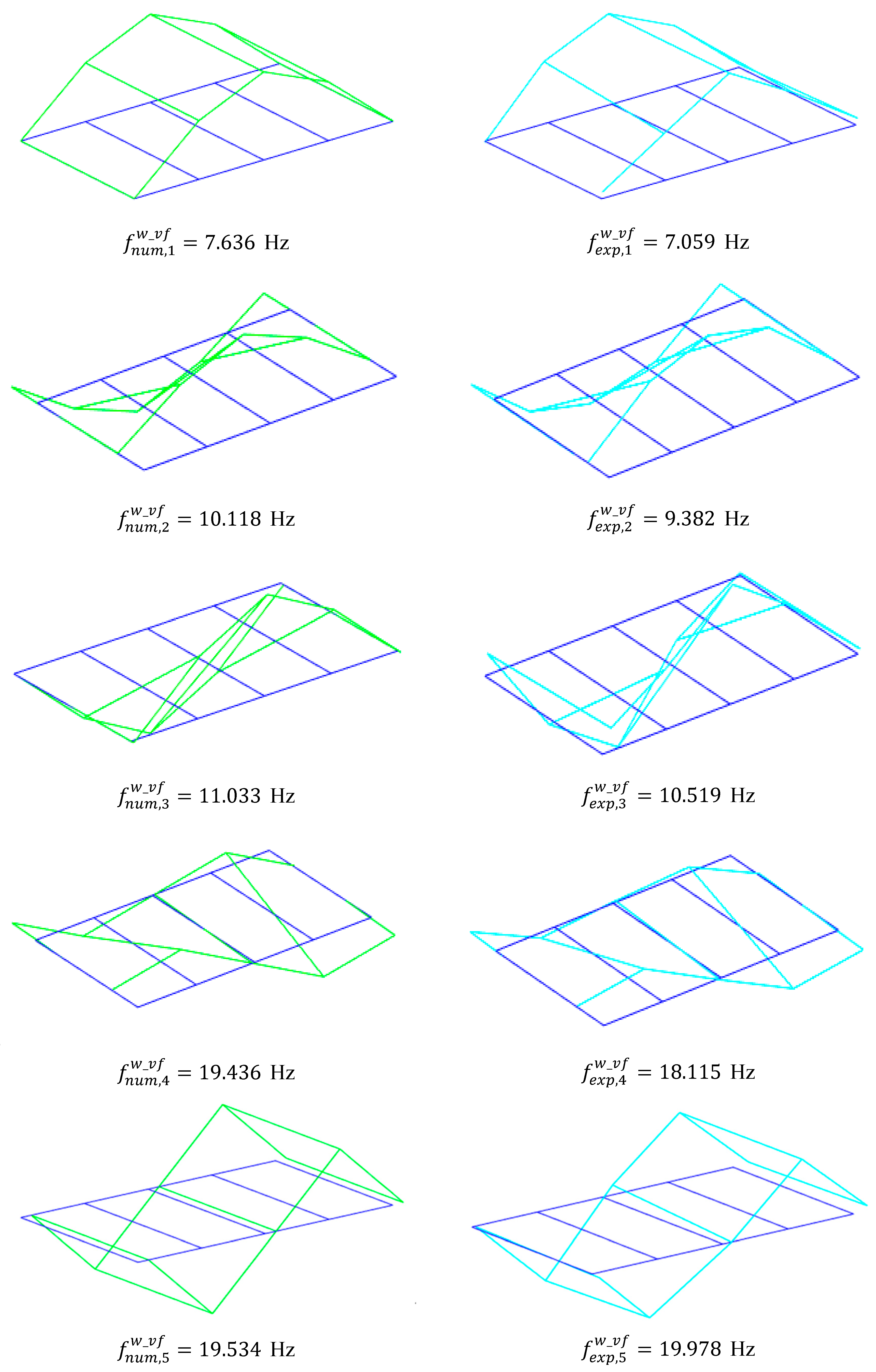
| Modes | Description | ||||||
|---|---|---|---|---|---|---|---|
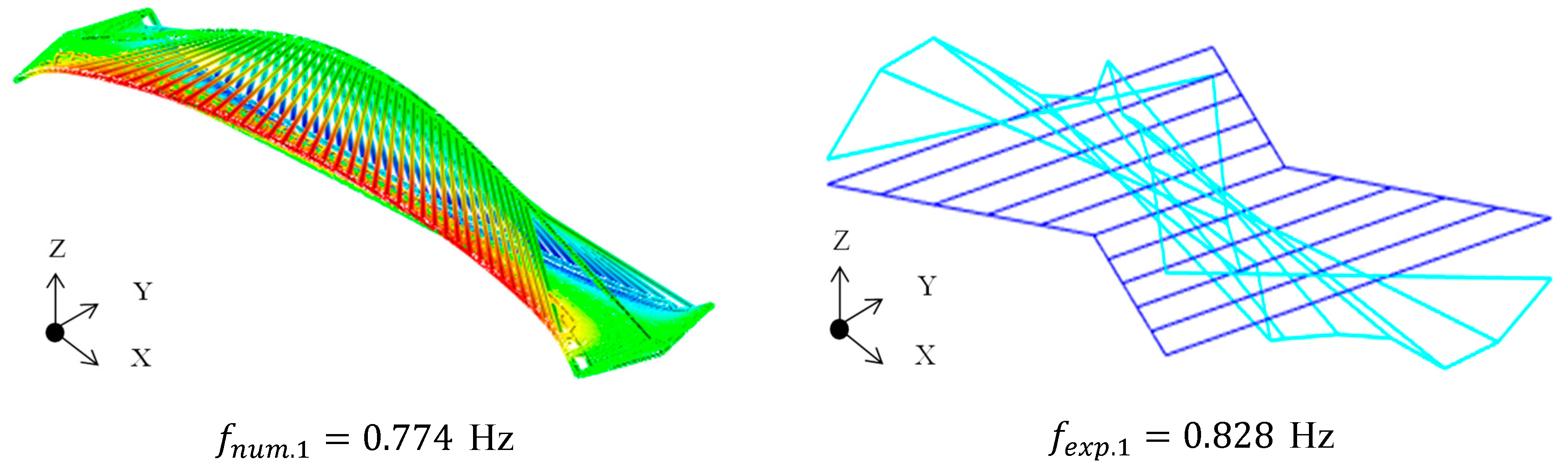
| 1 | 0.785 | 0.774 | 0.828 | 2.68 | −6.521 | 0.999 | Lateral + Torsion |
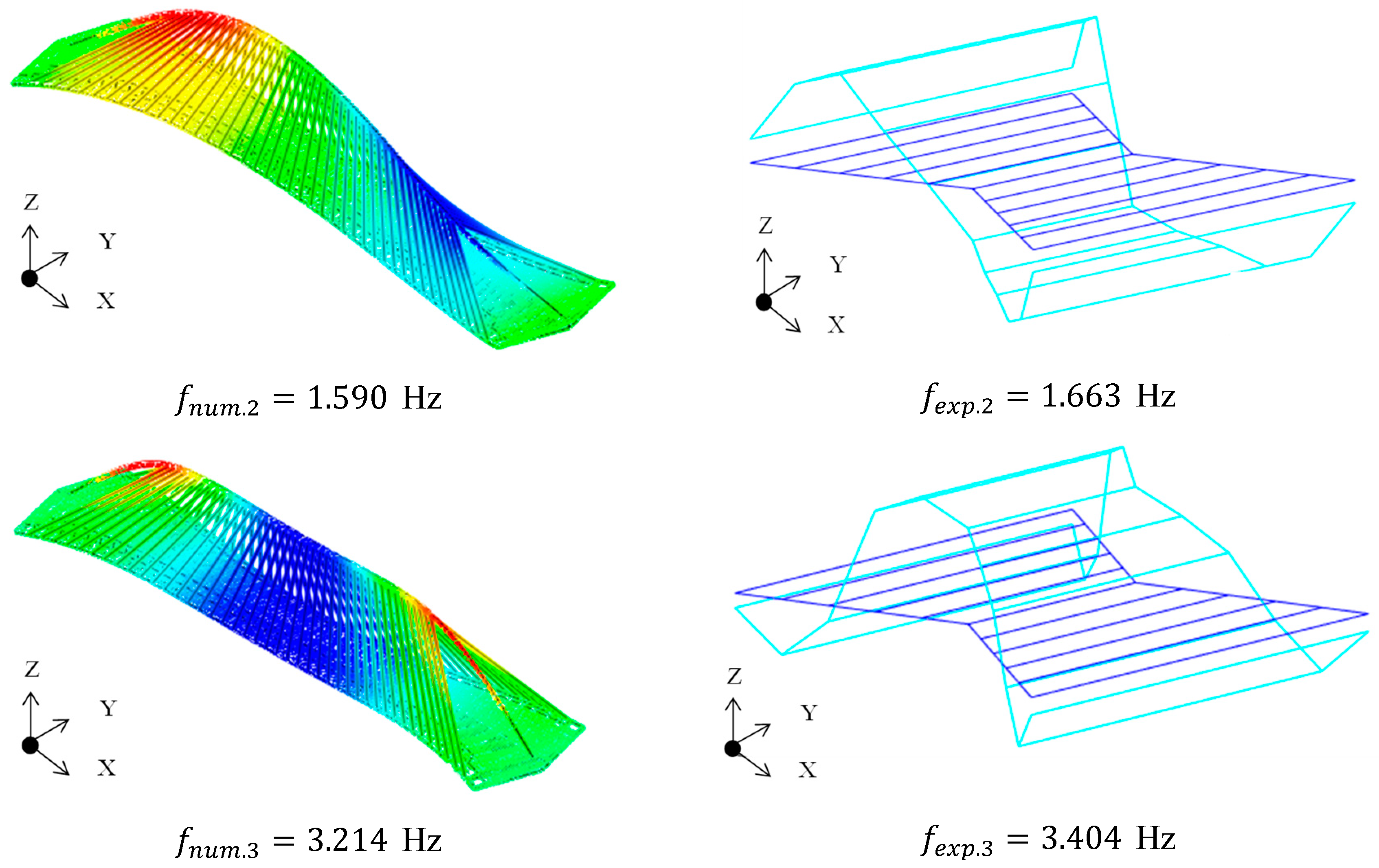
| 2 | 1.614 | 1.590 | 1.663 | 2.04 | −4.389 | 0.998 | Vertical |
| 3 | 3.262 | 3.214 | 3.404 | 1.61 | −5.581 | 0.951 | Vertical |
| Construction Type | ||||||
|---|---|---|---|---|---|---|
| French Guidelines [13] | European Guidelines [14] | |||||
| Serviceability Conditions | Large Vibrations | Serviceability Conditions | Large Vibrations | |||
| Minimum | Mean | Mean | Minimum | Mean | Mean | |
| Reinforced concrete | 0.80 | 1.30 | 5.00 | 0.80 | 1.30 | 5.00 |
| Prestressed Concrete | 0.50 | 1.00 | 2.00 | 0.50 | 1.00 | 2.00 |
| Steel welded joints | 0.20 | 0.40 | 2.00 | 0.20 | 0.40 | 2.00 |
| Steel bolted joints | 0.20 | 0.40 | 4.00 | 0.20 | 0.40 | 4.00 |
| Composite | 0.30 | 0.60 | - | 0.30 | 0.60 | - |
| Timber | 1.50 | 3.00 | - | 1.00 | 1.50 | - |
| Stress-ribbon | - | - | - | 0.70 | 1.00 | - |
| Modes | Description | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8.188 | 7.636 | 7.494 | 7.059 | 0.171 | 2.196 | 9.261 | 8.173 | 0.997 | 0.990 | Vertical |
| 2 | 11.056 | 10.118 | 10.157 | 9.382 | 0.293 | 1.797 | 8.851 | 7.844 | 0.904 | 0.992 | Lateral |
| 3 | 11.357 | 11.033 | 10.819 | 10.519 | 0.224 | 3.604 | 4.973 | 4.886 | 0.978 | 0.941 | Torsion |
| 4 | 20.042 | 19.436 | 19.627 | 18.115 | 0.513 | 2.187 | 2.114 | 7.292 | 0.995 | 0.995 | Lateral |
| 5 | 20.154 | 19.534 | 21.385 | 19.978 | 0.437 | 2.201 | −5.756 | −2.222 | 0.963 | 0.962 | Longitudinal |
| Modes | Description | |||
|---|---|---|---|---|
| 1 | 0.171 | 2.196 | 2.025 | Vertical |
| 2 | 0.293 | 1.797 | 1.504 | Lateral |
| 3 | 0.224 | 3.604 | 3.380 | Torsion |
| 4 | 0.513 | 2.187 | 1.674 | Lateral |
| 5 | 0.437 | 2.201 | 1.764 | Longitudinal |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-Alonso, J.F.; Pérez-Aracil, J.; Hernández Díaz, A.M.; Sáez, A. Effect of Vinyl Flooring on the Modal Properties of a Steel Footbridge. Appl. Sci. 2019, 9, 1374. https://doi.org/10.3390/app9071374
Jiménez-Alonso JF, Pérez-Aracil J, Hernández Díaz AM, Sáez A. Effect of Vinyl Flooring on the Modal Properties of a Steel Footbridge. Applied Sciences. 2019; 9(7):1374. https://doi.org/10.3390/app9071374
Chicago/Turabian StyleJiménez-Alonso, Javier Fernando, Jorge Pérez-Aracil, Alejandro Mateo Hernández Díaz, and Andrés Sáez. 2019. "Effect of Vinyl Flooring on the Modal Properties of a Steel Footbridge" Applied Sciences 9, no. 7: 1374. https://doi.org/10.3390/app9071374
APA StyleJiménez-Alonso, J. F., Pérez-Aracil, J., Hernández Díaz, A. M., & Sáez, A. (2019). Effect of Vinyl Flooring on the Modal Properties of a Steel Footbridge. Applied Sciences, 9(7), 1374. https://doi.org/10.3390/app9071374






