Investigating Quantum Coherence by Negative Excursions of the Wigner Quasi-Distribution
Abstract
Featured Application
Abstract
1. Quantum Information and The Wigner Function
1.1. The Wigner Function
1.2. Entanglement in the Wigner Function
- Quantum coherence is characterized by negative values of the Wigner function;
- In a virtual particle picture, coherent states are distinguished from classical states by the existence of particles with a negative weight.
2. A Simple Example Problem and Methods
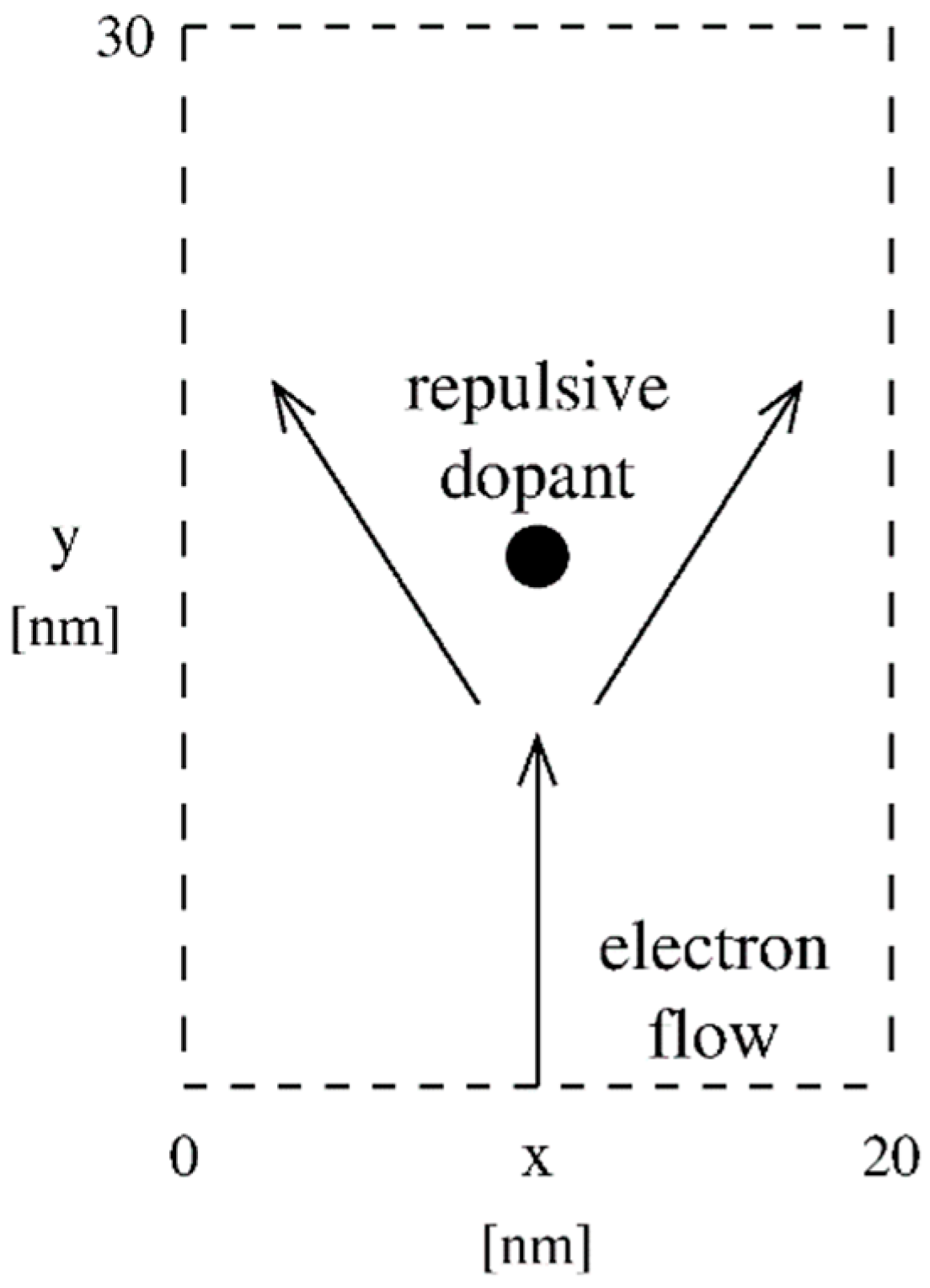
2.1. A Quasi-Two-Slit Electron Problem
2.2. Signed-Particles
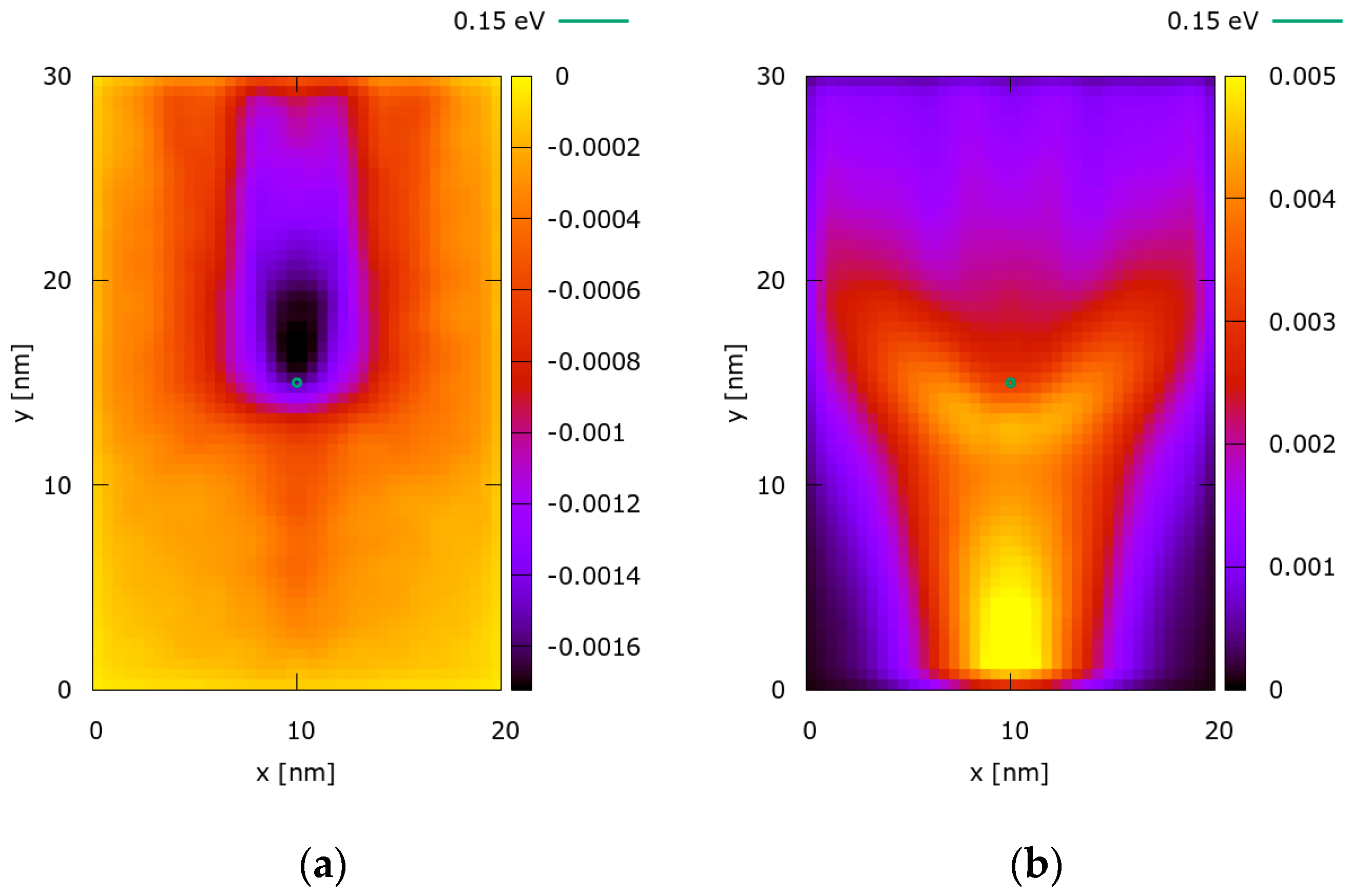
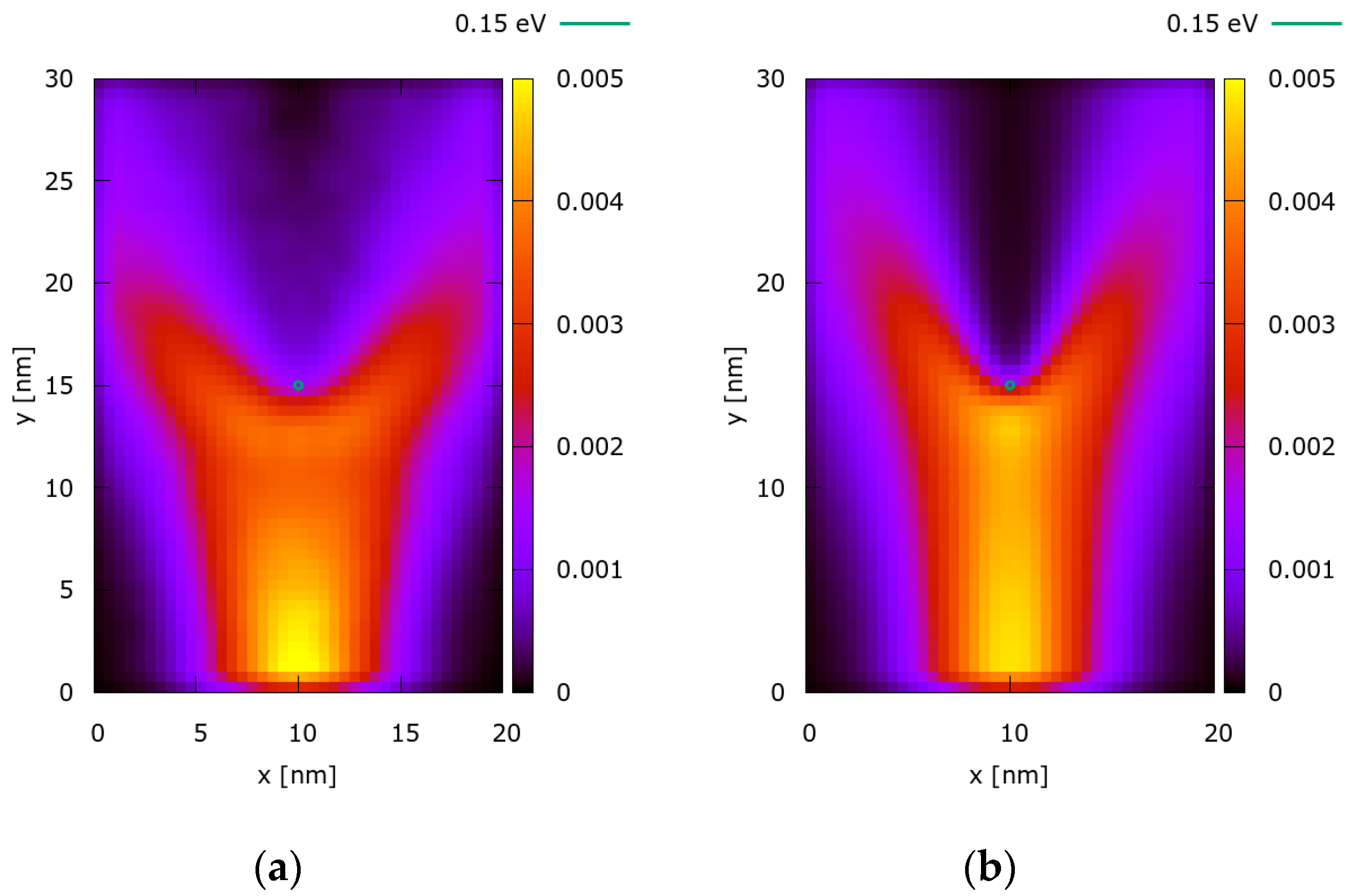
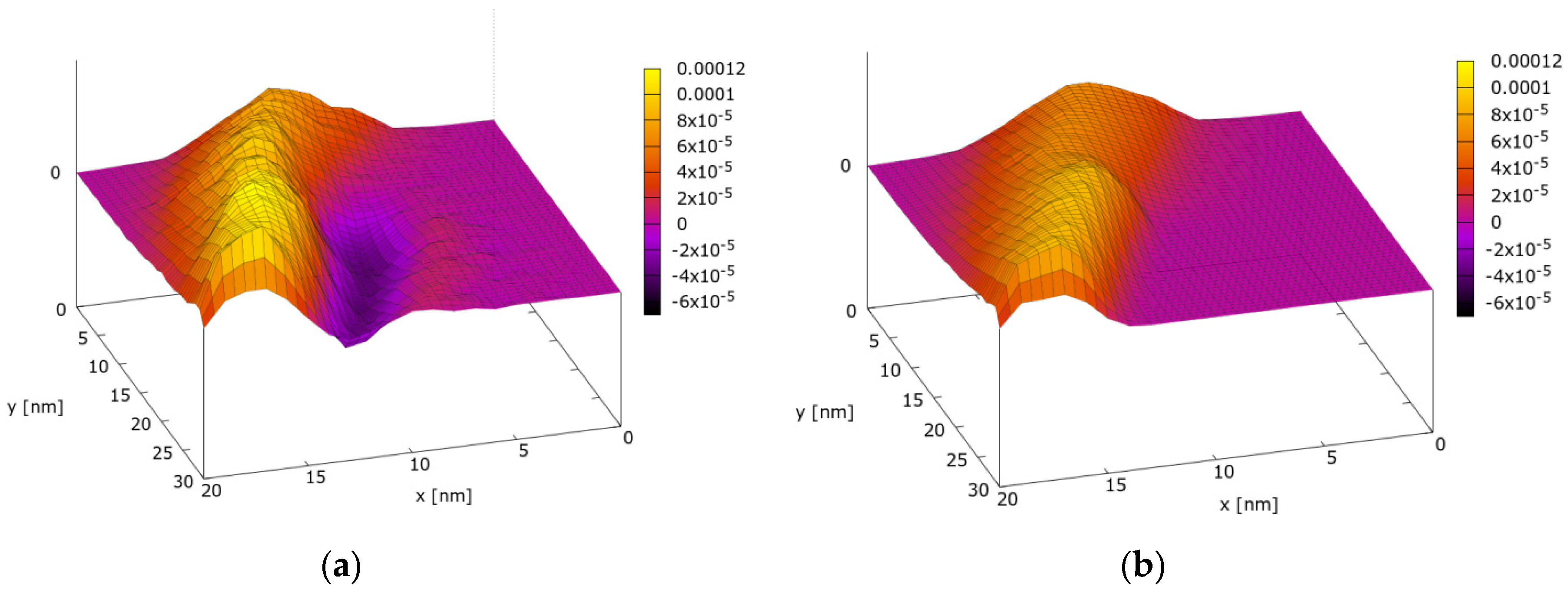
3. Results
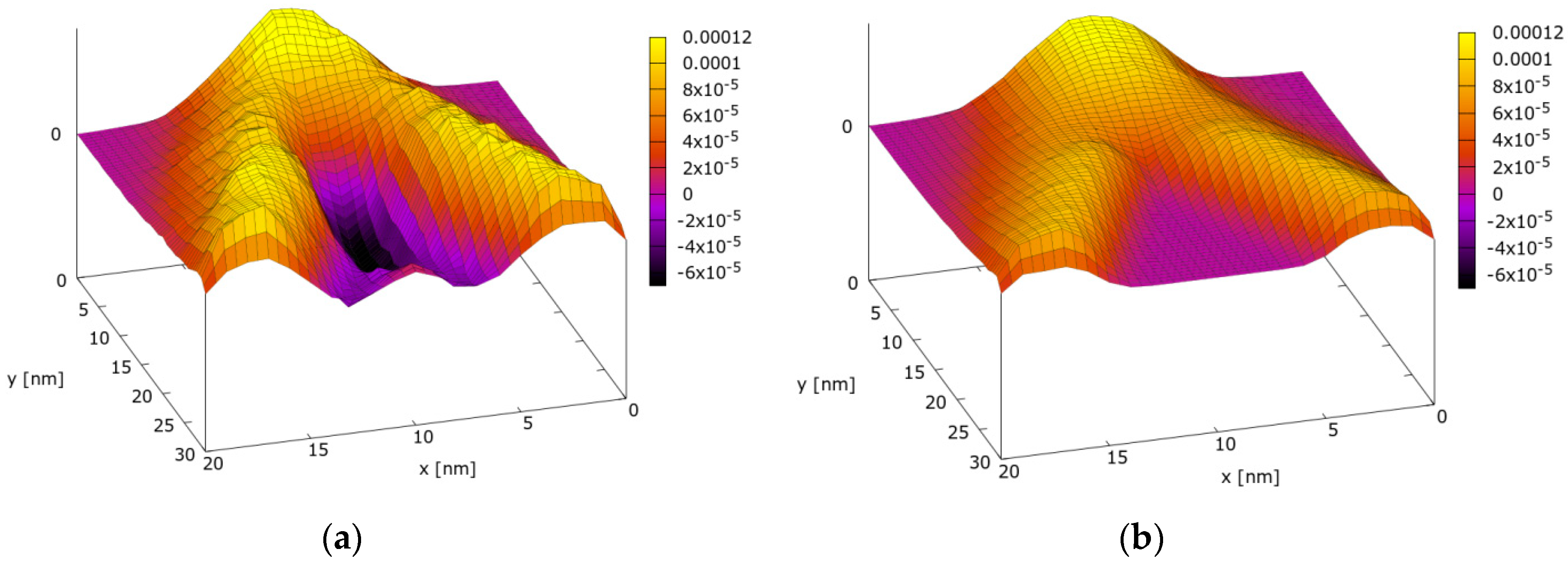
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Benioff, P.A. Quantum mechanical Hamiltonian models of discrete processes that erase their own histories: Application to Turing Machines. Int. J. Theor. Phys. 1982, 21, 177–201. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church-Turing principle, and the universal quantum computer. Proc. Roy. Soc. London A 1985, 400, 97–117. [Google Scholar] [CrossRef]
- Turing, A. On computable numbers, with an application to the Entscheidungs problem. London Math. Soc. Ser. II 1937, 42, 230–265. [Google Scholar] [CrossRef]
- Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik. Naturwiss 1935, 23, 807–812, 823–828, 844–849. [Google Scholar]
- Calderbank, A.R.; Shor, P.W. Good quantum error-correcting codes exist. Phys. Rev. A 1996, 54, 1098–1105. [Google Scholar] [CrossRef]
- Gea-Banacloche, J.; Kish, L.B. Comparison of energy requirements for classical and quantum information processing. Fluc. Noise Lett. 2003, 3, C3–C7. [Google Scholar] [CrossRef]
- Ferry, D.K.; Nedjalkov, M. The Wigner Function in Science and Technology; IOP Publishing: Bristol, UK, 2018; Chapter 8. [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Weinbub, J.; Ferry, D.K. Recent advances in Wigner function approaches. Appl. Phys. Rev. 2018, 5, 041104. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Gea-Banaloche, J. Collapse and revival of the state vector in the Jaynes-Cummings model: An example of state preparation by a quantum apparatus. Phys. Rev. Lett. 1990, 65, 3385–3388. [Google Scholar] [CrossRef]
- Birrittella, R.; Cheng, K.; Gerry, C.C. Photon-number parity oscillations in the resonant Jaynes-Cummings model. Optics Commun. 2015, 354, 286–290. [Google Scholar] [CrossRef]
- Douce, T.; Eckstein, A.; Walborn, S.P.; Khoury, A.K.; Ducci, S.; Keller, A.; Coudreau, T.; Milman, P. Direct measurement of the biphoton Wigner function through two-photon interference. Sci. Rep. 2013, 3, 3530. [Google Scholar] [CrossRef]
- Reboiro, M.; Civitarese, O.; Tielas, D. Use of discrete Wigner functions in the study of decoherence of a system of superconducting flux-qubits. Phys. Scripta 2015, 90, 074028. [Google Scholar] [CrossRef]
- Zhang, H.-L.; Yuan, H.-C.; Hu, L.-Y.; Xu, X.-X. Synthesis of Hermite excited squeezed vacuum states from two separate single-mode squeezed vacuum states. Opt. Commun. 2015, 356, 223–229. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying coherence. Phys. Rev. Let. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring quantum coherence with entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef] [PubMed]
- Svozilík, J.; Vallés, A.; Peřina, J., Jr.; Torres, J.P. Revealing Hidden Coherence in Partially Coherent Light. Phys. Rev. Lett. 2015, 115, 220501. [Google Scholar] [CrossRef]
- Kalaga, J.K.; Leoński, W.; Peřina, J., Jr. Einstein-Podolsky-Rosen steering and coherence in the family of entangled three-qubits states. Phys. Rev. A 2018, 97, 042110. [Google Scholar] [CrossRef]
- Ellinghaus, P.; Weinbub, J.; Nedjalkov, M.; Selberherr, S. Analysis of lense-governed Wigner signed particle quantum dynamics. Phys. Stat. Sol. RRL 2017, 11, 1700102. [Google Scholar] [CrossRef]
- Vitanov, P.; Nedjalkov, M.; Jacoboni, C.; Rossi, F.; Abramo, A. Unified Monte Carlo approach to the Boltzmann and Wigner equations. In Advances in Parallel Algorithms; Dimov, I., Tonev, O., Eds.; IOS Press: Amsterdam, Netherlands, 1994; pp. 154–196. [Google Scholar]
- Kenfack, A.; Życzkowski, K. Negativity of the Wigner function as an indicator of non-classicality. J. Opt. B 2004, 6, 396–404. [Google Scholar] [CrossRef]
- Ballicchia, M.; Weinbub, J.; Nedjalkov, M. Electron evolution around a repulsive dopant in a quantum wire: coherence effects. Nanoscale 2018, 10, 23037–23049. [Google Scholar] [CrossRef] [PubMed]
- Jacoboni, C. Theory of Electron Transport in Semiconductors; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Querlioz, D.; Dollfus, P. The Wigner Monte Carlo Method for Nanoelectronic Devices; ISTE-Wiley: London, UK; Hoboken, NJ, USA, 2010. [Google Scholar]
- Nedjalkov, M.; Querlioz, D.; Dollfus, P.; Kosina, H. Wigner Function Approach. In Nano-Electronic Devices, Semiclassical and Quantum Transport Modeling; Vasileska, D., Goodnick, S., Eds.; Springer: New York, NY, USA, 2011; pp. 289–358. [Google Scholar]
- Nedjalkov, M.; Kosina, H.; Selberherr, S.; Ringhofer, C.; Ferry, D.K. Unified particle approach to Wigner-Boltzmann transport in small semiconductor devices. Phys. Rev. B 2004, 70, 115319. [Google Scholar] [CrossRef]
- Ellinghaus, P. Two-Dimensional Wigner Monte Carlo Simulation for Time-Resolved Quantum Transport with Scattering. Doctoral Dissertation, TU Wien, Vienna, Austria, 2016. Available online: http://www.iue.tuwien.ac.at/phd/ellinghaus/ (accessed on 28 March 2019).
- Nedjalkov, M.; Schwaha, P.; Selberherr, S.; Sellier, J.M.; Vasileska, D. Wigner quasi-particle attributes - An asymptotic perspective. Appl. Phys. Lett. 2013, 102, 163113. [Google Scholar] [CrossRef]
- Weinbub, J.; Ballicchia, M.; Nedjalkov, M. Electron interference in a double-dopant potential structure. Phys. Stat. Sol. RRL 2018, 12, 1800111. [Google Scholar] [CrossRef]
- Ferry, D.K. An Introduction to Quantum Transport in Semiconductors; Pan Stanford Publishing: Singapore, 2018. [Google Scholar]
- Bordone, P.; Vasileska, D.; Ferry, D.K. Collision-duration time for optical-phonon emission in semiconductors. Phys. Rev. B 1996, 53, 3846. [Google Scholar] [CrossRef]
- Towie, E.A.; Watling, J.R.; Barker, J.R. Remotely screened electron-impurity scattering model for nanoscale MOSFETS. Semicond. Sci. Technol. 2011, 26, 055008. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballicchia, M.; Ferry, D.K.; Nedjalkov, M.; Weinbub, J. Investigating Quantum Coherence by Negative Excursions of the Wigner Quasi-Distribution. Appl. Sci. 2019, 9, 1344. https://doi.org/10.3390/app9071344
Ballicchia M, Ferry DK, Nedjalkov M, Weinbub J. Investigating Quantum Coherence by Negative Excursions of the Wigner Quasi-Distribution. Applied Sciences. 2019; 9(7):1344. https://doi.org/10.3390/app9071344
Chicago/Turabian StyleBallicchia, Mauro, David K. Ferry, Mihail Nedjalkov, and Josef Weinbub. 2019. "Investigating Quantum Coherence by Negative Excursions of the Wigner Quasi-Distribution" Applied Sciences 9, no. 7: 1344. https://doi.org/10.3390/app9071344
APA StyleBallicchia, M., Ferry, D. K., Nedjalkov, M., & Weinbub, J. (2019). Investigating Quantum Coherence by Negative Excursions of the Wigner Quasi-Distribution. Applied Sciences, 9(7), 1344. https://doi.org/10.3390/app9071344





