Three-Dimensional Wide-Band Electromagnetic Forward Modelling Using Potential Technique
Abstract
:1. Introduction
2. Theory and Methodology
2.1. Formulation of Maxwell’s Equations in the Secondary Field
2.2. Finite Volume Analysis
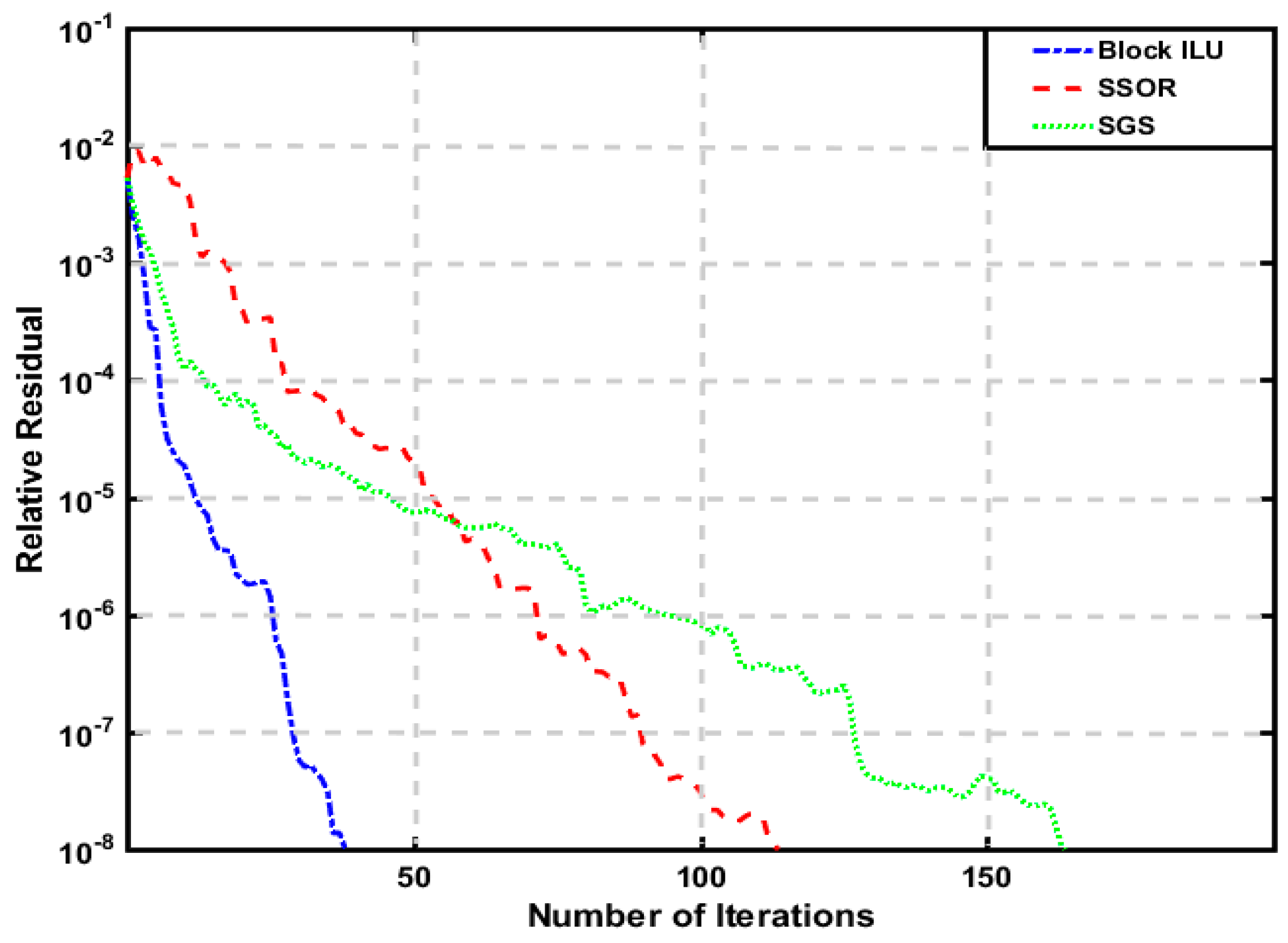
3. Results and Discussion
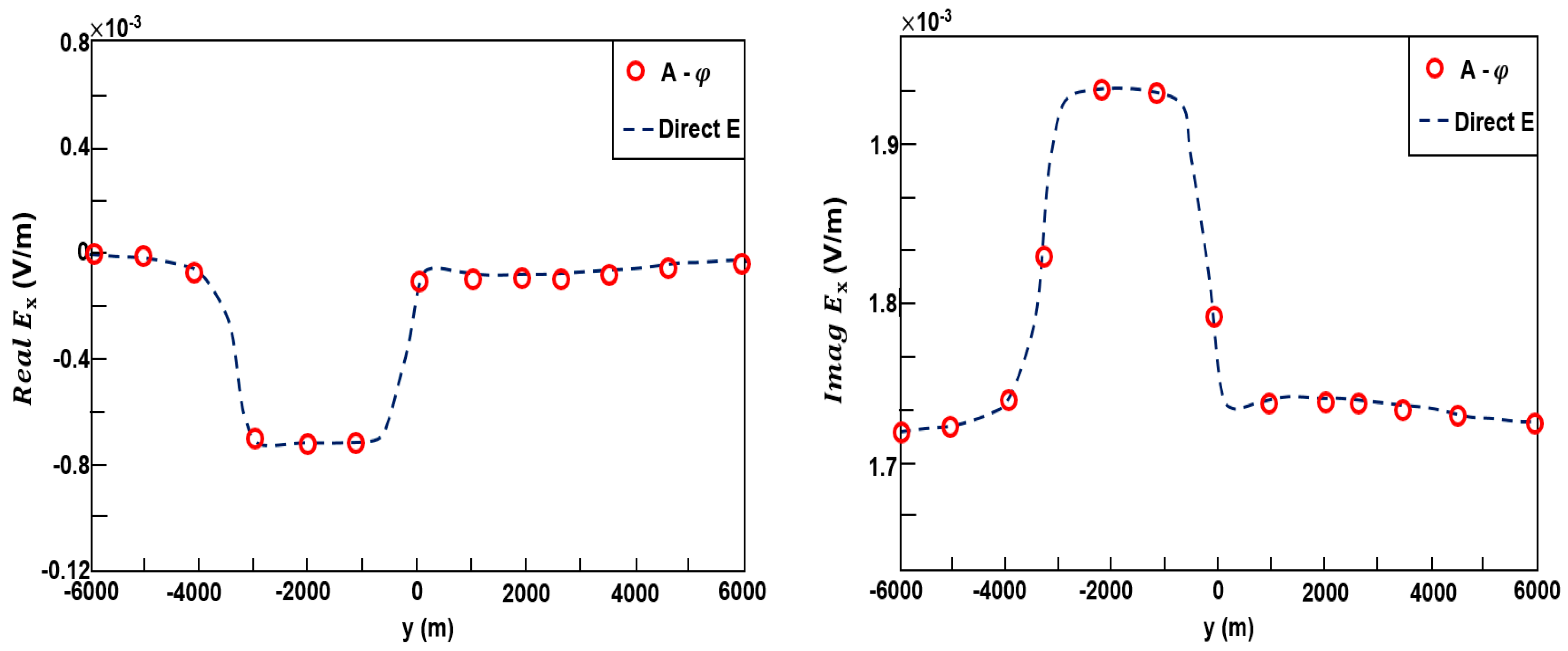
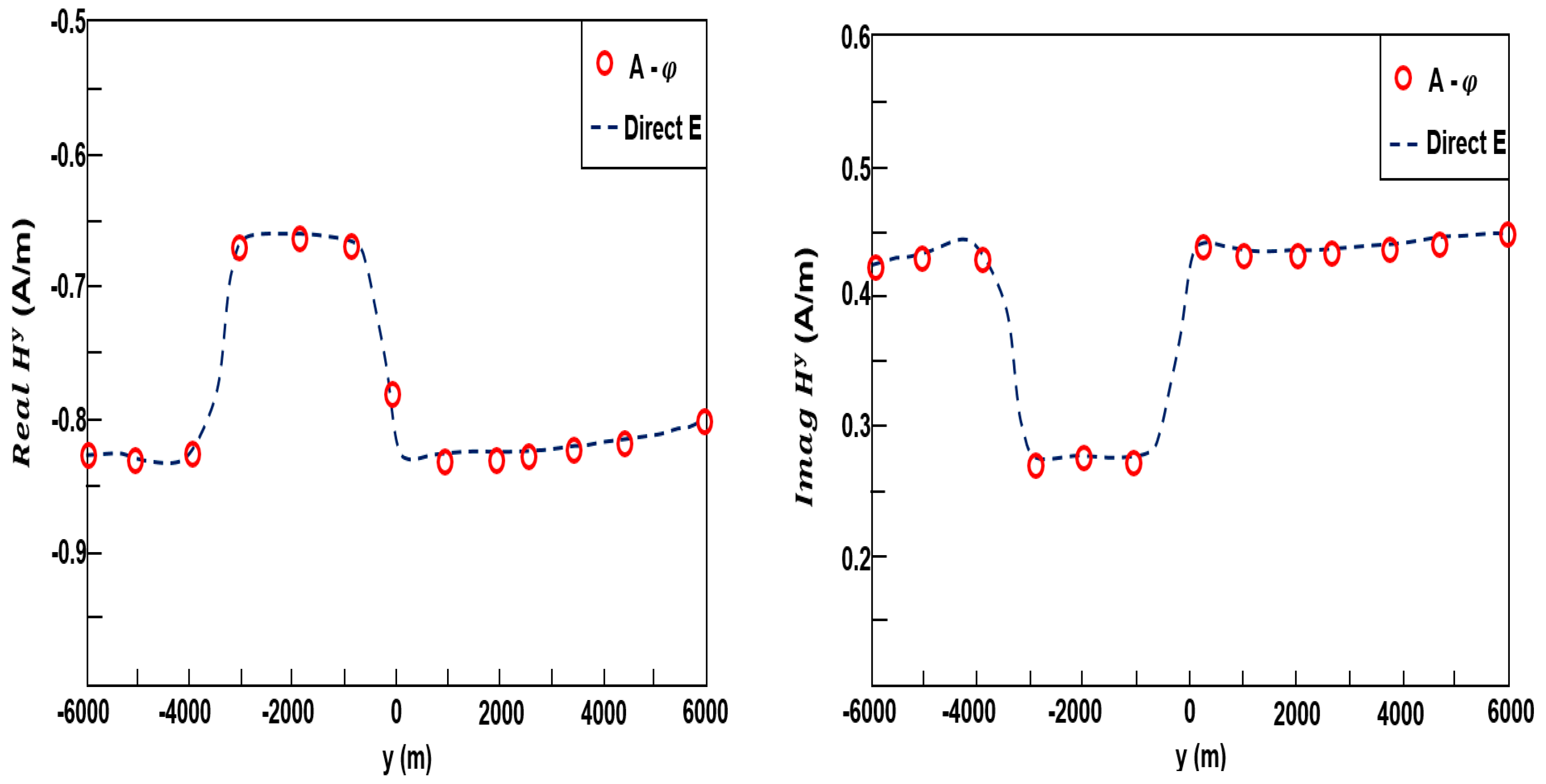
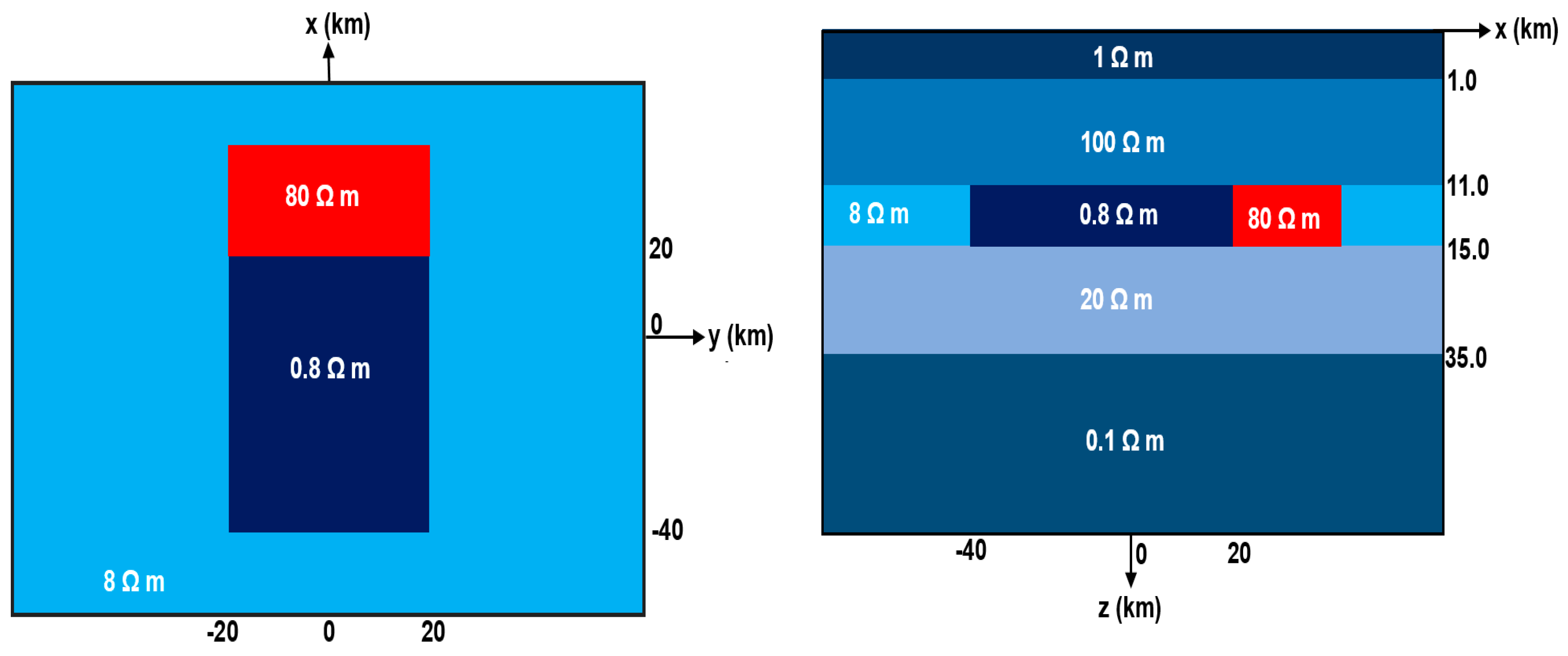
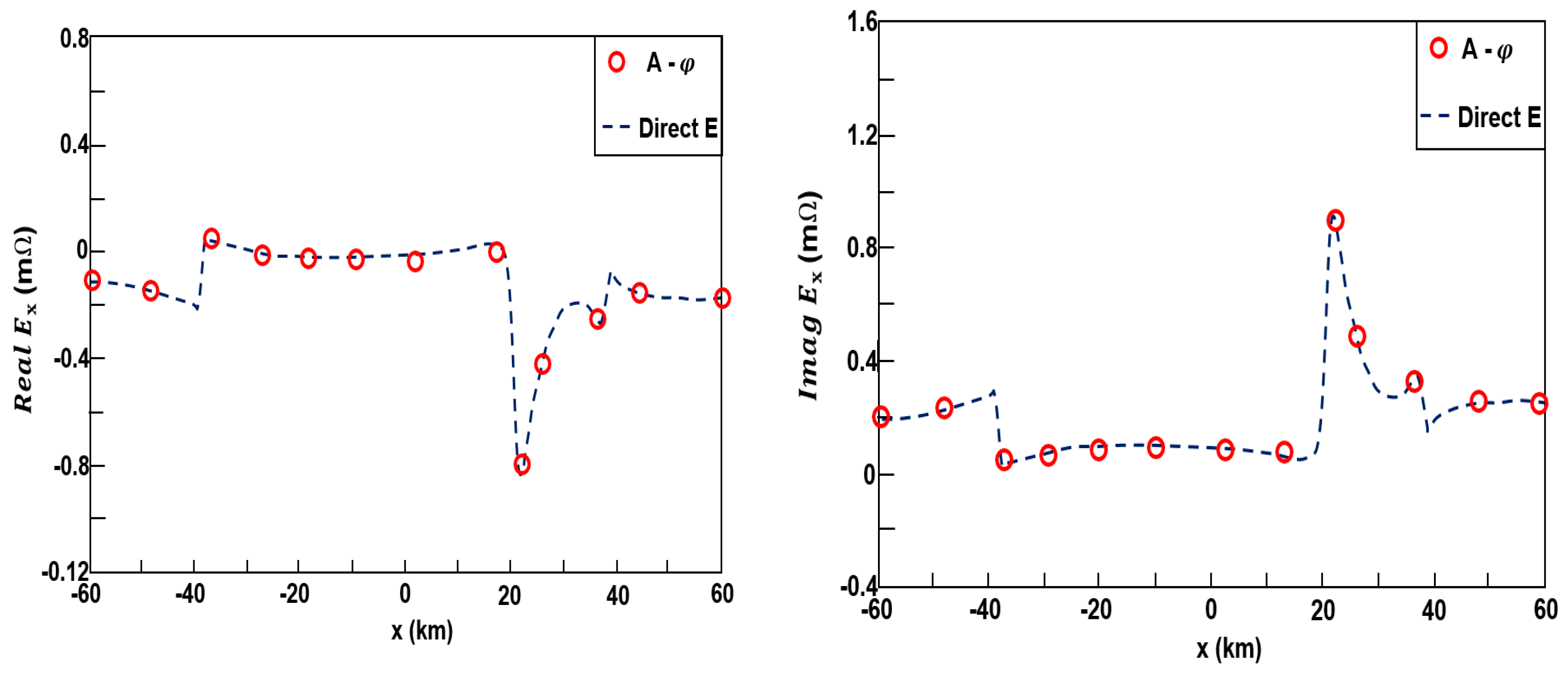
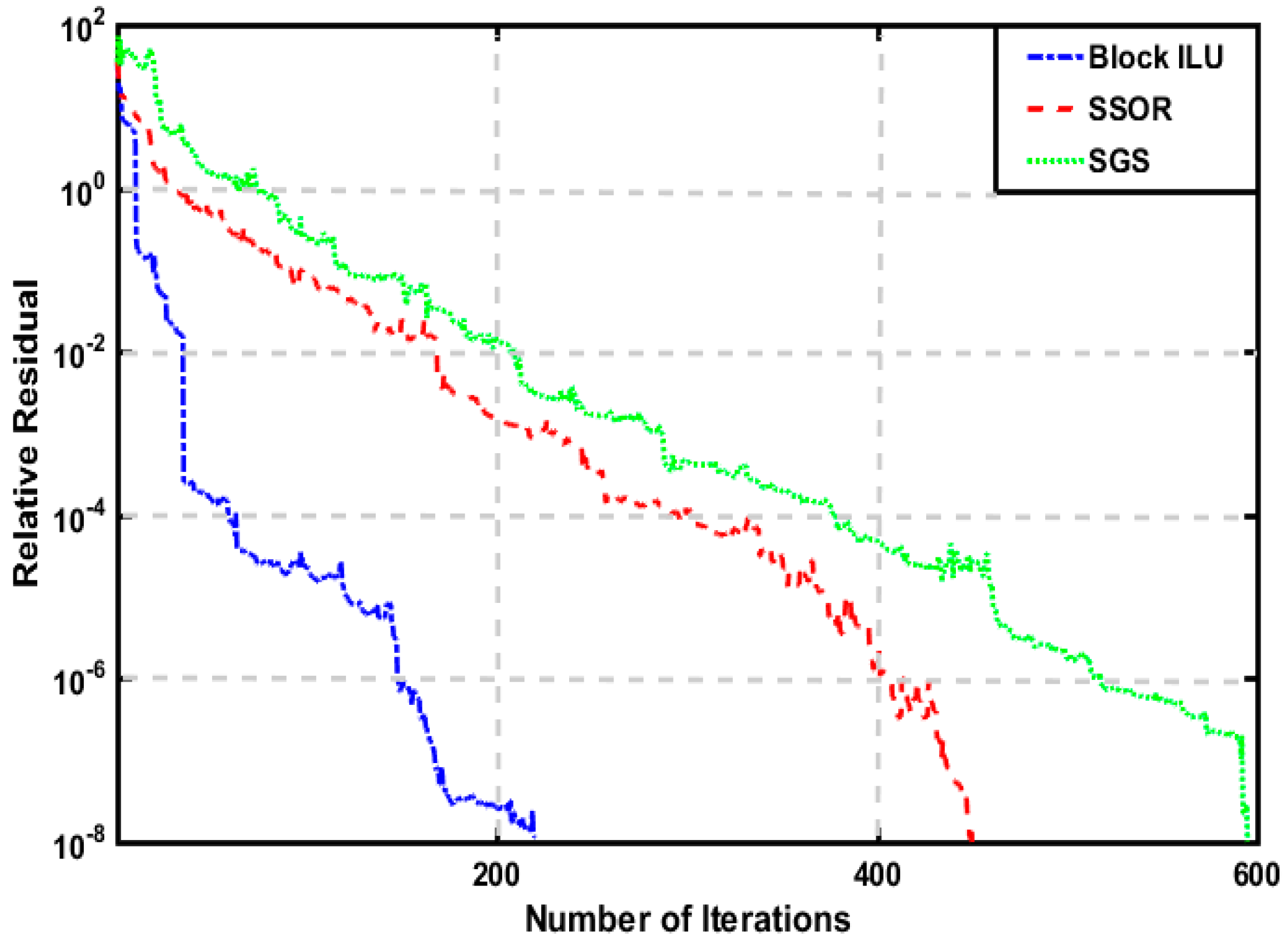
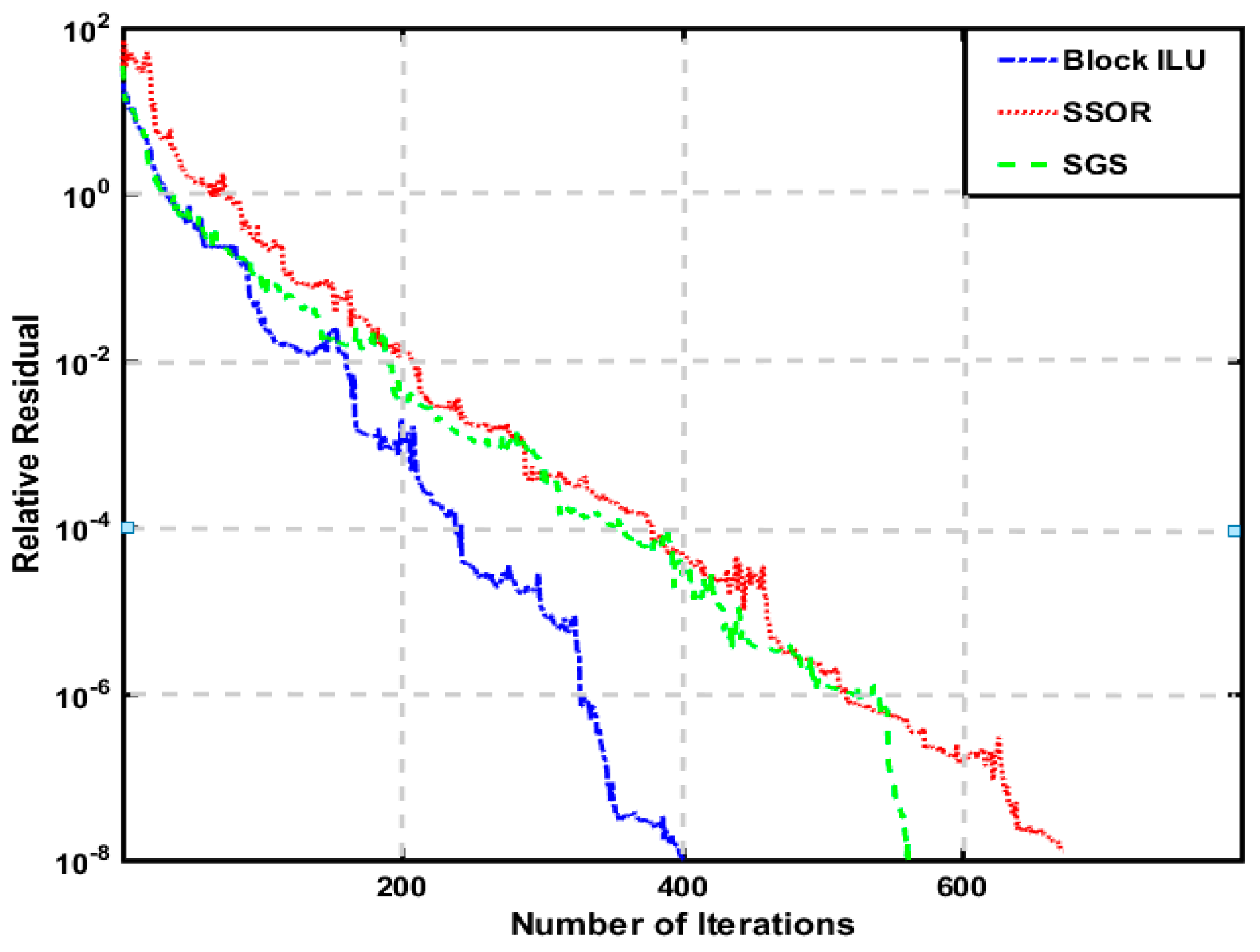
3.1. Model 1
3.2. Model 2
3.3. Model 3
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhdanov, M.S. Electromagnetic geophysics Notes from the past and the road ahead. Geophysics 2010, 75, 75A49–75A66. [Google Scholar] [CrossRef]
- Weiss, C. Project APhiD A Lorenz-gauged A-ϕ decomposition for parallelized computation of ultra-broadband electromagnetic induction in a fully heterogeneous earth. Comp. Geosci. 2013, 58, 40–52. [Google Scholar] [CrossRef]
- Avdeev, D.B. Three-dimensional electromagnetic modeling and inversion from theory to application. Surv. Geophys. 2005, 26, 767–799. [Google Scholar] [CrossRef]
- Wannamaker, P.E. Advances in three-dimensional magnetotelluric modeling using integral equations. Geophysics 1991, 56, 1716–1728. [Google Scholar] [CrossRef]
- Zhdanov, M.S. Geophysical Electromagnetic Theory and Methods; Elsevier: Oxford, UK, 2009. [Google Scholar]
- Liu, R.; Guo, R.W.; Liu, J.X.; Ma, C.Y.; Guo, Z.W. A hybrid solver based on the integral equation method and vector finite-element method for 3D controlled-source electromagnetic method modeling. Geophysics 2018, 83, E319–E333. [Google Scholar] [CrossRef]
- Avdeev, D.B.; Kushinov, A.V.; Pankratov, O.V.; Newman, G.A. High-Performance three-dimensional electromagnetic modelling using modified Neumann Series Wide-band numerical solution and examples. J. Geomag. Geoelectr. 1997, 49, 1519–1539. [Google Scholar] [CrossRef]
- Hursán, G.; Zhdanov, M.S. Contraction integral equation method in three-dimensional electromagnetic modelling. Radio Sci. 2002, 37, 1–13. [Google Scholar] [CrossRef]
- Singer, B. Electromagnetic integral equation approach based on contraction operator and solution optimization in Krylov subspace. Geophys. J. Int. 2008, 175, 857–884. [Google Scholar] [CrossRef]
- Kruglyakov, M.; Kuvshinov, A. Using high-order polynomial basis in 3-D EM forward modelling based on volume integral equation method. Geophys. J. Int. 2018, 213, 1387–1401. [Google Scholar] [CrossRef]
- Mackie, R.L.; Smith, J.T.; Madden, T.R. Three-dimensional electromagnetic modelling using finite difference equations. The magnetotelluric example. Radio Sci. 1994, 29, 923–993. [Google Scholar] [CrossRef]
- Streich, C. 3D finite-difference frequency-domain modeling of controlled source electromagnetic data: Direct solution and optimization for high accuracy. Geophysics 2009, 74, F95–F105. [Google Scholar] [CrossRef]
- Weiss, C.J. Triangulated finite difference methods for global-scale electromagnetic induction simulations of whole mantle electrical heterogeneity. Geochem. Geophys. Geosys. 2010, 11. [Google Scholar] [CrossRef]
- Egbert, G.D.; Kelbert, A. Computational recipes for electromagnetic inverse problems. Geophys. J. Int. 2012, 189, 251–267. [Google Scholar] [CrossRef]
- Simpson, F.; Bahr, K. Practical Magnetotellurics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Monk, P. Finite Element Methods for Maxwell’s Equations; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Ren, Z.; Kalscheuer, T.; Greenhalgh, S.; Maurer, H. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophys. J. Int. 2013, 194, 700–718. [Google Scholar] [CrossRef]
- Sugeng, F. Modeling the 3D TDEM response using the 3D full-domain finite element method based on the hexahedral edge-element technique. Explor. Geophys. 1998, 29, 615–619. [Google Scholar] [CrossRef]
- Mitsuhata, Y.; Uchida, T. 3D magnetotelluric modeling using the T-Omega finite-element method. Geophysics 2004, 1, 108–119. [Google Scholar] [CrossRef]
- Nam, M.; Kim, H.; Song, Y.; Lee, T.; Son, J.; Suh, J. 3D magnetotelluric modelling including surface topography. Geophys. Prosp. 2007, 55, 277–287. [Google Scholar] [CrossRef]
- Ansari, S.M.; Farquharson, C.G. 3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids. Geophysics 2014, 79, 1–17. [Google Scholar] [CrossRef]
- Puzyrev, V.; Koldan, J.; de la Puente, J.; Houzeaux, G.; Vázquez, M.; Cela, J.M. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling. Geophys. J. Int. 2013, 193, 678–693. [Google Scholar] [CrossRef]
- Börner, R.U.; Ernst, G.O.; Spitzer, K. Fast 3-D simulation of transient electromagnetic fields by model reduction in the frequency domain using Krylov subspace projection. Geophys. J. Int. 2008, 173, 766–780. [Google Scholar] [CrossRef]
- Haber, E.; Ascher, U.M. Fast finite volume simulation of 3D electromagnetic problems with highly discontinuous coefficients. SIAM J. Sci. Comput. 2001, 22, 1943–1961. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. Finite-volume modelling of geophysical electromagnetic data on unstructured grids using potentials. Geophys. J. Int. 2015, 202, 1859–1876. [Google Scholar] [CrossRef]
- Um, E.S.; Harris, J.M.; Alumbaugh, D.L. 3D time-domain simulation of electromagnetic diffusion phenomena: A finite-element electric-field approach. Geophysics 2010, 4, F115–F126. [Google Scholar] [CrossRef]
- Smith, J.T. Conservative modeling of 3-D electromagnetic fields Part II biconjugate gradient solution and an accelerator. Geophysics 1996, 61, 1319–1324. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Miensopust, M.P. Three-dimensional finite element modelling of magnetotelluric data with a divergence correction. J. Appl. Geophys. 2011, 75, 699–710. [Google Scholar] [CrossRef]
- Morisue, T. A comparison of the Coulomb gauge and Lorentz gauge magnetic vector potential formulations for 3D eddy current calculations. IEEE Trans. Mag. 1993, 29, 1372–1375. [Google Scholar] [CrossRef]
- Aruliah, D.A.; Ascher, U.M.; Haber, E.; Oldenburg, D.W. A method for the forward modelling of 3D electromagnetic quasi-static problems. Math. Models Meth. Appl. Sci. 2001, 11, 1–21. [Google Scholar] [CrossRef]
- Badea, E.A.; Everett, M.E.; Shen, L.C.; Weiss, C.J. Effect of background fields on three-dimensional finite element analysis of induction logging. Radio Sci. 2001, 36, 721–729. [Google Scholar] [CrossRef]
- Schwarzbach, C.; Boerner, R.U.; Spitzer, K. Three-dimensional adaptive higher-order finite element simulation for geo-electromagnetics—A marine CSEM example. Geophys. J. Int. 2011, 187, 63–74. [Google Scholar] [CrossRef]
- Haber, E.; Ascher, U.M.; Aruliah, D.A.; Oldenburg, D.W. Fast simulation of 3D electromagnetic problems using potentials. J. Comp. Phys. 2000, 163, 150–171. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Chave, A.; Jones, A. The Magnetotelluric Method—Theory and Practice; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Newman, G.A.; Alumbaugh, D.L. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences. Geophys. Prospect. 1995, 43, 1021–1042. [Google Scholar] [CrossRef]
- Freund, R.W.; Nachtigal, N.M. QMR: A quasi-minimal residual method for non-Hermitian linear systems. Numer. Math. 1991, 60, 315–339. [Google Scholar] [CrossRef]
- Van der Vorst, H.A. BI-CGSTAB A fast and smoothly convergent variant of BiCG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comp. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Wait, J.R. Propagation of radio waves over a stratified ground. Geophysics 1953, 20, 416–422. [Google Scholar] [CrossRef]
- Weiss, C.J.; Constable, S. Mapping thin resistor and hydrocarbons with marine EM methods part II—Modeling and analysis in 3D. Geophysics 2006, 71, G321–G332. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bello, M.; Liu, J.; Guo, R. Three-Dimensional Wide-Band Electromagnetic Forward Modelling Using Potential Technique. Appl. Sci. 2019, 9, 1328. https://doi.org/10.3390/app9071328
Bello M, Liu J, Guo R. Three-Dimensional Wide-Band Electromagnetic Forward Modelling Using Potential Technique. Applied Sciences. 2019; 9(7):1328. https://doi.org/10.3390/app9071328
Chicago/Turabian StyleBello, Musa, Jianxin Liu, and Rongwen Guo. 2019. "Three-Dimensional Wide-Band Electromagnetic Forward Modelling Using Potential Technique" Applied Sciences 9, no. 7: 1328. https://doi.org/10.3390/app9071328
APA StyleBello, M., Liu, J., & Guo, R. (2019). Three-Dimensional Wide-Band Electromagnetic Forward Modelling Using Potential Technique. Applied Sciences, 9(7), 1328. https://doi.org/10.3390/app9071328




