Research on Control Parameters for Voltage Source Inverter Output Controllers of Micro-Grids Based on the Fruit Fly Optimization Algorithm

Abstract

Due to the strong intermittency of micro-resources, the poor grid-tied power quality, and the high generation-demand sensitivity in micro-grids, research into the control methods of micro-grid systems has always been a notable issue in the field of micro-grids. The inverter is the core control equipment at the primary control level of the micro-grid, and the key factors affecting its output performance can be divided into three categories: control methods, hardware configuration, and control parameter design. Taking the classical active and reactive power (P-Q) control structure and the three-phase, two-stage inverter topology model as an example, this paper designs a parameter for offline tuning, and an online self-tuning optimization method for an inverter control system based on the fruit fly optimization algorithm (FOA). By simulating and comparing the inverter controllers with non-optimized parameters in the same object and environment, the designed parameter tuning method is verified. Specifically, it improves the dynamic response speed of the inverter controller, reduces the steady-state error and oscillation, and enhances the dynamic response performance of the controller.

1. Introduction

With the rapid development of micro-grid technologies in recent years, modern smart power grids, characterized by diversified energy types [1,2], an individualized energy supply [3,4], a multilayer control system [5,6], multi-type network structures [7,8], and flexible working modes [9,10] have gradually come into being. Since micro-grids have characteristics such as strong intermittency, low damping of output power, and high generation-demand sensitivity [11], the core goal of research on micro-grid control methods is to realize a stable, rapid, and reliable control system. As Figure 1 shows, in a modern micro-grid, primary control-level research has mainly focused on inverter output control, power sharing control [9], and coordinated control of inverters [12]. Secondary control mainly includes the control of the frequency and voltage error, and superior control mainly involves energy management and dispatch control.

In secondary control of a micro-grid, primary power dispatch control and voltage/current source inverter (VSI/CSI) internal output control jointly comprise a complicated, closed-loop control network consisting of multiple proportional integral (PI) controllers in serial and parallel structures. Since secondary control requires cascade control over multiple underlying inverters via bus communication, its control network structure is more complicated and changeable. Although different control levels have different control time domains [13], the uncertainty and time delay in control network communications will seriously influence the control performance of the entire system [14]. In the field of control science, tuning and optimization of the controller parameters are often carried out to improve the performance of a complicated PI-based control system [15]. However, in the process of parameter tuning, the control objects of different parameters vary in their damping coefficients, which leads to different overshoots, oscillations, durations of rise, and durations of adjustment [16]. Therefore, it is of great significance to explore the application of parameter tuning methods of PI controllers in improving the performance of the underlying control system of a micro-grid [17]. Research on PI controller parameter tuning can be divided into two major categories: offline tuning [18,19] and online tuning [20,21]. In Al-Saedi’s work [22], online optimization tuning is conducted for PI controller parameters of micro-grid inverters by the particle swarm optimization algorithm (PSO) and error performance index methods. However, as the update calculation process of an individual particle is relatively complex, the overall calculation time is long, which makes it more suitable for offline tuning [23,24]. Compared with PSO, the fruit fly optimization algorithm (FOA) [25] requires less in terms of the calculation process and a simpler structure, with the advantage of shorter calculation time for parameter tuning. Research works [26,27,28] have discussed the feasibility of optimizing PI controller parameter tuning in an industrial process by using FOA, and they have provided guidance for this paper.

In this paper, by taking the typical active and reactive power (PQ) control structure of the power controller, the voltage, and the current double closed-loop control structure in the internal output controller of the inverter in the micro-grid as the object of tuning, FOA is employed to study the methods of offline and online parameter tuning. Finally, simulation experiments for online PI parameter self-tuning optimization and offline PI parameter tuning in the same model environment are carried out to demonstrate the effectiveness of FOA in the tuning and optimization of the PI controller parameters of the inverter in the micro-grid.

The rest of this paper is organized as follows. In Section 2, a typical conversion circuit model as a controlled plant has been built, a typical output control structure and a typical power control structure have been introduced, and the necessity of the influence of the control parameter tuning on VSI control performance has been analyzed. In Section 3, the FOA offline parameter optimization method and the FOA online parameter self-tuning method have been described in detail. The main contents of Section 4 are simulation comparisons and experimental analysis. In the same experimental environment, the initial parameter controller, the offline optimization method, and the online parameter self-tuning method have undergone simulation comparisons and experimental comparisons in a family photovoltaic micro-grid platform. Finally, some conclusions have been drawn in Section 5.

2. Preliminary Knowledge: The Inverter Model and Voltage Source Inverter (VSI) Controller

2.1. The Inverter Model

In recent years, there have been more and more topological structures of inverter circuits designed for characterizing distributed generations (DGs) [29]. A typical three-phase, two-stage conversion circuit of inverters [29] (as Figure 2 shows) was taken as the controlled object for model building. The mathematical model of the inverter in this figure will be used as the controlled object to participate in offline tuning of the control parameters.

According to the Kirchhoff laws, the mathematical models of the circuit on the DC side can be expressed as the following:

$$\frac{\mathrm{d}{u}_{pv}}{dt}=\frac{i_{pv}}{C_1}-\frac{i_{L1}}{C_1},$$

(1)

$$\frac{{\mathrm{di}}_{L1}}{dt}=\frac{u_{pv}}{L_1}-\frac{s_k{u}_{dc}}{L_1}.$$

(2)

The mathematical models of the conversion circuit on the AC side can be expressed as the following:

$$U_a=i_{a}R+L_2\frac{d{i}_a}{dt}+e_a,$$

(3)

$$U_b=i_{a}R+L_2\frac{d{i}_b}{dt}+e_b,$$

(4)

$$U_c=i_{c}R+L_2\frac{d{i}_c}{dt}+e_c,$$

(5)

$$C_3\frac{d{u}_{dc}}{dt}=i_{ES}-(i_a{S}_a+i_b{S}_b+i_c{S}_c).$$

(6)

In the above models, u_pv is the output voltage of the inverter; I_PV is the input current at the DC side of the inverter; u_dc is the voltage between two ends of the capacitor C₂; S_k represents the duty cycle of the thyristor at the DC side of the main conversion circuit; S_a, S_b, and S_c represents the duty cycle of the thyristor at the AC side of the main conversion circuit; and the parameter i_ES can be expressed as the following:

$$i_{ES}=S_{K1}{i}_{L1}-C_2\frac{d{u}_{dc}}{dt}.$$

(7)

2.2. VSI Controller

In this paper, the classic PQ control method in inverter control was used for the power controller of the inverter shown in Figure 2. The voltage e_abc and output current i_abc, collected from the grid connection point, can be expressed as follows after abc/dq0 conversion:

The typical current control model of the inner control loop [22]:

$$I_d^{\ast }=(k_{pd1}+\frac{k_{id1}}{s})(P^{\ast }-P),$$

(8)

$$I_q^{\ast }=(k_{pq2}+\frac{k_{iq2}}{s})(Q^{\ast }-Q).$$

(9)

The typical voltage control model of the outer control loop [22]:

$$e_d^{\ast }=(k_{pd3}+\frac{k_{id3}}{s})(I_d^{\ast }-I_d),$$

(10)

$${\mathrm{e}}_q^{\ast }=(k_{pq4}+\frac{k_{iq4}}{s})(I_{\mathrm{q}}^{\ast }-I_q).$$

(11)

2.3. Necessity of VSI Controller Parameter Tuning

According to the model above, the output control module of VSIs in the primary control level contains many control loops, which are composed of multiple PI controllers with parallel and serial forms [30]. It is clear that the different parameters have different response performances to the PI controller (as Figure 3 shows). Figure 4 shows the step–response curves of the cascade control loop form, which includes two PI controllers. The response curves have shown great differences when one of the parameters changes, and the remaining three parameters remain unchanged. Comparing Figure 3 and Figure 4, it can be seen that the response curves of the PI control loop in the series have obvious overshooting and oscillation. Furthermore, the rising time, overshoot, and oscillation appear largely different when the proportionality coefficient parameters change, as shown in Figure 4. This situation also applies to changes in the remaining three parameters.

The inverter–output control module is composed of an outer voltage control loop and inner current control loop [9]. The power sharing control stage mainly divides into the master–slave control strategy and the peer-to-peer control strategy [30]. The master–slave control strategy, such as the voltage–frequency (V-f) control method and active–reactive power (P-Q) control method, is usually used in a centralized micro-grid control system [15]. The V-f control method has a single closed voltage control loop with DC voltage compensation and two PI controllers [30]. The typical P-Q control structure is contained in a cascade control, with an inner current control loop and outer voltage control loop. There are four PI controllers in the cascade control structure, which are parallel in the first part and cascaded in the second. The peer-to-peer control strategy, such as the droop control method, is usually adopted in a decentralized control system structure [31,32]. The droop control method contains more than four PI controllers, which are distributed in the voltage control loop and frequency control loop [33].

The PI controller has been adopted in all of the above control methods. It is easy to see that the micro-grid hierarchical control system is actually a complex control network with a large numbers of PI controllers, if the control loop has been introduced into the control system and topology of the control network. Parameter tuning of the PI controllers will have a huge impact on the output response performance. Therefore, it is necessary to study the control parameter tuning method for VSI control networks.

3. The Fruit Fly Optimization (FOA)-Based Parameter Tuning Method of VSI Output Control

To reduce the optimization time and achieve the goal of control performance improvement, this paper has adopted the FOA method to optimize the controller parameters. The FOA method is much simpler and more robust compared with PSO, and it has been applied in many areas. Its excellent global optimization ability and simple optimization process can help to improve the optimization time. Because of the complex structure of the conversion circuit and the multiple PI controllers in the VSI control structure, the control performance and dynamic characteristic of micro-grids would be improved by using the FOA algorithm for optimization and design.

3.1. The FOA-Based Offline Parameter Optimization Tuning Method

Offline parameter optimization and tuning of the parameters of the inverter controller requires the topological construction of the model for the controlled object as well as the identification of the optimal value through parameter optimization and tuning of the offline model. Figure 5 presents a block diagram of the control structure of FOA-based offline parameter optimization and tuning.

The integral absolute error (IAE) index is taken as the discrimination index of the offline parameter tuning process.

$$IAE={\displaystyle {\int }_{t_1}^{t_2}\left|error(t)\right|dt}.$$

(12)

The eight control parameters of the four PI controllers are divided into four categories. Take the proportionality coefficient as the x coordinate of the original location of the fruit fly, and the integral coefficient as the y coordinate of the original location of the fruit fly. Each generation of fruit fly swarm includes four types of fruit fly, and the distance from the fruit fly to the target is the smell concentration function built by using IAE as the main judgment index.

The flow chart of the FOA-based offline parameter optimization tuning process is shown in Figure 6, and the key computation steps are as follows:

Step 1: Initialize the location of the four types of fruit fly with the PI parameter values in the system:

$$x_{axis}1=kp1,y_{axis}1=ki1,x_{axis}2=kp2,y_{axis}2=ki2,$$

(13)

$$x_{axis}3=kp3,y_{axis}3=ki3,x_{axis}4=kp4,y_{axis}4=ki4,.$$

(14)

Step 2: Use the parameter RandomValue, which is random variables, to give a random direction and distance for the search values:

$$x_{i1}=x_{axis}1+RandomValue,y_{i1}=y_{axis}1+RandomValue,$$

(15)

$$x_{i1}=x_{axis}1+RandomValue,y_{i1}=y_{axis}1+RandomValue,$$

(16)

$$x_{i3}=x_{axis}3+RandomValue,y_{i3}=y_{axis}3+RandomValue,$$

(17)

$$x_{i4}=x_{axis}4+RandomValue,y_{i4}=y_{axis}4+RandomValue.$$

(18)

Step 3: Use the indicators (IAE) to build the distance function (Dist) and calculate the smell function (Si):

$$Dist1={\displaystyle {\int }_{t1}^{t2}\left|error1(t)\right|dt},Si1=1/Dist1,$$

(19)

$$Dist2={\displaystyle {\int }_{t1}^{t2}\left|error2(t)\right|dt},Si2=1/Dist2,$$

(20)

$$Dist3={\displaystyle {\int }_{t1}^{t2}\left|error3(t)\right|dt},Si3=1/Dist3,$$

(21)

$$Dist4={\displaystyle {\int }_{t1}^{t2}\left|error4(t)\right|dt},Si4=1/Dist4.$$

(22)

Step 4: Use smell function Si1, Si2, Si3, and Si4 to construct the smell concentration judgment set {Smell1}, {Smell2}, {Smell3}, and {Smell4} of the fruit fly swarm:

$$Smell{1}_i=Si1,$$

(23)

$$Smell{2}_i=Si2,$$

(24)

$$Smell{3}_i=Si3,$$

(25)

$$Smell{4}_i=Si4.$$

(26)

Step 5: Find out the maximal smell from the {Smell1}, {Smell2}, {Smell3}, and {Smell4} values. Then, the maximal value is sent to the local optimum variable bestSmellbestIndex of the current iteration:

$$[bestSmellbestIndex1]=\max (Smell{1}_i),$$

(27)

$$[bestSmellbestIndex2]=\max (Smell{2}_i),$$

(28)

$$[bestSmellbestIndex3]=\max (Smell{3}_i),$$

(29)

$$[bestSmellbestIndex4]=\max (Smell{4}_i).$$

(30)

Step 6: Compare bestSmellbestIndex with the global optimum value bestSmell, and update the bestSmell to keep the best smell value in all generations. Then, the fruit fly swarm will use vision to fly towards that location. This process can be expressed as the following Equations (31)–(33). The parameter bestIndex represents the global optimum flies.

$$Smellbest=bestSmell,$$

(31)

$$X_{axis}=X(bestIndex),$$

(32)

$$Y_{axis}=Y(bestIndex).$$

(33)

Step 7: Find the optimal value and end the optimization process.

3.2. The FOA-Based Online Parameter Optimization Tuning Method

FOA-based online optimization tuning refers to the search for optimized computation after each control step-size of the step–response and change in the controller parameters in real time according to the adjustment principle, so as to achieve the goal of increasing the response speed of the controller and improving its performance. As shown in the control diagram of online parameter optimization tuning in Figure 7, the tuning process involves real-time optimizing and self-tuning of parameters during the step–response. According to the rising characteristic of the step–response curve, the online parameter optimization tuning process shall conform to the following tuning rules:

• In the rising stage of the system (the set value of the curve ranging from 0 to 0.9), the variation slope of the real-time sampling point should be the maximum error change ratio (IE) value identified during the optimizing process, in order to shorten the rising response time of the system.
• In the oscillation and adjustment stages of the system, the slope of the real-time sampling point should be the minimum IE value (as the following Equation (34) expresses) in order to reduce the oscillation and overshot of the system, and gradually smooth the system curve.

  $$IE=\frac{d(error(t))}{dt}.$$

  (34)

According to the above-mentioned tuning rules, and compared with the offline tuning process, the difference lies in the smell function in Step 3 consisting of the IE values after each control step, rather than the integral errors after each entire simulation process. The online self-tuning parameter flow chart is shown in Figure 8.

Step 3*: Update the controller parameter and operate for one step, then compute the IE index:

$${D\mathrm{ist}1}^{\prime }=\frac{d{e}_{i1}}{dt},{D\mathrm{ist}2}^{\prime }=\frac{d{e}_{i2}}{dt},{D\mathrm{ist}3}^{\prime }=\frac{d{e}_{i3}}{dt},{D\mathrm{ist}4}^{\prime }=\frac{d{e}_{i4}}{dt},$$

(35)

$${Si1}^{\prime }=1/{Dist1}^{\prime },{Si2}^{\prime }=1/{Dist2}^{\prime },{Si3}^{\prime }=1/{Dist3}^{\prime },{Si4}^{\prime }=1/{Dist4}^{\prime }.$$

(36)

4. Simulation and Results Analysis

The control structure shown in Figure 1 was used as the simulation structure, and the circuit structure shown in Figure 2 was taken as the simulated structure of the inverter circuit model. The FOA offline optimization population scale was 100, and the online self-tuning was 20; the number of iterations was 100; the simulation time was 1 s; the sampling time was 50 × 10⁻⁶ s; the analog output power of the active power was 8 kW and the reactive power was 3 kVar; the output voltage was 220 V; and the frequency was 50 Hz. Offline optimization and online self-tuning optimization were performed for the inverter control parameters through analog simulation. Finally, the IAEs of the two optimizations in the step–response process were compared to verify the optimization effects.

4.1. Simulation of the Optimization Process

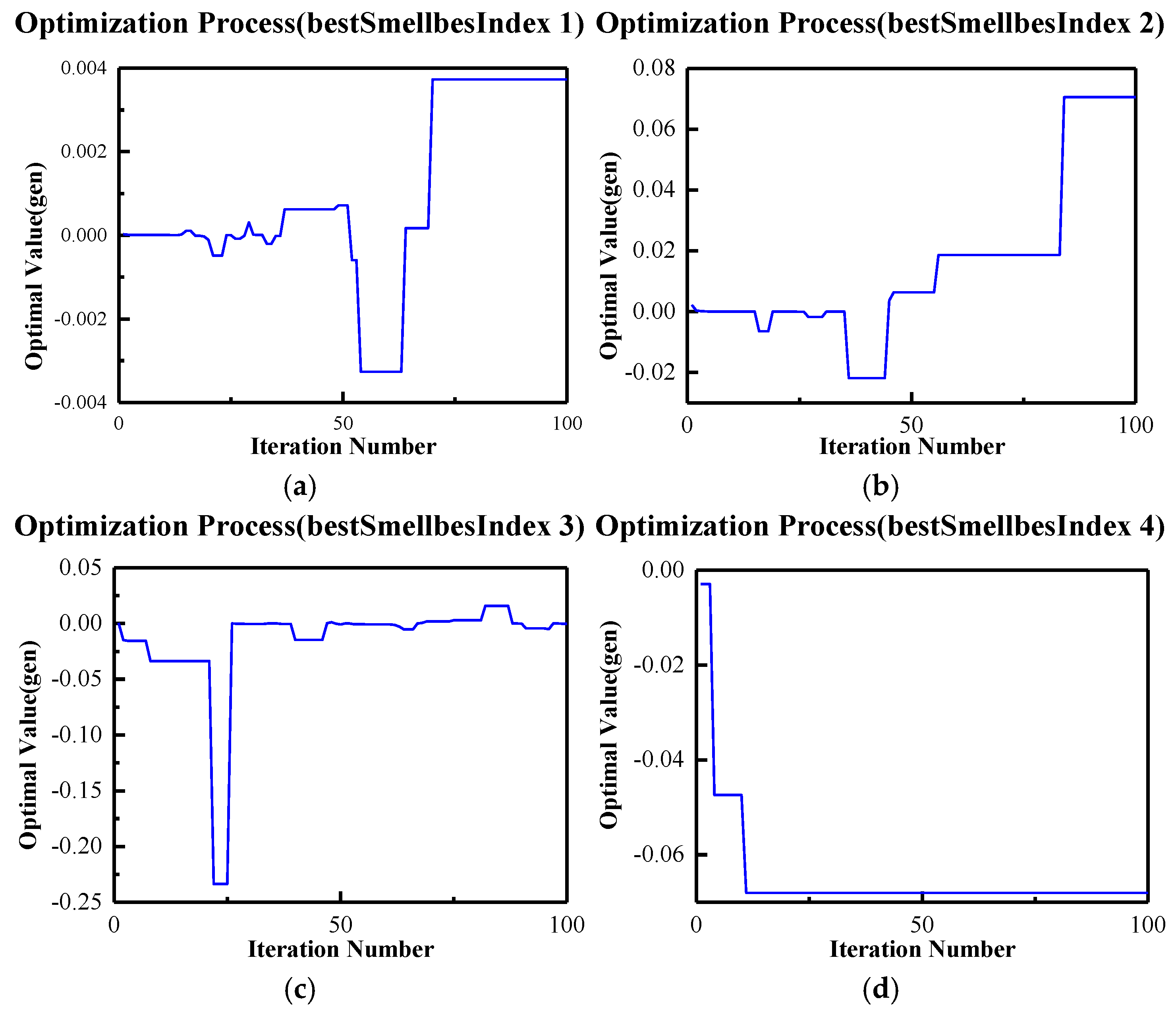
The main discrimination index of the offline optimization process was the smell function: bestSmellbestIndex, and the IAE time was 0.2 s. Figure 9 is an optimization iteration diagram composed of the reciprocal of the control error IAE index in each control loop. Figure 9a represents the reciprocal of the control error IAE index of reactive power; Figure 9b represents the index of reactive power; Figure 9c represents the index of the d-axis component of the output control error; and Figure 9d represents the index of the q-axis component of the output control error.

Table 1. Detailed comparison results of optimal values.

Optimum Variable	100-Population		200-Population
	Optimal Value	Iteration Number	Optimal Value	Iteration Number
bestSmellbestIndex1	0.007284	9	0.007321	16
bestSmellbestIndex2	0.021197	7	0.021093	5
bestSmellbestIndex3	0.037699	31	0.037472	16
bestSmellbestIndex4	0.010301	7	0.010189	5

shows the comparison of offline optimization key parameters between a population size of 100 and a population size of 200. The computation time of each fruit fly individual was 5.6 s in the offline optimization simulation process. Comparisons of the final optimized parameters suggested that the larger the population size, the larger the search space range and the smaller the number of iterations, but no significant difference was found between the final optimal values. Furthermore, the increase in the population scale meant the extension of optimization time. The total time for the offline optimization calculation was 15.7 h when the fruit fly population was 100. When the fruit fly population was 200, the total simulation time increased to 31.4 h.

Table 2. The initial parameters and offline optimal parameters comparison table.

Controller Parameters	Initial Parameters	Optimal Parameters
		100-Population	200-Population
Kp1	0.5	0.5112	0.5177
Ki1	20	20.0196	20.0368
Kp2	0.5	0.4978	0.5296
Ki2	20	20.0212	20.0249
Kp3	0.5	0.4894	0.4886
Ki3	20	20.0202	20.0265
Kp4	0.5	0.5588	0.5482
Ki4	20	20.0397	20.0291

shows the comparisons of the parameters between different controllers after population optimization. It can be seen from the table that the parameters of different controllers differed a lot in population scale.

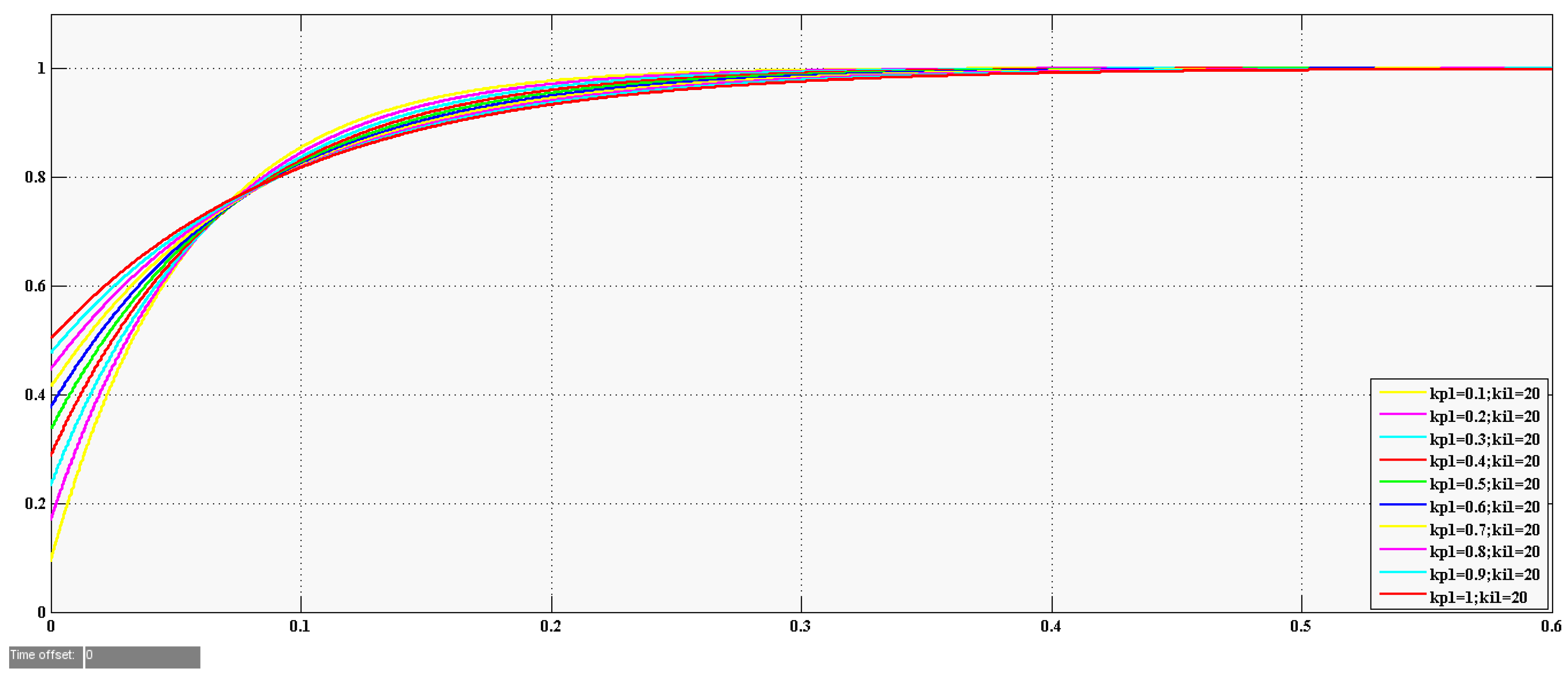
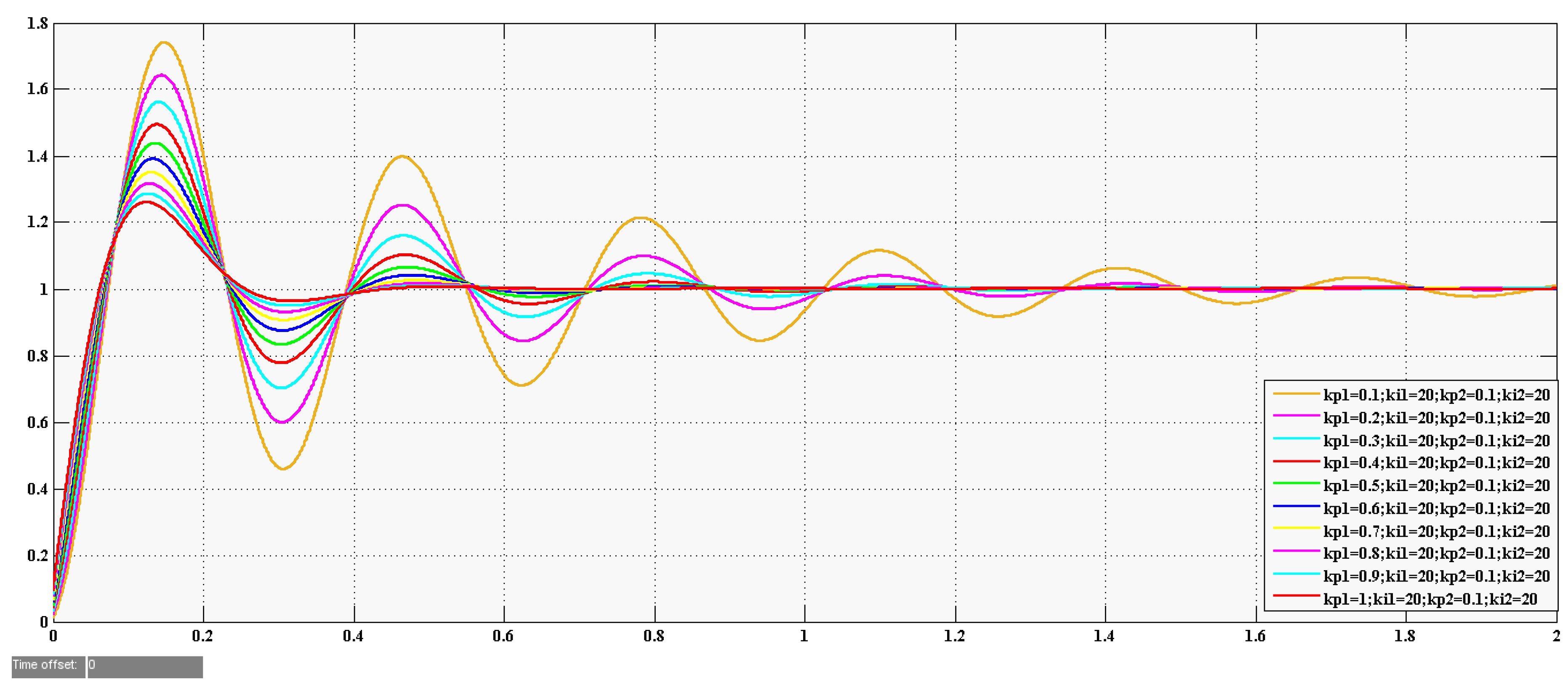
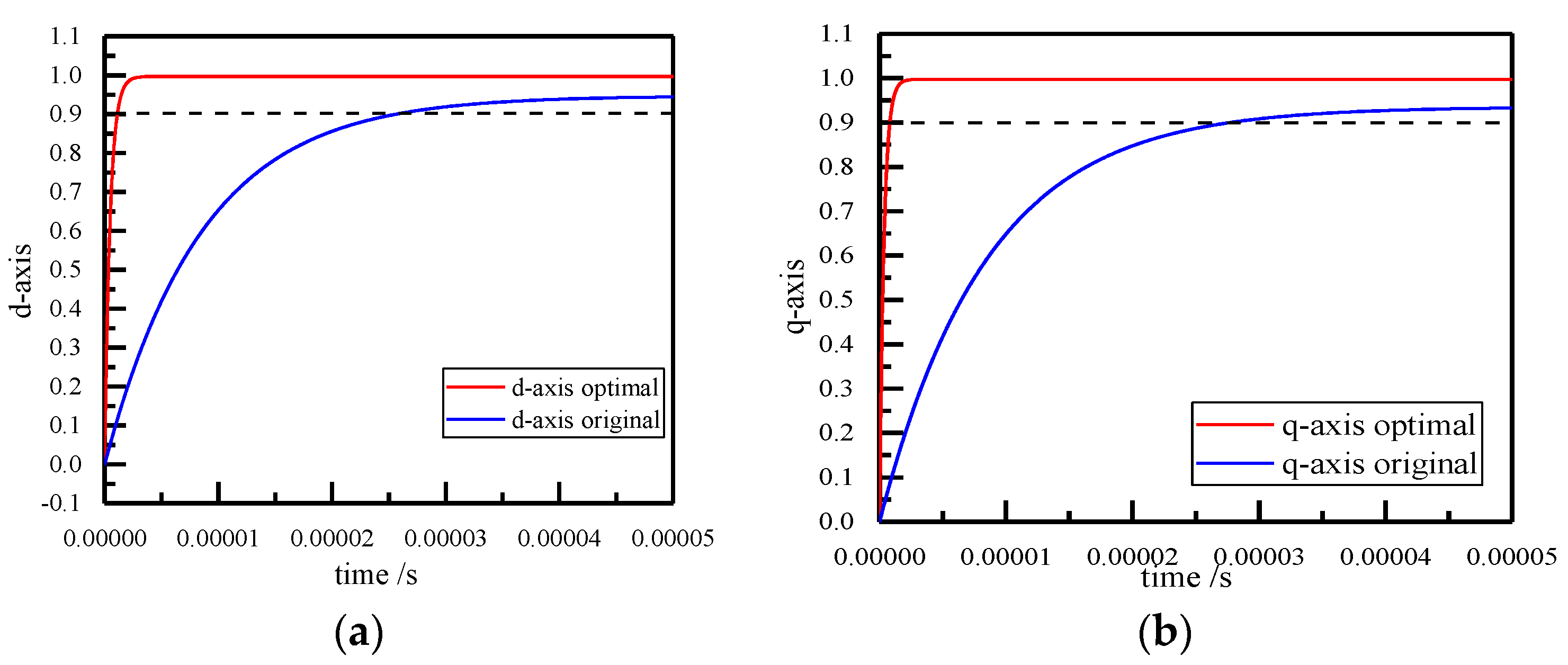
Figure 10 shows the comparison unit step–response curves between the initial value and the optimal unit step–response of the optimization calculation process. It can be seen from the figure that the step–response results of the optimal controller parameters significantly outperformed those of the initial controller parameters. The unit step–response rising time of the d-axis component was 1.11434 × 10⁻⁶ s, and the average deviation rate of steady-state error was 0.298%, while the initial controller was 2.56119 × 10⁻⁵ s and 5.542%, respectively. Correspondingly, the unit step–response rising time and the average deviation rate of the steady-state error of the q-axis component was 8.21158 × 10⁻⁷ s and 0.271%, respectively, while the initial controller increased to 2.77256 × 10⁻⁵ s and 6.727%, respectively. It was noted that the responses of the optimized controllers became faster with a smaller steady-state error, and the control performance of these controllers was improved.

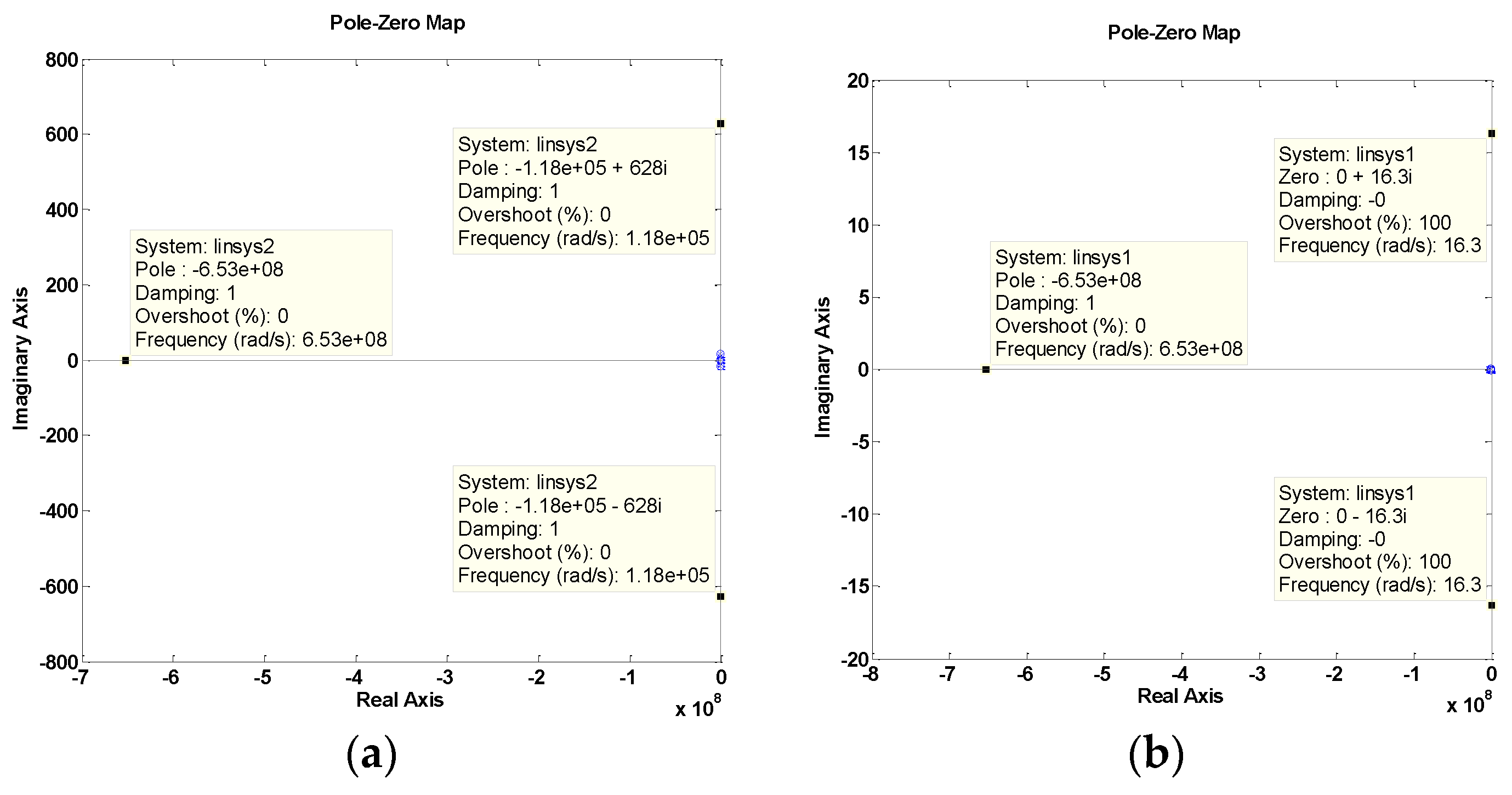
The improved dynamic performance of the controller after parameter optimization has been proven by Figure 10, shown above. Figure 11 shows the poles and zeros analysis results of the initial and optimal control loop. The initial control loop had three domain poles to influence the control performance (Figure 11a). The zeros were concentrated near the origin point. The three domain poles influenced each other. Figure 11b shows the new poles and zeros results after parameter optimization. There was only one domain pole on the negative real-axis. The other domain poles, which were close to the zero points, cannot be regarded as effective domain poles. The system changed to become more controllable and more stable.

The inverter output current and output power simulation comparison curves are shown in Figure 12 and Figure 13, and the parameters of the simulation circuit element are given in

Table A1. Main parameters of the simulation.

Load active power (kW)	12
Load reactive power (kVar)	3
L of the filter (H)	0.028
C of the filter (F)	0.000362
R of the filter (Ω)	25
DC Voltage (V)	750
carrier frequency of PWM generator (Hz)	4000
Sample period (s)	5 × 10−5
AC Voltage of urban grid (V)	220
Voltage Frequency (Hz)	50

in Appendix A. The detailed indicators comparing the results of dynamic performances have been listed in

Table 3. The detailed comparison index of dynamic performances.

Dynamic Performance Indicators	Initial	Offline
Rise time (Id, s)	0.143	0.115
Rise time (Iq, s)	0.145	0.125
Rise time (P, s)	0.147	0.115
Rise time (Q, s)	0.147	0.115
Overshoot (Id, %)	32.3%	9.1%
Overshoot (Iq, %)	12.73%	4.46%
Overshoot (P, %)	31.6%	8.3%
Overshoot (Q, %)	12.3%	3.3%
Peak time (Id, s)	0.302	0.2
Peak time (Iq, s)	0.25	0.25
Peak time (P, s)	0.306	0.205
Peak time (Q, s)	0.25	0.24
Settling time (Id, s)	1.151	0.38
Settling time (Iq, s)	0.4	0.375
Settling time (P, s)	1.146	0.353
Settling time (Q, s)	0.405	0.346
Average steady-state error (Id, %)	6.3%	0.37%
Average steady-state error (Iq, %)	1.27%	1.02%
Average steady-state error (P, %)	5.83%	0.96%
Average steady-state error (Q, %)	5.87%	1.1%

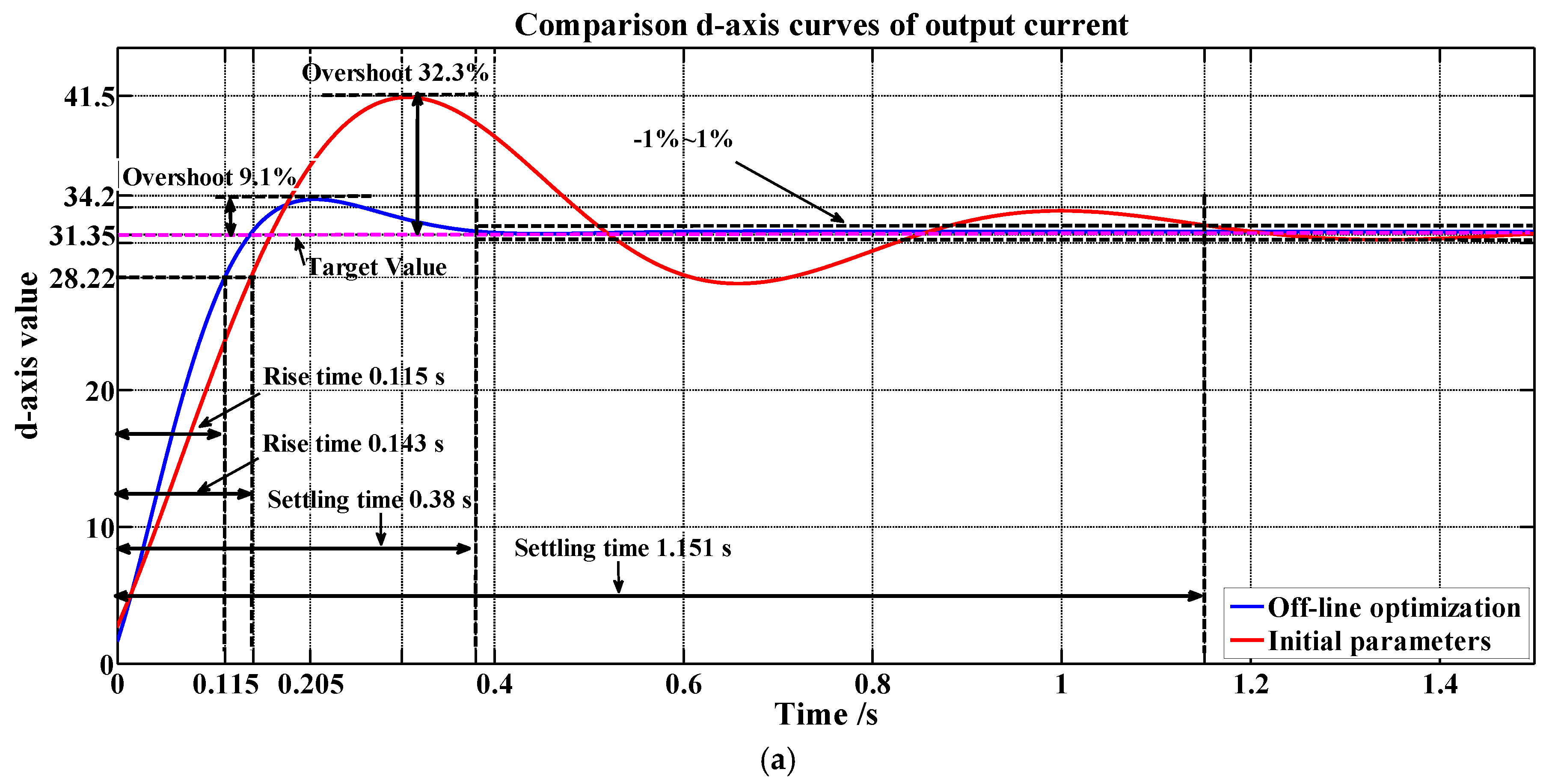
. The active power target was 12 kW, and the reactive power target was 3 kVar. The curves showed the VSI start operation process with grid support. The sampling time was 5 × 10⁻⁵ s, and the control time of the controller was 2 × 10⁻⁴ s in the simulation process. In Figure 12a, the results showed that the overshoot reduced from 32.3% to 9.1%, and the settling time shortened from 1.151 s to 0.38 s. 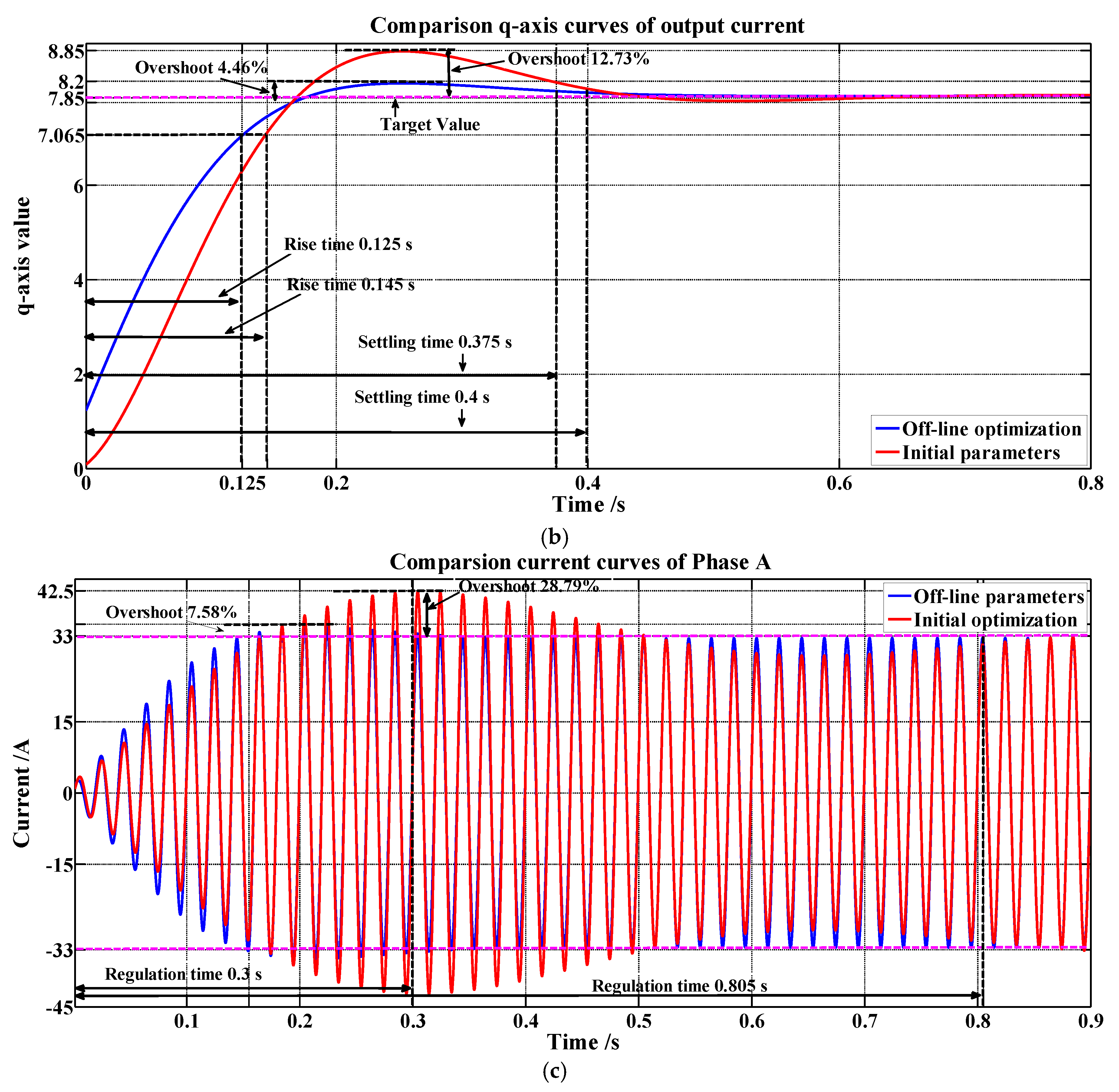These dynamic characteristic indicators in Figure 12b also reduced from 12.73% to 4.46% and shortened from 0.4 s to 0.375 s. With the improvement of the control performance of the d-axis and q-axis, the peak amplitude of current output exceeding the set value reduced from 28.79% to 7.58%, and the settling time shortened from 0.805 s to 0.3 s (as Figure 12c shows).

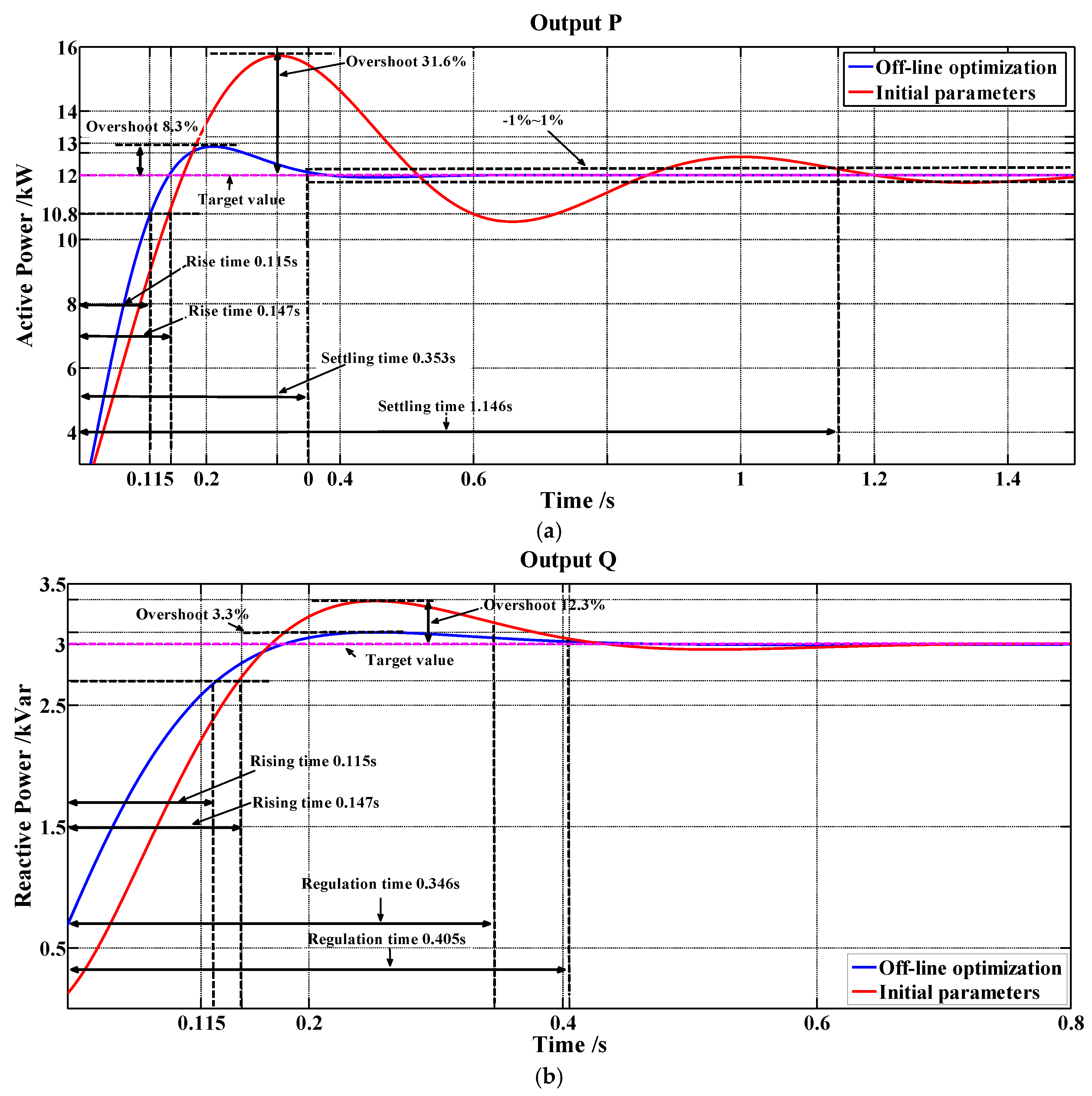
The curves of Figure 13 show active and reactive power output comparison results. According to Figure 13a and Table 3, the overshoot of the active power reduced from 31.6% to 8.3%, the settling time shortened from 1.146 s to 0.353 s, and the average steady-state error reduced from 5.83% to 0.96%. These characteristic indicators of the comparison results in Figure 13b also have been reduced and shortened (as Table 3 shows). With the improvement of settling time, overshoot time, and rise time, the dynamic performance of the output controller had comprehensively improved. Because of the difference between the actual system and the theoretical approximation model, the results of the simulation performance comparison under the same model need to be further verified by actual system experiments.

4.2. Comparison of Online Optimization

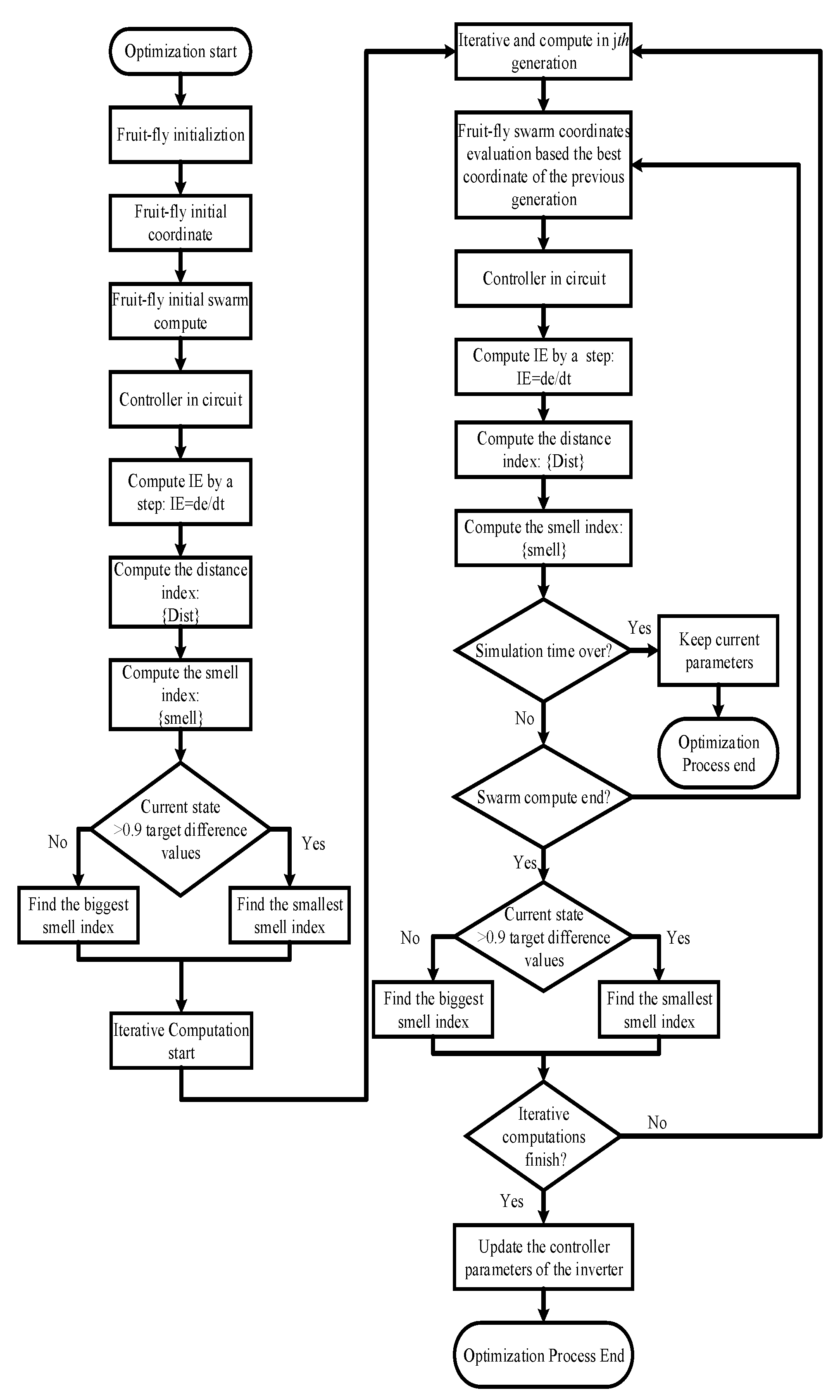
Unlike the offline optimization process, the FOA-based online optimization process refers to the online self-tuning optimization of the parameters on the basis of calculating the time sequence sampling data during the step–response in the practical operation of the controllers. In other words, the offline process involves a step–response simulation for each fruit fly via the object model, while online optimization refers to the self-tuning optimization of real-time parameters in the manner of time sequence optimizing for all the fruit fly populations in the same step–response process.

Figure 14 shows the optimization result curve of the parameter self-tuning process with a population size of 10, and a total number of iterations of 100.The curves in Figure 14a–c demonstrate a process of decline before rebound, which was because the main discrimination index of the online optimization consisted of the slope IE of the sampling point curve in the step–response. According to the above-mentioned rules for online optimization, we should first solve the maximum of the IE value and then the minimum in the step–response process of the system. Therefore, regarding the discrimination rules of the overall smell function (Si), we should first solve the minimum and then the maximum, so as to be consistent with the tendencies of the curves in Figure 14a,b.

Table 4. The initial parameters and online optimal parameters comparison table.

Optimum Value and Controller Parameters	Original Value	Optimal Value
bestSmellbestIndex1	2.42 × 10−5	0.00373
bestSmellbestIndex2	2.2 × 10−3	0.07049
bestSmellbestIndex3	4.49 × 10−4	−9.95 × 10−5
bestSmellbestIndex4	2.94 × 10−3	−0.06804
kp1	0.5	0.4264
ki1	20	19.7319
kp2	0.5	1.1136
ki2	20	19.7449
kp3	0.5	0.1799
ki3	20	10.2169
kp4	0.5	0.8494
ki4	20	19.6006

shows the comparisons of the major parameters in the self-tuning process.

Table 4 shows the major parameter indexes at the initial moment and the end moment of parameter self-tuning in the optimization process.

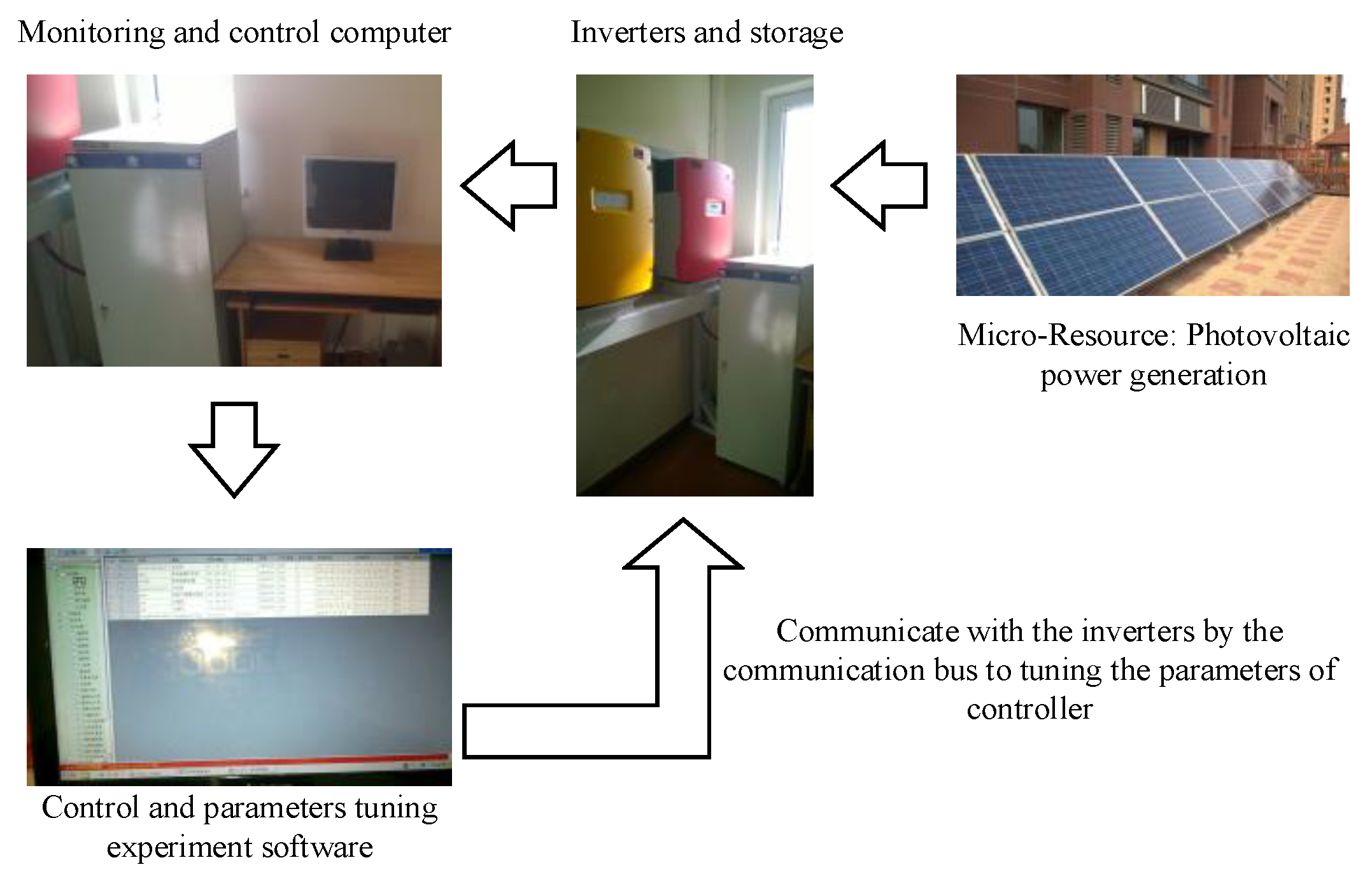
In order to fully compare the performance of the online self-tuning controller, the offline optimization controller, and the original controller, a comparison experiment was undertaken on an experimental verification platform (as Figure 15 shows). The experimental platform was a representative family photovoltaic micro-grid project in Binhai District, Tianjin, China. The micro-grid system had two photovoltaic arrays, two photovoltaic grid inverters as VSIs, and a monitoring software platform with a communication and control parameter adjustment function. Throughout the whole experimental process, the controller parameters at each sampling time were self-tuned. The complete power step–responses of the online optimization parameters, the offline optimization parameters, and the initial parameters during the startup process were compared (as Figure 16 shows).

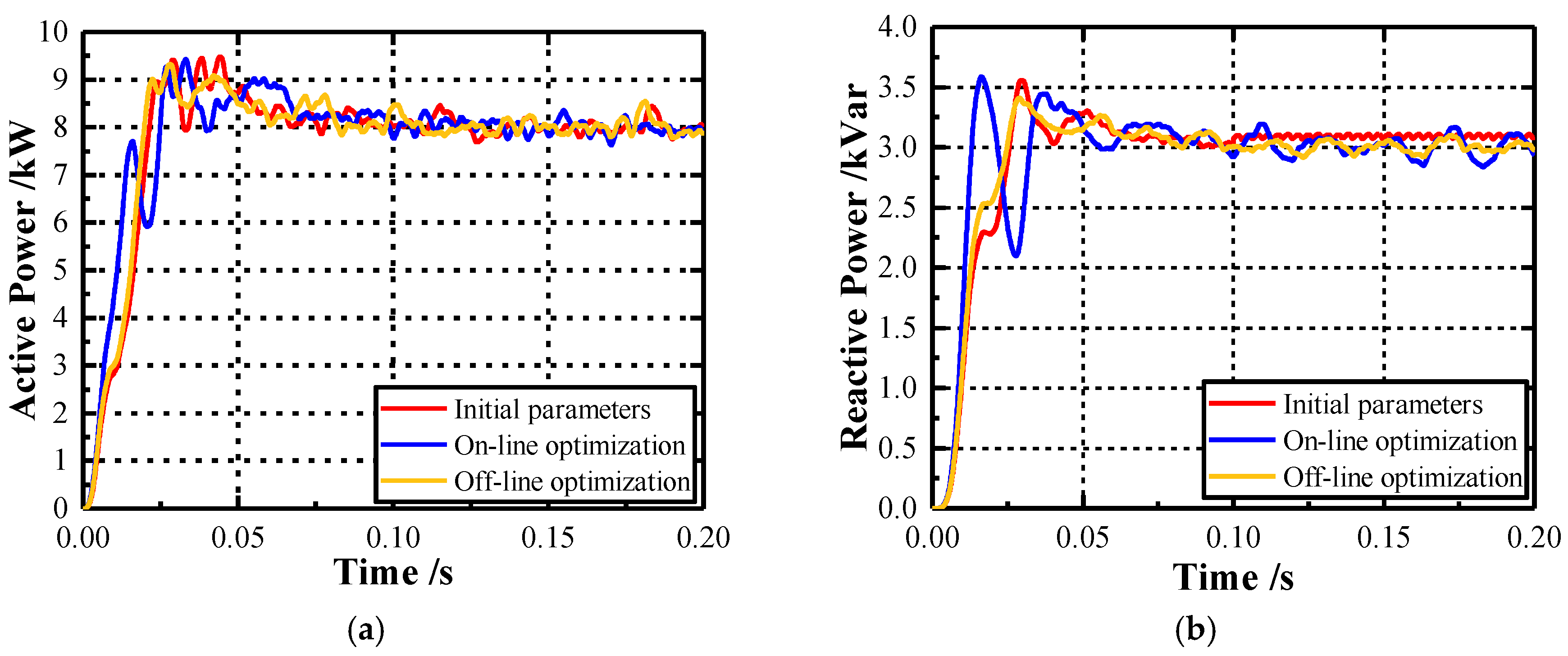
Figure 16a shows the contrast curves of the original controller, the self-tuning parameter controller, and the offline optimized controller with the active and reactive power response in the practical operation process of the system. Figure 16b presents the curves with the reactive power response. A comparison between the curves before optimization and after optimization indicated that the oscillation amplitude of the curve increased, but its frequency declined, in the process of the step–response. In particular, it can be seen from Figure 16b that, after achieving the steady-state, the fluctuation frequency and steady-state error in the curve after optimization were lowered, but the oscillation amplitude increased compared with the curve before optimization. It can be noted from the figure that there were many oscillations and fluctuations, both in the rising process and the steady process of the VSI startup. The oscillations and fluctuations of the curves also helped to verify the low inertia, high sensitivity, and the oscillation ripple wave with a small signal disturbance of VSIs, as described in Radwan’s work [34].

Table 5. The key parameters comparison table of the active and reactive power initial step–response during the VSI startup process.

Dynamic Performance Indicators	Initial	Offline	Online
Rise time (P, s)	0.0200	0.0184	0.0140
Average steady-state error (P, %)	1.3%	1.28%	1.22%
Overshoot (P, %)	18.4%	16.5%	17.8%
Rise time (Q, s)	0.0230	0.0220	0.0123
Average steady-state error (Q, %)	3.06%	1.35%	1.64%
Overshoot (Q, %)	18.7%	13.7%	18.3%

reveals that the response speed of the online self-tuned controller was improved with the online parameter self-tuning method, and the rising time during the step–response was longer than that of the initial controller and the offline optimized controller. In terms of steady-state error, the initial controller had steady-state error in the process of reactive power adjustment, while that of the offline controller was relatively smaller. The overshoot of the offline optimized controller was significantly smaller than that of the initial controller and the online self-tuned controller. In the steady-state of the controller after parameter optimization, the fluctuation amplitude was large, but the fluctuation frequency declined. Since the fluctuation amplitude still fell within an acceptable steady-state margin, no further optimization was needed. Therefore, we can introduce smell discrimination criteria (smell) to further improve the problem of fluctuation amplitude during the optimization.

The experimental results in Figure 16 are essentially a zero initial-state step–response. All state variables needed to be regulated from the zero initial-state to the target state. Therefore, the difference of the comparison curves was not obvious in Figure 16. In order to comprehensively compare the performance of the original controller, the offline optimized controller, and the online self-tuned controller, the IAEs in the process of the step–response in the zero initial-state were compared horizontally. 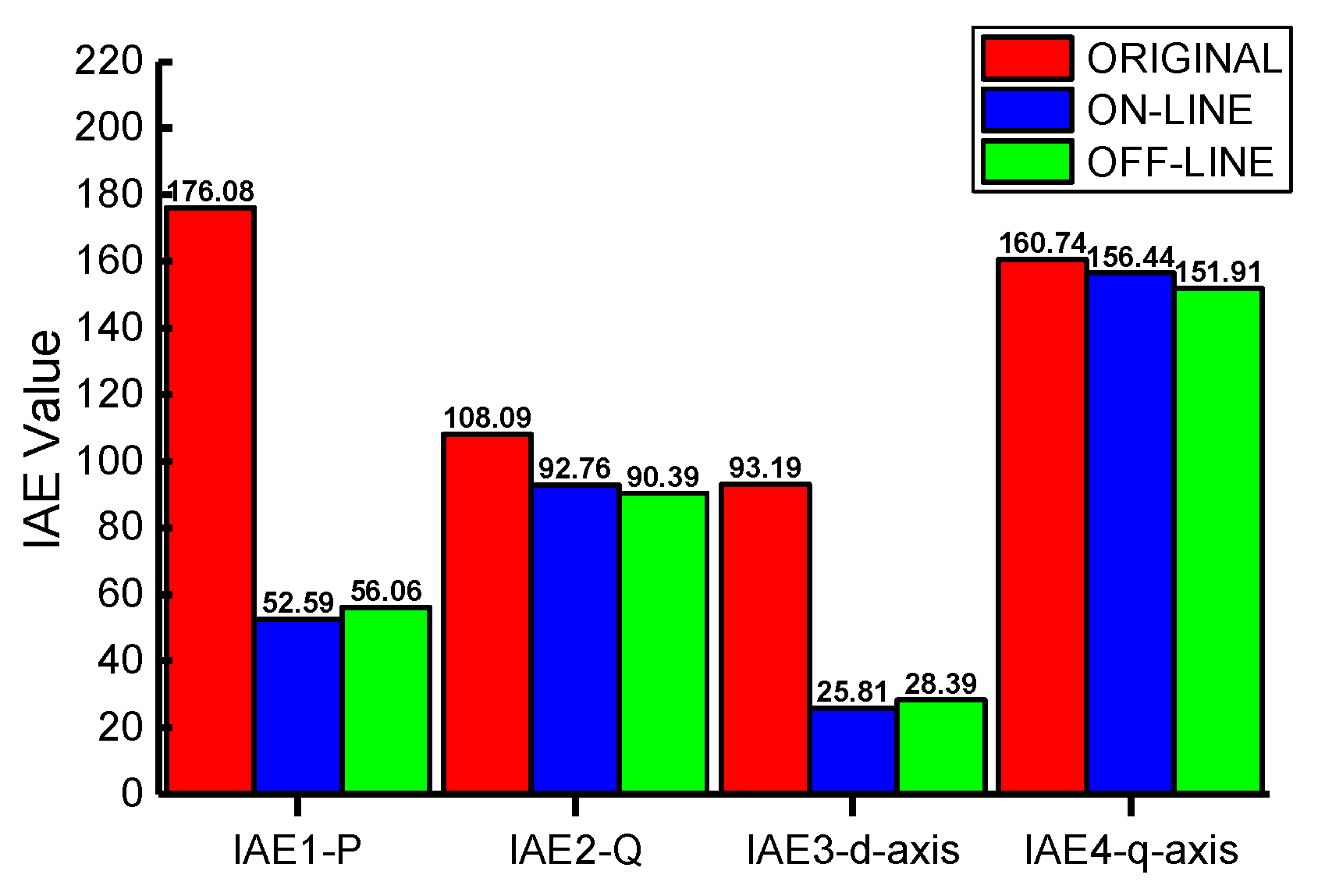Figure 17 gives the comparisons of the IAEs of different control loops. It can be seen from the figure that a dramatic drop was witnessed by the IAEs of online optimization in active power adjustment and q component adjustment, along with slight rises in reactive power adjustment and d component adjustment. This was a result of the fact that multiple PI controllers in serial and parallel structures worked together to constitute a complicated closed-loop control network, and any changes of a parameter affected other controller properties. Moreover, there were many zero initial-state variables that needed to be regulated in the zero initial step–response, and the step–response characteristics of each part were different for the zero initial-state. Under the comprehensive limitations of the reasons mentioned above and the various interferences (e.g., noise interference, communication delay, and response delay of the system components), the performance contrast shown in Figure 17 is not obvious.

As mentioned above, the result of IAE was affected by the parameter-coupling relationship of the PI controller in the parameter tuning process. The results of IAEs were affected by the parameter-coupling relationship of the PI controllers. A comparison result of the IAE values needed to be considered rather than one of the IAE values. The IAE indicator value was not fixed because of the influence of factors such as integration time, sampling time, control time, operating conditions, step amplitude, equipment parameters, environmental noise interference, and population size of the optimization algorithm. Therefore, the optimization tuning result was not judged according to the comparison value of the IAEs of a certain working condition or that of a certain control ring, but was based on the comprehensive comparison of the IAE values of all the control rings under different operating conditions.

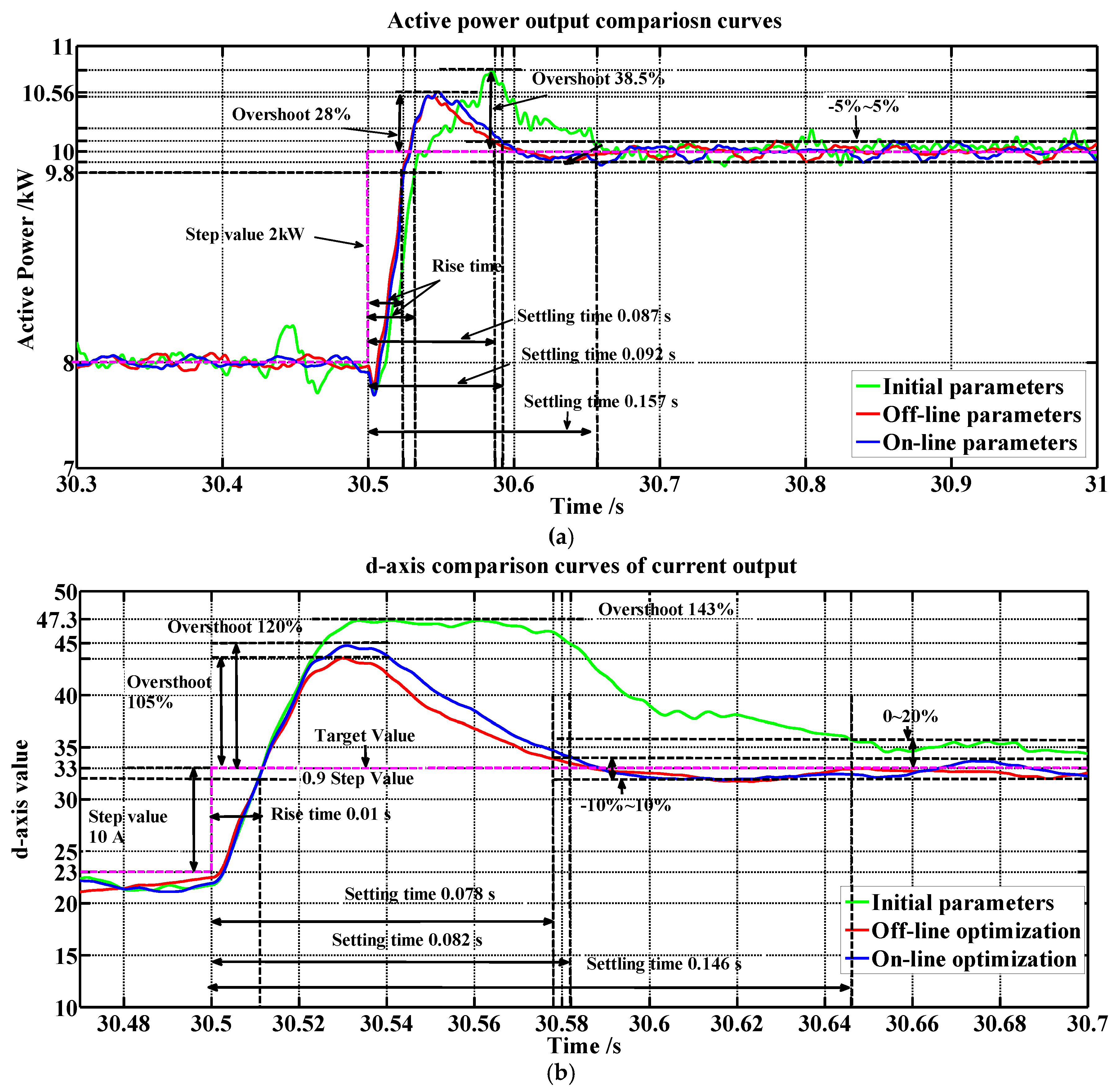
In order to further verify the improvement of VSI output performance by optimizing parameters, an experimental comparison of variable load output during normal operation of the system was conducted (as Figure 18 shows). Due to the change in load demand, the target-setting values of the VSI output changed from 10 kW and 3 kVar to 10 kW and 3 kVar when the operation time was 35.5 s. The detailed indicator comparison results of the step–response process are listed in

Table 6. The key parameters comparison table of the step–response.

Dynamic Performance Indicators	Initial	Offline	Online
Step value (Id, A)	10	10	10
Step value (P, kW)	2	2	2
Rise time (Id, s)	0.01	0.01	0.01
Rise time (P, s)	0.032	0.022	0.023
Overshoot (Id, %)	143%	105%	120%
Overshoot (P, %)	38.5%	26%	28%
Peak time (Id, s)	0.04	0.03	0.031
Peak time (P, s)	0.0085	0.042	0.047
Settling time (Id, s)	0.146	0.078	0.082
Settling time (P, s)	0.157	0.087	0.092
Average steady-state error (Id, %)	19.3%	10.1%	9.8%
Average steady-state error (P, %)	11.1%	4.9%	5.1%

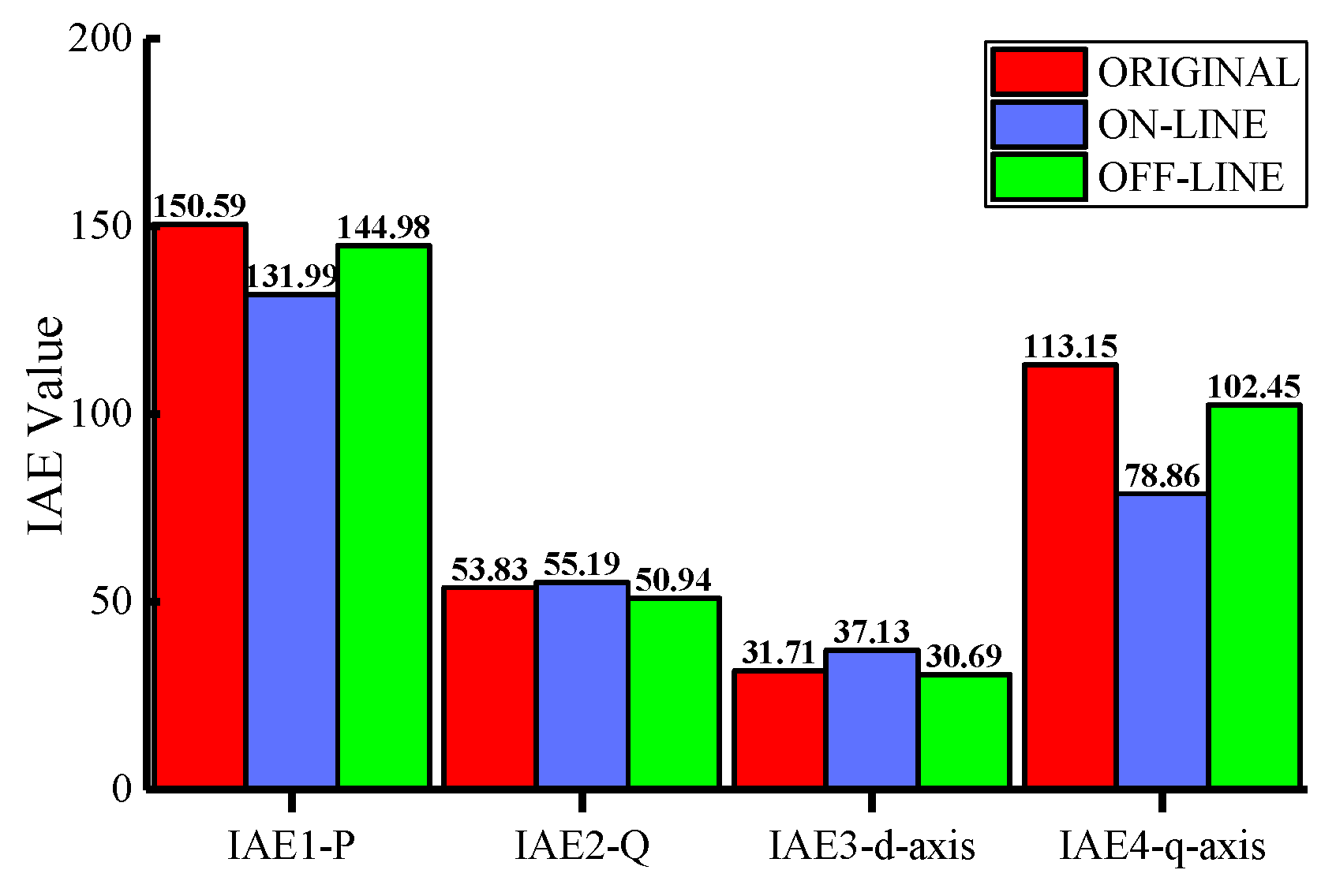
. Compared with the initial parameter results, the overshoot of response curves with online optimization and offline optimization (in Figure 18a) reduced from 38.5% to 28% and 26%, respectively. The settling time shortened from the 0.157 s to 0.092 s and 0.087 s, respectively. The indicators of d-axis in Figure 18b also have been improved. According to Figure 18 and Table 6, the response speed of the controller with optimization parameters improved, and the overshoot, oscillation, and average steady-state errors were reduced. The IAE comparison results of the variable load process are shown in Figure 19. It can be seen that the IAE value of the controller with optimized parameters was greatly reduced in each control loop. Compared with the startup phase in Figure 17, the performance improvement was more obvious during normal operation because of the reduction of the zero initial-state variables of the device.

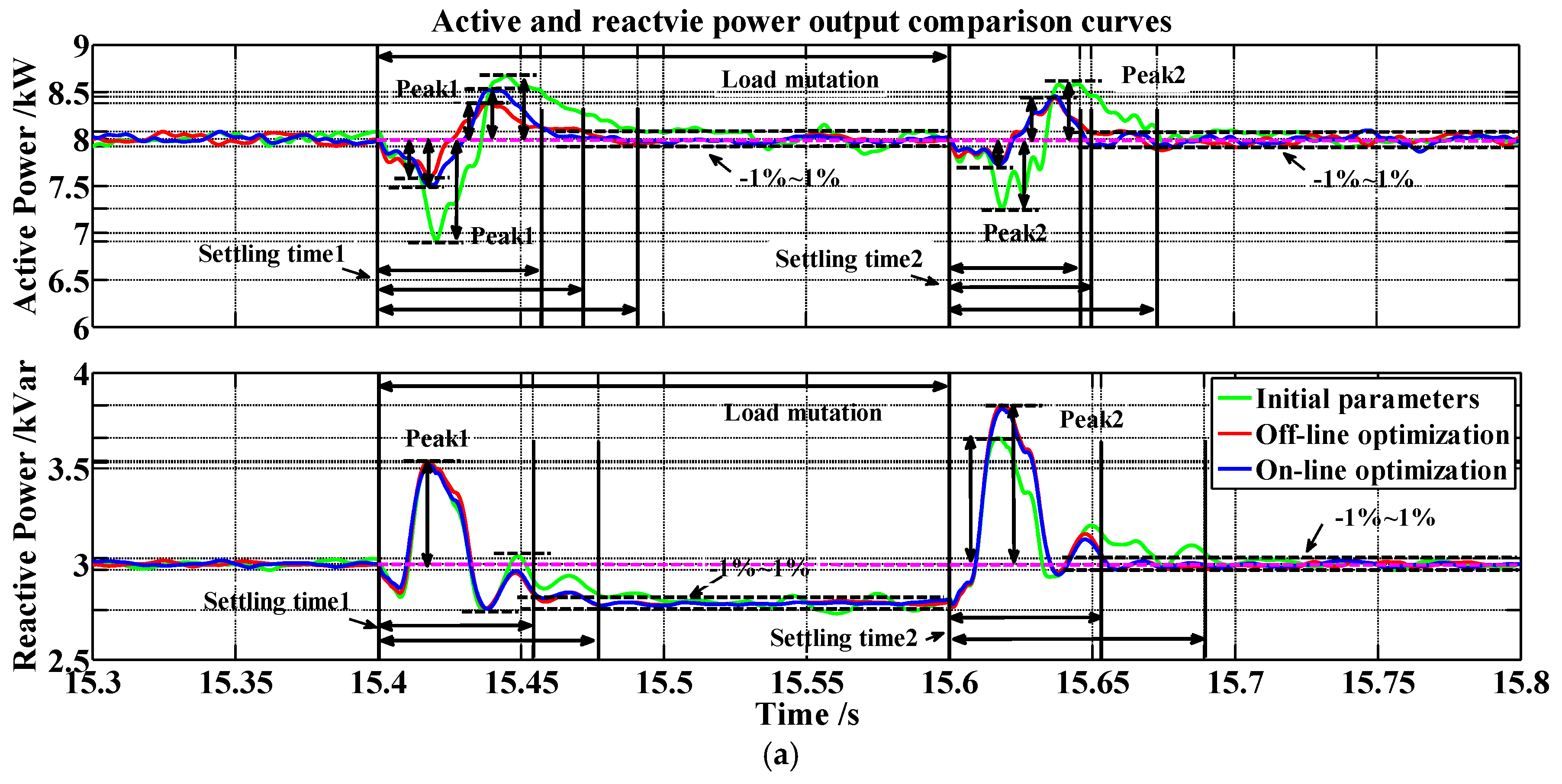
Due to the strong load randomness characteristics, high intermittent characteristics of the power supplies, low inertia characteristics, and the effect of random noise disturbances and delays, the oscillations and fluctuations cannot be avoided during the normal operation process of a micro-grid (as Figure 18 shows). To verify the anti-shock performance of the system caused by the strong randomness of the load, the impulse response of VSI was compared in this paper (as Figure 20 shows). The load mutation appeared when the operation time was 15.4 s, and disappeared at 15.6 s. Since the target-setting values of VSI output were changed, the control system experienced two impulse response processes as the power changed, caused by load mutations. The main dynamic comparison indicators are listed in

Table 7. The key parameters comparison table during the load mutation process.

Dynamic Performance Indicators	Initial	Offline	Online
Peak1 (P, kW)	1.09	0.38	0.51
Peak1 (Q, kVar)	0.53	0.54	0.53
Peak2 (P, kW)	0.74	0.43	0.45
Peak2 (Q, kVar)	0.66	0.83	0.82
Settling time1 (P, s)	0.092	0.072	0.057
Settling time1 (Q, s)	0.077	0.054	0.054
Settling time2 (P, s)	0.073	0.05	0.046
Settling time2 (Q, s)	0.089	0.053	0.053

. Compared with the initial parameter curve, the active power output curve with optimized parameters had smaller spike amplitudes in the process of the impulse response and a quicker recovery of the stable state. The IAE comparison results of this process are shown in Figure 21. The improvement of IAEs in active power control loops and the d-axis control loop was clear, while the improvement effect in other control loops was relatively small. Although the performance improvement of reactive power output was limited, the comprehensive performance of the control system improved by optimizing control parameters without changing the overall control structure, method, and usage of energy storage.

5. Conclusions

With the classic three-phase, two-stage inverter circuit as the model, this paper uses the traditional PQ control and double closed-loop output control as the objects of study. Through tuning and optimizing the parameters for the controllers in the control structure by using FOA, the methods of online self-tuning optimization control and offline optimization control are respectively designed. According to the simulation and experiment comparison results, the optimization parameters can help to improve the performance of VSI in micro-grids. The optimization of PI control parameters can shorten the regulation time, enhance the response speed, and lower the steady-state error and fluctuation. These improvements will help to shorten the secondary control time and improve the stability control performance of the whole hierarchical control system of micro-grids. Due to the lack of differentiation elements by the PI controller, although the dynamic response performance of VSI is enhanced, the improvement of the oscillation effect caused by its low inertia is relatively insignificant. Therefore, the improvement of VSI output performance has some limitations without changing the control structure and control method of the primary control system of the micro-grid. Due to the low inertia of micro-resources and high randomness of the load in micro-grids, the traditional control structure of VSIs has large oscillation ripple waves in the control output curve under a small signal disturbance. Compared with the traditional parameter tuning methods, the FOA optimization method has a higher computation speed and effectiveness. It can provide a reference for engineers in the process of micro-grid design and maintenance and help to improve the efficiency of parameter tuning.