1. Introduction
Conventional vapor-compression cooling systems require large amounts of electrical energy to operate: This promotes energy consumption based on fossil fuels [
1]. In recent years, research and technology development have been focused on efficient energy use as well as renewable energy sources to mitigate environmental problems (such as global warming or air, water, and soil pollution) and other related energy issues [
2]. Among renewable energies, geothermal energy is considered to be an abundant and constant source of thermal energy, unlike thermal solar energy [
3]. Geothermal resources of a high temperature are generally being utilized for electricity production, and the installed capacity is continuously growing [
4]. However, despite the vast potential of low-to-medium temperature geothermal resources, they are not being used because there are technical limitations to electricity generation (by low-temperature heat), low energy conversion efficiency, and high investment and production costs [
5,
6]. However, there is considerable potential for geothermal energy at a low-to-medium temperature (<150 °C): According to Stefansson [
7], there is a potential for 1410 EJ/year. Air conditioning absorption systems are some of the most interesting devices, since they use low-to-medium temperature heat sources [
8]. Air conditioning absorption systems operate with environmentally clean working fluids and require lower electricity consumption than conventional systems, so CO
2 emissions are very low [
9]. Absorption systems can be used for large-scale applications, their cost is lower with respect to other thermally driven systems, they consume a negligible amount of electrical energy, and they have few mechanical parts [
10]: This is an environmentally friendly method in order to produce air conditioning. However, a combination of renewable thermal energy and an absorption chiller mainly depends on the coupling temperature [
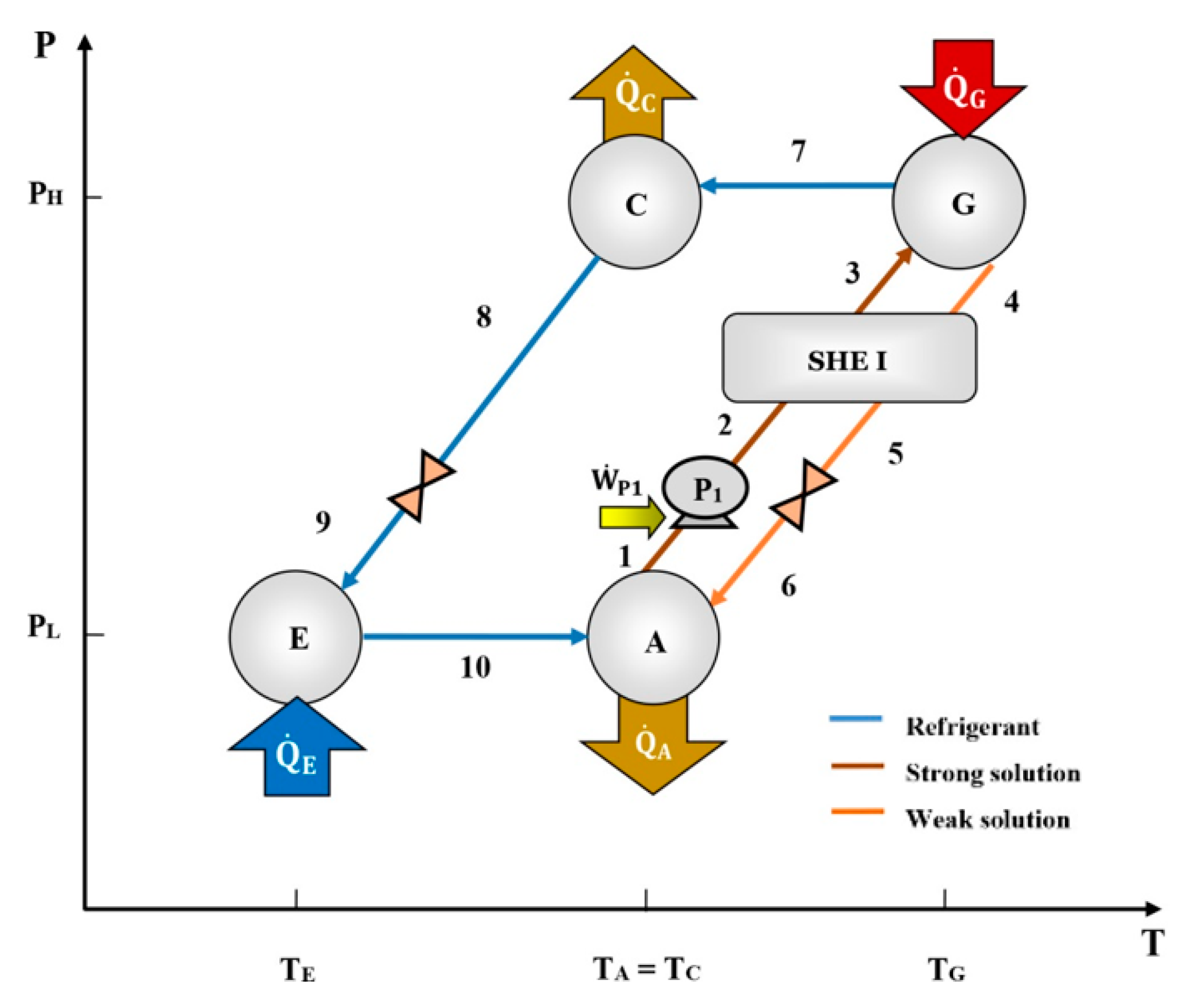
11]. A single-effect absorption cooling system consists of a generator (G), an absorber (A), a condenser (C), an evaporator (E), and a heat exchanger (SHE), as can be seen in
Figure 1. Heat is supplied to the generator to separate part of the refrigerant from the working mixture. The refrigerant goes to the condenser and then to the evaporator through the expansion valve. The refrigerant is evaporated, producing a cooling effect, and then goes to the absorber, where it is absorbed by the solution coming from the generator. The diluted solution is pumped to the generator, starting the cycle again.
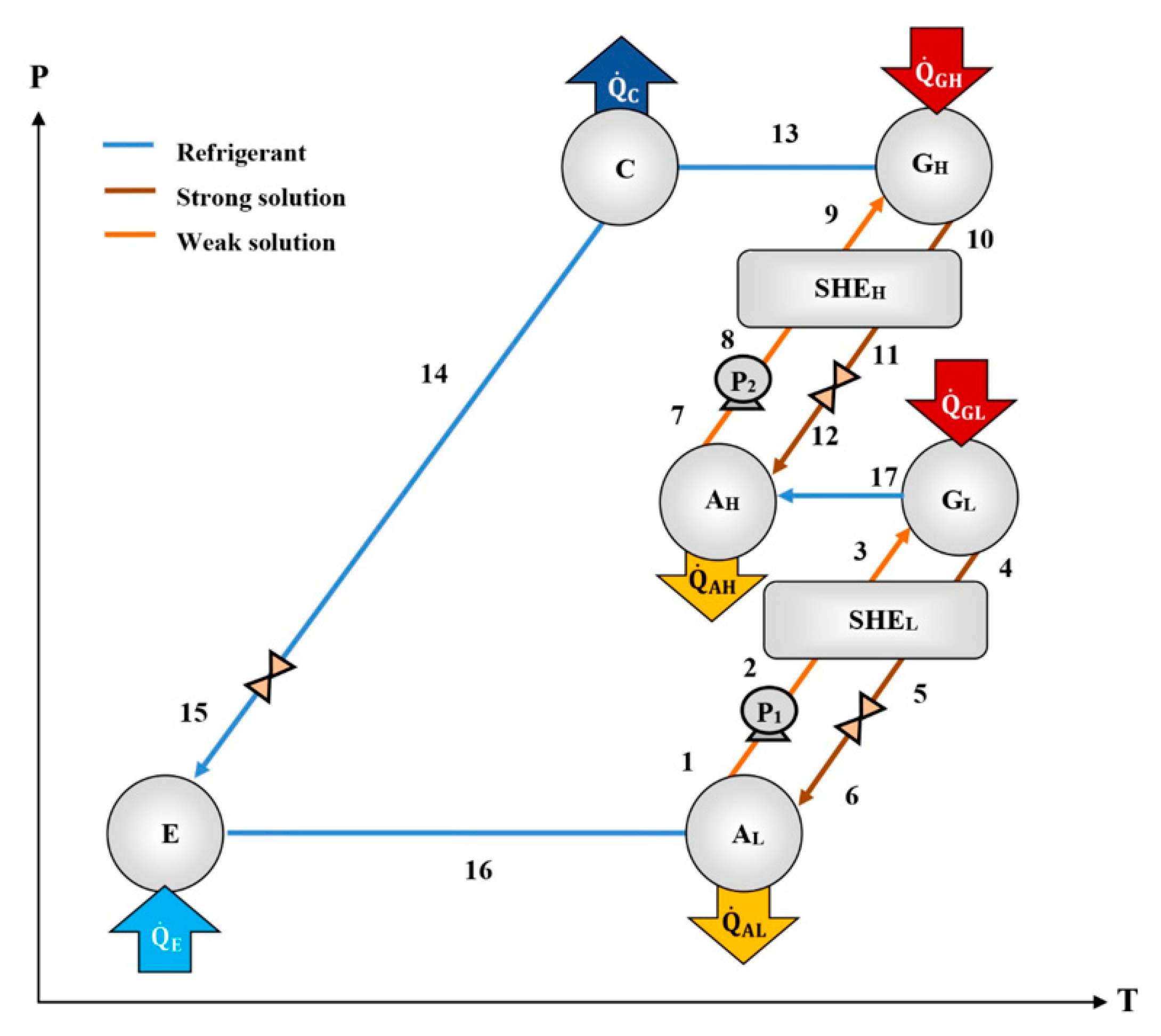
Compared to the single-effect cycle, the half-effect cycle has two solution circuits, one of them at high pressure and the other one at low pressure, as can be seen in
Figure 2 [
12]. The heat is supplied to both generators (G
HP and G
LP) at the same temperature. The refrigerant fluid produced by the first solution circuit (in G
LP) is absorbed in the second solution circuit (in A
HP). Meanwhile, the refrigerant fluid vapor produced in the high-pressure generator (G
HP) is condensed, expanded, and evaporated to produce a cooling effect. The refrigerant fluid leaving the evaporator goes to the low-pressure absorber (A
LP), where it is absorbed by the solution coming from G
LP. The new strong solution is pumped to G
L, starting the cycle again. The half-effect cycle, despite having relatively low values of the coefficient of performance (COP) compared to the simple effect cycle [
12,
13], has the peculiarity that it can operate at extreme operating conditions, such as high condensing temperatures and low generation temperatures.
In the literature, there have been many reports about theoretical and experimental works on single- and double-effect absorption systems: However, the literature about absorption half-effect systems is scarce. Cozzolino [
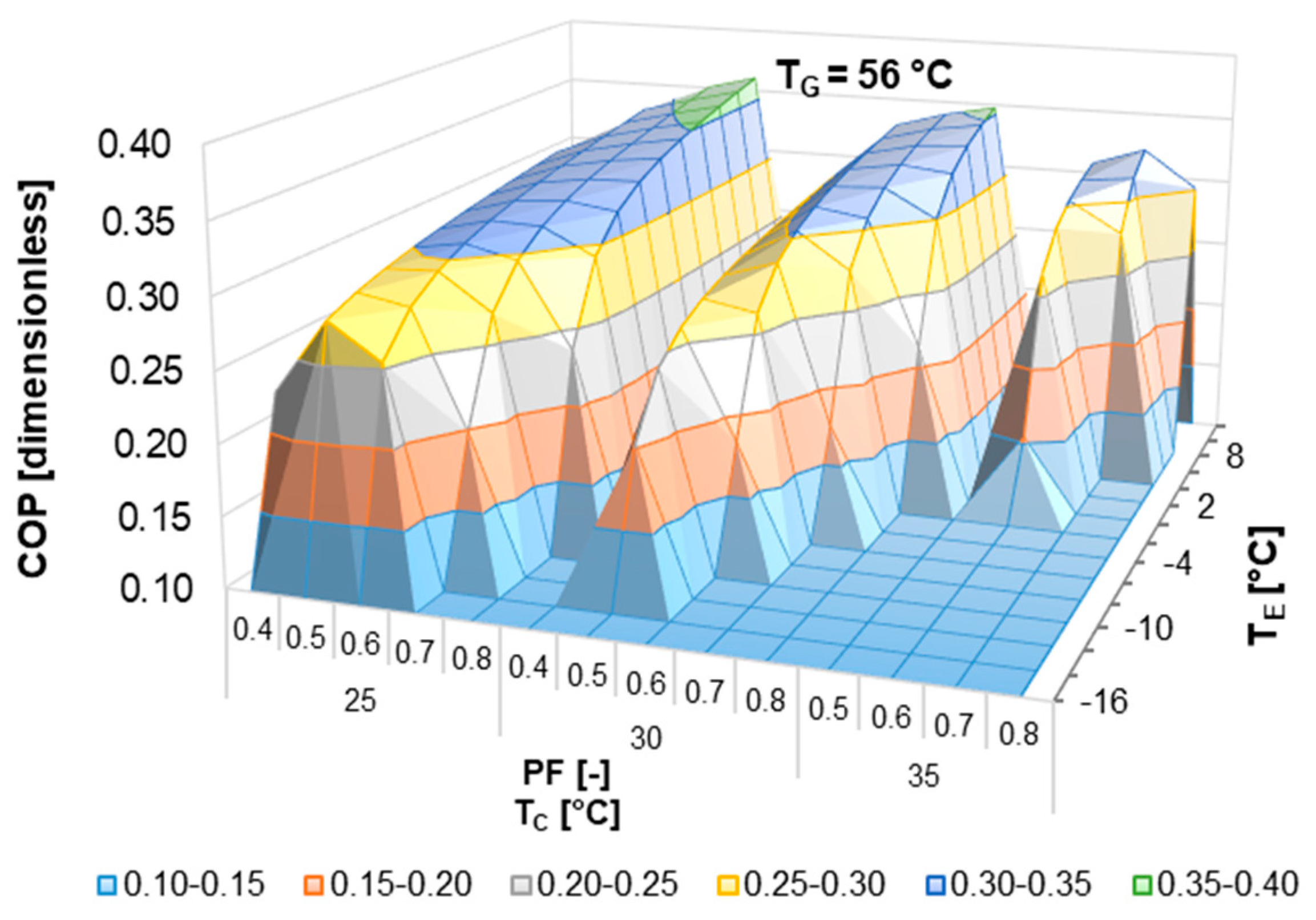
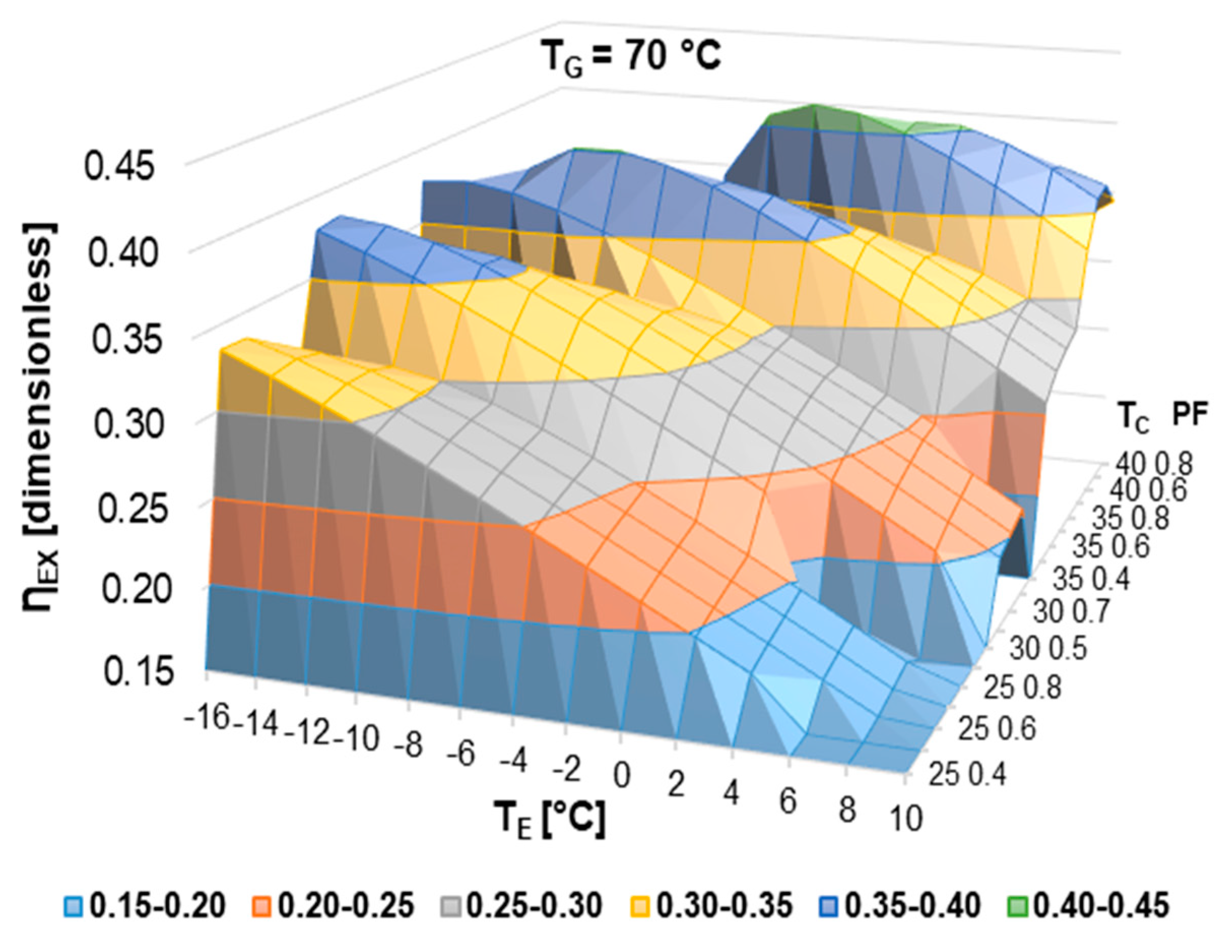
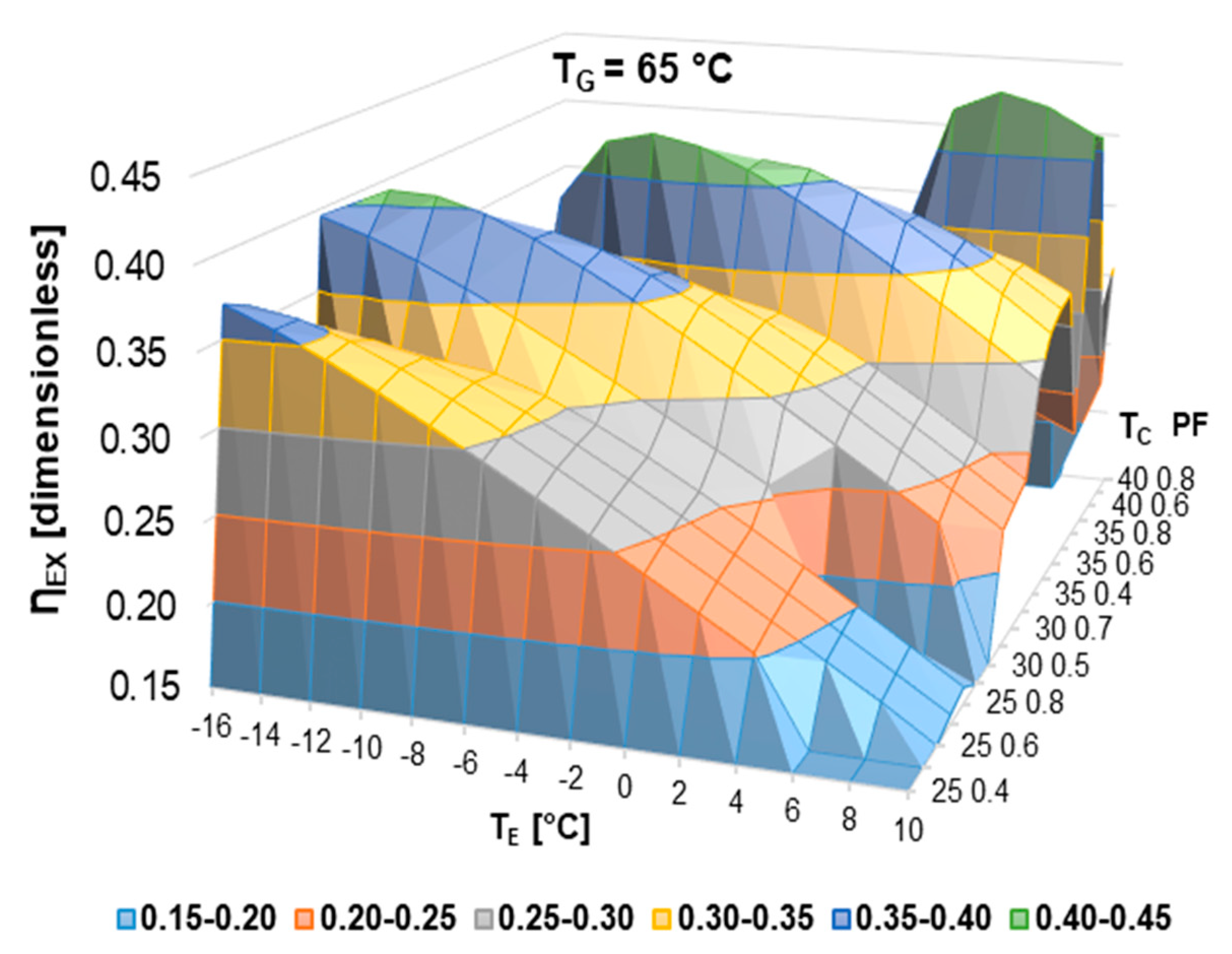
14] described a residential micro-Combined Cooling, Heating and Power (CCHP) system, including a low-temperature Proton Exchange Membrane Fuel Cell (PEMFC) power unit and a half-effect lithium bromide absorption chiller. The author carried out numerical simulations in order to demonstrate the energetic feasibility and performance of this configuration. According to the author’s results, the highest exergy utilization factor (ExUF) value was obtained for the minimum evaporator temperature (4 °C), minimum condenser temperature (27 °C), and 67 °C in both generators (high- and low-temperature) of the absorption chiller. Maryami and Dehghan [
13] carried out a comparative theoretical analysis of five configurations of LiBr/water absorption refrigeration systems, included the half-effect configuration. Based on the authors’ results, when the evaporator temperature was 4 °C with condenser temperatures of 33 °C and 39 °C, the half-effect system could be operated at lower generator temperatures, around 57 °C and 67 °C, respectively. The COP values calculated were approximately 0.40 and 0.42, respectively. This was a significant result because it meant that it was possible to use a heat source at a low thermal level that could be obtained from low-cost solar collectors or waste heat in order to produce air conditioning. Domínguez-Inzunza et al. [
12] analyzed, through mathematical simulations, the performance of five different configurations of absorption cooling systems operating with ammonia/lithium nitrate. The authors concluded that the half-effect system might reach evaporator temperatures around 0 °C at generator temperatures as low as 50 °C, with a COP value around 0.3. Gebreslassie et al. [
15] carried out an exergy analysis for single-, double-, triple-, and half-effect water/lithium bromide absorption cycles. According to the results, the highest exergy destruction rates in the cycle occurred on the two absorbers, followed by the two generators. As the heat source temperature increased, the concentration differences between incoming and leaving solutions in the generators and absorbers increased, which was accompanied by higher exergy destruction rates. Gomri [
16] carried out a comparative study between single-effect and half-effect absorption cycles with an identical cold output and water/LiBr as a working mixture. The author demonstrated that the calculated COP of the half-effect system was approximately half of the COP of the single-effect system, but the exergy efficiency of the latter was slightly lower. The results of the thermodynamic analysis showed that, when the evaporation temperature was maintained at 4 °C, condenser and absorber temperatures varied from 28 °C to 38 °C; generator temperature varied from 40 °C to 80 °C; the maximum COP values for half-effect cooling systems were from 0.408 to 0.435; and the maximum exergy efficiency was from 14.7% to 22.6%. Besides, the author concluded that for generator temperatures higher than 78 °C, a single-effect system must be used, but on the other hand, when generator temperatures are less than 78 °C, it is recommended to use a half-effect system. Arivazhagan et al. [
17] described a 1-kW cooling capacity half-effect absorption prototype, which used hydro chlorofluorocarbon (HFC)-based working fluids (R134a as refrigerant and N,N-dimethylacetamide (DMAC) as absorbent). According to the experimental performance evaluation, the evaporator temperature was as low as 7 °C, with generator temperatures from 55 to 75 °C. The optimum generator temperature was in the range of 65–70 °C, for which the coefficient of performance was 0.36.
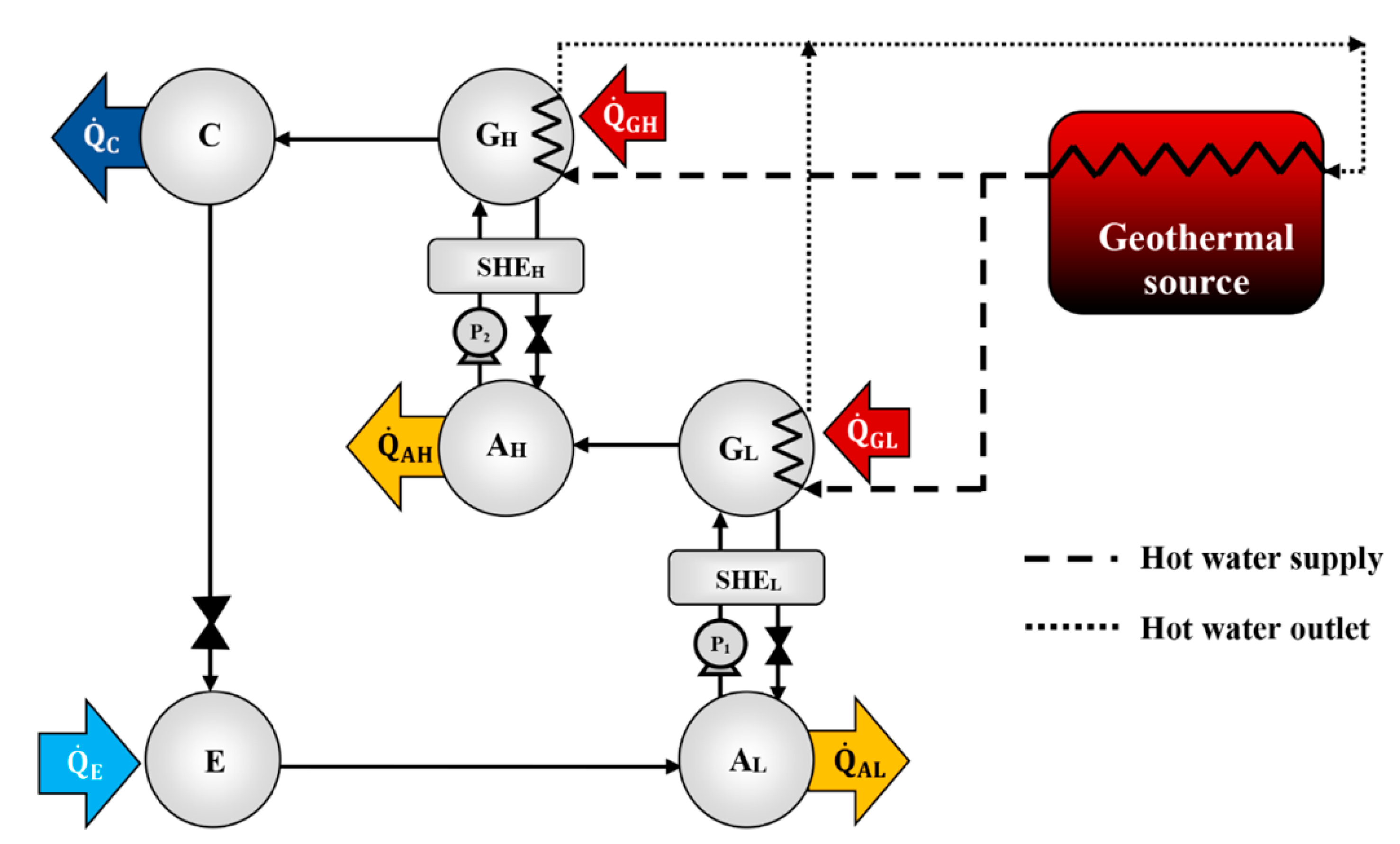
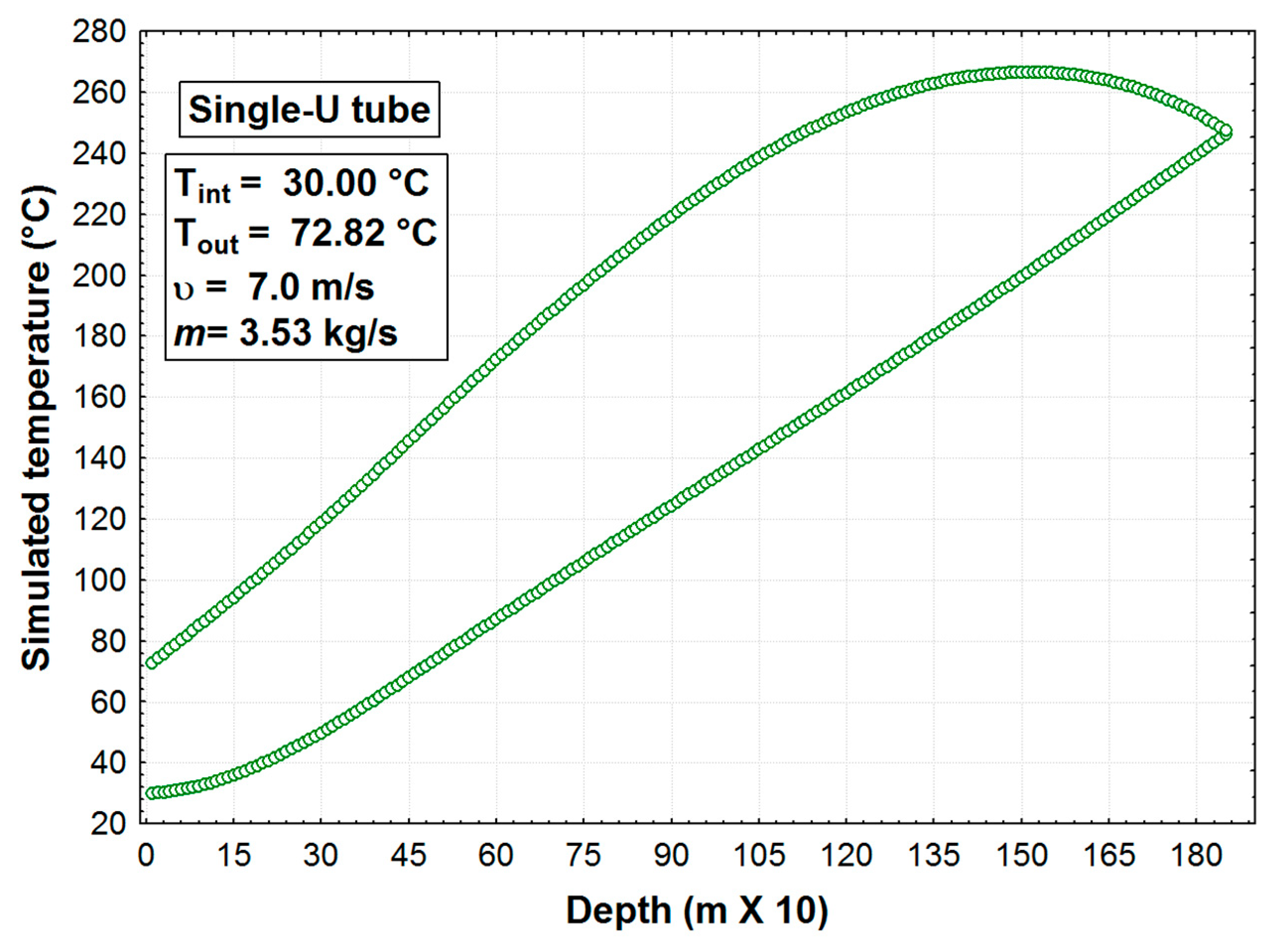
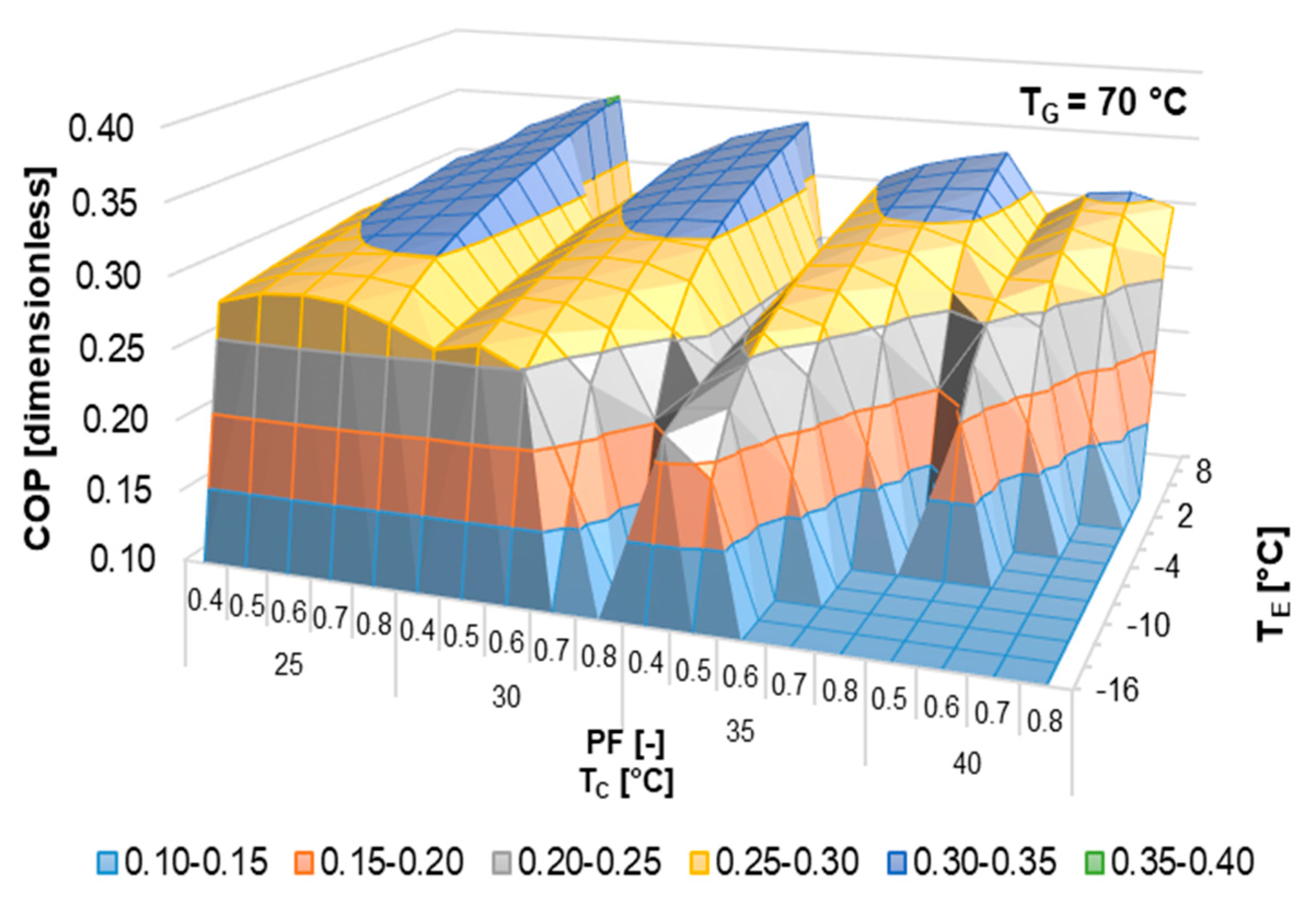
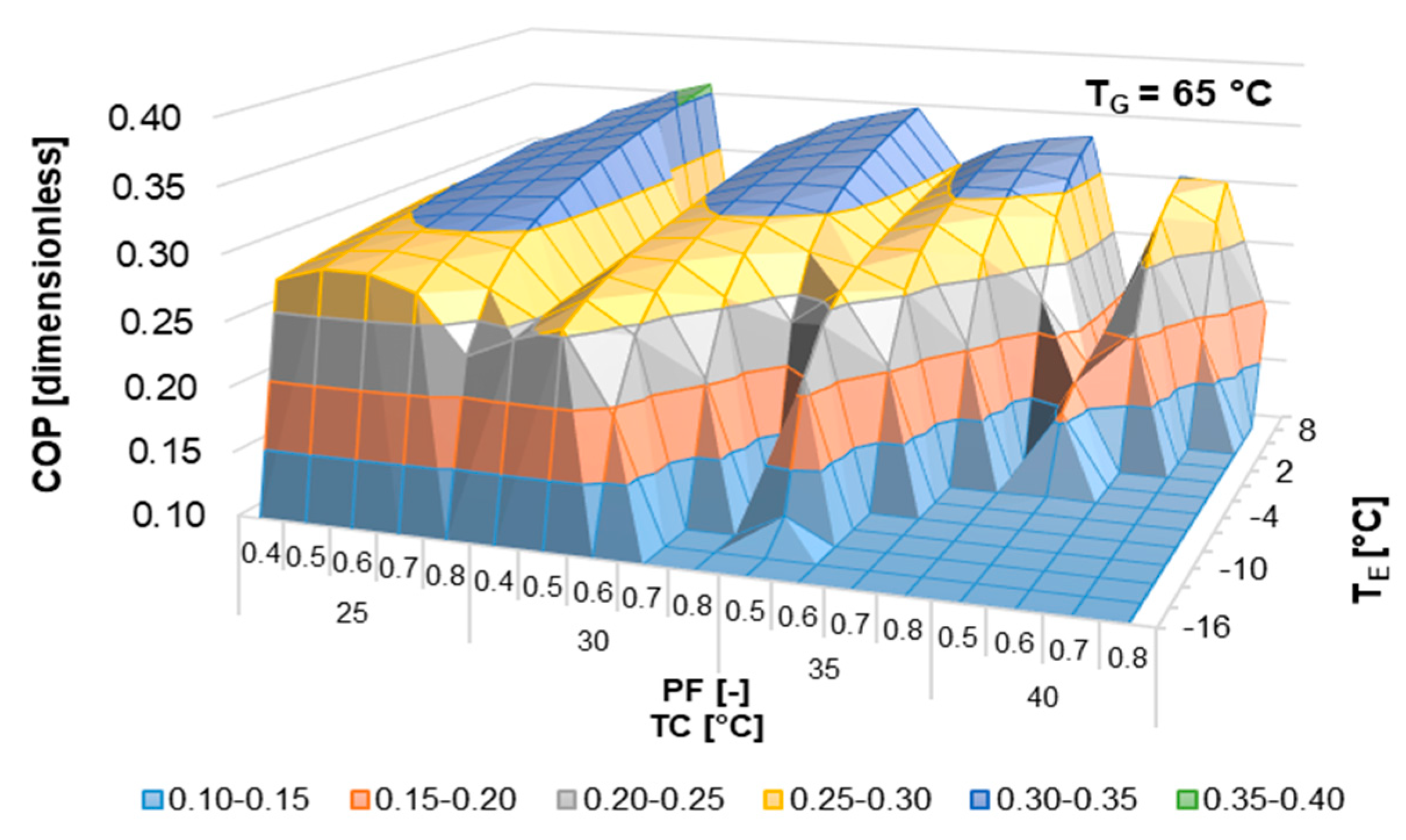
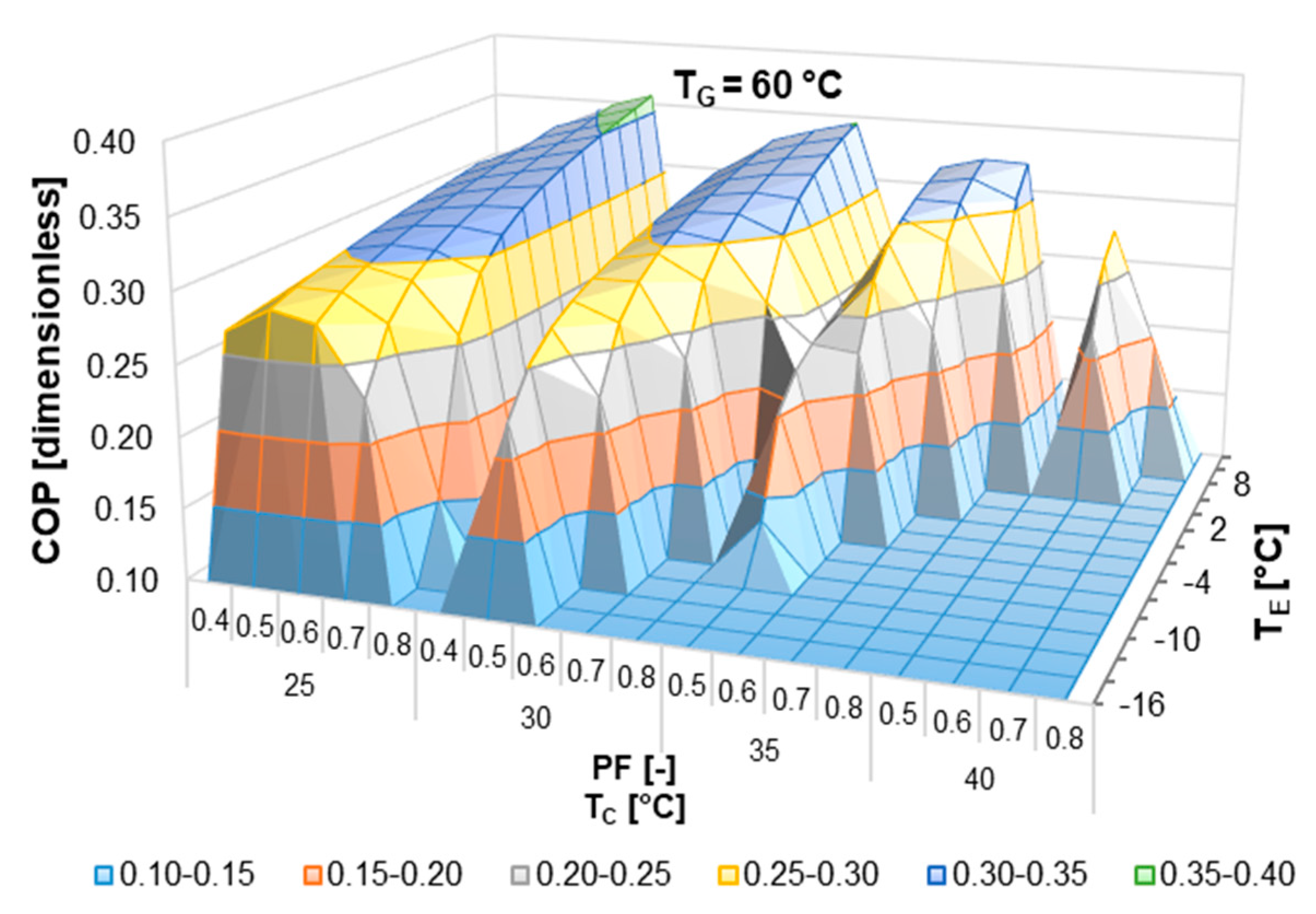
According to the literature review, half-effect absorption systems show great potential in using low-temperature heat sources. In the present paper, thermodynamic and numerical heat transfer analyses are presented in order to demonstrate the feasibility of a half-effect absorption system driven by a low-enthalpy geothermal source. Two cases were analyzed: The first of them was used as an extreme case due to its low thermal level (<65 °C), and the second was considered a medium-temperature level heat source (>70 °C).